Теорема безу

Рациональные корни

До сих пор мы работали лишь с приведёнными многочленами, где старший коэффициент равен единице. Однако теорема Безу прекрасно работает и для неприведённых многочленов — при условии что все коэффициенты остаются целыми.

Рассмотрим уравнение

\

где ${{a}_{n}},\ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}\ne 0$.

Это утверждение будет доказано в конце урока. Сейчас важен практический смысл, который состоит в том, что все рациональные корни уравнения

\

имеют вид $x=\color{red}{p}/\color{blue}{q}\;$, где $\color{red}{p}$ следует искать среди делителей ${{a}_{0}}$, а $\color{blue}{q}$ — среди положительных делителей ${{a}_{n}}$.

Пример 8. Простой многочлен

Решение. Делители свободного члена ${{a}_{0}}=-2$:

\

Положительные делители старшего коэффициента ${{a}_{4}}=2$:

\

Возможные рациональные корни многочлена $P\left( x \right)$ по Следствию 4 теоремы Безу:

\[x=\pm 1;\ \pm 2;\ \pm {1}/{2}\;\]

Проверять числа $x=\color{red}{\pm 1}$ нет смысла, поскольку все коэффициенты многочлена $P\left( x \right)$, за исключением одного, чётные. Следовательно, при подстановке нечётных чисел многочлен принимает нечётные значения, которые точно не равны нулю.

Остальные числа проверим по схеме Горнера:

\[\begin{array}{r|r|r|r|r|r|r}{} & \color{blue}{2} & \color{blue}{-1} & \color{blue}{0} & \color{blue}{0} & \color{blue}{4} & \color{blue}{-2}\\ \hline\color{red}{2} & 2 & 3 & 6 & 12 & 28 & \color{red}{54}\\ \hline\color{red}{-2} & 2 & -5 & 10 & -20 & 44 & \color{red}{-90}\\ \hline \color{red}{{1}/{2}\;} & 2 & 0 & 0 & 0 & 4 & \color{green}{0}\\ \hline \color{red}{-{1}/{2}\;} & 2 & -2 & 1 & -{1}/{2}\; & {17}/{4}\; & \color{red}{-{33}/{8}\;}\\ \end{array}\]

Подошло лишь одно число: $x=\color{red}{{1}/{2}\;}$. Следовательно, многочлен имеет лишь один рациональный корень.

Ответ: $x={1}/{2}\;$.

Обратите внимание: проверку дробных чисел можно прекращать, как только в строке таблицы появилась дробь. Потому что дальше это число будет лишь умножаться на новые дроби и складываться с другими целыми числами

При таких обстоятельствах получить $r=\color{green}{0}$ уже невозможно.

Пример 9. Сложный многочлен

Решение. Это многочлен с целыми коэффициентами. Делители свободного члена ${{a}_{0}}=5$:

\

Положительные делители старшего коэффициента ${{a}_{7}}=3$:

\

Кандидаты в корни согласно Следствию 4 теоремы Безу:

\[x=\pm 1;\ \pm 5;\ \pm {1}/{3}\;;\ \pm {1}/{5}\;\]

Всего восемь кандидатов. Проверим их все по схеме Горнера:

\[\begin{array}{r|r|r|r|r|c|c|c|c}{} & \color{blue}{3} & \color{blue}{2} & \color{blue}{-5} & \color{blue}{0} & \color{blue}{3} & \color{blue}{-1} & \color{blue}{-7} & \color{blue}{5}\\ \hline\color{red}{1} & 3 & 5 & 0 & 0 & 3 & 2 & -5 & \color{green}{0}\\ \hline\color{red}{-1} & 3 & 2 & -2 & 2 & 1 & 1 & \color{red}{-6} & {}\\ \hline\color{red}{5} & 3 & 20 & 100 & \color{red}{500} & \color{red}{-} & \color{red}{-} & \color{red}{-} & {}\\ \hline\color{red}{-5} & 3 & -10 & 50 & \color{red}{-250} & \color{red}{-} & \color{red}{-} & \color{red}{-} & {}\\ \hline\color{red}{{1}/{3}\;} & 3 & 6 & 2 & \color{red}{{2}/{3}\;} & \color{red}{-} & \color{red}{-} & \color{red}{-} & {}\\ \hline\color{red}{-{1}/{3}\;} & 3 & 4 & \color{red}{-{4}/{3}\;} & \color{red}{-} & \color{red}{-} & \color{red}{-} & \color{red}{-} & {}\\ \hline\color{red}{{5}/{3}\;} & 3 & 10 & \color{red}{{50}/{3}\;} & \color{red}{-} & \color{red}{-} & \color{red}{-} & \color{red}{-} & {}\\ \hline\color{red}{-{5}/{3}\;} & 3 & 0 & 0 & 0 & 3 & -3 & \color{green}{0} & {}\\ \end{array}\]

Обратите внимание: для чисел $x=\color{red}{5}$ и $x=\color{red}{-5}$ мы прекратили вычисления досрочно, поскольку получили явно неадекватные числа, которые дальше будут только расти. При проверке $x=\color{red}{{1}/{3}\;}$, $x=\color{red}{-{1}/{3}\;}$ и $x=\color{red}{{5}/{3}\;}$ мы в какой-то момент возникли дроби, после чего дальнейшие вычисления теряют смысл

При проверке $x=\color{red}{{1}/{3}\;}$, $x=\color{red}{-{1}/{3}\;}$ и $x=\color{red}{{5}/{3}\;}$ мы в какой-то момент возникли дроби, после чего дальнейшие вычисления теряют смысл.

Итого найдены два рациональных корня: $x=\color{red}{1}$ и $x=\color{red}{-{5}/{3}\;}$. Пожалуй, это одно из самых утомительных заданий на применение теоремы Безу, которые я когда-либо решал.:)

Теорема Безу и схема Горнера

Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:

Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.

Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.

Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:

И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:

(Картинка позаимствована здесь) Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:

Формулировка и доказательство теоремы Безу

При делении многочлена п-й степени относительно х, расположенного по убывающим степеням х, на двучлен (х — а остаток равен значению делимого при х = а буква а может обозначать любое действительное или мнимое число, т. е. любое комплексное число).

Прежде чем доказывать теорему, сделаем несколько подготовительных пояснений.

1. В формулировке теоремы не случайно сказано: «расположенного по убывающим степеням х».

Если производить деление, расположив делимое и делитель по возрастающим степеням х, то тогда нельзя утверждать, что остаток всегда будет равен значению делимого при х = а.

Например, если многочлен расположить по возрастающим степеням х и делить его на 2 + х, т. е. производить деление так:

то мы никогда не получим остатка, равного числу 4, т. е. значению делимого при x = — 2.

2. Мы знаем, что существуют такие алгебраические выражения, которые теряют смысл при некоторых отдельных значениях входящих в него букв. Например, теряет смысл при x = 0; выражение теряет смысл при x = 5 и при x = — 5.

Заметим, что многочлен любой целой положительной степени никогда не теряет смысла. При всяком значении переменной он принимает определенное значение.

3. Произведение двух множителей, из которых один обращается в нуль, а другой принимает определенное значение, всегда равно нулю. Если же один множитель обращается в нуль, а другой теряет смысл, то о таком произведении нельзя говорить, что оно равно нулю. О таком произведении ничего определенного сказать нельзя. В каждом отдельном случае необходимо особое исследование.

Рассмотрим, например, произведение

При х = 1 первый множитель обращается в нуль, а второй теряет смысл. Нельзя утверждать, что это произведение при х = 1 равно нулю.

Очевидно, что

Итак, при х = 1 само произведение смысла не имеет. Но его предел имеет смысл, а именно равен , а не нулю, как это ошибочно можно было предположить.

Схема Горнера. Теорема Безу.

ГЛАВНАЯ » Материалы для обучения

Схема Горнера

Теорема Безу

Рассмотрим более подробно процесс деления многочлена $P_n(x)$ на линейный двучлен вида $x — \alpha$. В этом случае деление упрощается и может быть проведено по специальной схеме, называемой обычно схемой Горнера.
Запишем основное равенство, определяющее частное и остаток, в случае делителя вида $x — \alpha$; частное имеет степень $n — 1$, а остаток — нулевую степень, т. е. просто является числом:
$a_0x^n + a_1x^{n-1} + \cdots + a_n = (x — \alpha)(b_0x^{n-1} + b_1 x^{n-2} + \cdots + b_{n-1}) + r$. (1)
Как уже указывалось, это равенство — тождественное, многочлены в его левой и правой частях совпадают; раскрыв скобки, получим равенства, выражающие совпадение коэффициентов при одинаковых степенях $x$:
$a_0 = b_0$,
$a_1 = — ab_0 + b_1$,
$a_2 = -ab_1 + b_2$,
$\cdots$
$a_{n-1} = — ab_{n-2} + b_{n-1} + r$.
Отсюда последовательно находим
$b_0 = a_0$,
$b_1 = a_1 + ab_0$,
$b_2 = a_2 + ab_1$,
$\cdots$
$b_{n-1} = a_{n-1} + ab_{n-2}$,
$r = a_n + ab_{n-1}$.
Вычисление коэффициентов частного и остатка располагают в такой таблице:
Верхняя строка таблицы заполняется сразу; в нижней строке помещаются коэффициенты частного и остаток; она заполняется постепенно, слева направо. В каждой клетке нижней строки записывается сумма коэффициентов из верхней строки и умноженного на а результата, записанного в соседней слева клетке нижней строки.
Замечательно, что остаток от деления многочлена на двучлен $x — \alpha$ может быть найден независимо от выполнения деления, без отыскания частного. Действительно, положим в равенстве
$P_{n} (x) = (x — \alpha)Q(x) + r$
$x = \alpha$. Так как равенство тождественное, то оно удовлетворится и мы найдем
$P_{n} ( \alpha ) = r$.
Остаток от деления многочлена $P_{n}(x)$ на двучлен вида $x — \alpha$ равен значению многочлена при $x = \alpha$:
$r = P_{n} (x)|_{x = \alpha}$.
Как следствие отсюда вытекает
Теорема Безу. Многочлен $P_{n}(x)$ делится без остатка на двучлен $x — \alpha$ в том и только в том случае, когда $\alpha$ — корень многочлена.
Пример. Найти остаток от деления многочлена $x^{3} + 6x^{2} — 2x + 5$ на двучлен $x — 3$ (не выполняя деления).
Решение. Значение остатка находим так:
$x^{3} + 6x^{2} — 2x + 5|_{x = 3} = 27 + 54 — 6 + 5 = 80$.
Пользуясь теоремой Безу, легко выяснить, при каких условиях выражения вида ($a \neq 0$)
$x^{n} — a^{n}, x^{n} + a^{n}$
будут делиться на $x — a, x + a$ без остатка.
1) $x^{n} — a^{n}$ делится на $x — a$ при любом $n$. Действительно,
$x^{n} — a^{n}|_{x=a} = a^{n} — a^{n} = 0$,
откуда делимость вытекает в силу теоремы Безу.
2) $x^{n} + a^{n}$ делится на $x + a$ при четном $n$ и не делится при нечетном $n$. Действительно, находим
$x^{n} — a^{n} |_{x = -a} = (-a)^{n} — a^{n} = \begin{cases} 0&, если \: n \: — \: четное, \\ -2a^{n}&, если \: n \: — \: нечетное, \end{cases}$
откуда и следует наше утверждение.
3) $x^{n} + a^{n}$ делится на $x + a$ при нечетном $n$ и не делится при четном $n; x^{n} + a^{n}$ не делится на $x — a$ ни при каком $n$.
Доказательство аналогично.

Применение онлайн-калькулятора

Как бы ни облегчала расчёт теорема всё равно приходится выполнять определённые арифметические действия. Когда уравнение до четвёртого порядка, выполнить операции несложно и самостоятельно. Но чем больше показатель в формуле, тем сложнее выполнять вычисления и больше возникает вероятность допущения ошибки. При этом затрачивается и много времени.

Поэтому резонно для сложных заданий использовать автоматически расчёт уравнений. Выполнить его можно используя любой специализированный сервис — онлайн калькулятор. Теорема Безу предлагает алгоритм расчётов, который запрограммирован в исполняющем приложении. Доступ к интернет-порталам предлагающих такого рода услугу бесплатен. При этом от пользователя не требуется даже регистрации или указания какой-либо информации.

Необходимо просто зайти на страничку онлайн-калькулятора и ввести в предложенную сайтом форму исследуемое уравнение, а после запустить программу нажатием одной кнопки, например, «Рассчитать». Нет необходимости в скачивании или установки программ. Система сама выполнит все вычисления и выдаст ответ. Только в сети рунета существует несколько десятков таких расчётчиков. Из популярных среди пользователей можно выделить следующие:

1. Math-solution. Основу сайта составляют различные приложения выполняющие вычисления. Кроме непосредственно решения, сервис предоставляет поэтапное описание действий. Подробное решение излагается в соответствии с принятой программой обучения в школе и вузах. Кроме этого, на сайте существует раздел «Книги». В нём каждый желающий сможет найти учебники, решебники и другую справочную информацию по математике или геометрии.
2. Planetcalc. Этот сервис позволит вычислить ответ любой сложности соотношения многочленов. Особенностью его является простой интерфейс, не содержащий загромождения информации. Кроме этого, предложенный поэтапный расчёт сопровождается лаконичными объяснениями.
3. Calc. Онлайн-калькулятор имеет интуитивно понятный интерфейс и всю необходимую теорию для понятия теоремы и возможностей её использования. На страничках сайта представлены примеры решений задач различной сложности с подробным описанием действий.

Решив несколько примеров с помощью онлайн-решателей, пользователь сможет самостоятельно научиться применять правила. Автоматические вычислители смогут как подтянуть знания, так и проверить выполненный расчёт.

Деление многочлена на двучлен по схеме Горнера

Рассмотрим частный случай деления многочленов – деление многочлена на двучлен вида x — b0. Алгоритм деления для этого случая называется схемой Горнера или методом сокращенного деления многочлена на двучлен.

Пусть требуется поделить многочлен

На двучлен b(x)= x — b0, то есть требуется представить многочлен a(x) в виде

A(x)=b(x)*c(x) + r(x), где степень частного c(x) равна n-1, а степень остатка r(x) равна 0. Пусть

Перемножим x — b0 и c(x), сложим с r0 и приравняем коэффициенты многочленов при одинаковых степенях x в левой и правой частях равенства. Получим рекуррентные формулы для определения значений ci и остатка r0.

R0=an + c0*b0. Для удобства вычислений по этим формулам создается таблица, заполняемая слева направо.

В первой строке записываются коэффициенты делимого в порядке убывания степеней x и число b0.

Во второй строке — соответствующие значения выражений сi*b0 (первое число 0, так как cn=0).

Числа в первой строке складываются с числами во второй и записываются в третью строку. В результате в третьей строке мы получаем коэффициенты частного, а последнее число – это остаток.

Заполняют эту таблицу в таком порядке:

Сначала заполняют первую строку. Под первым числом первой строки пишем 0.

Складываем числа в первом столбце, и результат будет первым числом третьей строки.

Затем первое число третьей строки cn-1 умножаем на последнее число первой строки b0, результат записываем на второе место второй строки.

Складываем числа второго столбца и получаем второе число третьей строки cn-2.

Это число опять умножаем на последнее число первой строки b0, результат записываем на третье место во второй строке.

Складываем числа третьего столбца, и получаем третье число третьей строки и т. д.

Хотя объяснение выглядит довольно громоздким, но выполнять деление с помощью схемы Горнера очень просто и удобно. Рассмотрим применение схемы Горнера на примерах.

Свойства целой рациональной функции

Теорема Гаусса позволяет открыть и доказать другие важные свойства целой рациональной функции.

1. Всякую целую рациональную функцию п-й степени можно представить в виде произведения коэффициента высшего члена на п линейных множителей, т. е.

Эти линейные множители могут быть все действительными или все мнимыми и могут быть частью действительными и частью мнимыми.

Доказательство:

Функцию

обозначим для краткости буквой М. По теореме Гаусса М имеет по крайней. мере один корень х, (действительный или мнимый). Тогда по следствию из теоремы Безу многочлен М должен делиться без остатка на .

Обозначив буквой частное от этого деления, получим:

будет целой рациональной функцией (п— 1)-й степени с коэффициентом при высшем члене, равном .

По теореме Гаусса функция также будет иметь по крайней мере один корень.

Обозначив этот корень буквой получим:

Число может оказаться отличным от xv но может оказаться и равным ему. Для нас это безразлично.

Применяя такие же рассуждения к функции , получим:

Степени функций будут соответственно

Продолжая этот процесс, мы придем к равенству

где есть функция вида , где b — постоянная. Но

Обозначив корень функции буквой получим, что

Пользуясь полученными равенствами, найдем последовательно:

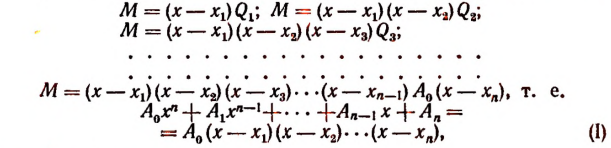
что и требовалось доказать.

Из равенства (I) непосредственно видно, что числа являются корнями данной целой рациональной функции.

Правая часть равенства (I) не может обратиться в нуль ни при каком значении переменной х, отличном от значений

Следовательно, целая рациональная функция п-й степени не может иметь более п корней.

Если все числа окажутся различными, то функция будет иметь ровно п различных корней.

Если же среди чисел окажутся равные, то различных корней будет меньше чем п.

Пусть оказалось, что

а остальные корни отличны от В этом случае говорят, что есть корень кратности k. Например, функция разлагается на множители

Значит, число — 1 есть простой ксрень, а число 4 есть корень кратности 2 или двукратный корень.

2. Если целая рациональная функция с действительными коэффициентами имеет комплексный корень то она обязательно будет иметь и корень

Доказательство. Выражение

в котором —действительные числа, будет представлять собой некоторое комплексное число Р + Qi, т. е.

Заменив в последнем равенстве i числом —i, получим:

Теперь допустим, что есть корень целой рациональной функции

тогда окажется, что P + Qi = 0. Отсюда следует, что Р = 0 и Q = 0. Но в таком случае окажется равным нулю и выражение Р—Qi, т. е. окажется корнем целой рациональной функции (1) и число что и требовалось доказать.

3. Всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима либо на действительные линейные множители, либо на действительные множители 2-й степени, либо на действительные множители, среди которых имеются и линейные и второй степени. (Доказательство 3-го свойства опускается.)

Примеры разложения целой рациональной функции с действительными коэффициентами степени выше второй на действительные неприводимые множители

Получилось разложение на действительные линейные множители.

Получилось разложение на действительные множители 2-й степени.

Получился один множитель линейный, а другой 2-й степени.

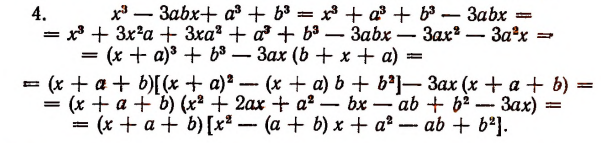
Получился один множитель линейный, а другой 2-й степени.

Теоретически доказано (как уже отмечалось), что всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима на действительные множители 1-й и 2-й степени.

Однако осуществление этого разложения не всегда достигается легко. Например, попробуем разложить на множители

Решим эту задачу двумя способами.

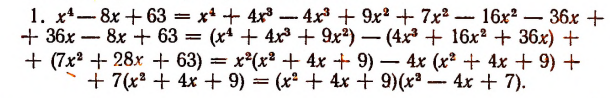
(Полученные многочлены 2-й степени имеют мнимые корни, а потому неразложимы на действительные линейные множители.)

Изложенный способ носит слишком искусственный характер. Его трудно придумать.

Второй способ, изложенный ниже, будет менее искусственным.

2. Прежде всего исследуем характер корней многочлена или, что то же самое, характер корней уравнения

Переписав это уравнение в виде

построим графики функций (рис. 208). Графики не пересекаются. Следовательно, корни уравнения

а значит, и многочлена

будут все мнимыми. Поэтому среди действительных множителей, на которые разлагается этот многочлен, не может быть ни одного линейного.

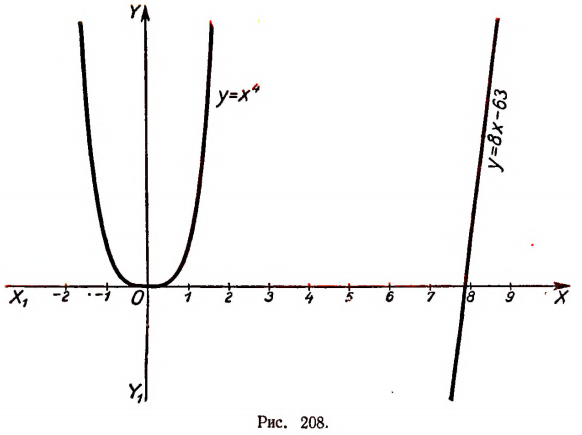
Итак, выяснено, что действительными множителями разложения многочлена будут только многочлены 2-й степени. Таких множителей будет два, так как данный многочлен имеет 4-ю степень.

Таким образом, будем иметь, что

Остается определить а, b, р и q.

Перемножив многочлены, стоящие в правой части последнего равенства, получим:

Но поскольку нам необходимо, чтобы правая часть этого равенства превратилась в такой же многочлен, который стоит в левой части, потребуем выполнения следующих условий:

Получилась система четырех уравнений с четырьмя неизвестными a, b, р, q.

Из первого уравнения

Подставив во второе и третье уравнение — а вместо р, получим систему:

Из второго уравнения этой системы

Подставив это в первое уравнение, получим систему:

Обозначим b + q буквой z. Тогда первое уравнение последней системы примет вид:

Делителями числа 64 являются: ± 1; ± 2; ± 4; ± 8; ± 16; ± 32; ± 64.

Испытывая эти делители, обнаружим, что число 16 является корнем уравнения

Значит, мы можем взять b + q = 16. Кроме того, bq = 63. Отсюда примем b = 7 и q = 9. Пользуясь равенством

получим, что а = —4. Наконец, из равенства р = —а найдем, что р = — 4.

Теперь задача решена полностью. Мы получили:

Имея это разложение, мы легко обнаруживаем все корни многочлена или, что то же самое, все корни уравнения

Этими корнями будут комплексные числа

Алгебра и начало анализа. Теорема Безу. 11-й класс

Класс: 11

Презентация к уроку

Цель урока:

• способствовать развитию навыков деления многочлена на многочлен и использованию схемы Горнера;
• закрепить навыки работы в электронных таблицах OpenOffice.org Calc;
• организовать деятельность учащихся по восприятию, осмысливанию и первичному запоминанию новых знаний;
• разобрать и доказать теорему Безу при решении проблемной ситуации: можно ли разложить многочлен третьей степени на множители;
• рассмотреть использование теорему Безу для решения уравнений высших степеней;
• содействовать развитию логического мышления, внимания, речи и умения работать самостоятельно.

Тип урока: урок ознакомления с новым материалом.

Оборудование: мультимедиа проектор, презентация к уроку, компьютерный класс.

«Для того, чтобы совершенствовать ум, надо больше рассуждать, чем заучивать». Декарт (1596 -1650). Французский математик, физик, филолог, философ.

Ход урока

I. Организационный момент

Наша задача сегодня в совместной деятельности подтвердить слова Декарта (слайд 1). Тема нашего урока (слайд 2) «Теорема Безу» настолько значима, что даже используется в заданиях ЕГЭ и различных олимпиадах. Теорема Безу облегчает решение многих заданий, содержащих уравнения высших степеней. К сожалению, она изучается только на профильном уровне.

II. Возникновение проблемной ситуации

На этом уроке мы научимся решать уравнения высших степеней, а алгоритм решения выведем сами.

Решить уравнение: x 3 — 2x 2 — 6x + 4=0 (Слайд 3). Возникает проблема: Мы понимаем, что было бы удобно представить левую часть уравнения в виде произведения, и так как произведение равно нулю, то приравнять к нулю каждый множитель. Для этого надо разложить многочлен 3-ей степени на множители. Но как? Можно ли сгруппировать или вынести общий множитель за скобку в нашем случае? (Нет).

III. Актуализация опорных знаний

Вспомним, как разложить на множители многочлен х 2 — 5х — 6? (Слайд 4).

(По формуле разложения на множители квадратного трехчлена:

ах 2 + bх + с = a(x – x₁)(x-x₂), где х₁ и х₂ корни трехчлена).

Найдите корни трехчлена двумя способами. Какими?

(по формуле корней квадратного уравнения и по теореме Виета).

Решают на доске от каждой группы по одному ученику. Остальные учащиеся в тетрадях. Получили: х 2 — 5х — 6 = (х — 6) (х + 1).

Это значит, что трехчлен делится на каждый из двучленов: х – 6 и х + 1.

Обратите внимание на свободный член нашего трехчлена и найдите его делители (±1, ±2, ±3, ±6). Какие из делителей являются корнями трехчлена? (-1 и 6)

Какие из делителей являются корнями трехчлена? (-1 и 6)

Какой вывод можно сделать? (Корни трехчлена являются делителями свободного члена).

IV. Выдвижение гипотезы

Так какой же одночлен поможет подобрать корни многочлена?

Р(х) = x 3 — 2x 2 — 6x + 4=0?

Выпишите его делители: ±1; ±2; ±4.

Найдите значения многочлена для каждого делителя. С помощью электронных таблиц и непосредственно:

Задания для самостоятельного решения

Задание 1. Выполните деление:

Решение:

Задание 2. Выполните деление:

Решение:

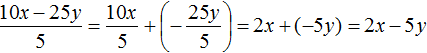
Задание 3. Выполните деление:

Решение:

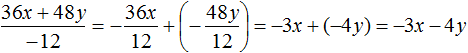
Задание 4. Выполните деление:

Решение:

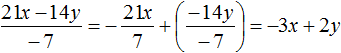
Задание 5. Выполните деление:

Решение:

Задание 6. Выполните деление:

Решение:

Задание 7. Выполните деление:

Решение:

Задание 8. Выполните деление:

Решение:

Задание 9. Выполните деление:

Решение:

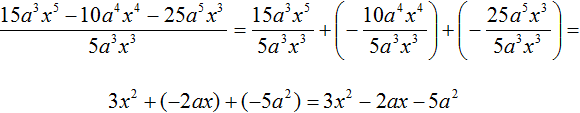
Задание 10. Выполните деление:

Решение:

Задание 11. Выполните деление:

Решение:

Задание 12. Выполните деление:

Решение:

Задание 13. Выполните деление:

Решение:

Задание 14. Выполните деление:

Решение:

Задание 15. Выполните деление:

Решение:

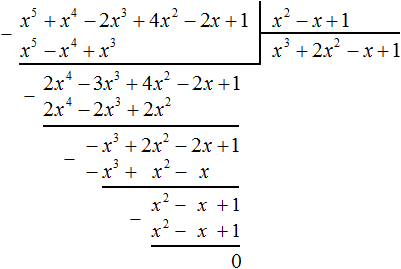
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Примеры решения

Теорема Безу применяется при решении степенных уравнений. Согласно её объяснению чтобы понять, чему будет равняться остаток от деления многочлена на двучлен, не нужно выполнять сложные утомительные действия. Достаточно просто подставить число в многочлен. Его значение как раз и будет являться искомым остатком от деления. Но чаще всего при решении задач используется не сама теорема, а следствие из неё — разложение многочленов на множители.

Пусть есть многочлен с целыми коэффициентами: x3 — 5x — 2x + 24. Свободным числом в формуле является двадцать четыре. Его нужно разложить на множители: 24 = 6 * 4 = 2 * 3 * 2 * 2 * 1. Единицу дописывают с целью поиска дополнительных корней. Для того чтобы разложить многочлен на множители нужно вспомнить начальную алгебру. Из неё известно, что если число x1 является корнем какого-либо многочлена P (x), то это выражение можно переписать в виде произведения: P (x) = (x — x1) *Q (x) где степень Q (x) меньше исходной формулы.

Так как у многочлена присутствует некий корень х1, то он обязательно будет делителем числа 24. Следовательно, собираться из множителей числа. Для этого нужно взять наименьшее число, подставив его в исходное выражение и проверить, является ли оно корнем. Тут стоит отметить, что для уравнений сложного вида можно использовать схему Горнера.

Для рассматриваемого примера первое число будет единица. Подставив его в многочлен вместо икса, получим: P (1) = 1 — 5 — 2 + 24 = 18. Ответ не равняется нулю, поэтому единица не будет корнем.

Теперь нужно подставить второй член разложения, цифру два: P (2) = 8 — 20 — 4 + 24 = 8. Ответ снова не подходит. Используем: x = -2: P (-2) = -8 — 20 + 4+ 24 =0. Результат означает, что x = -2 является корнем рассматриваемого многочлена.

Получив корень можно записать: P (x) = (x +2) * Q (x). Осталось найти Q (x). Для этого исходный многочлен нужно разделить на x +2. После деления получится квадратное уравнение вида: х2 — 7x + 12. Таким образом, исходное уравнение можно переписать как P (x) = (x + 2) * (x2 — 7x + 12) = (x + 2) + (x — 3) * (x — 4). Это и есть полное разложение многочлена на линейные множители. При этом корнями уравнения будут: x1 =- 2, x2 =3, x3 = 4.

Деление многочлена на многочлен с остатком

Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.

Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:

То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:

Рациональное число читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.

Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:

Например, разделим многочлен 2×3 − x2 − 5x + 4 на многочлен x − 3

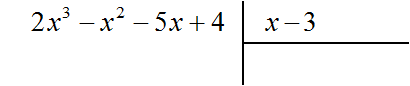
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2×2. Записываем 2×2 в частном:

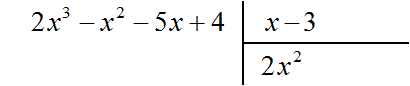
Умножим 2×2 на делитель x − 3 и полученный результат запишем под делимым:

Вычтем из делимого полученный многочлен 2×3 − 6×2

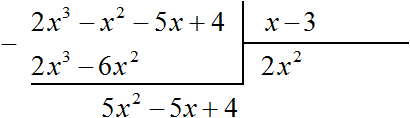
Теперь делим 5×2 − 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном:

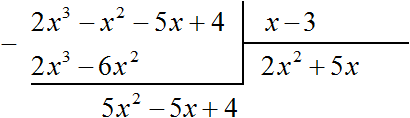
Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5×2 − 5x + 4

Вычтем из многочлена 5×2 − 5x + 4 многочлен 5×2 − 15x

Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном:

Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4. Сразу вычтем этот полученный результат из делимого 10x + 4

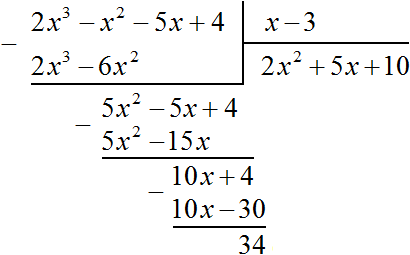
Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4, является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34.

Поэтому при делении многочлена 2×3 − 2×2 − 5x + 4 на многочлен x − 3 получается 2×2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:

Разложение на множители квадратного трехчлена.

Квадратный трехчлен раскладывается на два линейных множителя: , где и являются корнями (комплексными или действительными).

Таким образом, разложение на множители квадратного трехчлена сводится к решению квадратного уравнения.

Пример.

Разложить квадратный трехчлен на множители.

Решение.

Найдем корни квадратного уравнения .

Дискриминант уравнения равен , следовательно,

Таким образом, .

Для проверки можно раскрыть скобки: 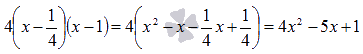. При проверке пришли к исходному трехчлену, поэтому разложение выполнено верно.

Пример.

Разложить на множители квадратный трехчлен .

Решение.

Соответствующее квадратное уравнение имеет вид .

Найдем его корни.

Поэтому, .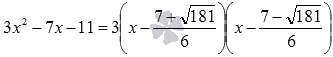

Пример.

Разложить многочлен на множители .

Решение.

Найдем корни квадратного уравнения .

Получили пару комплексно сопряженных корней.

Разложение многочлена будет именть вид .

Пример.

Разложить на множители квадратный трехчлен .

Решение.

Решим квадратное уравнение .

Поэтому,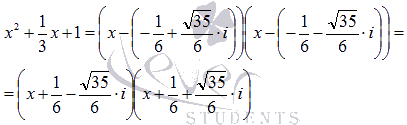

Замечание:

В дальнейшем, при отрицательном дискриминанте, мы будем оставлять многочлены второго порядка в исходном виде, то есть не будем раскладывать их на линейные множители с комплексными свободными членами.