Как извлечь корень из комплексного числа

Примеры решений

Пример 1

Извлечь корень $ sqrt <-1>$ над множеством $ mathbb $

Решение

Представим число в тригонометрической форме. Найдем модуль и аргумент:

$$ varphi = arctg frac<0> <-1>+pi = arctg 0 + pi = pi $$

Получаем: $$ z = (cos pi + isin pi) $$

Используем знакомую формулу Муавра для вычисления корней любой степени:

Так как степень $ n = 3 $, то по формуле $ k = 0,1,2 $:

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Онлайн калькулятор предназначен для вычисления корня n -ой степени из комплексного числа, с описанием подробного хода решения на русском языке. Для нахождения корня n -ой степени, сначала необходимо выбрать (алгебраическую, тригонометрческую или показательную) форму представления комплексного числа. Далее приведены минимальные теоретические сведения, необходимые для понимания решения, выдаваемого калькулятором.

Согласно теории, корень n -ой степени из любого числа ( n &#8712 Z ) имеет ровно n значений. Например:

Пример, по интереснее:

где i – мнимая единица. Можете попробовать возвести все значения в куб, и действительно получите 8. Возникает вопрос: как найти все n значений корня n -ой степени из числа? Для этого необходимо использовать формулу Муавра, причем комплексное число должно быть записано в тригонометрической форме. Наш калькулятор автоматически осуществит перевод введенного числа в тригонометрическую форму, если потребуется.

Рассматривать будем на таком примере:

Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:

Выполним проверку того, что эти корни и права оказываются решением уравнения:

Что и требовалось доказать.

Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: .

Такие корни являются сопряженными комплексными корнями.

Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:

, ,

,

,

В каждом случае получаем 2 сопряженных комплексных корня.

Решим квадратное уравнение .

Первым шагом определим дискриминант уравнения:

В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:

Как известно из формул дискриминанта у нас образуется 2 корня:

– сопряженные комплексные корни

Т.о., у уравнения есть 2 сопряженных комплексных корня:

,

Теперь можно решить любое квадратное уравнение!

У любого уравнения с многочленом n-ой степени есть ровно n корней, некоторые из них могут быть комплексными.

Как извлечь корень из произвольного комплексного числа?

Рассмотрим уравнение z n = w, либо, записав в другом виде: . Здесь n может принимать всякое натуральное значение, которое больше 1-цы.

В частности, при n = 2 получаем квадратный корень .

У уравнения типа есть ровно n корней ­z, z₁, z₂, … z_n-1, которые можно вычислить с помощью формулы:

,

где – это модуль комплексного числа w,

φ – его аргумент,

а параметр k принимает значения: .

Найдем корни уравнения: .

Перепишем уравнение как: .

В этом примере , , поэтому у уравнения будет 2 корня: z и z₁. Детализируем общую формулу:

, .

Далее найдем модуль и аргумент комплексного числа :

Число w находится в 1-ой четверти, значит:

Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.

Детализируем еще немного общую формулу:

, .

Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.

Подставляем в формулу значение k = 0 и получаем 1-й корень:

.

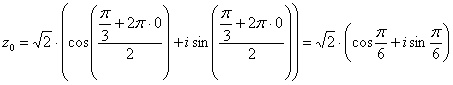Подставляем в формулу значение k = 1 и получаем 2-й корень:

.

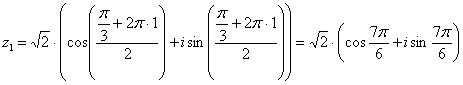Ответ: ,

Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.

Часто вычисленные корни нужно изобразить геометрически:

Как выполнить чертеж?

Для начала на калькуляторе вычисляем, чему равен модуль корней и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.

Далее берем аргумент 1-го корня и вычисляем, чему равен угол в градусах:

.

Отмеряем транспортиром 45° и ставим на чертеже точку z.

Берем аргумент 2-го корня и переводим его тоже в градусы: . Отмеряем транспортиром 165° и ставим на чертеже точку z₁.

По этому же алгоритму ставим точку z₂.

Видно, что корни располагаются геометрически правильно с интервалом между радиус-векторами. Чертеж обязательно делать при помощи транспортира.

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность:
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Теорема Виета для решения квадратных уравнений

Теорема Виета — это еще один способ упростить решение полных квадратных уравнений. Ее очень часто используют для решения несложных квадратных уравнений в уме и для анализа квадратного многочлена, особенно это актуально в сложных заданиях с параметром в ЕГЭ.

Прежде чем сформулировать теорему Виета, познакомимся с приведенными квадратными уравнениями.

Приведенное квадратное уравнение

Квадратные уравнения \(ax^2+bx+c=0\), у которых коэффициент \(a\) при \(x^2\) равен \(1\), называют приведенными.

Например:
$$x^2+4x-3=0;$$
$$x^2-140x-65=0;$$
Любое полное квадратное уравнение всегда можно свести к приведенному. Для этого надо поделить все уравнение на коэффициент \(a\):

Пример 17
Привести квадратное уравнение к приведенному.
$$3x^2-15x+9=0;$$
Разделим уравнение на \(a=3\). (Так можно делать: если левую и правую части уравнения поделить на одно и то же число, то корни уравнения от этого не изменятся.)
$$\frac{3x^2-15x+9}{3}=\frac{0}{3};$$
В результате каждое слагаемое поделится на \(3\):
$$\frac{3x^2}{3}-\frac{15x}{3}+\frac{9}{3}=0;$$
$$x^2-5x+3=0;$$

Формулы Виета

Сумма корней приведенного квадратного уравнения \(x^2+bx+c=0\) равна второму коэффициенту \(b\) со знаком минус, а произведение корней равно свободному члену \(c\).

Пусть \(x_1\), и \(x_2\) — корни квадратного уравнения \(x^2+bx+c=0\), тогда справедливы формулы:
$$ \begin{cases}
x_1+x_2=-b; \\
x_1*x_2=c. \\
\end{cases}$$
На первый взгляд может показаться, что это очень запутанно, но на самом деле, теорема Виета часто помогает решить уравнение в уме. Попробуем на практике:

Пример 18
$$x^2+4x+3=0;$$
$$a=1 \quad b=4 \quad c=3.$$
Воспользуемся теоремой Виета и выпишем формулы:
$$ \begin{cases}
x_1+x_2=-b; \\
x_1*x_2=c. \\
\end{cases}$$
Подставим коэффициенты:
$$ \begin{cases}
x_1+x_2=-4; \\
x_1*x_2=3. \\
\end{cases}$$

Нужно найти такие \(x_1\) и \(x_2\), которые удовлетворяют и первому, и второму уравнениям в системе. Подобрать корни достаточно просто: рассмотрим второе уравнение, какие два числа дают при умножении \(3ку\)?

Либо: \(3=1*3\);
Либо: \(3=(-1)*(-3)\).

Осталось проверить, будут ли найденные множители удовлетворять первому уравнению в системе, просто подставим их:
$$1+3 \neq -4;$$
$$-1+(-3) = -4;$$
Вот мы и нашли корни системы уравнений: \(x_1=-1\) и \(x_2=-3\). А самое главное, мы нашли корни исходного квадратного уравнения. Ответ: \(x_1=-1 \quad и \quad x_2=-3.\)

Если потренироваться, то все эти вычисления можно легко проводить в уме, если коэффициенты небольшие. Главное запомнить, что произведение корней должно быть равно свободному члену \(c\), а сумма корней равна \((-b)\).

Теорема Виета, если \(a\neq1\)

По теореме Виета можно решать не только приведенные квадратные уравнения (у которых \(a=1\)). Но перед тем, как применять формулы Виета, надо привести уравнение к приведенному, поделив на первый коэффициент \(a\):
$$ax^2+bx+c=0; \quad \mid :a$$
$$\frac{ax^2}{a}+\frac{bx}{a}+\frac{c}{a};$$
$$x^2+\frac{b}{a}*x+\frac{c}{a};$$
Получили приведенное квадратное уравнение, для которого можно записать формулы Виета, где вторым коэффициентом будет \(\frac{b}{a}\), а свободным членом \(\frac{c}{a}\):
$$ \begin{cases}
x_1+x_2=-\frac{b}{a}; \\
x_1*x_2=\frac{c}{a}. \\
\end{cases}$$

Пример 19
$$12x^2+x-1=0;$$
$$a=12 \quad b=1 \quad c=-1.$$
Коэффициент \(a=12 \neq 1\), поэтому разделим все уравнение на \(a=12\):
$$12x^2+x-1=0; \quad \mid :12$$
$$x^2+\frac{1}{12}x-\frac{1}{12}=0;$$
$$a=1 \quad b=\frac{1}{12} \quad c=-\frac{1}{12}.$$

Теорема Виета:
$$ \begin{cases}
x_1+x_2=-\frac{1}{12}; \\
x_1*x_2=-\frac{1}{12}. \\
\end{cases}$$

Подбираем корни:
$$x_1=-\frac{1}{3};$$
$$x_2=\frac{1}{4};$$

Ответ: \(x_1=-\frac{1}{3} \quad и \quad x_2=\frac{1}{4}.\)

Тригонометрическая и показательная форма комплексных чисел

Примеры решения задач

Задача 1

Задача

Необходимо найти частное пары комплексных чисел:

(z_1 = 3+i) и (z_2 = 2-3i)

Решение:

Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу.

(frac{z_1}{z_2} = frac{3+i}{2-3i} =)

Сопряженное комплексное число к знаменателю:

(overline{z_2} = 2+3i)

Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе:

(= frac{(3+i)(2+3i)}{(2-3i)(2+3i)} = frac{6 + 9i + 2i — 3}{4 + 6i — 6i + 9} =)

Далее следует привести подобные слагаемые и записать вывод с ответом:

(= frac{3 + 11i}{13} = frac{3}{13} + frac{11}{13}i)

Ответ: (frac{z_1}{z_2} = frac{3}{13} + frac{11}{13}i)

Задача 2

Задача

Требуется выполнить деление комплексных чисел:

(z_1 = 2(cos frac{pi}{3} + isin frac{pi}{6}))

(z_2 = 4(cos frac{pi}{6} + isin frac{pi}{6}))

Решение:

Комплексные числа в условии задачи записаны в тригонометрической форме. По этой причине необходимо использовать в расчетах соответствующую формулу. В данном случае следует определить деление модулей и разность аргументов:

Деление модулей:

(frac{r_1}{r_2} = frac{2}{4} = frac{1}{2})

Разность аргументов:

(varphi_1 — varphi_2 = frac{pi}{3} — frac{pi}{6} = frac{pi}{6})

Следующим шагом является деление чисел:

(frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Ответ: (frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Задача 3

Задача

Нужно найти частное комплексных чисел:

(z_1 = 3e^{frac{pi}{2}i})

(z_2 = 4e^{frac{pi}{4}i})

Решение:  Согласно формуле деления в показательной форме определяем разность аргументов и частное модулей:

(frac{r_1}{r_2} = frac{3}{4})

(varphi_1 — varphi_2 = frac{pi}{2} — frac{pi}{4} = frac{pi}{4})

При подстановке в формулу полученных значений уравнение будет преобразовано следующим образом:

(frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Ответ: (frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Задача 4

Задача

Определить частное:

(frac{-2+i}{1-i})

Решение:

В первую очередь следует домножить числитель и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю:

(1-i)

Данным числом является:

(1+i)

Таким образом:

(frac{-2+i}{1-i}=frac{-2+i}{1-i} cdot frac{1+i}{1+i}=frac{(-2+i)(1+i)}{(1-i)(1+i)})

Затем следует перемножить комплексные числа, как алгебраические двучлены, с учетом:

(i^{2}=-1)

(frac{-2+i}{1-i}=frac{(-2+i)(1+i)}{(1-i)(1+i)}=frac{-2-2 i+i-1}{1^{2}-i^{2}}=)

(=frac{-3-i}{1-(-1)}=frac{-3-i}{2}=-frac{3}{2}-frac{i}{2})

Ответ:( frac{-2+i}{1-i}=-frac{3}{2}-frac{i}{2})

Задача 5

Задача

Необходимо найти частное:

(frac{z_{1}}{z_{2}})

При условии, что:

(z_{1}=2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right))

(z_{2}=cos frac{pi}{4}+i sin frac{pi}{4})

Решение:

Искомое частное:

(frac{z_{1}}{z_{2}}=frac{2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right)}{cos frac{pi}{4}+i sin frac{pi}{4}}=)

(=frac{2}{1} cdotleft=)

(=2 cdotleft=2 cdot(0+i)=2 i)

Ответ: (frac{z_{1}}{z_{2}}=2 cdotleft(cos frac{pi}{2}+i sin frac{pi}{2}right)=2 i)

Задача 6

Задача

Необходимо разделить два комплексных числа:

(z_{1}=-1+3i)

(z_{2}=1+2i)

Решение:

С помощью соответствующей формулы можно записать уравнение:

(z_{1} div z_{2} = frac{-1+3i}{1+2i} = frac{(-1+3i)(1-2i)}{(1+2i)(1-2i)} = frac{-1 cdot 1 + 3 cdot 2}{1^{2}+2^{2}} + i frac{3 cdot 1 + (-1) cdot (-2)}{1^{2}+2^{2}} =)

(= frac{5}{5} + i frac{5}{5}=1+i)

Ответ: ( z_{1} div z_{2} = 1+i)

Задача 7

Задача

Необходимо вычислить частное комплексных чисел:

(z_{1}=sqrt{2} left( cos frac{pi}{2} + i sin frac{pi}{2} right))

(z_{2}=sqrt{2} left( cos frac{pi}{4} + i sin frac{pi}{4} right))

Решение:

Используя соответствующую формулу, запишем:

(z_{1} div z_{2} = frac{r_{1}}{r_{2}} (cos ( varphi _{1} — varphi _{2}) + i sin ( varphi _{1} — varphi _{2})) = frac{sqrt{2}}{sqrt{2}} left( cos left( frac{pi}{2}-frac{pi}{4} right) + i sin left( frac{pi}{2}-frac{pi}{4} right) right) =)

(= 1 cdot left( cos frac{pi}{4} + i sin frac{pi}{4} right) = cos frac{pi}{4} + i sin frac{pi}{4})

Ответ:( z_{1} div z_{2} = cos frac{pi}{4} + i sin frac{pi}{4})

Задача 8

Извлечение корней из дробных чисел

Перед тем, как начать вычисления, убедитесь, что дробное число представлено в виде обыкновенной дроби.

Перейдем к свойству корня из частного:

\{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\]

Далее нужно воспользоваться правилом извлечения корня из дроби, которое гласит: корень из дроби равен от деления корня числителя на корень знаменателя.

Пример 1:

Давайте возьмем любую десятичную дробь и на её примере посмотрим, как нужно извлекать корень.

Так, например, найдем кубический корень из 373,248.

Первый ход — это представление десятичной дроби в виде обыкновенной:

³√373248/³√1000. После этого найдем кубический корень в числе и знаменателе:

³√373248=2×2×2×2×2×2×2×2×2×3×3×3×3×3×3=2⁹×3⁶=72³

Эти действия происходят как с квадратными корнями, но здесь уже мы считаем числа 2 и 3 не по двойке, а тройке, т.е. 2⁹=2×2×2, а 3⁶=3×3. Или же сокращаем ⁹ и ⁶.

Проверим таким образом: из 9 вычитаем тройки до тех пор, пока не придем к 0: 9-3-3-3 – это значит, что двоек у нас будет именно 3. Так и с 3⁶. Если от 6 отнять 3 два раза, то будет 0. Выходит, что троек у нас именно две.

А 1000=10³.

Получается, ³√373248/³√1000=72/10=7,2.

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – .

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем

Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа

Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то ) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

x– 5 = 62

х = 36 + 5

х = 41

Ответ: 41.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

х – 5 = (– 6)3

х = – 216 + 5

х = – 211

Ответ: – 211.

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х2 – 14х = 25

х2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью :

D = b2– 4ac = (– 14)2 – 4•1•(– 32) = 196 + 128 = 324

х₁ = (14 – 18)/2 = – 2

х₂ = (14 + 18)/2 = 16

Итак, нашли два корня: (– 2) и 16.

Ответ: (– 2); 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = (х – 4)2

х – 2 = х2 – 8х + 16

х2 – 9х + 18 = 0

D = b2– 4ac = (– 9)2 – 4•1•18 = 81 – 72 = 9

х₁ = (9 – 3)/2 = 3

х₂ = (9 + 3)/2 = 6

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3     х – 4 = 3 – 4 = – 1

при х = 6     6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Ответ: 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х2 + 6х – 25 = (1 – х)3

3х2 + 6х – 25 = 1 – 3х + 3х2 – х3

х3 + 9х – 26 = 0

Получили кубическое ур-ние. Решить его можно . Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

23 + 9•2 – 26 = 0

8 + 18 – 26 = 0

0 = 0

Других корней нет. Это следует из того факта, что функция у = х3 + 9х – 26 является .

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2   1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Ответ: 2.

Пояснения к калькулятору

1. Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.
2. Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
3. ⌫ – удалить в поле ввода символ слева от курсора.
4. C – очистить поле ввода.
5. При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
6. Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
7. Ввод числа в n-ой степени и квадратного корня прозводится кнопками ab и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей →.

Что такое квадратные уравнения?

А теперь подробно с примерами обсудим квадратные уравнения.

Любые уравнения, сводящиеся к виду \(ax^2+bx+c=0\), называются квадратными. Где буквы \( b,\; с\) — любые числа, \(a\neq0\). Почему \(a\neq0\) мы обсудим ниже.

Обратите внимание на порядок слагаемых в квадратном уравнении: \(a\) — всегда стоит первая и обязательно умножается на \(x^2\), она называется старшим коэффициентом (или первым); \(b\) — принадлежит второму слагаемому и всегда умножается просто на переменную \(x\), это у нас второй коэффициент; \(c\) — называют свободным членом, она не умножается ни на какую переменную. В дальнейшем старайтесь приводить квадратное уравнение к виду \(ax^2+bx+c=0\), чтобы слагаемые стояли именно в таком порядке

Это очень важно при решении уравнений, и поможет избежать множества ошибок

В дальнейшем старайтесь приводить квадратное уравнение к виду \(ax^2+bx+c=0\), чтобы слагаемые стояли именно в таком порядке

Это очень важно при решении уравнений, и поможет избежать множества ошибок

Потренируемся определять значения коэффициентов \( a, \; b,\; с\), чтобы запомнить порядок:

Пример 1
$$2x^2+3x+4=0;$$
$$a=2 \quad b=3 \quad c=4.$$

Пример 2
$$5x^2-3x-0,7=0;$$
$$a=5 \quad b=-3 \quad c=-0,7.$$

Пример 3
$$-x^2+2x+10=0;$$
Минус перед \(x^2\) можно представить в виде \(-x^2=-1*x^2\). Единицу обычно не пишут, поэтому минус перед первым слагаемым означает, что \(a=-1\):
$$a=-1 \quad b=2 \quad c=10.$$

Пример 4
$$3+x^2-5x=0;$$
Слагаемые стоят в неправильном порядке. Так коэффициенты находить неудобно, поэтому переставим все слагаемые в нужном порядке. От перемены мест слагаемых сумма не меняется:
$$x^2-5x+3=0;$$
$$a=1 \quad b=-5 \quad c=3.$$

Пример 5
$$2x^2-3x=0;$$
В уравнении нет свободного члена \(c\), поэтому он будет равен \(0\):
$$a=2 \quad b=-3 \quad c=0.$$

Пример 6
$$-4x^2+1=0;$$
А здесь уже нет второго коэффициента \(b\):
$$a=-4 \quad b=0 \quad c=1.$$

Уравнения, приведенные в примерах №5 и 6, называются неполными квадратными уравнениями, так как в них коэффициенты \(b\) или \(c\) равны нулю.

А вот если в уравнении коэффициенты \( a, \; b,\; с\) не равны 0, то такое уравнение называется полным.

Как использовать комплексные числа для решения квадратных уравнений

Квадратные уравнения с комплексными корнями могут быть решены с помощью комплексных чисел. Этот метод особенно полезен, когда дискриминант отрицательный, что означает, что вещественные корни отсутствуют. В таком случае мы можем использовать комплексные числа, чтобы получить корни.

Для решения квадратного уравнения, содержащего комплексные числа, нужно знать как работать с комплексными числами: как складывать, вычитать, умножать и делить, а также как находить модуль комплексного числа. Кроме того, нужно знать формулу дискриминанта, которая позволяет нам определить, есть ли вещественные корни у уравнения или нет.

Если дискриминант отрицательный, мы можем использовать формулу для нахождения комплексных корней квадратного уравнения. Мы можем использовать следующую формулу: x = (-b ± √D) / 2a, где a, b и c — коэффициенты квадратного уравнения, а D — дискриминант. Если D отрицательный, мы можем записать его в виде D = -d², где d — вещественное число.

Тогда наша формула будет выглядеть таким образом: x = (-b ± di) / 2a. Таким образом, мы получим два комплексных корня, которые имеют вид a + bi и a — bi, где a — это вещественная часть, а bi — мнимая часть комплексного числа.

Выделение полного квадрата

Выделение полного квадрата — это преобразования многочленов второй степени. С его помощью квадратные уравнения НЕ решают. Метод может пригодиться при оценке квадратных многочленов, построении графиков квадратных функций и особенно его любят в сложных заданиях с параметрами.

Надеюсь, вы знакомы с формулами сокращенного умножения:
$$(a+b)^2=a^2+2ab+b^2;$$
$$(a-b)^2=a^2-2ab+b^2;$$
Еще они называются формулам полного квадрата. Часто их применяют, чтобы раскрыть квадрат суммы или разности, но иногда бывает нужно, наоборот, представить квадратный многочлен в виде скобок, то есть воспользоваться формулами справа налево:
$$x^2+2x+1=(x+1)^2;$$
$$4x^2-8x+4=(2x-2)^2;$$
К сожалению, далеко не любой квадратный многочлен можно представить в виде квадрата. Более того, такие многочлены встречаются не часто. Метод выделения полного квадрата позволяет представить практически любой многочлен в виде суммы/разности квадрата и числа. Например, многочлен \(x^2+6x+7\) невозможно свернуть по формулам сокращенного умножения, но можно представить в виде:
$$x^2+6x+7=x^2+6x+9-2=(x+3)^2-2;$$
Приведение многочлена второй степени к такому виду и называется методом выделения полного квадрата. Давайте разбираться, как я все это провернул:

• Первые два слагаемых, у которых есть \(x\), мы никогда не трогаем. Нас интересует только свободный член. Нужно дополнить слагаемые таким свободным членом, чтобы получилась формула полного квадрата.
• Соотнесем формулу \(a^2+2ab+b^2=(a+b)^2\) с многочленом \(x^2+6x+(?)\). В нашем примере:
  $$a^2=x^2 \Rightarrow a=\pm x;$$
  $$2ab=6*x=2*3*x;$$
  а знак вопроса — это \(b^2\), которое нам надо подобрать.
• Посмотрите еще раз на слагаемое удвоенного произведения \(2ab=6*x=2*3*x\), если \(a=x\), то \(b\) должно быть равно \(3\). То есть вместо знака вопроса нужно подставить \(b^2=3^2=9\).
• Но мы не можем просто к \(x^2+6x\) добавить \(9-ку\), тогда квадратный многочлен изменится. Если мы добавим \(9\), то и вычтем \(9\):
  $$x^2+6x+7=x^2+6x+9-9+7=(x+3)^2-9+7=(x+3)^2-2;$$

В общем виде алгоритм выделения полного квадрата будет выглядеть так:
$$ax^2\pm bx+c=a(x^2\pm \frac{b}{a}x)+c=a(x^2 \pm 2\frac{b}{2a}x)+c=$$
$$=a\left(x^2 \pm 2\frac{b}{2a}x+\left(\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2\right)+c=$$
$$=a\left(\left(x^2 \pm 2\frac{b}{2a}x+\left(\frac{b}{2a}\right)^2\right)-\left(\frac{b}{2a}\right)^2\right)+c=$$
$$=a\left(x\pm \frac{b}{2a}\right)^2-\frac{b^2}{4a}+c.$$