От теории к практике
 Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Чтобы найти площадь правильного шестиугольника онлайн по нужной вам формуле, введите в поля числа и нажмите кнопку «Посчитать онлайн».Внимание!
Числа с точкой (2.5) надо писать с точкой(.), а не с запятой!
1. Все углы правильного шестиугольника равны 120 °
2. Все стороны правильного шестиугольника идентичны друг другу
Регулярный шестиугольный периметр
4. Форма поверхности правильного шестиугольника
5. Радиус удаленной окружности правильного шестиугольника
6. Диаметр круглого круга нормального шестиугольника
7. Радиус введенной правильной шестиугольной окружности
8. Отношения между радиусами введенных и ограниченных кругов
как , и , и , из которого следует треугольник — прямоугольная с гипотенузой — это то же самое . Таким образом,
10. Длина AB равна
11. Формула сектора
[править] Формулы
Формула используется для области регулярного n-угольника в n = 6
:
S_6 = \ frac {3a ^ 2} {2} CTG \ frac {\ pi} {6} \ Leftrightarrow \ Leftrightarrow S_6 = 6S _ {\ triangle} \ S _ {\ triangle } = \ frac {e ^ 2} {4} CTG \ frac {\ pi} {6} \ Leftrightarrow \ Leftrightarrow S_6 = \ frac {1} {2} P_6r \ P_6 = \ right {\ math} {Math} \ Leftrightarrow S_6 = 6R ^ 2 \ sin \ frac {\ pi} {6} \ cos \ frac {{pi} Frac {\ pi} {6} \ R = \ frac {a} {2 \ sin \ frac {\ pi} {6}} \ Leftrightarrow \ Leftrightarrow S_6 = 6r ^ 2tg \ frac { pi} {6}, \ r = R \ cos \ frac {\ pi} {6}
Использование углов тригонометрического угла для углов α = π / 6
:
S_6 = \ FRAC {3 \ sqrt {3}} {2} ^ 2 \ Leftrightarrow \ Leftrightarrow S_6 = 6S _ {\ triangle} \ S _ {\ triangle} = \ FRAC { \ sqrt {3}} {4} ^ 2 \ Leftrightarrow \ Leftrightarrow S_6 = \ frac {1} {2} P_6r \ P_6 = 6a, \ r = \ FRAC {\ sqrt {3}} {2} A \ Leftrightarrow \ Leftrightarrow S_6 = \ FRAC {3 \ sqrt {3}} {2} R ^ 2, \ R = A \ Leftrightarrow \ \ r = \ frac {\ sqrt {3}} {2} R leftrightarrow S_6 = 2 \ sqrt {3} r ^ 2
где {Math} \ {pi \} sin \ frac {6} = \ frac {1} {2} \ cos \ frac {\ pi} {6} = \ FRAC {\ sqrt { 3}} {2} , tg \ frac {\ pi} {6} = \ frac {\ sqrt {3}} {3} pi} {6} = \ sqrt {3}
Шестиугольник в реальности
Гексагоны часто встречаются в реальной жизни. К примеру, сечения гаек или карандашей имеют шестиугольную форму, благодаря чему обеспечивается удобный обхват предмета. Шестиугольник — это эффективная геометрическая фигура, способная замостить плоскость без пробелов и наложений. Именно поэтому шестиугольную форму часто имеют декоративные отделочные материалы, например, кафельная и тротуарная плитка или гипсокартонные панели.
Эффективность гексагона делает его популярным и в природе. Пчелиные соты обладают именно шестиугольной формой, благодаря которой пространство улья заполняется без пробелов. Еще одним примером гексагонального замощения плоскости является Тропа Великанов — памятник живой природы, сформированный во время извержения вулкана. Вулканический пепел был спрессован в шестиугольные колонны, которые замостили поверхность побережья Северной Ирландии.
Свойства простые и интересные
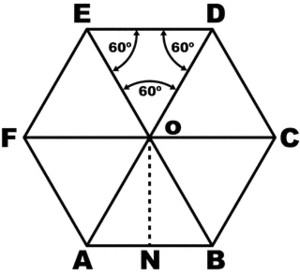
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
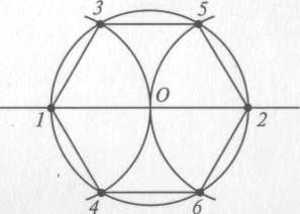
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
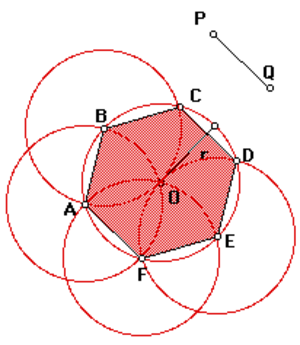
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
S=3(2r/√3)²(√3)/2=r²(2√3)
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
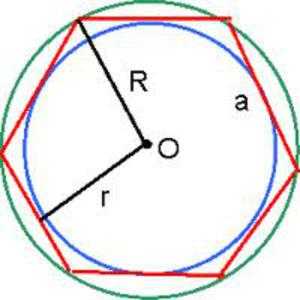
- Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
Как найти площадь неправильного шестиугольника
Формулы для вычисления площади неправильного шестиугольника – многоугольника, стороны которого не равны между собой.
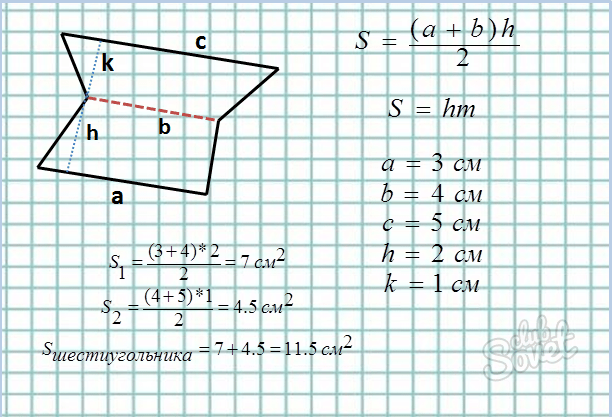
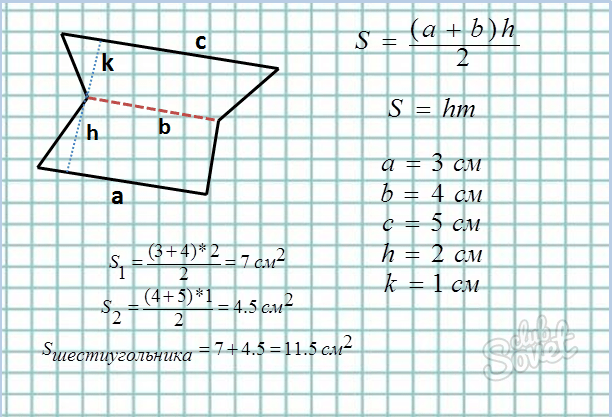
Метод трапеции:
- Делим шестиугольник на произвольные трапеции, вычисляем площадь каждой из них и складываем.
- Основные формулы площади трапеции: S = 1/2*(a + b)*h, где a и b – основания трапеции, h – высота.
S = h*m, где h – высота, m – средняя линия.
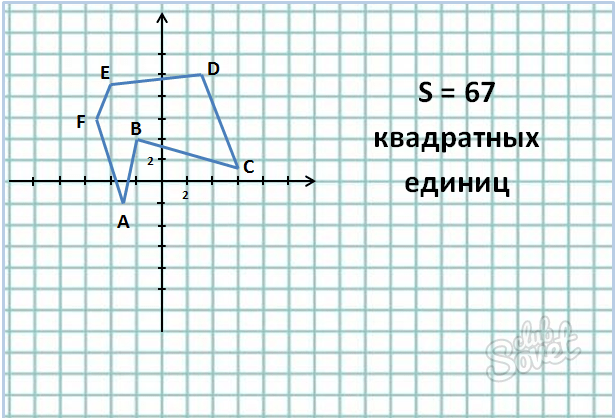
Известны координаты вершин шестиугольника:
- Для начала запишем координаты точек, причём, располагая их не в хаотичном порядке, а последовательно друг за другом. Например:
A: (-3, -2)
B: (-1, 4)
C: (6, 1)
D: (3, 10)
E: (-4, 9)
F: (-5, 6) - Далее, внимательно, умножаем координату x каждой точки на координату y следующей точки:
-3*4 = -12
-1*1 = -1
6*10 = 60
3*9 = 27
-4*6 = -24
-5*(-2) = 10
Результаты складываем:
-12 – 1 + 60 + 27 – 24 + 10 = 60
Далее умножаем координату y каждой точки на координату x следующей точки.
-2*(-1) = 2
4*6 = 24
1*3 = 3
10*(-4) = -40
9*(-5) = -45
6*(-3) = -18
Результаты складываем:
2 + 24 + 3 – 40 – 45 – 18 = -74
Из первого результата вычитаем второй:
60 -(-74) = 60 + 74 = 134
Полученное число делим на два:
134/2 = 67
Ответ: 67 квадратных единиц.
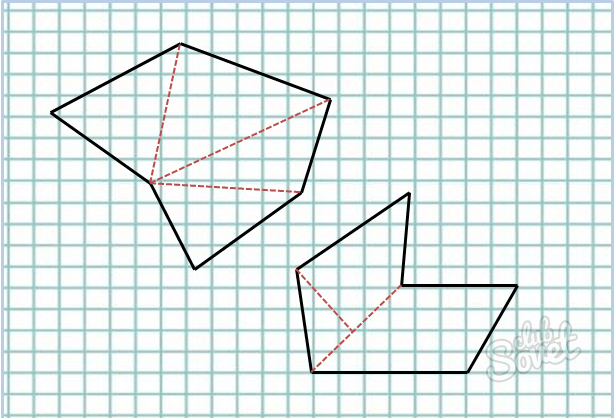
Также для нахождения площади шестиугольника вы можете разбить его на треугольники, квадраты, прямоугольники, параллелограммы и так далее. Найти площади составляющих его фигур и сложить.
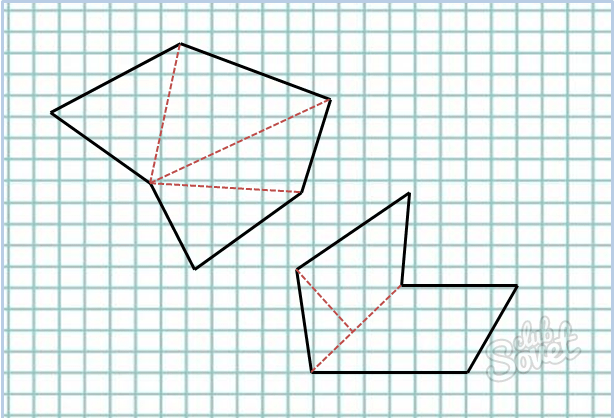
Итак, методы нахождения площади шестиугольника на все случаи жизни изучены. Теперь вперёд, применять полученные знания! Удачи!
Шестиугольник или гексагон — это правильный многоугольник, у которого стороны равны между собой, а каждый угол равен строго 120 градусов. Гексагон иногда встречается в человеческой повседневности, поэтому вам может понадобиться вычислить его площадь не только в школьных задачах, но и в реальной жизни.
От теории к практике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Презентация была опубликована 5 лет назад пользователемГригорий Оськин
Выбор расходных материалов для сварки
Чтобы варить алюминий инвертором без аргона применяются электроды, сделанные из близкого по составу материала. Их покрытие при нагреве создает газовую среду, которая препятствует проникновению воздуха в зону сварки. Лучшими отечественными признаны марки ОЗА, ОЗР, ОЗАНА. Аналоги зарубежного производства OK 96.20, OK 96.40, Kobatek-213 лучше по качеству, но стоят дороже. Аргонодуговая сварка выполняется неплавящимися электродами из вольфрама. Для создания шва используют присадочную проволоку диаметром от 2 до 5 мм. В составе популярных марок АО, АД, АК содержится много магния.
Чтобы сваривать алюминий инверторным полуавтоматом используется присадочная проволока диаметром от 0,8 до 1 мм в катушках по 0,5 кг. Большей популярностью пользуются марки ER 4043 и ER 5356, сделанные из сплава кремния с алюминием. Св-АК 5 и Св-АМг из алюминия с магнием применяются реже.
Описание фигуры
Непосредственно шестиугольник представляет собой плоскую фигуру, состоящую из шести отрезков, с расположением под углом 120 градусов относительно друг друга. Имеет научное название гексагон. Вокруг него или внутри можно вписать либо описать окружность. Между собой радиус и сторона многоугольника соотносятся по следующим формулам:
- R=2sin (pi/6)*a=a.
- r=0,866a.
- P=4*sqrt (3)*r или P=6*R.
Гексагон является очень популярной фигурой, ее имеют гайки, карандаши, соты, снежинки и многое другое. Является оптимальным вариантом для того, чтобы без пробелов замостить все пространство. Одним из примеров этого является Мостовая гигантов, образовавшаяся в результате соединения более чем 40 тысяч базальтовых колонн в результате извержения древнего вулкана и элегантно замостившая поверхность побережья в Северной Ирландии.
Поиски вышеописанного параметра гексагона являются простой, но в то же время довольно интересной задачей. Найдя периметр, можно убедиться в правильности замощенного пространства и отсутствии пробелов при составлении будущей документации.
Расчет
Требуемое значение можно рассчитать, разделив фигуру на шесть равносторонних треугольников.
Для расчета S используйте следующую формулу:
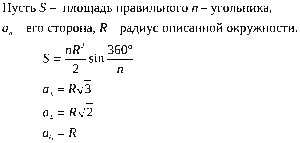
Вычислив S для одного из треугольников, легко определить общий. Простая формула, поскольку правильный шестиугольник на самом деле представляет собой шесть равных треугольников. Для его вычисления умножьте найденную площадь треугольника катетов на 6.
Если из центра шестиугольника провести перпендикуляр к любой из сторон, то получится отрезок — апофема.
Давайте посмотрим, как найти S шестиугольника, апофема которого известна:
- S =1/2×периметр×апофема.
- Возьмем апофему, равную 5√3 см.
- Находим периметр с помощью апофемы: так как апофема перпендикулярна стороне 6-угольника, то углы треугольника, образованного с апофемой, равны 30˚-60˚-90˚. Каждая сторона треугольника соответствует: xx√3-2x, где короткая сторона, направленная к углу 30˚, равна x; длинная сторона, противоположная углу 60˚, равна x√3, а гипотенуза равна 2x.
- Апофему x√3 можно заменить формулой a=x√3. Если апофема 5√3, подставляем это значение, получаем: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника равна 5 см, так как эта величина равна половине длины стороны 6-угольника. Умножая 5 на 2, получаем 10 см, что является значением длины стороны.
- Полученное значение умножаем на 6 и получаем значение окружности – 60 см.
Подставляем полученные результаты формулой: S=1/2×периметр×апофема
S=½×60см×5√3
Мы считаем:
Упростим ответ, чтобы избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150√3см=259,8 с м².
Где и как можно использовать шестиугольник?
Шестиугольник может быть применен в различных областях и имеет множество применений. Вот некоторые из них:
- Архитектура и строительство. Шестиугольники могут использоваться в архитектуре для создания уникальных фасадов зданий или в планировке помещений. Например, шестиугольные плитки могут использоваться для создания интересных и гармоничных дизайнов пола и стен.
- Упаковка. Шестиугольные упаковочные контейнеры могут обеспечивать более эффективное использование пространства и обеспечивать прочность и стабильность конструкции.
- Биология и природа. Многие ячейки и пчелиные соты имеют форму шестиугольника, поскольку это оптимальная форма для заполнения пространства с минимальными затратами энергии. Также шестиугольники можно найти в структурах медовых трутней и в некоторых природных образованиях, таких как гексагональные базальтовые колонны.
- Геометрические и математические исследования. Шестиугольники являются одним из простейших правильных многоугольников, и их свойства широко изучаются в математике и геометрии. Они могут использоваться в качестве примеров для изучения углов, сторон и свойств многоугольников в целом.
- Графика и дизайн. Шестиугольники могут быть использованы в графическом дизайне и создании паттернов. Их регулярная форма и симметрия позволяют создавать интересные и гармоничные композиции.
- Игры и головоломки. Шестиугольники могут использоваться в играх и головоломках, где требуется решать задачи, связанные с их свойствами и геометрией.
Это лишь некоторые примеры применения шестиугольника. Фактически, шестиугольник может использоваться везде, где требуется регулярная форма с определенными свойствами и характеристиками.
Через длину стороны
По той причине, что выпуклый шестиугольник включает в себя шесть равносторонних треугольников, формула нахождения искомого значения по длине стороны выглядит следующим образом:
S = (3√3*a²)/2
где а — длина стороны.
Рассмотрим пример. Пусть длина стороны равна 8. Значит, согласно этой формуле, заданная характеристика замкнутого выпуклого шестиугольника будет приблизительно равна 166.
Все довольно просто, если сайт известен заранее. Если это значение нам не дано, но известен периметр или апофема — высота одного из шести равносторонних треугольников, — то можно вычислить длину стороны.
Если периметр известен, его нужно разделить на шесть, получив таким образом длину стороны. Например, если периметр равен 36, то разделив 36 на 6, вы получите 6 — это длина стороны.
Если известна только апофема, то можно вычислить длину стороны, подставив апофему в формулу b = x√3 и умножив ответ на 2. Все это потому, что апофема – это сторона x√3 треугольника он составляет с углами 30, 60 и 90 градусов. Например, если апофема 11√3, то x = 11, а длина стороны будет равна 22.
Площадь треугольников
Зная базу и высоту
Когда мы знаем основание и высоту, это легко.
Это просто половина b умножить на
Площадь = 1 2 bh
(Более подробная информация на странице «Треугольники»)
Самое главное, чтобы основание и высота были под прямым углом. Поиграйте здесь:
Пример: Какова площадь этого треугольника?
(Примечание: 12 — это высота , а не длина левой стороны)
Высота = h = 12
База = b = 20
Площадь =
120
Знание трех сторон
Существует также формула для определения площади любого треугольника, когда мы знаем длины всех трех его сторон.
Его можно найти на странице формул Герона.
Зная две стороны и угол наклона
Когда мы знаем две стороны и включенный угол (SAS), мы можем использовать другую формулу (фактически, три эквивалентные формулы).
В зависимости от того, какие стороны и углы нам известны, формулу можно записать тремя способами:
Площадь = 1 2 ab sin C
Площадь = 1 2 до н.э. sin A
Площадь = 1 2 ca sin B
Это действительно та же формула, только с измененными сторонами и углом.
Пример: Найдите площадь этого треугольника:
Прежде всего мы должны решить, что мы знаем.
Нам известен угол C = 25º, а стороны a = 7 и b = 10.
Итак, приступим:
Площадь = (½) ab sin C
Введите известные нам значения: ½ × 7 × 10 × sin (25º)
Сделайте некоторую работу с калькулятором: 35 × 0,4226 …
Площадь = 14,8 с точностью до одного десятичного знака
Как помнить
Подумайте только о «abc»: Площадь = ½ a b sin C
Также хорошо помнить, что угол между двумя известными сторонами всегда равен , что называется «включенным углом».
Как это работает?
Площадь = ½ × основание × высота
|
В этом треугольнике:
|
Получаем:
Площадь = ½ × (c) × (b × sin A)
Что (проще):
Площадь = 1 2 до н.э. sin A
Изменив метки на треугольнике, мы также можем получить:
- Площадь = ½ ab sin C
- Площадь = ½ ca sin B
Еще один пример:
Пример: Найдите сколько земли
Фермер Джонс владеет треугольным участком земли.
Длина забора АВ составляет 150 м. Длина забора БЦ 231 м.
Угол между упором AB и ограждением BC составляет 123º.
Сколько земли принадлежит фермеру Джонсу?
Прежде всего мы должны решить, какие длины и углы нам известны:
- AB = c = 150 м,
- BC = a = 231 м,
- и угол B = 123º
Итак, мы используем:
Площадь = 1 2 ca sin B
Введите известные нам значения: ½ × 150 × 231 × sin (123º) м 2
Сделайте некоторую работу с калькулятором: 17,325 × 0.838 … м 2
Площадь = 14530 м
2
Фермер Джонс владеет 14530 м 2 земли
Получи пятерку
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля – до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Сразу после оплаты вы получите ссылки на скачивание видеокурсов и уникальные ключи к ним.
Задачи комплекта «Математические тренинги – 2019» непростые. В каждой – интересные хитрости, «подводные камни», полезные секреты.
Варианты составлены так, чтобы охватить все возможные сложные задачи, как первой, так и второй части ЕГЭ по математике.






























