Деление комплексных чисел в тригонометрической форме
Рассмотрим частное комплексных чисел , заданных в тригонометрической форме. Из определения частного имеем и, применяя к произведению правило умножения (формулы (1.10)), получаем .
Правило деления. Модуль частного, полученного в результате деления чисел, заданных в тригонометрической форме, равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя:
(1.11)
В результате деления чисел по формуле (1.11) может получиться аргумент честного, не являющийся главным значением.
Пример 1.20. Записать в тригонометрической форме комплексное число .
Решение. Обозначим . Для чисел и находим модули и аргументы: (см. пример 1.19). По формуле (1.11) получаем и
Извлечение корня.
Рассмотрим уравнение
$$
z^n=a,\label{ref22}
$$
где \(a\neq 0\) — комплексное число, \(n\) — натуральное число.
Если \(z=re^{i\varphi}, \ a=\rho e^{i\theta}\), то уравнение \eqref{ref22} примет вид
$$
r^n e^{in\varphi}=\rho e^{i\theta},\nonumber
$$
откуда
$$
r^n=\rho,\quad n\varphi=\theta+2k\pi,\quad k\in\mathbb{Z},\nonumber
$$
и поэтому
$$
r=\sqrt{\rho},\qquad \varphi_k=\frac{1}{n}(\theta+2k\pi),\quad k\in \mathbb{Z},\label{ref23}
$$
то есть числа
$$
z_k=\sqrt{\rho}e^{i\varphi_k}\label{ref24}
$$
являются корнями уравнения \eqref{ref22} и других корней это уравнение не имеет.
Заметим, что числа \(z_0,\ z_1,\ …,\ z_{n-1}\) различны, так как их аргументы \(\displaystyle\varphi_0=\frac{\theta}{n},\ \varphi_1=\frac{\theta}{n}+\frac{2\pi}{n},\ …,\ \varphi_{n-1}=\frac{\theta}{n}+\frac{2\pi(n-1)}{n}\) различны и отличаются друг от друга меньше, чем на \(2\pi\). Далее, \(z_n = z_0\), так как \(|z_n| = |z_0|=\displaystyle\sqrt{\rho}\) и \(\varphi_n=\varphi_0+2\pi\). Аналогично, \(z_{n+1} = z_1,\ z_{-1} = z_{n-1}\) и т. д.
Итак, при \(a\neq 0\) уравнение \eqref{ref22} имеет ровно \(n\) различных корней, определяемых формулами \eqref{ref23} и \eqref{ref24}, где \(k=0,1,…,n-1\).
На комплексной плоскости точки \(z_k\ (k=\overline{0,n-1})\) располагаются в вершинах правильного \(n\)-угольника, вписанного в окружность радиуса \(\displaystyle \sqrt{\rho}\) с центром в точке 0.
Пример 5.
Найти все корни уравнения \(z^4 = 1 + i\).
\(\triangle\) Корни \(z_k\ (k = \overline{0,3})\) этого уравнения определяются формулами \eqref{ref23} и \eqref{ref24}, где \(\displaystyle \rho=|1 + i| =\sqrt{2},\ \theta=\frac{\pi}{4}\), то есть
$$
z_k=\sqrt{2}e^{i\varphi_k},\nonumber
$$
где
$$
\varphi_k=\frac{\pi}{16}+\frac{\pi k}{2},\quad k=0,1,2,3.\nonumber
$$
Рис. 31.6
Точки \(z_k\) располагаются в вершинах квадрата (рис. 31.6). \(\blacktriangle\)
Расширенная комплексная плоскость. Сфера Римана
Из геометрии известно, что любой упорядоченной паре вещественных чисел соответствует точка $z$ на плоскости комплексного переменного. Определим
на комплексной плоскости бесконечно удаленную точку. Так условно будем называть «мысленную точку» $(x,y)$, координаты которой (обе сразу
или одна из них) — величины неограниченные, т.е. комплексные числа имеют формальный вид $z=x+i\infty$, $z=\infty+iy$ либо $z=\infty+i\infty$.
Тогда пишут $z=\infty$ (несобственное комплексное число), считая ее единственной бесконечно удаленной точкой.
Для несобственного комплексного числа понятия вещественной и мнимой части, а также понятие аргумента не вводятся; точнее говоря, объявляются
лишенными смысла (напомним, что понятие аргумента не имеет смысла и для числа 0). Что касается модуля числа $z=\infty$, то для него используется
символ $|\infty|=+\infty$.
Договорились, что имеют смысл следующие операции, в которых участвуют $z=\infty$ и собственное комплексное число $a$: $$
\frac{a}\infty=0,\quad\frac\infty{a}=\infty,\quad\frac{a}0=\infty.
$$ Такие операции, как $$
\infty\pm\infty,\quad 0\cdot\infty,\quad \dfrac00,\quad
\dfrac\infty\infty
$$ объявляются лишенными смысла.
Совокупность точек комплексной плоскости и бесконечно удаленной точки называется расширенной плоскостью комплексного переменного.
Наглядное представление о расширенной комплексной плоскости дает следующая интерпретация Римана (1826-1866).
Чтобы получить геометрическое изображение числа $\infty$, прибегают к представлению комплексных чисел точками сферы. Построим сферу (называемую сферой Римана) радиуса $r$, касающуюся плоскости $z$ в точке $z=0$ и отметим точку $N$ сферы, диаметрально противоположную началу
координат $O$.
Из точки $N(0,0,2r)$ сферы проведем проведем луч в любую точку $Z(x,y,0)$ плоскости $(x,y)$ и отметим точку $S$ пересечения данного луча и
сферы. Эта точка $S(\xi,\eta,\zeta)$ является новым геометрическим представлением комплексного числа $z$. В результате таких
построений лучей между точками плоскости $(x,y)$ и точками сферы устанавливается взаимно однозначное соответствие, называемое стереографической
проекцией, имеющей применение в картографии.
Точкам меридиана $NSO$ на сфере соответствуют точки луча $OZ$ на плоскости $(x,y)$, различным параллелям — круги на плоскости $(x,y)$.
Исключение составляет точка $N$. Северному полюсу $N$ сферы не соответствует пока никакое комплексное число. Однако точкам сферы, достаточно
близким к $N$, соответствуют точки $z$ плоскости, сколь угодно далеко отстоящие от начала координат, т.е. точка $z$ сколь угодно большого
модуля. Будем считать, что точке $N$ соответствует единственная точка $z=\infty$.
Покажем, что точка $z=\infty+\mathbf i \infty$ (или $z=x+\mathbf i \infty$, или $z=\infty+\mathbf i y$) будет при таком преобразовании переходить в точку $N(0,0,2r)$ и
наоборот. Координаты точек на такой сфере $(\xi,\eta,\zeta)$ связаны формулой
\begin{equation}\label{eq g1 p7 1}
\xi^2+\eta^2+(\zeta-r)^2=r^2\quad\hbox{или}\quad \xi^2+\eta^2=\zeta
(2r-\zeta).
\end{equation}
Из коллинеарности $NZ$ и $NS$ можно получить представление луча $NSZ$
$$
\frac{\xi-0}{x-0}=\frac{\eta-0}{y-0}=\frac{\zeta-2r}{0-2r}.
$$
Отсюда можно получить координаты точек плоскости через координаты точек сферы:
\begin{equation}\label{eq g1 p7 2}
x=\frac{2r\xi}{2r-\zeta},\quad y=\frac{2r\eta}{2r-\zeta}.
\end{equation}
Составим
$$ x^2+y^2=\frac{4r^2(\xi^2+\eta^2)}{(2r-\zeta)^2}, $$
$$ x^2+y^2 = \frac{4r^2\zeta}{2r-\zeta}. $$
Тогда
можно выразить координату
$$
\zeta=\frac{2r(x^2+y^2)}{x^2+y^2+4r^2},
$$
и другие координаты
$$
\xi=\frac{4r^2x}{x^2+y^2+4r^2},\quad\eta=\frac{4r^2y}{x^2+y^2+4r^2}.
$$
Устремим $x\to\infty$, $y\to\infty$ (по отдельности или вместе), тогда $\xi\to0$, $\eta\to0$, $\zeta\to2r$, а это и есть точка $N$.
Некоторые сведения о комплексных числах подробнее изложены в курсе Высшей алгебры А.Ю. Утешева ( здесь).
Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел
С алгебраической формой комплексного числа мы уже познакомились, – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.
Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.
Сложение комплексных чисел
Пример 1
Сложить два комплексных числа ,
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса: – от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2
Найти разности комплексных чисел и , если ,
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .
Рассчитаем вторую разность:
Здесь действительная часть тоже составная:
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
Пример 3
Найти произведение комплексных чисел ,
Очевидно, что произведение следует записать так:
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным.
Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Я распишу подробно:
Надеюсь, всем было понятно, что
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .
В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Деление комплексных чисел
Пример 4
Даны комплексные числа , . Найти частное .
Составим частное:
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем бородатую формулу и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть
Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!).
Распишу подробно:
Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:
Редко, но встречается такое задание:
Пример 5
Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).
Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :
Пример 6
Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что
Комплексные числа — простое объяснение
Для того, чтобы разобраться с комплексными числами, следует для начала рассмотреть множество действительных чисел. К этому множеству относятся целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.
Рассмотрим две точки на прямой А = 1 и Б = 2. Сложим эти две точки. Их сумма эта третья точка В = 1+2 = 3.
Точки также можно перемножать. Посмотрим, например, как действует умножения на минус 2. Данное действие преобразует точку 1 в минус 2. Если мы снова умножим на минус 2, то нужно будет повторить аналогичное передвижение на прямой, поменять стороны относительно начала координат и удвоить расстояние до него. В результате получим 4.
Умножение на минус 1 устроено просто. Каждая точка переходит в симметричную ей относительно начала координат. Другими словами нужно сделать пол оборота (повернуть на 180°). Повторение умножения на минус 1 приводит в исходное положение. Умножение на минус 1 переводит 1 в минус 1. Если еще раз умножить на минус 1, мы вернемся обратно в 1.
На данном этапе можно выделить правило, что если умножить число на себя, результат всегда будет положительным. Другими словами минус 1 не имеет квадратного корня. Но только не в случае с комплексными числами.
В начале 19 века Робер Арган высказал следующую идею. Поскольку умножить на минус 1 означает повернуть на 180°, то квадратный корень из минус 1 означает повернуть на половину (90°). Если повернуть дважды на четверть оборота, вы сделаете пол оборота. Квадрат четверти оборота — это пол оборота (минус 1). То есть квадратный корень из минус 1 отвечает точке, в которую минус 1 переходит при повороте на 90°. Поскольку такое построение, выходящее за пределы горизонтальной прямой, выглядит странным, говорят, что такая точка, являющаяся квадратным корнем из минус 1 — это мнимое число. И в математике оно обозначается — i.
Показательная форма комплексного числа:
Символом $e^{i\varphi}$ обозначается комплексное число $\cos\varphi+i\sin\varphi.$ С помощью этого обозначения всякое комплексное число $z=|z|(\cos\varphi+i\sin\varphi)$ может быть представлено в показательной форме $$z=|z|e^{i\varphi}.$$
Примеры.
Представить в показательной форме следующие комплексные числа:
1.475. $\frac{7+24i}{5}.$
Решение.
Приведем число $z=\frac{7+24i}{5}$ к алгебраическому виду:
$$z=x+iy=\frac{7+24i}{5}=\frac{7}{5}+\frac{24}{5}i.$$
$$|z|=\sqrt{\left(\frac{7}{5}\right)^2+\left(\frac{24}{5}\right)^2}=\sqrt{\frac{49+576}{25}}=\sqrt{\frac{625}{25}}=\sqrt{25}=5.$$
$$tg\varphi=\frac{y}{x}=\frac{\frac{24}{5}}{\frac{7}{5}}=\frac{24}{7}.$$ Поскольку число $z$ принадлежит первой четверти, то $\varphi=arctg\frac{24}{7}.$
Таким образом, $z=5e^{i arctg\frac{24}{7}}.$
Ответ: $z=5e^{i arctg\frac{24}{7}}.$
{jumi}
1.479. $\sin\alpha-i\cos\alpha.$
Решение.
$$z=x+iy=\sin\alpha-i\cos\alpha\Rightarrow \,\,x=\sin\alpha,\,\,y=-cos\alpha.$$
$$|z|=\sqrt{x^2+y^2}=\sqrt{\sin^2\alpha+\cos^2\alpha}=1.$$
$$tg\varphi=\frac{y}{x}=\frac{-\cos\alpha}{\sin\alpha}=-ctg\alpha=tg(\alpha+\frac{\pi}{2})=tg(\alpha+\frac{3\pi}{2}).$$
Кроме этого должны выполняться условия
$$\cos\varphi=\frac{x}{|z|}=\sin\alpha;\qquad \sin\varphi=\frac{y}{|z|}=\cos\alpha.$$
Отсюда находим
$$\varphi=\alpha+\frac{3\pi}{2}.$$
Таким образом, $$z=\sin\alpha-i\cos\alpha=e^{i\left(\alpha+\frac{3\pi}{2}\right)}.$$
Ответ: $e^{i\left(\alpha+\frac{3\pi}{2}\right)}.$
1.482 (а). Данные числа $z_1$ и $z_2$ представить в показательной форме и выполнить указанные действия над ними:
$z_1z_2;$ $\frac{z^2_1}{z_2},$ если $z_1=2\sqrt 3-2i,$ $z_2=3-3\sqrt 3i.$
Решение.
Запишем числа $z_1$ и $z_2$ в показательной форме:
$$|z_1|=\sqrt{x^2+y^2}=\sqrt{(2\sqrt 3)^2+(-2)^2}=\sqrt{16}=4.$$
$$tg\varphi=\frac{y}{x}=\frac{-2}{2\sqrt 3}=-\frac{1}{\sqrt 3}.$$
Поскольку число $z_1$ принадлежит четвертой четверти, то $\varphi_1=arctg{-\frac{1}{\sqrt 3}}=-\frac{\pi}{6}.$
Отсюда $$z_1=4e^{-i\frac{\pi}{6}}.$$
$$|z_2|=\sqrt{x^2+y^2}=\sqrt{3^2+(-3\sqrt 3)^2}=\sqrt{36}=6.$$
$$tg\varphi=\frac{y}{x}=\frac{-3\sqrt 3}{3}=-\sqrt 3.$$
Поскольку число $z_2$ принадлежит четвертой четверти, то $\varphi_2=arctg{\sqrt 3}=-\frac{\pi}{3}.$
Отсюда $$z_2=6e^{-i\frac{\pi}{3}}.$$
Далее находим $z_1z_2$ и $\frac{z^2_1}{z_2}:$
$$z_1z_2=4e^{-i\frac{\pi}{6}}6e^{-\frac{\pi}{3}}=24e^{i\left(\frac{-\pi}{6}-\frac{\pi}{3}\right)}=24e^{-i\frac{\pi}{2}}=$$
$$=24\left(\cos\left(-\frac{\pi}{2}\right)+i\sin\left(-\frac{\pi}{2}\right)\right)=24(0-1)=-24.$$
$$\frac{z^2_1}{z_2}=\frac{(4e^{-i\frac{\pi}{6}})^2}{6e^{-\frac{\pi}{3}}}=\frac{16}{6}e^{i\left(\frac{-2\pi}{6}+\frac{\pi}{3}\right)}=\frac{8}{3}e^{i\cdot 0}=\frac{8}{3}.$$
Ответ: $-24, \frac{8}{3}.$
Домашнее задание.
Следующие комплексные числа представить в тригонометрической форме и изобразить точками на комплексной плоскости:
1.436. $1-i\sqrt 3.$
Ответ: $2\left(\cos\frac{5\pi}{3}+i\sin\frac{5\pi}{3}\right).$
1.437. $-\frac{1}{2}+i\frac{\sqrt 3}{2}.$
Ответ: $\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}.$
1.440. $\sin\frac{\pi}{3}+i\cos\frac{\pi}{3}.$
Ответ: $\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}.$
Представить в показательной форме следующие комплексные числа:
1.476. $5-12i.$
Ответ: $13e^{-i arctg\left(-\frac{12}{5}\right)}.$
1.477. $-3-4i.$
Ответ: $5e^{i arctg\left(\frac{4}{3}+\pi\right)}.$
1.479.$\sin\alpha-i\cos\alpha.$
Ответ: $e^{i \left(\alpha+\frac{3\pi}{2}\right)}.$
1.480. $\sin\alpha+i(1-\cos\alpha).$
Ответ: $2\sin\frac{\pi}{2}e^{i \frac{\alpha}{2}}.$
1.482 (б). Данные числа $z_1$ и $z_2$ представить в показательной форме и выполнить указанные действия над ними:
$z^2_1\overline z_2;$ $\frac{\overline z_2}{z_1},$ если $z_1=-\sqrt 3+i\sqrt 2,$ $z_2=\sqrt 8-\sqrt 8.$
Ответ: $16e^{i\frac{7\pi}{4}}; 2e^{-i\frac{\pi}{2}}.$
Умножение комплексных чисел
Умножение комплексных чисел немного сложнее и заставляет задуматься:
А что значит перемножить два комплексных числа?
Самый простой способ понять мнимые числа — это интерпретировать умножение +1, -1 и √-1 (или, как Гаусс говорит прямые, обратные и боковые единицы) как вращение вокруг комплексной плоскости против часовой стрелки.
Умножение на +1
Умножение на +1 можно представить как вращение на 0˚ или 360˚ относительно начала координат, поскольку в любом случае вы вернетесь туда, откуда начали.
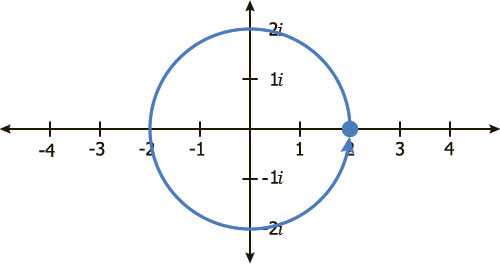Умножение на +1
Умножение на -1
Умножение на -1 можно интерпретировать как вращение на 180˚ против часовой стрелки вокруг начала координат. Например, если я начинаю с 2 и умножаю на -1, Я заканчиваю на -2, что составляет 180˚ против часовой стрелки. И если я умножу -2 на -1, я вернусь к положительному 2.
Умножение на i или √-1
А теперь самое интересное.
Умножая на i или √-1 мы поворачиваем плоскость на 90˚. Вот здесь мнимые числа и вступают в игру.
Обратите внимание, что если я умножу 2 на i, я получу 2i, что является поворотом на 90˚
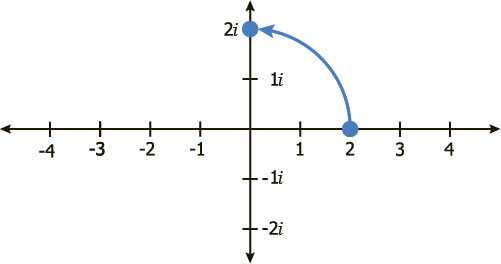
Если я умножу 2i на i, я получу 2i², что есть -2, так как i² фактически равно -1.
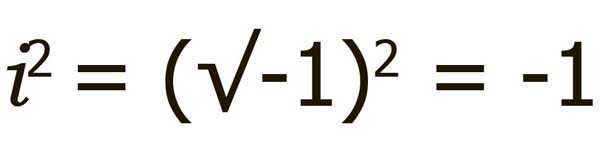
Итак, 2i ² = 2 (-1) или -2, еще 90° против часовой стрелки.
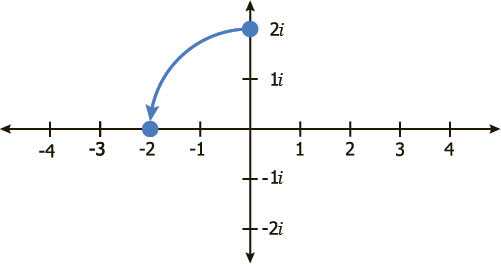Умножение на i или √-1
Точно так же, -2 умноженное на i равно -2i, еще четверть оборота.
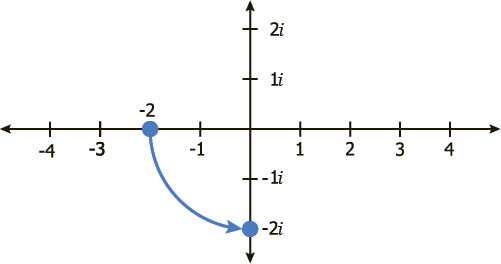
И наконец, -2i умноженное на i равно -2i² или -2(-1) что равно 2.
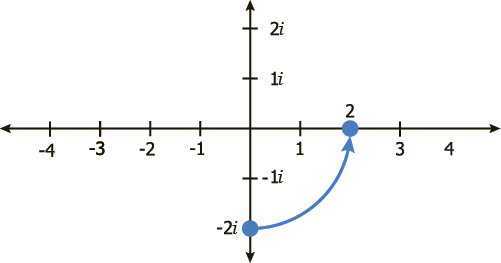
Мы могли бы продолжать умножать на i и вращаться вокруг плоскости, поэтому данный пример даёт нам шаблон, который повторяется каждые 4 цикла.
В общем, мы знаем, что
умножение на действительное число масштабирует значение, и мы чуть выше узнали,
что умножение на i поворачивает значение на 90° против часовой
стрелки, но как насчет этого?
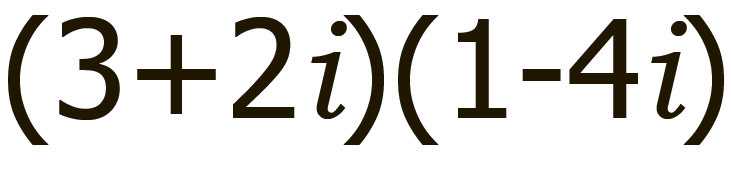
Чтобы лучше понять, давайте распишем.
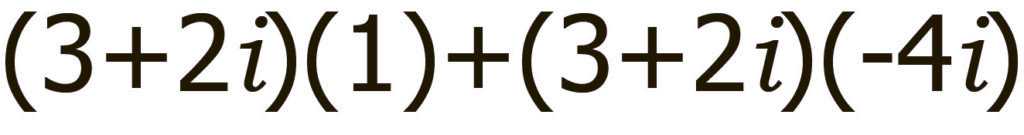
Хорошо, теперь мы можем выполнить сложение векторов. Первый вектор это (3+2i) (1), как мы рассмотрели выше (3+2i) поворачивается на 360˚, то есть остается на месте.
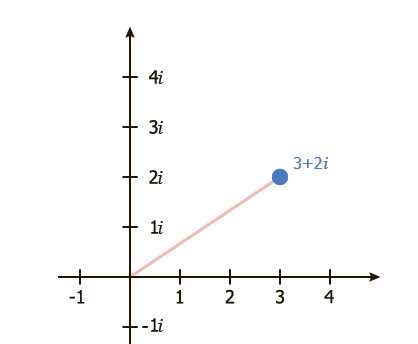
Теперь мы рассмотрим второй вектор (3 + 2i) (- 4i). Здесь происходит то же самое, что и с первым вектором: масштабирование и вращение. Вот как это происходит.
Сначала вектор (3 + 2i) умножаем на 4, и получаем (12 + 8i), этим мы растянули вектор (3 + 2i) в 4 раза.
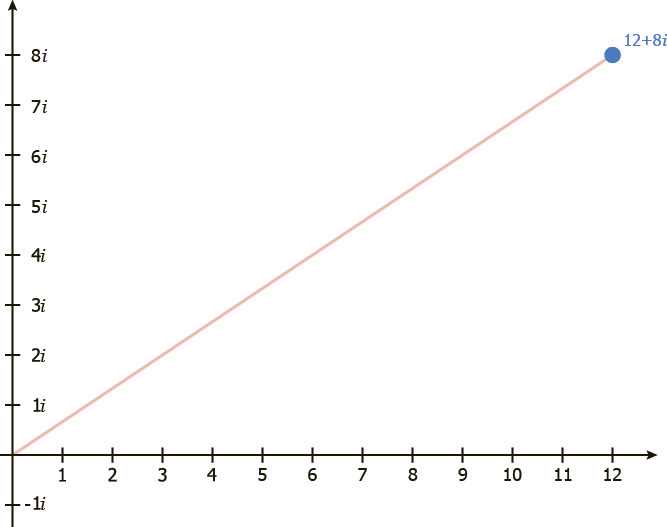
Нам также нужно умножить на -i. Напомним, умножая на -i мы поворачиваем на 90˚ по часовой стрелке.
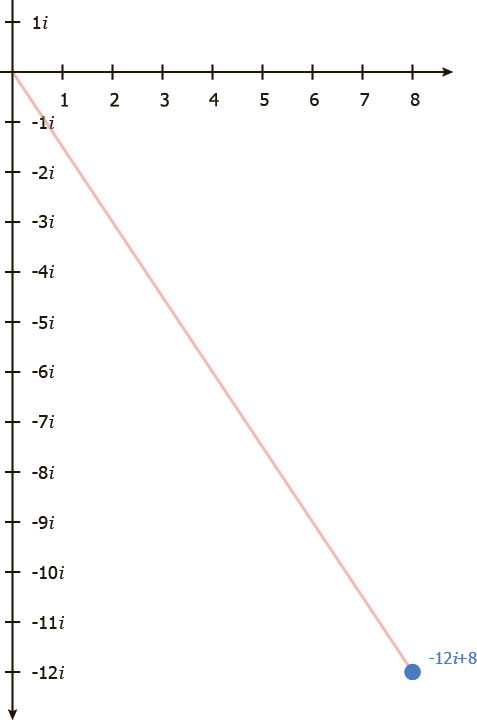
Теперь распишем полученное с помощью алгебры.
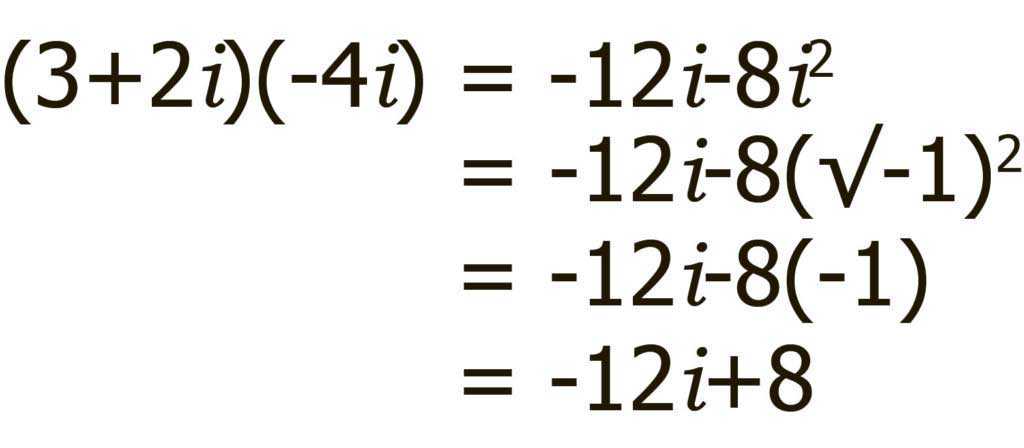
Последний шар — выполним сложение, перенеся параллельно начало одного вектора в конец другого.
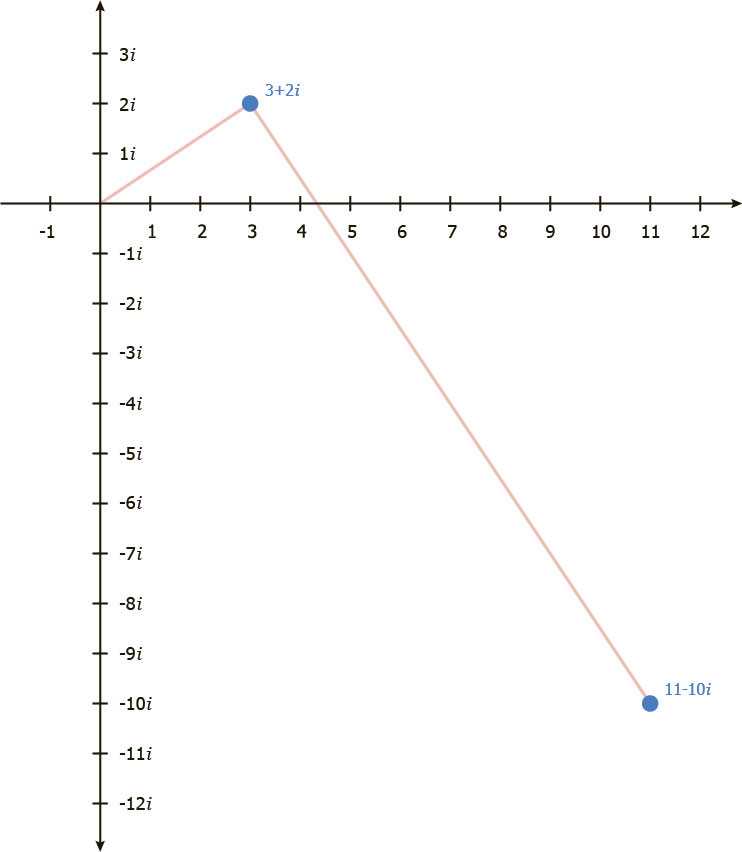
Наш окончательный ответ 11 — 10i.
Теперь у вас может возникнуть вопрос, почему мы не можем просто решить все с помощью алгебры?
И это так, мы можем решить это с помощью алгебры. На самом деле, это самый эффективный способ решения задачи (хотя ему не хватает понимания, которое вы получаете от построения графиков). Поэтому мы предложили вашему вниманию оба пути решения.
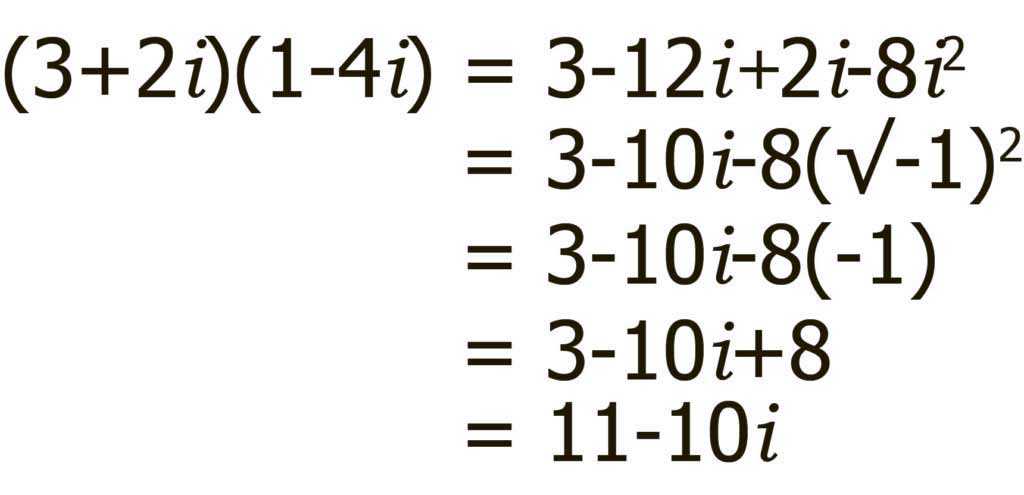
Понятие бесконечности на множестве комплексных чисел
Как и в реальной области, на множестве комплексных чисел вводится понятие бесконечности, бесконечно удаленной точки. Это можно сделать по аналогии с набором действительных чисел по геометрическим причинам.
Рассмотрим числовую прямую и круг, соприкасающиеся с линией в точке; будет указана точка, диаметрально противоположная точке.
Соединим разные точки оси точкой с прямыми линиями; точки пересечения прямых с кругом будут обозначены значком. Очевидно, каждая точка соответствует точке. Обратное верно для всех точек в круге, кроме точки. Но когда вы удаляетесь по прямой от точки (с увеличением расстояния, равным), ее изображение на окружности приближается к точке.
Для такой последовательности в анализе принято бесконечно большое имя (значение) последовательности. Ее предел обозначается и называется бесконечностью или бесконечно удаленной точкой. Следовательно, точку можно рассматривать как изображение бесконечно удаленной точки на окружности, а бесконечность — как «точку» оси, изображение которой на окружности является точкой .
По аналогии рассмотрим плоскость (плоскость) и касательную к ней сферу в начале координат, т.е в точке (рис. 1.2, а). Лучи, соединяющие точки с точкой, пересекают сферу в точках. В этом случае одна точка соответствует любой точке, и наоборот, одна точка соответствует любой точке. Очевидно, что чем дальше точка от начала координат (это длина радиус-вектора точки), тем ближе ее изображение к точке. Чтобы совпадение было полным, вводится «несоответствующий» элемент (символ), бесконечно удаленная точка, такая как точка на плоскости, изображение которой находится на этой точке .
Плоскость, объединенная элементом, называется расширенной комплексной плоскостью и обозначается значком .
Однозначное соответствие, построенное между точками сферы и целым, называется стереографической проекцией, а сфера — сферой Римана.
Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z.
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z.
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента, обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ, то мы можем найти вещественную и мнимую части по формулам
| (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y, то модуль этого числа, конечно же, определяется по формуле
| (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположениечисла z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественнаяполуось |
x > 0 , y = 0 |
φ = 2kπ | ||
|
x > 0 , y > 0 |
||||
| Положительнаямнимаяполуось |
x = 0 , y > 0 |
|||
|
x < 0 , y > 0 |
||||
| Отрицательнаявещественнаяполуось |
x < 0 , y = 0 |
π | φ = π + 2kπ | |
|
x < 0 , y < 0 |
||||
| Отрицательнаямнимаяполуось |
x = 0 , y < 0 |
|||
|
x > 0 , y < 0 |
| Расположениечисла z | Положительнаявещественнаяполуось |
| Знаки x и y |
x > 0 , y = 0 |
| Главноезначениеаргумента | |
| Аргумент | φ = 2kπ |
| Примеры |
| Расположениечисла z | |
| Знаки x и y |
x > 0 , y > 0 |
| Главноезначениеаргумента | |
| Аргумент | |
| Примеры |
| Расположениечисла z | Положительнаямнимаяполуось |
| Знаки x и y |
x = 0 , y > 0 |
| Главноезначениеаргумента | |
| Аргумент | |
| Примеры |
| Расположениечисла z | |
| Знаки x и y |
x < 0 , y > 0 |
| Главноезначениеаргумента | |
| Аргумент | |
| Примеры |
| Расположениечисла z | Отрицательнаявещественнаяполуось |
| Знаки x и y |
x < 0 , y = 0 |
| Главноезначениеаргумента | π |
| Аргумент | φ = π + 2kπ |
| Примеры |
| Расположениечисла z | |
| Знаки x и y |
x < 0 , y < 0 |
| Главноезначениеаргумента | |
| Аргумент | |
| Примеры |
| Расположениечисла z | Отрицательнаямнимаяполуось |
| Знаки x и y |
x = 0 , y < 0 |
| Главноезначениеаргумента | |
| Аргумент | |
| Примеры |
| Расположениечисла z | |
| Знаки x и y |
x < 0 , y < 0 |
| Главноезначениеаргумента | |
| Аргумент | |
| Примеры |
|
Расположение числа z : Положительная вещественная полуось Знаки x и y : x > 0 , y = 0 Главное значение аргумента: Аргумент: φ = 2kπ Примеры: |
|
Расположение числа z : Знаки x и y : x > 0 , y > 0 Главное значение аргумента: Аргумент: Примеры: |
|
Расположение числа z : Положительная мнимая полуось Знаки x и y : x = 0 , y > 0 Главное значение аргумента: Аргумент: Примеры: |
|
Расположение числа z : Знаки x и y : x < 0 , y > 0 Главное значение аргумента: Аргумент: Примеры: |
|
Расположение числа z : Отрицательная вещественная полуось Знаки x и y : x < 0 , y = 0 Главное значение аргумента: π Аргумент: φ = π + 2kπ Примеры: |
|
Расположение числа z : Знаки x и y : x < 0 , y < 0 Главное значение аргумента: Аргумент: Примеры: |
|
Расположение числа z : Отрицательная мнимая полуось Знаки x и y : x = 0 , y < 0 Главное значение аргумента: Аргумент: Примеры: |
|
Расположение числа z : Знаки x и y : x < 0 , y < 0 Главное значение аргумента: Аргумент: Примеры: |
