Геометрическая интерпретация комплексного числа

Математика. Комплексные числа. Введение

Начнём с самого важного — это название темы. Расставим правильно ударение, нужно говорить «комплЕксные числа», это очень важно

Как говорил один препод в универе: «обед у вас кОмплексный, а числа комплЕксные!».

Если таких мелочей не знать, то математичка в ваших знаниях сильно усомнится.

Комплексные числа являются одной из самой главных тем в теории чисел, считая что вещественные числа являются частным случаем.

Они подразумевают под собой, что число состоит из действительной и мнимой частей. Записывается в виде:

Где а-действительная часть, а b-мнимая (нереальная, несуществующая).

Не сложно догадаться почему вещественные числа являются частным случаем, ведь их можно записать в виде:

Имея в виду что мнимая часть будет равняться нулю и останется только действительная.

Забыли затронуть что такое «i» у нас в записи. Это мнимая единица и равняется она «квадратному корню из минус единицы».

Любое число умноженное на «i», будет являться мнимым.

Как и вещественные числа, комплексные тоже можно изобразить, только не на обычной плоскости, а на «комплексной». Где ось «y» будет называться «мнимая — Im(z) — (Imaginary)», а ось «x» «действительная — Re(z) — (Real)».

Комплексное число на плоскости изображается в виде радиус вектора.

Разберёмся с обозначениями на графике, там присутствует «|z|», это модуль, он обозначает длину радиус вектора. Другое обозначение это «φ», с её помощью вводится понятие угла отклонения радиус вектора от действительной оси. Длина вектора и угол вычисляются по формулам:

Формула вычисления угла может изменяться в зависимости от четверти в которой находится комплексное число.

Все знают что с числами можно выполнять различные операции, такие как: сложение, вычитание, умножение, деление. делается всё это немного сложней, потому что у нас есть помимо вещественной части ещё и мнимая. Разберёмся со сложением и вычитанием на данный момент. Посмотрим как это делается на примере, таким образом проще понять.

Ничего затруднительного нет, действительную часть складываем с действительной, мнимую с мнимой. Очевидно же.

Вот с умножением и делением придётся «попотеть», вспомнить формулы сокращённого умножения в некоторых случаях. Разберём тоже на примерах.

Метод умножения: фонтанчиком. Первая циферка из первой скобки умножается на циферки второй скобки с соответствующими знаками, после вто… Так, вы это знаете, не стоит продолжать, всё ясно.

Приступим к делению, цифры те же.

Изначально наша задача записать всё это действие в виде «отдельно действительная часть, отдельно мнимая». Для этого потребовалось избавиться от мнимой части в знаменателе, мы домножили числитель и знаменатель на число «комплексно сопряжённое» знаменателю. После этого действия идут алгебраические вычисления, которые в итоге приводят нас к ответу.

Поясним за комплексно сопряжённое. Это обычное комплексное число, только записанное со знаком минус.

Обозначается оно с чёрточкой сверху.За сегодня ознакомились с самыми элементарными понятиями в теории комплексных числе. В следующий раз разберёмся с видами записи комплексных чисел. Оставляйте в х что необходимо разобрать в другой раз

Спасибо за внимание

Примеры решения задач

Задача 1

Задача

Необходимо найти частное пары комплексных чисел:

(z_1 = 3+i) и (z_2 = 2-3i)

Решение:

Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу.

(frac{z_1}{z_2} = frac{3+i}{2-3i} =)

Сопряженное комплексное число к знаменателю:

(overline{z_2} = 2+3i)

Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе:

(= frac{(3+i)(2+3i)}{(2-3i)(2+3i)} = frac{6 + 9i + 2i — 3}{4 + 6i — 6i + 9} =)

Далее следует привести подобные слагаемые и записать вывод с ответом:

(= frac{3 + 11i}{13} = frac{3}{13} + frac{11}{13}i)

Ответ: (frac{z_1}{z_2} = frac{3}{13} + frac{11}{13}i)

Задача 2

Задача

Требуется выполнить деление комплексных чисел:

(z_1 = 2(cos frac{pi}{3} + isin frac{pi}{6}))

(z_2 = 4(cos frac{pi}{6} + isin frac{pi}{6}))

Решение:

Комплексные числа в условии задачи записаны в тригонометрической форме. По этой причине необходимо использовать в расчетах соответствующую формулу. В данном случае следует определить деление модулей и разность аргументов:

Деление модулей:

(frac{r_1}{r_2} = frac{2}{4} = frac{1}{2})

Разность аргументов:

(varphi_1 — varphi_2 = frac{pi}{3} — frac{pi}{6} = frac{pi}{6})

Следующим шагом является деление чисел:

(frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Ответ: (frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Задача 3

Задача

Нужно найти частное комплексных чисел:

(z_1 = 3e^{frac{pi}{2}i})

(z_2 = 4e^{frac{pi}{4}i})

Решение:  Согласно формуле деления в показательной форме определяем разность аргументов и частное модулей:

(frac{r_1}{r_2} = frac{3}{4})

(varphi_1 — varphi_2 = frac{pi}{2} — frac{pi}{4} = frac{pi}{4})

При подстановке в формулу полученных значений уравнение будет преобразовано следующим образом:

(frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Ответ: (frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Задача 4

Задача

Определить частное:

(frac{-2+i}{1-i})

Решение:

В первую очередь следует домножить числитель и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю:

(1-i)

Данным числом является:

(1+i)

Таким образом:

(frac{-2+i}{1-i}=frac{-2+i}{1-i} cdot frac{1+i}{1+i}=frac{(-2+i)(1+i)}{(1-i)(1+i)})

Затем следует перемножить комплексные числа, как алгебраические двучлены, с учетом:

(i^{2}=-1)

(frac{-2+i}{1-i}=frac{(-2+i)(1+i)}{(1-i)(1+i)}=frac{-2-2 i+i-1}{1^{2}-i^{2}}=)

(=frac{-3-i}{1-(-1)}=frac{-3-i}{2}=-frac{3}{2}-frac{i}{2})

Ответ:( frac{-2+i}{1-i}=-frac{3}{2}-frac{i}{2})

Задача 5

Задача

Необходимо найти частное:

(frac{z_{1}}{z_{2}})

При условии, что:

(z_{1}=2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right))

(z_{2}=cos frac{pi}{4}+i sin frac{pi}{4})

Решение:

Искомое частное:

(frac{z_{1}}{z_{2}}=frac{2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right)}{cos frac{pi}{4}+i sin frac{pi}{4}}=)

(=frac{2}{1} cdotleft=)

(=2 cdotleft=2 cdot(0+i)=2 i)

Ответ: (frac{z_{1}}{z_{2}}=2 cdotleft(cos frac{pi}{2}+i sin frac{pi}{2}right)=2 i)

Задача 6

Задача

Необходимо разделить два комплексных числа:

(z_{1}=-1+3i)

(z_{2}=1+2i)

Решение:

С помощью соответствующей формулы можно записать уравнение:

(z_{1} div z_{2} = frac{-1+3i}{1+2i} = frac{(-1+3i)(1-2i)}{(1+2i)(1-2i)} = frac{-1 cdot 1 + 3 cdot 2}{1^{2}+2^{2}} + i frac{3 cdot 1 + (-1) cdot (-2)}{1^{2}+2^{2}} =)

(= frac{5}{5} + i frac{5}{5}=1+i)

Ответ: ( z_{1} div z_{2} = 1+i)

Задача 7

Задача

Необходимо вычислить частное комплексных чисел:

(z_{1}=sqrt{2} left( cos frac{pi}{2} + i sin frac{pi}{2} right))

(z_{2}=sqrt{2} left( cos frac{pi}{4} + i sin frac{pi}{4} right))

Решение:

Используя соответствующую формулу, запишем:

(z_{1} div z_{2} = frac{r_{1}}{r_{2}} (cos ( varphi _{1} — varphi _{2}) + i sin ( varphi _{1} — varphi _{2})) = frac{sqrt{2}}{sqrt{2}} left( cos left( frac{pi}{2}-frac{pi}{4} right) + i sin left( frac{pi}{2}-frac{pi}{4} right) right) =)

(= 1 cdot left( cos frac{pi}{4} + i sin frac{pi}{4} right) = cos frac{pi}{4} + i sin frac{pi}{4})

Ответ:( z_{1} div z_{2} = cos frac{pi}{4} + i sin frac{pi}{4})

Задача 8

Геометрическая интерпретация комплексных чисел

В 1799 году датчанин Каспар Вессель определил комплексное число как упорядоченную пару вещественных чисел $(x,y)$. Известно, что на декартовой
плоскости упорядоченной паре соответствует точка. Выберем на плоскости прямоугольную систему координат и установим взаимно однозначное
соответствие между комплексными числами и точками плоскости, при котором комплексному числу $z=x+\mathbf i y$ отвечает точка $M$ с координатами
$x,y$. Точку $M$ мы рассматриваем как изображение комплексного числа $z=x+\mathbf i y$.

При этом множество всех вещественных чисел изображается осью абсцисс, называемой поэтому вещественной осью, множество всех чисто мнимых
чисел лежит на оси ординат, называемой мнимой осью. Плоскость $XOY$, точки которой изображают комплексные числа, называется комплексной плоскостью (иногда гауссовой плоскостью) или просто плоскостью $z$. Термины «комплексное число $z$» и «точка $z$ на комплексной плоскости» употребляются как синонимы.

Комплексное число $z=x+\mathbf i y$ может также изображаться вектором с проекциями $x$ и $y$ на координатные оси, который, таким образом, равен
радиус-вектору точки $z$. Иногда термины «комплексное число» и «вектор» употребляют также как синонимы.

Именно поэтому, глядя на координатную плоскость,
естественно сделать вывод, что комплексные числа невозможно сравнивать, т.е. нельзя говорить, что какое-то комплексное число больше или меньше другого.

Комплексное число равное сумме или разности двух комплексных чисел $z_1\pm z_2$ соответствует вектору на комплексной плоскости, который получится при сложении/вычитании векторов, соответствующих числам $z_1$ и $z_2$. Для произведения $z_1\cdot z_2$ этой аналогии уже не будет.

Напомним, что в полярных координатах точка $M$ имеет координаты $(r,\varphi)$. В нашем случае полярные координаты имеют следующий смысл:

полярный радиус (или длина вектора) называется модулем комплексного числа $z=x+\mathbf i y$ и вычисляется по формуле

$$
r=|z|=\sqrt{x^2+y^2}=\sqrt{z\bar z},
$$

полярный угол $\varphi$ (угол между положительным направлением оси $OX$ и отрезком $OM$) называется аргументом комплексного числа $z$ и обозначается $\varphi=\mbox{Arg }z$.

Модуль и аргумент — две важнейшие характеристики комплексного числа.

Условия равенства двух комплексных чисел $z_1$ и $z_2$ — равенство их модулей: $|z_1|=|z_2|$ и аргументов: $\mbox{Arg }z_1=\mbox{Arg }z_2$.

Особый разговор об аргументе

Угол $\varphi=\mbox{Arg }z$ — аргумент комплексного числа $z=x+\mathbf i y$. Этот угол, изменяясь от положительного направления оси $OX$ против часовой
стрелки, увеличивается до $2\pi$, а далее его величины повторяются. Поэтому аргумент комплексного числа бесконечнозначен, так как все его
значения отличаются друг от друга на слагаемые, кратные $2\pi$.

Аргумент $\varphi$ определяется из формул
\begin{equation}
\left\{\begin{array}{l}
x=r\cos\varphi, \\
y=r\sin\varphi
\end{array}\right.
\end{equation}
с точностью до слагаемого $2\pi k$: $$
\mbox{Arg }z=\mbox{arg }z+2\pi k,\quad k=0,\pm1,\pm2,\ldots\ .
$$

Из множества значений аргумента особо выделяется главное значение $\mbox{arg }z$, удовлетворяющее неравенству $-\pi<\mbox{arg } z\le\pi$. При этом полезны
формулы
\begin{equation}
\arg z=\left\{\begin{array}{ll}
\mbox{arctg }\dfrac{y}{x},&x>0, \\
\mbox{arctg }\dfrac{y}{x}+\pi,&x<0,\ y\ge0, \\
\mbox{arctg }\dfrac{y}{x}-\pi,&x<0,\ y<0.\\
\end{array}\right.
\end{equation}

Для комплексного числа $z=0+\mathbf i 0$ понятие аргумента не
имеет смысла.

Условие сопряжения двух чисел $z$ и $\bar{z}$:
$$|z|=|\bar{z}|,\quad \arg z=-\arg \bar{z}.$$

Некоторые свойства модуля:
$$
\left| z_1 + z_2 \right| \le \left| z_1\right| + \left| z_2\right| \ ,
$$
$$
\left| z_1 + z_2 \right| \ge \big| | z_1 | — | z_2 | \big| \ ,
$$
$$
\left| z_1 — z_2 \right| \ge \big| | z_1 | — | z_2 | \big|.
$$

Комплекснозначные функции действительного переменного.

Если каждому значению \(t\in \) поставлено в соответствие комплексное число \(z=z(t)\), то говорят, что на отрезке \(\) задана комплекснозначная функция действительного переменного.

Пусть \(\operatorname{Re}z(t) = x(t),\ \operatorname{Im}z(t) = y(t)\), тогда \(z(t) = x(t)+iy(t)\). Функцию \(z(t)\) можно рассматривать как вектор-функцию \(z(t)=(x(t),y(t))\). Определения предела, непрерывности, производной для комплекснозначной функции аналогичны соответствующим определениям для вектор-функции.

Например, производная функции \(z(t) = x(t) + iy(t)\) определяется формулой
$$
z'(t) = x'(t) + iy'(t).\label{ref25}
$$
Следовательно, производная \(z'(t)\) существует, если существуют производные \(x'(t)\) и \(y'(t)\).

Применяя формулу \eqref{ref25} к функции \(e^{it}=\cos t+i\sin t\), получаем \((e^{it})’=-\sin t+i\cos t=i^2\sin t + i\cos t = i(\cos t + i\sin t)\), то есть
$$
(e^{it})’=i e^{it}.\label{ref26}
$$

Таким образом, формула для производной комплексной функции \(e^{it}\) имеет такой же вид, как и для функции \(e^{\alpha t}\), где \(\alpha\in\mathbb{R}\).

Определим теперь показательную функцию \(\displaystyle e^{(\alpha+i\beta)t}\), где \(\alpha,\beta\) — заданные действительные числа, \(t\) — действительное переменное. Функция \(f(t) = e^t\), где \(t\in\mathbb{R}\), удовлетворяет условию
$$
f(t_1)f(t_2) = f(t_1+t_2).\label{ref27}
$$

Аналогично функция \(e^{i\beta t}\), где \(\beta\in\mathbb{R}\), обладает свойством \eqref{ref27} в силу первого из равенств \eqref{ref18}.

Поэтому функцию    \(e^{(\alpha+i\beta)t}\) естественно определить так, чтобы для нее выполнялось условие \eqref{ref27}, то есть
$$
e^{(\alpha+i\beta)t}=e^{\alpha t}e^{i\beta t}.\nonumber
$$

Используя формулу \eqref{ref15}, отсюда находим
$$
e^{(\alpha+i\beta)t} = e^{\alpha t} (\cos \beta t+i\sin\beta t).\label{ref28}
$$
Применяя к функции \(e^{\lambda t}\), где \(\lambda=\alpha+i\beta\), правило дифференцирования \eqref{ref25}, легко показать, что
$$
(e^{\lambda t})=\lambda e^{\lambda t},\quad \lambda=\alpha+i\beta.\label{ref29}
$$

По аналогии с производной неопределенный интеграл от комплекснозначной функции \(z(t)=x(t)+iy(t)\) определяется формулой
$$
\int z(t) dt = \int x(t) dt + i\int y(t) dt.\nonumber
$$

Если комплексная функция \(\omega(t) = \xi(t) + i\eta (t)\) такова, что \(\omega'(t)=z(t)\), то
$$
\int z(t)=\int \omega'(t)dt=\int \xi'(t)dt+i\int \eta'(t)dt = \xi(t) + C_1 + i\eta(t)+iC_2.\nonumber
$$
Следовательно,
$$
\int z(t) dt = \omega(t) + C,\quad C = C_1+iC_2.\nonumber
$$
Применяя это утверждение к функции \(e^{(\alpha+i\beta)t}\) и используя формулу \eqref{ref29}, получаем
$$
\int e^{(\alpha+i\beta)t}=\displaystyle \frac{e^{(\alpha+i\beta)t}}{\alpha+i\beta}+C_1+iC_2.\label{ref30}
$$

Выделяя в равенстве \eqref{ref30} действительные и мнимые части, находим
$$
\int e^{\alpha t}\cos\beta t dt + i\int e^{\alpha t}\sin\beta t dt = \frac{\alpha-i\beta}{\alpha^2+\beta^2}e^{\alpha t}(\cos\beta t+i\sin\beta t)+C_1+C_2,\nonumber
$$
откуда получаем
$$
\int e^{\alpha t}\cos\beta t dt=\frac{e^{\alpha t}}{\alpha^2+\beta^2}(\alpha\cos\beta t+\beta\sin\beta t)+C_1,\label{ref31}
$$
$$
\int e^{\alpha t}\sin\beta t dt=\frac{e^{\alpha t}}{\alpha^2+\beta^2}(\alpha\sin\beta t-\beta\cos\beta t)+C_2,\label{ref32}
$$

Заметим, что формула \eqref{ref31} была получена с помощью в .

Алгебраическая форма комплексного числа

Комплексным числом $z$
называется выражение вида $z=x+\mathbf i y$, где $x$ и $y$ — вещественные числа, $\mathbf i$ — символ, называемый мнимой единицей, $\mathbf i^2=-1$.

Выражение $z=x+\mathbf i y$ называют алгебраической формой комплексного числа, $x$ называется вещественной частью числа $z$ и обозначается $\mathfrak{Re}(z)$ или $\mathfrak{Re}\,z$ ($\mathfrak{Re}$ — начальные буквы латинского слова realis — вещественный), $y$ называется мнимой частью $z$ и обозначается $\mathfrak{Im}(z)$ или $\mathfrak{Im}\,z$ ($\mathfrak{Im}$ — начальные буквы латинского слова imaginarius — мнимый).

Например, $\mathfrak{Re}(1-2\mathbf i)=1$, $\mathfrak{Im}(1-2\mathbf i)=-2$. Если $y=\mathfrak{Im}\,z=0$, то $z=x$ является вещественным числом, а если $\mathfrak{Re}\,z=x=0$ и $y\ne0$, то $z=\mathbf i y$ является чисто мнимым числом.

Два комплексных числа $z_1$ и $z_2$ равны тогда и только
тогда, когда $\mathfrak{Re} z_1=\mathfrak{Re} z_2$ и $\mathfrak{Im} z_1=\mathfrak{Im} z_2$ одновременно.

Сопряженным с комплексным числом $z=x+\mathbf i y$ называют
комплексное число вида $x-\mathbf i y$, его обозначают $\overline{z}=x-\mathbf i y$.

Свойства сопряжения
\begin{equation*}
\overline{\bar{z}}=z, \quad \overline{z_1z_2}=\bar{z}_1\bar{z}_2, \quad \overline{\frac{z_1}{z_2}}=\frac{\bar{z}_1}{\bar{z}_2}.
\end{equation*}

Комплексное число $-x-\mathbf i y=-z$ называется противоположным
комплексному числу $z=x+\mathbf i y$.
Их сумма равна так называемому нулевому комплексному числу $x+\mathbf i y+(-x-\mathbf i y)=0+\mathbf i 0$.

Для комплексных чисел $\alpha,\beta,\gamma$ выполняются следующие законы арифметики.

а) Коммутативный (переместительный) закон:

для сложения
$$ \alpha+\beta=\beta+\alpha;$$
для умножения
$$ \alpha\beta=\beta\alpha.$$

б) Ассоциативный (сочетательный) закон:

для сложения
$$ \alpha+\beta+\gamma=\alpha+(\beta+\gamma)=(\alpha+\beta)+\gamma=
\beta+(\alpha+\gamma);$$
для умножения
$$ \alpha\beta\gamma=\alpha(\beta\gamma)=(\alpha\beta)\gamma=\beta
(\alpha\gamma). $$

в) Дистрибутивный (распределительный) закон:
$$
\alpha(\beta+\gamma)=\alpha\beta+\alpha\gamma.
$$

Действия над комплексными числами, записанными в алгебраической форме $\alpha=a+b\mathbf i $, $\beta=c+d\mathbf i $, выражаются следующими формулами:

для сложения и вычитания
$$
\alpha\pm\beta=(a+b\mathbf i )\pm(c+d\mathbf i )=(a\pm c)+(b\pm d)\mathbf i ,
$$

для умножения (учитывая, что $\mathbf i ^2=-1$)
$$
\alpha\beta=(a+b\mathbf i )(c+d\mathbf i )=ac+ad\mathbf i +bc\mathbf i +bd\mathbf i ^2=(ac-bd)+(ad+bc)\mathbf i ,
$$
заметим также, что $\alpha\bar\alpha=a^2+b^2\in R$, $i^3=-i$, $i^4=1$, и, наконец,

для деления
$$
\frac\alpha\beta=\frac{\alpha\bar\beta}{\beta\bar\beta}=
\frac{(a+b\mathbf i )(c-d\mathbf i )}{c^2+d^2}=\frac{ac+bc\mathbf i -ad\mathbf i -bd\mathbf i ^2}{c^2+d^2}=
$$
$$
=\frac{ac+bd+(bc-ad)\mathbf i }{c^2+d^2}=\frac{ac+bd}{c^2+d^2}+
\frac{bc-ad}{c^2+d^2}\,\mathbf i .
$$

Множество всех комплексных чисел с арифметическими операциями образует поле комплексных чисел. Его обычно
обозначают символом $\mathbb C_{} $ (от лат. complex — тесно связанный).

Множество вещественных чисел $\mathbb R_{} $ является подмножеством множества комплексных чисел $\mathbb{C}$, то есть $\mathbb{R}\subset \mathbb{C}$.

П

Пример.
\begin{equation*}
\begin{split}
&z_1=-3+4\mathbf i , \,\, z_2=5-\mathbf i .\\
&z_1+z_2=2+3\mathbf i ,\,\, z_1-z_2=-8+5\mathbf i , \,\, z_1z_2=-11+23\mathbf i ,\\
&\overline{z}_2=5+\mathbf i , \,\, z_2\overline{z_2} =26, \,\, \frac{z_1}{z_2}=-\frac{19}{26}+\frac{17}{26}\mathbf i .
\end{split}
\end{equation*}

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность:
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Комплексные числа — простое объяснение

Для того, чтобы разобраться с комплексными числами, следует для начала рассмотреть множество действительных чисел. К этому множеству относятся целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.

Рассмотрим две точки на прямой А = 1 и Б = 2. Сложим эти две точки. Их сумма эта третья точка В = 1+2 = 3.

Точки также можно перемножать. Посмотрим, например, как действует умножения на минус 2. Данное действие преобразует точку 1 в минус 2.  Если мы снова умножим на минус 2, то нужно будет повторить аналогичное передвижение на прямой, поменять стороны относительно начала координат и удвоить расстояние до него. В результате получим 4.

Умножение на минус 1 устроено просто. Каждая точка переходит в симметричную ей относительно начала координат. Другими словами нужно сделать пол оборота (повернуть на 180°). Повторение умножения на минус 1 приводит в исходное положение. Умножение на минус 1 переводит 1 в минус 1. Если еще раз умножить на минус 1, мы вернемся обратно в 1.

На данном этапе можно выделить правило, что если умножить число на себя, результат всегда будет положительным. Другими словами минус 1 не имеет квадратного корня. Но только не в случае с комплексными числами.

В начале 19 века Робер Арган высказал следующую идею. Поскольку умножить на минус 1 означает повернуть на 180°, то квадратный корень из минус 1 означает повернуть на половину (90°). Если повернуть дважды на четверть оборота, вы сделаете пол оборота. Квадрат четверти оборота — это пол оборота (минус 1). То есть квадратный корень из минус 1 отвечает точке, в которую минус 1 переходит при повороте на 90°. Поскольку такое построение, выходящее за пределы горизонтальной прямой, выглядит странным, говорят, что такая точка, являющаяся квадратным корнем из минус 1 — это мнимое число. И в математике оно обозначается — i.

Расширенная комплексная плоскость. Сфера Римана

Из геометрии известно, что любой упорядоченной паре вещественных чисел соответствует точка $z$ на плоскости комплексного переменного. Определим
на комплексной плоскости бесконечно удаленную точку. Так условно будем называть «мысленную точку» $(x,y)$, координаты которой (обе сразу
или одна из них) — величины неограниченные, т.е. комплексные числа имеют формальный вид $z=x+i\infty$, $z=\infty+iy$ либо $z=\infty+i\infty$.
Тогда пишут $z=\infty$ (несобственное комплексное число), считая ее единственной бесконечно удаленной точкой.

Для несобственного комплексного числа понятия вещественной и мнимой части, а также понятие аргумента не вводятся; точнее говоря, объявляются
лишенными смысла (напомним, что понятие аргумента не имеет смысла и для числа 0). Что касается модуля числа $z=\infty$, то для него используется
символ $|\infty|=+\infty$.

Договорились, что имеют смысл следующие операции, в которых участвуют $z=\infty$ и собственное комплексное число $a$: $$
\frac{a}\infty=0,\quad\frac\infty{a}=\infty,\quad\frac{a}0=\infty.
$$ Такие операции, как $$
\infty\pm\infty,\quad 0\cdot\infty,\quad \dfrac00,\quad
\dfrac\infty\infty
$$ объявляются лишенными смысла.

Совокупность точек комплексной плоскости и бесконечно удаленной точки называется расширенной плоскостью комплексного переменного.

Наглядное представление о расширенной комплексной плоскости дает следующая интерпретация Римана (1826-1866).

Чтобы получить геометрическое изображение числа $\infty$, прибегают к представлению комплексных чисел точками сферы. Построим сферу (называемую сферой Римана) радиуса $r$, касающуюся плоскости $z$ в точке $z=0$ и отметим точку $N$ сферы, диаметрально противоположную началу
координат $O$.

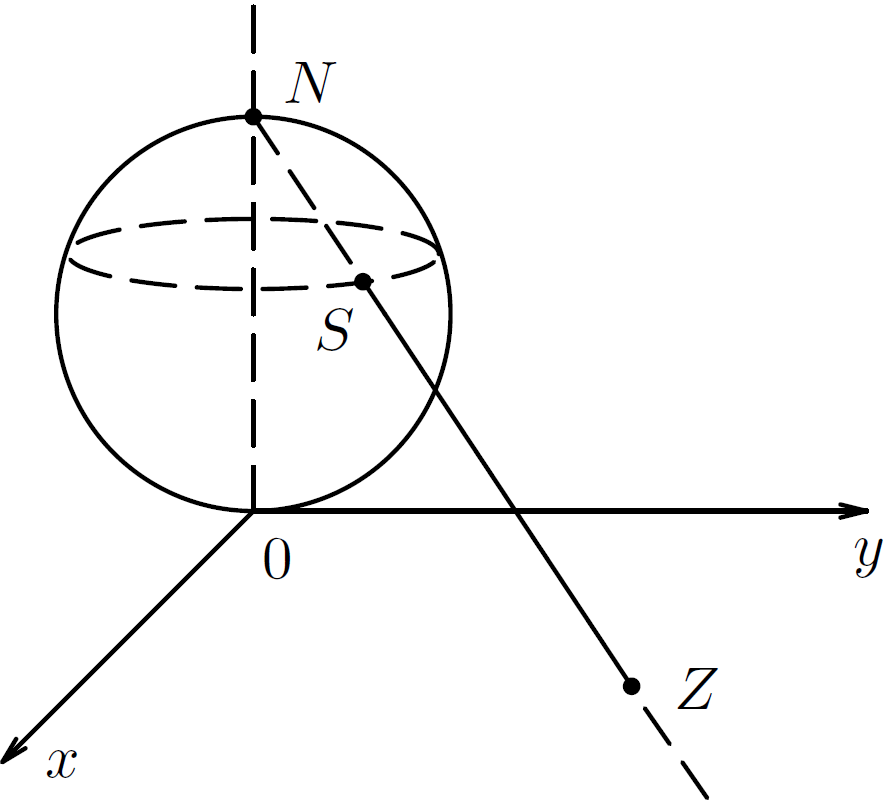
Из точки $N(0,0,2r)$ сферы проведем проведем луч в любую точку $Z(x,y,0)$ плоскости $(x,y)$ и отметим точку $S$ пересечения данного луча и
сферы. Эта точка $S(\xi,\eta,\zeta)$ является новым геометрическим представлением комплексного числа $z$. В результате таких
построений лучей между точками плоскости $(x,y)$ и точками сферы устанавливается взаимно однозначное соответствие, называемое стереографической
проекцией, имеющей применение в картографии.

Точкам меридиана $NSO$ на сфере соответствуют точки луча $OZ$ на плоскости $(x,y)$, различным параллелям — круги на плоскости $(x,y)$.
Исключение составляет точка $N$. Северному полюсу $N$ сферы не соответствует пока никакое комплексное число. Однако точкам сферы, достаточно
близким к $N$, соответствуют точки $z$ плоскости, сколь угодно далеко отстоящие от начала координат, т.е. точка $z$ сколь угодно большого
модуля. Будем считать, что точке $N$ соответствует единственная точка $z=\infty$.

Покажем, что точка $z=\infty+\mathbf i \infty$ (или $z=x+\mathbf i \infty$, или $z=\infty+\mathbf i y$) будет при таком преобразовании переходить в точку $N(0,0,2r)$ и
наоборот. Координаты точек на такой сфере $(\xi,\eta,\zeta)$ связаны формулой
\begin{equation}\label{eq g1 p7 1}
\xi^2+\eta^2+(\zeta-r)^2=r^2\quad\hbox{или}\quad \xi^2+\eta^2=\zeta
(2r-\zeta).
\end{equation}

Из коллинеарности $NZ$ и $NS$ можно получить представление луча $NSZ$
$$
\frac{\xi-0}{x-0}=\frac{\eta-0}{y-0}=\frac{\zeta-2r}{0-2r}.
$$
Отсюда можно получить координаты точек плоскости через координаты точек сферы:
\begin{equation}\label{eq g1 p7 2}
x=\frac{2r\xi}{2r-\zeta},\quad y=\frac{2r\eta}{2r-\zeta}.
\end{equation}

Составим
$$ x^2+y^2=\frac{4r^2(\xi^2+\eta^2)}{(2r-\zeta)^2}, $$
$$ x^2+y^2 = \frac{4r^2\zeta}{2r-\zeta}. $$
Тогда
можно выразить координату
$$
\zeta=\frac{2r(x^2+y^2)}{x^2+y^2+4r^2},
$$
и другие координаты
$$
\xi=\frac{4r^2x}{x^2+y^2+4r^2},\quad\eta=\frac{4r^2y}{x^2+y^2+4r^2}.
$$

Устремим $x\to\infty$, $y\to\infty$ (по отдельности или вместе), тогда $\xi\to0$, $\eta\to0$, $\zeta\to2r$, а это и есть точка $N$.

Некоторые сведения о комплексных числах подробнее изложены в курсе Высшей алгебры А.Ю. Утешева ( здесь).

Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным. Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

• когда положительное число находится внутри модуля, достаточно просто избавиться от него,
• если есть выражение, нужно его упростить, прежде чем найти абсолютное значение,
• если равенство содержит две переменные, нужно решать его с помощью системы уравнений и за основу брать методы решения выражений с абсолютными величинами.

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.