Основные тригонометрические формулы и тождества sin, cos, tg, ctg

Как вспомнить забытую тригонометрическую формулу? Вывести!

На олимпиаде по математике с большой степенью вероятности, а на внешнем независимом тестировании – уж наверняка встретятся задания по тригонометрии.

Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами.

На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.

А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела.

Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот.

Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.

Будем опираться на следующие формулы:

1. Основное тригонометрическое тождество: sin2a+cos2a = 1
2. Определение тангенса:
3. Определение котангенса:
4. Формула синуса суммы: sin(a+b) = sinacosb+cosasinb
5. Формула косинуса суммы: cos(a+b) = cosacosb-sinasinb

Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:

1. Синус разности: sin(a-b) = sinacos(-b)+cosasin(-b) = sinacosb-cosasinb
2. Косинус разности: cos(a-b) = cosacos(-b)-sinasin(-b) = cosacosb+sinasinb

Поставляя в эти же формулы a = b, получаем формулы синуса и косинуса двойных углов:

1. Синус двойного угла: sin2a = sin(a+a) = sinacosa+cosasina = 2sinacosa
2. Косинус двойного угла: cos2a = cos(a+a) = cosacosa-sinasina = cos2a-sin2a

Аналогично получаются и формулы других кратных углов:

1. Синус тройного угла: sin3a = sin(2a+a) = sin2acosa+cos2asina = (2sinacosa)cosa+(cos2a-sin2a)sina = 2sinacos2a+sinacos2a-sin3a = 3sinacos2a-sin3a = 3sina(1-sin2a)-sin3a = 3sina-4sin3a
2. Косинус тройного угла: cos3a = cos(2a+a) = cos2acosa-sin2asina = (cos2a-sin2a)cosa-(2sinacosa)sina = cos3a-sin2acosa-2sin2acosa = cos3a-3sin2acosa = cos3a-3(1-cos2a)cosa = 4cos3a-3cosa

Прежде чем двигаться дальше, рассмотрим одну задачу. Дано: угол — острый. Найти его косинус, если Решение, данное одним учеником:

Т.к. , то sina = 3,а cosa = 4.

(Из математического юмора)

Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin2a+cos2a = 1 и разделим его на cos2a. Получим:

1. Связь тангенса и косинуса:

1. Аналогично получаем связь котангенса и синуса:

Формула тангенса суммы – ещё одна, тяжело поддающаяся запоминанию. Выведем её так:

1. Формула тангенса суммы: . Разделив числитель и знаменатель на произведение косинусов, получим:

Сразу выводится и

1. Формула тангенса двойного угла:

Из формулы косинуса двойного угла можно получить формулы синуса и косинуса для половинного. Для этого к левой части формулы косинуса двойного угла: cos2a = cos2a-sin2a прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.

cos2a+1 = cos2a-sin2a+cos2a+sin2a

2cos2a = cos2a+1 Выражая cosa через cos2a и выполняя замену переменных, получаем:

1. Косинус половинного угла:

Знак берётся в зависимости от квадранта.

Аналогично, отняв от левой части равенства единицу, а от правой — сумму квадратов синуса и косинуса, получим: cos2a-1 = cos2a-sin2a-cos2a-sin2a 2sin2a = 1-cos2a

1. Cинус половинного угла:

И, наконец, чтобы преобразовать сумму тригонометрических функций в произведение, используем следующий приём. Допустим, нам нужно представить в виде произведения сумму синусов sina+sinb. Введём переменные x и y такие, что a = x+y, b+x-y.

Тогда sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosxsiny+sinxcosy-cosxsiny = 2sinxcosy. Выразим теперь x и y через a и b.

Поскольку a = x+y, b = x-y, то . Поэтому

1. Представление суммы синусов в виде произведения:

Сразу же можно вывести

1. Формулу для разбиения произведения синуса и косинуса в сумму: sinacosb = 0.5(sin(a+b)+sin(a-b))

Рекомендуем потренироваться и вывести самостоятельно формулы для преобразования в произведение разности синусов и суммы и разности косинусов, а также для разбиения в сумму произведений синусов и косинусов. Проделав эти упражнения, вы досконально освоите мастерство вывода тригонометрических формул и не потеряетесь даже на самой сложной контрольной, олимпиаде или тестировании.

Формулы тригонометрии (более сложные)

Название формулы	Формула
Синус суммы и разности:	\( \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \)
Косинус суммы и разности:	\( \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \)
Тангенс суммы и разности:	\( \displaystyle tg\left( \alpha \pm \beta \right)=\frac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta }\)
Синус двойного угла (следствие формулы 1)	\( \displaystyle sin2a=2sina\cdot cosa\)
Косинус двойного угла (следствие формулы 2)	\( \displaystyle cos2a=co{{s}^{2}}a-si{{n}^{2}}a\)\( \displaystyle cos2a=2co{{s}^{2}}a-1=1-2si{{n}^{2}}a\)
Тангенс двойного угла:	\( \displaystyle tg2a=\frac{2tga}{1-t{{g}^{2}}a}\)

Формулы приведения

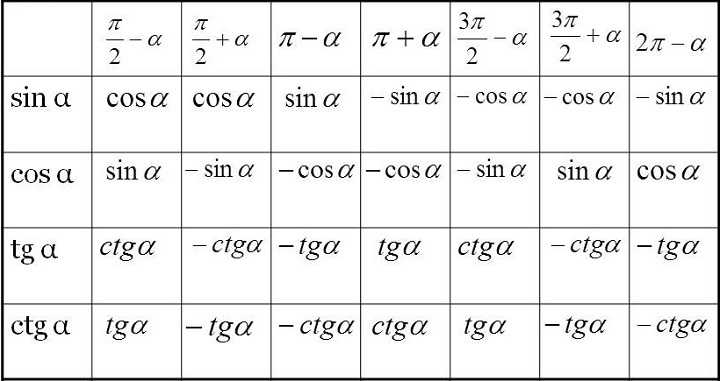
Что позволяют формулы

С их помощью значение тригонометрической функции любого угла можно привести к значению как той же, так и другой функции острого угла. Это позволяет, имея тупой угол, перейти к работе с острым, что намного удобнее для решения задач.

Часто в таблицах приводятся формулы только для синуса и косинуса, из которых легко получить формулы для тангенса и котангенса. При необходимости их можно переписать, заменяя радианы на градусы. Для этого нужно подставить вместо числа пи 180 градусов.

Формулы приведения не нужно заучивать наизусть. Достаточно запомнить закономерность, известную как мнемоническое правило:

1. Представить аргумент исходной функции в виде:

   \(\pm\;\alpha\;+\;2\pi\;\times\;z,\;\frac{\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\pi\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\frac{3\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\)

2. Определить знак исходной функции — тот же знак будет иметь функция в правой части формулы приведения.

3. Сохранить название исходной функции для углов: 

   \( \pm\;\alpha\;+\;2\pi\;\times\;z,\;\pi\;\pm\;\alpha\;+\;2\pi\;\times\;z\)

4. Заменить название исходной функции на название кофункции (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангес) для углов:

   \(\frac{\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\frac{3\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z\)

Важно, чтобы угол \(\alpha\) был не больше 90 градусов

Следствием чего являются

Формулы приведения следуют из свойств тригонометрических функций:

• периодичности;
• симметричности;
• сдвига на данный угол.

Формулы приведения для котангенса

ctg(π/2-α) = tg(α)
ctg(π/2+α) = -tg(α)
ctg(π-α) = -ctg(α)
ctg(π+α) = ctg(α)
ctg(3π/2-α) = tg(α)
ctg(3π/2+α) = -tg(α)
ctg(2π-α) = -ctg(α)
ctg(2π+α) = ctg(α)

Запомнить все формулы приведения достаточно непросто, ибо в них не прослеживается какой-либо явной закономерности.

Однако, это можно сделать, если понять принцип по которому в приведенной формуле происходит или не происходит смена функции на кофункцию и смена или не смена знака функции.

Когда надо менять название функции в формуле приведения?

Смена или не смена функции в формуле приведения зависит от того, к какому диаметру тригонометрического круга прилежит угол α в формуле приведения.

π/2±α и 3π/2±α — это вертикальный диаметр тригонометрического круга (ось Y), поскольку точки π/2 и π3/2 лежат на оси Y. Если помотать головой вверх-вниз, как бы скользя взглядом по оси ординат, то автоматически получим ответ на вопрос «надо ли менять название функции в формуле приведения?» — да, надо.

π±α и 2π±α — это горизонтальный диаметр тригонометрического круга (ось X), поскольку точки π и 2π лежат на оси Х. Если помотать головой влево-вправо, как бы скользя взглядом по оси абсцисс, то автоматически получим ответ на вопрос «надо ли менять название функции в формуле приведения?» — нет, не надо.

Когда надо менять знак функции в формуле приведения?

Для ответа на этот вопрос надо знать знаки функций синуса, косинуса, тангенса и котангенса в каждом квадранте тригонометрического круга.

Для синуса и косинуса — это просто, если помнить, что синус — это ордината (Y), а косинус — абсцисса (X):

• sin — это ось Y или вертикальная ось, поэтому, все, что лежит выше оси абсцисс — это «плюс» (I, II квадранты), что лежит ниже — «минус» (III, IV квадранты);
• cos — это ось X или горизонтальная ось, поэтому, все, что лежит правее оси ординат — это «плюс» (I, IV квадранты), что лежит левее — «минус» (II, III квадранты);
• tg и ctg — это отношение синуса и косинуса, поэтому, тангенс и котангенс будут положительны в тех квадрантах, в которых синус и косинус имеют одинаковый знак — это нечетные квадранты (I, III); соответственно, в четных квадрантах тангенс и котангенс будут отрицательны.

Знак функции в формуле приведения ставится по квадранту исходного угла, при этом считаем, что сам угол α является острым.

Например, для угла π-α получается, что угол находится во II квадранте, т.к., π-α будет лежать в пределах от 90° до 180° (см. рисунок выше). Во втором квадранте синус положителен, поэтому, в формуле приведения надо будет ставить знак, идентичный знаку исходной функции, т. е., «плюс». Поскольку угол π-α прилежит к горизонтальному диаметру, то сама функция не меняется. Получается, что sin(π-α) = sin(α).

Для косинуса надо будет сменить знак, т.к., во втором квадранте косинус отрицателен: cos(π-α) = -cos(α).

Для тангенса и котангенса: в четном квадранте — знак «минус», а функция остается прежней: tg(π-α) = -tg(α); ctg(π-α) = -сtg(α).

Для угла π+α получается, что угол находится во III квадранте, т.к., π+α будет лежать в пределах от 180° до 270° (см. рисунок). В третьем квадранте синус отрицателен, поэтому, в формуле приведения надо будет сменить знак. Поскольку угол π+α прилежит к горизонтальному диаметру, то функция не меняется. Получается, что sin(π+α) = -sin(α). Аналогично для косинуса: cos(π+α) = -cos(α).

Для тангенса и котангенса: в нечетном квадранте — знак «плюс», а функция остается прежней: tg(π+α) = tg(α); ctg(π+α) = сtg(α).

Десятиминутный ролик на ЮТуб, посмотрев который, вы навсегда запомните, как легко и просто приводить углы в тригонометрических функциях:

Пример решения уравнения с помощью формул приведения:

√2·sin(13π/4)
√2·sin(3π+π/4)
√2·sin(π+π/4)
sin(π+π/4)=-sin(π4)=-√2/2
√2·(-√2/2)=-1

Формулы суммы и разности тригонометрических функций

1. Синус суммы и разности:
   $$\mathbf{\sin(\alpha+\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha);}$$
   $$\mathbf{\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);}$$
2. Косинус суммы и разности:
   $$\mathbf{\cos(\alpha+\beta)=\cos(\alpha)*\cos(\beta)-\sin(\beta)*\sin(\alpha);}$$
   $$\mathbf{\cos(\alpha-\beta)=\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha);}$$
3. Тангенс суммы и разности:
   $$\mathbf{tg(\alpha+\beta)=\frac{tg(\alpha)+tg(\beta)}{1-tg(\alpha)*tg(\beta)};}$$
   $$\mathbf{tg(\alpha-\beta)=\frac{tg(\alpha)-tg(\beta)}{1+tg(\alpha)*tg(\beta)};}$$
4. Котангенс суммы и разности:
   $$\mathbf{сtg(\alpha+\beta)=\frac{-1+сtg(\alpha)*ctg(\beta)}{ctg(\alpha)+ctg(\beta)};}$$
   $$\mathbf{сtg(\alpha-\beta)=\frac{-1-сtg(\alpha)*ctg(\beta)}{ctg(\alpha)-ctg(\beta)};}$$

Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.

Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:

Пример 3
Упростить выражение \(sin(\frac{\pi}{2}+\alpha)\).

Воспользуемся формулой синуса суммы:
$$\sin(\alpha+\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha);$$
$$\sin(\frac{\pi}{2}+\alpha)=\sin(\frac{\pi}{2})*\cos(\alpha)+\sin(\alpha)*\cos(\frac{\pi}{2})=$$
$$=1*\cos(\alpha)+\sin(\alpha)*0=\cos(\alpha);$$

Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:

Пример 4
Найдите значение \(\sin(15^o)=?\)

\(15^o\) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим \(15^o\) в виде разности стандартных углов \(15^o=45^o-30^o\). И воспользуемся формулой синуса разности:
$$\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);$$
$$\sin(15^o)=\sin(45^o-30^o)=\sin(45^o)*\cos(30^o)-\sin(30^o)*\cos(45^o)=$$
$$=\frac{\sqrt{2}}{2}*\frac{\sqrt{3}}{2}-\frac{1}{2}*\frac{\sqrt{2}}{2}=$$
$$=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4};$$
Вот мы наши синус \(15^o\). Получилось такое иррациональное некрасивое выражение, так и оставляем.

Ответ: \(\sin(15^o)=\frac{\sqrt{6}-\sqrt{2}}{4}.\)

Пример 5
Найдите значение \(\cos(75^o)=?\)

\(75^o\) можно представить в виде суммы стандартных углов \(75^o=30^o+45^o\). Здесь воспользуемся формулой косинуса суммы:
$$\cos(\alpha+\beta)=\cos(30^o)*\cos(45^o)-\sin(30^0)*\sin(45^0)=$$
$$=\frac{\sqrt{3}}{2}*\frac{\sqrt{2}}{2}-\frac{1}{2}*\frac{\sqrt{2}}{2}=$$
$$=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что \(\cos(75^o)=\sin(15^o)\). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.

Ответ: \(\cos(75^o)=\frac{\sqrt{6}-\sqrt{2}}{4}.\)

Мы не будем выводить эти формулы — это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.

Применение основных тригонометрических формул для решения уравнений

Тригонометрические тождества можно выражать различным способом, для облегчения решения уравнения.

Рассмотрим характеристики тригонометрических функций для косинуса, синуса, тангенса и котангенса.

а) Сложение и вычитание тригонометрических функций.

Сложение и вычитание тригонометрических функций можно представить как — произведение. Преобразовать на множители косинус или синус, и тем самым упростить процесс вычисления.

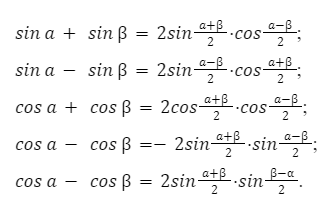
б) Произведение тригонометрических функций.

Произведение функций можно вычислить путем сложения и вычитания тождеств.

В свою очередь произведение тригонометрических функций, позволяет вычислить сумму. Эти два действия являются противоположными по отношению к друг другу.

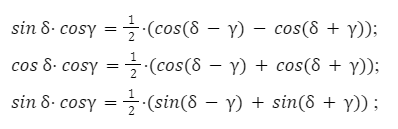
в) Тригонометрические формулы сложения.

При их применении можно сложение и вычитание углов выразить через тригонометрические функции заданных значений угла.

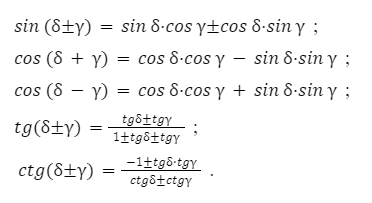
Преобразовав формулы сложения, мы получим тригонометрические уравнения угла.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Тригонометрические функции в прямоугольном треугольнике[]

Чтобы определить тригонометрические функции произвольного угла α,{\displaystyle \alpha ,} возьмём произвольный прямоугольный треугольник, содержащий угол α{\displaystyle \alpha }. Стороны этого треугольника мы будем называть так:

• Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона c.{\displaystyle c.}
• Противолежащий катет — катет, лежащий напротив угла. Например, катет a{\displaystyle a} — противолежащий по отношению к углу A.{\displaystyle A.}
• Прилежащий катет — катет, являющийся стороной угла. Например, катет b{\displaystyle b} — прилежащий по отношению к углу A.{\displaystyle A.}

Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна π.{\displaystyle \pi .} Это означает, что углы между катетами и гипотенузой лежат между {\displaystyle 0} и π2.{\displaystyle {\frac {\pi }{2}}.} Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.

Си́нус угла — отношение противолежащего катета к гипотенузе: sin⁡α=ac.{\displaystyle \sin \alpha ={\frac {a}{c}}.} Это отношение не зависит от выбора треугольника ABC{\displaystyle {ABC}}, содержащего угол α,{\displaystyle \alpha ,} так как все такие треугольники подобны.

Ко́синус угла — отношение прилежащего катета к гипотенузе: cos⁡α=bc.{\displaystyle \cos \alpha ={\frac {b}{c}}.} Так как sin⁡β=bc,{\displaystyle \sin \beta ={\frac {b}{c}},} синус одного острого угла в треугольнике равна косинусу второго, и наоборот.

Та́нгенс угла — отношение противолежащего катета к прилежащему: tgα=ab.{\displaystyle \operatorname {tg} \,\alpha ={\frac {a}{b}}.}

Кота́нгенс угла — отношение прилежащего катета к противолежащему: ctgα=ba.{\displaystyle \operatorname {ctg} \,\alpha ={\frac {b}{a}}.} Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.

Се́канс угла — отношение гипотенузы к прилежащему катету: sec⁡α=cb.{\displaystyle \sec \alpha ={\frac {c}{b}}.}

Косе́канс угла — отношение гипотенузы к противолежащему катету: cosecα=ca.{\displaystyle \operatorname {cosec} \,\alpha ={\frac {c}{a}}.}

Из определений тригонометрических функций следует:

a=csin⁡α,{\displaystyle a=c\sin \alpha \,,}

b=ccos⁡α,{\displaystyle b=c\cos \alpha \,,}

a=btgα,{\displaystyle a=b\,\operatorname {tg} \,\alpha ,}

b=actgα,{\displaystyle b=a\,\operatorname {ctg} \,\alpha ,}

c=bsec⁡α,{\displaystyle c=b\sec \alpha \,,}

c=acosecα,{\displaystyle c=a\,\operatorname {cosec} \,\alpha ,}

и симметрично:

b=csin⁡β,{\displaystyle b=c\sin \beta \,,}

a=ccos⁡β,{\displaystyle a=c\cos \beta \,,}

b=atgβ,{\displaystyle b=a\,\operatorname {tg} \,\beta ,}

a=bctgβ,{\displaystyle a=b\,\operatorname {ctg} \,\beta ,}

c=asec⁡β,{\displaystyle c=a\sec \beta \,,}

c=bcosecβ.{\displaystyle c=b\,\operatorname {cosec} \,\beta .}

Формулы тройного угла

Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$\cos(3*\alpha)=\cos^3(\alpha)-3*\sin^2(\alpha)*\cos(\alpha)=-3*\cos(\alpha)+4*\cos^3(\alpha);$$
$$\sin(3*\alpha)=3*\sin(\alpha)*\cos^2(\alpha)-\sin^3(\alpha)=3*\sin(\alpha)-4*\sin^3(\alpha);$$
$$tg(3*\alpha)=\frac{3*tg(\alpha)-tg^3(\alpha)}{1-3*tg^2(\alpha)};$$
$$ctg(3*\alpha)=\frac{ctg^3(\alpha)-3*ctg(\alpha)}{3*ctg^2(\alpha)-1};$$

Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$\cos(3*\alpha)=\cos(2\alpha+\alpha)=\cos(2\alpha)*\cos(\alpha)-\sin(2\alpha)*\sin(\alpha)=$$
$$=(\cos^2(\alpha)-\sin^2(\alpha))*\cos(\alpha)-2\sin(\alpha)*\cos(\alpha)*\sin(\alpha)=$$
$$=\cos^3(\alpha)-\sin^2(\alpha)*\cos(\alpha)-2\sin^2(\alpha)*\cos(\alpha)=$$
$$=\cos^3(\alpha)-3\sin^2(\alpha)*\cos(\alpha);$$

Если расписать \(sin^2(\alpha)=1-\cos^2(\alpha)\), то получим еще один вариант формулы тройного угла:
$$\cos(3*\alpha)=cos^3(\alpha)-3\sin^2(\alpha)*\cos(\alpha)=cos^3(\alpha)-3(1-\cos^2(\alpha))*\cos(\alpha)=$$
$$=4\cos^3(\alpha)-3\cos(\alpha);$$

Аналогично выводится формула синуса тройного угла:
$$\sin(3\alpha)=\sin(2\alpha+\alpha)=\sin(2\alpha)*\cos(\alpha)+\sin(\alpha)*\cos(2\alpha)=$$
$$=2\sin(\alpha)*\cos(\alpha)*\cos(\alpha)+\sin(\alpha)*(\cos^2(\alpha)-\sin^2(\alpha))=$$
$$=2\sin(\alpha)*\cos^2(\alpha)+\sin(\alpha)*\cos^2(\alpha)-\sin^3(\alpha)=3\sin(\alpha)*\cos^2(\alpha)-\sin^3(\alpha);$$
Распишем по основному тригонометрическому тождеству \(\cos^2(\alpha)=1-\sin^2(\alpha)\) и подставим:
$$\sin(3\alpha)=3\sin(\alpha)*\cos^2(\alpha)-\sin^3(\alpha)=$$
$$=3\sin(\alpha)*(1-\sin^2(\alpha))-\sin^3(\alpha)=3\sin(\alpha)-4\sin^3(\alpha);$$

Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.

Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.

I группа. Основные тождества

sin2α + cos2α = 1;

tgα = ____sinαcosα ;     ctgα = ____cosαsinα ;

tgα·ctgα = 1;

1 + tg2α = _____   1cos2α;     1 + ctg2α = _____   1sin2α .

Эта группа содержит самые простые и самые востребованные формулы. Большинство учащихся их знает. Но если всё-таки есть трудности, то чтобы запомнить первые три формулы, мысленно представьте себе прямоугольный треугольник с гипотенузой равной единице. Тогда его катеты будут равны, соответственно, sinα по определению синуса (отношение противолежащего катета к гипотенузе) и cosα по определению косинуса (отношение прилежащего катета к гипотенузе).

Первая формула представляет собой теорему Пифагора для такого треугольника — сумма квадратов катетов равна квадрату гипотенузы (12 = 1), вторая и третья — это определения тангенса (отношение противолежащего катета к прилежащему) и котангенса (отношение прилежащего катета к противолежащему). Произведение тангенса на котангенс равно 1 потому, что котангенс, записанный в виде дроби (формула третья) есть перевернутый тангенс (формула вторая). Последнее соображение, кстати, позволяет исключить из числа формул, которые необходимо обязательно заучить, все последующие длинные формулы с котангенсом. Если в каком-либо сложном задании Вам встретится ctgα, просто замените его на дробь ___  1tgα и пользуйтесь формулами для тангенса.

Последние две формулы можно не запоминать досимвольно. Они встречаются реже. И если потребуются, то Вы всегда сможете вывести их на черновике заново. Для этого достаточно подставить вместо тангенса или контангенса их определения через дробь (формулы вторая и третья, соответственно) и привести выражение к общему знаменателю

Но важно помнить, что такие формулы, которые связывают квадраты тангенса и косинуса, и квадраты котангенса и синуса существуют. Иначе, Вы можете не догадаться, какие преобразования необходимы для решения той или иной конкретной задачи

Если рекомендации понятны, нажмите кнопку , чтобы убрать «лишние» формулы.

Формулы преобразования суммы или разности тригонометрических функций в произведение (восьмая группа)

Основными формулами преобразования суммы и разности тригонометрических функций являются следующие:

Первая из этих формул читается так: сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.

Соответствующим образом читаются и остальные формулы.

Вывод этих формул.

Складывая и вычитая почленно известные нам равенства

получим соответственно:

Положим,

Тогда

При этих обозначениях получим:

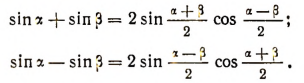
Складывая и вычитая почленно равенства

и изменяя обозначения, получим:

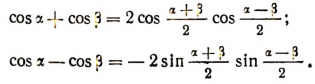
Выведенные формулы справедливы при любых значениях , так как, каковы бы ни были числа , можно подобрать такие х и у, чтобы соблюдались соотношения

в чем легко убедиться, разрешив эту систему относительно х и у.

Сумма и разность тангенсов

Аналогично

Формулы деления (шестая группа)

Основными формулами деления являются следующие:

Складывая и вычитая, получим соответственно:

Отсюда легко получаются написанные выше две формулы деления.

Формулы деления позволяют находить значение тригонометрической функции половинного угла по данному значению функции самого угла.

Например, если

Выведем еще формулы и для :

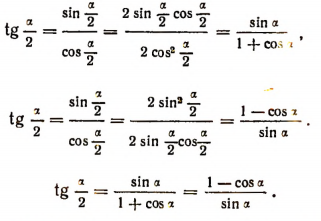
Полезно знать формулы для 1+ cos a и 1—cos a. Складывая и вычитая почленно равенства

получим соответственно:

Полезность этих двух последних формул заключается, в частности, в том, что они преобразовывают выражения 1 + cos а и 1 — cos а к виду, удобному для логарифмирования. Этими формулами приходится очень часто пользоваться.

Формулы понижения степени для позволяют вторые степени sin а и cos а выражать через первую степень cos 2а.

Действительно, складывая и вычитая почленно равенства

получим соответственно:

Отсюда

Формулы двойного угла (аргумента)

\sin(2\alpha)=2 \cdot \cos \alpha \cdot \sin \alpha\sin(2\alpha)=\dfrac{2 \cdot \tg \alpha}{1+\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{1+\ctg ^2 \alpha}=\dfrac{2}{\tg \alpha + \ctg \alpha}\cos(2\alpha)=\cos ^2 \alpha- \sin ^2 \alpha = 2 \cdot \cos ^2 \alpha- 1 = 1- 2 \cdot \sin ^2 \alpha\cos(2\alpha)=\dfrac{1 -\tg ^2 \alpha}{1+\tg ^2 \alpha}=\dfrac{\ctg ^2 \alpha- 1}{\ctg ^2 \alpha +1}=\dfrac{\ctg \alpha-\tg \alpha}{\ctg \alpha + \tg \alpha}\tg(2\alpha) = \dfrac{2 \cdot \tg \alpha}{1-\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{\ctg ^2 \alpha- 1}=\dfrac{2}{\ctg \alpha- \tg \alpha}\ctg(2\alpha) = \dfrac{\ctg ^2 \alpha-1}{2 \cdot \ctg \alpha}=\dfrac{\ctg \alpha- \tg \alpha}{2}