Как найти координаты вектора — формула, правило и примеры вычислений

Характеристики вектора: длина, направление, координаты

У любого вектора есть 2 главные характеристики:

• длина (математики говорят «модуль вектора»)
• направление (в какую сторону вектор на рисунке направлен)

Третья характеристика вектора – это его координаты.

Примечание:

Зная координаты вектора, можно найти его длину и направление. Поэтому, задавать информацию о векторе можно двояко: либо указав его длину и направление, либо его координаты.

Что такое координаты вектора

Координаты вектора – это длины его теней на осях координат (его проекции на оси).

Координаты вектора указывают так:

\( a_ \) – это «x» координата вектора, проекция вектора \( \vec \) на ось Ox;

\( a_ \) — это «y» координата вектора, проекция вектора \( \vec \) на ось Oy;

Координаты вектора можно получить из координат его начальной и конечной точек:

«координата вектора» = «конец» — «начало»

Пример:

\( A \left( 1;1 \right) \) — начальная точка,

\( B \left( 4;3 \right) \) — конечная точка,

\

\

Длина вектора (в чем измеряется, как посчитать)

Длину вектора (его модуль) обозначают так:

Как вычислить длину вектора по его координатам

Когда известны координаты вектора, его длину считают так:

\( a_ \) и \( a_ \) — это числа, координаты вектора \( \vec \)

Для двухмерного вектора:

Для трехмерного вектора:

Как вычислить длину вектора с помощью рисунка

Если вектор нарисован на клетчатой бумаге, длину считаем так:

1). Если вектор лежит на линиях клеточек тетради:

— считаем количество клеточек.

Зная масштаб клеток, легко получить длину вектора – умножаем масштаб на количество клеток.

2). Если вектор не лежит вдоль линий:

— проводим вертикаль и горизонталь пунктиром.

\( \Delta x \) — горизонталь; \( \Delta y \) — вертикаль;

— затем применяем формулу:

Как указать направление вектора

Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.

Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.

Для двумерного вектора

Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:

• угол \( \alpha \) между вектором и горизонталью (осью Ox),
• или угол \( \beta \) вежду вектором и вертикалью (осью Oy).

Словами указать направление вектора можно так:

• вектор длиной 5 единиц направлен под углом 30 градусов к горизонтали;
• Или же: вектор длиной 5 единиц направлен под углом 60 градусов к вертикали.

Такой способ указания координат используют в полярной системе координат.

Для трехмерного вектора

Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.

• угол между вектором и осью Oz;
• и один из углов: между вектором и осью Oy, или между вектором и осью Ox;

Такой способ указания координат используют в сферической системе координат.

Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).

Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.

Координаты точки

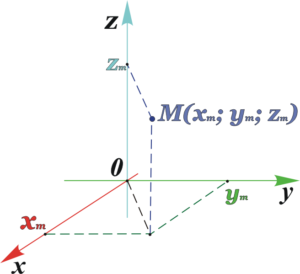
Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).

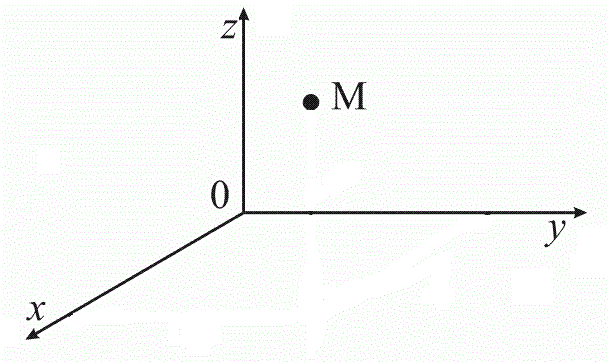Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ

Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).

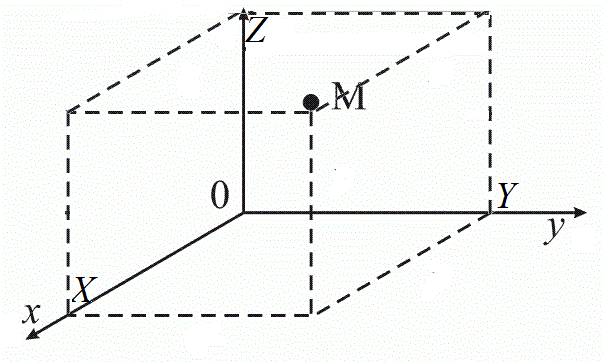Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ

Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.

Пример 1

Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.

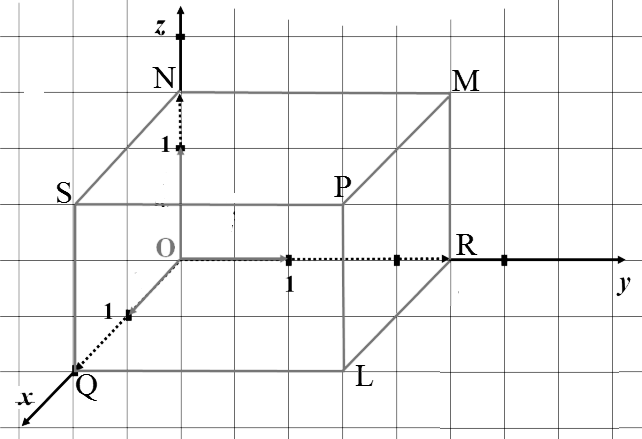Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ

Решение.

Точка $O$ начало координат, следовательно, $O=(0,0,0)$.

Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит

$Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$

Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит

$S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$

Точка $P$ имеет координаты $P=(2,2.5,1.5)$

Определитель третьего порядка

Отныне и впредь, когда ты будешь иметь дело с методом координат на плоскости, тебе очень часто будут встречаться эти самые определители.

Что же такое определитель третьего порядка? Как ни странно, это всего-навсего число. Осталось понять, какое конкретно число мы будем сопоставлять с определителем.

Давай вначале запишем определитель третьего порядка в более общем виде:

\( \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right|\),Где \( {{a}_{ij}}\) – некоторые числа.

Причем под первым индеком \( \displaystyle i\) мы понимаем номер строки, а под индеком \( \displaystyle j\) – номер столбца.

Например, \( {{a}_{23}}\) означает, что данное число стоит на пересечении второй строки и третьего столбца.

Давай поставим следующий вопрос: каким именно образом мы будем вычислять такой определитель?

То есть, какое конкретно число мы будем ему сопоставлять?

Для определителя именно третьего порядка есть эвристическое (наглядное) правило треугольника оно выглядит следующим образом:

Как его читать? А понимать его надо следующим образом: мы составляем два выражения:

• Произведение элементов главной диагонали (с верхнего левого угла до нижнего правого) \( \displaystyle +\) произведение элементов, образующих первый треугольник «перпендикулярный» главной диагонали \( \displaystyle +\) произведение элементов, образующих второй треугольник «перпендикулярный» главной диагонали;
• Произведение элементов побочной диагонали (с верхнего правого угла до нижнего левого) \( \displaystyle +\) произведение элементов, образующих первый треугольник «перпендикулярный» побочной диагонали \( \displaystyle +\) произведение элементов, образующих второй треугольник «перпендикулярный» побочной диагонали;
• Тогда определитель равен разности значений, полученных на шаге \( \displaystyle 1\) и \( \displaystyle 2\).

Если записать все это цифрами, то мы получим следующее выражение:

\( \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right| = \)\( = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{21}}{a_{32}}{a_{13}} — \left( {{a_{13}}{a_{22}}{a_{31}} + {a_{23}}{a_{32}}{a_{11}} + {a_{21}}{a_{12}}{a_{33}}} \right)\)Тем не менее, запоминать способ вычисления в таком виде не нужно, достаточно в голове просто держать треугольники и саму идею, что с чем складывается и что из чего затем вычитается).

Уравнения прямой и плоскости

           Вспомните, как вас знакомили с системой координат и объясняли, что положение каждой точки в системе координат можно определять координатами х и у. Это точки M(x_m; y_m) и N(x_n; y_n)

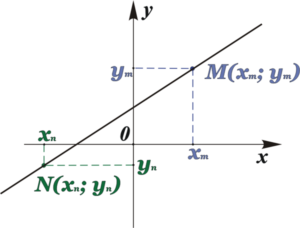          Как известно, прямую можно провести через две точки, и при том, только одну. Задача по определению уравнения прямой на плоскости, проходящей через две точки, координаты которых известны, решалась очень просто. В этом случае в уравнение прямой y=kx+b подставляли сначала координаты точки М, затем – точки N.

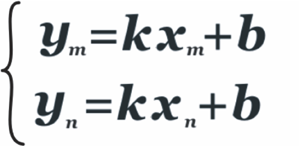
       Получали систему двух линейных уравнений относительно неизвестных коэффициентов k и b, которые находили при решении  этой системы.

        Но уравнение прямой на плоскости можно задать и по-другому:

Ax + By + C = 0,       (A² + B² ≠ 0)

И суть от этого не изменится, изменятся только коэффициенты. Условие в скобках означает, что А и В не могут быть равны нулю одновременно.

        Стереометрия рассматривает фигуры в пространстве, где каждая точка описывается уже тремя координатами – (x, y, z).

       Уравнение прямой в пространстве задается через направляющий вектор. Но это уже не входит в рамки программы средней школы, поэтому просто принимаем к сведению.

            Если известны две точки пространства  M( x_m ; y_m ; z_m ) и  N( x_n ; y_n ; z_n ) , то уравнения прямой, проходящей через данные точки, выражаются формулами:

             Но вот что мы с вами можем, так это воспользоваться вектором этой прямой, который будет определяться расстоянием между точками в пространстве. И об этом подробно поговорим в следующем разделе — 

          Привязка фигур к  системе координат позволяет не только определять координаты точек, но и записать уравнение плоскости. Как известно, на трех точках можно построить плоскость, притом, только одну. Соответственно, можно и записать плоскость уравнением. Выглядит это уравнение следующим образом:

  Ax + By + Cz + D = 0

 Очень похоже на вторую запись уравнения прямой на плоскости. Значит, и коэффициенты  А, В, С и D мы будем находить также, как и коэффициенты для прямой на плоскости, по точкам.

       Это действие сродни тому, что вы производили, определяя уравнение прямой, проходящей через две точки, заданные координатами.

       Прямую можно провести через две точки, и мы составляли два уравнения для двух точек.

         Плоскость можно провести через три точки, значит, и уравнений будет три!

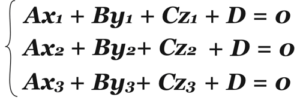
        Но уравнений три, а неизвестных – четыре! Ну, и что! Мы же можем разделить все уравнения на D, при этом они не изменятся, будут равнозначны первоначальным! Так и будем поступать! Тогда   вместо D   будет единица, а все остальные коэффициенты будут делиться на D,  назовем их также, А, В, С. И это уже вполне решаемая система!

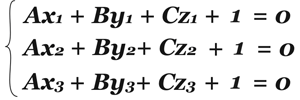
          Здесь значения всех x, y и z известны, это координаты точек, принадлежащих данной плоскости.

          Итак, точку описать можем, прямую описать можем, плоскость –  можем. Осталось вспомнить сами векторы и их координаты, они нам тоже пригодятся при решении задач.

21 Условие перпендикулярности векторов

Если
ненулевые векторы

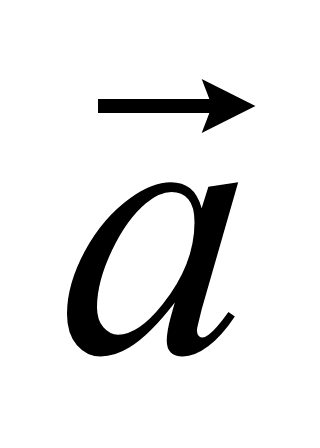
= (x₁; y₁;
z₁) и

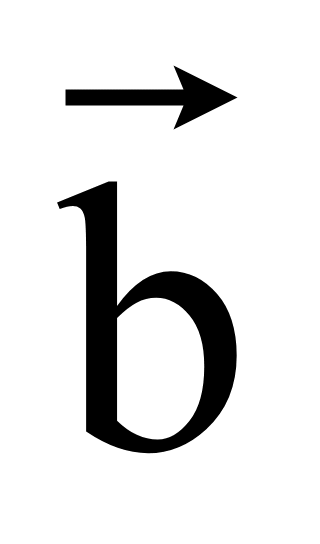
= (x₂; y₂;
z₂) перпендикулярны, то их
скалярное произведение равно нулю

=
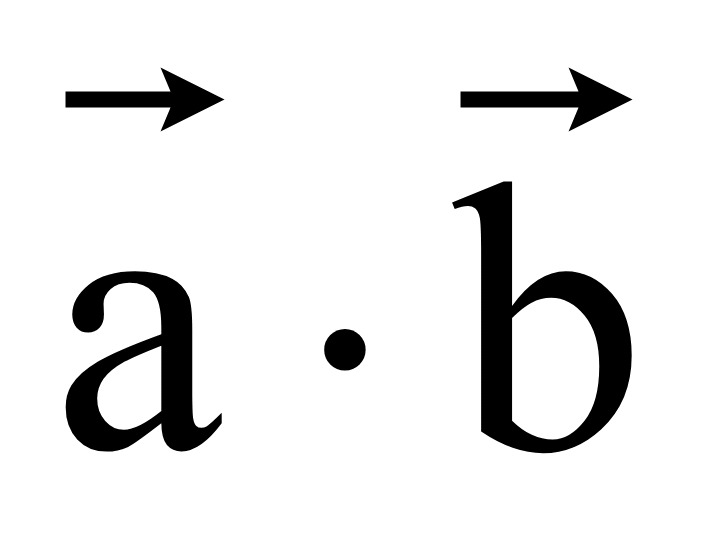0,

=
x₁x₂
+ y₁y₂
+ z₁z₂
= 0.

Если
задан один ненулевой вектор

= (x₁; y₁;
z₁), то координаты
перпендикулярного (нормального) ему ненулевого
вектора

= (x₂; y₂;
z₂) должны удовлетворять
равенству

x₁x₂
+ y₁y₂
+ z₁z₂
= 0.

Таких
векторов

бесконечное множество.

Если
на плоскости задан один ненулевой вектор

= (x₁; y₁),
то координаты перпендикулярного (нормального) ему вектора

= (x₂; y₂)
должны удовлетворять равенству

x₁x₂
+ y₁y₂
= 0.

Отсюда
можно выразить произведение координат y

y₁y₂
= — x₁x₂.

Если
на плоскости задан ненулевой вектор

= (x₁; y₁),
то достаточно задать произвольно одну из координат перпендикулярного
(нормального) ему вектора

= (x₂; y₂)
и из условия перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

выразить
вторую координату вектора

.

Например,
если подставить произвольную координату x₂,то из равенства

y₁y₂
= — x₁x₂

выражается
вторая координата вектора

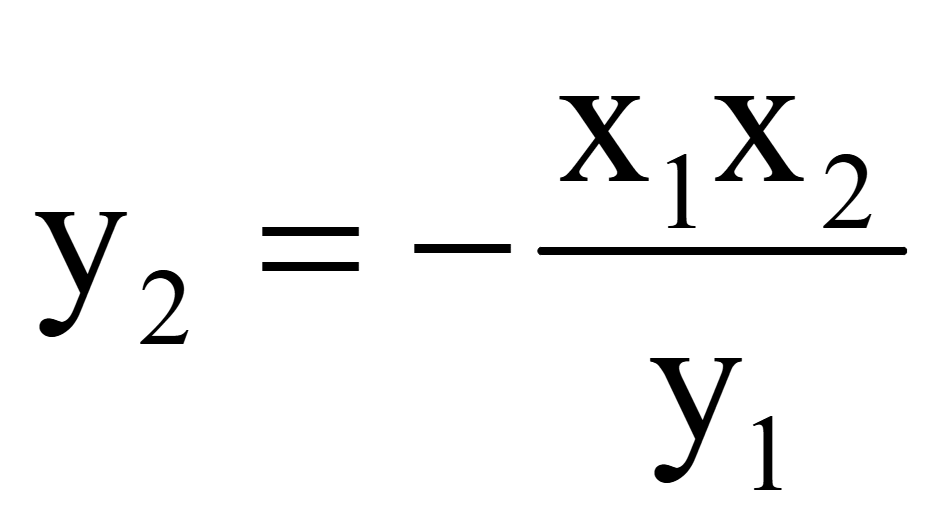
Если
произвольно придать x₂ = y₁,
то вторая координата вектора

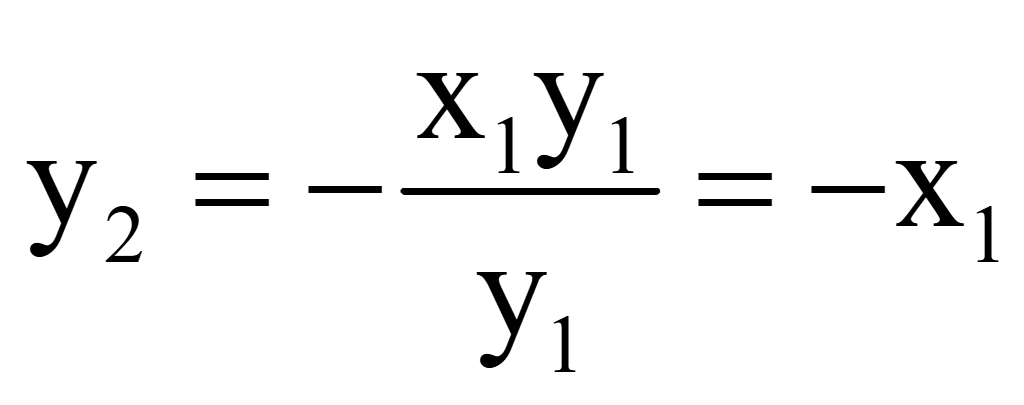
Если
на плоскости задан ненулевой вектор

= (x₁; y₁),
то перпендикулярный (нормальный) ему вектор

= (y₁; -x₁).

Если
одна из координат ненулевого вектора

равна нулю, то у перпендикулярного ему ненулевого вектора

такая же координата не равна нулю, а вторая координата равна нулю.
Такие векторы лежат на осях координат, поэтому перпендикулярны.
Например, если

= (; y₁),
то этот вектор лежит на оси Oy, тогда
перпендикулярный ему ненулевой вектор

= (x₂;
0) лежит на оси Ox.

Определим
второй вектор, перпендикулярный вектору

= (x₁; y₁),
но противоположный вектору

= (y₁; -x₁),
то есть вектор —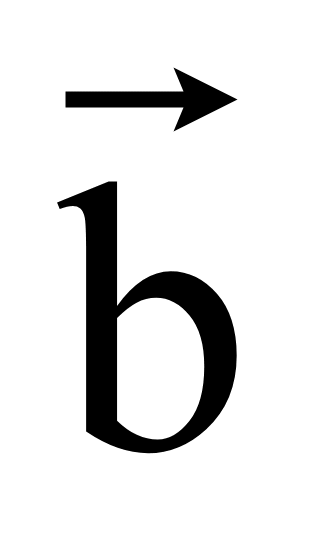
.
Тогда достаточно поменять знаки координат вектора

—

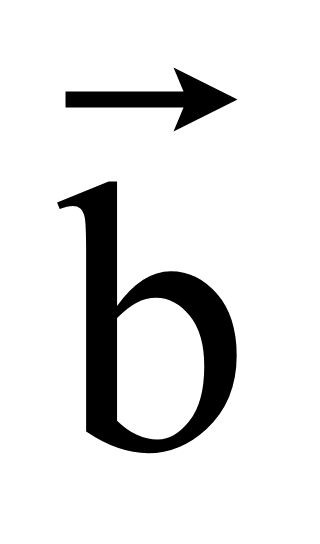
= -1·

= (-1·y₁;
-1·(-x₁))=
(-y₁; x₁).

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

₁
= (y₁; -x₁),

₂
= (-y₁; x₁).

Для
получения координат ненулевых векторов, перпендикулярных заданному
ненулевому вектору на плоскости, достаточно поменять местами
координаты заданного вектора и поменять знак одной из координат.

Задача.
Задан вектор

= (3; -5). Найти два нормальных вектора с различной ориентацией.

Решение

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

₁
= (y₁; -x₁),

₂
= (-y₁; x₁).

Подставляем
координаты вектора

= (3; -5)

₁
= (-5; -3),

₂
= (-(-5); 3) = (5; 3).

Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

3·(-5)
+ (-5)·(-3) = -15 + 15 = 0

верно!

3·5
+ (-5)·3 = 15 — 15 = 0

верно!

Ответ:
₁
= (-5; -3),
₂
= (5; 3).

Если
присвоить x₂ = 1, подставить

x₁
+ y₁y₂
= 0.

y₁y₂
= -x₁

Получим
координату y₂ вектора,
перпендикулярного вектору

= (x₁; y₁)

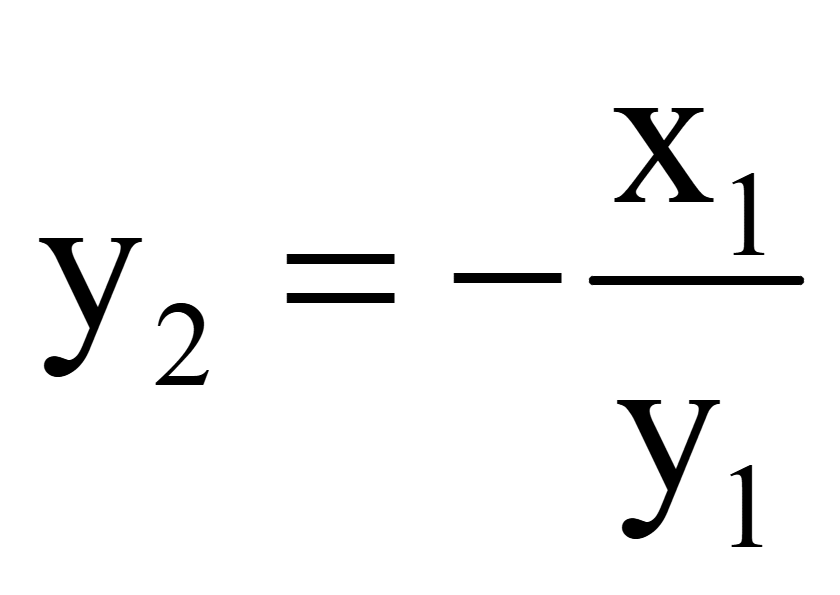
Координаты
одного вектора, перпендикулярного на плоскости ненулевому вектору

= (x₁; y₁)

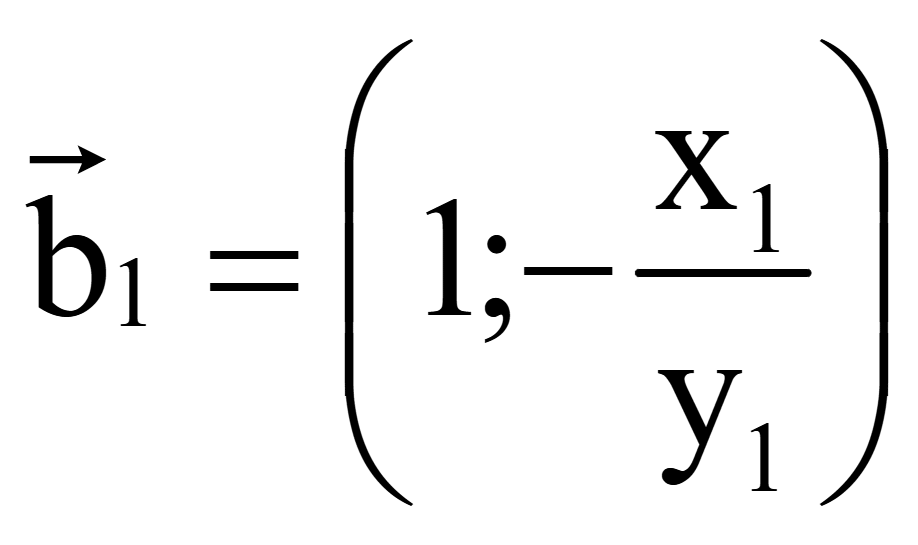
Для
получения второго вектора, перпендикулярного вектору

= (x₁; y₁),
но противоположно направленного вектору

.
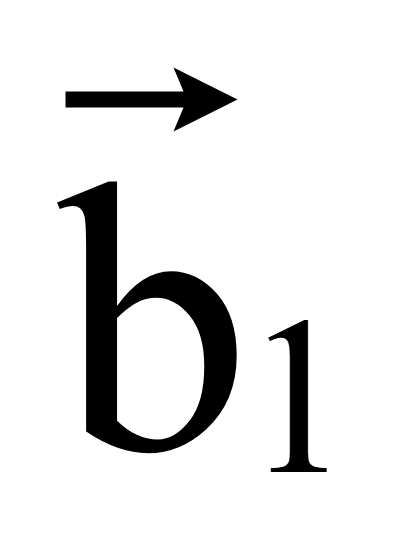
Пусть

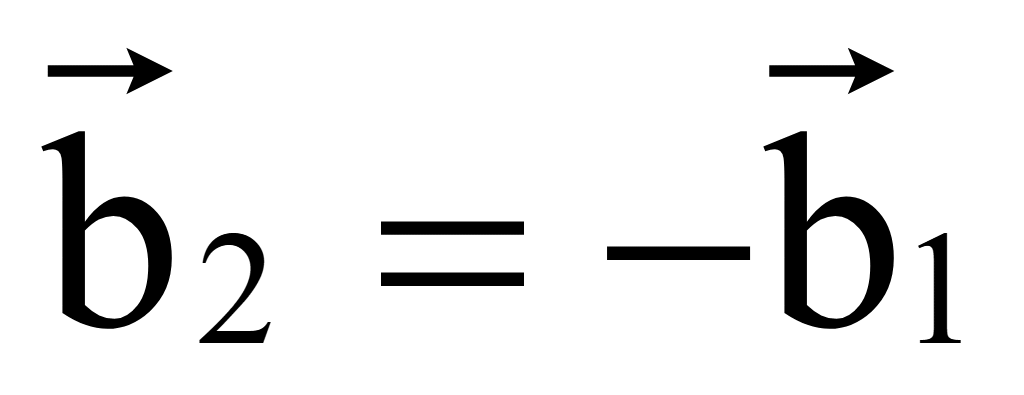
Тогда
достаточно поменять знаки координат вектора

.

Координаты
второго вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

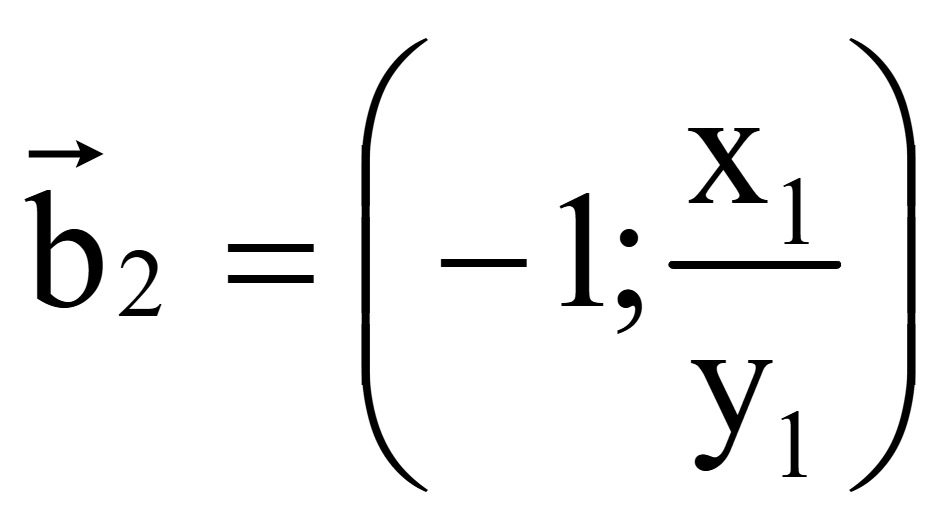
Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

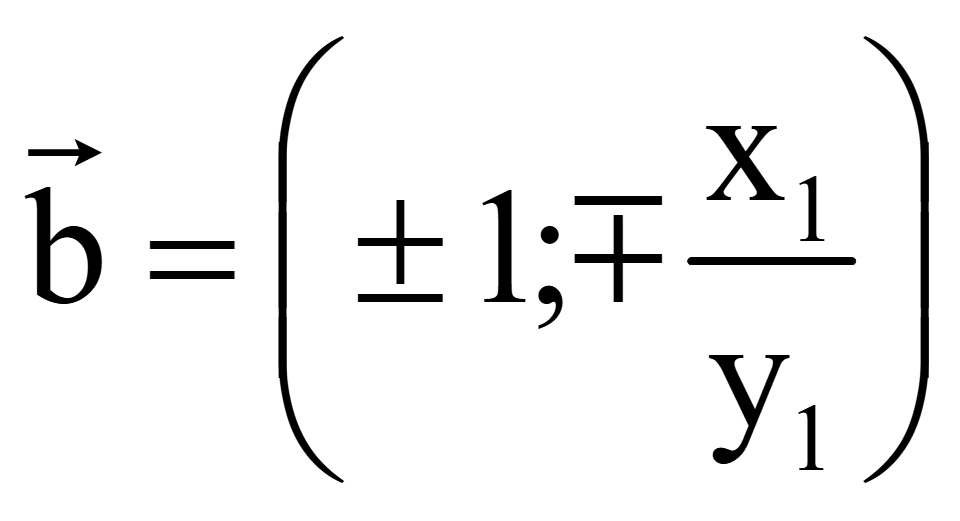
Задача.
Задан вектор

= (3; -5). Найти два нормальных вектора с различной ориентацией.

Решение

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

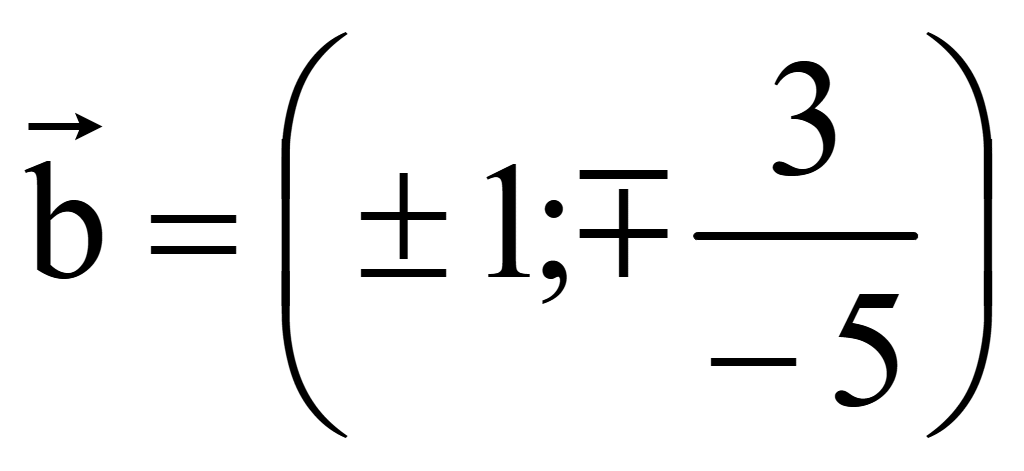
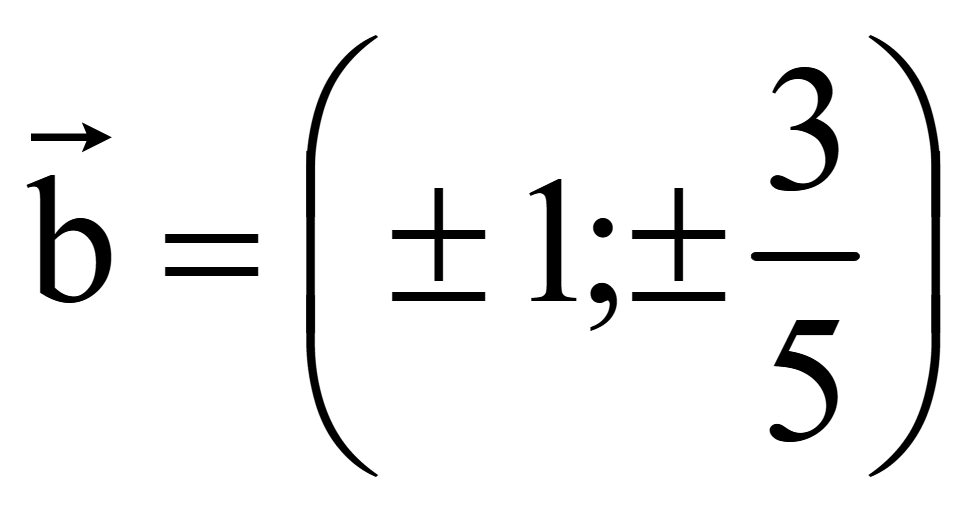
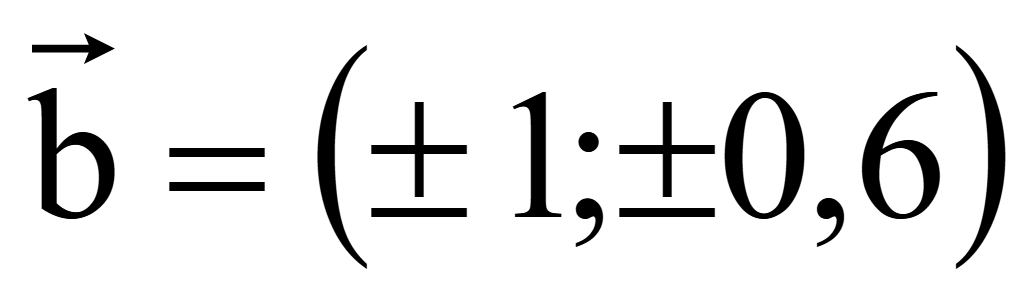
Координаты
одного вектора

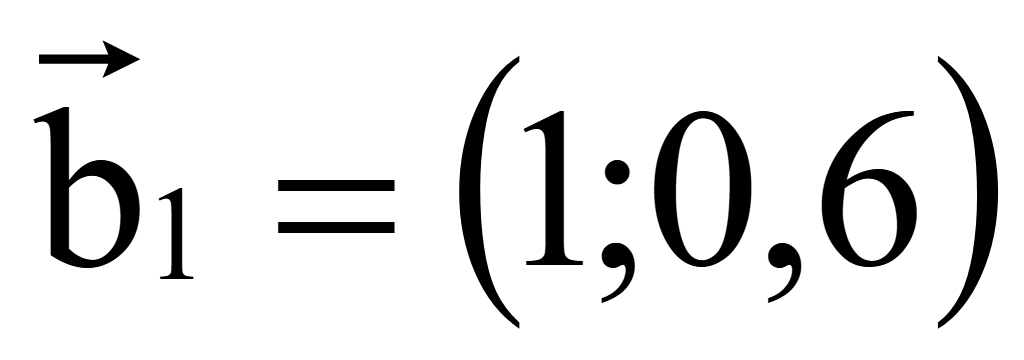
Координаты
второго вектора

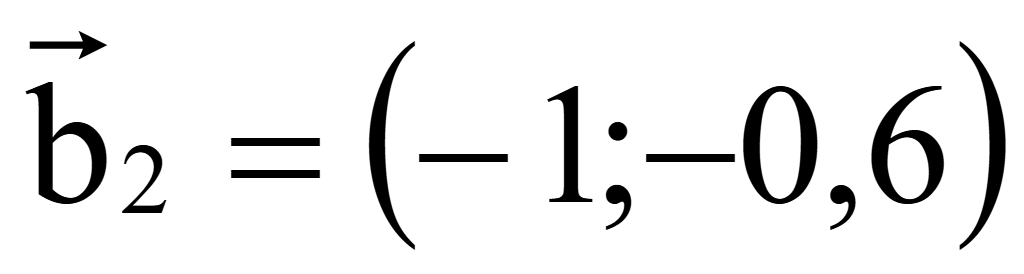
Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

3·1
+ (-5)·0,6 = 3 — 3 = 0

верно!

3·(-1)
+ (-5)·(-0,6) = -3 + 3 = 0

верно!

Ответ:

и

.

Если
присвоить x₂ = — x₁,
подставить

x₁(-x₁)
+ y₁y₂
= 0.

-x₁2
+ y₁y₂
= 0.

y₁y₂
= x₁2

Получим
координату вектора, перпендикулярного вектору

Если
присвоить x₂ = x₁,
подставить

x₁x₁
+ y₁y₂
= 0.

x₁2
+ y₁y₂
= 0.

y₁y₂
= -x₁2

Получим
координату y второго вектора,
перпендикулярного вектору

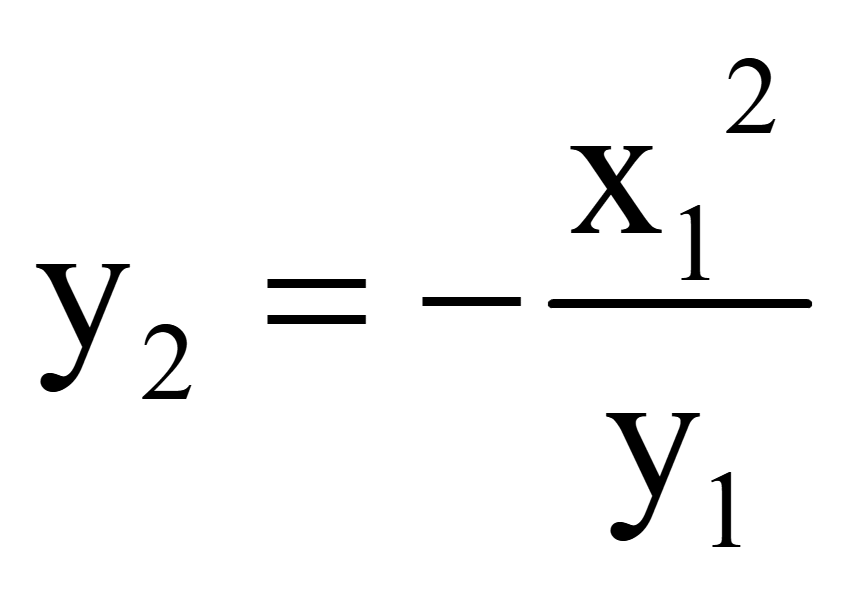
Координаты
одного вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

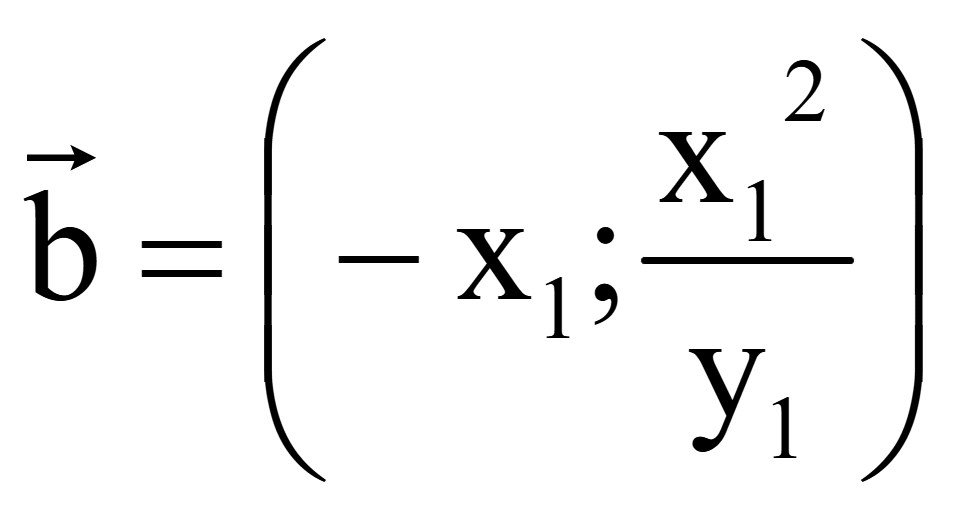
Координаты
второго вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

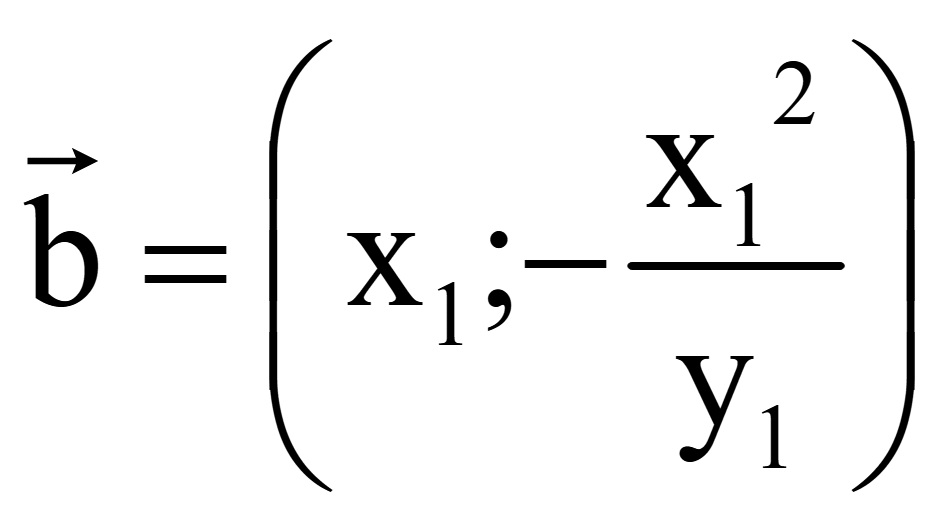
Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

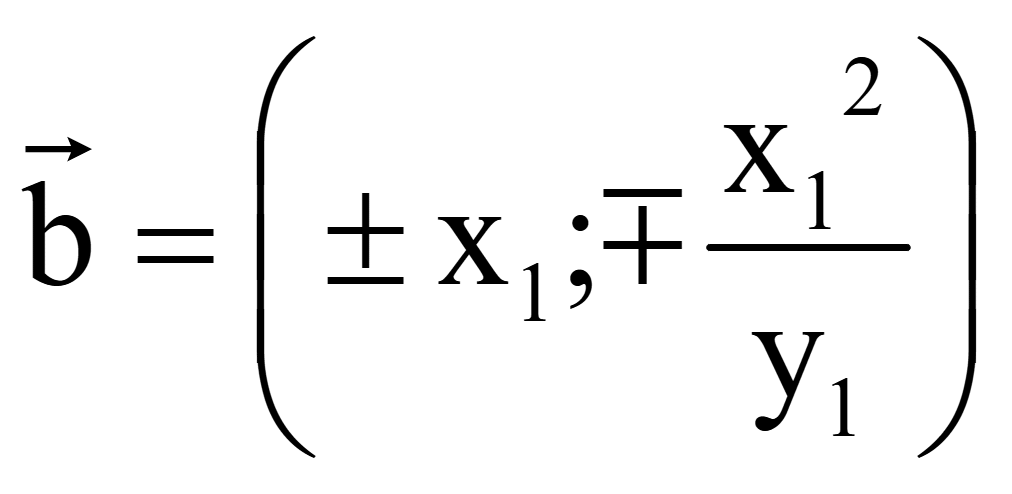
Нахождение длины вектора по координатам.

Длину вектора  будем обозначать . Аналогичное обозначение имеет модуль числа, и длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор  и он имеет координаты . Получим формулу, позволяющую находить длину вектора  через координаты  и .

Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как  и  соответственно и рассмотрим прямоугольник  с диагональю ОА.

В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что  и , а по построению длина ОА равна длине вектора , следовательно, .

Таким образом, формула для нахождения длины вектора  по его координатам на плоскости имеет вид .

Если вектор  представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты  и  являются координатами вектора  в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора , заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам :

Ответ:

.

Теперь получим формулу для нахождения длины вектора  по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор  и обозначим проекции точки А на координатные оси как  и . Тогда мы можем построить на сторонах  и прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае  (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .

Таким образом, длина вектора  в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле .

Пример.

Вычислите длину вектора , где  — орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора  по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .

Ответ:

.

Длина вектора через координаты точек его начала и конца.

А как найти длину вектора, если даны координаты точек его начала и конца?

В предыдущем пункте мы получили формулы для нахождения длины вектора по его координатам на плоскости и в трехмерном пространстве. Тогда мы можем ими воспользоваться, если найдем координаты вектора по координатам точек его начала и конца.

Таким образом, если на плоскости заданы точки  и , то вектор  имеет координаты  и его длина вычисляется по формуле , а формула для нахождения длины вектора  по координатам точек  и  трехмерного пространства имеет вид .

Рассмотрим решения примеров.

Пример.

Найдите длину вектора , если в прямоугольной декартовой системе координат .

Решение.

Можно сразу применить формулу для нахождения длины вектора по координатам точек начала и конца на плоскости :

Вторым вариантом решения является определение координат вектора через координаты точек и применение формулы :

Ответ:

.

Пример.

Определите, при каких значениях  длина вектора  равна , если .

Решение.

Длина вектора  по координатам точек начала и конца может быть найдена как

Приравняв полученное значение длины вектора к , вычислим искомые :

Ответ:

при .

Нахождение длины вектора по теореме косинусов.

Большинство задач на нахождение длины вектора решаются в координатах. Однако, когда координаты вектора не известны приходится искать другие пути решения.

Пусть известны длины двух векторов ,  и угол между ними (или косинус угла), а требуется найти длину вектора  или . В этом случае можно по теореме косинусов в треугольнике АВС вычислить длину стороны ВС, которая равна искомой длине вектора.

Разберем решение примера для пояснения сказанного.

Пример.

Длины векторов  и  равны 3 и 7 соответственно, а угол между ними равен . Вычислите длину вектора .

Решение.

Длина вектора  равна длине стороны ВС в треугольнике АВС. Из условия нам известны длины сторон АВ и АС этого треугольника (они равны длинам соответствующих векторов), а также угол между ними, поэтому нам достаточно данных для применения теоремы косинусов:

Таким образом, .

Ответ:

.

Итак, для нахождения длины вектора по координатам используем формулы или ,
по координатам точек начала и конца вектора — или ,
в некоторых случаях к результату приводит теорема косинусов.

Вычисление углов между двумя плоскостями

Алгоритм решения будет таков:

• По трем точкам ищем уравнение первой плоскости: \( {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+{{D}_{1}}=0\)
• По другим трем точкам ищем уравнение второй плоскости: \( {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+{{D}_{2}}=0\)
• Применяем формулу: \( cos\varphi =\frac{\left| {{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}~ \right|}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}\cdot \sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}\)

Как видишь, формула очень похожа на две предыдущие, при помощи которых мы искали углы между прямыми и между прямой и плоскостью.

Так что запомнить эту тебе не составит особого труда. Сразу переходим к разбору задач:

Формула координат

При построении отрезка единичный вектор выбирается исходя из удобства размещения его в плоскости. Начальная и конечная точка могут быть определены в координатной плоскости. Чаще всего для этого используется декартова система координат. К расположениям осей жёстких требований нет, но принято по горизонтали рисовать ось икс в правом направлении, а по вертикали снизу вверх — ось игрек. Пересекаются эти оси между собой под прямым углом и место их пересечения называют началом отсчёта. В этой точке координата записывается как (0, 0).

Задать координаты, значит, присвоить точке два числа. Так, если точка имеет координаты x = 4; y = -2, то обозначаться она будет как A (4, -2). Ось от нуля в направлении икса называется абсциссой, а совпадающая с игреком — ординатой. В плоскости каждая точка заданного отрезка характеризуются двумя значениями. Одно из них соответствует оси ординат, а другое абсцисс. Например, A (1, 5); B (3, 2). Здесь единица и тройка соответствуют значению точек на оси икс, а пятёрка и двойка — на оси игрек.

Исходя из этого, чтобы нарисовать вектор на плоскости, нужно узнать координаты его начальной и конечной точек, а также направление. Для получения рисунка вектора нужно просто соединить эти две точки. Из знания значений, ограничивающих точки отрезка, довольно легко определить координаты вектора.

Существует простое правило, которое гласит, что для этого необходимо из координат конечной точки вычесть координаты начальной. Для рассмотренного примера с точками A (1, 5); B (3, 2) координаты вектора будут: AB = (2 — 1); (3 — 5). То есть справедливо будет записать: AB (1; -2). Для общего случая можно сказать, что формула координаты вектора по двум точкам имеет следующий вид: AB (x2 — x1, y2 − y1), где икс и игрек один — положение первой точки, а икс и игрек два — второй.

Это выражение справедливо не только для плоскости, но и для нахождения координат в пространстве. В этом случае добавляется третья осью. Обозначается она часто буквой Z. Соответственно, каждая точка будет описываться уже не двумя координатными значениями, а тремя — по числу осей: A (x1, y1, z1) и B (x2, y2, z2). Отсюда следует, что координаты вектора определяются уже по формуле: AB = (x2 — x1; y2 — y1; z2 — z1).

При сложении, умножении, вычитании двух ограниченных линий нужно выполнять поэлементно действия над их координатами. Например, AB (x 1, y 1) + BC (x 2, y 2) = AC (x 1 + x 2, y 1 + y 2).

Расстояние между двумя точками на координатной плоскости

Давай рассмотрим теперь следующую задачу: у нас есть две точки на координатной плоскости. Как найти расстояние между ними?

Пусть первая точка будет \( {{P}_{1}}({{x}_{1}},{{y}_{1}})\), а вторая \( {{P}_{2}}\left( {{x}_{2}},{{y}_{2}} \right)\).

Обозначим расстояние между ними через \( d\). Давай сделаем для наглядности следующий чертеж:

Что я сделал?

Я, во-первых, соединил точки \( {{P}_{1}}\left( {{x}_{1}},{{y}_{1}} \right)\) и \( {{P}_{2}}\left( {{x}_{2}},{{y}_{2}} \right)\).

А также из точки \( {{P}_{1}}\) провел линию, параллельную оси \( Ox\), а из точки \( {{P}_{2}}\) провел линию, параллельную оси \( Oy\).

Они пересеклись в точке \( R\), образовав при этом замечательную фигуру. Чем она замечательна?

Да мы с тобой почти что все знаем про прямоугольный треугольник. Ну уж теорему Пифагора – точно!

Искомый отрезок – это гипотенуза этого треугольника, а отрезки \( {{P}_{1}}R,~{{P}_{2}}R\) – катеты.

Чему равны координаты точки \( R\)?

Да, их несложно найти по картинке: \( R\left( {{x}_{2}},{{y}_{1}} \right).~\)

Так как отрезки \( {{P}_{1}}R,~{{P}_{2}}R\) параллельны осям \( Ox\) и \( Oy\) соответственно, то их длины легко найти: если обозначить длины отрезков \( {{P}_{1}}R,~{{P}_{2}}R\) соответственно через \( \left| {{P}_{1}}R\left| ,~ \right|{{P}_{2}}R \right|\), то\( \left| {{P}_{1}}R \right|={{x}_{2}}-{{x}_{1}}\)\( \left| {{P}_{2}}R \right|={{y}_{2}}-{{y}_{1}}\)Теперь воспользуемся теоремой Пифагора. Длины катетов нам известны, гипотенузу мы найдем:

Легко заметить, что расстояние между точками не зависит от направления.

Тогда:

Отсюда делаем три вывода:

• Длина вектора = корень из суммы квадратов его координат;
• Найти расстояние между двумя точками = найти длину вектора, их соединяющего (в любом направлении);
• Длины векторов, соединяющих две точки в разном направлении, равны.

Векторы в системе координат

Координатная прямая, координатный луч

Получите представление о координатной (числовой) прямой, узнайте что называют координатой точки.

Прямоугольная система координат

Узнайте как вводится прямоугольная декартова система координат на плоскости и в пространстве и как в ней определяются координаты точек.

Координаты вектора

Познакомьтесь с определениями координатных векторов, с разложением произвольного вектора по координатным векторам и определением координат вектора.

Координаты вектора по координатам точек его начала и конца

На примерах разобрано применение формулы для нахождения координат вектора по известным координатам его начала и конца.

Нахождение длины вектора

Научитесь находить длину вектора по его известным координатам, запомните соответствующую формулу и разберите представленные решения примеров.

Угол между векторами

Узнайте что называют углом между векторами и научитесь находить угол по известным координатам векторов с использованием соответствующей формулы.

Проекция вектора на ось, числовая проекция вектора

Даны определения проекции вектора на ось (направление) и числовой проекции вектора, рассмотрены примеры.

Операции с векторами

Сложение и умножение вектора на число в координатах

Подробно показано как выполняется сложение векторов и умножение вектора на число, когда известны их координаты, приведены примеры с доступно изложенными решениями.

Скалярное произведение векторов

Введено определение скалярного произведения векторов, перечислены его свойства, дан его физический смысл и формулы для его вычисления, показаны решения характерных примеров.

Векторное произведение векторов

Познакомьтесь с векторным произведением векторов, его свойствами, геометрическим и механическим смыслом, рассмотрите решения характерных примеров и задач.

Смешанное произведение векторов

Изучите смешанное произведение векторов: ознакомьтесь с определением, свойствами и геометрическим смыслом, научитесь вычислять смешанное произведение и решать другие задачи.

Коллинеарность, перпендикулярность, компланарность

Условие коллинеарности векторов

Познакомьтесь с необходимым и достаточным условием коллинеарности двух векторов, научитесь находить вектор, коллинеарный данному.

Условие перпендикулярности векторов

Показано как проверять перпендикулярность векторов посредством вычисления их скалярного произведения, приведены решения характерных примеров.

Компланарные векторы

Разобрано как выявить являются ли три вектора компланарными с помощью вычисления смешанного произведения, показаны решения примеров.

Приложения

Расстояние от точки до точки

Получена формула для вычисления расстояния от точки до точки по координатам, разобраны решения примеров.

Координаты середины отрезка

Научитесь находить координаты середины отрезка, когда известны координаты его концов, изучите теорию и рассмотрите готовые решения примеров.

Деление отрезка в данном отношении

Выведены формулы для нахождения координат точки, которая делит отрезок в заданном отношении, показаны решения характерных примеров.

Интуитивное изображение сложения

Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.

Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма. 

Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.

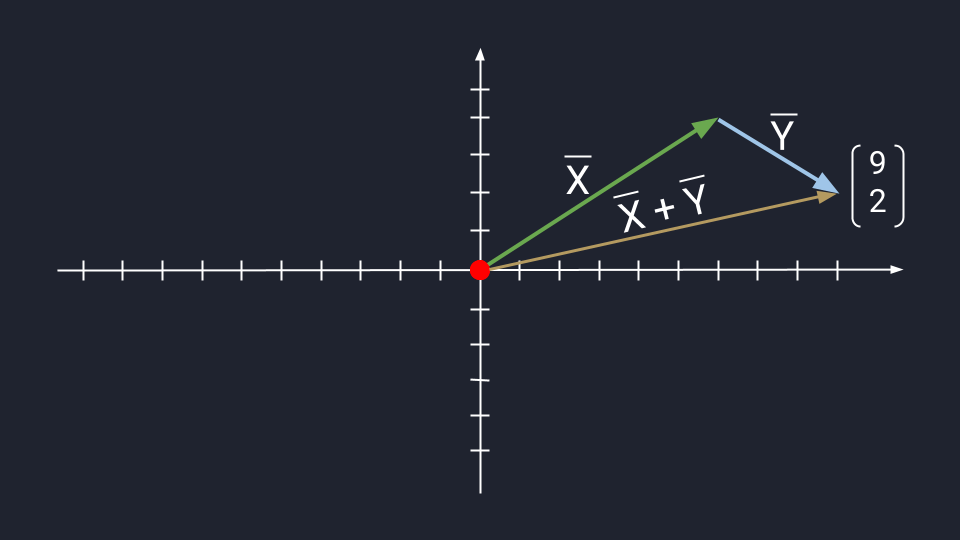Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)

Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y. 

Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.

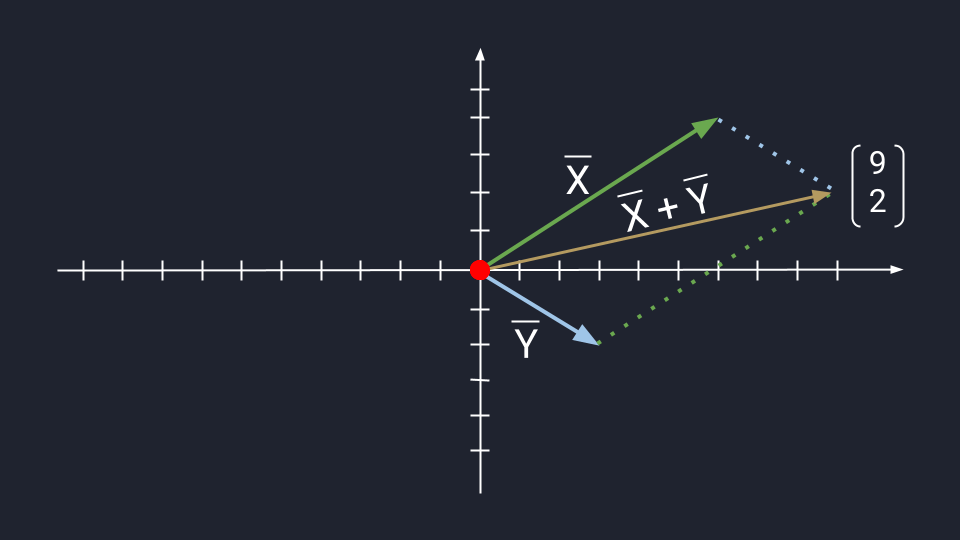Сложение векторов по методу параллелограмма: X = (6, 4); Y = (3, -2); Х + Y = (9, 2)

6 Произведение вектора на число

Произведение
ненулевого вектора

на число k дает вектор

=
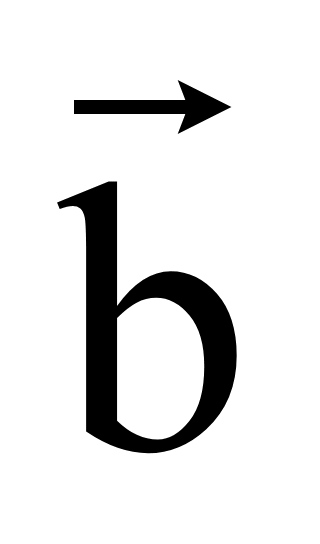k
,

коллинеарный
вектору

.

Например,
вектор

= 2

дает вектор
сонаправленный вектору

и в 2 раза длиннее вектора

.

Например,
вектор

= -4

дает вектор

противоположно направленный вектору

и в 4 раза длиннее вектора

.

Длина
вектора

:

|
|
= |k|·|
|.

Для
соотношения векторов

=
k

проанализируем
все возможные варианты в зависимости от коэффициента k:

—
если k > 0, то
векторы

и

сонаправленные.

—
если k = 0, то
вектор

нулевой.

—
если k < 0, то
векторы

и

противоположно направленные.

—
если |k| = 1, то
векторы

и

равной длины.

—
если k = 1, то

и

равные векторы.

—
если k = -1, то

и

противоположные векторы.

—
если |k| > 1,
то длина вектора

больше длины вектора

.

—
если k > 1, то
векторы

и

сонаправленные и длина

больше длины вектора

.

—
если k < -1,
то векторы

и

противоположно направленные и длина

больше длины вектора

.

—
если |k| < 1,
то длина вектора

меньше длины вектора

.

—
если 0 < k <
1, то векторы

и

сонаправленные и длина

меньше длины вектора

.

—
если -1 < k <
0, то векторы

и

противоположно направленные и длина

меньше длины вектора

.

Произведение
нулевого вектора на любое число дает нулевой вектор.

Задача.
Дан вектор

Построить
векторы 2
,
-3
,
0,5
,
-1,5
.

Задача.
Даны векторы

и

.

Построить
векторы 3
+
2
.

Решение

Векторы
2

— 2
,
-2

—

предлагается построить самостоятельно.

Законы,
описывающие умножение вектора на число

1.
Сочетательный закон (kn)
=
k(n
)

2.
Первый распределительный закон k(
+

)
= k
+
k
.

3.
Второй распределительный закон (k + n)

= k
+
n
.

Для
коллинеарных векторов

и

,
если

≠ 0, существует единственное число k,
позволяющее выразить вектор

через

:

=
k
.

Это
число равно

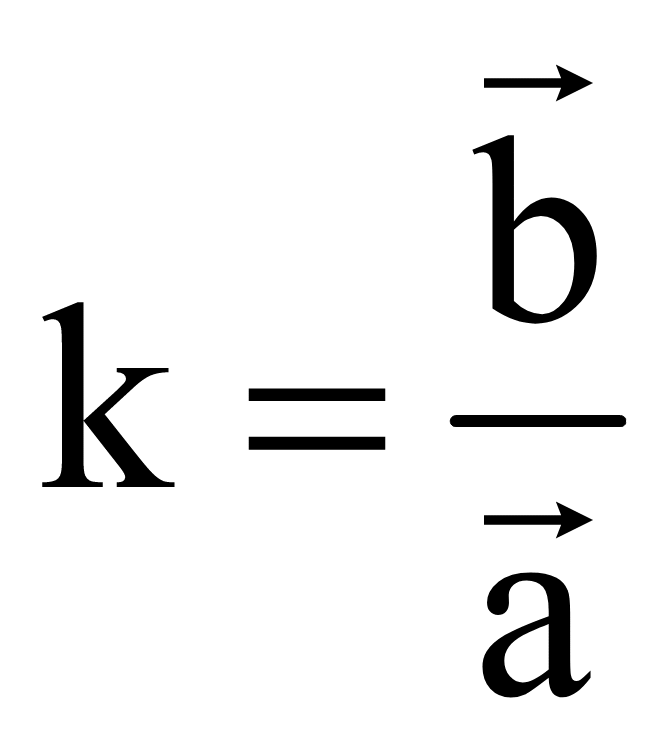
18 Скалярное произведение векторов

Скалярное
произведение двух векторов – это число (скаляр), равное
произведению длин векторов на косинус угла между векторами

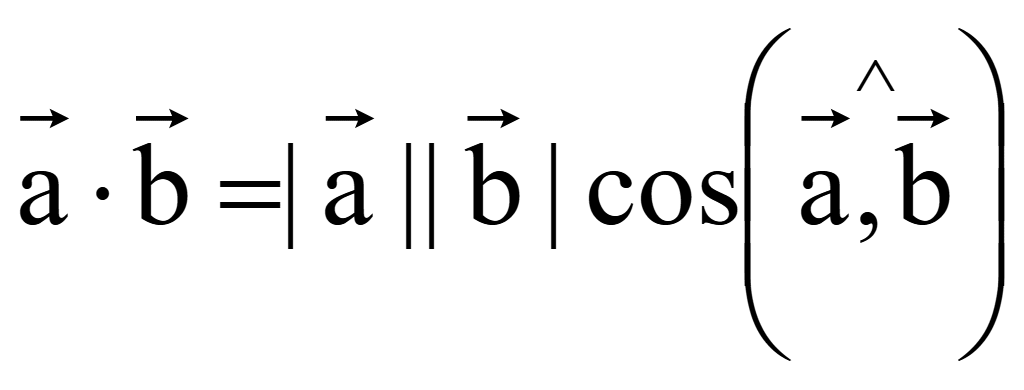
Если

=
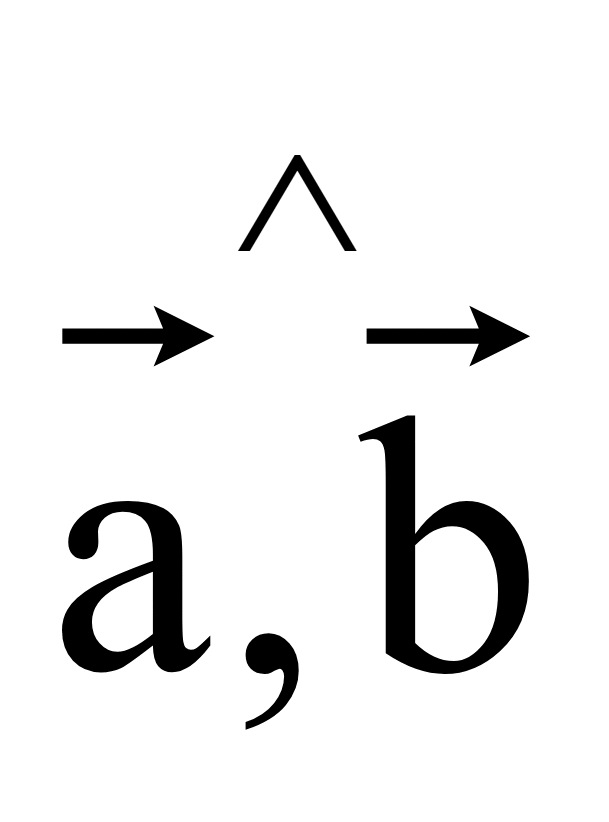
0, то векторы сонаправлены

и

=
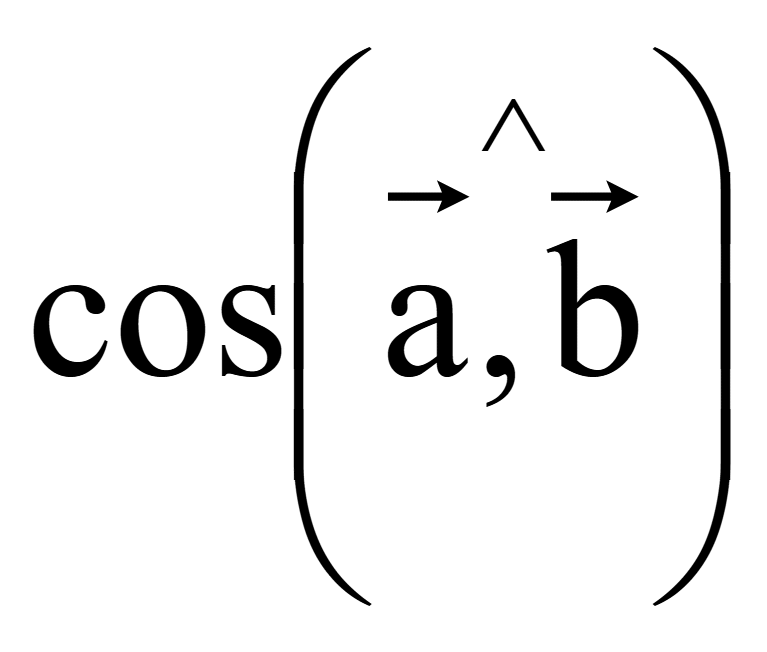cos 0 = 1,

следовательно,
скалярное произведение сонаправленных векторов равно произведению их
длин (модулей)

.

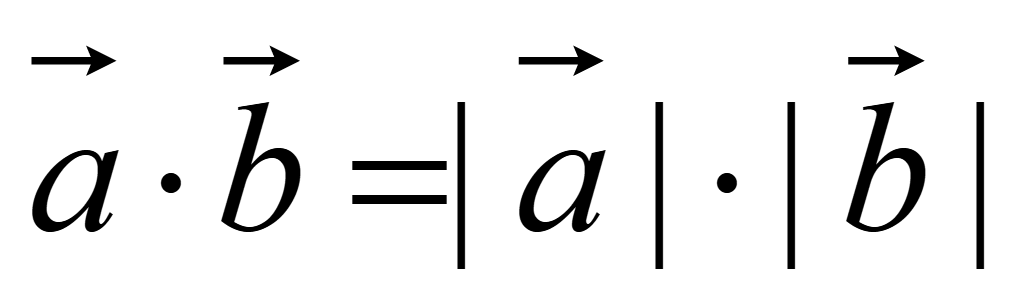Если
угол между векторами 0 <

< 90, то косинус угла между такими векторами больше
нуля

,
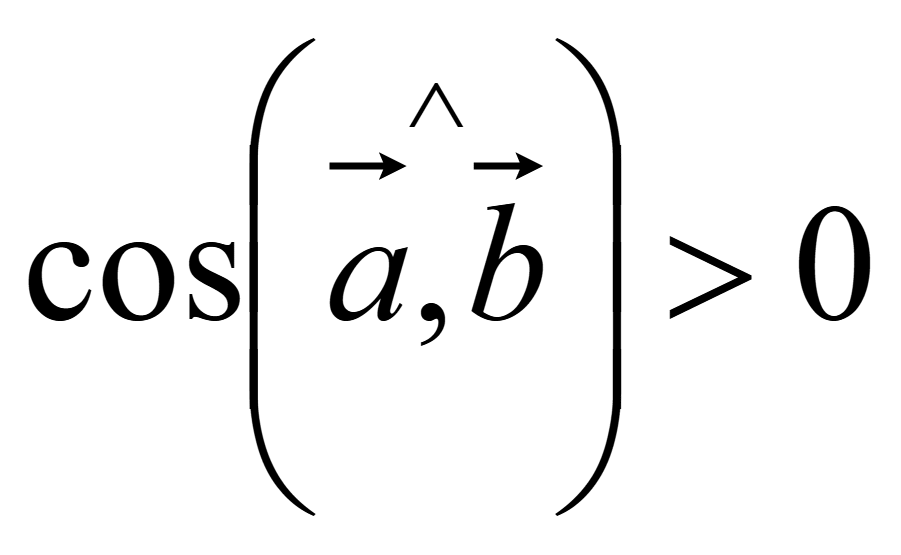
следовательно скалярное произведение больше нуля

.

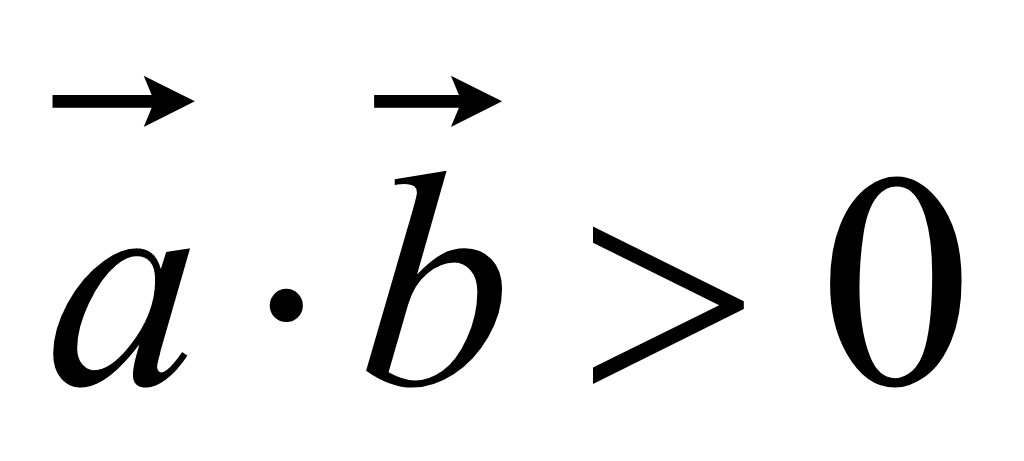
Если
ненулевые векторы перпендикулярны, то их скалярное произведение равно
нулю

,
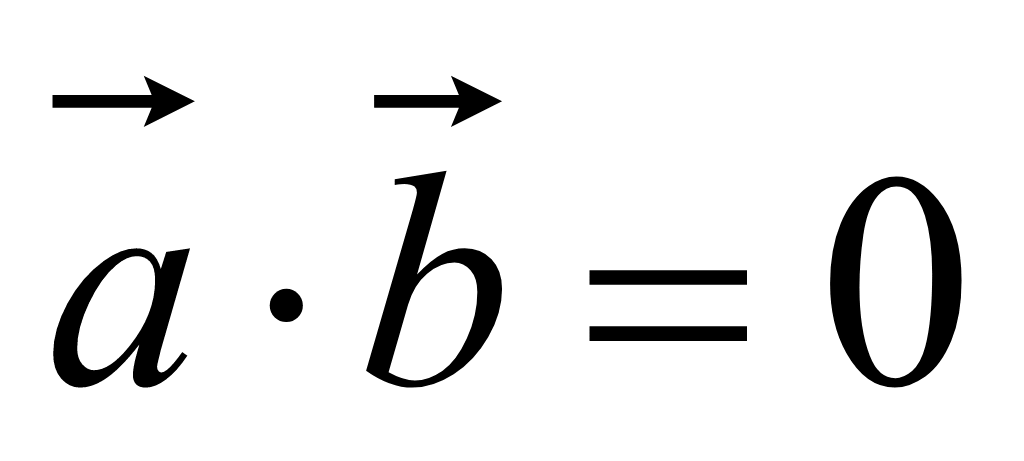
так как cos90 = 0. Скалярное
произведение перпендикулярных векторов равно нулю.

Если

,
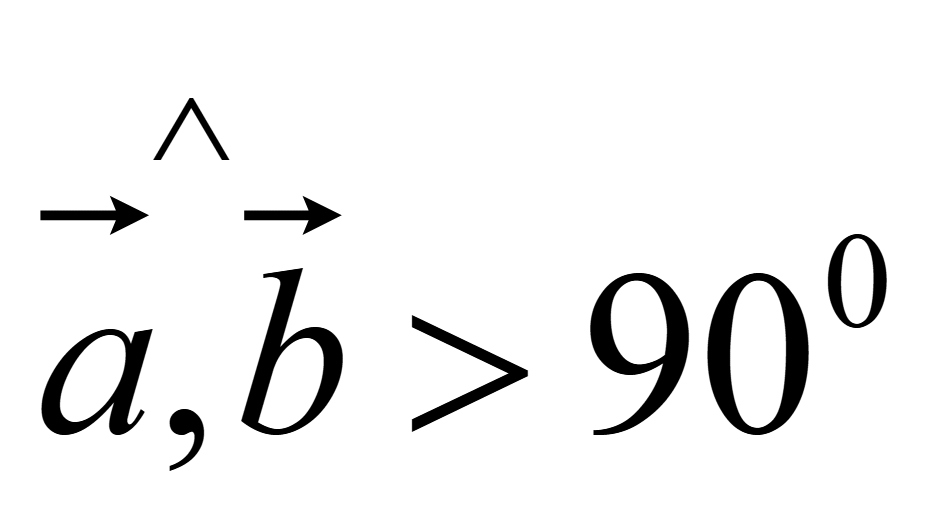
то косинус угла между такими векторами меньше нуля

,
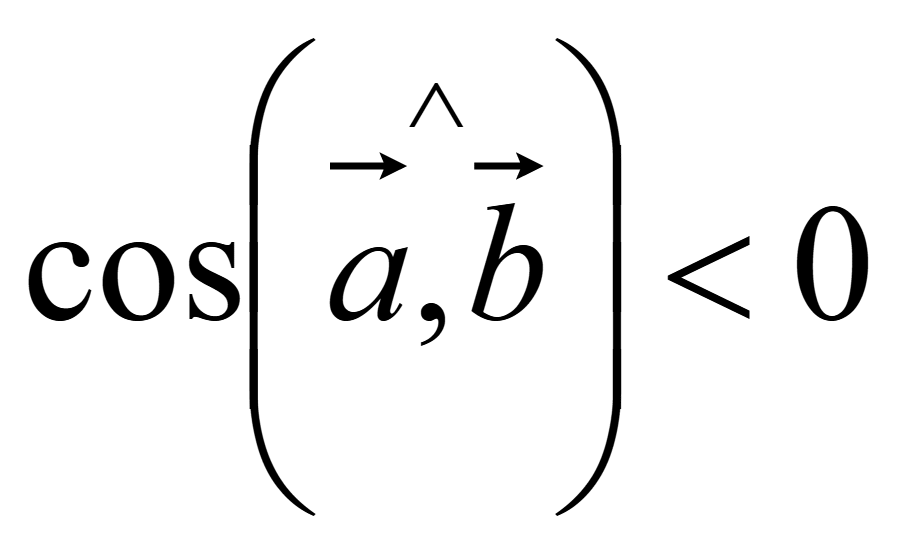
следовательно скалярное произведение меньше нуля

.

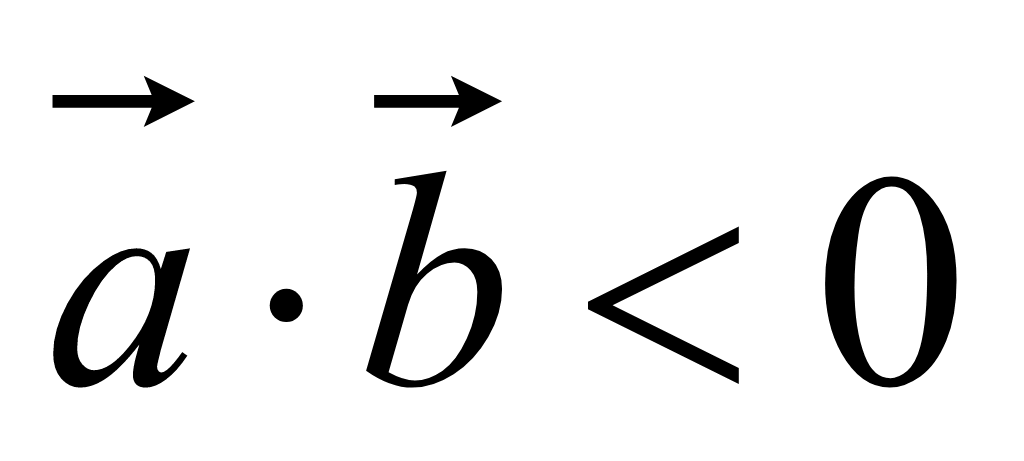
При
увеличении угла между векторами косинус угла между ними

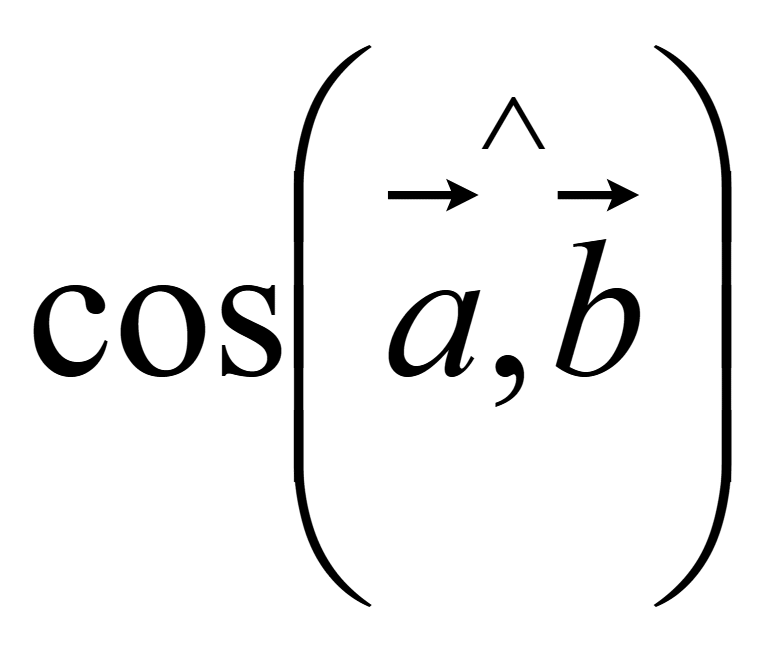
уменьшается и достигает минимального значения при

=
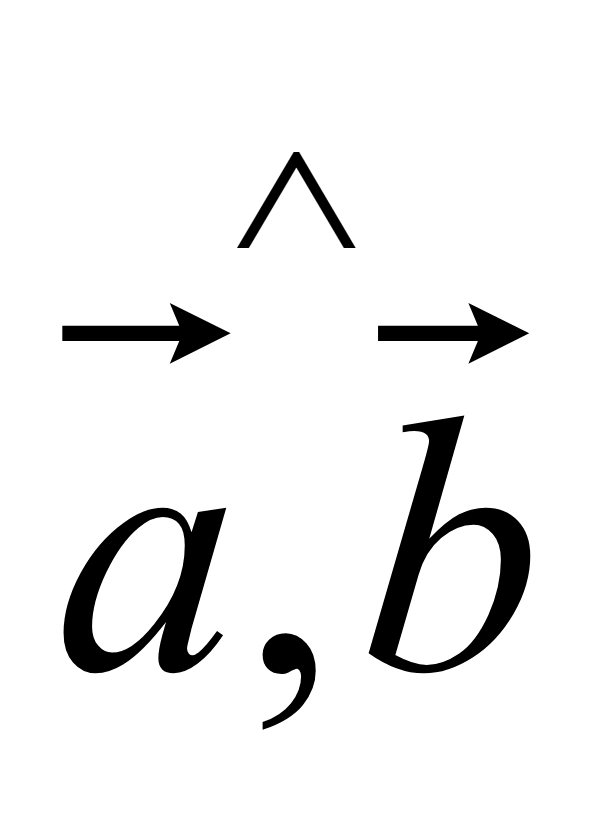
180, когда векторы противоположно направлены

.
Так как cos180=-1, то

.
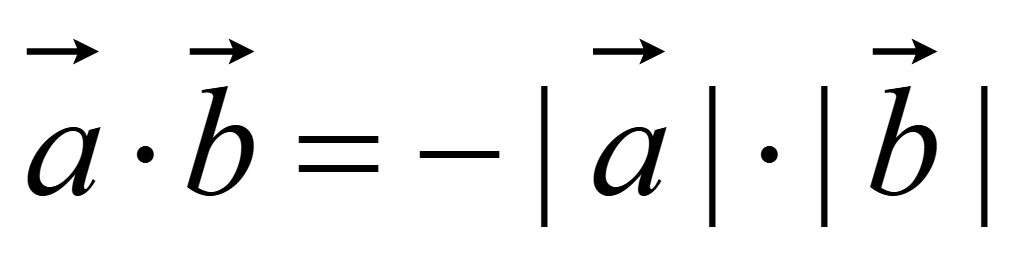
Скалярное произведение противоположно направленных векторов равно
отрицательному произведению их длин (модулей).

Скалярный
квадрат вектора равен модулю вектора в квадрате

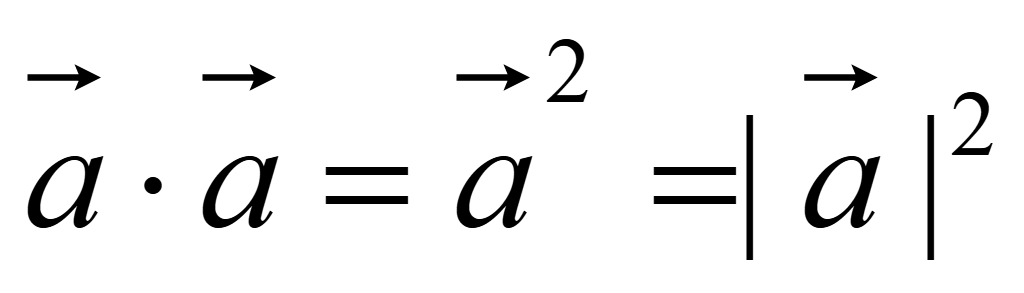
Скалярное
произведение векторов, по крайней мере один из которых нулевой, равно
нулю.

Нахождение координат вектора в пространстве

Теперь рассмотрим векторы в трехмерном пространстве, здесь все почти так же, как на плоскости, но будет добавлена ​​только одна дополнительная координата.

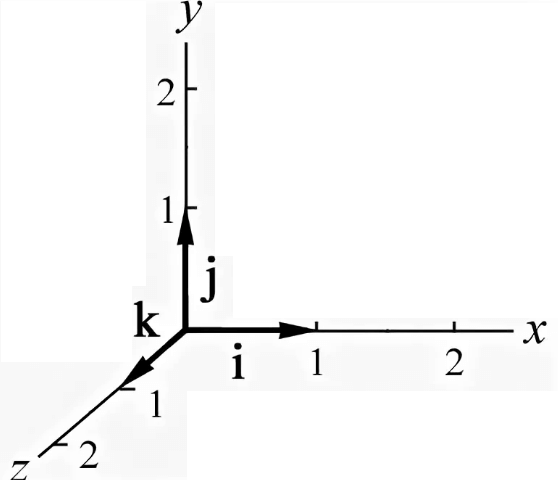Рис. 5.

Любой вектор в пространстве выражается следующим образом:

\, где координаты вектора (числа) в заданном базисе.

Пример 2

Нужно найти вектор, соединяющий точку А (начало) с координатами (4, 5, 6) с точкой В (конец) с координатами (10, 11, 12).

Решение:

Вектор направлен из точки А в точку В и может быть обозначен как \. Таким образом:

\

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь