Скалярное произведение векторов и его свойства с примерами решения и образцами выполнения

Доказательство формулы скалярного произведения – точка b

Мой опыт работы с скалярным произведением

Когда я впервые столкнулся с скалярным произведением в школе, мне пришлось немало потрудиться. Скалярное произведение двух векторов $\mathbf{a}$ и $\mathbf{b}$ определяется как $\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{ б}| \cos \theta$, где $\theta$ — угол между двумя векторами. Это определение стало для меня камнем преткновения. До этого момента большинство определений становились довольно интуитивными (и если не поначалу, то обычно через неделю или две после работы с ними они начинают казаться достаточно естественными). Эта формула или определение кажется просто вырванным из воздуха.

Далее была механика выполнения скалярного произведения: дано, что $\begin{pmatrix} a \\ b \\ c \end{pmatrix} \cdot \begin{pmatrix} d \\ e \\ f \end {pmatrix} = объявление + be + cf$. Естественной операцией было покомпонентное умножение элементов для получения вектора $\begin{pmatrix} ad \\ be \\ cf \end{pmatrix}$, так почему же это не так? Более того, если бы я просто принял результат, что «означало бы» количество $ad+be+cf$?

Потребовалось довольно много времени, чтобы «просто принять формулы и использовать их для решения вопросов», прежде чем я научился лучше разбираться в этом в школе.

Нам даны два вектора, $\begin{pmatrix} a \\ b \\ c \end{pmatrix}$ и $\begin{pmatrix} d \\ e \\ f \end{pmatrix}$, и мы надеемся «сочетать/умножать» их каким-либо образом. Мы можем определить естественную операцию $\begin{pmatrix} a \\ b \\ c \end{pmatrix} \otimes \begin{pmatrix} d \\ e \\ f \end{pmatrix} = \begin{pmatrix} ad \\ be \\ cf \end{pmatrix}$. Оказывается, это совершенно верно, и на самом деле это то, что мы можем проанализировать в теме абстрактной алгебры и колец. Однако на данный момент нас интересуют векторы как способ изучения геометрии (и интересуют такие величины, как длина, площади и углы). Насколько я знаю, операция, определенная как «естественно», для этого, к сожалению, не очень полезна.

Таким образом, мы определяем скалярное произведение как $\begin{pmatrix} a \\ b \\ c \end{pmatrix} \cdot \begin{pmatrix} d \\ e \\ f \end{pmatrix} = ad + быть + ср$.

Некоторые свойства скалярного произведения, полученные из определения

Прежде чем вывести окончательную формулу, нам понадобятся некоторые свойства скалярного произведения. Сначала у нас есть A: $k (\mathbf{a} \cdot \mathbf{b}) = (k\mathbf{a}) \cdot \mathbf{b}$. Как это можно доказать, проверив это: слева мы сначала выполняем скалярное произведение, чтобы получить $k (ad+be+cf)$, если $\mathbf{a}=\begin{pmatrix}a \\ b \ \ c \end{pmatrix}$ и $\mathbf{b} = \begin{pmatrix}d \\ e \\ f \end{pmatrix}$. Расширение наших обычных действительных чисел дает нам $kad + kbe + kcf$. Если теперь мы вычислим правую часть $(k\mathbf{a}) \cdot \mathbf{b}$ независимо, сначала выполнив скалярное умножение $k\mathbf{a}$, чтобы получить $\begin{pmatrix}ka \\ kb \\ kc \end{pmatrix}$ и затем скалярное произведение мы получим тот же ответ $kad+kbe+kcf$.

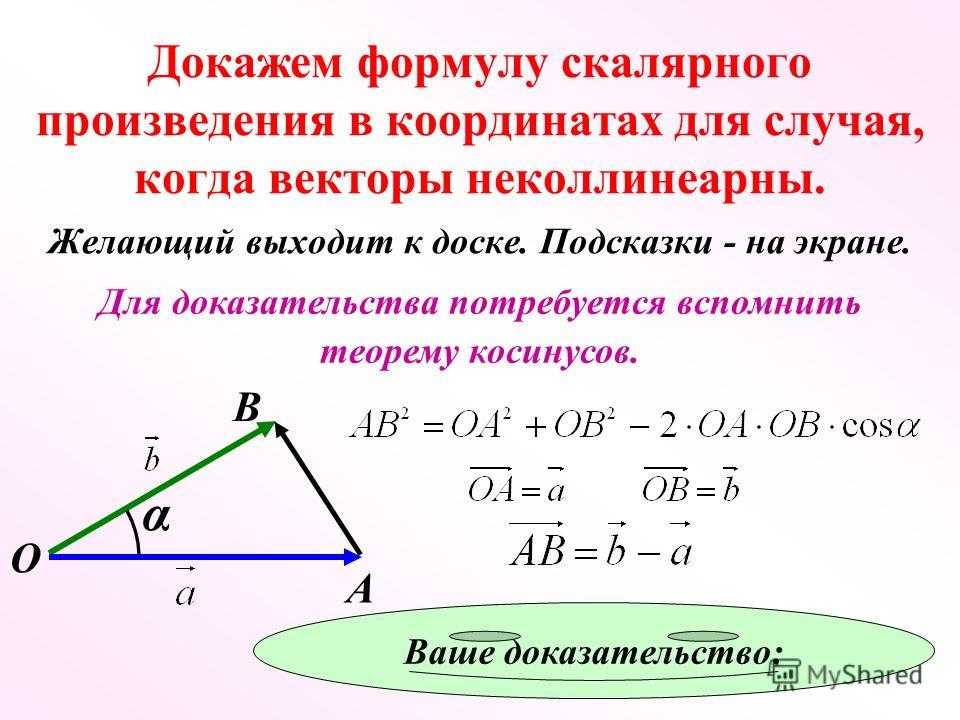
Угол между векторами

Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=<∠(→a; →b)=<180° либо 0°=<∠(→a; →b)=<>

Значок угла ∠ можно опустить и писать просто: (→a;→b).

Пусть даны два вектора →a, →b.

Отложим их от некоторой точки О пространства: →OA = →a; →OB = →b. Тогда угол между векторами — это угол ∠AOB = (→a, →b).

Угол между векторами может быть прямым, тупым или острым. Рассмотрим каждый случай:

Если векторы сонаправлены, то угол между ними равен 0°.

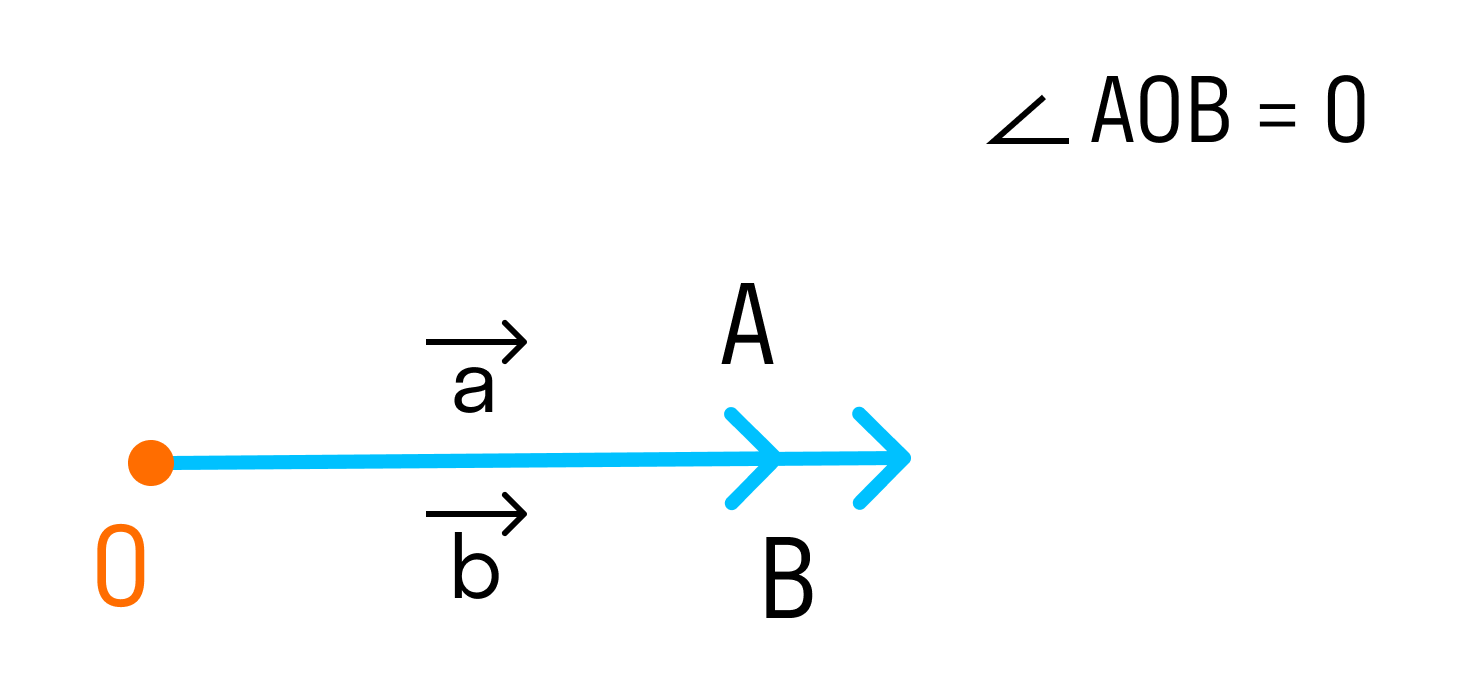
Так как косинус угла в 0° равен единице, то скалярное произведение сонаправленных векторов является произведением их длин. Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.

Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

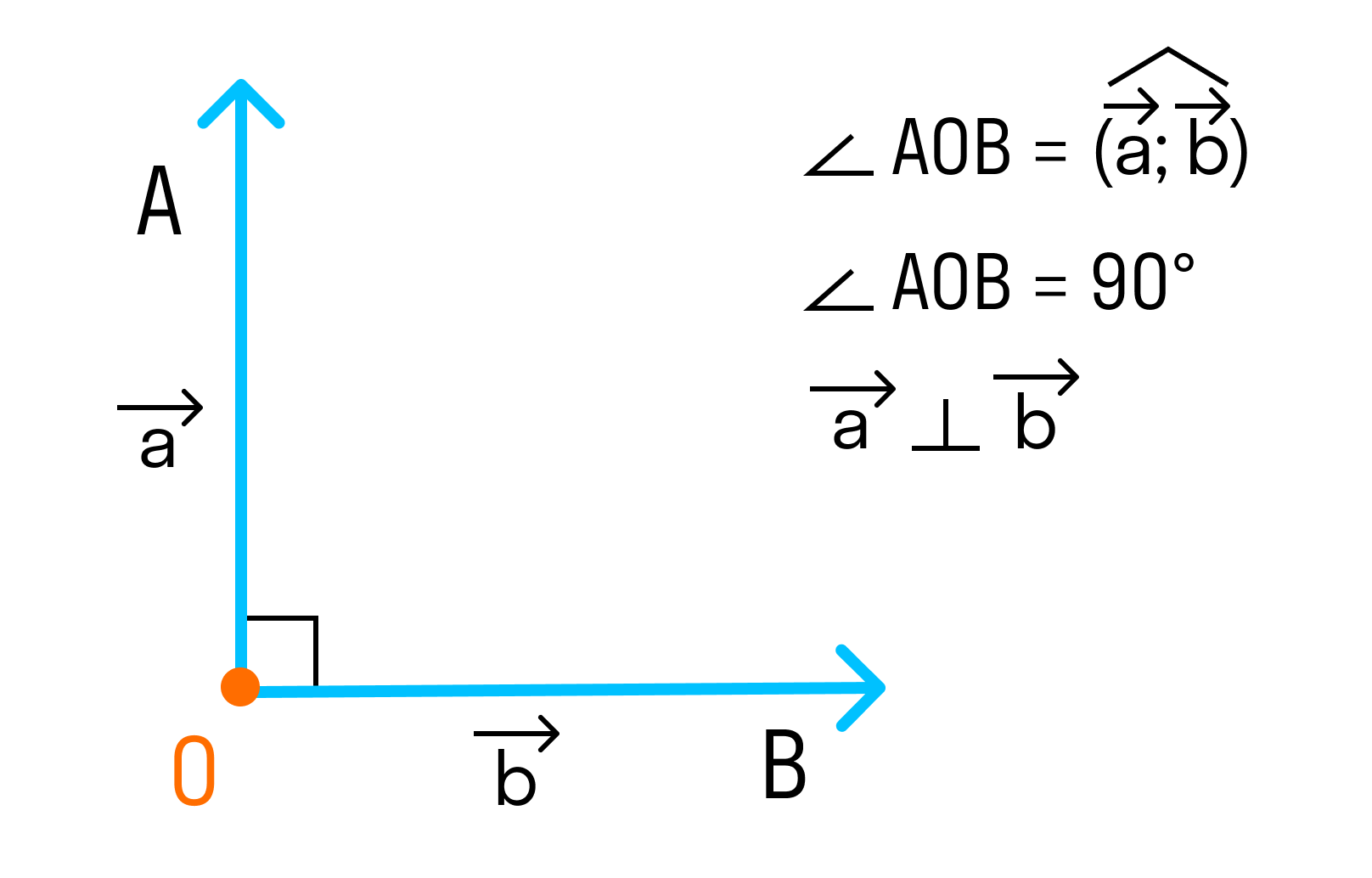
Так как косинус прямого угла равен 0, то скалярное произведение перпендикулярных векторов равно 0.

Если векторы направлены в разные стороны, тогда угол между ними 180°.

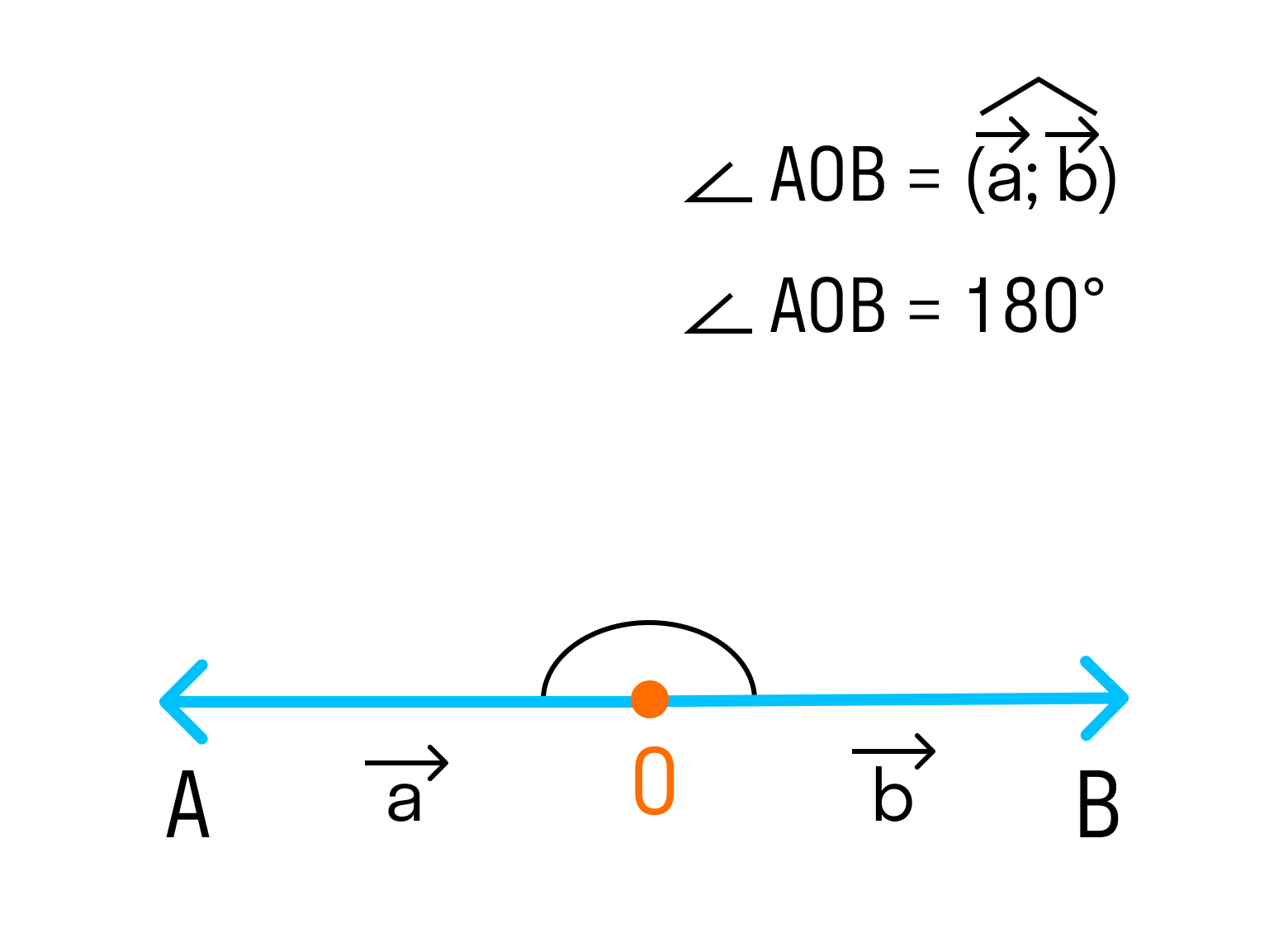
Так как косинус угла в 180° равен -1, то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.

Также векторы могут образовывать тупой угол. Это выглядит так:

Свойства скалярного произведения

1. $\vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a}$;
2. $(k\vec{a})\cdot \vec{b}=k(\vec{a}\cdot \vec{b})$;
3. $(\vec{a}+\vec{b})\cdot \vec{c}=\vec{a}\cdot \vec{c}+\vec{b}\cdot \vec{c}$.

Доказательство

Первое свойство очевидно в силу определения скалярного произведения.

Действительно, $\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos{\angle (\vec{a};\vec{b})}=|\vec{b}||\vec{a}|\cos{\angle (\vec{b};\vec{a})}=\vec{b}\cdot \vec{a}$.

Докажем второе свойство, используя теорему \ref{149}.

Пусть $\vec{a}$ имеет координаты $(x_1;y_1)$, а вектор $\vec{b}$ имеет координаты $(x_2;y_2)$.

Тогда вектор $(k\vec{a})\cdot\vec{b}=kx_1;ky_1)\cdot(x_2;y_2)=kx_1x_2+ky_1y_2=k(x_1x_2+y_1y_2)=k\vec{a}\cdot\vec{b}$.

Докажем третье свойство, используя теорему \ref{149}.

Пусть вектор $a$ имеет координаты $(x_a;y_a)$, вектор $b$ имеет координаты $(x_b;y_b)$, вектор $c$ имеет координаты $(x_c;y_c)$.

Тогда $(\vec{a}+\vec{b})\cdot \vec{c}=(x_a+x_b;y_a+y_b)\cdot(x_c;y_c)=(x_a+x_b)x_c+(y_a+y_b)y_c=\\=x_ax_c+x_bx_c+y_ay_c+y_by_c=(x_ax_c+y_ay_c)+(x_bx_c+y_by_c)=\vec{a}\cdot\vec{c}+\vec{b}\cdot \vec{c}$.

почему мы используем косинус как выражение векторного скалярного произведения?

Спросил 7 лет, 7 месяцев назад

Изменено
1 год, 1 месяц назад

Просмотрено
49 тысяч раз

$\begingroup$

Когда мы делаем векторные продукты, мы используем два разных метода.

Почему мы используем косинус в качестве выражения?

векторов

$\endgroup$

2

$\begingroup$

Пусть $\vec{\mathbf a} = (x_1, y_1) = (a \cos\alpha, a \sin\alpha)$

Пусть $\vec{\mathbf b} = (x_2, y_2) = (b \cos\beta, b\sin\beta)$

Тогда $\theta = |\beta — \alpha|$

По определению,

\begin{align}
\vec{\mathbf a} \circ \vec{\mathbf b}
&= x_1x_2 + y_1y_2 \\
&= ab(\cos\alpha\cos\beta+\sin\alpha\sin\beta) \\
&= аб \cos(\бета — \альфа)\\
&= аб \ соз \ тета
\end{выравнивание}

(Примечание: $\cos(\theta) = \cos(-\theta)$)

$\endgroup$

2

$\begingroup$

Скалярное произведение двух векторов $A$ и $B$ — это просто произведение величины одного вектора на скалярную проекцию другого на самого себя.

$\endgroup$

1

$\begingroup$

Скалярный продукт определяется таким образом.
Обратите внимание, что $cos\theta$ — подходящая функция; так как по неравенству Шварца:
$$|\mathbf{A} \cdot \mathbf{B}| \leq |\mathbf{A}| |\mathbf{B}|$$
и, таким образом, скалярное произведение постоянно находится в диапазоне от -1 до 1, как $ cos \ theta $ для $ \ theta \ in $. $\endgroup$

$\endgroup$

$\begingroup$

Это полностью определяется тем, что мы считаем вращением в плоскости.

Пусть $u, v$ — два единичных вектора. Пусть угол между ними равен $\theta$, и мы можем естественно записать $v$ как

$$v = u \cos \theta + u_\perp \sin \theta$$

, где $u_\perp$ единичный вектор, перпендикулярный $u$.

Но , если вы больше не находитесь в евклидовой плоскости, эта связь больше не выполняется. Например, в лоренцевом пространстве вместо косинуса и синуса вместо них мы получаем гиперболические функции:

$$v = u \cosh \theta + u_\perp \sinh \theta$$

И скалярное произведение равно $u \cdot v = \cosh \theta$. Физик должен признать, что эта $\theta$ является «быстротой», и что приведенная здесь форма $v$ в точности соответствует любому бусту Лоренца.

Итак, причина, по которой мы используем синус и косинус в евклидовом пространстве, заключается в том, что они продиктованы использованием синуса и косинуса при поворотах. В других пространствах с другими операторами поворота вместо этого вы используете функции, связанные с этими поворотами.

$\endgroup$

2

$\begingroup$

В точечном произведении мы используем cos theta, потому что в этом типе произведения
1.

$\endgroup$

$\begingroup$

Потому что здесь косинус отвечает за выполнение любого типа работы, например, работа, выполненная косинусом, используется. Здесь одна ось используется для выполненной работы, т. е. ось x, а для оси x мы используем косинус

.
$\endgroup$

$\begingroup$

Косинус используется для того, чтобы оба вектора указывали в одном направлении.

$\endgroup$

$\begingroup$

На самом деле это определение скалярного произведения двух векторов.

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Угол между векторами

Рассмотрим два данных вектора $\overrightarrow{a}$ и $\overrightarrow{b}$. Отложим от произвольно выбранной точки $O$ векторы $\overrightarrow{a}=\overrightarrow{OA}$ и $\overrightarrow{b}=\overrightarrow{OB}$, тогда угол $AOB$ называется углом между векторами $\overrightarrow{a}$ и $\overrightarrow{b}$ (рис. 1).

Рисунок 1.

Отметим здесь, что если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены или один из них является нулевым вектором, тогда угол между векторами равен $0^0$.

Обозначение: $\widehat{\overrightarrow{a},\overrightarrow{b}}$

Применение в физике

Впервые скалярное произведение ввёл У. Гамильтон в 1846 году. Одновременно учёные начали использовать в своих работах векторное произведение, сумму скаляров. Понятие получило широкое применение и в физике. На его основе сформулированы главные законы электродинамики и механики.

Скаляр является физической величиной. Чтобы его задать, используется одно число. Примеры скаляров в физике:

• масса тела, равная 4 кг;
• температура воздуха на уровне +10 градусов.

В каждом предложенном варианте величина задаётся с помощью одного числа, поэтому масса тела и температура относятся к скалярам. Но это понятие в физике не считается простым числом. Для него характерна размерность.

Если в условиях задачи известно, что масса тела равна 3, необходимо указывать единицу измерения (килограммы, граммы). В математике можно сложить числа 3 и 10, а в физике суммируются только скаляры с одинаковой размерностью: массы с массой, градусы с градусами.

Если рассматривать векторную физическую величину, она характеризуется следующим образом:

1. Неотрицательность.
2. Направленность в пространстве.

Понятие скаляр — модуль вектора либо абсолютная величина. Если предположить, что транспортное средство двигается со скоростью 60 км/ч, такая информация считается неполной

В физике важно знать направление движения. Кроме модуля скорости как абсолютной величины, потребуется знать направление в пространстве, поэтому скорость считается векторной величиной.

Если сила идёт вдоль горизонта, тогда объект поедет горизонтально. При вертикальном воздействии силы вниз кирпич останется на прежнем месте. Он будет вжиматься в землю. Подобные явления указывают на то, что сила является вектором, поэтому для неё характерна размерность, модуль.

Для обозначения вектора в физике используются латинские буквы и стрелка:

• вектор скорости: →v;
• вектор силы: →F.

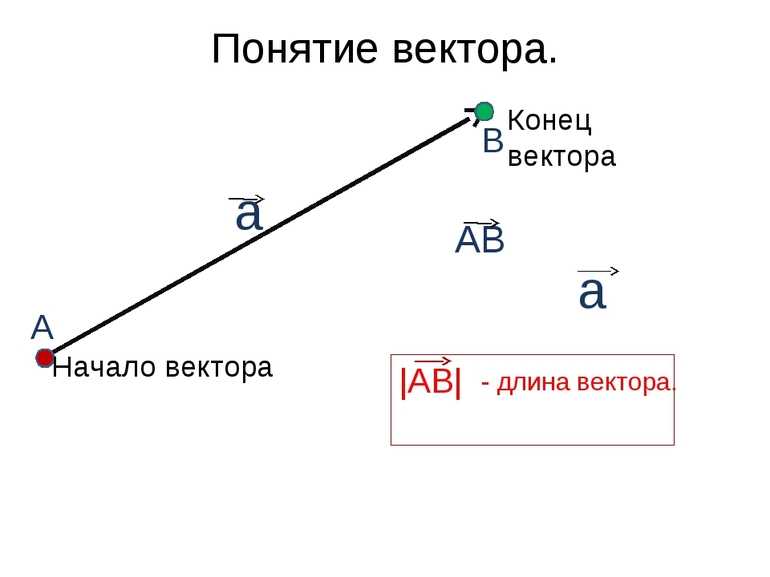
Стрелка является направленным отрезком. Её начальная точка — начало вектора, а конечная или остриё — конец вектора. В математике величина с начальной точкой А и концом В обозначается →АВ. Если начало и конец направленного отрезка совпадают, тогда получается нулевой вектор. Он обозначается →0.

Такой отрезок считается точкой. У него нет конкретного направления, а длина равняется нулю. К безразмерным скалярам относятся коэффициенты трения и полезного действия, показатель преломления света.

Скалярное произведение в ортонормированной системе координат[править]

Пусть заданы координаты двух векторов a={a1,a2,a3}{\displaystyle \mathbf {a} =\{a_{1},a_{2},a_{3}\}} и b={b1,b2,b3}{\displaystyle \mathbf {b} =\{b_{1},b_{2},b_{3}\}} в ортонормированной системе координат.

a⋅b=(a1e1+a2e2+a3e3)⋅(b1e1+b2e2+b3e3)==a1b1e1⋅e1+a2b2e2⋅e2+a3b3e3⋅e3+(a1b2+a2b1)e1⋅e2+(a1b3+a3b1)e1⋅e3+(a2b3+a3b2)e2⋅e3{\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3})\cdot (b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+b_{3}\mathbf {e} _{3})=\\&=a_{1}b_{1}\mathbf {e} _{1}\cdot \mathbf {e} _{1}+a_{2}b_{2}\mathbf {e} _{2}\cdot \mathbf {e} _{2}+a_{3}b_{3}\mathbf {e} _{3}\cdot \mathbf {e} _{3}+(a_{1}b_{2}+a_{2}b_{1})\mathbf {e} _{1}\cdot \mathbf {e} _{2}+(a_{1}b_{3}+a_{3}b_{1})\mathbf {e} _{1}\cdot \mathbf {e} _{3}+(a_{2}b_{3}+a_{3}b_{2})\mathbf {e} _{2}\cdot \mathbf {e} _{3}\end{aligned}}}

В ортонормированной системе координат e1⋅e1=e2⋅e2=e3⋅e3=1{\displaystyle \mathbf {e} _{1}\cdot \mathbf {e} _{1}=\mathbf {e} _{2}\cdot \mathbf {e} _{2}=\mathbf {e} _{3}\cdot \mathbf {e} _{3}=1} и e1⋅e2=e1⋅e3=e2⋅e3={\displaystyle \mathbf {e} _{1}\cdot \mathbf {e} _{2}=\mathbf {e} _{1}\cdot \mathbf {e} _{3}=\mathbf {e} _{2}\cdot \mathbf {e} _{3}=0}, так как cos⁡=1,cos⁡π2={\displaystyle \cos 0=1,\;\cos {\tfrac {\pi }{2}}=0}.
Поэтому

a⋅b=a1b1+a2b2+a3b3{\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}

Определение перпендикулярности векторов и прямых

Напомним, что скалярное произведение оказывается нулевым исключительно в случае перпендикулярности векторов. Это позволяет использовать его для проверки перпендикулярности векторов.

Задание. Проверьте, являются ли перпендикулярными вектора:

Решение. В каждом случае мы должны скалярно перемножить пару векторов. Если результат окажется нулевым, то можно сделать вывод о перпендикулярности векторов. В противном случае они не перпендикулярны. Первый вектор будет обозначать буквой а, а второй – буквой b:

Ответ: а) да; б) нет; в) да; г) нет.

Задание. При каком значении переменной х вектора а{4; 5} и b{x; – 6} окажутся перпендикулярными?

Решение. Перемножим скалярно вектора и получим некоторое выражение с переменной x:

Найдем, при каком х это выражение обращается в нуль, то есть вектора становятся перпендикулярными:

Задание. Определите, перпендикулярны ли прямые АВ и CD, если даны координаты точек: А(3; 8), В(4; 10), С(7;12) и D(5;13).

Решение. В этой задаче сначала надорассчитать координаты векторов АВ и CD по координатамих начальной и конечной точки:

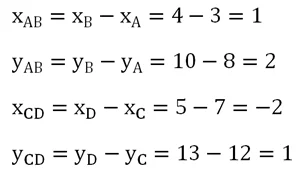
Мы вычислили координаты векторов: АВ{1; 2} и CD{– 2; 1}. Теперь мы можем проверить их перпендикулярность, скалярно перемножив вектора:

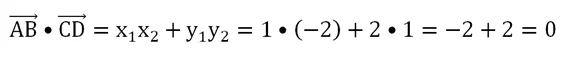
Мы получили ноль. Это означает, что АВ и CD – перпендикулярные вектора. Значит, и прямые, на которых они лежат, также перпендикулярны.

Ответ: перпендикулярны.

Задание. Перпендикулярны ли друг другу прямые, задаваемые уравнениями

Названия точкам в данном примере присвоены произвольно. На следующем шаге по координатам точек мы находим координаты векторов, лежащих на исследуемых прямых:

Полученный ноль показывает, что исходные прямые перпендикулярны.

Ответ: перпендикулярны.

В случае, когда прямые заданы уравнениями, необязательно проделывать столь длительные вычисления для определения их перпендикулярности. Есть теорема, сокращающая объем вычислений.

Докажем это утверждение. Пусть две прямые заданы уравнениями

Найдем какие-нибудь точки этих прямых. Для этого подставим в уравнения значения х = 0 и х = 1:

Прямые окажутся перпендикулярными исключительно в том случае, если это выражение будет нулевым. Это условие перпендикулярности можно записать как уравнение:

В результате мы получили доказываемую нами формулу.

Задание. Проверьте, какие из этих пар прямых перпендикулярны:

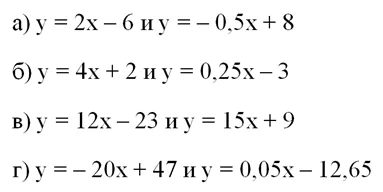
Решение. В каждом случае надо просто перемножить угловые коэффициенты прямых, то есть числа, стоящие перед переменной х. Другие числа в этих уравнениях (свободные коэффициенты) никак не влияют на перпендикулярность. Если вычисленное произведение окажется равным (– 1), то из этого будет вытекать перпендикулярность прямых.

Векторное произведение векторов

Так иногда бывает, что для полного счастья математикам нужно что-то еще, и если скалярное произведение еще может быть знакомо со школы, то векторное произведение чаще всего изучают в ВУЗе на курсах вышмата.

Обрадую всех вас — если все, что происходило до этого работало и в двухмерном и в трехмерном пространстве, то векторное произведение векторов подразумевает работу ТОЛЬКО с трехмерным пространством. (Стало проще, да ведь?)

В данном произведении участвуют также 2 вектора. Отличие от скалярного произведения тех же двух векторов будет в том, что в результате векторного произведения получается ВЕКТОР, а не число.

Формальное определение:
 

Векторным произведением  ā x b̅  неколлинеарных векторов  ā и b̅, взятых в определенном порядке, называется ВЕКТОР ā x b̅ , длина которого численно равна площади параллелограмма, построенного на данных векторах; вектор ā x b̅  ортогонален векторам  ā и b̅, и направлен так, что базис (ā; b̅;ā x b̅) имеет правую ориентацию.

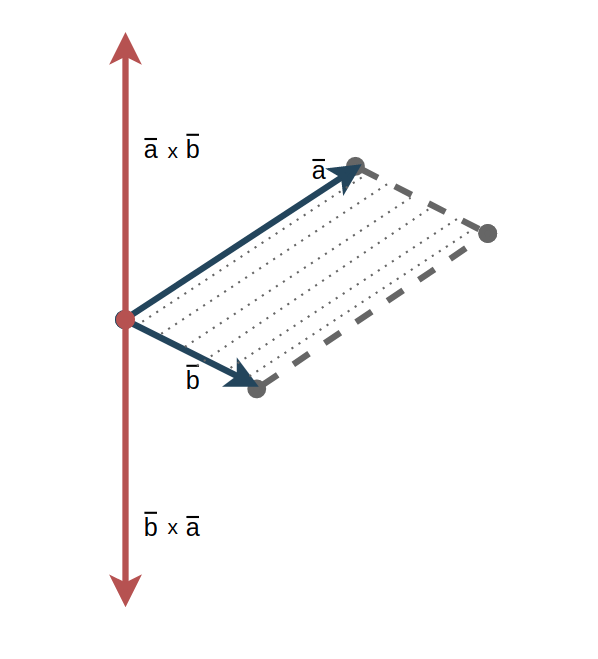
Это определение сложное и требует некоторых комментариев:

1. 

Векторы ā и b̅ по определению должны быть неколлинеарны. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Таким образом такие векторы могут называться параллельными, но так называть вектора просто не принято — их называют коллинеарными. Касаемо ситуации с векторным произведением — векторы должны быть, наоборот, непараллельными.

2.

 Важен порядок векторов. От этого зависит направление результата.

3.

Длина результирующего вектора равна площади заштрихованного параллелограмма. 

4.

Результирующий вектор ортогонален векторам  ā и b̅, т.е.  ā ┴   и  b ┴ 

5.

Результирующий вектор  направлен так, что базис (ā; b̅;ā x b̅) имеет правую ориентацию. 

Мысленно совместите указательный палец с вектором ā и средний палец с вектором b̅. Безымянный палец и мизинец прижмите к ладони. В результате большой палец – результирующий вектор будет смотреть вверх. Это правоориентированный базис.

Указательный палец левой руки с тем же вектором  ā, а средний – с вектором b̅. При этом большой палец будет неизбежно смотреть вниз – по направлению вектора . Это левый или левоориентированный базис.

Эти базисы не являются чем-то абстрактным. Примером может служить изображение и его отражение в зеркале. Самое обычное зеркало меняет ориентацию пространства, а изображение и зеркальное отражение этого отображения невозможно просто наложить друг на друга (попробуйте совместить «базисы» левой и правой руки, после чего станет понятно, что указательные и средние пальцы не совмещаются).

Что же будет, если вектора  ā и b̅ будут коллинеарны (т.е. параллельны, говоря на простом языке) — все просто, параллелаграм, который образуется этими векторами “складывается” в плоскую прямую, а площадь такой прямой равна нулю, из-за чего и результирующий вектор равен нулевому.  

Скалярное произведение векторов

Пусть векторы a и b заданы своими координатами в прямоугольной системе координат:

a ={ax , ay , az } и b ={bx ,by ,bz } .

Скалярным произведением векторов a и b называется число равное сумме произведений соответствующих координат:

a b = axbx + ayby + azbz .	(13)
Для обозначения скалярного произведения a b	используется также
выражение (a, b).

Теорема. Скалярное произведение векторов a и b равно произведению длин векторов на косинус угла между ними:

a b = a bcosθ .

Доказательство: Выберем такую прямоугольную систему координат, чтобы векторы a и b лежали в плоскости x,y, а вектор a был бы направлен вдоль положительного направления оси x.

В этой системе координат ax = a,	ay = az = 0 и	bx =bcos θ.

Следовательно, a b = axbx + ayby + azbz = abcosθ .

Бывает полезным представить эту теорему в несколько ином виде: a b = a Pr ojab = b Pr ojba

или

cosθ = aa bb .

Согласно последней формулировке косинус угла между векторами a

и b равен скалярному произведению единичных векторов aa и bb .

Рассмотрим несколько частных случаев.

1. Если a b , то cosθ =cos π2 =0 , что приводит нас к следующему условию ортогональности векторов a ={ax , ay , az } и b ={bx ,by ,bz } :

16

Если

axbx + ayby + azbz = 0 ,

то a b .

2. Если b = a, то θ = 0 и cosθ =1. Тогда

a a = a2 = ax2 +a2y +az2 .

Следовательно, длина вектора a выражается формулой

a = ax2 +a2y +az2 .

Используя две различных формулы для скалярного произведения векторов, и зная координаты векторов, мы можем легко найти угол между ними:

	cosθ =	a b	=	axbx +ayby +azbz
	a b	ax2 +a2y	+az2 bx2 +by2 +bz2

Большинство приложений скалярного произведения связано именно с нахождением угла между векторами, а также с использованием условия ортогональности векторов.

9.1. Свойства скалярного произведения

Нижеприведенные свойства основаны на определении скалярного произведения или непосредственно вытекают из доказанной теоремы. Их доказательство не приводится в виду своей очевидности.

1) Скалярное произведение векторов коммутативно: a b = b a .

2) Скалярное произведение векторов дистрибутивно:

(a +b) c = a c +b c .

3) Если скалярное произведение двух ненулевых векторов равно нулю, то векторы перпендикулярны друг другу и обратно, если два вектора перпендикулярны, то их скалярное произведение равно нулю:

a b a b =0 .

9.2. Примеры

Пример 1. Легко проверить, что векторы

i = {1, 0, 0}, j = {0, 1, 0} и k = {0, 0, 1}

образуют ортонормированный базис, т.е. являются единичными взаимно перпендикулярными векторами:

i i =1, j j =1, k k =1, i j = i k = j k =0 .

17

Пример 2. Если a = {2, –1, 3}, b = {5, 7, 4} и θ – угол между векторами a и b, то

a b = 2 5 +(−1) 7 +3 4 =15 ,

a =| a |= a a = 22 +(−1)2 +32 = 14 , b =| b |= b b = 52 +72 +42 = 80 = 4 5

и, следовательно,	a b		15			3
cosθ =	=	5	=	70 .
	| a | | b |		4 14		56

Пример 3. Найти угол между векторами a ={3, 2, −5} и b ={5, 7, 4}.

Решение. Так как

a b =3 1+4 3 +(−5) 3 =0 ,

то векторы являются ортогональными.

Пример 4. Выразить скалярное произведение векторов p и q через длины векторов a и b, если p = a + b и q = a – b.

Решение.

p q = (a +b) (a −b) = a 2 −a b +b a −b2 = a2 −b2 .

Пример 5. Зная две стороны AB и AC треугольника ABC и угол θ между этими сторонами, найти третью сторону треугольника.

→	→	→
Решение. Обозначим a = AB ,	b = AC и	c = CB .
Тогда
c = a −b
c2 = (a −b)2 = a2 +b2 −2a b

c2 = a2 + b2 − 2ab cosθ ,

что представляет собой известную из элементарной математики теорему косинусов. 5, a 1 6. Как насчет тебя? = (A, 5) = тогда cos (p = cos ~ = 0. ab- \ a \ -16 | • 0 = 0. Если a-5 = 0 и | a | φ0, \ b \ φ0, то cos (a, 5) = 0. Следовательно, tp = (a, b) = 90 °, т.е. a _L b. В частности: я •] -] — к = к-г = 0. ►

Пример: вершина A (-4; -4; 4), B (-3; 2; 2), C (2; 5; 1), £> (3; -2; Докажи диагонали) перпендикулярно друг другу. Построить векторы AC и BD по диагонали заданного четырехугольника. AS- (6; 9; -3) и BD = (6; -4; 0). Найти скалярное произведение этих векторов. AC • BD = 36-36 до 0 = 0. Результат AC -L BD.

Угол между векторами

Любую пару векторов можно отложить от одной точки. Если при этом вектора не сонаправлены друг с другом, то они образуют некоторый угол. Его и именуют углом между векторами.

Если же пара векторов сонаправлена, то принято считать, что угол между такими векторами составляет 0°.

На рисунке показаны два вектора, a и b. Чтобы определить угол между a и b, надо отложить их от одной и той же точки:

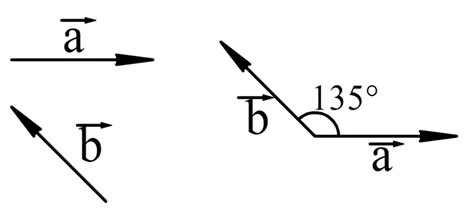
В приведенном примере угол составил 135°. Для обозначения этого угла может быть использована такая запись:

Задание. В квадрате АВСD проведены диагонали, они пересекаются в точке О. Определите, какой угол образуют вектора:

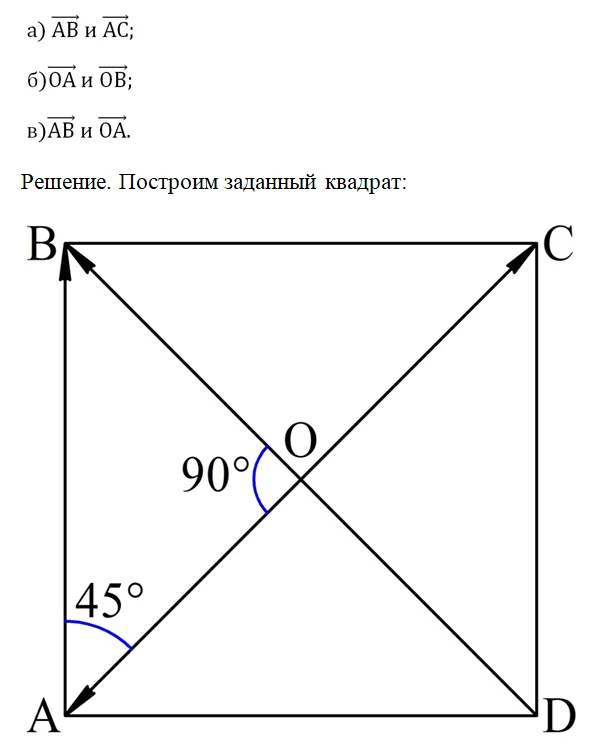
Так как в квадрате диагонали пересекаются под углом 90°, а со сторонами образуют угол 45°, то мы легко определим, что

Здесь нам помог тот факт, что вектора из пунктов а) и б) изначально отложены из одной точки. С пунктом в) ситуация сложнее. Надо отложить от точки А вектор ОА и определить угол, образующийся при этом:

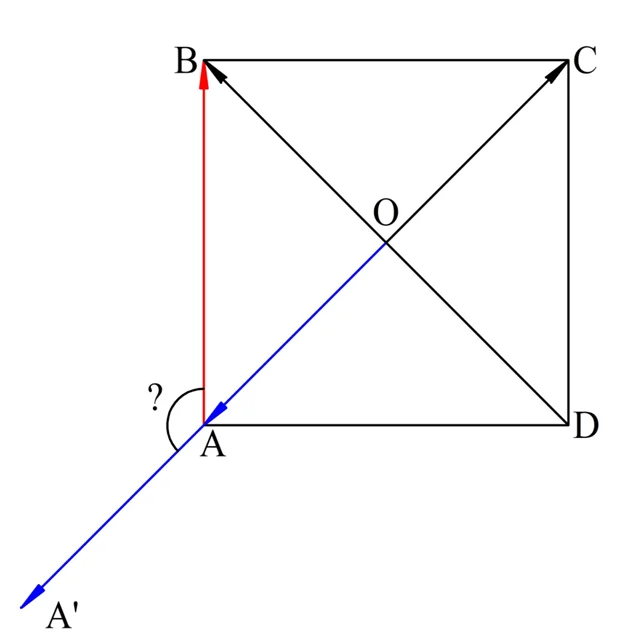
Пусть после откладывания вектора ОА от А получился вектора АА’. Нам надо найти ∠ВАА’. Нам уже известен ∠ОАВ, который является смежным с ∠ВАА’, поэтому можно записать равенство:

Ответ: а) 45°; б) 90°; в) 135°.

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.