Формула угла между векторами

Расчет угла, если вектор задан координатами

В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде \(\overrightarrow a=\left(a_x;a_y\right)\) и \(\overrightarrow b=\left(b_x;b_y\right)\), то угол между ними можно найти следующим образом:

\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}=\frac{a_x\cdot b_x+a_y\cdot b_y}{\sqrt{a_x^2+a_y^2}\cdot\sqrt{b_x^2+b_y^2}}\)

Если же координаты находятся в трехмерном пространстве и заданы в виде:

\(\overrightarrow a=\left(a_x;a_y;a_z\right)\)

\( \overrightarrow b=\left(b_x;b_y;b_z\right)\)

то формула принимает такой вид:

\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}=\frac{a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z}{\sqrt{a_x^2+a_y^2+a_z^2}\cdot\sqrt{b_x^2+b_y^2+b_z^2}}\)

Плоскость — как «обобщение» прямой

Однако с пространством не все так просто.

Как ты понимаешь, добавление еще одной координаты вносит существенное разнообразие в спектр фигур, «живущих» в этом пространстве. И для дальнейшего повествования мне потребуется ввести некоторое, грубо говоря, «обобщение» прямой.

Этим «обобщением» будет плоскость. Что ты знаешь про плоскость? Попробуй ответить на вопрос, а что такое плоскость? Очень сложно сказать.

Однако мы все интуитивно представляем, как она выглядит:

Грубо говоря, это некий бесконечный «лист», засунутый в пространство. «Бесконечность» следует понимать, что плоскость распространяется во все стороны, то есть ее площадь равна бесконечности.

Однако, это объяснение «на пальцах» не дает ни малейшего представления о структуре плоскости. А нас будет интересовать именно она.

Давай вспомним одну из основных аксиом геометрии: через две различные точки на плоскости проходит прямая, притом только одна.

Или ее аналог в пространстве: через три точки, не лежащие на одной прямой, проходит плоскость, притом только одна.

Нахождение угла между векторами

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

1. Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70

1. Также можно определить угол по формуле:

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70

Ответ: a → , b → ^ = — a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,

b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

37 Угол между двумя плоскостями

Две
плоскости могут быть параллельны или пересекаться по прямой.

Угол
между двумя пересекающимися плоскостями равен углу между двумя
пересекающимися прямыми, проведенными перпендикулярно линии
пересечения плоскостей.

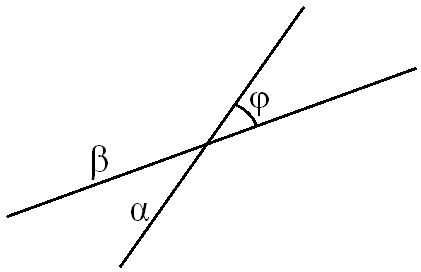
Поэтому
угол между плоскостями 0 ≤ φ ≤ 90.

Если
заданы две плоскости

a₁x
+ b₁y
+ c₁z
+ d₁ = 0

и

a₂x
+ b₂y
+ c₂z
+ d₂ = 0,

то
соответствующие нормальные векторы этих плоскостей
₁
(a₁; b₁;
c₁) и
₂
(a₂; b₂;
c₂). Косинус угла θ между
нормальными векторами плоскостей

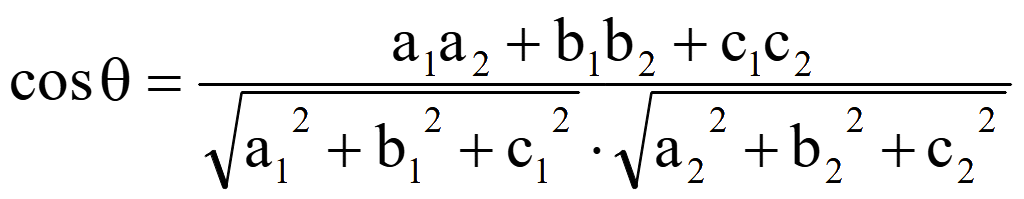
Если
угол φ между плоскостями α и β равен углу θ
между нормальными векторами этих плоскостей φ = θ, то

cos
φ = cos θ.

Если
угол между плоскостями φ = 180 — θ, то

cos
φ = cos (180
— θ) = — cos θ.

cos
φ = — cos θ.

Косинус
угла между плоскостями

a₁x
+ b₁y
+ c₁z
+ d₁ =
0

и

a₂x
+ b₂y
+ c₂z
+ d₂ =
0

равен
модулю косинуса угла между нормальными векторами
₁
(a₁; b₁;
c₁) и
₂
(a₂; b₂;
c₂) этих плоскостей

cos
φ = |cos θ| =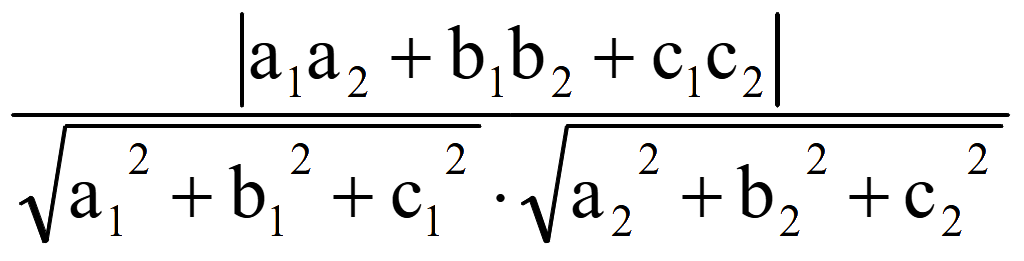

или
можно записать так

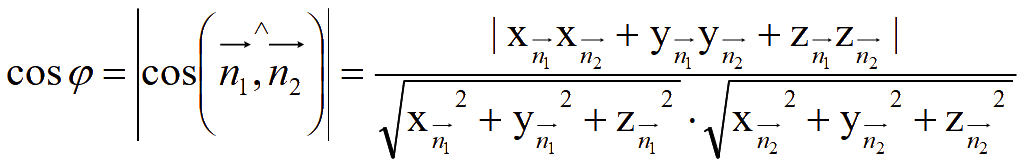
Для
лучшего запоминания сформулируем следующее правило. Плоскости
являются одинаковыми геометрическими объектами, поэтому и одинаковые
тригонометрические функции cos присутствуют
в формуле.

Косинус
угла между плоскостями

cos
φ =

Угол
между плоскостями

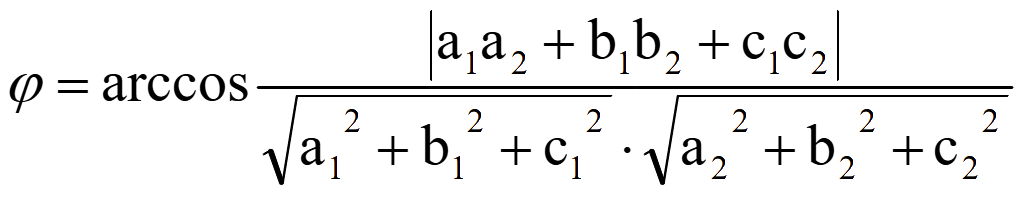
Если
cos φ = 1, то угол φ между
плоскостями равен 0, можно принять для этих плоскостей
один из нормальных векторов этих плоскостей, плоскости параллельны
или совпадают. Если плоскости не совпадают, то они параллельны. Если
плоскости совпадают, то любая точка одной плоскости принадлежит
другой плоскости.

Если
скалярное произведение нормальных ненулевых векторов
₁
(a₁; b₁;
c₁) и
₂
(a₂; b₂;
c₂) плоскостей равно нулю

a₁a₂
+ b₁b₂
+ c₁c₂= 0

и,
следовательно, cos φ = 0, то угол φ
между плоскостями 90 (плоскости перпендикулярны),
плоскости пересекаются по прямой.

Если
0 ≤ cos φ < 1, то угол между
плоскостями 0 < φ ≤ 90, плоскости
пересекаются по прямой.

37.1 Алгоритм
нахождения угла между двумя плоскостями

1.
Задать систему координат с началом на линии пересечения плоскостей.
Плоскости проходят через начало координат, поэтому d
= 0.

2.
В системе координат построить не менее двух точек, задающих каждую
плоскость, между которыми требуется определить угол. Эти две точки
необходимо задать так, чтобы прямая, соединяющая эти точки не
проходила через начало координат.

3.
Определить координаты заданных двух точек для каждой плоскости.

4.
Задать один коэффициент уравнения плоскости равным 1, обычно
принимается a = 1. Если какая-то координата
равна 0, то принять за 1 необходимо коэффициент, соответствующий этой
координате.

5.
Составить систему двух уравнений для каждой из 2-х плоскостей. В
каждой системе уравнений каждое уравнение соответствует каждой из 2-х
точек на плоскости.

6.
Решить системы уравнений и составить уравнения двух плоскостей, из
которых определяются координаты двух нормальных векторов.

7.
Косинус угла между плоскостями равен модулю косинуса угла между
нормальными векторами этих плоскостей

cos
φ = |cos θ| =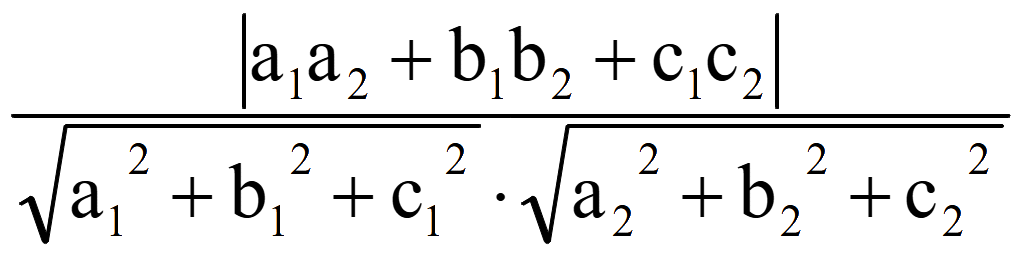

Задача.
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁
заданы ребра: AB = 16, AD
= 14, СС₁ = 24. Найти угол между плоскостями ABC
и A₁DB.

Вычисление углов между двумя плоскостями

Алгоритм решения будет таков:

• По трем точкам ищем уравнение первой плоскости: \( {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+{{D}_{1}}=0\)
• По другим трем точкам ищем уравнение второй плоскости: \( {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+{{D}_{2}}=0\)
• Применяем формулу: \( cos\varphi =\frac{\left| {{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}~ \right|}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}\cdot \sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}\)

Как видишь, формула очень похожа на две предыдущие, при помощи которых мы искали углы между прямыми и между прямой и плоскостью.

Так что запомнить эту тебе не составит особого труда. Сразу переходим к разбору задач:

Выбор системы координат

Ну вот, теперь у нас есть весь необходимый фундамент знаний, чтобы решать сложные стереометрические задачи по геометрии.

Однако прежде чем приступать непосредственно к примерам и алгоритмам их решения, я считаю, что будет полезно остановиться еще вот на каком вопросе: как именно выбирать систему координат для той или иной фигуры.

Ведь именно выбор взаимного расположения системы координат и фигуры в пространстве в конечном счете определит, насколько громоздкими будут вычисления.

Я напомню, что в этом разделе мы рассматриваем следующие фигуры:

• куб;
• Прямоугольный параллелепипед;
• Прямая призма (треугольная, шестиугольная…);
• Пирамида (треугольная, четырехугольная);
• Тетраэдр (одно и то же, что и треугольная пирамида).

Определение перпендикулярности векторов и прямых

Напомним, что скалярное произведение оказывается нулевым исключительно в случае перпендикулярности векторов. Это позволяет использовать его для проверки перпендикулярности векторов.

Задание. Проверьте, являются ли перпендикулярными вектора:

Решение. В каждом случае мы должны скалярно перемножить пару векторов. Если результат окажется нулевым, то можно сделать вывод о перпендикулярности векторов. В противном случае они не перпендикулярны. Первый вектор будет обозначать буквой а, а второй – буквой b:

Ответ: а) да; б) нет; в) да; г) нет.

Задание. При каком значении переменной х вектора а{4; 5} и b{x; – 6} окажутся перпендикулярными?

Решение. Перемножим скалярно вектора и получим некоторое выражение с переменной x:

Найдем, при каком х это выражение обращается в нуль, то есть вектора становятся перпендикулярными:

Задание. Определите, перпендикулярны ли прямые АВ и CD, если даны координаты точек: А(3; 8), В(4; 10), С(7;12) и D(5;13).

Решение. В этой задаче сначала надорассчитать координаты векторов АВ и CD по координатамих начальной и конечной точки:

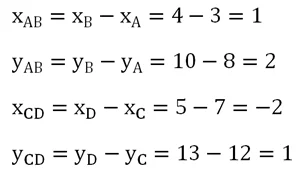
Мы вычислили координаты векторов: АВ{1; 2} и CD{– 2; 1}. Теперь мы можем проверить их перпендикулярность, скалярно перемножив вектора:

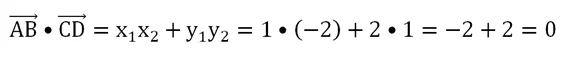
Мы получили ноль. Это означает, что АВ и CD – перпендикулярные вектора. Значит, и прямые, на которых они лежат, также перпендикулярны.

Ответ: перпендикулярны.

Задание. Перпендикулярны ли друг другу прямые, задаваемые уравнениями

Названия точкам в данном примере присвоены произвольно. На следующем шаге по координатам точек мы находим координаты векторов, лежащих на исследуемых прямых:

Полученный ноль показывает, что исходные прямые перпендикулярны.

Ответ: перпендикулярны.

В случае, когда прямые заданы уравнениями, необязательно проделывать столь длительные вычисления для определения их перпендикулярности. Есть теорема, сокращающая объем вычислений.

Докажем это утверждение. Пусть две прямые заданы уравнениями

Найдем какие-нибудь точки этих прямых. Для этого подставим в уравнения значения х = 0 и х = 1:

Прямые окажутся перпендикулярными исключительно в том случае, если это выражение будет нулевым. Это условие перпендикулярности можно записать как уравнение:

В результате мы получили доказываемую нами формулу.

Задание. Проверьте, какие из этих пар прямых перпендикулярны:

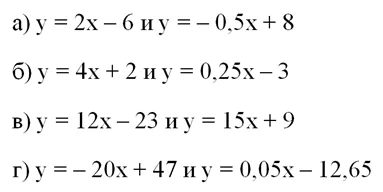
Решение. В каждом случае надо просто перемножить угловые коэффициенты прямых, то есть числа, стоящие перед переменной х. Другие числа в этих уравнениях (свободные коэффициенты) никак не влияют на перпендикулярность. Если вычисленное произведение окажется равным (– 1), то из этого будет вытекать перпендикулярность прямых.

Нахождение угла между векторами с помощью скалярного произведения

Скалярное произведение двух векторов — число или скаляр, которое равно произведению длин двух векторов с косинусом угла между этими векторами.

Если перевести слова на язык знаков, тогда получится, что скалярное произведение двух векторов: \( \overrightarrow{a}\overrightarrow{b}=\mid{\overrightarrow{a}}\mid\mid\overrightarrow{b}\mid\cos<(\overrightarrow{a},\overrightarrow{b})\).

Кроме непосредственно определения выше можно использовать такую теорему для нахождения значения скалярного произведения:

Теорема

Скалярное произведение двух векторов \(\overrightarrow{a}\)  и \(\overrightarrow{b}\) с координатами \(\overrightarrow{a}=(a_{1},a_{2},a_{3})\) и \(\overrightarrow{b}=(b_{1},b_{2},b_{3}\) будет равно сумме произведений конкретных координат.

Представим математически: \(\overrightarrow{a}\times\overrightarrow{b}=a_{1}\times{b_{1}}+a_{2}\times{b_{2}}+a_{3}\times{b_{3}}\).

Скалярное произведение обычно обозначается таким образом: \(\overrightarrow{a}\times\overrightarrow{b}\).

При помощи скалярного произведения возможно найти косинус угла между векторами. Разберем на примерах. Представим, что нам дали векторы \(\overrightarrow{a}\) и \(\overrightarrow{b}\) с координатами \(\overrightarrow{a}=(a_{1},a_{2},a_{3})\) и \(\overrightarrow{b}=(b_{1},b_{2},b_{3}\). Получится, что \(\cos<(\overrightarrow{a}\overrightarrow{b})=\frac{\overrightarrow{a}\overrightarrow{b}}{\mid\overrightarrow{a}\mid\mid\overrightarrow{b}\mid}.\)

Исходя из теоремы получаем, что \(\overrightarrow{a}\times\overrightarrow{b}=a_{1}\times{b_{1}}+a_{2}\times{b_{2}}+a_{3}\times{b_{3}}\). Значит \(\cos\overbrace{\overrightarrow{a}\overrightarrow{b}}==\frac{a_{1}\times{b_{1}}+a_{2}\times{b_{2}}+a_{3}\times{b_{3}}}{\mid{a}\mid\mid{b}\mid}\). Получаем:

\(\cos\overbrace{\overrightarrow{a}\overrightarrow{b}}=\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\sqrt{{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}}\).

При помощи значения косинуса просто найти величину угла.

Нахождение угла между векторами при помощи векторного произведения

Векторное произведение двух векторов — определенный вектор, перпендикулярный двум векторами, чья длина равна произведению длин данных векторов с синусом угла между этими векторами. Вектор и два остальных вектора будет иметь такое же направление, как и декартова система координат.

Обозначают обычно векторное произведение так: \(\overrightarrow{a}x\overrightarrow{b}\).

В математической форме будет так:

1. \(\mid\overrightarrow{a}x\overrightarrow{b}\mid=\mid\overrightarrow{a}\mid\mid\overrightarrow{b}\mid\sin<(\overrightarrow{a},\overrightarrow{b}).\)
2. \(\overrightarrow{a}x\overrightarrow{b}\perp\overrightarrow{a},\overrightarrow{a}x\overrightarrow{b}\perp\overrightarrow{b}.\)
3. \((\overrightarrow{a}\times\overrightarrow{b},\overrightarrow{a},\overrightarrow{b})\) и \((\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) являются ориентированными.

Для нахождения вектора векторного произведения можно использовать эту формулу:

25 Направляющий вектор прямой

Направляющий
вектор прямой — это ненулевой вектор, лежащий на заданной прямой или
на прямой, параллельной данной прямой.

Если
прямая M₁M₂
задана двумя точками M₁(x₁;
y₁; z₁)
и M₂(x₂;
y₂; z₂),
то направляющим является вектор

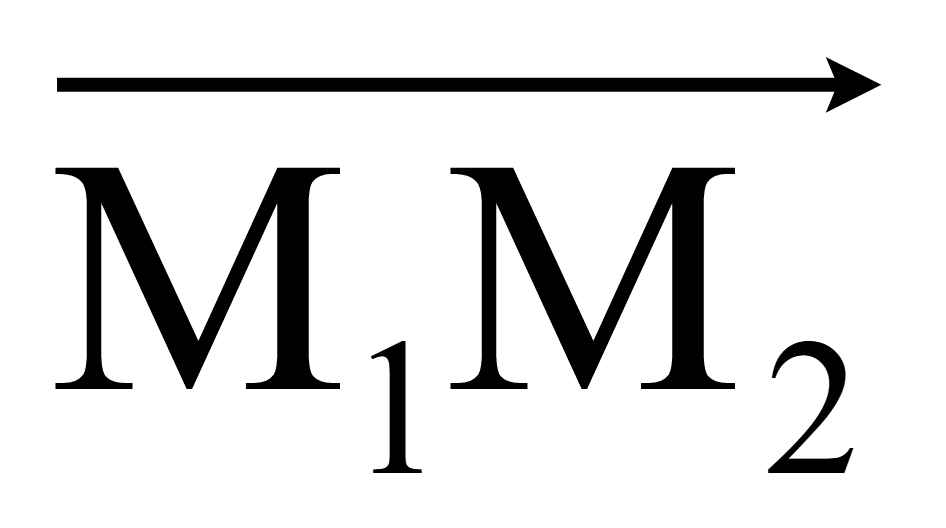
или противоположный ему вектор

=
—
.
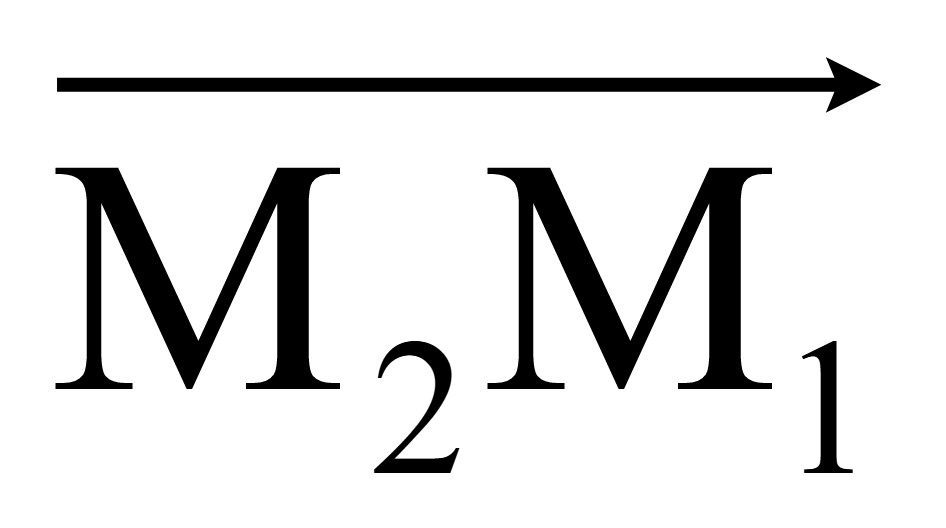
Координаты направляющих векторов прямой M₁M₂

=
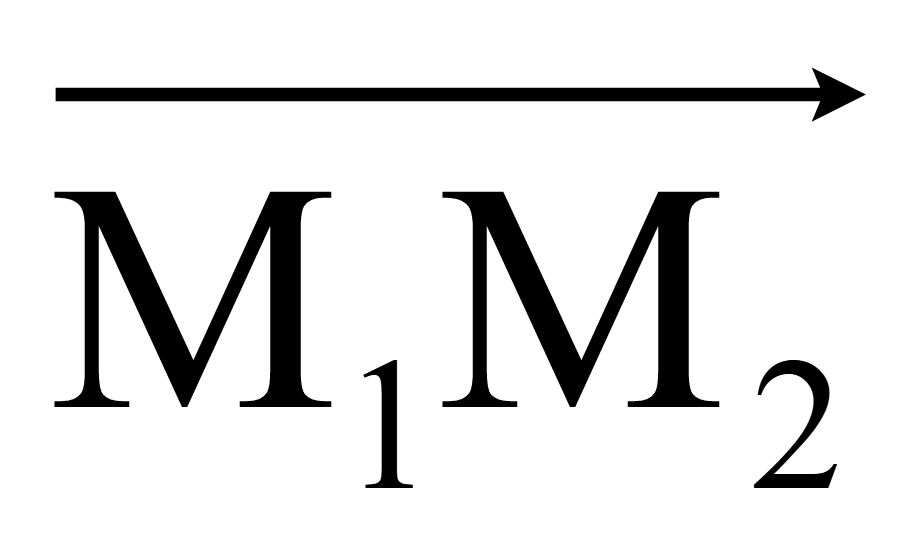(x₂
— x₁;
y₂
— y₁;
z₂
– z₁);

=
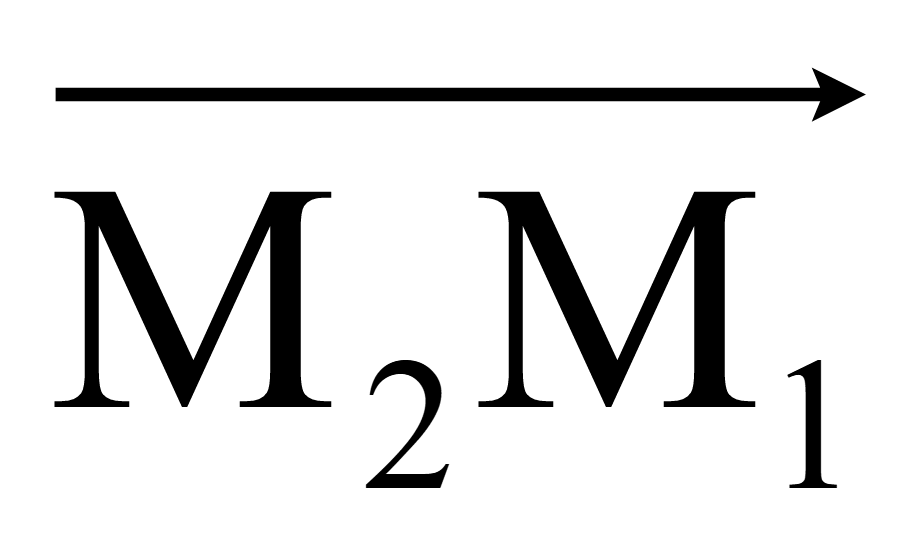(x₁
— x₂;
y₁
— y₂;
z₁
— z₂).

Систему
координат желательно задать так, чтобы прямая проходила через начало
координат, тогда координаты единственной точки на прямой, не
совпадающей с началом координат и будут координатами направляющего
вектора этой прямой.

Задача.
Определить координаты направляющего вектора прямой, проходящей через
точки M₁ (1; 0; 0), M₂
(0; 1; 0).

Решение

Построим
заданные точки в системе координат Oxyz.

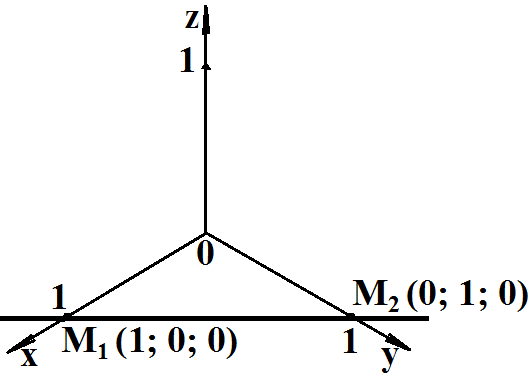
Направляющий
вектор прямой проходящей через точки M₁(1;
0; 0), M₂ (0; 1; 0) обозначим
.
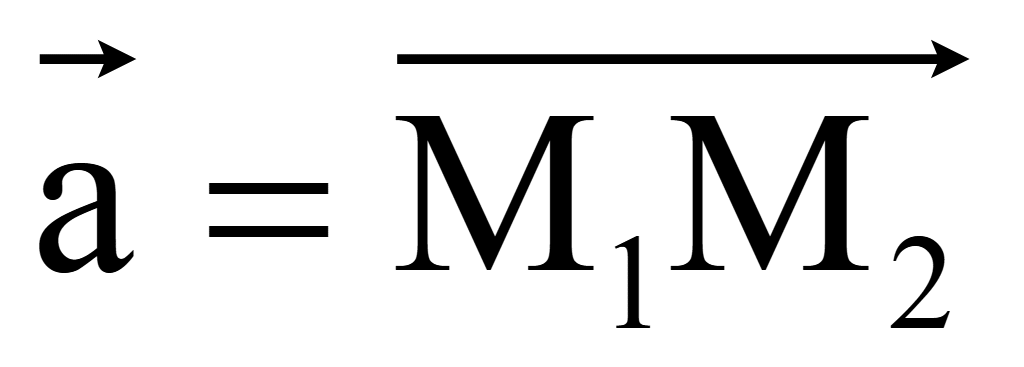Каждая из его координат равна разности соответствующих координат
конца и начала вектора

=
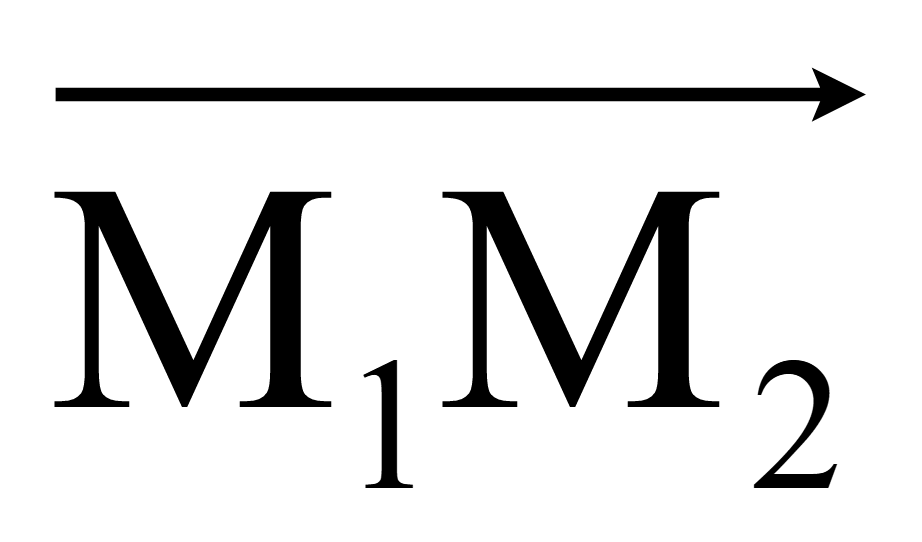(x₂
— x₁;
y₂
— y₁;
z₂
– z₁)

=
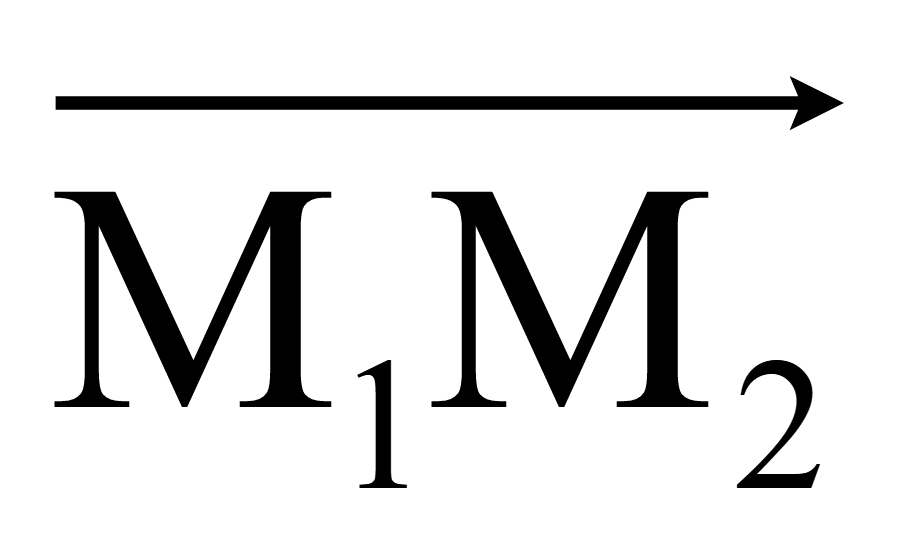(0 — 1; 1 — 0; 0 — 0) = (-1; 1; 0)

Изобразим
направляющий вектор прямой в системе координат с началом в точке M₁,
с концом в точке M₂ и равный ему
вектор

из начала координат с концом в точке M(-1; 1; 0)

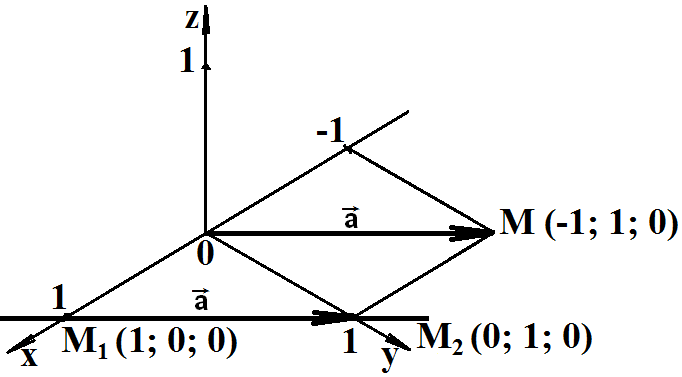
39 Расстояние от точки до плоскости

Если
известны координаты точки M(x;
y; z)
и уравнение плоскости ax + by
+ cz + d = 0 (a2
+ b2 + c2
≠ 0, то есть a, b и c
одновременно не равны нулю), то
расстояние от данной точки до плоскости определяется следующим
образом.

Проекцией
точки M на плоскость является
точка M₁ (x₁;
y₁; z₁),
поэтому вектор

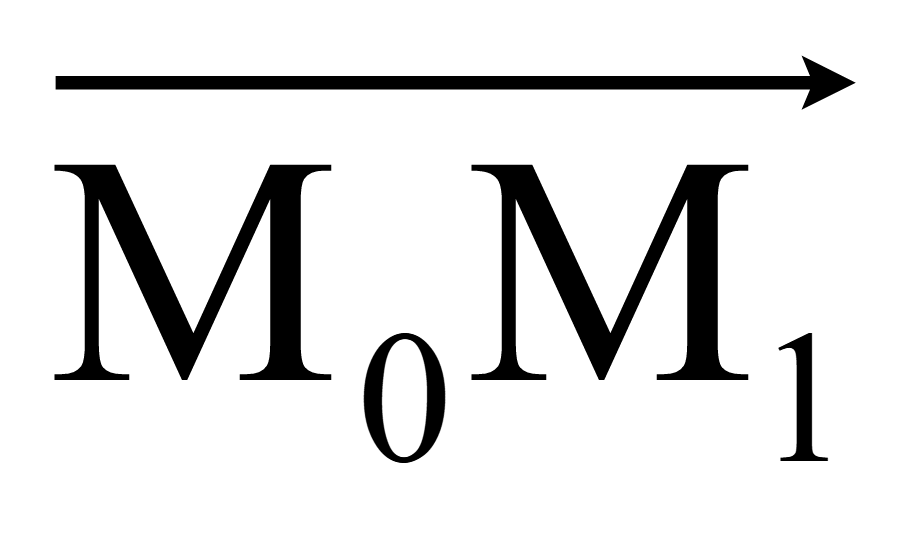
перпендикулярен плоскости и коллинеарен нормальному вектору плоскости

(a; b; c).
Следовательно,

=
k
.

Так
как координаты нормального вектора плоскости

(a; b; c), то координаты коллинеарного вектора k

(ka; kb; kc).

Координаты
вектора

равны разности координат конца и начала вектора

= (x₁ — x;
y₁ — y;
z₁ — z),
поэтому

=
(x₁ —
x; y₁
— y;
z₁ –
z) =
k

= (ka; kb;
kc);

x₁
— x =
ka; y₁
— y =
kb; z₁
— z =
kc.

Отсюда

x₁
= ka + x;
y₁ =
kb + y;
z₁ =
kc + z.

Расстояние
между точкой M и плоскостью
равно длине вектора
,
которая равна

|
|=
|k|||

Длина
нормального вектора равна корню квадратному из
суммы квадратов его координат

||=
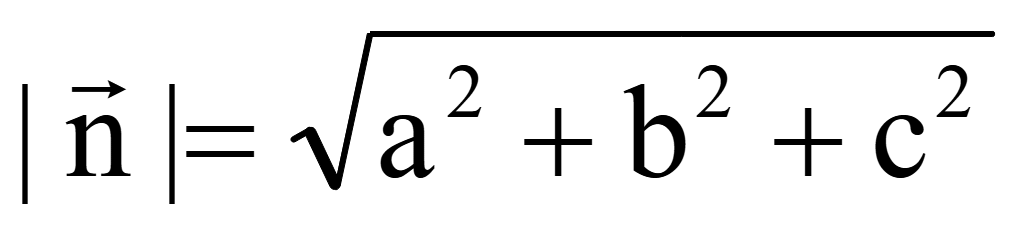
|k|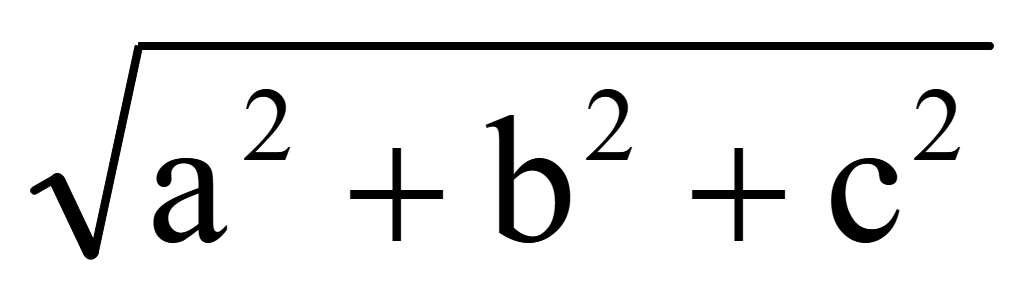

Подстановка
координат точки M₁ (x₁;
y₁; z₁)
в уравнение плоскости дает равенство

ax₁
+ by₁ + cz₁
+ d = 0.

Подставляем
полученные ранее значения x₁,
y₁, z₁

a(ka
+ x)
+ b(kb + y)
+ c(kc + z)
+ d = 0

Путем
преобразований выразим k. Раскроем
скобки

ka2
+ ax + kb2
+ by + kc2
+ cz + d
= 0,

сгруппируем

ka2
+ kb2
+ kc2
+ ax
+ by
+ cz
+ d = 0.

Вынесем
k за скобку и перенесем члены, не
содержащие k в правую часть равенства

k(a2
+ b2 +
c2) =
-(ax
+ by
+ cz
+ d).

Выразим
k

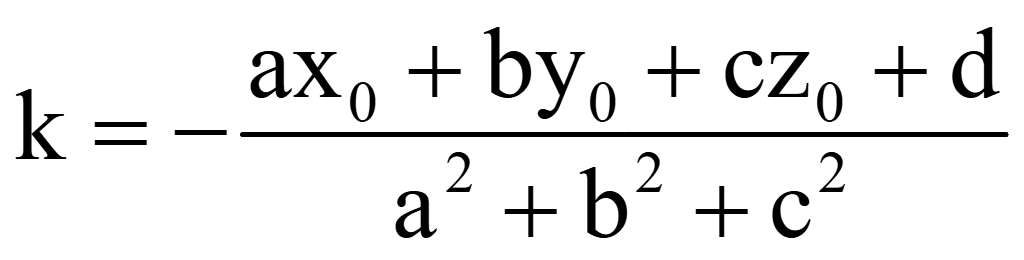
Модуль
k

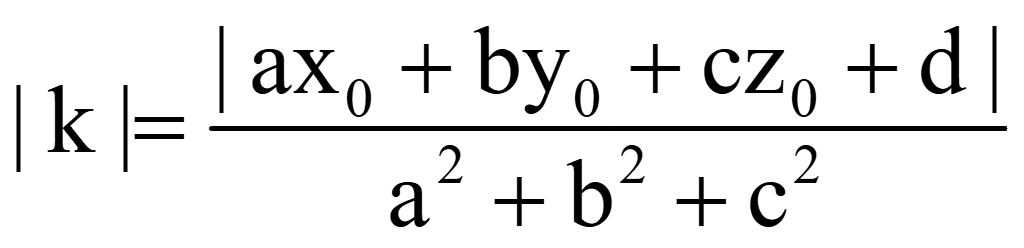
Подставим
|k|

||=

||=

||=

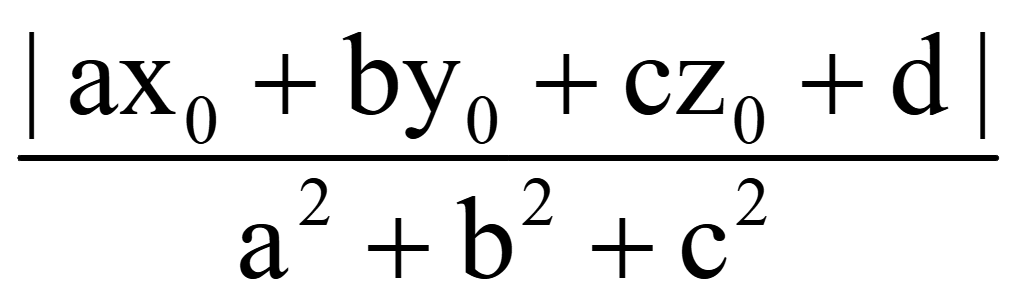
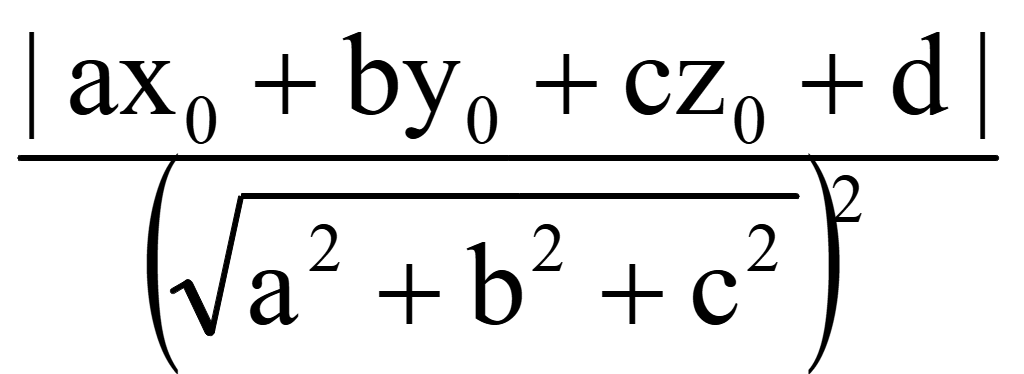
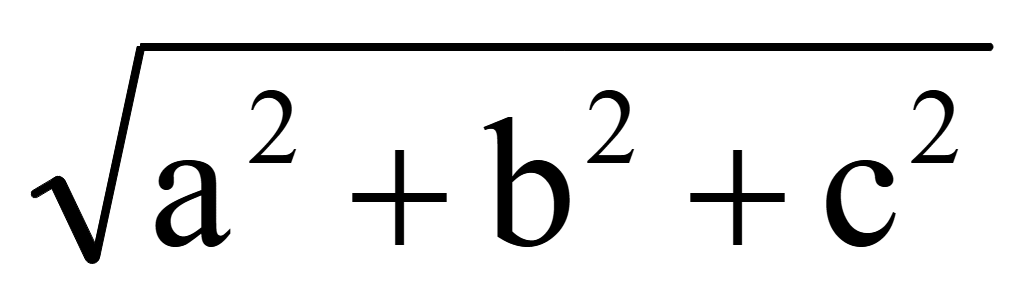
Расстояние
от точки M(x;
y; z)
до плоскости, заданной уравнением ax + by
+ cz + d = 0 (a2
+ b2 + c2
≠ 0)

ℓ =

Расстояние
между точкой и плоскостью равно модулю суммы произведений
соответствующих координат нормального вектора и точки плюс d,
деленного на длину (модуль) нормального вектора плоскости.

Другими
словами расстояние между точкой и плоскостью равно модулю
левой части уравнения плоскости, в которую подставили координаты
точки, деленного на длину (модуль) нормального вектора плоскости.

Желательно
выбрать систему координат так, чтобы искомая плоскость проходила
через начало координат, а так же, чтобы заданная
точка M(x;
y;
z)
находилась на одной из осей координат. Тогда решаемая задача
значительно упрощается за счет того, что d
и две координаты точки нулевые. Уравнение расстояния от точки до
плоскости значительно упрощается

ℓ =

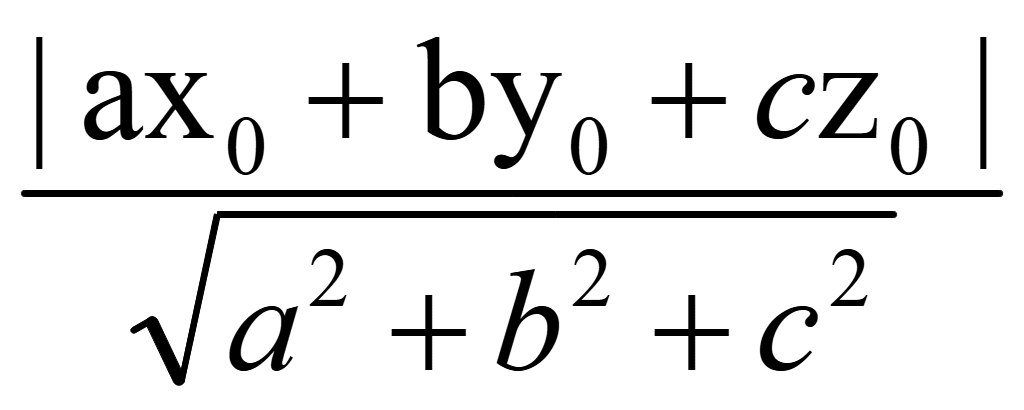
в
этом уравнении два члена в числителе
обнулятся и останется один член.

Если
заданная точка M(x;
y;
z)
совпадает с ось Ox, то
координаты y, z точки
равны нулю и получаем простейшее уравнение искомого расстояния,
содержащее лишь координату x
точки

ℓ =

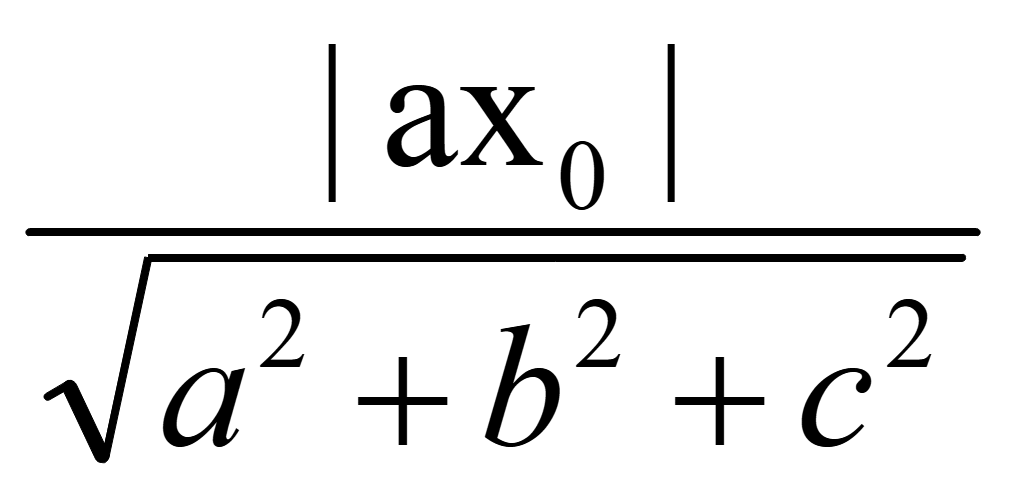
Таким
образом, если точка совпадает с ось Ox,
то в уравнении присутствует лишь координата
x точки.

Если
заданная точка
M
совпадает с ось Oy,
то координатыx,
z точки равны нулю и получаем простейшее
уравнение искомого расстояния

ℓ =

Таким
образом, если точка совпадает с ось Oy,
то используется
лишь координата yточки.

Если
заданная точка
M
совпадает с ось Oz,
то координатыx,
yточки
равны нулю и получаем простейшее уравнение искомого расстояния

ℓ =

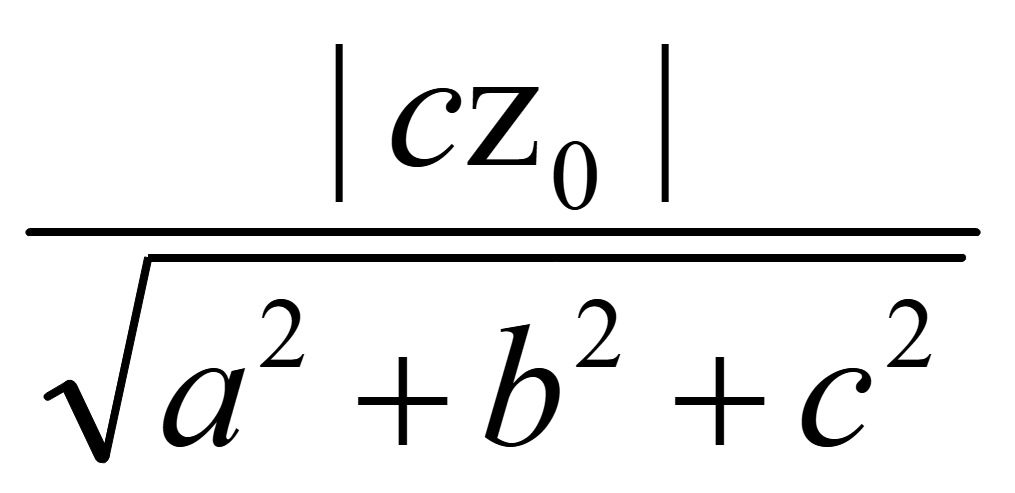
Таким
образом, если точка совпадает с ось Oz,
то используется
лишь координата zточки.

Задача.
Все ребра правильной четырехугольной пирамиды SABCD
равны 1. Найти расстояние между плоскостью SAD исерединой ребра AB.

Задача.
Определить общее уравнение плоскости

ax
+ by + cz + d
= 0,

проходящей
через точки M₁ (1; 0; 0), M₂
(0; 1; 0) и M₃ (0; 0; 1).
Найти расстояние от этой плоскости до точки M(10; -3; -7).

Решение

Построим
заданные точки M₁ (1; 0; 0), M₂
(0; 1; 0) и M₃ (0; 0; 1) в
системе координат Oxyz.

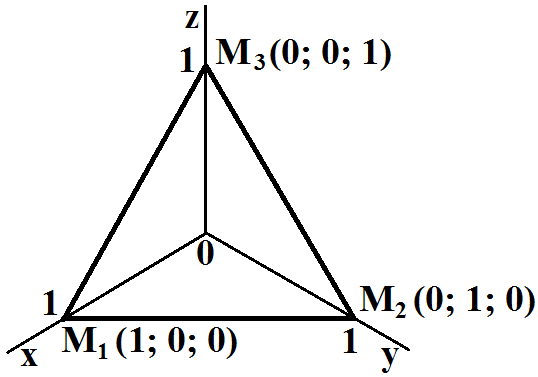
Примем
a = 1. Подстановка координат трех точек в
общее уравнение плоскости дает систему 3-х уравнений

;

;

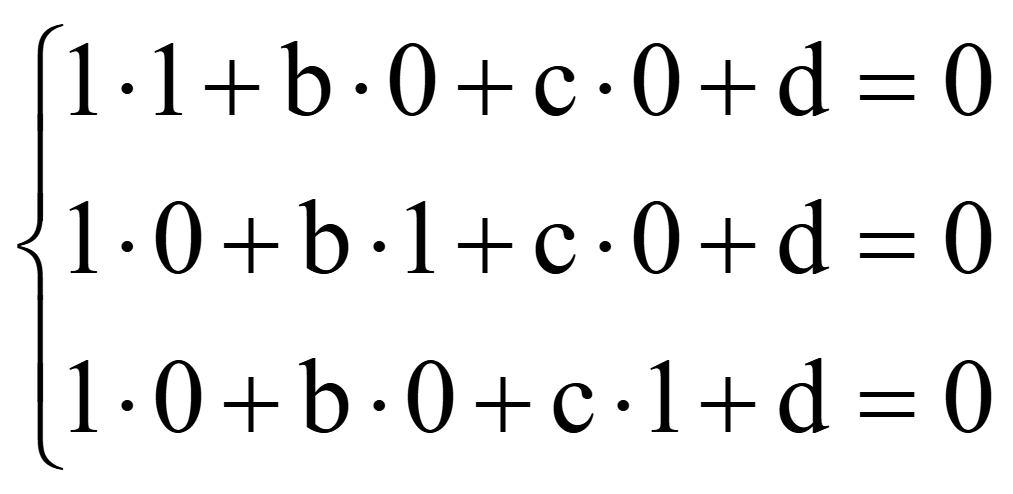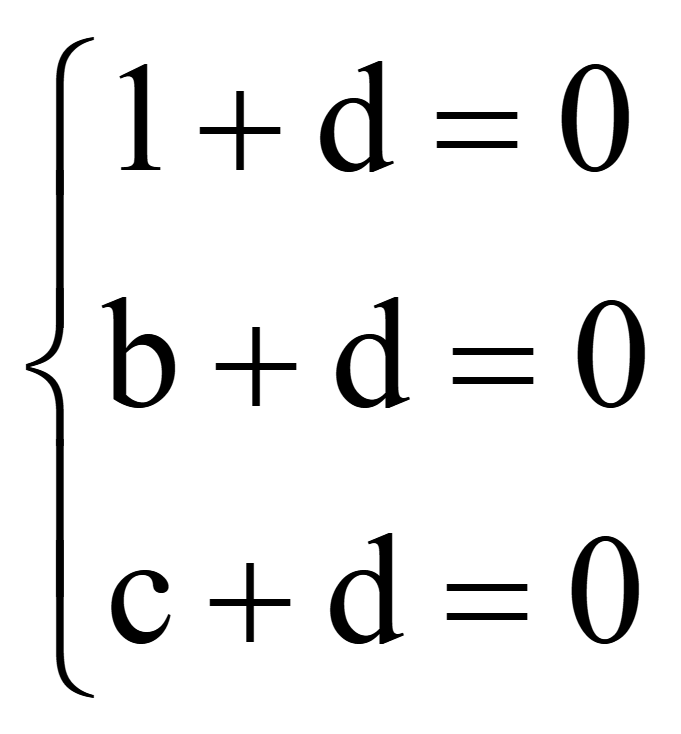
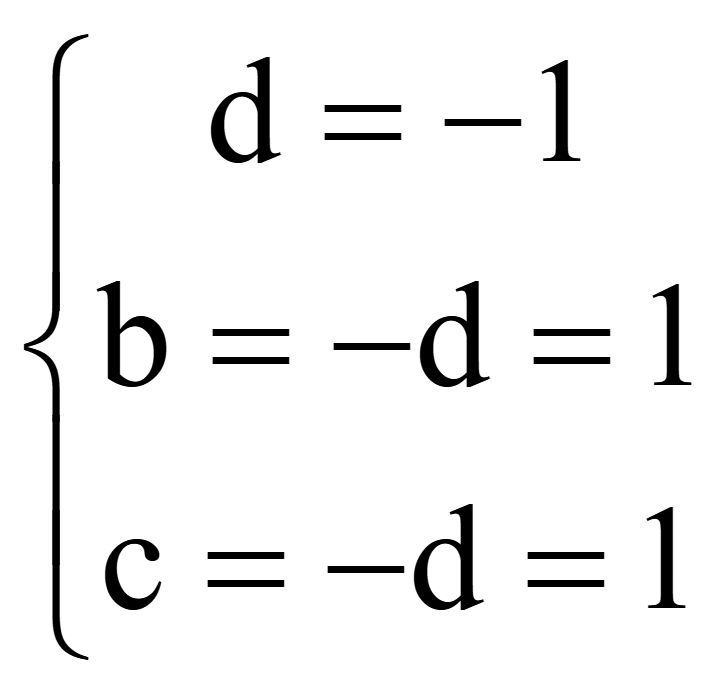
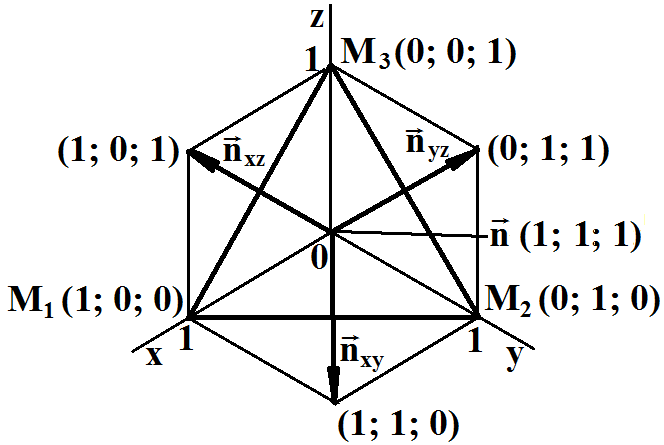
Координаты
нормального ненулевого вектора плоскости

(1;
1; 1), в изображенной ранее системе координат он будет изображен
точкой, поэтому покажем проекции нормального вектора на плоскости
xOy, yOz, xOz.

Общее
уравнение плоскости

x
+ y + z — 1 = 0.

Расстояние
от точки M до плоскости

ℓ =

ℓ =

Определитель третьего порядка

Отныне и впредь, когда ты будешь иметь дело с методом координат на плоскости, тебе очень часто будут встречаться эти самые определители.

Что же такое определитель третьего порядка? Как ни странно, это всего-навсего число. Осталось понять, какое конкретно число мы будем сопоставлять с определителем.

Давай вначале запишем определитель третьего порядка в более общем виде:

\( \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right|\),Где \( {{a}_{ij}}\) – некоторые числа.

Причем под первым индеком \( \displaystyle i\) мы понимаем номер строки, а под индеком \( \displaystyle j\) – номер столбца.

Например, \( {{a}_{23}}\) означает, что данное число стоит на пересечении второй строки и третьего столбца.

Давай поставим следующий вопрос: каким именно образом мы будем вычислять такой определитель?

То есть, какое конкретно число мы будем ему сопоставлять?

Для определителя именно третьего порядка есть эвристическое (наглядное) правило треугольника оно выглядит следующим образом:

Как его читать? А понимать его надо следующим образом: мы составляем два выражения:

• Произведение элементов главной диагонали (с верхнего левого угла до нижнего правого) \( \displaystyle +\) произведение элементов, образующих первый треугольник «перпендикулярный» главной диагонали \( \displaystyle +\) произведение элементов, образующих второй треугольник «перпендикулярный» главной диагонали;
• Произведение элементов побочной диагонали (с верхнего правого угла до нижнего левого) \( \displaystyle +\) произведение элементов, образующих первый треугольник «перпендикулярный» побочной диагонали \( \displaystyle +\) произведение элементов, образующих второй треугольник «перпендикулярный» побочной диагонали;
• Тогда определитель равен разности значений, полученных на шаге \( \displaystyle 1\) и \( \displaystyle 2\).

Если записать все это цифрами, то мы получим следующее выражение:

\( \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right| = \)\( = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{21}}{a_{32}}{a_{13}} — \left( {{a_{13}}{a_{22}}{a_{31}} + {a_{23}}{a_{32}}{a_{11}} + {a_{21}}{a_{12}}{a_{33}}} \right)\)Тем не менее, запоминать способ вычисления в таком виде не нужно, достаточно в голове просто держать треугольники и саму идею, что с чем складывается и что из чего затем вычитается).

Как найти длину вектора

Понятие длины вектора

Для того, чтобы разобраться с понятием длины вектора, прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям:
1. Они сонаправлены;
1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Решение.

Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).

Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит

$=x$, $=y$

Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим

$|\overline{α}|^2=^2+^2$

$|\overline{α}|^2=x^2+y^2$

$|\overline{α}|=\sqrt{x^2+y^2}$

Ответ: $\sqrt{x^2+y^2}$.

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Решение.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что

$\overline{XY}=(7+1,3-5)=(8,-2)$

Теперь, найдя длину этого вектора по формуле, выведенной выше, мы и получим искомую длину. Получим:

$d=\sqrt{8^2+(-2)^2}=\sqrt{64+4}=\sqrt{68}=2\sqrt{17}$

Ответ: $2\sqrt{17}$.

Замечание 1

Из этой задачи можно вывести формулу для вычисления такого расстояния. Пусть две точки имеют координаты ${(x’,y’)}$ и ${(x»,y»)}$. Тогда длину между такими точками можно найти по следующей формуле:

$d=\sqrt{(x’-x»)^2+(y’-y»)^2}$

Пример 3

Пусть нам дан треугольник своими координатами вершин $(5,-9)$, $(12,-2)$ и $(4,0)$. Найдем его периметр.

Решение.

Найдем для начала длины всех его сторон по формуле из замечания к задаче 2.

Первая сторона равняется:

$\sqrt{(5-12)^2+(-9+2)^2}=\sqrt{(-7)^2+(-7)^2}=\sqrt{98}=7\sqrt{2}$

Вторая сторона равняется:

$\sqrt{(5-4)^2+(-9-0)^2}=\sqrt{1^2+(-9)^2}=\sqrt{82}$

Третья сторона равняется:

$\sqrt{(12-4)^2+(-2-0)^2}=\sqrt{8^2+(-2)^2 }=\sqrt{68}=2\sqrt{17}$

Складывая, получим

Ответ: $7\sqrt{2}+\sqrt{82}+2\sqrt{17}$

Метод координат (продвинутый уровень)

Мы с тобой продолжаем изучать метод координат. В прошлой части мы вывели ряд важных формул, которые позволяют:

• Находить координаты вектора;
• Находить длину вектора (альтернативно: расстояние между двумя точками);
• Складывать, вычитать векторы. Умножать их на вещественное число;
• Находить середину отрезка;
• Вычислять скалярное произведение векторов;
• Находить угол между векторами.

Конечно, в эти 6 пунктов не укладывается весь координатный метод.

Он лежит в основе такой науки, как аналитическая геометрия, с которой тебе предстоит познакомиться в ВУЗе. Я лишь хочу построить фундамент, который позволит тебе решать задачи ЕГЭ любого уровня сложности!

Этот раздел будет посвящен методу решения тех задач, в которых будет разумно перейти к методу координат. Эта разумность определяется тем, что в задаче требуется найти, и какая фигура дана.

Физический смысл скалярного произведения

Распространенное понятие такое, как скалярное произведение обладает физическим смыслом. Его можно объяснить так, что работа А является результатом умножения силы F, которая производится постоянно во время движения тела, вектора а и составляющий с направлением силы F угол :

В качестве презентации введенного понятия рассмотрим рисунок:

На рисунке изображены следующие величины, с которыми можно часто встретиться в классе на уроках алгебры, геометрии и физики при рассмотрении различных теорем и доказательств:

• A является скалярной величиной и обозначением работы;
• a представляет собой вектор перемещения (смещения) материальной точки;
• F определяется, как вектор силы, которая оказывает воздействие на данную точку;
•  является углом силы F, действующим к смещению a.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

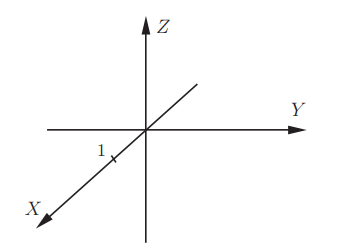
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

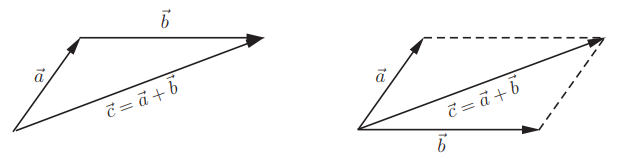
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

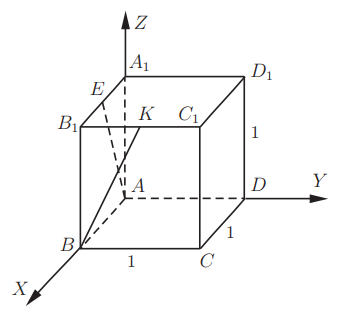
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

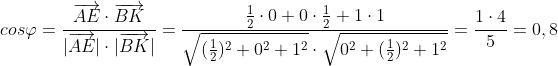
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

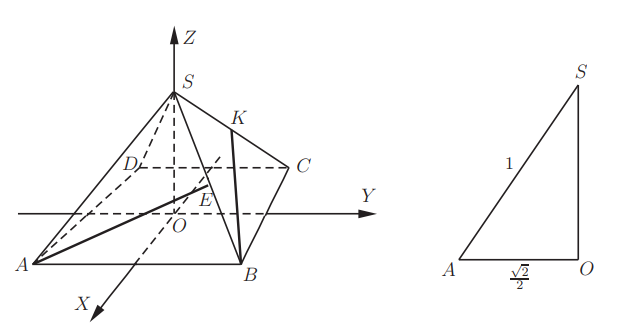
3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.