Как доказать параллельность векторов

Координатная форма условия коллинеарности векторов

Исходные данные: вектор a→ задан в некоторой прямоугольной системе координат на плоскости и имеет координаты (ax, ay), тогда, согласно полученному выше условию, вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay).

По аналогии: если вектор a→ задан в трехмерном пространстве, то он будет представлен в виде координат a=(ax, ay, az) , а вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay, λ·az). Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.

Определение 3

1. ​​​Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями:  bx=λ·axby=λ·ay  или ax=μ·bxay=μ·by
2. Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями:bx=λ·axby=λ·ay bz=λ·azили ax=μ·bxay=μ·by az=μ·bz

Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.

Если ненулевые векторы a→=(ax, ay, az) и b→=(bx, by, bz) коллинеарны, то согласно векторному определению произведения a→×b→=0→. И это также соответствует равенству: i→j→k→axayazbxbybz=0→, что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b→=λ·a→ и a→=μ·b→ , где μ – произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.

Определение 4

Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Рассмотрим применение условия коллинеарности на конкретных примерах.

Пример 1

Исходные данные: векторы  a→=(3-22, 1) и b→=(12+1, 2+1) . Необходимо определить, коллинеарны ли они.

Решение

Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: bx=λ·axby=λ·ay Подставив заданные значения координат, получим: bx=λ·ax⇔12+1=λ·(3-22)⇒λ=1(2+1)·(3-22)=132-4+3-22=12-1by=λ·ay⇔2+1=12-1·1⇔(2+1)·(2-1)=1 ⇔1≡1

Т.е. b→=12-1·a→, следовательно, заданные векторы коллинеарны.

Ответ: заданные векторы коллинеарны.

Пример 2

Исходные данные: векторы a→=(1, 0, -2) и b→=(-3, 0, 6) . Необходимо убедиться в их коллинеарности.

Решение

Т.к. bx=λ·axby=λ·ay bz=λ·az⇔-3=-3·10=-3·06=-3·(-2) , то верным будет равенство: b→=-3·a→ , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.

Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a→×b→=i→j→k→axayazbxbybz=i→j→k→10-2-306=i→·0·6+j→·(-2)·(-3)+k→·1·0-k→·0·(-3)-j→·1·6-i→·(-2)·0=0→Ответ: заданные векторы коллинеарны.

Пример 3

Исходные данные: векторы a→=(2, 7) и b→=(p, 3) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.

Решение

Согласно выведенному выше условию, векторы коллинеарны, если

b→=λ·a→⇔bx=λ·axby=λ·ay⇔p=λ·23=λ·7

тогда λ=37, а p=λ·2⇔p=67 . 

 Ответ: при p=67 заданные векторы коллинеарны.

Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.

Пример 4

Исходные данные: вектор a→=(2, -6) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.

Решение

Ответом может послужить, например, 12·a→=(1, -3) или вектор 3·a→=(6, -18) .

Ответ: вектор, коллинеарный заданному имеет координаты (1, -3).

Пример 5

Коллинеарность векторов

Онлайн калькулятор вычисления коллинеарности векторов. Поможет определить являются ли два вектора коллинеарными.

Коллинеарные векторы – это векторы, которые расположены параллельно друг к другу, то есть при наложении дают угол в градусов. Поэтому чтобы проверить коллинеарность векторов, нужно доказать что угол между векторами равен , а это проще всего сделать через функцию синуса, так как sin⁡0°=0. В аналитической геометрии синус используется для нахождения векторного произведения двух векторов, которое равно произведению длин векторов на синус угла между ними.

Поэтому когда между ними нулевой угол, то синус равен нулю, и все векторное произведение становится равно нулю. Из этого можно сделать и обратный вывод: если векторное произведение двух векторов равно нулю, то эти векторы коллинеарны. Формулы: \ = |\vec||\vec| \medspace sin⁡α \] \

Понятие коллинеарности векторов

Чтобы понять, что значит коллинеарные векторы, сперва надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Определение 1

Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.

Концами отрезка будем называть точки, которые его ограничивают.

Для введения определения вектора один из концов отрезка назовем его началом.

Определение 2

Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

Обозначение: $overline{AB}$ – вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.

Иначе одной маленькой буквой: $overline{a}$ (рис. 1).

Рисунок 1. Обозначение векторов. Автор24 — интернет-биржа студенческих работ

Определение 3

Нулевым вектором будем называть любую точку, которая принадлежит плоскости.

Обозначение: $overline{0}$.

Далее рассмотрим, какие векторы называются коллинеарными.

Определение 4

Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой. Кроме того, понятие коллинеарность наблюдается в случается параллельности векторов (рис.2).

Рисунок 2. Коллинеарность векторов. Автор24 — интернет-биржа студенческих работ

Также введем определение векторного произведения, которое будет нам необходимо далее.

Определение 5

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.

Обозначение: $overline{α}хoverline{β}$.

Чтобы найти векторное произведение, будем пользоваться формулой

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$

7 Компланарные векторы

Компланарными
называются векторы, лежащие в одной плоскости или в параллельных
плоскостях. Если провести векторы, равные данным компланарным
векторам из одной точки, то они будут лежать в одной плоскости.
Поэтому можно сказать, что компланарными называются векторы, если
имеются равные им векторы, лежащие в одной плоскости.

Два
произвольных вектора всегда компланарны потому что всегда можно
подобрать две параллельные плоскости, в которых будут лежать эти
векторы. Три вектора могут быть компланарными или не компланарными.
Три вектора, из которых хотя бы два коллинеарные, всегда компланарны.
Коллинеарные векторы всегда компланарны.

Базис.

Ранее было дано определение . Введем теперь определение базиса.

Определение.

Базисом в векторном пространстве называется упорядоченная линейно независимая система векторов такая, что любой вектор этого пространства по ней раскладывается.

Из доказанной выше сразу вытекает, что

• В нулевом пространстве базиса не существует.
• В одномерном пространстве (на прямой линии) базис состоит из одного ненулевого вектора.
• В двумерном пространстве (на плоскости) базис — упорядоченная пара неколлинеарных векторов.
• В трехмерном пространстве базис — упорядоченная тройка некомпланарных векторов.

Требование упорядоченности означает, что, например, в случае плоскости \(\boldsymbol{a}\), \(\boldsymbol{b}\) и \(\boldsymbol{b}\), \(\boldsymbol{a}\) — два разных базиса.

Так как векторы базиса линейно независимы, коэффициенты разложения по базису для каждого вектора пространства определены однозначно. Они называются компонентами или координатами вектора в этом базисе.

Таким образом, если \(\boldsymbol{e_{1}}\), \(\boldsymbol{e_{2}}\), \(\boldsymbol{e_{3}}\) — базис трехмерного пространства, то по формуле \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\) каждому вектору сопоставлена единственная упорядоченная тройка чисел \(\alpha_{1}\), \(\alpha_{2}\), \(\alpha_{3}\) и каждой тройке чисел — единственный вектор. Аналогично, вектор на плоскости имеет две компоненты, а на прямой — одну.

Компоненты пишутся в скобках после буквенного обозначения вектора, например \(\boldsymbol{a}\)(1,0,1).

В аналитической геометрии геометрические рассуждения о векторах сводятся к вычислениям, в которых участвуют компоненты этих векторов. Следующее предложение показывает, как производятся линейные операции над векторами, если известны их компоненты.

Утверждение 5.

При умножении вектора на число все его компоненты умножаются на это число. При сложении векторов складываются их соответствующие компоненты.

Действительно, если \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\), то

$$
\lambda\boldsymbol{a} = \lambda(\alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}) = (\lambda\alpha_{1})\boldsymbol{e_{1}} + (\lambda\alpha_{2})\boldsymbol{e_{2}} + (\lambda\alpha_{3})\boldsymbol{e_{3}}.\nonumber
$$
Если \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\) и \(\boldsymbol{b} = \beta_{1}\boldsymbol{e_{1}} + \beta_{2}\boldsymbol{e_{2}} + \beta_{3}\boldsymbol{e_{3}}\), то

$$
\boldsymbol{a} + \boldsymbol{b} = (\alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}) + (\beta_{1}\boldsymbol{e_{1}} + \beta_{2}\boldsymbol{e_{2}} + \beta_{3}\boldsymbol{e_{3}}) =\\= (\alpha_{1} + \beta_{1})\boldsymbol{e_{1}} + (\alpha_{2} + \beta_{2})\boldsymbol{e_{2}} + (\alpha_{3} + \beta_{3})\boldsymbol{e_{3}}.\nonumber
$$

Для одномерного и двумерного пространств доказательство отличается только числом слагаемых.

8 Разложение вектора по двум неколлинеарным векторам

Любой
вектор

единственным образом разлагается на плоскости по двум неколлинеарным
ненулевым векторам

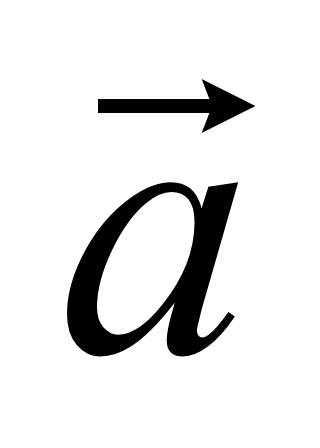
и

с единственными коэффициентами разложения x
и y:

=
x

+ y

Любой
вектор

,
компланарный ненулевым неколлинеарным векторам

и

,
единственным образом разлагается по этим двум векторам

и

с единственными коэффициентами разложения x
и y:

=
x

+ y

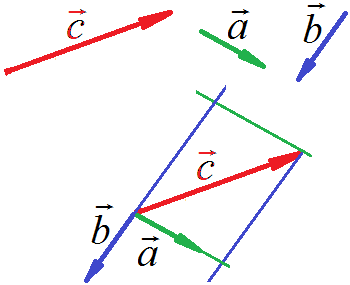
Разложим
на плоскости заданный ненулевой вектор

по данным ненулевым неколлинеарным векторам

и

:

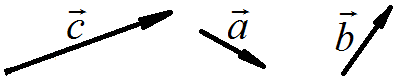
Если
векторы

,

и

компланарные, то на плоскости проведем их из одной точки, построив
векторы равные заданным компланарным векторам

Из
конца вектора

проведем прямые, параллельные векторам

и

до пересечения с прямыми, проведенными через вектора

и

.
Получим параллелограмм

Длины
сторон параллелограмма получаются путем умножения длин векторов

и

на числа x и y,
которые определяются путем деления длин сторон параллелограмма на
модули (длины) соответствующих им векторов

и

.
Получаем разложение вектора

по заданным неколлинеарным векторам

и

:

=
x

+ y

В
решаемой задаче x ≈ 1,3, y
≈ 1,9, поэтому разложение вектора

по заданным неколлинеарным векторам

и

можно записать в виде

=
1,3

+ 1,9
.

Разложим
на плоскости заданный ненулевой вектор

по данным ненулевым неколлинеарным векторам

и

:

В
решаемой задаче x ≈ 1,3, y
≈ -1,9, поэтому разложение вектора

по заданным неколлинеарным векторам

и

можно записать в виде

=
1,3

— 1,9
.

Линейные операции над векторами

3.1. Суммой векторови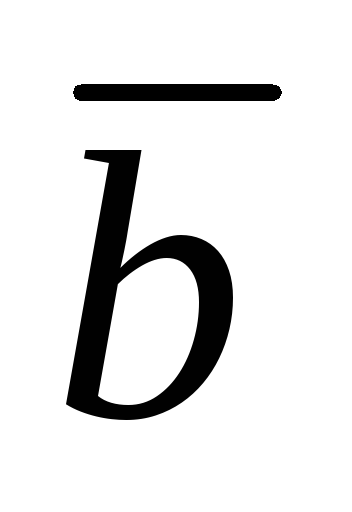называется вектор, который находится
либо по правилу параллелограмма (рис.
2), либо по правилу треугольника (рис.
3). В первом случае для нахождения суммы
оба вектора откладываются от одной
точки, на этих векторах строится
параллелограмм. Тогда сумма данных
векторов есть вектор, начало которого
совпадает с началами обоих векторов-слагаемых
и направленный по диагонали параллелограмма
(рис. 2). Чтобы найти сумму двух векторови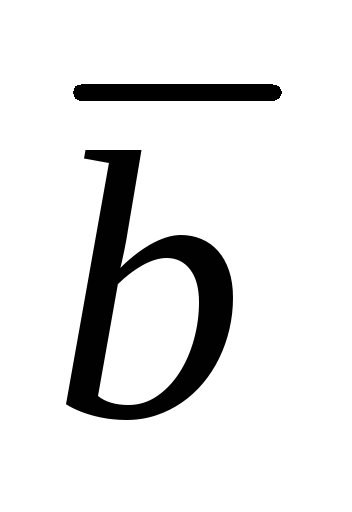по правилу треугольника, нужно расположить
векторы последовательно (от концавектораотложить вектор).
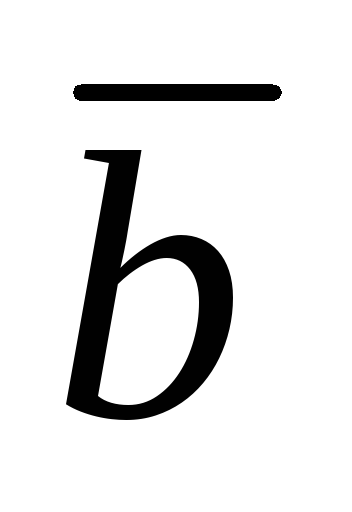Тогда их сумма – это вектор, начало
которого совпадает с началом первого
вектора (вектора),
а конец совпадает с концом второго
вектора (вектора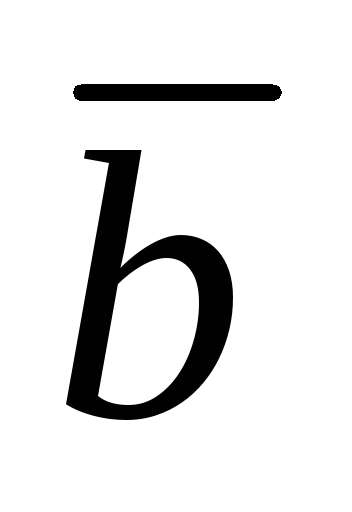)(рис.
3).

Рис. 2
Рис. 3

3.2. Сумму любого числа векторовнаходят по правилу многоугольника (рис.
4).

Рис. 4

По правилу многоугольника путем
параллельного переноса начало каждого
последующего вектора помещают в конец
предыдущего. Вектор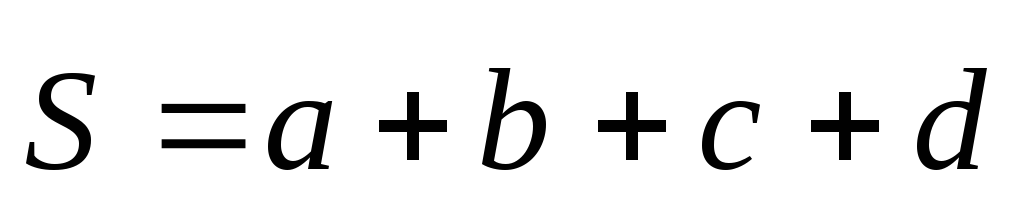получен путем соединения начала первого
вектора и конца последнего вектора.

3.3. Произведением векторана числоназывается вектор,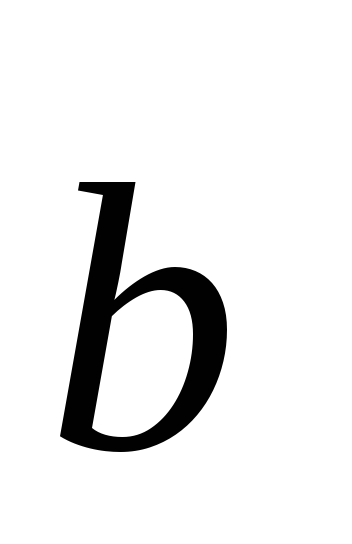
удовлетворяющий условиям:

1.,
если>
0;

,
если<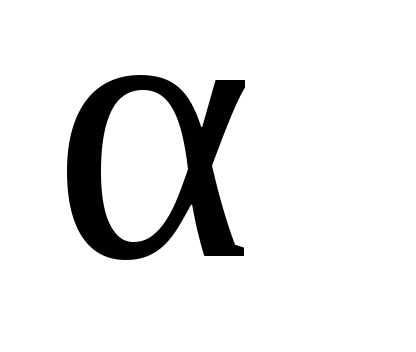
0.

2. .

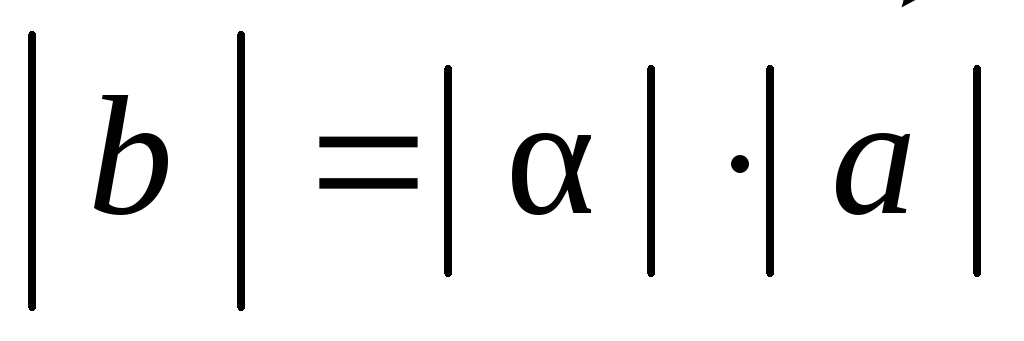3..

При этом
принята запись.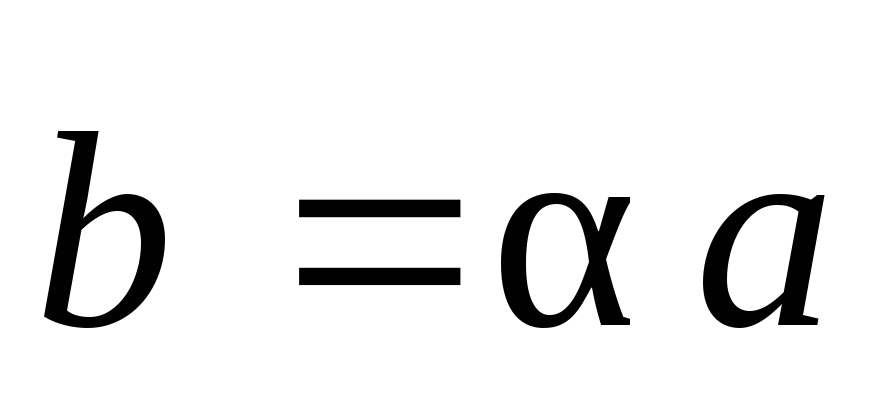

На рис.5 изображены векторы.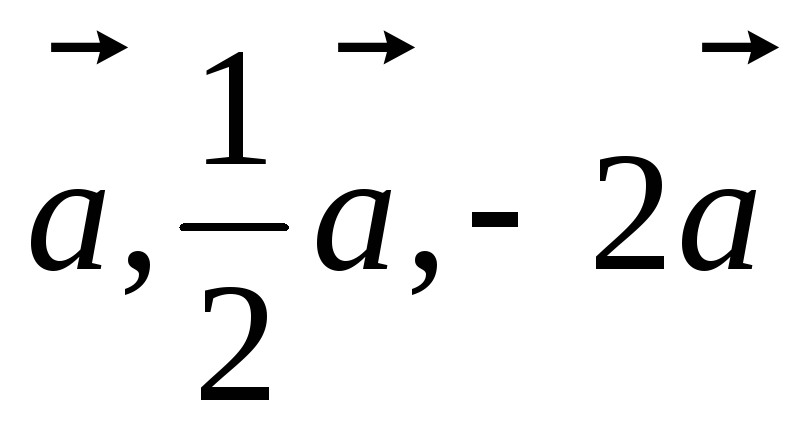

Рис. 5

Разложение вектора на некомпланарные вектора

Иногда вектор можно разложить не на два, а на три вектора. Выглядит такое разложение так:

Для доказательства рассмотрим три некомпланарных вектора а, bи c, а также произвольный вектор р. Отложим их от одной точки О. Обозначим концы этих векторов большими буквами А, В, С и Р:

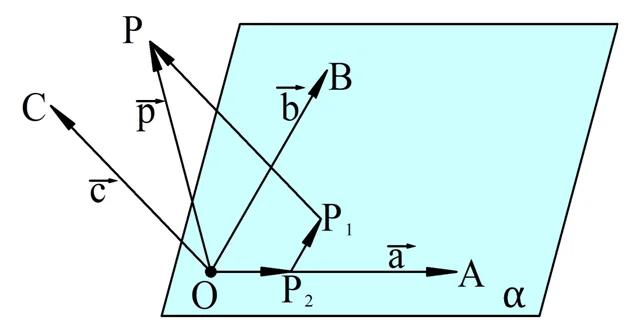
Через ОВ и ОА можно провести некоторую плос-ть α. Точка С ей принадлежать не может, ведь ОА, ОВ и ОС – некомпланарные вектора. Проведем через Р прямую, параллельную ОС. Так как ОС пересекает α, то и параллельная ей прямая также пересечет α в некоторой точке Р₁. (Примечание. Если Р принадлежит α, то точки Р и Р₁ совпадут, то есть вектор Р₁Р будет нулевым).

Далее через точку Р₁ в плос-ти α проведем прямую, параллельную ОВ, которая пересечет ОА в точке Р₂. Заметим, что вектор ОР₂ находится на той же прямой, что и вектор ОА, то есть они коллинеарны, поэтому существует такое число х, что

Итак, мы показали, что у произвольного вектора p есть разложение на заранее заданные некомпланарные вектора. Осталось показать, что существует только одно такое разложение. Докажем это методом от противного. Пусть есть второе разложение с другими коэффициентами х₁, у₁ и z₁:

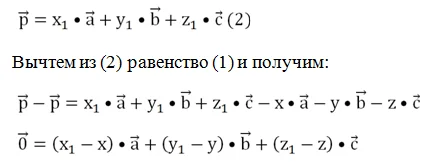
В правой части находятся три вектора, которые в сумме нулевой вектор. По правилу сложения векторов это означает, что эти вектора образуют треугольник, то есть находятся в одной плос-ти:

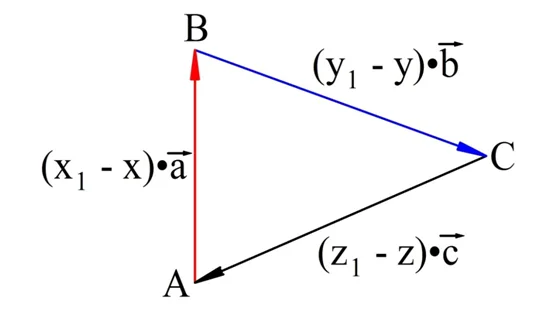
Значит, они компланарны. Тогда компланарны и вектора a, b и с, что противоречит условию теоремы. Значит, второго разложения р на заданные некомпланарные векторы не существует, ч. т. д.

Задание. АВСD и А₁В₁С₁D₁ – параллелограммы, располагающиеся в разных плос-тях. Докажите, что тройка векторов ВВ₁, СС₁ и DD₁ компланарна.

Решение. Сначала построим рисунок по условию задачи:

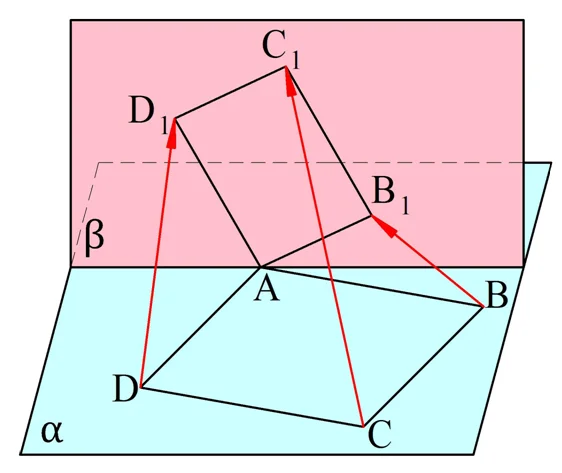
Для доказательства используем признак компланарности векторов. Для этого надо один из векторов, отмеченных на рисунке красным, разложить на два других вектора.

В результате нам удалось разложить СС₁ на вектора BB₁ и CC₁. Значит, эти три вектора коллинеарны.

Задание. В параллелепипеде АВСDA₁B₁C₁D₁ запишите разложение вектора BD₁ по векторам ВА, ВС и ВВ₁.

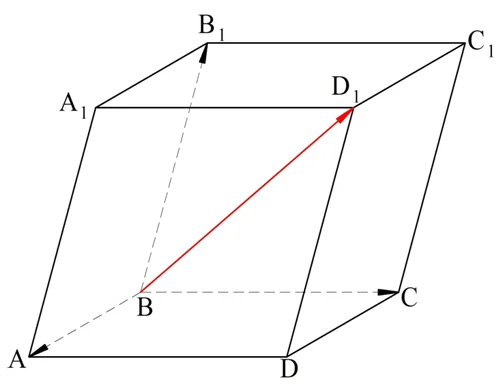
Решение. Сначала представим вектор BD₁ как сумму трех векторов:

Теперь заметим, что вектора С₁D₁ и ВА соответствуют ребрам параллелепипеда. Эти ребра одинаковы по длине и параллельны, поэтому и вектора будут равными. Аналогично равны вектора СС₁ и ВВ₁:

Задание. АВСD – тетраэдр, а точка К делит его ребро ВС пополам. Разложите вектор DK по векторам DA, AB и AC.

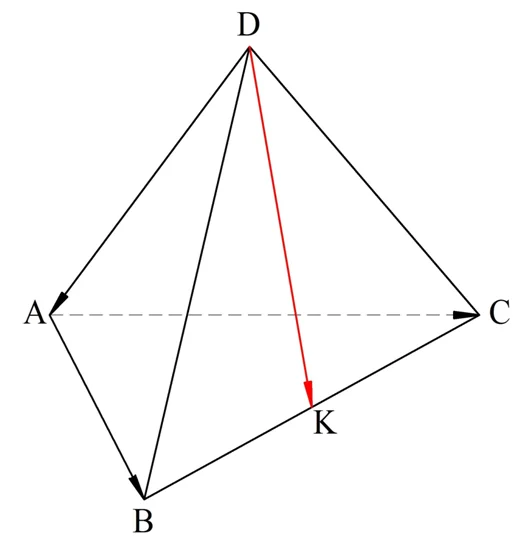
Решение. Сначала запишем очевидное выражение для вектора DK:

Задание. В точке М пересекаются медианы треугольника АВС, а О – произвольная точка в пространстве. Разложите вектор ОМ по векторам ОА, ОВ и ОС.

Решение. Медиану, проходящую через точку А, мы обозначим как АА₁, то есть А₁ – это середина отрезка ВС. Также буквой К обозначим середину ОВ:

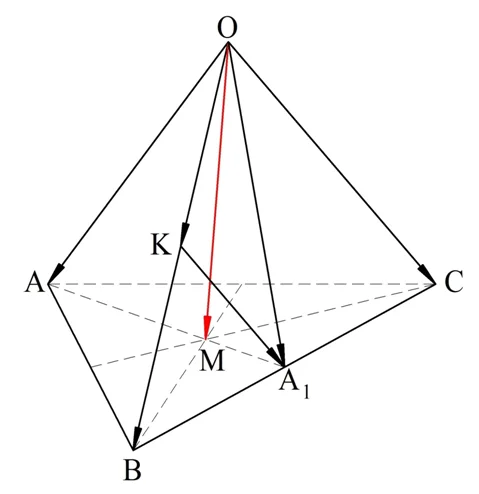
Сначала разложим вектор ОА₁ на ОВ и ОС. Это можно сделать, ведь они компланарны. КА₁ – это средняя линия ∆ОСВ, поэтому КА₁||ОС и КА₁ вдвое короче ОС. Это значит, что

Так как АА₁ – медиана, то точка М делит ее в отношении 2:1. Отсюда вытекает следующее соотношение:

Только что решенная задача может быть использована и при решении другого, более сложного задания.

Задание. Докажите, что в параллелепипеде АВСDА₁В₁С₁D₁ плос-ти А₁ВD и СB₁D₁ делят диагональ АС₁ на три равных отрезка.

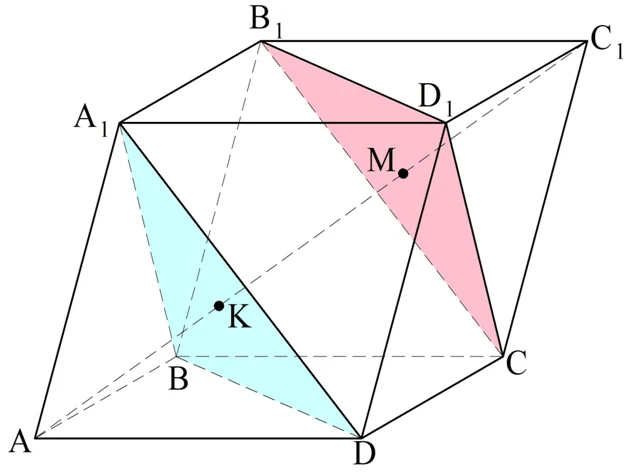
Решение. Обозначим точкой K точку пересечения медиан ∆А₁ВD. Тогда по формуле, выведенной в предыдущей задаче, мы получаем, что

Это соотношение означает, что вектора АК и АС₁ коллинеарны, поэтому они располагаются на одной прямой (они не могут находиться на параллельных прямых, ведь у них есть общая точка А). Значит, точка K принадлежит диагонали АС₁, и отрезок АК втрое короче диагонали.

Аналогично можно показать, что и

Из этого также вытекает, что М принадлежит диагонали АС₁, и МС₁ втрое короче АС₁. Значит, точки М и К делят диагональ на три равных отрезка, ч. т. д.

Сегодня мы расширили понятие векторов и научились их применять не только в планиметрических, но и в стереометрических задачах. При сохраняются все правила, по которым выполняются действия над векторами. Также в стереометрии появляется новое понятие компланарных и некомпланарых векторов.

Признак коллинеарности векторов

Напомним, что если два вектора (обозначим их как a и b) коллинеарны, то обязательно существует такое число k, что 

Из равенства (1) и рассмотренного нами правила умножения вектора на число вытекают два соотношения между этими координатами:

x₁ = k * x₂

y₁ = k * y₂

Если числа х₂ и у₂ не равны нулю, то можно выразить из каждого уравнения число k, после чего выражения можно будет приравнять:

Получили соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратную сторону – если координаты векторов удовлетворяют выведенному отношению, то можно смело утверждать, что вектора – коллинеарны.

Примечание. Формулировка «тогда и только тогда» означает, что правило действует в обе стороны – из пропорциональности координат следует коллинеарность векторов, а из коллинеарности векторов следует пропорциональность координат.

Покажем, как пользоваться этим признаком коллинеарности векторов. Пусть вектор а имеет координаты {8; 5}, а у вектора b они равны {24; 15}. Нам надо определить, коллинеарны ли они. Для этого поделим друг на друга их координаты х:

24:8 = 3

Получили число 3. Далее поделим и координаты у:

15:5 = 3

Снова получили тройку. То, что в обоих случаях получилось одно и тоже число, указывает на то, что вектора коллинеарны. Более того, можно даже записать, что вектор b втрое больше a:

В данном примере мы делили координаты второго вектора b на координаты первого вектора a. Но можно было поступить и наоборот, делить координаты а на координаты b:

Естественно, снова получилось одинаковое число.

Особняком стоит случай, когда одна из координат вектора равна нулю. Например, пусть вектор имеет координаты {0; у₁}, причем у₁≠ 0. Любой коллинеарный ему вектор можно получить, умножив вектор на какое-то число k. В этом случае его координаты {x₂; у₂} составят:

Получается, что и у коллинеарного вектора координата х обязательно будет равняться нулю. В свою очередь координаты у₂ и у₁ могут быть любыми, ведь мы всегда можем найти такое число k, для которого будет выполняться условие

y₂ = ky₁

Например, есть вектор {0; 5}. Можно сказать, что ему будет коллинеарен любой вектор, у которого первая координата также равна нулю, в частности,

Но любой вектор, у которого координата х НЕ равна нулю, НЕ будет коллинеарен вектору {0; 5}. В частности, ему не будут коллинеарны вектора:

Аналогичная логика действует и тогда, когда нулю равна не координата х, а координата у.

Если же у вектора обе координаты равны нулю, то он является нулевым вектором, то есть точкой. Напомним, что такой вектор считается коллинеарным любому другому вектору.

Задание. Определите, являются ли коллинеарными два вектора, если их координаты равны:

Решение. В первых пяти случаях все координаты – ненулевые, а поэтому надо просто проверить их пропорциональность. Для этого надо делить координаты друг на друга:

Числа различны, поэтому вектора НЕ коллинеарны.

В следующих примерах как минимум одна из координат равна нулю, поэтому делить координаты уже не нужно.

е) {0; 5} и {0; 12}

У обоих векторов координаты х нулевые, этого достаточно, чтобы утверждать, что они коллинеарны.

ж) {0; 3} и {2; 6}

У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.

з) {9; 0} и {4; 0}

У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.

и) {0; 3} и {12; 0}

Здесь у первого вектора нулю равна координата х, а у второго она ненулевая, поэтому вектора не коллинеарны.

к) {0; 0} и {5; 8}

Здесь имеет место особый случай, ведь первый вектор – нулевой, то есть представляющий собой точку. Считается, что он коллинеарен любому вектору, поэтому в данном примере вектора коллинеарны.

Ответ: а) да; б) нет; в) да; г) да; д) нет; е) да; ж) нет; з) да; и) нет; к) да.

Пока что мы рассматривали задачи, в которых фигурируют только вектора. Однако в будущем мы научимся с помощью метода координат решать и другие задачи, в которых рассматриваются отрезки, треугольники, окружности и прочие геометрические фигуры.

Действия с векторами. Коллинеарность векторов

В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.

Правило сложения векторов по правилу треугольников

Рассмотрим два произвольных ненулевых вектора  и :

Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор  от конца вектора :

Суммой векторов  и  является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов  представляет собой вектор результирующего перемещения  с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.

Кстати, если вектор  отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.

Умножение вектора на число

Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».

Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Обозначения: коллинеарность векторов записывают привычным значком параллельности: , при этом возможна детализация:  (векторы сонаправлены) или  (векторы направлены противоположно).

Произведением ненулевого вектора  на число  является такой вектор , длина которого равна , причём векторы   и  сонаправлены при  и противоположно направлены при .

Правило умножения вектора на число легче понять с помощью рисунка: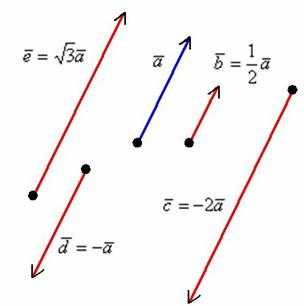

Разбираемся более детально:

1) Направление. Если множитель  отрицательный,  то вектор меняет направление на противоположное.

2) Длина. Если множитель заключен в пределах  или , то длина вектора уменьшается. Так, длина вектора  в два раза меньше длины вектора . Если множитель  по модулю больше единицы, то длина вектора увеличивается в  раз.

3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например,. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно  коллинеарны

Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.

4) Векторы  сонаправлены. Векторы  и  также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.

Какие векторы являются равными?

Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».

С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.