Объем шара и его частей

Шар, сфера и их части

Введем следующие определения, относящиеся к шару, сфере и их частям.

Определение 1. Сферой с центром в точке O и радиусом r называется множество точек, расстояние до точки O которых равно r (рис. 1).

Определение 2. Сферой с центром в точке O и радиусом r называется множество точек, расстояние от которых до точки O не превышает r (рис. 1).

Рисунок 1

Таким образом, сфера с центром в точке O и радиусом r является поверхностью сферы с центром в точке O и радиусом r.

Примечание: Радиус сферы (радиус сферы) — это отрезок, соединяющий любую точку на сфере с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом сферы).

Определение 3. Сферический пояс (сферический пояс) – это часть сферы, заключенная между двумя параллельными плоскостями параллельных плоскостей (рис. 2).

Определение 4. Сферический слой – это часть сферы, заключенная между двумя параллельными плоскостями параллельных плоскостей (рис. 2).

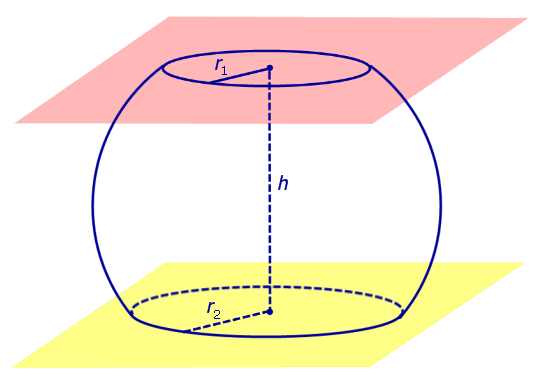
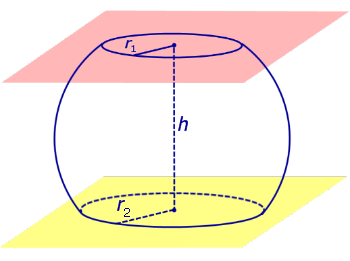
Рис.2

Окружности, ограничивающие сферический пояс, называются основаниями сферического пояса.

Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называется высотой сферического пояса.

Из определений 3 и 4 следует, что сферический слой ограничен сферическим поясом и двумя окружностями, плоскости которых параллельны и параллельны друг другу. Эти окружности называются основаниями сферического слоя.

Высота сферического слоя — это расстояние между плоскостями, расстояние между плоскостями оснований сферического слоя.

Определение 5. Сферическим сегментом называется каждая из двух частей, на которые шар делится секущей его плоскостью (рис. 3).

Определение 6. Каждая из двух частей, на которые шар делится секущей его плоскостью, называется сферическим сегментом (рис. 3).

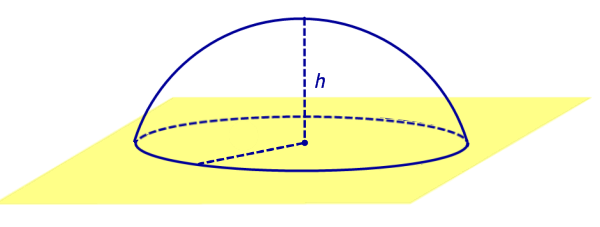
Рис.3

Из определений 3 и 5 следует, что сферический сегмент представляет собой сферический пояс, в котором одна из плоскостей основания касается сферы (рис. 4). Высота такого сферического пояса называется высотой сферического сегмента.

Соответственно сферический сегмент представляет собой сферический слой, в котором одна из плоскостей оснований касается шара (рис. 4). Высота такого сферического слоя называется высотой сферического сегмента.

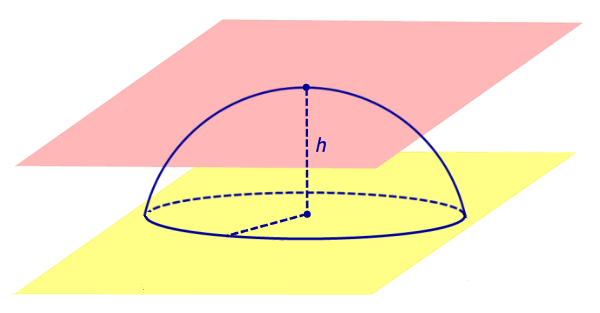
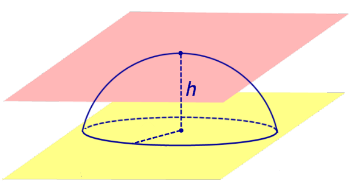
Рис.4

По той же причине всю сферу можно рассматривать как сферический пояс, где обе плоскости заземления соприкасаются со сферой (рис. 5). Следовательно, весь шар представляет собой сферический слой, где обе плоскости основания касаются шара (рис. 5).

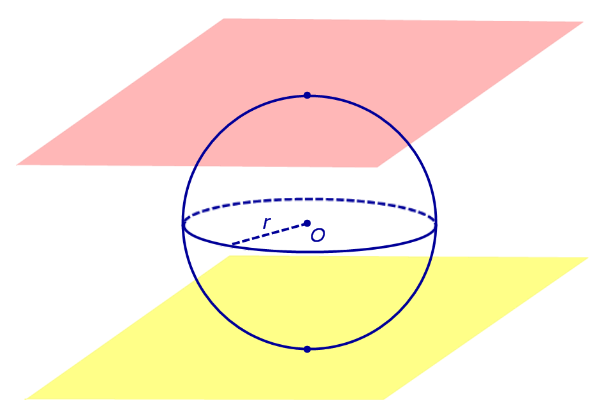
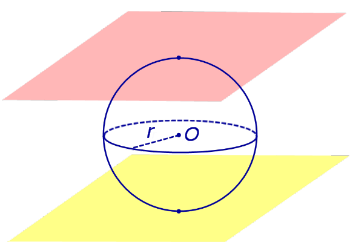
Рис.5

Определение 7. Сферическим сектором называется фигура, состоящая из всех отрезков, соединяющих точки сферического отрезка с центром сферы (рис. 6).

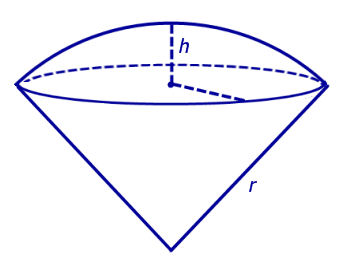
Рис. 6

Высота сферического сектора равна высоте его сферического сегмента .

Комментарий. Сферический сектор состоит из сферического сегмента и конуса с общим основанием. Вершина конуса является центром сферы.

Определение шарового слоя

Сферический слой (или разрез шара) — это часть шара, которая остается между двумя пересекающими его параллельными плоскостями. Изображение ниже окрашено в желтый цвет.

• R — радиус шара;
• r1 — радиус первой режущей базы;
• r2 — радиус второй режущей базы;
• h — высота сферического слоя; перпендикулярно из центра первого основания к центру второго.

Сферическая поверхность

Чтобы найти площадь сферической поверхности сферического слоя, нужно знать радиус шара, а также высоту надреза.

Сферы пов. = 2πRh

Площадь оснований разреза шара равна произведению квадрата соответствующего радиуса на число π.

S1 = пр12

S2 = пр22

Полная поверхность

Общая площадь поверхности сферического слоя равна сумме площадей его сферической поверхности и двух его оснований.

Полная пов. = 2πRh + πr12 + πr22 = π(2Rh + r12 + r22)

Примечания:

• если диаметры (d) даны вместо радиусов (R, r1 или r2), последние следует разделить на 2, чтобы найти искомые радиусы.
• значение числа π при выполнении вычислений обычно округляют до двух знаков после запятой — 3,14.

Шар и его части. Объем, площадь поверхности. |

Рассмотрим понятие таких геометрических тел как шар и его части:

• шаровой сегмент;
• шаровой сектор;
• шаровой слой.

Также представим формулы для вычисления объемов и площадей поверхностей шара и его частей.

Об элементах шара и понятии “сфера” будет опубликовано в отдельной статье.

Шар. 

Определение.

Шаром называется геометрическое тело, состоящее из точек пространства, находящихся от центра на расстоянии, не больше заданного.

Площадь поверхности шара вычисляется по формуле:

S_пов. = 4*π*R2 = π*D2 , где R –  радиус шара,   D – диаметр шара.

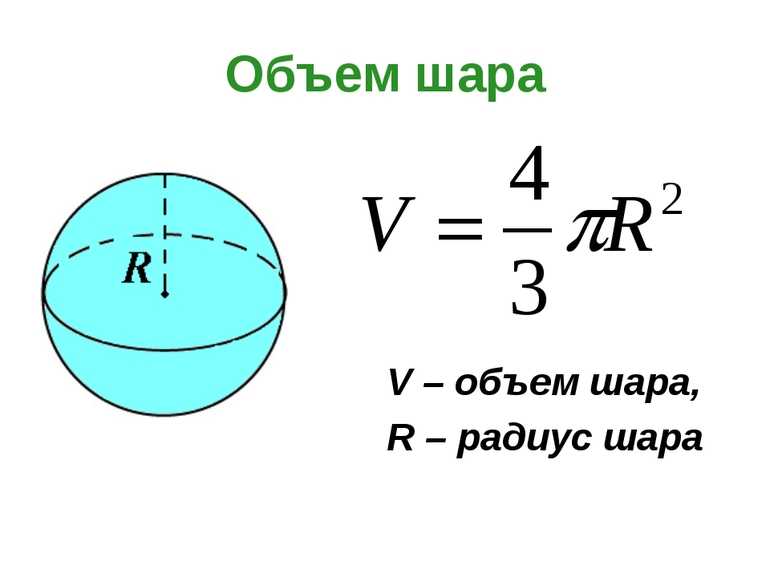
В школьной программе объем шара представлен одной формулой:

V = 4/3* π*R3 , где R –  радиус шара.

Учитывая, что диаметр шара вдвое больше радиуса шара, имеем формулу объема шара такую:

V = 1/6 * π* D3, где D – диаметр шара.

Но объем шара может быть задан и другими соотношениями . Опишем их ниже.

Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара:

V = 1/3 R*S, где R –  радиус шара.

А вот теорема Архимеда:

Объем шара в 1,5 раза меньше объема описанного вокруг него цилиндра, а поверхность шара – в 1,5 раза меньше полной поверхности того же цилиндра.

V = 2/3 * V_ц., где V_ц – объем цилиндра.

S_пов. = 2/3 * S_{пов. ц.} , где S_{пов. ц.} – полная поверхность цилиндра.

Части шара.

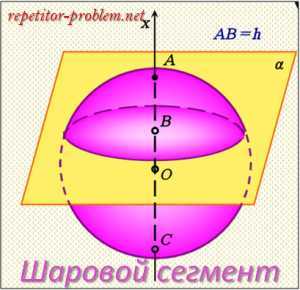Шаровой сегмент.

Определение.

Шаровой сегмент – это  часть шара, отсекаемая от нее плоскостью.

Кривая поверхность шарового сегмента равна произведению его высоты на длину окружности большого круга шара:

S_сегм. = 2πR* h, где R –  радиус шара, h – высота сегмента.

Еще формула площади поверхности сегмента:

S_сегм. = π*(r2 + h2), где r – радиус основания сегмента, h – высота сегмента.

Объем шарового сегмента вычисляется по формуле:

V = π* h2 *(R – 1/3*h) = 1/6*π*h(h2 + 3r2), где r – радиус основания сегмента, h – высота сегмента.

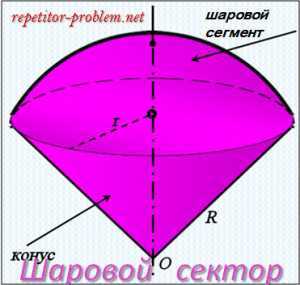Шаровой сектор.

Определение.

Шаровой сектор – часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной – центр шара.

Согласно определению формула площади поверхности шарового сектора выглядит так:

S_{шар. сектор} = S_{бок.конус.} + S_{шар. сегм.}

Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезанная сектором часть шаровой поверхности (S), а высота равна радиусу шара (R)

V = 1/3*R*S = 2/3*π*R2*h, где h – высота шарового сегмента, принадлежащая шаровому сектору.

Шаровой слой.

Определение.

Часть шара, заключенная между двумя секущими параллельными плоскостями, называется шаровым слоем, а кривая поверхность шарового слоя называется шаровым поясом (или зоной).

S_{шар. слоя} = h*2πR , где R –  радиус шара, h – высота шарового слоя.

Объем шарового слоя:

V = 1/6 * π* h3 +  1/2 * π*(r₁2 + r₂2)*h, где r_1, r₂  – радиусы оснований шарового слоя, h – высота шарового слоя.

Площади сферы и ее частей. Объемы шара и его частей

В следующей таблице приведены формулы для расчета объема сферы и объемов ее частей, а также площади сферы и площадей ее частей.

Фигура	Рисунок	Формула	Описание
Прохладный		S = 4πr2, где r — радиус сферы.	Диапазон пуль
Мяч	где r — радиус шара.	Объем мяча
Сферический ремень		S = 2пр, где r — радиус сферы, h – высота сферического пояса. Площадь сферического пояса не зависит от радиусов r1 и r2 !	Площадь сферического пояса
Мяч команда	где r1, r2 — радиусы оснований сферического слоя, h – высота сферического слоя.	Объем сферического слоя
Сферический сегмент		S = 2пр, где r — радиус сферы, h – высота сферического сегмента.	Площадь сферического сегмента
Шаровой сегмент	где r — радиус шара, h – высота сферического сегмента.	Объем сферического сегмента
Сектор мяча		где r — радиус шара, h — высота сферического сектора.	Объем сферического сектора

Прохладный

Диапазон мяча: S = 4πr2, где r — радиус сферы.

Мяч

Объем мяча: где r — радиус шара.

Сферический ремень

Площадь сферического пояса: S = 2пр, где r — радиус сферы, h – высота сферического пояса. Площадь сферического пояса не зависит от радиусов r1 и r2 !

Мяч команда

Объем шаровой кровати: где r1, r2 — радиусы оснований сферического слоя, h – высота сферического слоя.

Сферический сегмент

Площадь сферического сегмента: S = 2пр, где r — радиус сферы, h – высота сферического сегмента.

Шаровой сегмент

Объем шарового сегмента: где r — радиус шара, h – высота сферического сегмента.

Сектор мяча

Объем сектора сферы: где r — радиус шара, h — высота сферического сектора.

Терминология и сферическая геометрия

Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).

Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.

Сферическая геометрия

Большой круг на сфере

Основными элементами геометрии евклидовой плоскости являются точки и линии . На сфере точки определяются в обычном смысле. Аналог «линии» — геодезическая , представляющая собой большой круг ; Определяющей характеристикой большого круга является то, что плоскость, содержащая все его точки, также проходит через центр сферы. Измерение по длине дуги показывает, что кратчайший путь между двумя точками, лежащими на сфере, — это более короткий сегмент большого круга, который включает эти точки.

Многие теоремы классической геометрии верны и для сферической геометрии, но не все, потому что сфера не удовлетворяет некоторым постулатам классической геометрии , включая постулат параллельности . В сферической тригонометрии , углы определяются между большими кругами. Сферическая тригонометрия во многом отличается от обычной тригонометрии . Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Кроме того, любые два подобных сферических треугольника конгруэнтны.

Резюме

И шар, и сфера являются абстрактными геометрическими объектами (геометрическими фигурами), задаваемыми через некоторое геометрическое место точек пространства — например, с помощью понятия центра шара/сферы и радиуса шара/сферы. Однако только шар является полноценным геометрическим телом, поскольку включает в себя не только описание ограничивающей его поверхности, но и всей той части пространства, что в себя эта поверхность заключает. С такой точки зрения сфера — лишь внешняя абстрактная граница (поверхность) задаваемого в пространстве шара.

Символ шара-глобальность шара Земли. Символ будущего, он отличается от креста тем, что последний олицетворяет собой страдание и человеческую смерть. В Древнем Египте впервые пришли к заключению, что земля шарообразна. Это предположение послужило основой для многочисленных размышлений о бессмертии земли и возможности бессмертия населяющих ее живых организмах.

Данная точка (О) называется центром сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы (R-радиус сферы). Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Очевидно, что диаметр сферы равен 2R.

Определение шара Шар – это тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки (или фигура, ограниченная сферой). Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Шар

Плоскость,проходящая через центр шара,называется диаметральной плоскостью.Плоскость,проходящая через центр шара,называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью.Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью.

X²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.
R, то сфера и плоскость не имеют общих точек.»>
R, то сфера и плоскость не имеют общих точек.»>
R, то сфера и плоскость не имеют общих точек.» title=»x²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.»>
title=»x²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.»>

Касательная плоскость к сфере касательной плоскостью к сфереПлоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, точкой касания А плоскости и сферы.а их общая точка называется точкой касания А плоскости и сферы.

Теорема: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Доказательство: Рассмотрим плоскость α, касающуюся сферы с центром О в точке А. Докажем, что ОА перпендикулярен α. Предположим, что это не так. Тогда радиус ОА является наклонной к плоскости α, и, следовательно расстояние от центра сферы до плоскости меньше радиуса сферы. Поэтому сфера и плоскость пересекаются по окружности. Это противоречит тому, что-касательная, т.е. сфера и плоскость имеют только одну общую точку. Полученное противоречие доказывает, что ОА перпендикулярен α.

Определение.

Сфераповерхность шарацентром сферы

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шарцентром шара

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение.Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула.Объём шара:

V =	4	π R 3 =	1	π D 3
3	6

Формула.Площадь поверхности сферы через радиус или диаметр:

S = 4π
R 2 = π
D 2

Интегрирование формулы площади боковой поверхности шарового слоя: как избежать грубых ошибок

Шаровой слой — это регион, получаемый путем среза шара двумя плоскостями параллельными его базовой плоскости. Площадь боковой поверхности шарового слоя является важным параметром при решении различных математических задач. Интегрирование формулы для вычисления этой площади может быть сложным процессом, и неконтролируемые ошибки могут привести к неверным результатам. В этой статье мы рассмотрим некоторые методы, которые помогут избежать грубых ошибок при интегрировании формулы площади боковой поверхности шарового слоя.

1. Учтите ограничения интегрирования

При интегрировании формулы площади боковой поверхности шарового слоя, важно правильно ограничить пределы интегрирования. Наши ограничения должны быть связаны с параметрами шарового слоя, такими как радиус внешнего и внутреннего шаров и высота среза

Неправильно выбранные пределы интегрирования могут привести к неверным результатам. Поэтому перед началом интегрирования внимательно изучите параметры задачи и убедитесь, что ограничения выбраны правильно.

2. Используйте правильную формулу площади боковой поверхности шарового слоя

Существует несколько известных формул для вычисления площади боковой поверхности шарового слоя, в зависимости от задачи. Наиболее распространенными формулами являются:

• Формула площади боковой поверхности шарового слоя с вырезанным конусом:

• Формула площади боковой поверхности шарового слоя с участием угла выреза:

Убедитесь, что вы используете правильную формулу для вашей конкретной задачи, чтобы избежать ошибочных результатов.

3. Правильно выберите систему координат

Правильный выбор системы координат также важен при интегрировании формулы площади боковой поверхности шарового слоя. Если ваша задача алгебраически сложна, то грубые ошибки могут возникнуть из-за неправильного выбора системы координат. Вообще, удобно использовать сферические или цилиндрические координаты, чтобы упростить интегрирование и увеличить точность вашего результата.

4. Проверьте свои алгебраические вычисления

Из-за сложности формулы площади боковой поверхности шарового слоя, ошибки в алгебраических вычислениях могут стать причиной неверных результатов

Поэтому очень важно проверить свои алгебраические вычисления на предмет возможных ошибок. Однако, даже с правильными вычислениями, могут возникнуть неточности из-за использования дискретной аппроксимации интеграла вместо его точного вычисления

Использование численных методов интегрирования, таких как метод Монте-Карло, может помочь уменьшить эти неточности.

5. Практикуйтесь и проверяйте свои результаты

Как и в любой математической задаче, практика играет важную роль. Практикуйтесь в интегрировании формулы площади боковой поверхности шарового слоя на различных примерах, чтобы лучше понять процесс и избежать грубых ошибок

Также важно проверять свои результаты: сравните их с известными значениями площадей шаровых слоев, найденных аналитически или с использованием других методов. Это поможет вам лучше понять аккуратность и точность ваших вычислений

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №14. Объем шара и его частей

Перечень вопросов, рассматриваемых в теме

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10-11 учебник для общеобразов. учрежд.: база и профильн. М: Просвещение.2009

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни и др. – М.: Просвещение, 2014. – 255, сс. 121-126.

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.

Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.

Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.

Концы любого диаметра шара называются диаметрально противоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.

Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями

Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями

Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость.

Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.

Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы

Объем шара равен

Объем шарового сегмента равен

Объем шарового сектора равен

Объем шарового слоя равен

Примеры и разбор решения заданий тренировочного модуля

№1. Круговой сектор радиуса R с центральным углом 60 градусов вращается вокруг одного из радиусов, образующих этот угол. Найдите объем тела вращения.

№2. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.

Решение: запишем формулу для вычисления объема шарового слоя.

Чтобы найти объём шарового слоя нам необходимо знать его высоту и радиусы двух его оснований.

По условию задачи нам дано расстояние между сечениями, как раз-таки это расстояние и есть высота данного шарового слоя, и она равна

Теперь найдём чему равны радиусы оснований шарового слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга вычисляется по формуле

Подставим радиусы оснований и высоту шарового слоя в формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен

Как вычислить площадь поверхности вращения, если линия задана в полярной системе координат?

Если кривая задана в полярных координатах уравнением , и функция   имеет непрерывную производную  на данном промежутке, то площадь поверхности, полученной вращением данной кривой вокруг полярной оси, рассчитывается по формуле , где  – угловые значения, соответствующие концам кривой.

В соответствии с геометрическим смыслом задачи подынтегральная функция , а это достигается только при условии  ( и  заведомо неотрицательны). Следовательно, необходимо рассматривать значения угла из диапазона , иными словами кривая должна располагаться выше полярной оси и её продолжения. Как видите, та же история, что и в двух предыдущих параграфах.

Пример 5

Вычислить площадь поверхности, образованной вращением кардиоиды  вокруг полярной оси.

Решение: график данной кривой можно посмотреть в Примере 6 урока о полярной системе координат. Кардиоида симметрична относительно полярной оси, поэтому рассматриваем её верхнюю половинку на промежутке  (что, собственно, обусловлено и вышесказанным замечанием).

Поверхность вращения будет напоминать яблочко.

Техника решения стандартна. Найдём производную по «фи»:

Составим и упростим корень:
Надеюсь, с заштатными тригонометрическими формулами ни у кого не возникло затруднений.

Используем формулу:

На промежутке , следовательно:  (о том, как правильно избавляться от корня, я подробно рассказал в статье Длина дуги кривой).

Ответ:

Интересное и короткое задание для самостоятельного решения:

Пример 6

Вычислить площадь шарового пояса ,

Что такое шаровой пояс? Положите на стол круглый неочищенный апельсин и возьмите в руки нож. Сделайте два параллельных разреза, разделив тем самым фрукт на 3 части произвольных размеров. Теперь возьмите серединку, у которой сочная мякоть обнажилась с обеих сторон. Данное тело называется шаровым слоем, а ограничивающая её поверхность (оранжевая кожура) – шаровым поясом.

Читатели, хорошо знакомые с полярными координатами, легко представили чертёж задачи: уравнение  задаёт окружность с центром в полюсе радиуса , от которой лучи  отсекают меньшую дугу. Данная дуга вращается вокруг полярной оси и таким образом получается шаровой пояс.

Теперь можно с чистой совестью и лёгким сердцем съесть апельсинку, на этой вкусной ноте и завершим занятие, не портить же вам аппетит другими примерами =)

Решения и ответы:

Пример 2: Решение: вычислим площадь поверхности, образованной вращением верхней ветви  вокруг оси абсцисс. Используем формулу .В данном случае: ;Таким образом:Ответ

Пример 4: Решение: используем формулу . Первая арка циклоиды определена на отрезке .Найдём производные:Составим и упростим корень:Таким образом, площадь поверхности вращения:На промежутке , поэтому Первый интеграл интегрируем по частям:Во втором интеграле используем тригонометрическую формулу .Ответ

Пример 6: Решение: используем формулу:Ответ

(Переход на главную страницу)

О шаре и цилиндре

Так называлась работа, опубликованная античным математиком Архимедом. Она вышла в двух томах в 225 году до н. э. Он был первым, кто сделал полный и подробный трактат по основам вычисления площади поверхности сферы, объёма шара и аналогичных значений для таких элементов, как цилиндр. Результатами его деятельности пользуются до сих пор.

Архимед особенно гордился формулой объёма шара, где он доказал, что эта величина составляет две трети объёма описанного цилиндра. Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.

Аргумент, который Архимед использовал для доказательства формулы V шара, был довольно сложным и сильно вовлечён в его геометрию. Поэтому во многих современных учебниках используется упрощённая версия, основанная на концепции предела, которого, конечно, не было в античные времена. Великий математик создавал в сфере усечённый конус путём построения и вращения геометрических фигур, и только после этого он определил объём.

Сейчас кажется, что он специально выбирал такие оригинальные методы. Однако это был всего лишь лучший из тех, которые были ему доступны в греческой математике. Его основные работы были вновь открыты в XX веке. Например, Метод механических теорем, как он назывался в трактате автора.

Шар, сфера и их части

      Введем следующие определения, связанные с шаром, сферой и их частями.

      Определение 1. Сферой с центром в точке   O   и радиусом   r   называют множество точек, расстояние от которых до точки   O   равно   r   (рис. 1).

      Определение 2. Шаром с центром в точке   O   и радиусом   r   называют множество точек, расстояние от которых до точки   O   не превосходит   r   (рис. 1).

Рис.1

      Таким образом, сфера с центром в точке   O   и радиусом   r   является поверхностью шара с центром в точке   O   и радиусом   r.

      Замечание. Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом шара).

      Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

      Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями   (рис. 2).

Рис.2

      Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.

      Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.

      Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.

      Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя.

      Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).

      Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).

Рис.3

      Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.

      Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента.

Рис.4

      По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).

Рис.5

      Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).

Рис.6

      Высотой шарового сектора называют высоту его сферического сегмента.

      Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.