Что первое в координатах х или у?

Определение декартовой системы координат

Координаты – это записанный по определенным правилам своего рода точный “адрес”, по которому можно найти тот или иной объект.

Примеры координат:

• географические широта и долгота;
• расположение какой-либо отметки на числовой оси;
• номер ряда и места в самолете и т.д.

Когда требуется указать координаты какой-либо точки на плоскости, чаще всего используется декартовая (прямоугольная) система, названная так в честь французского математика и физика Рене Декарта.

1. На плоскости проводятся две прямые числовые оси, перпендикулярные друг к другу (т.е. расположенные под углом 90°). Их пересечение в точке O является началом координат (отсчета) для каждой из осей.

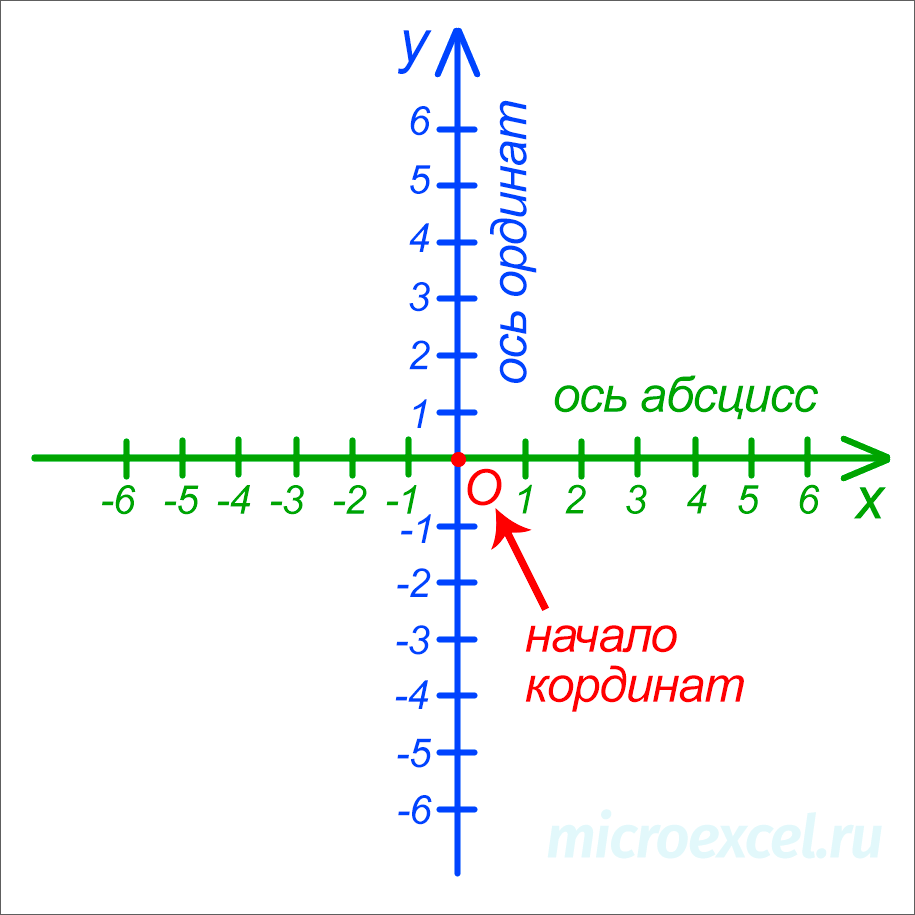
Таким образом, прямоугольная система координат включает следующие основные элементы:

1. Координатная плоскость – плоскость, в которой расположена система координат. Записывается как “xOy” .
2. Координатные оси: ось абсцисс ( Ox ) и ось ординат ( Oy ).
3. Единичные отрезки (цена деления) – расстояния между черточками на обеих числовых осях, которые обычно равны по длине.

Коллинеарность векторов

Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что

Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:

Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю

Например, пусть

В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами {0; 0; 0}. Он условно признается коллинеарным любому вектору.

Задание. Выясните, какие из этих пар векторов коллинеарны:

Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:

Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.

Повторяем эти действия в задании б):

На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.

В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.

В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:

Коэффициент k получился одинаковым, поэтому вектора коллинеарны.

В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.

Ответ: а) да; б) нет; в) нет; г) да; д) да.

Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).

Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.

Сначала вычислим коорд-ты векторов АВ и ВС:

Теперь проверяем, коллинеарны ли эти вектора:

Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.

Цилиндрическая и сферическая системы координат

Декартова система координат обеспечивает простой способ описания расположения точек в пространстве. Однако некоторые поверхности сложно смоделировать с помощью уравнений, основанных на декартовой системе. Рассмотрим два разных способа описания положения точек в пространстве, оба из которых основаны на расширениях полярных координат. Как следует из названия, цилиндрические координаты полезны для решения задач, связанных с цилиндрами, таких как расчет объема круглого резервуара для воды или количества масла, протекающего по трубе. Точно так же сферические координаты полезны для решения задач, связанных со сферами.

Цилиндрическая система координат

Когда мы расширили традиционную декартову систему координат с двух измерений до трех, мы просто добавили новую ось для моделирования третьего измерения. Начиная с полярных координат, мы можем следовать тому же процессу, чтобы создать новую трехмерную систему координат, называемую цилиндрической системой координат. Таким образом, цилиндрические координаты обеспечивают естественное расширение полярных координат до трех измерений.

В цилиндрической системе координат точка в пространстве (рис. 3) представлена ​​упорядоченными тремя скалярами \ где \ полярные координаты проекции точки на плоскость \, а z-координата в декартовой системе координат.

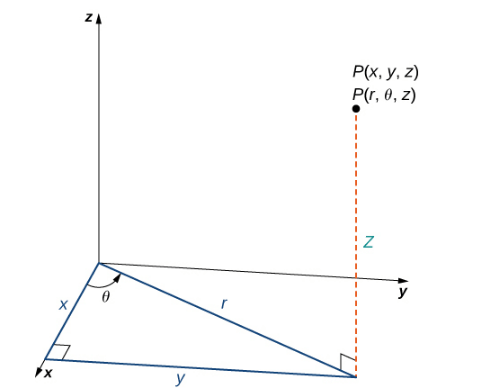Рис. 3 Правый треугольник лежит в плоскости xy

Длина гипотенузы равна r и θ — мера угла, образованного положительной осью x и гипотенузой. Г координата описывает местоположение точки выше или ниже х плоскости.

На плоскости xy прямоугольный треугольник, показанный на рис. 3, дает ключ к преобразованию между цилиндрическими и декартовыми (прямоугольными) координатами.

Преобразование между цилиндрическими и декартовыми координатами

Прямоугольные координаты (x,y,z)  и цилиндрические координаты  (r,θ,z)  точки связаны следующим образом:

\
\ — уравнения для преобразования из цилиндрических координат в декартовые

\ и \

\ — уравнения для преобразования из декартовых в цилиндрические

\

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Вычисление длины векторов и расстояния между точками

Рассмотрим радиус-вектор ОМ с коорд-тами {x; у; z}. Попытаемся найти его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор окажется диагональю:

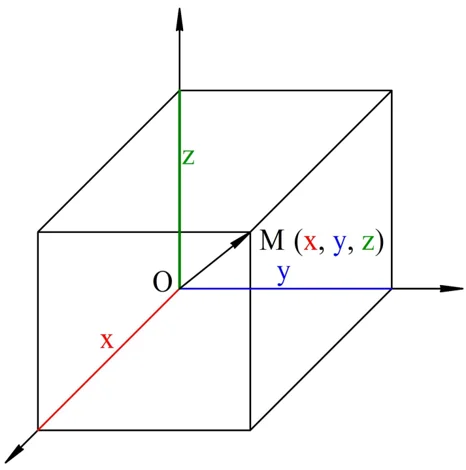
Напомним, что квадрат длины диагонали в прямоугольном параллелепипеде равен сумме квадратов его измерений. Но в полученном параллелепипеде измерения – это коорд-ты х, у и z, поэтому можно записать:

Так как равные вектора имеют как одинаковы и коорд-ты, и длина, то ясно, что каждый вектор с коорд-тами {x; y; z} будет равен рассмотренному радиус-вектору, а значит и его длина будет рассчитываться по такой же формуле.

Задание. Найдите длину вектора m{– 2; 9; 6}.

Решение. Просто используем формулу:

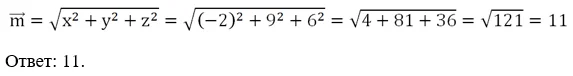
Рассмотрим отрезок АВ с известными коорд-тами его концов. Можно построить вектор АВ, его коорд-ты будут определяться так:

Задание. Найдите расстояние между точкой K(10; 15; 5) и M(16; 21; – 2).

Решение. Просто подставляем коорд-ты точек в формулу:

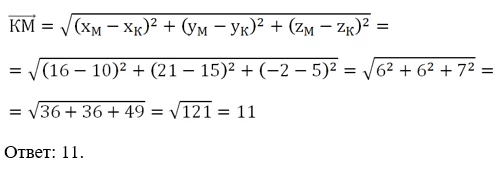
Задание. Найдите длину медианы KM в ∆ KPN, если известны коорд-ты его вершин: P(2; 5; 8), N (6; 9; 12) и K(16; 11; 13).

Решение. Для нахождения длины медианы достаточно знать коорд-ты ее концов. Коорд-ты K уже известны, а M – середина PN, что позволяет вычислить и ее коорд-ты:

Метод координат в задачах типа С2.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. 1

Си с т е м а к оо р д и н а т в п р о с т р а н с т в е

1. Си с т е м а к оо р д и н а т в п р о с т р а н с т в е.

В ы б е р е м н а ч а л о к оо р д и н а т . П р о в е д е м т ри в з а и м н о п е р п е н д и к у л яр ны е о с и х , y и z . Выберем м а с ш т а б .

П о л у ч и л а с ь с и с т е м а к о о р д и н а т в т р е х м е р н о м п р о с т р а н с т в е .

К а ж д а я т о ч к а х а р а к т е р и з у е т с я т р е м я ч и с л а м и — к оо р д и н а т а м и п о x , y и z . З а п и с ь M ( − 1 ; 3 ; 2 ) о з н а ч а е т , ч т о к оо р д и н а т а т о ч к и M п о x ( а б с ц и сс а ) р а в н а − 1 , к оо р д и н а т а п о y ( о р д и н а т а ) р а в н а 3 , а к оо р д и н а т а п о z ( а пп л и к а т а ) р а в н а 2 .

В е к т о р ы в п р о с т р а н с т в е о п р е д е л яю т с я т а к ж е , к а к и н а п л о с к о с т и.

Э т о н а п р а в л е н ны е о т р е з к и, и м е ю щ и е н а ч а л о и к о н е ц . Т о л ь к о в п р о с т р а н с т в е в е к т о р з а д а е т с я т р е м я к оо р д и н а т а м и x , y и z :

ﺂ؟ ( x a ; y a ; z a )

Чтобы н а й т и к о о р д и н а т ы в е к т о р а , так же, как и на плоскости, и з к оо р д и н а т ы к о н ц а надо в ы ч есть к оо р д и н а т у н а ч а ла.

Если точка M – середина отрезка AB , то ее координаты находятся по формуле:

Декартовы координаты в пространстве

Принцип строительства будет таким же. В аффинном пространстве размерности 3 система координат (декартова) представляет собой объединенные данные:
E{\ displaystyle E}

• точка отправления ,О{\ displaystyle O}
• и три вектора не компланарны , и .я→{\ displaystyle {\ vec {i}}}j→{\ displaystyle {\ vec {j}}}k→{\ displaystyle {\ vec {k}}}

В координатных осях являются одновременно аффинными линиями , и .
(ОИкс)знак равно(О;я→){\ Displaystyle (Ох) = (О; {\ vec {я}})}(Оy)знак равно(О;j→){\ Displaystyle (Оу) = (О; {\ vec {j}})}(Оz)знак равно(О;k→){\ Displaystyle (Оз) = (О; {\ vec {k}})}

Для точки мы имеем право нарисовать:
M{\ displaystyle M}

• плоскость, параллельная плоскости, разрезающей по оси абсцисс ,Оyz{\ displaystyle Oyz}ОИкс{\ displaystyle Ox}мИкс{\ displaystyle m_ {x}}Икс{\ displaystyle x}
• плоскость, параллельная плоскости, разрезающей по оси абсцисс ,ОИксz{\ displaystyle Oxz}Оy{\ displaystyle Oy}мy{\ displaystyle m_ {y}}y{\ displaystyle y}
• плоскость, параллельная плоскости, разрезающей по оси абсцисс .ОИксy{\ displaystyle Oxy}Оz{\ displaystyle Oz}мz{\ displaystyle m_ {z}}z{\ displaystyle z}

Тройка действительных чисел определяется только положением точки . Это называется координата (декартово) из в кадре  :
(Икс,y,z){\ Displaystyle (х, у, г)}M{\ displaystyle M}M{\ displaystyle M}(О;я→,j→,k→){\ displaystyle (O; {\ vec {i}}, {\ vec {j}}, {\ vec {k}})}

• реальное называется абсциссой .Икс{\ displaystyle x}
• реальное называется ординатой или глубиной .y{\ displaystyle y}
• реальное называется размером или высотой .z{\ displaystyle z}

И наоборот, любой тройке вещественных чисел соответствует одна точка абсциссы , ординаты и измерения . Эта точка получается как пересечение:
(Икс,y,z){\ Displaystyle (х, у, г)}M{\ displaystyle M}Икс{\ displaystyle x}y{\ displaystyle y}z{\ displaystyle z}

• плоскости, параллельной плоскости, проходящей через точку абсциссы ,Оyz{\ displaystyle Oyz}ОИкс{\ displaystyle Ox}Икс{\ displaystyle x}
• плоскости, параллельной плоскости, проходящей через точку абсцисс иОИксz{\ displaystyle Oxz}Оy{\ displaystyle Oy}y{\ displaystyle y}
• плоскости, параллельной плоскости, проходящей через точку абсциссы .ОИксy{\ displaystyle Oxy}Оz{\ displaystyle Oz}z{\ displaystyle z}

Эти три самолета, а также три базовые плоскости , и нарисовать параллелепипед.
ОИксy{\ displaystyle Oxy}ОИксz{\ displaystyle Oxz}Оyz{\ displaystyle Oyz}

Между любой точкой и любой тройкой действительных чисел существует взаимно однозначное соответствие, называемое системой координат .
M{\ displaystyle M}M{\ displaystyle M}

Как и на плоскости, эти координаты интерпретируются с помощью векторной записи:

ОM→знак равноИкся→+yj→+zk→{\ displaystyle {\ overrightarrow {OM}} = x {\ vec {i}} + y {\ vec {j}} + z {\ vec {k}}}

Ортонормальные ориентиры

В евклидовом аффинном пространстве размерности 3, маркер , как говорят ортонормированный , когда векторы , и являются унитарными и попарно ортогональны. Это второе условие записано:
(О;я→,j→,k→){\ displaystyle (O; {\ vec {i}}, {\ vec {j}}, {\ vec {k}})}я→{\ displaystyle {\ vec {i}}}j→{\ displaystyle {\ vec {j}}}k→{\ displaystyle {\ vec {k}}}

⟨я∣j⟩знак равно{\ Displaystyle \ langle \ mathbf {я} \ mid \ mathbf {j} \ rangle = 0} ;  ;⟨j∣k⟩знак равно{\ Displaystyle \ langle \ mathbf {j} \ mid \ mathbf {k} \ rangle = 0}⟨k∣я⟩знак равно{\ Displaystyle \ langle \ mathbf {к} \ mid \ mathbf {я} \ rangle = 0}

Как и на плоскости, необходимо будет использовать ортонормированную систему координат, если кто-то хочет работать с расстояниями и углами. Тогда расстояние будет записано:

ОMзнак равноИкс2+y2+z2{\ displaystyle OM = {\ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}}}

Числовая ось

Числовой осью называют направленную прямую, на которой указывается начальная точка О и задается некоторый «эталон» длины Е. Каждой точке этой прямой отвечает вещественное число, равное длине отрезка если расположено правее точки О, и равное этой

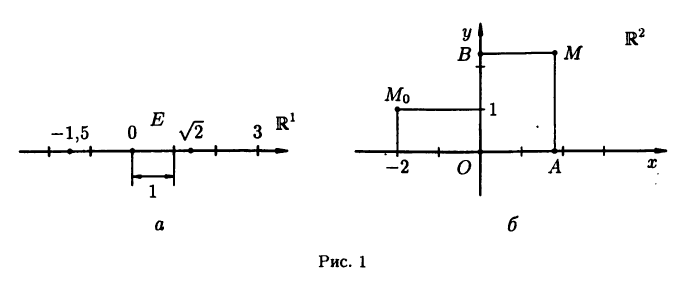
длине со знаком минус — в противном случае (см. рис. 1 а). Числовую ось будем обозначать (смысл этого обозначения прояснится ниже).

Указанное соответствие между точками числовой оси и множеством вещественных чисел является взаимно однозначным, т. е. каждой точке соответствует единственное число , обратно, каждому числу соответствует единственная точка Таким образом, множество . вещественных чисел можно отождествлять с числовой осью , чем мы будем впредь постоянно пользоваться.

Обозначения и соглашения

Декартовы координаты точки обычно записываются в скобки и через запятую, как в (10, 5) или же (3, 5, 7). Место происхождения часто обозначается заглавной буквой. О. В аналитической геометрии неизвестные или общие координаты часто обозначаются буквами (Икс, y) в плоскости и (Икс, y, z) в трехмерном пространстве. Этот обычай исходит из соглашения об алгебре, которое использует буквы в конце алфавита для неизвестных значений (таких как координаты точек во многих геометрических задачах) и буквы в начале для заданных величин.

Эти общепринятые имена часто используются в других областях, таких как физика и техника, хотя могут использоваться и другие буквы. Например, на графике, показывающем, как давление варьируется в зависимости от время, координаты графика можно обозначить п и т. Каждая ось обычно называется в честь координаты, которая измеряется вдоль нее; так говорят ось абсцисс, то ось Y, то Таксис, так далее.

Другое распространенное соглашение для именования координат — использование индексов, например (Икс₁, Икс₂, …, Икс_п) для п координаты в п-мерное пространство, особенно когда п больше 3 или не указано. Некоторые авторы предпочитают нумерацию (Икс, Икс₁, …, Икс_п−1). Эти обозначения особенно удобны в компьютерное программирование: сохраняя координаты точки как множество, вместо записывать, то нижний индекс может служить для индексации координат.

В математических иллюстрациях двумерных декартовых систем первая координата (традиционно называемая абсцисса ) измеряется по горизонтальный ось, ориентированная слева направо. Вторая координата ( ордината ) затем измеряется по вертикальный ось, обычно ориентированная снизу вверх. Маленькие дети, изучающие декартову систему, обычно учат порядок чтения значений, прежде чем закрепить Икс-, y-, и zконцепции осей, начиная с двумерной мнемоники (например, «Пройдите по коридору, затем поднимитесь по лестнице», как прямо через Иксось затем вертикально вверх по y-ось).

Компьютерная графика и обработка изображений, однако часто используют систему координат с y— ось направлена ​​вниз на дисплее компьютера. Это соглашение разработано в 1960-х годах (или ранее) из того, как изображения изначально хранились в отображать буферы.

Для трехмерных систем принято изобразить ху-плоскость по горизонтали, с z-ось добавлена ​​для представления высоты (положительное значение вверх). Кроме того, существует соглашение об ориентации Икс— ось к зрителю со смещением вправо или влево. Если диаграмма (3D проекция или же 2D чертеж в перспективе ) показывает Икс— и y-оси по горизонтали и вертикали соответственно, то z— ось должна быть указана «за пределы страницы» в сторону зрителя или камеры. На такой двумерной диаграмме трехмерной системы координат z— ось будет выглядеть как линия или луч, указывающий вниз и влево или вниз и вправо, в зависимости от предполагаемого зрителя или камеры перспектива. На любой диаграмме или отображении ориентация трех осей в целом произвольна. Однако ориентация осей относительно друг друга всегда должна соответствовать правило правой руки, если специально не указано иное. Все законы физики и математики предполагают это , что обеспечивает согласованность.

Для трехмерных диаграмм имена «абсцисса» и «ордината» редко используются для Икс и y, соответственно. Когда они есть, z-координату иногда называют прикладывать. Слова абсцисса, ордината и прикладывать иногда используются для обозначения осей координат, а не значений координат.

Квадранты и октанты

Четыре квадранта декартовой системы координат

Оси двумерной декартовой системы делят плоскость на четыре бесконечные области, называемые квадранты, каждая ограничена двумя полуосями. Они часто нумеруются с 1-го по 4-й и обозначаются римские цифры: I (где знаки двух координат — I (+, +), II (-, +), III (-, -) и IV (+, -). Когда оси нарисованы в соответствии с математическим обычаем , нумерация идет против часовой стрелки начиная с правого верхнего («северо-восточного») квадранта.

Точно так же трехмерная декартова система определяет разделение пространства на восемь областей или октанты, по знакам координат точек. Соглашение, используемое для наименования определенного октанта, состоит в перечислении его знаков, например (+ + +) или же (− + −). Обобщением квадранта и октанта до произвольного числа измерений является ортодоксальный, и применяется аналогичная система именования.

Координаты вектора

Введем в пространстве прямоугольную систему коорд-т, а далее от ее начала отложим вектора i, j и k, которые соответственно будут лежать на координатных осях Ох, Оу и Оz, и длина которых составит единицу. Эти вектора именуют координатными векторами, единичными векторами или просто ортами.

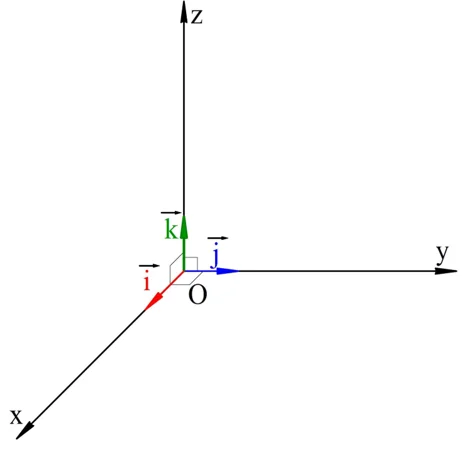
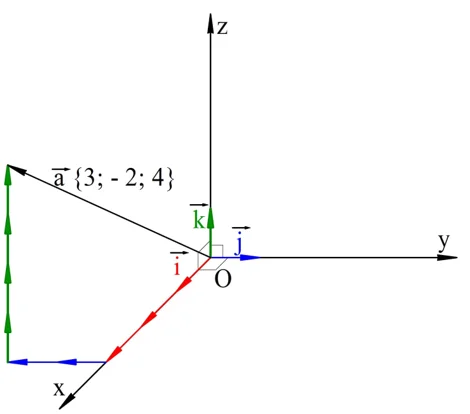
Ясно, что орты находятся в разных плоскостях, то есть они образуют тройку некомпланарных векторов. Это означает, что любой вектор а в пространстве можно разложить на орты:

где х, у и z – какие-то действительные числа. Они как раз и считаются координатами вектора а. Записываются коорд-ты вектора в фигурных скобках. На следующем рисунке показан вектор а{3; – 2; – 4}.

Задание. Разложите на орты вектор

Если начало вектора ОМ располагается в начале системы координат О, то вектор ОМ именуют радиус-вектором. В таком случае коорд-ты точки конца вектора, то есть точки М, совпадают с коорд-тами самого вектора ОМ.

Это свойство радиус-вектора мы уже изучали в 9 классе в планиметрии, и в стереометрии оно сохраняется.

Задание. О – начало координат, а точка М имеет коорд-ты (2; 5; – 3). Найдите коорд-ты вектора ОМ.

Решение. Всё очень просто – коорд-ты вектора будут совпадать с коорд-тами его конца, так его начало совпадает с началом коорд-т:

Также в стереометрии остаются справедливыми ещё несколько правил, которые были доказаны в курсе планиметрии:

Задание. Найдите сначала сумму, а потом разность векторов а{3; 7; 5} и b{2; 4; 6}.

Решение. Будем обозначать коорд-ты векторов через индексы. Например, коорд-ты вектора а – это х_а, у_а и z_а. Пусть сумма векторов будет вектором с, а их разность – вектором d. Для вычисления суммы надо складывать соответствующие координаты:

Для вычисления разности надо из коорд-т вектора а вычитать коорд-ты вектора b:

Задание. Вычислите коорд-ты вектора р, зная, что:

Решение. Для вычисления координат надо в выражении для вектора р сами векторы заменить на их координаты:

Получается, что вектор p имеет координаты {0; – 2; 3}.

Теперь мы можем доказать ещё одно утверждение, уже известное из курса планиметрии:

Действительно, пусть есть некоторый вектор АВ, причем коорд-ты точек А и В известны. Построим радиус-вектора OА и OВ:

Координаты радиус-векторов будут совпадать с координатами их концов:

ч. т. д.

Задание. Определите коорд-ты вектора CD, если даны коорд-ты точек С и D: С(3; 8; – 5) и D(5; 4; 1).

Решение. Здесь надо просто из коорд-т точки D, являющейся концом вектора, вычесть коорд-ты точки С:

Задание. От точки K(10; 6; 13) отложен вектор m{3; 2; 5}, конец совпал в точку H. Найдите коорд-ты точки H.

Решение. Коорд-ты вектора m и его концов связаны формулами:

Сферическая система координат

В декартовой системе координат положение точки в пространстве описывается с помощью упорядоченной тройки осей, в которой каждая координата представляет собой расстояние. В цилиндрической системе координат положение точки в пространстве описывается двумя расстояниями (r и z ) и угла (θ). В сферической системе координат мы снова используем упорядоченную тройку осей для описания положения точки в пространстве. В данном случае оси описывают одно расстояние и два угла. Сферические координаты упрощают описание сферы, так же как цилиндрические координаты упрощают описание цилиндра. Линии сетки для сферических координат основаны на измерениях углов, как и для полярных координат.

Теорема

В сферической системе координат точка P в пространстве (рис. 4) представлена упорядоченной тройкой
\

Где:

\ — это расстояние между P и началом координат \;

\ — тот же угол, который используется для описания местоположения в цилиндрических
координатах;

\ — это угол, образованный положительной осью z и отрезком прямой OP, где О это начало
координат и \

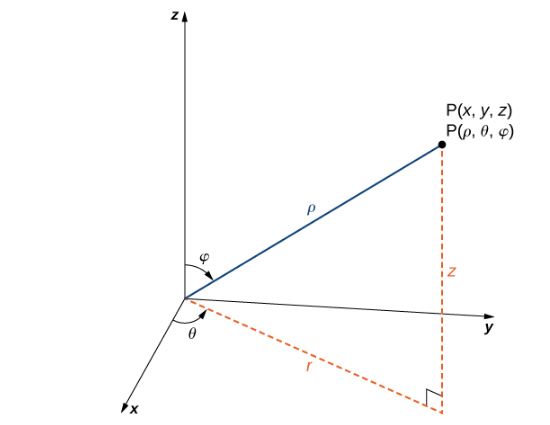Рис. 4 Связь между сферическими, декартовыми и цилиндрическими координатами.

Условно начало координат представлено как (0,0,0) в сферических координатах.

Преобразование между сферическими, цилиндрическими и прямоугольными координатами

Декартовые координаты \ и сферические координаты \ связаны следующим образом:

\

\ — уравнения для преобразования из сферических координат в   квадратные (декартовы).

\ и \

\ — уравнения для преобразования из декартовых в сферические.

\

Если точка имеет цилиндрические координаты \, тогда эти уравнения определяют связь между цилиндрическими и сферическими координатами.

\

\ — уравнения для преобразования из сферических координат в цилиндрические.

\ и \

\  — уравнения для преобразования из цилиндрических в сферические.

\

Формулы для преобразования сферических координат в прямоугольные могут показаться сложными, но это простые приложения тригонометрии. Глядя на рисунок 5, легко увидеть, что \. Затем, глядя на треугольник на плоскости xy с \ в качестве его гипотенузы имеем \.  Вывод формулы для y похож. Рисунок 3 также показывает, что \ и  \.  Решая это последнее уравнение для  \  а затем подставив  \ (из первого уравнения) дает  \

Также обратите внимание, что, как и прежде, мы должны быть осторожны при использовании формулы \ выбрать правильное значение \

Существуют и другие криволинейные системы координат, с помощью которых можно найти координаты заданной точки: параболические, гиперболические, эллиптические и другие. Система отсчета подбирается для каждого случая индивидуально с учетом особенности движения тела, с помощью которой определяется простейший закон движения того или иного тела или точки.

Обозначения и соглашение

Декартовы координаты точки обычно записываются в скобках и разделяются запятыми, как в (10, 5) или (3, 5, 7). Начало координат часто обозначается заглавной буквой О. В аналитической геометрии неизвестные или общие координаты часто обозначаются буквами (x, y) на плоскости и (x, y, z) в трехмерном пространстве. Этот обычай исходит из соглашения об алгебре, которая использует буквы в конце алфавита для неизвестных значений (таких как координаты точек во многих геометрическихх) и буквы в начале для заданных величин.

Эти общепринятые имена часто используются в других областях, например, в физике и технике, хотя местные и буквы. Например, на графике, показывающем, как давление изменяется с временем, координаты графика могут быть обозначены p и t. Каждая ось обычно называется в честь координаты, которая измеряется вдоль нее; поэтому говорят, что ось x, ось y, ось t и т. д.

Другое распространенное соглашение для именования координат — использование индексов, как (x 1, x 2,…, x n) для n координат в n-мерном пространстве, особенно когда n больше 3 или не указано. Некоторые авторы предпочитают нумерацию (x 0, x 1,…, x n — 1). Эти обозначения особенно полезны в компьютерном программировании : при сохранении точки координат в виде вместо записи нижний индекс может служить для индексации координат.

В математических иллюстрациях двумерных декартовых систем первая координатаанная (традиционно называемая абсциссой ) измеряется вдоль горизонтальной оси , ориентация слева направо. Вторая координата (ордината ) проходит вдоль вертикальной оси , обычно ориентированной снизу вверх. Маленькие дети, изучающие декартову, обычно изучают порядок чтения значений перед тем, как закрепить концепции x, y и z, начиная с двумерной мнемоники (например, «Пройдите по коридору, поднимитесь по лестнице», похожую на прямую). по оси X, затем вверх по вертикали по оси Y).

Компьютерная графика и обработка изображений, однако, часто используют систему координат с осью Y, ориентированной вниз на компьютерный дисплей. Это было разработано в 1960-х (или ранее) на основе соглашения, которым изображения изначально хранились в буферах отображения.

. Для трехмерных систем принято изображать плоскость xy по горизонтали с добавлением оси Z для представления высоты (положительное значение вверх). Существует соглашение о том, что ось x ориентирована к наблюдателю, смещенная вправо или влево. Если на диаграмме (трехмерная проекция или двухмерный перспективный чертеж ) оси x и y отображаются по горизонтали и вертикали, соответственно, то ось z должна быть указывающей «из страницы» к зрителю или камере. На любой диаграмме или отображении ориентации трех осей в зависимости от предполагаемого зрителя или перспективы камеры на любой диаграмме или отображении ориентации трех осей в двумерной диаграмме трехмерной системы системы ось будет указана ориентация влево или вправо. Все законы физики и математики предполагают эту праворукость, что обеспечивает согласованность.

правилу правой руки

Для трехмерных диаграмм используются «абсцисса» и «ордината» редко для x и y, соответственно, когда это так, координата z иногда называется аппликатой . иногда используются для обозначения осей координат, а не координат.

Квадранты и октанты

Оси двухмерной системы координат. Декартова система измерений делит плоскость на четыре бесконечные области, называемые квадрантами, каждая из которых ограничена двумя полуосями. Они часто нумеруются с 1-го по 4-й и обозначаются римскими цифрами : I (где знаки двух координат — I (+, +), II (-, +), III (-, -), Когда оси строятся в соответствии с математическим обычаем, нумерация идет против часовой стрелки, начиная с верхнего правого («северо-восточного») квадранта.

Точно так же трехмерная декартова система определяет разделение пространства на восемь областей или октантов в соответствии со знаками координат точек. Условие, используемое для наименования конкретного октанта, заключается в перечислении его знаки, например (+ + +) или (- + -). Обобщение квадранта и октанта до произвольного числа измерений — это ортант, и применяется аналогичная система имен.