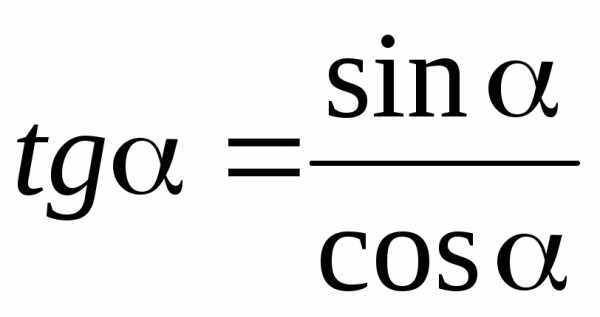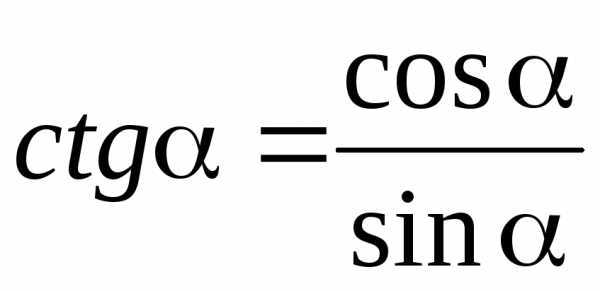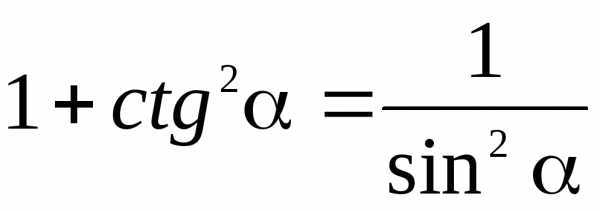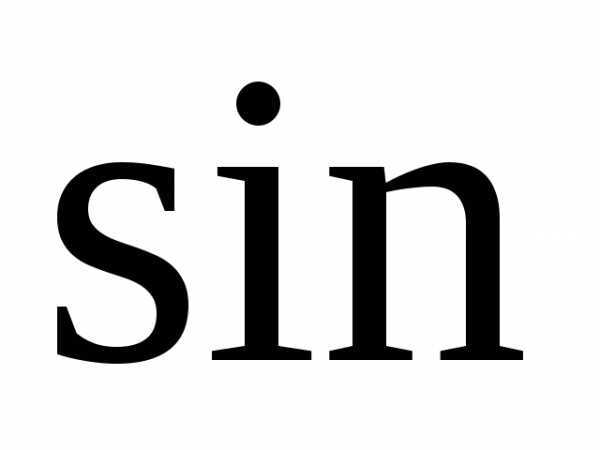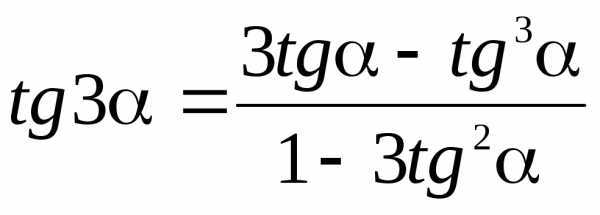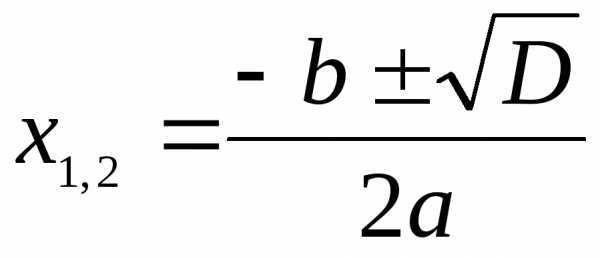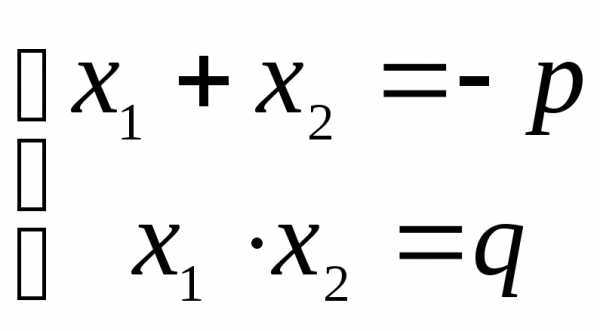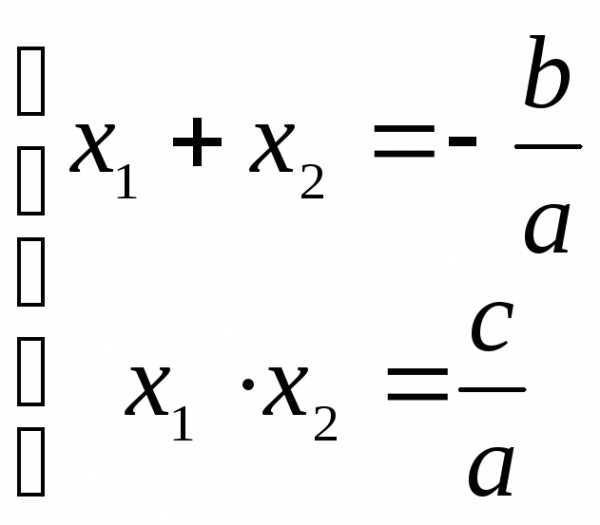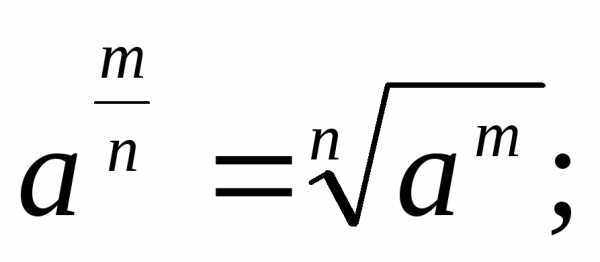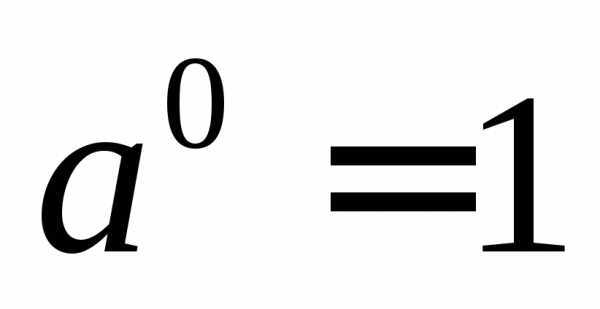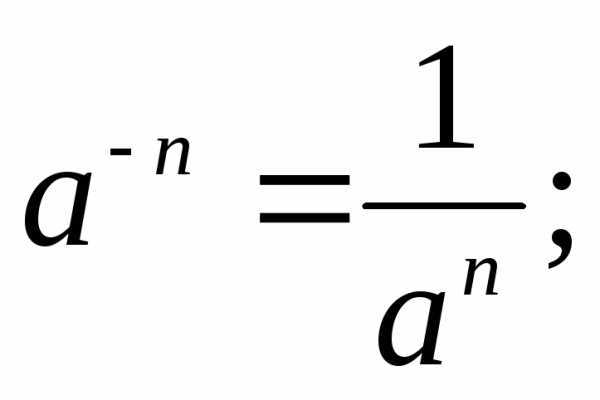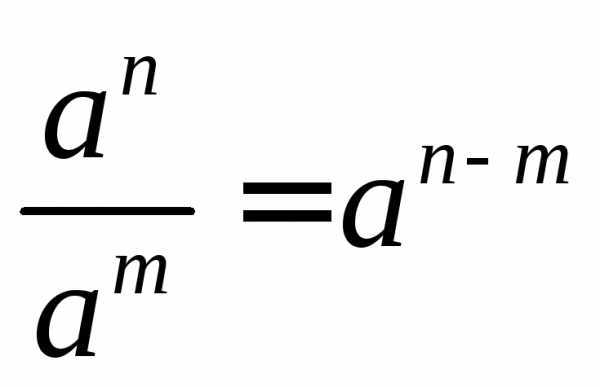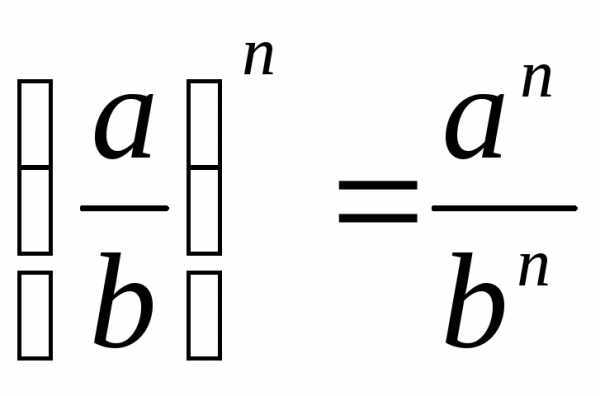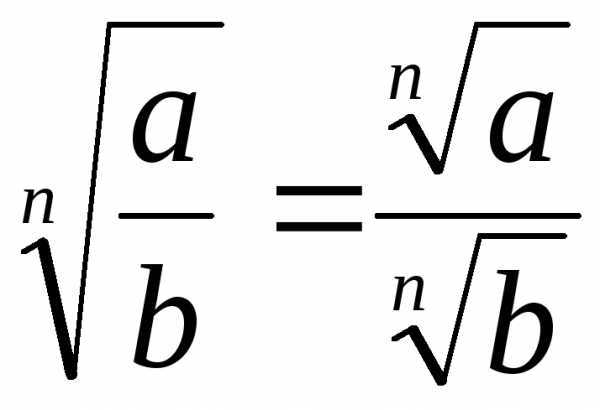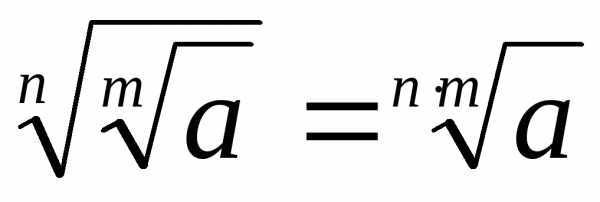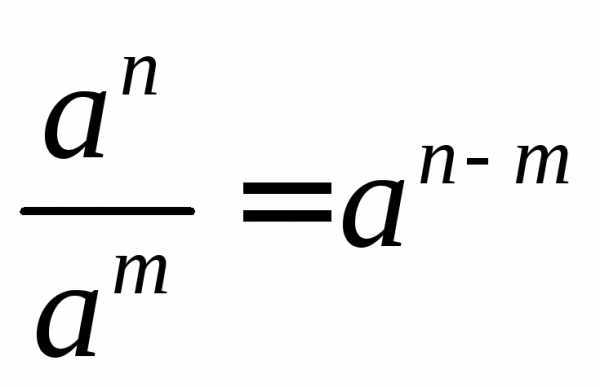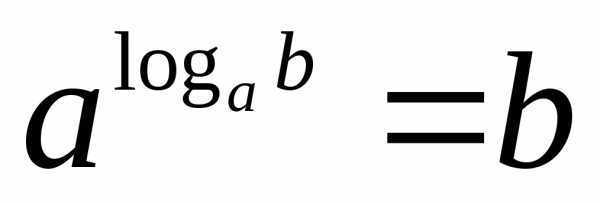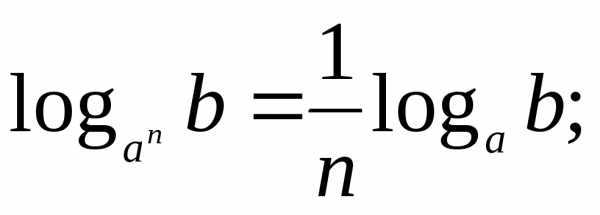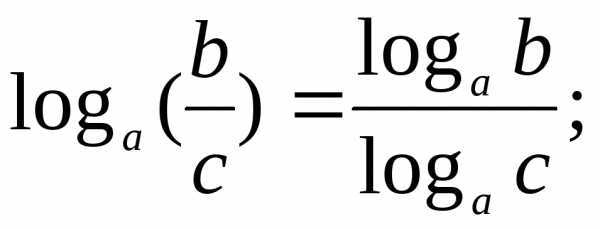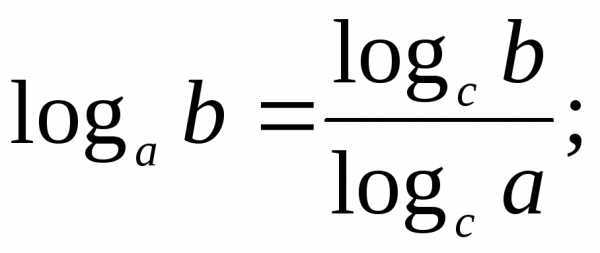Пример использования формул
Зная, как найти сумму арифметической прогрессии, стоит рассмотреть простой пример использования приведенных формул.
Ниже дана числовая последовательность, следует найти сумму ее членов, начиная с 5-го и заканчивая 12-м:
Приведенные числа свидетельствуют, что разность d равна 3. Используя выражение для n-го элемента, можно найти значения 5-го и 12-го членов прогрессии. Получается:
Зная значения чисел, стоящих на концах рассматриваемой алгебраической прогрессии, а также зная, какие номера в ряду они занимают, можно воспользоваться формулой для суммы, полученной в предыдущем пункте. Получится:
Стоит отметить, что это значение можно было получить иначе: сначала найти сумму первых 12 элементов по стандартной формуле, затем вычислить сумму первых 4 элементов по той же формуле, после этого вычесть из первой суммы вторую.
Важные формулы
Приведем теперь основные формулы, которые понадобятся для решения задач с использованием арифметической прогрессии. Обозначим символом a n n-й член последовательности, где n — целое число. Разность обозначим латинской буквой d. Тогда справедливы следующие выражения:
- Для определения значения n-го члена подойдет формула: a n = (n-1)*d+a 1 .
- Для определения суммы первых n слагаемых: S n = (a n +a 1)*n/2.
Чтобы понять любые примеры арифметической прогрессии с решением в 9 классе, достаточно запомнить эти две формулы, поскольку на их использовании строятся любые задачи рассматриваемого типа. Также следует не забывать, что разность прогрессии определяется по формуле: d = a n — a n-1 .
Геометрическая прогрессия. Формулы п-го члена и суммы п первых членов геометрической прогрессии. Характеристическое свойство геометрической прогрессии.
О.Геометрической прогрессией
О.Это число называетсязнаменателемгеометрической прогрессииqгеометрической
прогрессии.
Геометрическая
прогрессия задаётся своим первым членом
и знаменателем. Из определения
геометрической прогрессии следует,
что отношение любого её члена, начиная
со второго, к предыдущему члену равно q, т.е. при любом
натуральномnверно
равенство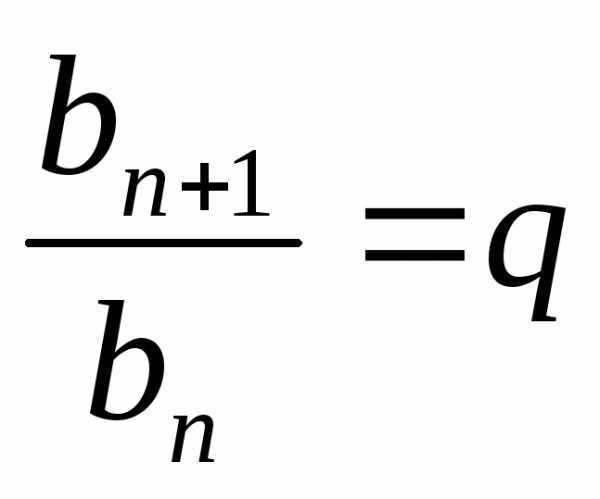
Формула n-го
члена геометрической прогрессии.
Любой член
геометрической прогрессии можно
вычислить по формуле 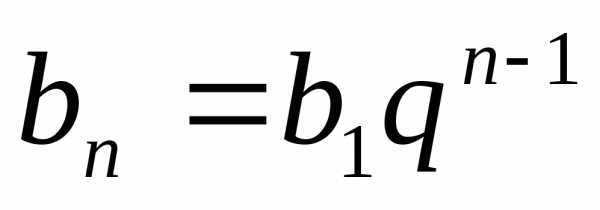 ,где
,где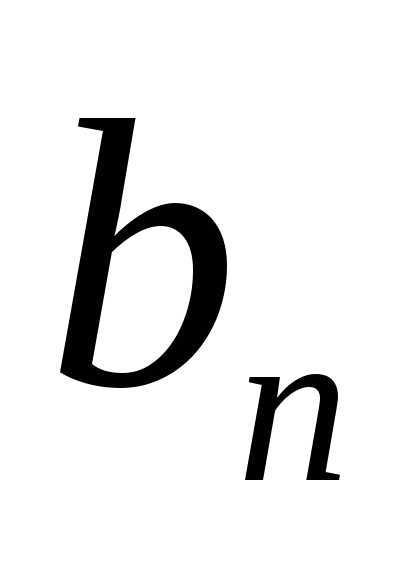
n,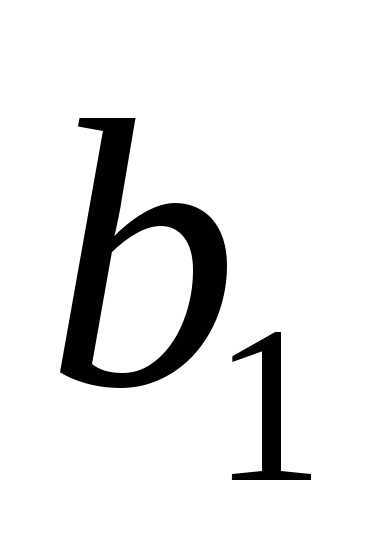 q
q
Возьмём произвольное
натуральное n.Из
определения геометрической прогрессии
следует.
Эта цепочка состоит
из nравенств, поэтому
для любого конечногоnона может быть выписана. Следовательно,
любой член геометрической прогрессии
можно вычислить, зная его номер, первый
член прогрессии и её знаменатель.
Характеристическое
свойство геометрической прогрессии с
положительными членами.
Если
последовательность положительных
чисел является геометрической
прогрессией, то все её члены, начиная
со
второго, являются средним
геометрическим предшествующего и
последующего членов.
Доказательство.
Из определения
геометрической прогрессии следует,
что 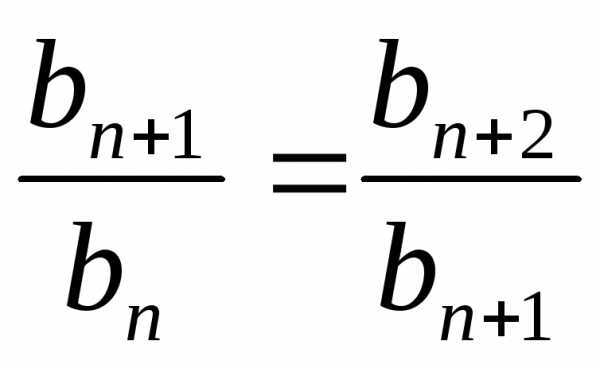 .
.
Выразив из этого
равенства 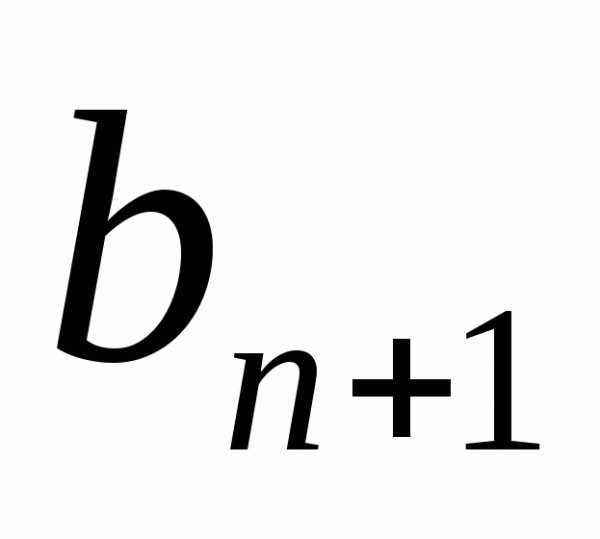
Так как все члены
прогрессии положительны, то последнее
равенство равносильно следующему
.
Теорема.
(формула суммы n первых членов
геометрической прогрессии).
Сумма nпервых членов геометрической
прогрессии равна 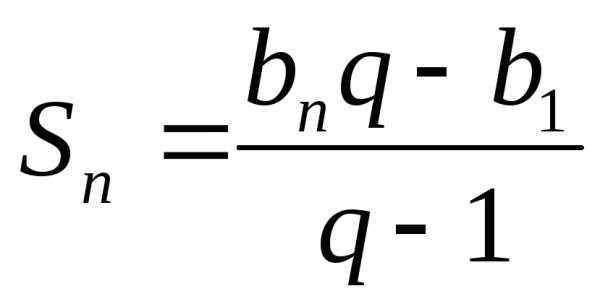 ,при
,при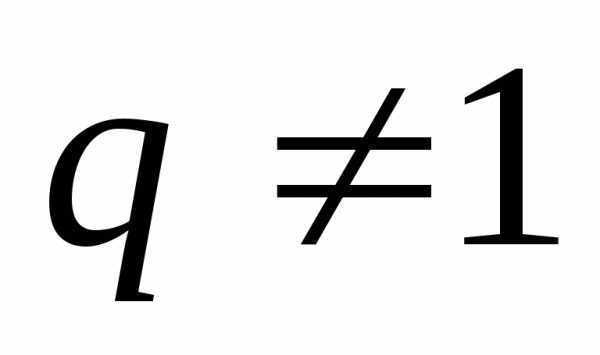
Доказательство.
Сумма nпервых членов
геометрической прогрессии равна
. 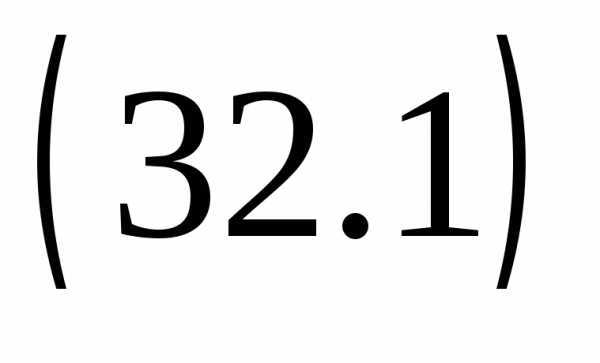
Домножим обе части
этого равенства на знаменатель
геометрической прогрессии
.
Следовательно,
.
Вычтем полученное равенство из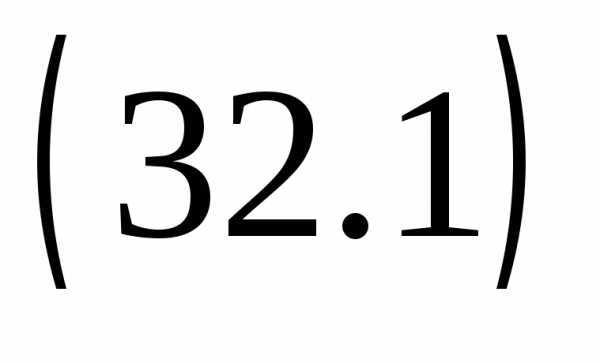
.
Отсюда следует,
что
.
При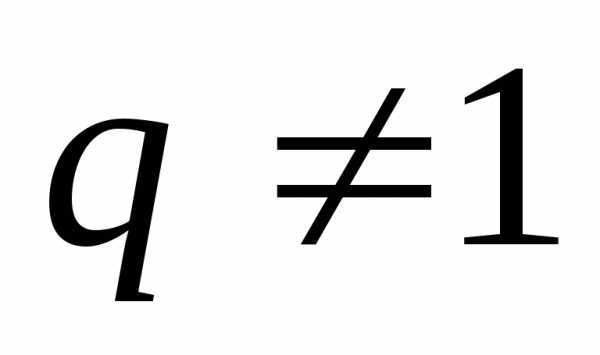
Следствие. 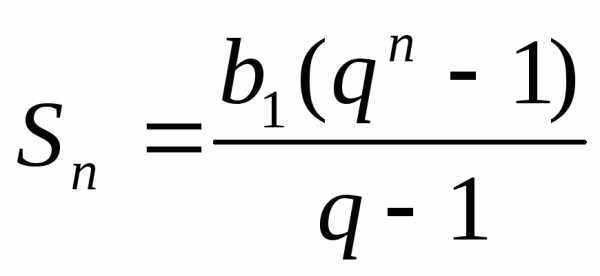 ,при
,при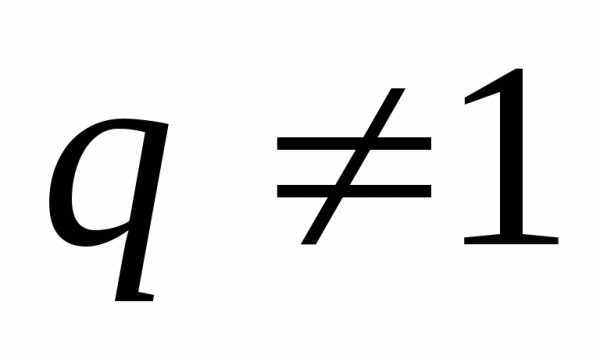
Доказательство.
Выразим 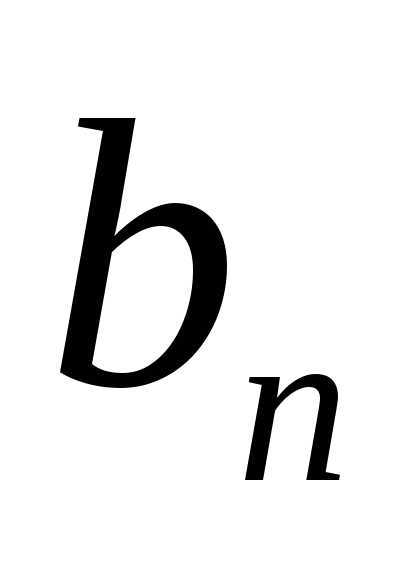
n
Геометрическая
прогрессия называется бесконечно
убывающей, если её знаменательq по абсолютной величине меньше
единицы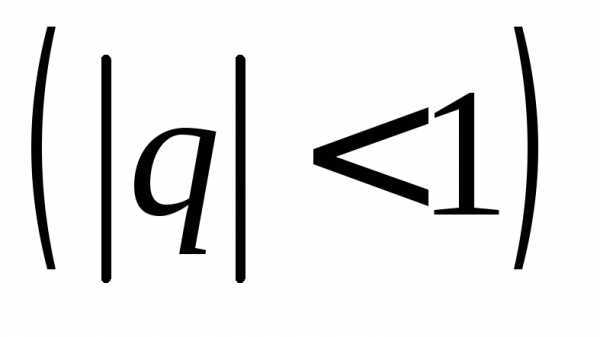
О.Суммой бесконечно
убывающей геометрической прогрессииназывается число, к которому неограниченно
приближается суммаnпервых членов бесконечно убывающей
геометрической прогрессии при
неограниченном увеличенииn.
Сумма
бесконечно убывающей геометрической
прогрессии равна 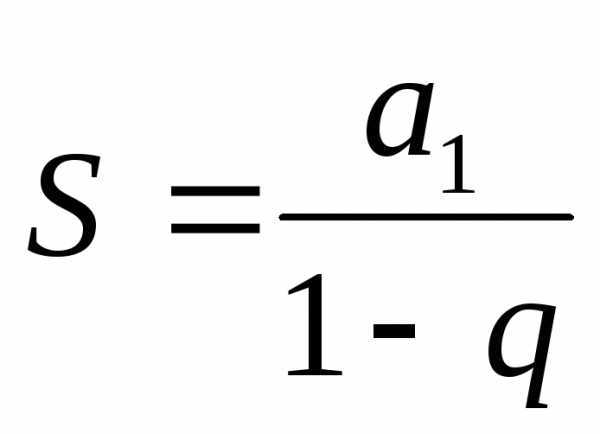
Приложение

Сборник формул
|
ТРИГОНОМЕТРИЯ Основные
Знаки
Тригонометрические Выражение отрицательного аргумента Решение Функция Преобразование суммы
Функции Функции половинного Функции |
АЛГЕБРА Корни квадратных Теорема
Разложение Степени
Логарифмы
Степень Извлечение |
Понятие числовой последовательности
Введем два определения числовой последовательности:
Определение 1
Числовая функция, у которой область определения совпадает с натуральным рядом чисел, будет называться числовой последовательностью.
Определение 2
Отображения натурального ряда чисел на множество действительных чисел будет называться числовой последовательностью: $f:N→R$
Числовая последовательность обозначается следующим образом:
${p_k }={p_1,p_2,…,p_k,…}$
где $p_1,p_2,…,p_k,…$ — действительные числа.
Есть три различных способа для задания числовых последовательностей. Опишем их.
-
Аналитический.
В этом способе последовательность задается в виде формулы, с помощью которой можно найти любой член этой последовательности, подставляя в нее вместо переменной натуральные числа.
-
Рекуррентный.
Данный способ задания последовательности заключается в следующем: Дается первый (или несколько первых) член данной последовательности, а затем формула, которая связывает любой член ее с предыдущим членом или предыдущими членами.
-
Словесный.
При этом способе числовая последовательность просто описывается без введения каких-либо формул.
Двумя частными случаями числовых последовательностей являются арифметическая и геометрическая прогрессии.
Формулы геометрической прогрессии
Прогрессия в формате математических переменных выглядит так:
Начнем с формулы для вычисления знаменателя. Из расположенного ниже рисунка мы видим, что разные виды прогрессии зависят от значения знаменателя.
Формулы n-го члена:
А вот формула для нахождения суммы n первых членов:
Характеристическое свойство этой последовательности (bn) выражается формулой:
Формула суммы геометрической прогрессии:
Рассмотрим несколько примеров.
Первый член ГП равен 27, а ее знаменатель – 1/3. Найдите шесть первых членов ГП.
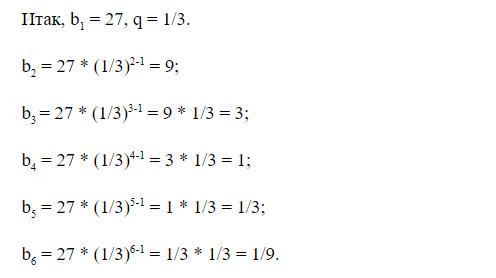
ГП выглядит таким образом: 27; 9; 3; 1; 1/3; 1/9…
Следующий пример. Посчитайте
Нам необходимо найти сумму ГП, первый член которой , знаменатель q=17, а количество членов n=20.
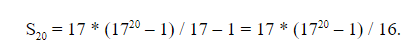
Но есть и сложные задачи с применением ГП. Чтобы школьник хорошо усвоил этот материал, необходимо решать по 10-20 заданий всех уровней сложности.
А лучше нанять профессионального репетитора, которой может просто и наглядно объяснить ребенку разные способы решений и показать, что математика – это нечто интересное и увлекательное. Используйте сайт BUKI для поиска квалифицированного преподавателя.
Задача № 4. Восстановление ряда чисел
Пусть даны 2 элемента числового ряда, например, 5-й равен 30 и 10-й равен 60. Необходимо по этим данным восстановить весь ряд, зная, что он удовлетворяет свойствам прогрессии геометрической.
Чтобы решить задачу, необходимо для начала записать для каждого известного члена соответствующее выражение. Имеем: a5 = b4 * a1 и a10 = b9 * a1. Теперь разделим второе выражение на первое, получим: a10 / a5 = b9 * a1 / (b4 * a1) = b5. Отсюда определяем знаменатель, взяв корень пятой степени от отношения известных из условия задачи членов, b = 1,148698. Полученное число подставляем в одно из выражений для известного элемента, получаем: a1 = a5 / b4 = 30 / (1,148698)4 = 17,2304966.
Таким образом, мы нашли, чему равен знаменатель прогрессии bn, и геометрическую прогрессию bn-1 * 17,2304966 = an, где b = 1,148698.
Геометрическая прогрессия — это… Что такое Геометрическая прогрессия?
Геометри́ческая прогре́ссия — последовательность чисел (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии), где , : .
Описание
Любой член геометрической прогрессии может быть вычислен по формуле:
Если и , прогрессия является возрастающей последовательностью, если , — убывающей последовательностью, а при — знакочередующейся.
Своё название прогрессия получила по своему характеристическому свойству:
то есть каждый член равен среднему геометрическому его соседей.
Примеры
- Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата:8-9.
- Последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
- 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — прогрессия со знаменателем 2 из тринадцати членов.
- 50; −25; 12,5; −6,25; 3,125; … — бесконечно убывающая прогрессия со знаменателем -½.
- — геометрическая прогрессия со знаменателем 1 (и арифметическая прогрессия с шагом 0).
Свойства
Доказательство
Пусть — последовательность :
- Полученное соотношение является характеристическим для арифметической прогрессии.
Доказательство
Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:,
Доказательство
Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:
Доказательство
Сумма первых членов геометрической прогрессии:
Доказательство
Через сумму:
Примеры некоторых классических задач
Чтобы лучше понять, что такое геометрическая прогрессия, примеры с решением для 9 класса могут помочь.
Условия:
a
1
= 3,
a
3
= 48. Найти
q
.
Решение: каждый последующий элемент больше предыдущего в
q
раз.
Необходимо выразить одни элементы через другие с помощью знаменателя.
Следовательно,
a
3
=
q
2
·
a
1
При подстановке
q
=
4
Условия:
a
2
= 6,
a
3
= 12. Рассчитать S 6 .
Решение:
Для этого достаточно найти q, первый элемент и подставить в формулу.
a
3
=
q
·
a
2
, следовательно,
q
=
2
a 2 = q
· a 1 ,
поэтому
a 1 =
3
S 6 =
189
·
a
1
= 10,
q
= -2. Найти четвертый элемент прогрессии.
Решение: для этого достаточно выразить четвертый элемент через первый и через знаменатель.
a 4 = q 3
·
a 1 = -80
Формулы арифметической прогрессии
Одно из важнейших свойств заключается в возможности вычисления любого числа конкретного места ряда.

Чтобы решать это, необходима формула, показывающая, как находится член арифметической прогрессии. В общем виде она будет выглядеть, как значение предыдущего числа в ряду (an-1), к которому прибавляют разность (d):
Также может возникнуть задача, когда надо просуммировать все числа ряда арифметической прогрессии (сумма членов). Если их малое количество, то можно посчитать это вручную, но если количество чисел перевалит за сотню, то проще будет воспользоваться специальной формулой для обработки.
Итак, нам понадобится значение первого числа в ряду (a1) и последнего (an), а также информация об общем количестве чисел в ряду. Рекуррентная формула, показывающая, как искать сумму, будет выглядеть в таком случае следующим образом:
Обратите внимание: под значением n подразумевается именно количество членов ряда, для которых производится нахождение суммы. Произведение членов арифметической прогрессии можно находить по похожей формуле:
Произведение членов арифметической прогрессии можно находить по похожей формуле:
где, Pn – произведение, b1 и bn – соответственно первое и последнее числа, а n – количество членов.
Отдельно следует коснуться такого понятия, как характеристическое свойство прогрессии. Оно сводится к выполнению определенного условия для каждого элемента:
Определение прогрессии геометрической
Для начала приведем определение этого числового ряда. Прогрессией геометрической называют такой ряд рациональных чисел, который формируется путем последовательного умножения его первого элемента на постоянное число, носящее название знаменателя.
Например, числа в ряду 3, 6, 12, 24, … — это прогрессия геометрическая, поскольку если умножить 3 (первый элемент) на 2, то получим 6. Если 6 умножить на 2, то получим 12, и так далее.
Члены рассматриваемой последовательности принято обозначать символом ai, где i — это целое число, указывающее на номер элемента в ряду.
Приведенное выше определение прогрессии можно записать на языке математики следующим образом: an = bn-1 * a1, где b — знаменатель. Проверить эту формулу легко: если n = 1, то b1-1 = 1, и мы получаем a1 = a1. Если n = 2, тогда an = b * a1, и мы снова приходим к определению рассматриваемого ряда чисел. Аналогичные рассуждения можно продолжить для больших значений n.
Определение числовой последовательности
Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.
Последовательности можно задавать разными способами:
- Словесно — когда правило последовательности объясняется словами: «Последовательность простых чисел: 4, 6, 10, 19, 21, 33…»
- Аналитически — когда указана формула ее n-го члена: yn = f(n). Последовательность yn = C называют постоянной или стационарной.
- Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.
Арифметическая прогрессия — (an), задана таким соотношением:
a1 = a, an+1= an + d.
Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: an+1 = an + an-1.
Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Графически — когда график последовательности состоит из точек с абсциссами
1, 2, 3, 4…
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.
Свойства числовых последовательностей:
- Последовательность {yn} называют возрастающей, если каждый ее член кроме первого больше предыдущего:y1 < y2 < y3 < … < yn < yn+1 < …
- Последовательность {yn} называют убывающей, если каждый ее член кроме первого меньше предыдущего: y1 > y2 > y3 > … > yn > yn+1 > …
Запишем числа, которые первые пришли в голову: 7, 19, 0, -1, 2, -11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.
Пример числовой последовательности выглядит так:
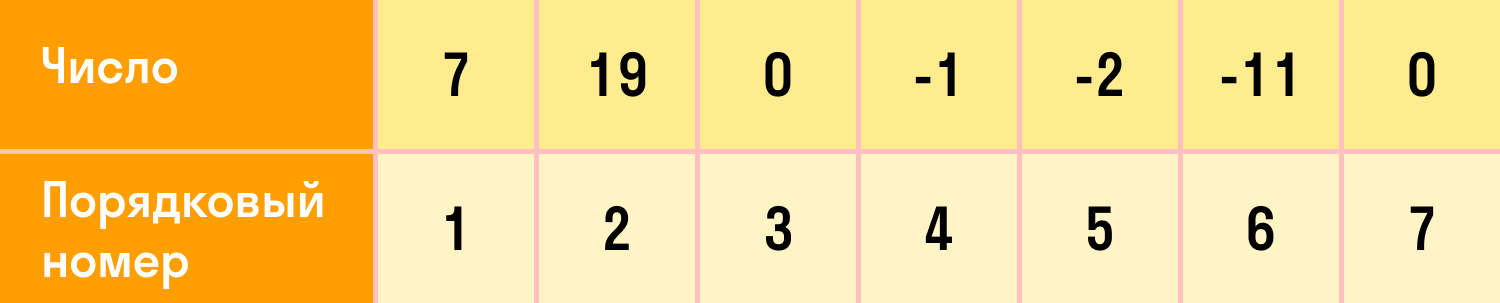
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.
N-ный член алгебраической последовательности — это число с порядковым номером n.
Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1, a2,…, a10…, an.
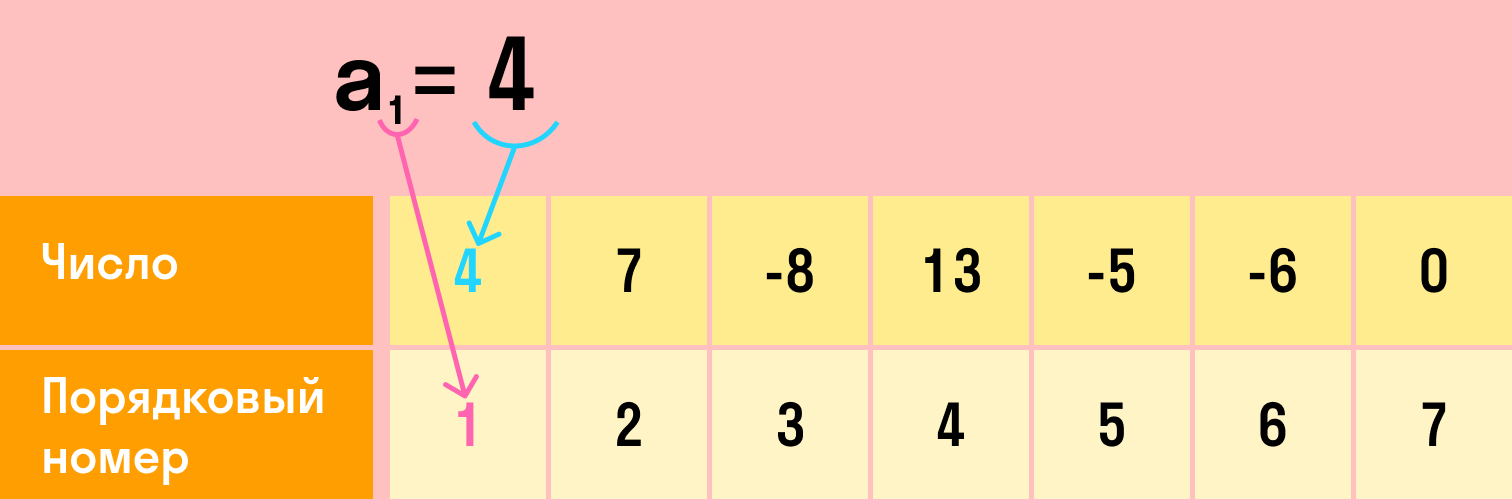
N-ый член последовательности можно задать формулой. Например:
- Формула an = 3n — 5 задает последовательность: −2, 1, 4, 7, 10…
- Формула an = 1 : (n + 2) задает последовательность: 13, 14, 15, 16…
Знаменатель прогрессии геометрической
Число b полностью определяет, какой характер будет носить весь числовой ряд. Знаменатель b может быть положительный, отрицательный, а также иметь значение больше единицы или меньше. Все перечисленные варианты приводят к разным последовательностям:
- b > 1. Имеет место возрастающий ряд рациональных чисел. Например, 1, 2, 4, 8, … Если элемент a1 будет отрицательным, тогда вся последовательность будет возрастать только по модулю, но убывать с учетом знака чисел.
- b
- -1
- b = 1. Часто такой случай не называют прогрессией, поскольку имеет место обычный ряд одинаковых рациональных чисел. Например, -4, -4, -4.
Формула суммы n первых членов геометрической прогрессии
Формула суммы n первых членов геометрической прогрессии имеет вид:
Sn = (bn*q — b1)/(q-1), где q не равно 1.
Рассмотрим простой пример:
В геометрической прогрессии b1=6, q=3, n=8 найти Sn.
Для нахождения S8 воспользуемся формулой суммы n первых членов геометрической прогрессии.
S8= (6*(3^8 -1))/(3-1) = 19 680.
Например
, последовательность \(3\); \(6\); \(12\); \(24\); \(48\)… является геометрической прогрессией, потому что каждый следующий элемент отличается от предыдущего в два раза (иначе говоря, может быть получен из предыдущего умножением его на два):
Как и любую последовательность, геометрическую прогрессию обозначают маленькой латинской буквой. Числа, образующие прогрессию, называют ее членами
(или элементами). Их обозначают той же буквой, что и геометрическую прогрессию, но с числовым индексом, равным номеру элемента по порядку.
Задача № 3. Чему равен знаменатель?
Пусть a1 = 2, найдите знаменатель прогрессии геометрической, при условии, что ее бесконечная сумма составляет 3, и известно, что это убывающий ряд чисел.
По условию задачи нетрудно догадаться, какой формулой следует пользоваться для ее решения. Конечно же, для суммы прогрессии бесконечно убывающей. Имеем: S∞ = a1 / (1 — b). Откуда выражаем знаменатель: b = 1 — a1 / S∞. Осталось подставить известные значения и получить требуемое число: b = 1 — 2 / 3 = -1 / 3 или -0,333(3). Можно качественно проверить этот результат, если вспомнить, что для этого типа последовательности модуль b не должен выходить за пределы 1. Как видно, |-1 / 3|
Разновидности
В зависимости от q и a 1, данная прогрессия разделяется на несколько видов:
Если и a 1 , и q больше единицы, то такая последовательность — возрастающая с каждым следующим элементом геометрическая прогрессия. Пример таковой представлен далее.
Пример: a 1 =3, q=2 — оба параметра больше единицы.
Тогда числовая последовательность может быть записана так:
3 6 12 24 48 …
Если |q| меньше единицы, то есть, умножение на него эквивалентно делению, то прогрессия с подобными условиями — убывающая геометрическая прогрессия. Пример таковой представлен далее.
Пример: a 1 =6, q=1/3 — a 1 больше единицы, q — меньше.
Тогда числовую последовательность можно записать таким образом:
6 2 2/3 … — любой элемент больше элемента, следующего за ним, в 3 раза.
Знакопеременная. Если q
Пример: a 1 = -3 , q = -2 — оба параметра меньше нуля.
Тогда числовую последовательность можно записать так:
3, 6, -12, 24,…
Сумма элементов от m до n: формула
Формула, приведенная в предыдущем пункте, дает ответ на вопрос, как найти сумму арифметической прогрессии (первых элементов), но часто в задачах необходимо просуммировать ряд чисел, стоящих в середине прогрессии. Как это сделать?
Ответить на этот вопрос проще всего, рассматривая следующий пример: пусть необходимо найти сумму членов от m-го до n-го. Для решения задачи следует представить заданный отрезок от m до n прогрессии в виде нового числового ряда. В таком представлении m-й член a m будет первым, а a n станет под номер n-(m-1). В этом случае, применяя стандартную формулу для суммы, получится следующее выражение:
Задача № 1. Вычисление неизвестных элементов прогрессии и суммы
Дана прогрессия геометрическая, знаменатель прогрессии 2, а ее первый элемент 3. Чему будут равны ее 7-й и 10-й члены, и какова сумма ее семи начальных элементов?
Условие задачи составлено достаточно просто и предполагает непосредственное использование вышеназванных формул. Итак, для вычисления элемента с номером n используем выражение an = bn-1 * a1. Для 7-го элемента имеем: a7 = b6 * a1, подставляя известные данные, получаем: a7 = 26 * 3 = 192. Аналогичным образом поступаем для 10-го члена: a10 = 29 * 3 = 1536.
Воспользуемся известной формулой для суммы и определим эту величину для 7-ми первых элементов ряда. Имеем: S7 = (27 — 1) * 3 / (2 — 1) = 381.
Определение и примеры арифметической прогрессии
Это последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой.
Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (аn) называется единичное число из последовательности.
Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии.
Кроме этого, существуют виды таких рядов:
- возрастающая – числа ряда увеличиваются по своему значению,
- убывающая – каждое последующее число ряда уменьшается.
В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6.
Возрастающие и убывающие геометрические прогрессии
У рассмотренной в самом начале статьи прогрессии \(b_n = \{3; 6; 12; 24; 48…\}\) знаменатель \(q\) больше единицы и поэтому каждый следующий член больше предыдущего. Такие прогрессии называются возрастающими
.
Если же \(q\) меньше единицы, но при этом положителен (то есть, лежит в пределах от нуля до единицы), то каждый следующий элемент будет меньше чем предыдущий. Например, в прогрессии \(4\); \(2\); \(1\); \(0,5\); \(0,25\)… знаменатель \(q\) равен \(\frac{1}{2}\).
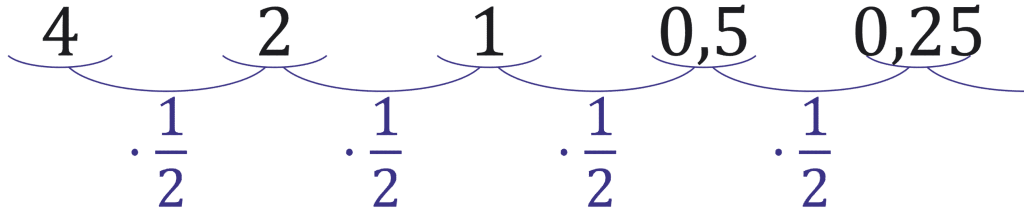
Эти прогрессии называются убывающими
Обратите внимание, что ни один из элементов такой прогрессии не будет отрицателен, они просто становятся всё меньше и меньше с каждым шагом. То есть, мы будем постепенно приближаться к нулю, но никогда его не достигнем и за него не перейдем
Математики в таких случаях говорят «стремиться к нулю».
Отметим, что при отрицательном знаменателе элементы геометрической прогрессии будут обязательно менять знак. Например
, у прогрессии \(5\); \(-15\); \(45\); \(-135\); \(675\)… знаменатель \(q\) равен \(-3\), и из-за этого знаки элементов «мигают».
Рассмотрим некоторый ряд.
7 28 112 448 1792…
Совершенно ясно видно, что значение любого его элемента больше предыдущего ровно в четыре раза. Значит, данный ряд является прогрессией.
Геометрической прогрессиейименуется бесконечная последовательность чисел, главной особенностью которой является то, что следующее число получается из предыдущего посредством умножения на какое-то определенное число. Это выражается следующей формулой.
a z +1 =a z ·q, где z — номер выбранного элемента.
Соответственно, z ∈ N.
Период, когда в школе изучается геометрическая прогрессия — 9 класс. Примеры помогут разобраться в понятии:
0.25 0.125 0.0625…
Исходя из этой формулы, знаменатель прогрессии возможно найти следующим образом:
Ни q, ни b z не могут равняться нулю. Так же каждый из элементов прогрессии не должен равняться нулю.
Соответственно, чтобы узнать следующее число ряда, нужно умножить последнее на q.
Чтобы задать данную прогрессию, необходимо указать первый ее элемент и знаменатель. После этого возможно нахождение любого из последующих членов и их суммы.
Что это за прогрессия?
Прежде чем переходить к рассмотрению вопроса (как найти сумму арифметической прогрессии), стоит понять, о чем пойдет речь.
Любая последовательность действительных чисел, которая получается путем добавления (вычитания) некоторого значения из каждого предыдущего числа, называется алгебраической (арифметической) прогрессией. Это определение в переводе на язык математики принимает форму:
Здесь i — порядковый номер элемента ряда a i . Таким образом, зная всего одно начальное число, можно с легкостью восстановить весь ряд. Параметр d в формуле называется разностью прогрессии.
Можно легко показать, что для рассматриваемого ряда чисел выполняется следующее равенство:
То есть для нахождения значения n-го по порядку элемента следует n-1 раз добавить разность d к первому элементу a 1 .
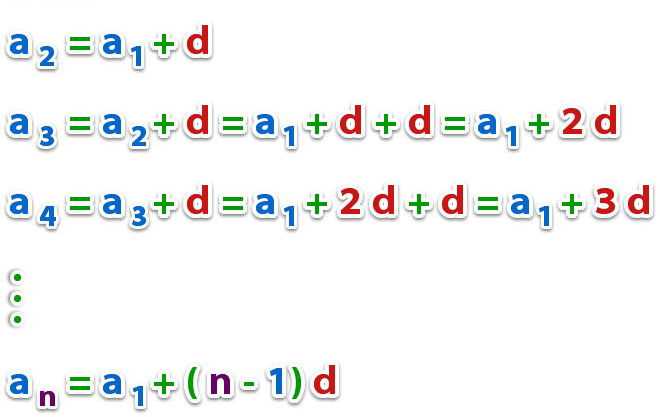
Что такое геометрическая прогрессия?
Возьмите лист бумаги и сложите его столько раз, сколько сможете. Какая получилась толщина бумаги после этого? И как это определить? Ответом будет геометрическая прогрессия. В ней последующее число в серии является двойным по сравнению с предыдущим числом.

Другими словами, когда 1 умножается на 2, получается 2. Когда 2 умножается на 2, получается 4. Точно так же, когда 4 умножается на 2, мы получаем 8 и так далее. Можно ли сказать, что соотношение двух следующих друг за другом членов геометрического ряда постоянно?

Таким образом, соотношение двух последовательных членов этой конкретной последовательности является фиксированным числом. Такая последовательность чисел называется геометрической прогрессией (ГП).
Кроме того, первый член не равен нулю, а каждый последующий член получается путем умножения предыдущего члена на фиксированную величину. К примеру, рассмотрим последовательность 1, 2, 4, 8, 16, 32… . Здесь общее отношение r=2 – это знаменатель геометрической прогрессии.
Знание прогрессии и умение проводить необходимые вычисления чрезвычайно полезно в самых различных отраслях деятельности.
Например, в строительстве определение площади поперечного сечения колонн, равномерно удаленных друг от друга, являет собой геометрическую прогрессию.
По законам прогрессии установлена размерность станков и инструментов по резке металла. Вообще вычисления прогрессии становят математическую основу стандартизации промышленной продукции. С ее помощью можно вычислять проценты по банковским вкладам и многое другое.
Геометрическая прогрессия, ее свойства — Алгебра — Мастер-класс
Геометрическая прогрессия, ее свойства.
Формула n-го члена геометрической прогрессии
Некоторые результаты естественных процессов образуют
последовательность называется геометрической прогрессией.
Геометрическая прогрессия —
это последовательность, каждый член которой, начиная со второго, равен предыдущему
члену, умноженному на одно и то же отличное от нуля число, которое называется знаменателем
геометрической прогрессии. В геометрической прогрессии каждый член, начиная с
второго, является срединно геометрическим между двумя соседними членами: .
Знаменатель геометрической прогрессии ( bn обозначается q и равна отношению любого члена прогрессии,
начиная со второго, к предыдущему члену: . Вообще, если bi и bj — два данные члены геометрической прогрессии ( bn, причем i j, то .
Любой член геометрической прогрессии можно вычислить,
зная первый член прогрессии
1qnbnb1qn-1
Свойства геометрической прогрессии с первым членом b1 и знаменателем q:
1. Если первый член геометрической прогрессии — число положительное (b1 >
0) и знаменатель прогрессии q > 1, то такая геометрическая прогрессия является возрастающей; или если первый член
геометрической прогрессии — число отрицательное (b1 0) и
знаменатель прогрессии 0 > q 1, то такая геометрическая прогрессия является возрастающей.
2. Если первый член геометрической прогрессии — число отрицательное (b1 0) и знаменатель прогрессии q > 1, то такая геометрическая прогрессия является убывающей; или если первый член
геометрической прогрессии — число положительное (b1 > 0) и
знаменатель прогрессии 0 q 1, то такая прогрессия является убывающей; При q 0 геометрическая прогрессия не является ни убывающей, ни растущей.
3. Произведение двух членов конечной геометрической
прогрессии, равноотстоящих от ее концов, равен произведению крайних членов.
Что собой представляет арифметическая прогрессия?
Чтобы это понять, необходимо дать определение рассматриваемой прогрессии, а также привести основные формулы, которые далее будут использованы при решении задач.
Арифметическая или алгебраическая прогрессия — это такой набор упорядоченных рациональных чисел, каждый член которого отличается от предыдущего на некоторую постоянную величину. Эта величина называется разностью. То есть, зная любой член упорядоченного ряда чисел и разность, можно восстановить всю арифметическую прогрессию.
Приведем пример. Следующая последовательность чисел будет прогрессией арифметической: 4, 8, 12, 16, …, поскольку разность в этом случае равна 4 (8 — 4 = 12 — 8 = 16 — 12). А вот набор чисел 3, 5, 8, 12, 17 уже нельзя отнести к рассматриваемому виду прогрессии, поскольку разность для него не является постоянной величиной (5 — 3 ≠ 8 — 5 ≠ 12 — 8 ≠ 17 — 12).
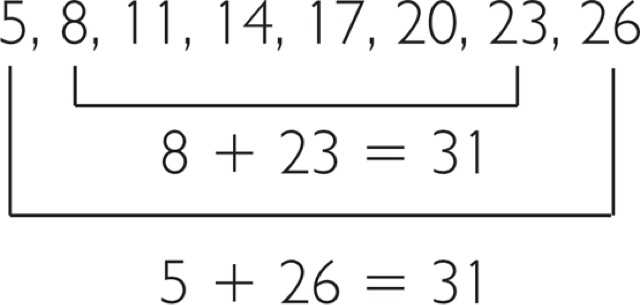
Пример №4: первый член прогрессии

Продолжим приводить примеры арифметической прогрессии с решением. Во всех предыдущих задачах было известно первое число алгебраической прогрессии. Теперь рассмотрим задачу иного типа: пусть даны два числа, где a 15 = 50 и a 43 = 37. Необходимо найти, с какого числа начинается эта последовательность.
Формулы, которыми пользовались до настоящего времени, предполагают знание a 1 и d. В условии задачи об этих числах ничего неизвестно. Тем не менее выпишем выражения для каждого члена, о котором имеется информация: a 15 = a 1 + 14 * d и a 43 = a 1 + 42 * d. Получили два уравнения, в которых 2 неизвестные величины (a 1 и d). Это означает, что задача сводится к решению системы линейных уравнений.
Указанную систему проще всего решить, если выразить в каждом уравнении a 1 , а затем сравнить полученные выражения. Первое уравнение: a 1 = a 15 — 14 * d = 50 — 14 * d; второе уравнение: a 1 = a 43 — 42 * d = 37 — 42 * d. Приравнивая эти выражения, получим: 50 — 14 * d = 37 — 42 * d, откуда разность d = (37 — 50) / (42 — 14) = — 0,464 (приведены лишь 3 знака точности после запятой).
Зная d, можно воспользоваться любым из 2 приведенных выше выражений для a 1 . Например, первым: a 1 = 50 — 14 * d = 50 — 14 * (- 0,464) = 56,496.
Если возникают сомнения в полученном результате, можно его проверить, например, определить 43 член прогрессии, который задан в условии. Получим: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Небольшая погрешность связана с тем, что при вычислениях использовалось округление до тысячных долей.