Площадь прямоугольной трапеции через угол и основания ️ свойства

Задачи

№1. На определение углов при нижнем основании трапеции.

Условие.
Дана равнобедренная трапеция, боковая сторона которой 5 см. Ее основания равны 6 и 12 см. Требуется найти синус острого угла.

Решение.
Для удобства следует ввести обозначение. Пусть левая нижняя вершина будет А, все остальные по часовой стрелке: В, С, Д. Таким образом, нижнее основание будет обозначено АД, верхнее — ВС.

Нужно провести высоты из вершин В и С. Точки, которые укажут концы высот будут обозначены Н 1 и Н 2 , соответственно. Поскольку в фигуре ВСН 1 Н 2 все углы прямые, то она является прямоугольником. Это означает, что отрезок Н 1 Н 2 равен 6 см.

Теперь нужно рассмотреть два треугольника. Они равны, так как являются прямоугольными с одинаковыми гипотенузами и вертикальными катетами. Отсюда следует, что и меньшие катеты у них равны. Поэтому их можно определить как частное от разности. Последняя получится от вычитания из нижнего основания верхнего. Делиться оно будет на 2. То есть 12 — 6 нужно поделить на 2. АН 1 = Н 2 Д = 3 (см).

Теперь из теоремы Пифагора нужно найти высоту трапеции. Она необходима для нахождения синуса угла. ВН 1 = √(5 2 — 3 2) = 4 (см).

Воспользовавшись знанием о том, как находится синус острого угла в треугольнике с прямым углом, можно записать такое выражение: sin α= ВН 1 / АВ = 0,8.

Ответ.
Искомый синус равен 0,8.

№2. На нахождение высоты трапеции по известному тангенсу.

Условие.
У равнобедренной трапеции нужно вычислить высоту. Известно, что ее основания равны 15 и 28 см. Дан тангенс острого угла: 11/13.

Решение.
Обозначение вершин такое же, как в предыдущей задаче. Снова нужно провести две высоты из верхних углов. По аналогии с решением первой задачи нужно найти АН 1 = Н 2 Д, которые определятся как разность 28 и 15, деленная на два. После подсчетов получается: 6,5 см.

Поскольку тангенс — это отношение двух катетов, то можно записать такое равенство: tg α= АН 1 / ВН 1 . Причем это отношение равно 11/13 (по условию). Так как АН 1 известен, то можно вычислить высоту: ВН 1 = (11 * 6,5) / 13. Простые расчеты дают результат в 5,5 см.

Ответ.
Искомая высота равна 5,5 см.

№3. На вычисление высоты по известным диагоналям.

Условие.
О трапеции известно, что ее диагонали равны 13 и 3 см. Нужно узнать ее высоту, если сумма оснований составляет 14 см.

Решение.
Пусть обозначение фигуры будет таким же, как раньше. Предположим, что АС — меньшая диагональ. Из вершины С нужно провести искомую высоту и обозначить ее СН.

Теперь потребуется выполнить дополнительное построение. Из угла С нужно провести прямую, параллельную большей диагонали и найти точку ее пересечения с продолжением стороны АД. Это будет Д 1 . Получилась новая трапеция, внутри которой начерчен треугольник АСД 1 . Он-то и нужен для дальнейшего решения задачи.

Искомая высота окажется еще и ей же в треугольнике. Поэтому можно воспользоваться формулами, изученными в другой теме. Высота треугольника определяется как произведение числа 2 и площади, деленное на сторону, к которой она проведена. А сторона оказывается равна сумме оснований исходной трапеции. Это исходит из правила, по которому выполнено дополнительное построение.

В рассматриваемом треугольнике все стороны известны. Для удобства введем обозначения х = 3 см, у = 13 см, z = 14 см.

Теперь можно сосчитать площадь, воспользовавшись теоремой Герона. Полупериметр будет равен р = (х + у + z)/ 2 = (3 + 13 + 14) / 2 = 15 (см). Тогда формула для площади после подстановки значений будет выглядеть так: S = √(15 * (15 — 3) * (15 — 13) * (15 — 14)) = 6 √10 (см 2).

Ответ.
Высота равна 6√10 / 7 см.

№4. Для поиска высоты по сторонам.

Условие.
Дана трапеция, три стороны которой равны 10 см, а четвертая 24 см. Нужно узнать ее высоту.

Решение.
Поскольку фигура равнобедренная, то потребуется формула под номером 2. В нее нужно просто подставить все значения и сосчитать. Это будет выглядеть так:

н = √(10 2 — (10 — 24) 2 /4) = √51 (см).

Ответ.
н = √51 см.

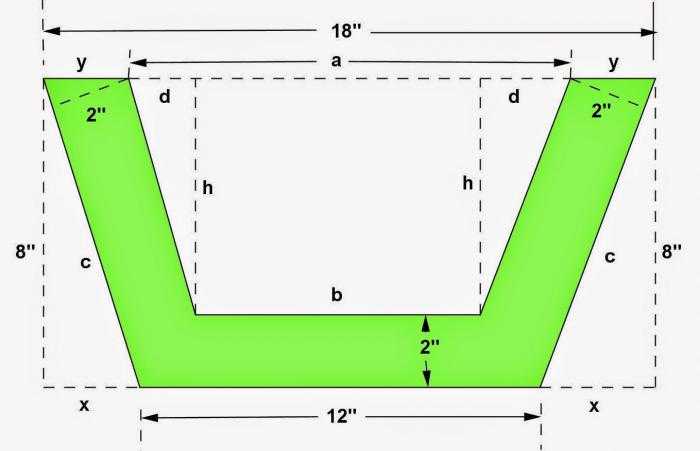
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.

Найти высоту равнобедренной трапеции

Итак, если с = d, то h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 = √c 2 -(a-b) 2 /4,
a, b – стороны-основания четырехугольника,
c = d – его боковые стороны.

При наличии величины углов, образованных двумя сторонами (основанием и боковой), высоту трапеции определяет следующее соотношение:

h = c* sinα,
h = с * tgα *cosα = с * tgα * (b – a)/2c = tgα * (b-a)/2,

α – угол в основании фигуры,
a, b (a
c = d – его боковые стороны.

Если даны величины диагоналей фигуры, то выражение для нахождения высоты фигуры видоизменится, т.к. d1 = d2:

h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,

h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Особенности и свойства трапеций

Прежде чем разобраться, как найти площадь прямоугольной трапеции, следует подробнее рассмотреть свойства этого класса фигур. Все они представляют собой выпуклые четырехугольники, у которых две и всего две стороны параллельны между собой. Они называются основаниями и имеют разную длину. Оставшиеся две стороны наклонены друг относительно друга под определенным и неравным нулю углом. Они называются боковыми.

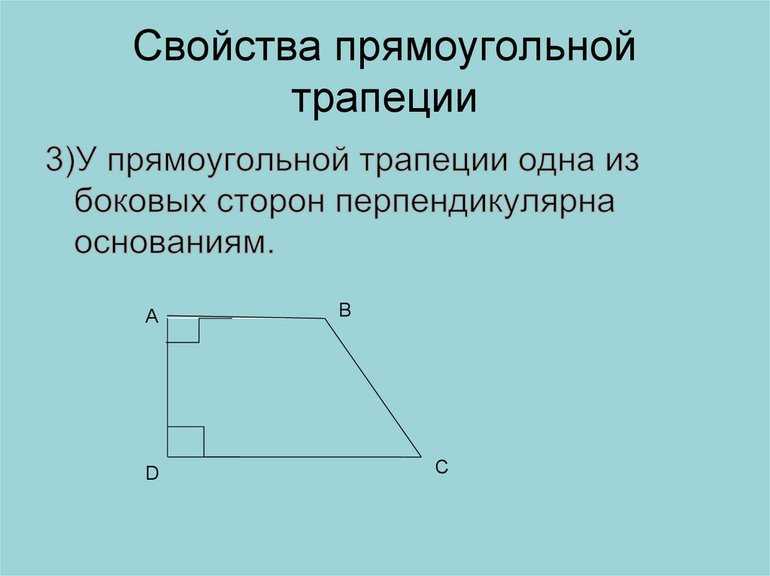
Терминология и элементы

Из определения трапеции следует, что эта фигура состоит из двух оснований и двух боковых сторон. Помимо них, в геометрии выделяют также следующие линейные характеристики:

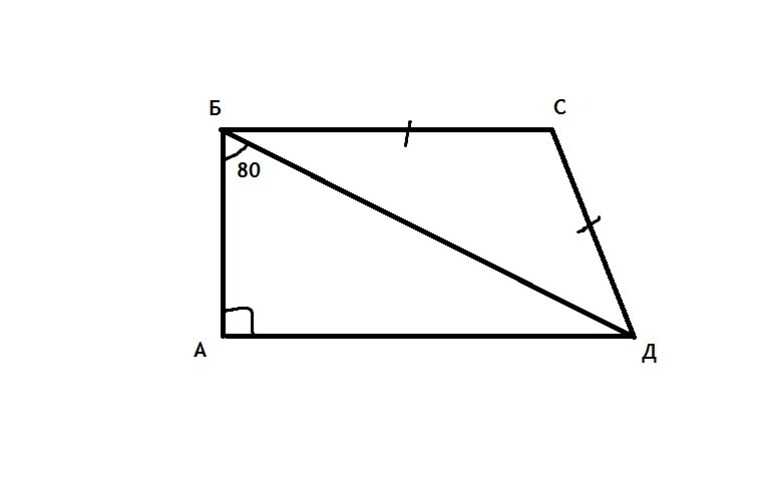
Диагонали — соединяющие несмежные (противоположные) вершины отрезки, в общем случае они имеют разную длину и могут быть вычислены из знания всех длин сторон фигуры. Соответствующие формулы имеют вид: D1 = (a*b + d 2 — a*(d 2 -c 2 )/(a-b))^0,5 и D2 = (a*b + c 2 — a*(c 2 -d 2 )/(a-b))^0,5. Здесь буквами a и b обозначены основания, c и d — это боковые стороны.
Высота — расстояние между параллельными основаниями, она соответствует длине перпендикуляра, опущенного от малого основания к большому. Обычно ее обозначают буквой h. Через четыре стороны фигуры она так же, как и диагонали, может быть рассчитана. Соответствующая формула является несколько громоздкой. Она имеет вид: h = (4*(a-b)^2*d 2 — (d 2 + (a-b)^2 — c 2 )^2)^0,5/(2*(a-b)).
Средняя линия или медиана M — отрезок, который соединяет середины сторон боковых, его длина однозначно рассчитывается из знания длин обоих оснований. Выражение для M имеет следующую форму: M = (a+b)/2 — полусумма длин оснований.
В некоторых задачах также встречается отрезок n, который соединяет середины обеих диагоналей. Его длина рассчитывается как полуразница оснований: n = (a-b)/2.

Все формулы для нахождения длин соответствующих линейных элементов трапеции справедливы независимо от значений ее сторон и внутренних углов.

Существующие типы

Несмотря на простоту построения трапеции, она бывает нескольких типов. Последние определяются однозначно с учетом значения внутренних углов фигуры. В геометрии выделяют следующие типы:

Общий. Этот тип фигуры является наименее симметричным. В ней все четыре угла отличаются друг от друга, при этом два из них являются тупыми, и два острыми. Их расположение может быть либо попарным, либо противоположным. Кроме того, трапеция общего типа имеет разные длины боковых сторон.
Равнобедренный. Это самый симметричный тип фигуры. Равнобедренная трапеция по определению имеет две одинаковые по длине боковые стороны и, как следствие, равные попарно углы при основаниях (два острых и два тупых). Прямая, проходящая через середины оснований, является осью симметрии фигуры. Ее диагонали равны, а противоположные углы в сумме составляют 180 °. В такую трапецию можно вписать окружность, радиус которой составит половину высоты фигуры (r = h/2), однако, это не всегда возможно.
Прямоугольный. Как следует из названия, для этого типа трапеции характерно наличие внутренних прямых углов, то есть таких, мера которых составляет 90 °. Поскольку сумма односторонних углов, заключенных между параллельными прямыми, всегда составляет 180 °, то в прямоугольной трапеции всегда существует два прямых угла. Два других угла являются острым и тупым.

Для всех перечисленных типов трапеции справедлив тот факт, что сумма четырех углов составляет 360 °. В любой тип фигуры можно вписать окружность. Для этого необходимо, чтобы выполнялось следующее условие:

a + b = c + d.

Другими словами, сумма длин оснований должна быть в точности равна сумме боковых сторон.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной
:

Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

шаг

Метод 1 из 2: определение площади по длине параллелей и высоте

Добавьте длину параллельных сторон.

Например, предположим, вы знаете, что значение стороны параллельно вершине (b1) составляет 8 см, а нижняя параллель (b2) составляет 13 см, общая длина параллельных сторон 8 см + 13 см = 21 см (что отражает часть «b = b1 + b2″в формуле).

Как следует из названия, параллельные стороны — это 2 параллельные стороны трапеции. Если вы еще не знаете длины двух параллельных сторон, измерьте их линейкой. После этого сложите два вместе.
Измерьте высоту трапеции.

Длина гипотенузы или основания трапеции не равна высоте трапеции. Линия высоты должна быть перпендикулярна двум параллельным сторонам.

Высота трапеции — это расстояние между двумя параллельными сторонами. Проведите линию между двумя параллельными сторонами и с помощью линейки или другого измерительного инструмента найдите длину линии. Делайте заметки, чтобы не забыть и не потерять их.
Умножьте количество параллельных сторон на высоту.

В этом примере 21 см x 7 см = 147 см, что отражает часть уравнения «(b) t».

Далее вам нужно умножить сумму сторон (b) на высоту (t) трапеции. Ответы должны быть в квадратных единицах.
Умножьте результат на ½, чтобы найти площадь трапеции.

В этом примере площадь (W) трапеции составляет 147 см / 2 = 73,5 см.

Вы можете умножить произведение на 1/2 или разделить на 2, чтобы найти конечную площадь трапеции. Убедитесь, что единицы ответа выражены в квадратных единицах.

Метод 2 из 2: расчет площади трапеции, если вы знаете размер сторон

Разбейте трапецию на 1 прямоугольник и 2 прямоугольных треугольника.

Этот метод работает только со стандартной равнобедренной трапецией.

Нарисуйте прямую линию из каждого угла верхней стороны трапеции перпендикулярно нижней стороне. Теперь у трапеции есть 1 прямоугольник посередине и 2 правых и левых правых треугольника. Рекомендуется провести эту линию, чтобы вы могли более четко видеть форму и рассчитать высоту трапеции.
Найдите длину одного из оснований треугольника.

Например, если верхний (b1) по длине 6 см и нижней стороной по (b2) 12 см, что означает, что основание треугольника равно 3 см (поскольку b = (b2 — б1) / 2 и (12 см — 6 см) / 2 = 6 см, что может быть упрощено до 6 см / 2 = 3 см).

Отнимите длину нижней стороны трапеции от верхней. Разделите результат на 2, чтобы найти длину основания треугольника. Теперь у вас есть длина основания и гипотенуза треугольника.
Используйте теорию Пифагора, чтобы найти высоту трапеции. Подставьте длины основания и гипотенузы (самой длинной стороны треугольника) в формулу Пифагора A + B = C, где A — основание, а C — гипотенуза. Решите уравнение для B, чтобы найти высоту трапеции. Если длина стороны основания 3 см, а длина гипотенузы 5 см, вот расчет:
- Подставьте переменные: (3 см) + B = (5 см)
- Возведите числа в квадрат: 9 см + B = 25 см.
- Отнимите 9 см с каждой стороны: B = 16 см.
- Найдите квадратный корень из каждой стороны: B = 4 см.
Подсказки: Если у вас нет идеального квадрата в уравнении, просто упростите его насколько возможно и оставьте остаток как квадратный корень, например √32 = √ (16) (2) = 4√2.
Подставьте длину и высоту трапеции в формулу площади и решите. Подставьте длину и высоту основания в формулу L = ½ (b₁ + b₂) t, чтобы найти площадь трапеции. Максимально упростите числа и дайте им квадратные единицы.
- Установите формулу: L = ½ (b₁+ b₂) т
- Подставьте переменные: L = ½ (6 см + 12 см) (4 см)
- Упростите термины: A = ½ (18 см) (4 см)
- Умножьте числа: W = 36 см.

Как решить задачу на поиск периметра трапеции по её основаниям и площади:

Для решения задачи на поиск периметра трапеции по её основаниям и площади следует использовать соответствующую формулу периметра и известные данные.

Дано:

Длина первого основания трапеции (a);
Длина второго основания трапеции (b);
Площадь трапеции (S).

Для нахождения периметра трапеции необходимо выполнить следующие шаги:

Найти высоту трапеции (h) по формуле h = S / ((a + b) / 2), где S — площадь трапеции.
Найти боковые стороны трапеции (с) по формуле c = √(h^2 + (b — a)^2), где h — высота трапеции, a и b — основания трапеции.
Найти периметр трапеции (P) по формуле P = a + b + 2c, где a и b — основания трапеции, c — боковая сторона трапеции.

Таким образом, чтобы решить задачу на поиск периметра трапеции по её основаниям и площади, нужно применить формулы для нахождения высоты, боковых сторон и периметра трапеции, в зависимости от известных данных.

Шаги решения задачи на поиск периметра трапеции

Для решения задачи на поиск периметра трапеции необходимо выполнить следующие шаги:

Определить данные, из которых можно вычислить периметр трапеции. В данном случае нам даны основания трапеции и ее площадь.
Найти длину бокового стороны трапеции. Для этого можно воспользоваться формулой площади трапеции: S = (a + b) * h / 2, где S — площадь трапеции, a и b — основания трапеции, h — высота трапеции.
Определить длины всех сторон трапеции. Для этого можно использовать теорему Пифагора или формулы для прямоугольных треугольников, составленных из сторон трапеции и высоты.
Найти сумму всех сторон трапеции. Для этого сложите длины всех сторон.
Вычислить периметр трапеции, сложив сумму всех сторон.

Итак, шаги решения задачи на поиск периметра трапеции сводятся к нахождению длин боковых сторон трапеции, нахождению суммы всех сторон и вычислению периметра. Последовательное выполнение этих шагов приведет к решению задачи.

Пример задачи с решением

Рассмотрим пример задачи, в которой нужно найти периметр трапеции по её основаниям и площади.

Условие задачи:

Дана трапеция с основаниями a = 6 см и b = 10 см. Известно, что площадь трапеции S = 36 см2. Найдите её периметр.

Решение:

Найдем высоту трапеции h. Для этого воспользуемся формулой площади трапеции: S = (a + b) * h / 2. Подставим известные значения: 36 = (6 + 10) * h / 2. Решим уравнение относительно h: 36 * 2 = 16 * h, 72 = 16 * h. Получаем h = 72 / 16 = 4.5 см.
Найдем боковые стороны трапеции. Для этого воспользуемся теоремой Пифагора. Рассмотрим прямоугольный треугольник, образованный боковым ребром трапеции, его высотой и основанием. По теореме Пифагора получаем: a2 = h2 + x2, где x — длина боковой стороны. Подставляем известные значения: 62 = 4.52 + x2, 36 = 20.25 + x2, x2 = 36 — 20.25, x2 = 15.75, x = √15.75 ≈ 3.97 см. Так как боковые стороны трапеции параллельны и равны по длине, то x = y ≈ 3.97 см.
Найдем периметр трапеции. Периметр трапеции равен сумме длин всех её сторон. Имеем: P = a + b + 2 * y. Подставляем известные значения: P = 6 + 10 + 2 * 3.97, P ≈ 23.94 см.

Итак, периметр трапеции составляет около 23.94 см.

Свойства диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.
Данный отрезок параллелен основаниям трапеции.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или
LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.

Свойства трапеции, достроенной до треугольника

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Как найти высоту трапеции

Через стороны

Если нам известны стороны фигуры, мы можем найти ее высоту по формуле:

\(h=\sqrt{b^2-(\frac{{(a-d)}^2+d^2+c^2}{2\cdot(a-b)}})^2\)

Где h — высота, a — большее основание, b — меньшее основание, c и d — боковые стороны.

Через среднюю линию и площадь

Если в условии есть данные о величине средней линии и площади, можем использовать формулу:

\(h=\frac Sm\)

Где m — средняя линия трапеции.

Через боковую сторону и угол

Когда нам известна величина одной из боковых сторон и угол между этой стороной и большим основанием, используем формулу:

\(h=c\cdot\sin\left(\alpha\right)\)

Где \alpha — это угол между стороной c и большим основанием a.

Через диагонали, угол между ними и основания

Если нам известны длины обоих диагоналей трапеции, а также угол между ними, можем найти высоту следующим образом:

\(h=\frac{d_1d_2}{a+b}\cdot\sin\left(\gamma\right)\)

Где \(d_1\) и \(d_2\) — диагонали трапеции, а \(\gamma\) — угол между ними.

Через диагонали, угол и среднюю линию

В том случае, если нам известны сразу длины диагоналей, угол между ними и величина средней линии, мы можем узнать высоту трапеции по формуле:

\(h=\frac{d_1d_2}{2m}\cdot\sin\left(\gamma\right)\)

Через радиус вписанной окружности

Если в трапецию можно вписать окружность, то ее высота будет равна диаметру этой окружности, то есть d=h. Другими словами, высота фигуры будет равна удвоенному радиусу вписанной в нее окружности:

\(h=2r\)

Где r — радиус выписанной окружности.

Обучающее видео

Отличным подспорьем в изучении основных типов вычислений площади являются видеоматериалы с доступным, легким языком изложения, подробными объяснениями и примерами решения задач.

Видео «Площадь трапеции»

Видео содержит максимально полную информацию о видах трапеций, правильных буквенных обозначениях и вариантах решений разноплановых задач при помощи всех известных методов и принципов расчета.

Все перечисленные формулы и способы вычисления широко применимы во время изучения геометрии в школах и ВУЗах. Студенту, школьнику и абитуриенту предоставленная информация пригодится в качестве онлайн шпаргалки в период интенсивной подготовки к экзаменам, контрольным работам, написания рефератов, курсовых и подобных работ.

Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.

В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.

трапеция и ее теоремы

Введение в геомантию

Пожалуйста, включите JavaScript

Введение в геомантию

Мы в ask-math считаем, что образовательный материал должен быть бесплатным для всех. Пожалуйста, используйте содержимое этого веб-сайта для более глубокого понимания концепций. Кроме того, мы создали и разместили видеоролики на нашем YouTube.

Мы также предлагаем индивидуальные / групповые занятия / помощь в выполнении домашних заданий по математике с 4 по 12 классы по алгебре, геометрии, тригонометрии, предварительному исчислению и исчислению для учащихся из США, Великобритании, Европы, Юго-Восточной Азии и ОАЭ.

Также приветствуются связи со школами и учебными заведениями.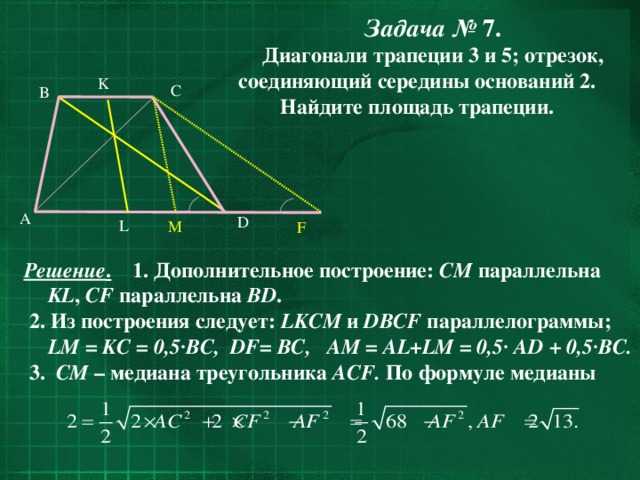

Мы также будем рады разместить видео в соответствии с вашими требованиями. Напишите нам.

В этом разделе мы обсудим некоторые трапеции и их теоремы.

Трапеция – это четырехугольник, по крайней мере, с одной парой параллельных сторон. АБ || CD. (если есть две пары параллельных прямых, то это параллелограмм)

Если непараллельные стороны трапеции равны, то она называется равнобедренной трапецией. Теорема 1. Трапеция равнобедренная тогда и только тогда, когда углы при основании равны.

Дано: ABCD — равнобедренная трапеция. AD = ВС и АВ || CD.

Заявления

Причины

0045 1) ABCD — трапеция.

1) Дано
2) AB || CD
2) Дано
3) AD = BC
3) Дано
4) DA || CE
4) По конструкции
5) ADCE является параллелограммом.
5) По свойствам параллелограмма.
6) DA = CE и DC = AE
6) По свойствам параллелограмма.
7) BC = CE
7) BC = AD и AD = CE (переходное свойство)
∠CEB ≅ &CBE
Если BC ≅ CE, то противоположные им углы равны.
9) ∠DAB ≅ ∠ABC
9) свойство параллелограмма и линейной пары углов
10) ∠A + ∠D = 180 и ∠B + 1002 ∠90 на внутренних углах 180 те же стороны трансверсали являются дополнительными. 11) ∠A + ∠D = ∠C + ∠B
11) Транзитивность (правые стороны одинаковы, поэтому левые равны)
12) ∠D = ∠C
12) Сверху (∠A = ∠B)

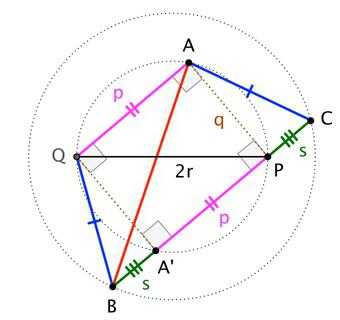
Пример: В трапеции QRS и.

Решение:

Теоремы

1. Трапеция равнобедренная тогда и только тогда, когда углы при основании равны.

2. Трапеция равнобедренная тогда и только тогда, когда диагонали конгруэнтны.

Если трапеция равнобедренная, то противоположные углы дополнительные.

Медиана (или середина) трапеции параллельна каждому основанию, и ее длина составляет половину суммы длин оснований.

Никогда не предполагайте, что трапеция равнобедренная, если вы не получили (или не можете доказать) эту информацию.

Практика

1) В трапеции ABCD,AB|| CD и ВС = AD. Если m∠C=65 , то найти m∠D. 2) PQRS — трапеция, в которой PQ || РС. Если ∠P = ∠Q = 40, найдите величины двух других углов. 3) В трапеции ABCD ∠B= 120 Найти m∠C. 4) В четырехугольнике HELP, если EP = LH, то какой это четырехугольник? 5) В четырехугольнике углы относятся как 4:5:3:6. Найдите величины каждого угла.

Четырехугольник

• Введение в четырехугольник • Типы четырехугольника • Свойства четырехугольника • Параллелограмм и его теоремы • Rectangle and its Theorems • Square and its Theorems • Rhombus and its Theorems • Trapezoid and its Theorems • Kite and its Theorems • Mid Point Theorem

Geometry

Home Page

Домашняя страница
Видео по математике
Чувство чисел
Алгебра
Бизнес-математика
Геометрия
Измерение
Статистика
Тригонометрия
75 Измерения
750275
11th grade math
Hindi Numbers
Formula 1
Ask Experts
f UN zONE
Link Partners
About us/Disclaimer
Contact Us
Privacy Policy
Math Blog
CBSE Sample Papers

сообщите об этом объявлении

Заключение

Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.

Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.

Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.

Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.

Трапеции обладают некоторыми интересными свойствами:

Средняя линия трапеции равна полусумме оснований и параллельна им.
У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.

Как найти площадь трапеции
.

Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:

где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.

Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.

Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.

В этом случае площадь трапеции может быть найдена по формуле:

S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2

где S-площадь, a,b-основания, c,d-боковые стороны трапеции.

Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.

Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.