Способы вычитания натуральных чисел

Математические действия с разностью чисел

Чтобы узнать разность чисел, нужно совершить такое арифметическое действие как вычитание, в результате которого по одному данному слагаемому и данной сумме можно найти другое слагаемое.

Вычитание принято обозначать знаком «–» (минус).

Примечание

Обычно вычитание натуральных чисел возможно только в том случае, если уменьшаемое больше вычитаемого. Однако если уменьшаемое меньше вычитаемого, то значение разности получается отрицательным.

Следует привести некоторые особенности действий с нулем:

1. Прибавление к числу нуля не изменяет этого числа.

   Пример

   20+0=20

2. Если первое слагаемое равно второму, то их разность равна нулю.

   Пример

   150-150=0.

Необходимо также обозначить свойства вычитания:

1. x-(y+z)=x-y-z: 26-(14+4)=26-4-14=22-14=8.
2. (x+y)-z=(x-z)+y=x+(y-z): (37+28)-5=(37-5)+28=60.
3. x+(y-z)=x+y-z: 51+(34-7)=51+32=19.
4. x-(y-z)=x-y+z: 66-(34-7)=(66-34)+7=39.
5. если x-y=z, то x=y+z: х-7=6, х=7+6, х=13.
6. если x-y=z, то y=x-z: 46-у=16, у=46-16, у=30.
7. если x-y=z, то (x+n)-y=z+n и (x-n)-y=z-n: 19-11=8, (19+6)-11=8+6, (19-1)+11=8-1.
8. если x-y=z, то x-(y+n)=z-n и x-(y-n)=z+n: 46-11=35, 46-(11+4)=35+4, 46-(11-9)=35-9.
9. если x-y=z, то (x+n)+(y-n)=z: 100-50=50, (100+10)+(50-10)=50.
10. если x-y=z, то (x+n)-(y+n)=z и (x-n)-(y-n)=z: 300-150=150, (300+25)-(150+25)=150, (300-25)-(150-25)=150.

Определение

Однозначное число — это число, состоящее из одной цифры.

Определение

Многозначное число — включающее две и более цифры.

Чтобы найти разницу между однозначными числами, стоит вычесть из первого слагаемого второе. В этом поможет таблица вычитания, которую заучивают наизусть.

Чтобы посчитать результат вычитания многозначных чисел, можно воспользоваться счетом «в столбик». Этот способ подразумевает, что вычитаемое записывают под уменьшаемым в соответствии с десятками, сотнями, тысячами и так далее. После этого, начиная с конца, то есть с десятков, производят вычисление.

Пример

653-132

Сначала находим разность единиц, то есть от 3 отнимаем 2. Получаем 1.

Затем вычисляем десятки, то есть от 5 отнимаем 3. Результат равен 2.

И, наконец, считаем сотни, то есть от 6 отнимаем 1 и получаем 5.

Ответ: 521.

Если одно и то же число вычитается из другого множество раз, то можно умножить данное значение на столько раз, сколько представлено в примере, и таким образом получить одно вычитаемое число.

Пример

440-10-10-10=440-(10*3)=440-30=410.

Сложение натуральных чисел и его свойства

Для начала предлагаю вспомнить, что такое ряд натуральных чисел.

Натуральный ряд — это неограниченная последовательность натуральных чисел, расположенных в порядке их возрастания. Значит в натуральном ряду каждое последующее число больше предыдущего на единицу.

Как определить неизвестное число из натурального ряда?

Нужно прибавить к предыдущему числу единицу. Какое число следует за тройкой? Прибавляем единицу и получаем 4. То есть в натуральном ряду за тройкой следует четвёрка.

Как использовать это свойство натурального ряда при сложении?

Давайте сложим 2 и 3. Три — это три единицы, значит, к двойке прибавляем по одной по порядку:

2+1=3

3+1=4

4+1=5

В конечном результате действия с числами 2 и 3 появилось число 5. Вроде бы просто да? Но такой способ сложения лёгкий лишь когда, мы работаем с маленькими числами. С большими числами не по единичке же добавлять? Правильно?

Представим ситуацию, при которой в корзине лежит 20 яблок, добавляем к ним и ещё 15. Как определить, сколько всего яблок оказалось в корзине? Чтобы освободиться от необходимости перебирать объекты по одному, давайте определим операцию сложения.

Определение:

Сложение — это арифметическая операция, после проведения которого наши вещи, подвергаемые счету, соединяются воедино. В данном случае единое целое — это общее количество яблок в корзине. Общее количество в переводе на латиницу – это сумма. Слышали это слово?

Сумма — это результат операции сложения.

Для записи операции сложения используется знак «+». Он располагается между складываемыми числами.

Числа, которые мы складываем, называют слагаемыми. Для отображения результата сложения используют знак «=».

Давайте посчитаем, сколько же яблок оказалось в той самой корзине:

20 (яблок) +  15 (яблок) = 35 (яблок) в корзине

Теперь попробуем представить сложение небольших натуральных чисел на координатном луче.

Мы уже складывали числа 2 и 3. Возьмём теперь числа 2 и 4 и найдём их сумму с помощью координатного луча с началом отсчета в точке 0.

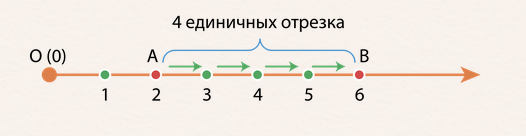
Его единичный отрезок (одно деление) равен  единице. Мы помним, что любому числу координатного луча соответствует одна единственная точка. Учитывая это знание, выполним сложение натуральных чисел 2 и 4 на координатном луче.

Отмечаем число 2 там, где два деления, далее прибавляем 4, то есть двигаемся право на 4 единичных отрезка, где мы окажемся в точке, равной 6. Следовательно, суммы чисел 2 и 4 равна 6. Это мы и так уже знали, но теперь увидели это и на координатном луче.

Переходим к следующему разделу и рассмотрим свойства сложения натуральных чисел.

Переместительное свойство

У нас есть корзина, и в ней лежат 8 бананов. Затем мы кладем туда ещё 5 бананов. Таким образом, в ней оказывается 13 бананов.

А мы выберем немного другой порядок. Представим, что сначала в корзине было 5 бананов, и мы туда положили ещё 8 бананов. В итоге фруктов в корзине будет 13. Почему? Потому что и в первом и во втором случае общее количество фруктов, которые положили в корзину одинаковое. Без разницы, в каком порядке выполнялись эти действия 8 + 5 или 5 + 8. В обоих случаях в сумме получается 13. Переместительное свойство сложения обязательно нужно запомнить.

Определение:

От перестановки слагаемых сумма не меняется.

Сочетательное свойство

Второе сложения натуральных чисел – сочетательное свойство. Мы можем положить в корзину 3 банана и 4 яблока, а потом доложить еще 5 мандаринов. Или наоборот, мы можем положить 4 яблока и 5 мандаринов, а потом доложить еще 3 банана

Порядок добавления фруктов не имеет значения, потому неважно, в каком сочетании суммировались эти числа. В обоих случаях итог был бы одинаковым – 12 фруктов в корзине

Говоря математически,  результат сложения числа 5 с суммой чисел 3 и 4 равен результату сложения числа 3 и суммы чисел 4 и 5.

Определение:

«Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить к нему первое слагаемое, а потом к полученной сумме второе».

Отметим, что последовательность действий при суммировании значение не имеет.

Сложение с числом 0

Еще одно свойство сложения – это свойство сложения 0 с натуральным числом.

При сложении 0 с каким-либо числом всегда получается это самое число. Или наоборот, если к числу прибавлять 0, то есть ничего не прибавлять, то получится исходное число.

Определение:

«Сумма двух слагаемых, если одно из слагаемых равно нулю, будет всегда равна другому слагаемому».

Теоретический материал

Алгебра

Глава 1. Натуральные числа

1.2. Запись натуральных чисел

Учитель

Рассмотрим запись натуральных чисел в десятичной системе счисления, т.е. при помощи десяти цифр: , , , , , , , , , .

Имейте ввиду, что цифр всего (именно поэтому система счисления и называется десятичной), а чисел бесконечно много. Числа составляются из цифр.

И вообще, чтобы иметь дело с числами, необходимо прежде всего уметь называть и записывать их. Правильно это все сделать позволяет понятие системы счисления.

Ученик

А что такое система счисления?

Определение

Системой счисления принято называть совокупность приемов наименования и обозначения (записи) чисел. Условные знаки, применяемые при обозначении чисел, обычно называют цифрами. В ряде систем счисления числа записывают как последовательности цифр. Например, , , .

Учитель

Более подробную информацию ты можешь прочитать здесь.

Цифры, при помощи которых записано натуральное число, при чтении справа налево указывают последовательно, сколько в данном числе содержится единиц, десятков, сотен, тысяч и т.д.

Ученик

Если честно, пока мне ничего не понятно. Может примерчик.

Учитель

Да пожалуйста, например, — цифра единиц, — цифра десятков, — цифра сотен, — цифра тысяч,т.е. .

Ученик

А если число будет очень большое. Скажем, из 20 цифр?

Учитель

В общем случае систематическая запись натурального числа определяется при помощи цифр следующим образом.

Определение

Систематической записью натурального числа называют представление этого числа в виде суммы:, где , причем .

Ученик

Мне незнаком символ . Что он обозначает?

Учитель

— это символ принадлежности множеству. Например, , но . Вообще говоря, математики в фигурные скобки заключают элементы множества: — одноэлементное множество, содержащее единичку. — четырехэлементное множество, элементами которого являются, например, ваши оценки в дневнике.

Элементы в множестве можно указывать в произвольном порядке, поэтому . — бесконечное множество (в данном случае — натуральный ряд).{} = Ø — пустое множесто, т.е. такое множество, в котором нет элементов.Т.о. множество — это неупорядоченный набор элементов.

Ученик

Вот вы говорите все множество да множество, интересно, кто ввел это понятие ?

Учитель

Конечно «кто-то» ввел понятие множества. И этим «кто-то» является известный в мире математиков человек Георг Кантор. Вообще, это тебе для общего развития, понятие множества — простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д.Ну как, интересно?

Ученик

Интересно, но не совсем понятно: почему в определении систематической записи ?

Учитель

Давайте рассмотрим конкретный пример:

Пусть дано число .Его систематическая запись следующая: .. — порядок числа — наибольшая степень десятки входящей в систематическую запись числа.В данном случае , т.к. первое ненулевое число стоит при Если бы (т.е. мы бы имели дело с числом ), то систематическую запись числа мы бы начали писать с сотен (с ), а не с тысяч.Итак, (правильная систематическая запись: порядок числа , )(неправильная систематическая запись: ,) (неправильная систематическая запись: , )Таким образом, условие обеспечивает нам единственность систематической записи числа.

В математике строго доказывается, что всякое натуральное число может быть единственным образом представлено в виде систематической записи. Вместо громоздкой записи используют запись

Ученик

А зачем «крышка» над ?

Учитель

Черту сверху пишут для того, чтобы отличить эту запись от произведения чисел . Однако, ты можешь встретить в математической литературе запись (шесть факториал), что означает .

Ученик

Значит, чтобы коротко изобразить произведение всех натуральных чисел от до , достаточно написать .

Вычитание в столбик

Многозначные числа удобнее всего вычитать в столбик. Для того чтобы вычесть число из числа в столбик, необходимо:

1. Правильно записать числа. Первым записываем уменьшаемое, под уменьшаемым пишем вычитаемое, так чтобы каждый разряд вычитаемого находился строго под соответствующим разрядом вычитаемого. Слева поставим знак «-» под столбиком, состоящим из уменьшаемого и вычитаемого проводим черту

2. Справа налево последовательно вычитаем из разряда уменьшаемого соответствующий разряд вычитаемого. Результат запишем под чертой, это будет разность.

3 Если разряд уменьшаемого окажется меньше разряда вычитаемого занимаем 10 у разряда стоящего слева (см. рисунок).

Как проверить действия сложение и вычитание?

После того, как вы закончили арифметическое действие, нужно проверить правильность ответа, то есть, удостовериться, что вычисление было сделано без ошибок.

Проверить сложение можно двумя способами: обратным сложением и вычитанием.

Обратное сложение означает, что мы меняем слагаемые местами, и складываем их еще раз. Если результат будет такой же, как и после первого сложения, значит, вычисление было верным.

Например, в уроке сложение чисел мы находили сумму: 5728+803 = 6531 . Проверим правильность результата способом обратного сложения :

Как видите, сложив слагаемые в другом порядке, мы получили тот же самый результат, а значит, вычисление было правильным.

Проверка сложения вычитанием – это способ, при котором нужно из суммы, которую получили после выполнения действия сложение, отнять одно из слагаемых. Если результат этого вычитания будет равен второму слагаемому (или сумме остальных слагаемых, если их больше двух), значит сложение было выполнено верно.

Проверим эту же сумму вычитанием : отнимем от результата 6531 слагаемое 5728 .

И этот способ проверки показал правильность нашего решения.

Проверить вычитание также возможно и сложением, и другим вычитанием.

Проверка вычитания сложением основана на взаимосвязи вычитания и сложения. Зная, что уменьшаемое – это сумма, а остаток и вычитаемое – это слагаемые, мы можем сложить между собой вычитаемое и остаток, и, если получим в результате уменьшаемое, значит, мы правильно сделали действие.

Вот так выглядит проверка вычитания сложением на примере вычисленной на этом уроке разницы 50063-4825 = 45238 :

Проверка вычитания вычитанием также основывается на взаимосвязи вычитания и сложения, а также на переместительном законе сложения. Так как уменьшаемое – это сумма двух слагаемых: вычитаемого и остатка, и сумма не зависит от порядка сложения слагаемых, то очевидно, что мы можем отнять от уменьшаемого остаток. Если результат этого действия будет равен вычитаемому, значит наша первая разность вычислена верно.

Проверка той же самой разницы вычитанием:

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 2

Оценок пока нет. Поставьте оценку первым.

Так как вы нашли эту публикацию полезной.

Подписывайтесь на нас в соцсетях!

Я недаром написал в правиле, что нужно отнимать от подходящего слагаемого суммы, потому что, если оно будет меньше вычитаемого, то оно нам не подходит. Так, в нашем примере 65 .

Вычитание натуральных чисел

Мы можем не только собирать в группы различные предметы, то есть, складывать их, но и забирать из существующей группы определенное их количество.

Например, в кошельке было 1850 рублей. В магазине было потрачено 780 рублей. Чтобы узнать, сколько осталось денег, можно вытащить кошелек и пересчитать их. Но можно поступить по-другому: из той суммы, которая была в кошельке, отнять ту сумму, что была потрачена в магазине. Разница этих чисел, то есть, на сколько единиц изначальная сумма денег больше той суммы, которую потратили, и будет остатком денег.

Разность (или Остаток) – это такое число, которое получится, если от одного числа отнять другое, то есть, от всех единиц одного числа отнять все единицы, которые содержатся в другом числе.

Уменьшаемое – это то число, от которого мы отнимаем единицы другого числа.

Вычитаемое – это число, которое мы вычитаем из другого числа. То есть, то число, на количество единиц которого мы уменьшаем другое число.

Вычитание – это арифметическое действие, которое выполняется для получения разности двух или нескольких чисел.
То есть, Совершить действие вычитания – это найти такое число, которое получится, если от данного числа отнять определенное количество единиц другого числа.

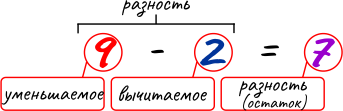
Про действие вычитание также говорят, что нужно из одного числа вычесть другое, или одно число уменьшить на другое.

Совершая вычитание натуральных чисел, вы должны помнить, что из одного натурального числа можно вычесть только равное ему или меньшее натуральное число. Действительно, мы никак не можем отобрать единиц предметов больше, чем их есть в наличии.

Поэтому, уменьшаемое натуральное число всегда больше или равное вычитаемому. Другими словами, мы всегда вычитаем из большего меньшее или из равного равное.

Проверка той же самой разницы вычитанием:

Как меняется разность при изменении вычитаемого или уменьшаемого

Если уменьшаемое увеличить на некоторое количество единиц, то и разность увеличится на такое же количество единиц.

14.11.2020 6:31:36

2020-11-14 06:31:36

Любые данныеЛюбые данные Любые данные

Примеры использования свойств сложения и вычитания

Основные свойства сложения и вычитания мы изучили — осталось потренироваться. Чтобы ничего не забыть, воспользуйтесь этой шпаргалкой:

Загрузка

Пример 1

Вычислите сумму терминов, используя различные свойства:

а) 4 + 6 + 5

б) 9+11+2

в) 30 + 0 + 13

Как мы решаем:

а) 4 + 6 + 8 = (4 + 6) + 5 = 10 + 5 = 15

б) 9 + 11 + 2 = (9 + 11) + 2 = 20 + 2 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Используйте разные свойства при вычислении разницы:

а) 25 — 0 — 2

б) 22 — 7 — 5

в) 55 — 55

Как мы решаем:

а) 25 — 0 — 2 = 25 — 2 = 23

б) 22 — 7 -5 = 22 — (7 + 5) = 22 — 12 = 10

в) 55 — 55 = 0

Пример 3

Найдите значение выражения на практике:

а) 11+10+3+9

б) 16 — (6+5)+7

в) 0 + 2 + 4 — 0

Как мы решаем:

а) 11 + 10 + 3 + 9 = (11 + 9) + (10 + 3) = 20 + 13 = 33

б) 16 — (6 + 5) + 7 = (16 — 6) — 5 + 7 = 10 — 5 + 7 = 5 + 7 = 12

в) 0 + 2 + 4 — 0 = 2 + 4 = 6

Свойства сложения

1. Переместительное свойство сложения: от перестановки слагаемых сумма не меняется.

a + b = b + a

В этом равенстве a и b могут принимать любые натуральные значения и значение 0.

2. Сочетательное свойство сложения: чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.

В буквенном виде:

(a + b) + c = a + (b + c)

Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто a + b + с.

(a + b) + c = a + (b + c) = a + b + c

Переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.

3. Свойство нуля при сложении

Сумма двух натуральных чисел всегда больше каждого из слагаемых. Но это не так, если хотя бы одно из слагаемых равно нулю.

Если к числу прибавить нуль, получится само число.

a + О = О + a = a

Поднятие степени из знаменателя в числитель и наоборот

Если знаменатель дробного выражения содержит степень, то данную степень можно поднять в числитель, изменив знак показателя этой степени на противоположный. Значение выражения при этом не меняется. Данное преобразование иногда используется при упрощении выражений.

Рассмотрим следующее равенство:

Данное равенство является верным, поскольку выражение  равно 2, а любое число в нулевой степени есть единица.

Попробуем поднять степень 22 из знаменателя в числитель, изменив знак показателя этой степени на противоположный. При этом, поднятую степень и ту степень, которая располагалась в числителе, соединим знаком умножения:

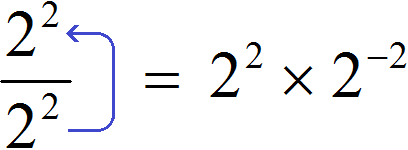
Получили выражение 22 × 2−2. Чтобы его вычислить, воспользуемся основным свойством степени:

22 × 2−2 = 22 + (−2) = 2 = 1

Получился тот же результат, что и раньше. Значит значение выражения не изменилось. Как это работает?

Если в равенстве  поменять местами левую и правую часть, то получим равенство . Это позволяет заменять в выражениях дробь вида  на тождественно равное ей выражение a−n.

Теперь представим выражение  в виде произведения . То есть . Напомним, что при замене деления умножением, делимое умножают на число, обратное делителю. А обратное делителю число в данном случае это дробь 

Теперь воспользуемся правилом . В произведении  заменим дробь  на тождественно равное ей выражение 2−2

Далее, как и раньше применяем основное свойство степени:

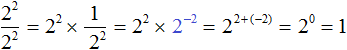
Получился тот же результат 1.

Таким же образом можно опустить степень из числителя в знаменатель, изменив знак показателя этой степени на противоположный.

Рассмотрим выражение . Чтобы найти его значение, воспользуемся правилом деления степеней с одинаковыми основаниями. В результате получим

Теперь попробуем решить этот пример, опустив степень 2−2 из числителя в знаменатель, изменив знак показателя этой степени на противоположный. При этом, опущенную степень 2−2 и ту степень, которая располагалась в знаменателе, соединим знаком умножения. А в числителе останется единица:

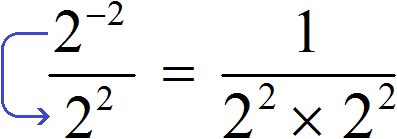
Дальнейшее вычисление не составит особого труда:

Как и в прошлом примере выражение  представимо в виде произведения 

Этим и объясняется появление единицы в числителе, после того как степень 2−2 была опущена в знаменатель.

Переносимых в знаменатель либо в числитель степеней может быть несколько. Например, знаменатель дроби  содержит степени 32, a3, b4. Перенесём эти степени в числитель, изменив знаки их показателей на противоположные. В результате получим выражение 3−2a−3b−4.

Пример 2. Поднять степени из знаменателя дроби  в числитель

Пример 3. Поднять степени из знаменателя дроби  в числитель

Пример 4. Поднять степень из знаменателя дроби  в числитель

Пример 5. Опустить степень из числителя дроби  в знаменатель

Пример 6. Степень из числителя дроби  опустить в знаменатель, а степень из знаменателя поднять в числитель

Представлять дробь  в виде произведения  вовсе не обязательно. Если пропустить эту запись, то данный пример можно решить короче:

Пример 7. В дроби  перенести из знаменателя в числитель только те степени, которые имеют отрицательные показатели:

Пример 8. Представить произведение 3x−5 в виде дроби, не содержащей степени с отрицательным показателем.

Перепишем произведение 3x−5 с помощью знака умножения:

3 × x−5

Сомножитель 3 оставим без изменений, а сомножитель x−5 заменим на тождественно равную ему дробь 

Теперь согласно правилу , умножим множитель 3 на числитель дроби . В результате образуется дробь 

Пример 9. Представить произведение 3(x + y)−4 в виде дроби, не содержащей степени с отрицательным показателем.

Выражение состоит из сомножителей 3 и (x + y)−4. Сомножитель 3 оставим без изменений, а сомножитель (x + y)−4 заменим на тождественно равную ему дробь 

Теперь умножим множитель 3 на числитель дроби . В результате образуется дробь 

Пример 10. Представить дробь  в виде произведения.

Чтобы решить этот пример, достаточно поднять степень x2 в числитель, изменив знак показателя этой степени на противоположный:

Как и в прошлых примерах дробь  можно было представить в виде произведения . Затем воспользовавшись правилом , заменить сомножитель  на тождественно равный ему сомножитель x−2.

Пример 11. Представить дробь  в виде произведения.

Пример 12. Найти значение выражения 

Поднимем степень 2−3 из знаменателя в числитель, а степень 10−2 из числителя опустим в знаменатель:

Вычислим значения степеней, содержащихся в числителе и в знаменателе:

Сократим полученную дробь на 25. Тогда останется дробь , значение которой равно 2.

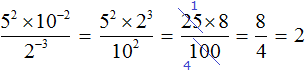
А если бы мы не подняли степень 2−3 в числитель, и степень 10−2 не опустили в знаменатель, а стали вычислять каждую степень по отдельности, то получили бы не очень компактное решение:

Вычитание единиц из десятков, сотен, тысяч

От числа 10 можно любое число от 1 до 9 . Используем таблицу, представленную выше. Но что делать в других случаях? Необходимо уменьшаемое представить, как сумму двух слагаемых, одно из которых равно 10 , после чего вычесть его из суммы. Закрепим знание материала примером:

Необходимо вычесть из 60 число 5 .

Число 60 представляем в виде суммы двух чисел, одно из которых равно 10 . Второе числа находим, вычитая из 60 число 10 . Так как 60 − 10 = 50 , то 60 = 50 + 10 . Заменим 60 суммой 50 + 10 , получая 60 − 5 = ( 50 + 10 ) − 5 . Получаем, что: ( 50 + 10 ) − 5 = 50 + ( 10 − 5 ) = 50 + 5 = 55 .

Рассмотрев вычитание единиц из десятков, перейдем к вычитанию единиц из сотен.

Чтобы из 100 вычесть число от 1 до 10 нужно 100 представить, как 90+10 90 + 10 и прибегнуть к правилу.

Необходимо найти разность 100 − 7 .

Представим 100 как 90 + 10 и выполняем: 100 − 7 = ( 90 + 10 ) − 7 = 90 + ( 10 − 7 ) = 90 + 3 = 93 . Усложним пример. Отнимем от числа 500 число 3 . Представим 500 в виде суммы. Второе слагаемое = 500 − 100 , то есть, 400 . Имеем 500 = 400 + 100 . 100 = 90 + 10 , 500 = 400 + 90 + 10 .

Таким образом, 500 − 3 = ( 400 + 90 + 10 ) − 3 .

Закончим вычисление: ( 400 + 90 + 10 ) − 3 = 400 + 90 + ( 10 − 3 ) = 400 + 90 + 7 = 497 .

Перейдем к вычитанию единиц из тысяч.

Необходимо вычислить разность 1 000 − 8 .

Так как 1 000 = 900 + 100 , а 100 = 90 + 10 , то 1 000 = 900 + 90 + 10 .

Тогда 1 000 − 8 = ( 900 + 90 + 10 ) − 8 = 900 + 90 + ( 10 − 8 ) = 900 + 90 + 2 = 992 .

Необходимо вычесть из 7 000 единицу.

7 000 запишем как 7 000 = 6 000 + 1 000 = 6 000 + 900 + 100 = 6 000 + 900 + 90 + 10 .

Делаем вывод: 7 000 − 1 = ( 6 000 + 900 + 90 + 10 ) − 1 = 6 000 + 900 + 90 + ( 10 − 1 ) = 6 000 + 900 + 90 + 9 = 6 999 .

Используя данный пример, мы сможем вычитать любые числа, также тысячные и десятитысячные.

Необходимо вычислить разность 100 000 − 4 .

Так как 100 000 = 90 000 + 10 000 = 90 000 + 9 000 + 1 000 = = 90 000 + 9 000 + 900 + 100 = 90 000 + 9 000 + 900 + 90 + 10 то 100 000 − 4 = ( 90 000 + 9 000 + 900 + 90 + 10 ) − 4 = = 90 000 + 9 000 + 900 + 90 + ( 10 − 4 ) = 90 000 + 9 000 + 900 + 90 + 6 = 99 996 .

Необходимо вычесть из 4 000 000 число 5 .

Так как 4 000 000 = 3 000 000 + 1 000 000 = 3 000 000 + 900 000 + 100 000 = = 3 000 000 + 900 000 + 90 000 + 10 000 = 3 000 000 + 900 000 + 90 000 + 9 000 + 1 000 = = 3 000 000 + 900 000 + 90 000 + 9 000 + 900 + 100 = = 3 000 000 + 900 000 + 90 000 + 9 000 + 900 + 90 + 10 то 4 000 000 − 5 = ( 3 000 000 + 900 000 + 90 000 + 9 000 + 900 + 90 + 10 ) − 5 = = 3 000 000 + 900 000 + 90 000 + 9 000 + 900 + 90 + ( 10 − 5 ) = = 3 000 000 + 900 000 + 90 000 + 9 000 + 900 + 90 + 5 = 3 999 995 .

Числовые и буквенные выражения

Как вы уже, наверное, заметили, математические операции сложения и вычитания мы записывали в какой-то новой для нас форме, со знаками «-«, «+» и «=».

Такой способ записи математической информации на бумаге, в компьютере или где-нибудь еще можно назвать математическим языком.

А определенную последовательность символов этого математического языка, которая несет в себе некий смысл, мы будет называть математическим выражением.

Существуют числовые и буквенные выражения. Ниже приведем пример таких выражений.

Под цифрами 1, 2 и 4 записаны числовые выражения.

Числовые выражения — это математические выражения, состоящие из чисел, знаков арифметических действий и скобок.

Под цифрами 2, 5 и 6 записаны буквенные выражения.

Буквенное выражение составлено также из знаков арифметических действий и скобок. Но в отличие от числовых выражений, здесь есть ещё и буквы. Буквами в буквенных выражениях обозначаются некоторые числа, которые пока нам не известны.

Следует учесть то, что две одинаковые буквы подразумевают под собой одно и то же число.

Если, например, известно какое число скрывается за каждой буквой в буквенном выражении, то такое выражение можно перевести в числовое.

Посмотрите на буквенное выражение:

a + b = 9

Если a = 5, а b = 4, то это буквенное выражение можно представить в виде числового

5 + 4 = 9

Способы вычитания

Можно двумя способами вычесть одно число из другого:

1. или можно отнять от большего числа столько единиц, сколько их содержится в меньшем. Так, из 9 вычесть 6 значит от 9 отнять 6. Число 3 будет искомый остаток;

2. или можно к меньшему числу прибавлять по единице до тех пор, пока не получим большее число. Так, вычитая 6 из 9, мы к 6 прибавляем 3 единицы. Число единиц, которое нужно прибавить к меньшему числу, чтобы уравнять его с большим, определяет разность. Меньшее число с разностью должно равняться большему числу, следовательно, меньшее число и разность суть слагаемые, а большее — их сумма. На этом основано другое определение вычитания:

Вычитание есть такое действие, в котором по данной сумме и одному слагаемому отыскивается другое слагаемое.

В этом случае данная сумма есть уменьшаемое, данное слагаемое — вычитаемое, а искомаяразность — другое слагаемое.

Определение вычитания

Вычесть значит отнять одно число от другого.

Вычитание есть такое действие, в котором отнимают меньшее число от большего. При вычитании целых чисел большее число уменьшается на столько единиц, сколько их содержится в меньшем. Вычесть одно число из другого значит убавить одно число другим, поэтому вычитание есть действие обратное сложению.

В вычитании два данных числа называются уменьшаемым и вычитаемым, а искомое — разностью.

Уменьшаемым называют большее число, от которого отнимают другое. Оно уменьшается от вычитания.

Вычитаемым называют меньшее число, которое отнимают от большего.

Разностью называют вывод, полученный от вычитания. Разность определяет, чем одно число больше другого или показывает разницу между двумя числами.

Знак вычитания. Действие вычитания обозначается знаком — (минус).

Правило встречается в следующих упражнениях:

5 класс

Задание 257 ,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 582,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 646,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1061,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1133,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1171,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1406,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1678,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 261,
Мерзляк, Полонский, Якир, Учебник

Номер 1,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 32,
Мерзляк, Полонский, Якир, Учебник

Номер 97,
Мерзляк, Полонский, Якир, Учебник

Номер 598,
Мерзляк, Полонский, Якир, Учебник

Номер 1183,
Мерзляк, Полонский, Якир, Учебник

Номер 1184,
Мерзляк, Полонский, Якир, Учебник

Номер 1191,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Задание 619,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 701,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 891,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 6,
Мерзляк, Полонский, Якир, Учебник

Номер 7,
Мерзляк, Полонский, Якир, Учебник

Номер 11,
Мерзляк, Полонский, Якир, Учебник

Номер 12,
Мерзляк, Полонский, Якир, Учебник

Номер 17,
Мерзляк, Полонский, Якир, Учебник

Номер 18,
Мерзляк, Полонский, Якир, Учебник

Номер 78,
Мерзляк, Полонский, Якир, Учебник

Номер 177,
Мерзляк, Полонский, Якир, Учебник

Номер 498,
Мерзляк, Полонский, Якир, Учебник

Номер 671,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 485,
Мерзляк, Полонский, Якир, Учебник

Номер 578,
Мерзляк, Полонский, Якир, Учебник

Открытый урок по математике в 5-м классе по теме: «Применение свойств сложения и вычитания к решению уравнений»

Разделы: Математика

Цели урока: реализация компетентностного подхода к обучению через различные формы самостоятельной работы на уроке; развитие интереса к предмету математики через новые способы выполнения традиционных заданий.

Задачи урока:

Образовательные: продолжить отработку ранее полученных навыков упрощения выражений, используя свойства сложения и вычитания; сформировать умение решать уравнения способом, основанном на упрощении выражения, стоящего в левой части.
Развивающие: развивать память, логическое мышление, умение сравнивать, выявлять закономерности, анализировать и обобщать факты.
Воспитательные: продолжить формирование таких качеств личности как организованность, дисциплинированность; способствовать поддержанию общей работоспособности на высоком уровне и снижению утомляемости на уроке.

Оборудование: доска, мел, карточки для индивидуальной работы и карточки с раздаточным материалом.

I. Организационный момент.

II. Постановка цели урока.

Мы повторили действия сложение и вычитание, повторили и расширили перечень свойств этих действий, ввели понятия числового и буквенного выражений, научились упрощать буквенные выражения, используя законы сложения и вычитания, вспомнили способ решения уравнений путём последовательного нахождения неизвестных компонентов.

Цель урока — научиться решать уравнения способом, основанном на упрощении выражения, стоящего в левой части.

— Перед вами лежат карточки с заданиями. Закончите запись соответствующих свойств сложения и вычитания.

См. приложение 1.

Карточки с выполненными заданиями собрать.

III. Устная фронтальная работа.

Используя свойства сложения и вычитания, вычислите удобным способом:

а) 653 + (281 + +347),

б) (747 + 599) — 647,

2) Упростите выражения:

3) Что называется уравнением?

4) Что значит решить уравнение?

5) Что называется корнем уравнения?

6) Придумайте уравнение,

• имеющее 1 корень в натуральных числах,
• не имеющее корней в натуральных числах.

Посчитайте, сколько треугольников изображено на рисунке. (35)

IV. Изучение нового материала.

1. Подготовительная работа.

573 — (а + 173) = 286

Один ученик записывает решение уравнения на доске, проговаривая вслух правила нахождения неизвестных компонентов.

а + 173 = 573 -286

Наиболее подготовленные учащиеся решают уравнения на индивидуальных карточках. (См. приложение 2.)

Карточки затем собрать и оценить к концу урока.

2. Работа над новой темой.

— А теперь решим первое уравнение по-другому, упростив его левую часть.

Запись в тетради: II способ.

— Напомните, как из числа можно вычесть сумму?

Ученик формулирует соответствующее свойство.

Запись в тетради:

573 — (а + 173) = 286

V. Закрепление изученного материала.

— На доске записаны уравнения. Решите их, упростив левую часть.

(Уравнения 2), 3) решают самостоятельно, затем проверяют по записям на «крыле» доски. Первые 6 работ оценить.)

1) (524 + у) — 124 = 807	2) х — 68 — 114 = 215	3) 67 — (34 + х) + 56 = 73
400 + у = 807	х — 182 = 215	89 — х = 73
у = 407	х = 397	х = 16
Ответ: 407.	Ответ: 397.	Ответ: 16.

Тем, кто справится с работой раньше, дать карточку.

См. приложение 3.

VII. Тест. (См. приложение 4.)

По окончании работы учащиеся проверяют ответы и оценивают результаты теста.

Решившим тест раньше — карточка. (См. приложение 6.)

Сегодня на уроке мы познакомились еще с одним способом решения уравнений, но для его применения необходимо хорошо знать и владеть свойствами сложения и вычитания. У вас на столе фигуры. Я предлагаю вам выбрать символ и оценить свою деятельность. Дети, уходя с урока, прикрепляют выбранный символ к магнитной доске.

Дом. задание: повторить свойства сложения и вычитания в п. 9,

445 (б, в, г) — решить уравнения двумя способами,

447 (а) — составить уравнение для решения задачи и решить его.

Дополн. задание. Каким числом можно заменить а, чтобы корнем уравнения 38 — (а + 13) = х + 13 было число 8?

Вычитание натуральных чисел

Вычитание — операция, обратная сложению.

Пример 2

На тарелке лежало $7$ яблок, съели $3$ яблока. Сколько яблок осталось на тарелке?

Очевидно, что если к оставшемуся числу яблок $(x)$ добавить $3$ яблока, то их станет $7$:

$x + 3 = 7.$

Таким образом, известно одно слагаемое и сумма, нужно найти второе слагаемое.

Для этого используется вычитание:

$x = 7 — 3 = 4$, т.к. $3 + 4 = 7.$

Число, из которого вычитают, называется уменьшаемым, а число, которое вычитают, — вычитаемым. Результат вычитания называется разностью.

Из данной задачи получаем:

$7$ — уменьшаемое, $3$ — вычитаемое, $8$ — разность.

В общем виде

Если $b + c = a$, то

Рисунок 4.

При вычитании натуральных чисел уменьшаемое обязательно должно быть больше вычитаемого:

$11 — 3 = 8; 8 > 3.$

Разность двух чисел находят, чтобы узнать на сколько уменьшаемое больше вычитаемого или на сколько вычитаемое меньше уменьшаемого:

$11$ больше $3$ на $8$.