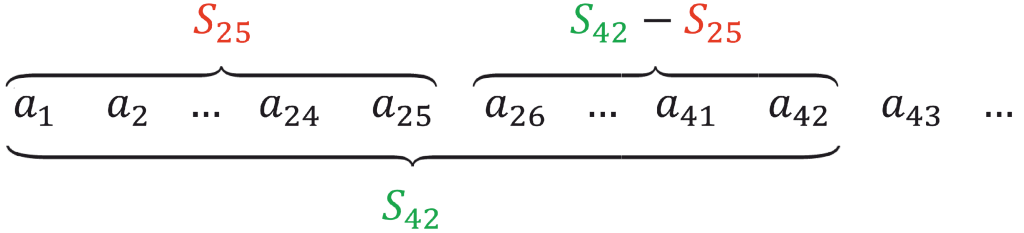Как найти d в прогрессии формула. арифметическая прогрессия

Свойства и формулы арифметической прогрессии

Разность арифметической прогрессии вычисляется по следующей формуле:

\(a_{n+1}\;-\;a_n\;=\;d\)

Существует несколько формул для нахождения членов арифметической прогрессии с номером n:

\(a_n\;=\;a_1\;+\;(n\;-\;1)d\)

\(a_n\;=\;a_m\;-\;(m\;-\;n)d\)

В обоих случаях \(a_1\) будет обозначать первый член прогрессии, d здесь будет являться разностью прогрессии, а a_m обозначает член арифметической прогрессии с номером m.

Характеристическое свойство арифметической прогрессии выражается следующим образом: последовательность \(a_1\), \(a_2\), \(a_3\), которая интерпретируется как арифметическая прогрессия \Leftrightarrow для всех элементов указанной прогрессии справедливо условие:

\(a_n\;=\;\frac{a_{n-1\;}+\;a_{n+1}}2,\;n\;\geq\;2\)

Сумма первых членов арифметической прогрессии вычисляется с использованием следующих формул:

\(S_n\;=\;\frac{a_{1\;}+\;a_n}2\;\cdot\;n\)

В данной формуле \(a_1\) является обозначением первого члена прогрессии, \(a_n\) — обозначением члена прогрессии с номером n, а n — обозначением суммируемых членов прогрессии.

\(S_n\;=\;\frac{2a_{1\;}+\;d(n-1)}2\;\cdot\;n\)

Дополнительно к предыдущим обозначениям в этой формуле d — это шаг прогрессии, а n — число суммируемых членов прогрессии.

Вывод этой формулы выглядит следующим образом:

\(S_n\;=\;a_1\;+\;a_2\;+\;a_3\;+\;…\;+\;a_{n-2}\;+\;a_{n-1}\;+\;a_n\)

\(S_n\;=\;a_n\;+a_{n-1}\;+\;a_{n-2}\;+\;…\;a_3\;+\;a_2\;+\;a_1\)

\(2S_n\;=\;(a_{1\;}+\;a_n)\;+\;(a_2\;+\;a_{n-1})\;+\;(a_3\;+\;a_{n-2})\;+\;…\;+\;(a_{n-1}\;+\;a_2)\;+\;(a_n\;+\;a_1)\)

Предоставим объяснение того, что выражения, заключенные в скобки, равны как между собой, так и выражению \(a_1 + a_n\):

\(a_2\;+\;a_{n-1}\;=\;(a_1+d)\;+\;(a_n-d)\;=\;a_1+a_n\)

\(a_3\;+\;a_{n-2}\;+\;(a_2\;+d)\;+\;(a_{n-1}\;-\;d)\;=\;a_2\;+\;a_{n-1}\;=\;a_1+a_n\)

Тогда мы можем записать:

\(2S_n\;=(a_1\;+\;a_n)\;\cdot n\)

Из этого выводится формула, дающая в результате сумму первых n членов арифметической прогрессии:

\(S_n\;=\frac{(a_1\;+\;a_n)}2\cdot n\)

Еще одно свойство арифметической прогрессии — сходность. Арифметическая прогрессия будет являться расходящейся при \(d\;\neq0\) и сходящейся при d = 0.

\(\lim_{n\rightarrow\infty}a_n\;=\;\left\{\begin{array}{c}+\infty,\;d>0\\-\infty,\;d<0\\a_1,\;d=0\end{array}\right.\)

Существует также связь между геометрической и арифметической прогрессиями. Если в арифметической прогрессии \(a_1\), \(a_2\), \(a_3\), … число a > 0, то последовательность вида \(a^{a_1},\;a^{a_2},\;a^{a_3},\;…\) будет геометрической прогрессией со значением \(a^d.\)

Алгебра. Урок 6. Задания. Часть 1.

Найдем первые несколько членов данной последовательности.

n = 1 ⇒ c 1 = 1 2 − 1 = 1 − 1 = 0

n = 2 ⇒ c 2 = 2 2 − 1 = 4 − 1 = 3

n = 3 ⇒ c 3 = 3 2 − 1 = 9 − 1 = 8

Число 3 является членом данной последовательности.

Правильный ответ под номером 3 .

№2. Последовательность задана формулой c n = n + ( − 1 ) n n . Какое из следующих чисел не является членом этой последовательности?

1. 2 1 2
2. 4 1 4
3. 5 1 5
4. 6 1 6

Решение:

Найдем несколько первых членов данной последовательности.

n = 1 ⇒ c 1 = 1 + ( − 1 ) 1 1 = 1 + − 1 1 = 1 − 1 = 0

n = 2 ⇒ c 2 = 2 + ( − 1 ) 2 2 = 2 + 1 2 = 2 1 2

n = 3 ⇒ c 3 = 3 + ( − 1 ) 3 3 = 3 + − 1 3 = 3 − 1 3 = 2 2 3

n = 4 ⇒ c 4 = 4 + ( − 1 ) 4 4 = 4 + 1 4 = 4 1 4

n = 5 ⇒ c 5 = 5 + ( − 1 ) 5 5 = 5 + − 1 5 = 5 − 1 5 = 4 4 5

n = 6 ⇒ c 6 = 6 + ( − 1 ) 6 6 = 6 + 1 6 = 6 1 6

Приходим к выводу, что число 5 1 5 не является членом данной последовательности.

Правильный ответ под номером 3.

№3. Последовательность задана формулой a n = 11 n + 1. Сколько членов в этой последовательности больше 1?

1. 8
2. 9
3. 10
4. 11

Решение:

Решим неравенство 11 n + 1 > 1 относительно n .

Для того, чтобы дробь была больше 1 , знаменатель должен быть меньше числителя. n + 1 < 11 ⇒ n < 10.

Поскольку n – натуральное число, то все возможные значения, которые может принимать n для выполнения исходного неравенства это: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Правильный ответ под номером 2.

№4. Последовательности заданы несколькими первыми членами. Одна из них – арифметическая прогрессия. Укажите её.

1. 1 ; 2 ; 3 ; 5 ; …
2. 1 ; 2 ; 4 ; 8 ; …
3. 1 ; 3 ; 5 ; 7 ; …
4. 1 ; 1 2 ; 2 3 ; 3 4 ; …

Решение:

Для того, чтобы последовательность была арифметической, должны выполняться условия:

a 2 = a 1 + d a 3 = a 2 + d a 3 = a 2 + d a n = a n − 1 + d

То есть каждый следующий член последовательности должен отличаться от предыдущего на одно и то же число. Начнем проверку:

1. 1 ; 2 ; 3 ; 5 ; … d = 2 − 1 = 1 d = 3 − 2 = 1 d = 5 − 3 = 2 – противоречие.
2. 1 ; 2 ; 4 ; 8 ; … d = 2 − 1 = 1 d = 4 − 2 = 2 – противоречие.
3. 1 ; 3 ; 5 ; 7 ; … d = 3 − 1 = 2 d = 5 − 3 = 2 d = 7 − 5 = 2

Условия соблюдены. Данная прогрессия является арифметической.

1. 1 ; 1 2 ; 2 3 ; 3 4 ; … d = 1 2 − 1 = − 1 2 d = 2 \ 2 3 − 1 \ 3 2 6 = 2 ⋅ 2 − 1 ⋅ 3 6 = 4 − 3 6 = 1 6 – противоречие.

Правильный ответ под номером 3.

№5. Одна из данных последовательностей является геометрической прогрессией. Укажите эту последовательность.

1. 10 ; 6 ; 2 ; − 2 ; …
2. 5 ; 5 2 ; 5 4 ; 5 8 ; …
3. 1 ; 2 ; 3 ; 5 ; …
4. 1 2 ; 1 3 ; 1 4 ; 1 5 ; …

Решение:

Для того, чтобы последовательность была геометрической, должны выполняться условия: b 2 = b 1 ⋅ q b 3 = b 2 ⋅ q = b 1 ⋅ q 2 … b n = b n − 1 ⋅ q = b 1 ⋅ q n − 1

То есть каждый следующий член последовательности должен отличаться от предыдущего в q раз ( q одно и то же для всех членов последовательности). Начнем проверку:

1. 10 ; 6 ; 2 ; − 2 ; … q = 6 10 = 0,6 q = 2 6 = 1 3 – противоречие.
2. 5 ; 5 2 ; 5 4 ; 5 8 ; … q = 5 2 ÷ 5 = 5 2 ⋅ 1 5 = 1 2 q = 5 4 ÷ 5 2 = 5 4 ⋅ 2 5 = 1 2 q = 5 8 ÷ 5 4 = 5 8 ⋅ 4 5 = 4 8 = 1 2

Условия соблюдены. Данная прогрессия является геометрической.

1. 1 ; 2 ; 3 ; 5 ; … q = 2 1 = 2 q = 3 2 = 1,5 – противоречие.
2. 1 2 ; 1 3 ; 1 4 ; 1 5 ; … q = 1 3 ÷ 1 2 = 1 3 ⋅ 2 1 = 2 3 q = 1 4 ÷ 1 3 = 1 4 ⋅ 3 1 = 3 4 – противоречие.

Правильный ответ под номером 2.

№6. Какая из следующих последовательностей является арифметической прогрессией?

1. Последовательность натуральных степеней числа 2.
2. Последовательность натуральных чисел, кратных 5.
3. Последовательность кубов натуральных чисел.
4. Последовательность всех правильных дробей, числитель которых на 1 меньше знаменателя.

Решение:

Для того, чтобы последовательность была арифметической, должны выполняться условия:

a 2 = a 1 + d a 3 = a 2 + d a 3 = a 2 + d a n = a n − 1 + d

1. Последовательность натуральных степеней числа 2.

Данная последовательность представляет собой следующий ряд:

5 ; 10 ; 15 ; 20 ; … d = 4 − 2 = 2 d = 8 − 4 = 4 – противоречие.

1. Последовательность натуральных чисел, кратных 5.

Данная последовательность представляет собой следующий ряд:

5 ; 10 ; 15 ; 20 ; … d = 10 − 5 = 5 d = 15 − 10 = 5 d = 20 − 15 = 5

Условие соблюдено. Данная прогрессия является арифметической.

1. Последовательность кубов натуральных чисел.

Данная последовательность представляет собой следующий ряд:

1 ; 8 ; 27 ; 81 ; … d = 8 − 1 = 7 d = 27 − 8 = 19 – противоречие.

1. Последовательность всех правильных дробей, числитель которых на 1 меньше знаменателя.

Данная последовательность представляет собой следующий ряд:

1 2 ; 2 3 ; 3 4 ; 4 5 ; … d = 2 \ 2 3 − 1 \ 3 2 6 = 2 ⋅ 2 − 3 6 = 4 − 3 6 = 1 6 d = 3 \ 3 4 − 2 \ 4 3 12 = 3 ⋅ 3 − 2 ⋅ 4 12 = 9 − 8 12 = 1 12 – противоречие.

Нахождения n-ого члена арифметической прогрессии

Способ I

Мы можем прибавлять к предыдущему значению числа прогрессии \( d=4\) , пока не дойдем до \( \displaystyle 6\)-го члена прогрессии. Хорошо, что суммировать нам осталось немного – всего три значения:

\( \begin{array}{l}{{a}_{4}}=11+4=15\\{{a}_{5}}=15+4=19\\{{a}_{6}}=19+4=23\end{array}\)Итак, 6-ой член описанной арифметической прогрессии равен 23.

Способ II

А что если нам нужно было бы найти значение \( \displaystyle 140\)-го члена прогрессии? Суммирование заняло бы у нас не один час, и не факт, что мы не ошиблись бы при сложении чисел.

А теперь очень важно! Чтобы облегчить себе работу, нужно найти закономерность, потом описать ее формулой и потом пользоваться этой формулой, чтобы вычислять в разы быстрее. Это и есть математика!

Это и есть математика!

Важно научиться находить закономерности, а потом уже запоминать формулы. Потому что, даже если ты забудешь формулу, ты сможешь ее вывести

И, самое главное, ты сможешь проверить подходит та или иная формула для решения задачи, а не просто подставлять их как обезьянка. 

Давай попробуем вывести формулу. Это легко и тебе понравится! Чтобы найти закономерности, надо пользоваться тем, что мы знаем.

Что мы знаем?

• У нас есть арифметическая прогрессия: 3, 7, 11, 15, 19 и т.д.
• У нас есть номера прогрессии: 1, 2, 3, 4, 5, и т.д.
• Мы все время прибавляем 4, значит разница прогрессии d = 4.

Чему равен 2-й член арифметической прогрессии? Попробуй сначала написать числами, а потом в более общем виде, заменив числа буквами.

7=3+4 или 7=3+d

Закономерности пока не видны. Ок. Идем дальше. Чему равен 3-й член арифметической прогрессии?

11=3+4+4 или 11=3+d+d

Похоже что вырисовывается закономерность! Чтобы узнать значение 2-го члена прогрессии, мы прибавляли одно d, а чтобы узнать 3-го — два d! Иными словами, нам надо прибавлять каждый раз на одно d меньше, чем номер члена прогрессии.

Давай проверим? Чему равен 4-й член арифметической прогрессии?

15=3+4+4+4 или 15=3+d+d+d

Бинго! Закономерность подтверждается. Теперь осталось описать закономерность формулой и пользоваться ею!

А теперь запомни эту формулу и используй ее для быстрого счета. А если забудешь — то легко выведешь.

Например, посмотрим, из чего складывается значение \( \displaystyle 4\)-го члена данной арифметической прогрессии:

Попробуй самостоятельно найти таким способом значение члена \( \displaystyle n=6\) данной арифметической прогрессии.

Рассчитал? Сравни свои записи с ответом:

Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно прибавляли \( \displaystyle d\) к предыдущему значению членов арифметической прогрессии. Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

Кстати, таким образом мы можем посчитать и \( \displaystyle 140\)-ой член данной арифметической прогрессии (да и \( \displaystyle 169\)-ый тоже можем, да и любой другой вычислить совсем несложно).

Возрастающие и убывающие арифметические прогрессии

Например:

Например:

Выведенная формула применяется в расчете членов как в возрастающих, так и в убывающих членах арифметической прогрессии.

Проверим это на практике.

Нам дана арифметическая прогрессия, состоящая из следующих чисел: \( \displaystyle 13;\text{ }8;\text{ }4;\text{ }0;\text{ }-4.\)

Проверим, какое получится \( \displaystyle 4\)-ое число данной арифметической прогрессии, если при его расчете использовать нашу формулу:

Так как \( \displaystyle d=-5\), то:\( {{a}_{4}}=13-5\left( 4-1 \right)=13-15=-2\)

Таким образом, мы убедились, что формула действует как в убывающей, так и в возрастающей арифметической прогрессии.

Попробуй самостоятельно найти \( \displaystyle 140\)-ой и \( \displaystyle 169\)-ый члены этой арифметической прогрессии.

Более сложные задачи на арифметическую прогрессию

Теперь у вас есть вся необходимая информация для решения практически любой задачи на арифметическую прогрессию. Завершим тему рассмотрением задач, в которых надо не просто применять формулы, но и немного думать (в математике это бывает полезно )

Пример (ОГЭ).Найдите сумму всех отрицательных членов прогрессии: \(-19,3\); \(-19\); \(-18,7\)…Решение:

\(S_n=\)\(\frac{2a_1+(n-1)d}{2}\)\(\cdot n\)		Задача очень похожа на предыдущую. Начинаем решать также: сначала найдем \(d\).
\(d=a_2-a_1=-19-(-19,3)=0,3\)		Теперь бы подставить \(d\) в формулу для суммы… и вот тут всплывает маленький нюанс – мы не знаем \(n\). Иначе говоря, не знаем сколько членов нужно будет сложить. Как это выяснить? Давайте думать. Мы прекратим складывать элементы тогда, когда дойдем до первого положительного элемента. То есть, нужно узнать номер этого элемента. Как? Запишем формулу вычисления любого элемента арифметической прогрессии: \(a_n=a_1+(n-1)d\) для нашего случая.
\(a_n=a_1+(n-1)d\)
\(a_n=-19,3+(n-1)·0,3\)		Нам нужно, чтоб \(a_n\) стал больше нуля. Выясним, при каком \(n\) это произойдет.
\(-19,3+(n-1)·0,3>0\)		Решаем полученное неравенство. Переносим \(-19,3\) через знак сравнения.
\((n-1)·0,3>19,3\)           \(|:0,3\)		Делим обе части неравенства на \(0,3\).
\(n-1>\)\(\frac{19,3}{0,3}\)		Переносим минус единицу, не забывая менять знаки
\(n>\)\(\frac{19,3}{0,3}\)\(+1\)		Вычисляем…
\(n>65,333…\)		…и выясняется, что первый положительный элемент будет иметь номер \(66\). Соответственно, последний отрицательный имеет \(n=65\). На всякий случай, проверим это.
\(n=65;\)      \(a_{65}=-19,3+(65-1)·0,3=-0,1\) \(n=66;\)      \(a_{66}=-19,3+(66-1)·0,3=0,2\)		Таким образом, нам нужно сложить первые \(65\) элементов.
\(S_{65}=\)\(\frac{2 \cdot (-19,3)+(65-1)0,3}{2}\)\(\cdot 65\) \(S_{65}=\)\({-38,6+19,2}{2}\)\(\cdot 65=-630,5\)		Ответ готов.

Ответ:   \(S_{65}=-630,5\).

Пример (ОГЭ).Арифметическая прогрессия задана условиями: \(a_1=-33\); \(a_{n+1}=a_n+4\). Найдите сумму от \(26\)-го до \(42\) элемента включительно.Решение:

\(a_1=-33;\) \(a_{n+1}=a_n+4\)	В этой задаче также нужно найти сумму элементов, но начиная не с первого, а с \(26\)-го. Для такого случая у нас формулы нет. Как решать? Легко — чтобы получить сумму с \(26\)-го до \(42\)-ой, надо сначала найти сумму с \(1\)-ого по \(42\)-ой, а потом вычесть из нее сумму с первого до \(25\)-ого (см картинку).
	Для нашей прогрессии \(a_1=-33\), а разность \(d=4\) (ведь именно четверку мы добавляем к предыдущему элементу, чтоб найти следующий). Зная это, найдем сумму первых \(42\)-ух элементов.
\(S_{42}=\)\(\frac{2 \cdot (-33)+(42-1)4}{2}\)\(\cdot 42=\) \(=\)\(\frac{-66+164}{2}\)\(\cdot 42=2058\)	Теперь сумму первых \(25\)-ти элементов.
\(S_{25}=\)\(\frac{2 \cdot (-33)+(25-1)4}{2}\)\(\cdot 25=\) \(=\)\(\frac{-66+96}{2}\)\(\cdot 25=375\)	Ну и наконец, вычисляем ответ.
\(S=S_{42}-S_{25}=2058-375=1683\)

Ответ:   \(S=1683\).

Для арифметической прогрессии существует еще несколько формул, которые мы не рассматривали в данной статье ввиду их малой практической полезности. Однако вы без труда можете найти их здесь.

Числовая последовательностьГеометрическая прогрессия

Понятие числовой последовательности

Введем два определения числовой последовательности:

Определение 1

Числовая функция, у которой область определения совпадает с натуральным рядом чисел, будет называться числовой последовательностью.

Определение 2

Отображения натурального ряда чисел на множество действительных чисел будет называться числовой последовательностью: $f:N→R$

Числовая последовательность обозначается следующим образом:

${p_k }={p_1,p_2,…,p_k,…}$

где $p_1,p_2,…,p_k,…$ — действительные числа.

Есть три различных способа для задания числовых последовательностей. Опишем их.

• Аналитический.

  В этом способе последовательность задается в виде формулы, с помощью которой можно найти любой член этой последовательности, подставляя в нее вместо переменной натуральные числа.

• Рекуррентный.

  Данный способ задания последовательности заключается в следующем: Дается первый (или несколько первых) член данной последовательности, а затем формула, которая связывает любой член ее с предыдущим членом или предыдущими членами.

• Словесный.

  При этом способе числовая последовательность просто описывается без введения каких-либо формул.

Двумя частными случаями числовых последовательностей являются арифметическая и геометрическая прогрессии.

Числовая последовательность

Итак, сядем и начнем писать какие-нибудь числа. Например: \( \displaystyle 4,\text{ }7,\text{ }-8,\text{ }13,\text{ }-5,\text{ }-6,\text{ }0,\text{ }\ldots \)

Писать можно любые числа, и их может быть сколько угодно (в нашем случае их \( \displaystyle 7\)). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать.

Это и есть пример числовой последовательности.

Например, для нашей последовательности:

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и \( \displaystyle n\)-ное число) всегда одно.

Число с номером \( \displaystyle n\) называется \( \displaystyle n\)-ным членом последовательности.

Всю последовательность мы обычно называем какой-нибудь буквой (например, \( \displaystyle a\)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: \( \displaystyle {{a}_{1}},\text{ }{{a}_{2}},\text{ }…,\text{ }{{a}_{10}},\text{ }…,\text{ }{{a}_{n}}\).

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

1. Словесно — когда правило последовательности объясняется словами:

«Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23. »

Аналитически — когда указана формула ее n-го члена: y_n = f(n).

Последовательность y_n = C называют постоянной или стационарной.

Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.

Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a_n+1 = a_n + a_n-1.

Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

Графически — когда график последовательности состоит из точек с абсциссами 1, 2, 3, 4.

Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

Свойства числовых последовательностей:

1. Последовательность n> называют возрастающей, если каждый ее член кроме первого больше предыдущего:

Возрастающие и убывающие последовательности называют монотонными последовательностями.

Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: y_n = y_n+T. Число T — длина периода.

Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.

Пример числовой последовательности выглядит так:

В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

N-ный член алгебраической последовательности — это число с порядковым номером n.

Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a₁, a₂. a₁₀. a_n.

N-ый член последовательности можно задать формулой. Например:

• Формула a_n = 3n − 5 задает последовательность: −2, 1, 4, 7, 10…
• Формула a_n = 1 : (n + 2) задает последовательность: 1/3, 1/4, 1/5, 1/6.

Последовательности чисел

Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной. 

Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.

Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.

Что такое числовая последовательность? 

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.

Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N. 

Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.

На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.

Пример №2: разность прогрессии

Теперь усложним немного задачу, приведем пример, как найти разность прогрессии арифметической.

Известно, что в некоторой прогрессии алгебраической 1-й член равен 6, а 7-й член равен 18. Необходимо найти разность и восстановить эту последовательность до 7 члена.

Воспользуемся формулой для определения неизвестного члена: an = (n — 1) * d + a1. Подставим в нее известные данные из условия, то есть числа a1 и a7, имеем: 18 = 6 + 6 * d. Из этого выражения можно легко вычислить разность: d = (18 — 6) /6 = 2. Таким образом, ответили на первую часть задачи.

Чтобы восстановить последовательность до 7 члена, следует воспользоваться определением алгебраической прогрессии, то есть a2 = a1 + d, a3 = a2 + d и так далее. В итоге восстанавливаем всю последовательность: a1 = 6, a2 = 6 + 2=8, a3 = 8 + 2 = 10, a4 = 10 + 2 = 12, a5 = 12 + 2 = 14, a6 = 14 + 2 = 16, a7 = 18.

Сумма элементов от m до n: формула

Формула, приведенная в предыдущем пункте, дает ответ на вопрос, как найти сумму арифметической прогрессии (первых элементов), но часто в задачах необходимо просуммировать ряд чисел, стоящих в середине прогрессии. Как это сделать?

Ответить на этот вопрос проще всего, рассматривая следующий пример: пусть необходимо найти сумму членов от m-го до n-го. Для решения задачи следует представить заданный отрезок от m до n прогрессии в виде нового числового ряда. В таком представлении m-й член a m будет первым, а a n станет под номер n-(m-1). В этом случае, применяя стандартную формулу для суммы, получится следующее выражение:

Последовательности

Будем выписывать в порядке возрастания положительные четные числа. Первое такое число равно 2, второе 4, третье 6, четвертое 8 и т. д. Получим последовательность

2; 4; 6; 8; … .

Очевидно, что на пятом месте в этой последовательности будет число 10, на десятом — число 20, на сотом — число 200. Вообще для любого натурального числа п можно указать соответствующее ему положительное четное число; оно равно 2n.

Рассмотрим еще одну последовательность. Будем выписывать в порядке убывания правильные дроби с числителем, равным 1:

Для любого натурального числа n мы можем указать соответствующую ему дробь; она равна Так, на шестом месте должна стоять дробь на тридцатом дробь , на тысячном — дробь

Числа, образующие последовательность, называют соответственно первым, вторым, третьим, четвертым и т. д. членами последовательности. Члены последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена. Например, (читают: «а первое, а второе, а третье, а четвертое» и т. д.). Вообще член последовательности с номером n, или, как говорят, n-й член последовательности, обозначают Саму последовательность будем обозначать так:

Заметим, что последовательность может содержать конечное число членов. В таком случае ее называют конечной. Например, конечной является последовательность двузначных чисел:

Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.

Часто последовательность задают с помощью формулы n-го члена последовательности. Например, последовательность положительных четных чисел можно задать формулой последовательность правильных дробей с числителем, равным 1, — формулой Приведем другие примеры.

Пример:

Пусть последовательность задана формулой Подставляя вместо n натуральные числа 1, 2, 3, 4, 5 и т. д., получаем:

Рассматриваемая последовательность начинается так:

Пример:

Пусть последовательность задана формулой Все члены этой последовательности с нечетными номерами равны —10, а с четными номерами равны 10:

Получаем последовательность

Пример:

Формулой задается последовательность, все члены которой равны 5:

Рассмотрим еще один способ задания последовательности.

Пример:

Пусть первый член последовательности равен 3, а каждый следующий член равен квадрату предыдущего, т. е.

С помощью формулы можно по известному первому члену последовательности вычислить второй, затем по известному второму найти третий, по известному третьему — четвертый и т. д. Получим последовательность

Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro — возвращаться).

Определение и примеры арифметической прогрессии

Это последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой.

Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (аn) называется единичное число из последовательности.

Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии.

Кроме этого, существуют виды таких рядов:

• возрастающая – числа ряда увеличиваются по своему значению,
• убывающая – каждое последующее число ряда уменьшается.

В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6.

Арифметическая прогрессия .

Арифметическая прогрессия – это ряд чисел, в котором все член получаются из предыдущего методом добавления к нему 1-го и того же числа d, которое называется разностью арифметической прогрессии.

Или другими словами: арифметическая прогрессия — численная последовательность, которая имеет вид:

,

т.е. последовательность чисел (членов прогрессии), в которой числа, начиная со 2-го, получаются из предыдущего путем добавления к нему постоянного числа  (шаг либо разность прогрессии):

Всякий (n-й) член прогрессии можно вычислить с помощью формулы общего члена:

Арифметическая прогрессия – это монотонная последовательность. При  она возрастает, а при  — убывает. Если , то последовательность – стационарная. Это следуют из соотношения  для членов арифметической прогрессии.

Чему равна сумма арифметической прогрессии: формула

Прежде чем приводить формулу для указанной суммы, стоит рассмотреть простой частный случай. Дана прогрессия натуральных чисел от 1 до 10, необходимо найти их сумму. Поскольку членов в прогрессии немного (10), то можно решить задачу в лоб, то есть просуммировать все элементы по порядку.

Стоит учесть одну интересную вещь: поскольку каждый член отличается от последующего на одно и то же значение d = 1, то попарное суммирование первого с десятым, второго с девятым и так далее даст одинаковый результат. Действительно:

Как видно, этих сумм всего 5, то есть ровно в два раза меньше, чем число элементов ряда. Тогда умножая число сумм (5) на результат каждой суммы (11), вы придете к полученному в первом примере результату.

Если обобщить эти рассуждения, то можно записать следующее выражение:

Это выражение показывает, что совсем не обязательно суммировать подряд все элементы, достаточно знать значение первого a 1 и последнего a n , а также общего числа слагаемых n.

Считается, что впервые до этого равенства додумался Гаусс, когда искал решение на заданную его школьным учителем задачу: просуммировать 100 первых целых чисел.

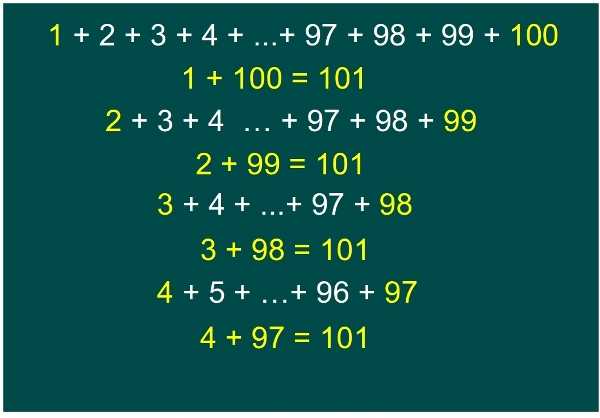
Важные формулы

Приведем теперь основные формулы, которые понадобятся для решения задач с использованием арифметической прогрессии. Обозначим символом a n n-й член последовательности, где n — целое число. Разность обозначим латинской буквой d. Тогда справедливы следующие выражения:

1. Для определения значения n-го члена подойдет формула: a n = (n-1)*d+a 1 .
2. Для определения суммы первых n слагаемых: S n = (a n +a 1)*n/2.

Чтобы понять любые примеры арифметической прогрессии с решением в 9 классе, достаточно запомнить эти две формулы, поскольку на их использовании строятся любые задачи рассматриваемого типа. Также следует не забывать, что разность прогрессии определяется по формуле: d = a n — a n-1 .