Что такое образующая конуса: формулы и вычисления

Правильное изображение конуса карандашом — объем

Для того, чтобы придать нашему конусу объем, нам стоит добавить свет и тень. Обозначаем границу света и тени, найти самый светлый участок. В конусе присутствуют следующие теневые участки:

• полутон;
• свет;
• блик;
• свет;
• полутон;
• тень;
• блик.

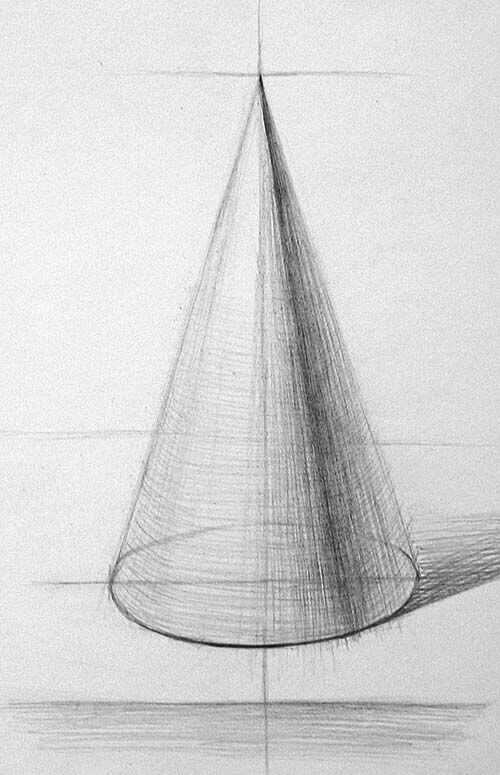
Именно это распределение света и тени смогут сделать конус объемным. Центр блика зависит от того, откуда идет освещение.

Штрихи идут по форме, при этом четких границ между светом и тенью отсутствует.

На занятиях наши педагоги рассказывают, каким образом правильно создавать рисунок конуса, проводят лекционные и практические группы.

Did you find apk for android? You can find new Free Android Games and apps.

Понятие конуса

Построим на плос-ти α окруж-ть L с центром в точке О. Далее через О проведем перпендикуляр к α и отметим на нем точку Р. Если мы отрезками соединим точку Р с каждой точкой окруж-ти L, то получим поверх-ть, которая именуется конической поверхностью. При этом:

• прямая ОР – это ось конической поверх-ти;
• прямые, соединяющие Р с точками на окруж-ти L, именуются образующими конической поверх-ти;
• сама точка Р – это вершина конической поверх-ти.

Объемное тело, ограниченное окруж-тью L и конической поверх-тью, именуется конусом. Соответственно вершина конической поверх-ти, её ось и образующие будут одновременно являться вершиной, осью и образующими конуса. Окруж-ть L – это основание конуса.

Ещё несколько терминов:

• коническая поверх-ть конуса именуется его боковой поверх-тью;
• если же к этой площади прибавить ещё и площадь основания, то в итоге получится полная площадь конуса;
• отрезок ОР – это не только ось конуса, но и высота конуса.

Как и в случае с цилиндром, мы в данном случае рассматриваем особый случай конуса – прямой круговой конус. В более общем случае ось конуса может не быть перпендикуляром к плос-ти основания (так называемый косой конус). Также в его основании может находиться не окруж-ть, а другая плоская фигура.

В общем случае любая пирамида может рассматриваться как частный случай конуса. Однако в рамках школьного курса под конусом подразумевается исключительно прямой круговой конус, если только не обговорено иное.

Докажем важное утверждение:

Действительно, рассмотрим две произвольные образующие РА и РВ у конуса с вершиной Р, у которой О – центр основания:

Так как ось ОР перпендикулярна основанию, то ∆РОА и ∆РОВ – прямоугольные. У них общий катет РО, а катеты АО и ОВ одинаковы как радиусы окруж-ти. Тогда ∆РОА и ∆РОВ равны, поэтому одинаковы и образующие РА и РВ, ч. т. д.

Заметим, что конус получается при вращении прямоугольного треуг-ка вокруг его катета. Так, на следующем рисунке конус получается при вращении ∆РОА с прямым углом О относительно катета РО:

Если сечение конуса проходит через его ось, то оно именуется осевым сечением. Ясно, что это сечение будет являться треуг-ком, причем две его стороны – это образующие конуса, а третья сторона диаметр основания. Образующие конуса одинаковы, поэтому осевое сечение будет равнобедренным треуг-ком.

Теперь рассмотрим сечение, параллельное плос-ти основания. Пусть оно пересекает ось РО в какой-то точке О₁. Также пусть А₁ – точка пересечения образующей АР исходного конуса с секущей плос-тью α:

Заметим, что раз ось РО перпендикулярна основанию, то она также будет перпендикулярна и секущей плос-ти, ведь основание и плос-ть α параллельны. Тогда ∠РО₁А₁ будет прямым.

Теперь рассмотрим ∠РОА и ∠РО₁А₁. Они прямоугольные и у них есть общие угол ∠АРО. Значит, это подобные треуг-ки. Обозначим радиус ОА как r, а длину А₁О₁ как r₁. Тогда из подобия получаем:

Рассмотрим теперь другую образующую ВР, которая пересекает секущую плос-ть в точке В₁. Отрезки АО и ОВ одинаковы. Повторяя предыдущие рассуждения, легко доказать подобие ∆РОВ и ∆РО₁В₁, откуда можно вычислить длину О₁В₁:

Получили, что точки А₁и В₁ находятся на одинаковом расстоянии r₁ от точки О₁. Мы выбрали точки А и В произвольно, поэтому для любых двух точек, принадлежащих сечению конуса, можно утверждать, что они равноудалены от точки О₁. Это значит, что все точки сечения лежат на окруж-ти с центром в точке О₁ и радиусом r₁, то есть сечение имеет форму окруж-ти.

Как определить площадь боковой поверхности конуса? Для этого ее надо «разрезать» вдоль одной из образующих и развернуть на плос-ти. В результате получится круговой сектор.

Напомним, что площадь сектора может быть рассчитана по формуле

Теперь обозначим длину образующей буквой l, а радиус основания конуса как r. Тогда

Для вычисления полной площади конуса к боковой поверх-ти необходимо добавить ещё и площадь основания:

Врезка конуса в куб вид снизу

Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса.

Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите

где S —площадь основания, а h — высота конуса. Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в

Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?

где S — площадь основания, а h — высота конуса. При уменьшении высоты в 3 раза объем конуса также уменьшится в 3 раза.

V=1/3Sh-это формула объёма пирамиды!

Она же формула объема конуса.

Уважаемый редактор! Условие данной задачи некорректно по причине, похожей на указанную для задания N 27137 (содержится в условии для этой задачи). В самом деле, высоту конуса можно уменьшить в 3 раза (вообще говоря, в n раз) : 1) полагая неизменным основание (радиус основания) конуса (на этом предположении и основано приведённое на сайте решение данной задачи); или 2) полагая неизменным телесный угол при вершине конуса: в данном случае параллельно основанию конуса проводится сечение, делящее высоту в отношении 1:3 (1:n), и получается отсечённый конус с высотой, уменьшенной в 3 раз (в n раз). Во втором случае, учитывая, что меньший конус подобен большему с коэффициентом 1/3, а объемы подобных тел относятся как куб коэффициента подобия, — объем меньшего конуса в 27 раз меньше объема большего конуса.

В добавление замечу, что возможен ещё третий случай, когда высота конуса уменьшается в 3 раза (вообще говоря, в n раз): если образующая не меняется. При этом изменяются телесный угол (увеличивается), а радиус основания (увеличивается), так как образующая, высота и радиус основания конуса соответствующим образом связаны теоремой Пифагора. В данном случае ответ будет соответствующим образом зависеть от соотношения между образующей и радиусом основании исходного конуса. Например, если у исходного конуса положить угол между образующей и плоскость основания равным 45 град., то, в результате несложных вычислений, мы получим объём конуса (с уменьшенной в 3 раза высотой и той же самой образующей): V2 = 17/27*V1 или V2/V1 = 17/27.

Аналитическое описание

Вертикальный круговой конус (двойной конус) с острием в начале координат и осью z в ​​качестве оси симметрии можно выразить уравнением

Икс2+у2знак равноР.2z2{\ displaystyle x ^ {2} + y ^ {2} = R ^ {2} z ^ {2}}

описывать. Число — это радиус высот кружков высот . Is уравнение упрощается до
Р.{\ displaystyle R}zзнак равно±1{\ displaystyle z = \ pm 1}Р.знак равно1{\ Displaystyle R = 1}

Икс2+у2знак равноz2{\ displaystyle x ^ {2} + y ^ {2} = z ^ {2}}

и в этом случае конус называется единичным конусом (аналог единичной окружности).

Подобно тому, как любой эллипс является , любой конус (как квадрика ) является аффинным образом единичного конуса . Простейшие аффинные отображения — это масштабирование координат. Масштабирование осей x и y приводит к конусам с уравнениями

Kаб:Икс2а2+у2б2знак равноz2;а,б>0.{\ displaystyle K_ {ab} \ двоеточие \, {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = z ^ {2}; \; \; a, b> 0.}

Векторы для параметрического представления эллиптического конуса

Вертикальные сечения таких конусов представляют собой эллипсы. Пересечение с плоскостью возвышения — это эллипс . Конус равен объединению всех прямых (образующих), проходящих через вершину и точки эллипса. Если эллипс описывается параметрическим представлением, а генераторы представлены в параметрической форме, получается следующее параметрическое представление конуса :
zзнак равно1{\ displaystyle z = 1}Э.Икс2а2+у2б2знак равно1{\ displaystyle E \ двоеточие {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1}Э.{\ displaystyle E}Икс→(т)знак равно(апотому что⁡т,бгрех⁡т,1){\ Displaystyle {\ vec {x}} (т) = (а \ соз т, б \ грех т, 1)}Kаб{\ displaystyle K_ {from}}

Kаб:Икс→(s,т)знак равноs⋅(апотому что⁡т,бгрех⁡т,1)Т;s∈Р.,0≤т

Уравнение конуса, расположенного где-либо в пространстве, дать сложно. С другой стороны, параметрическое представление любого конуса относительно просто:

Икс→(s,т)знак равноq→0+sж→1потому что⁡т+sж→2грех⁡т+sж→3; s∈Р.,0≤ т

Вот вершина конуса и три линейно независимых вектора. указывает в направлении оси конуса (см. рисунок). Для каждого постоянного параметра есть эллипс, с помощью которого можно представить (вместе с острием) генерируемый конус.
q→{\ displaystyle {\ vec {q}} _ {0}}ж→1,ж→2,ж→3{\ displaystyle {\ vec {f}} _ {1}, {\ vec {f}} _ {2}, {\ vec {f}} _ {3}}ж→3{\ displaystyle {\ vec {f}} _ {3}}s{\ displaystyle s}

Если три вектора попарно ортогональны и равны , то параметрическое представление описывает перпендикулярный круговой конус.
ж→1,ж→2,ж→3{\ displaystyle {\ vec {f}} _ {1}, {\ vec {f}} _ {2}, {\ vec {f}} _ {3}}|ж→1|знак равно|ж→2|{\ displaystyle | {\ vec {f}} _ {1} | = | {\ vec {f}} _ {2} |}

Тот факт, что любой эллиптический конус всегда содержит круги, показан в плоскости кругового сечения.

Врезка куба и конуса .geometric body inset

Врезка куба и цилиндра .geometric body insetПодробнее

Врезка куба с кубом и куба с пирамидой .Подробнее

врезка куба и конуса — Костромина Татьяна АлександровнаПодробнее

ТЕМА 6. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА ШЕСТИГРАННОЙ ПРИЗМЫ, ПИРАМИДЫ И КОНУСА.Подробнее

ТЕМА 4. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА: ШАР, КУБ, ЦИЛИНДРПодробнее

ТЕМА 7. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА. ПРОДОЛЖЕНИЕ.Подробнее

#1 как рисовать ВРЕЗКУ геометрических фигурПодробнее

врезка куб и цилиндр — Костромина Татьяна АлександровнаПодробнее

врезка куб и шар — Костромина Татьяна АлександровнаПодробнее

ВРЕЗКА из 4-х ГЕОМЕТРИЧЕСКИХ ТЕЛПодробнее

врезка куб в куб — Костромина Татьяна АлександровнаПодробнее

врезка куб и шестигранник — Костромина Татьяна АлександровнаПодробнее

Простые врезки Конус и кубПодробнее

Вступительные испытания по академическому рисунку в МГХПА им. С.Г. Строганова, 2020г. «Врезка».Подробнее

врезка куба и треугольной призмыПодробнее

врезка куб и пирамида — Костромина Татьяна АлександровнаПодробнее

Врезка геометрических тел. Часть 1.Подробнее

Развертка конуса или как построить развертку конусаПодробнее

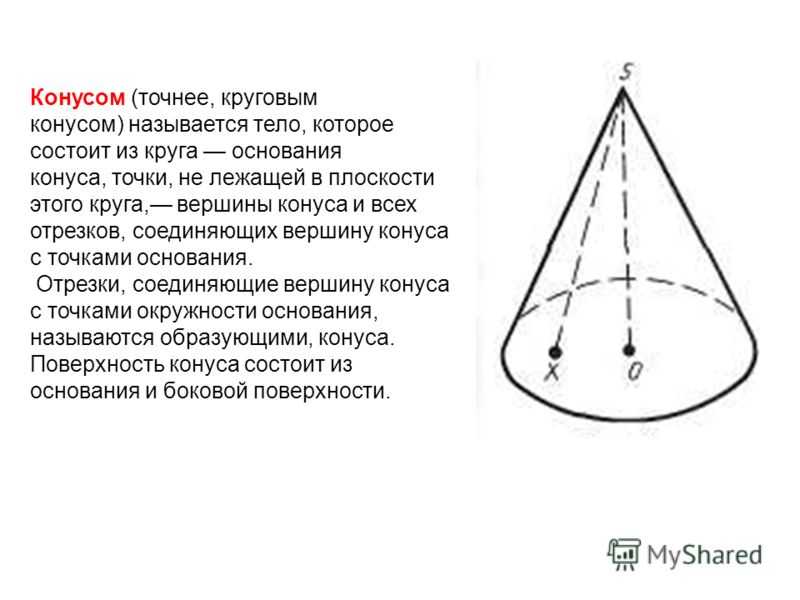
Презентация на тему: » Конусом (точнее, круговым конусом) называется тело, которое состоит из круга основания конуса, точки, не лежащей в плоскости этого круга, вершины конуса.» — Транскрипт:

2

Конусом (точнее, круговым конусом) называется тело, которое состоит из круга основания конуса, точки, не лежащей в плоскости этого круга, вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности.

3

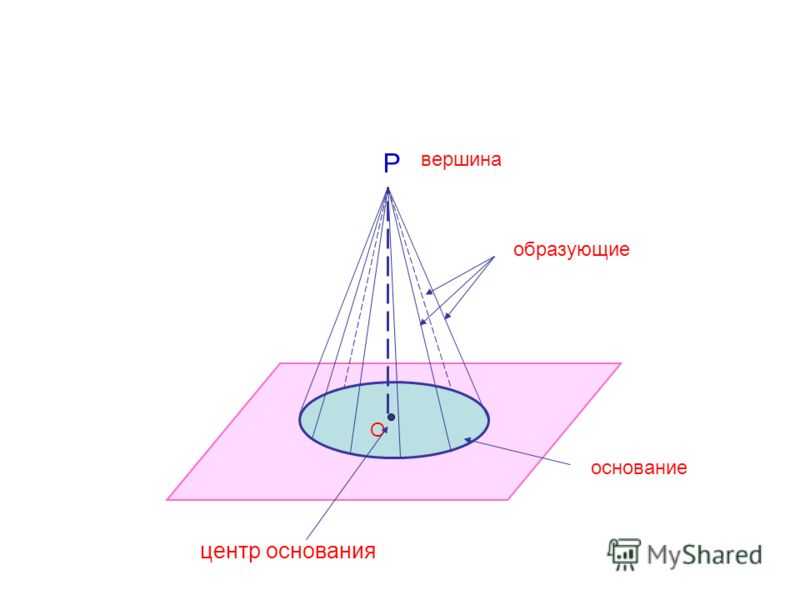
Р вершина образующие основание О центр основания

4

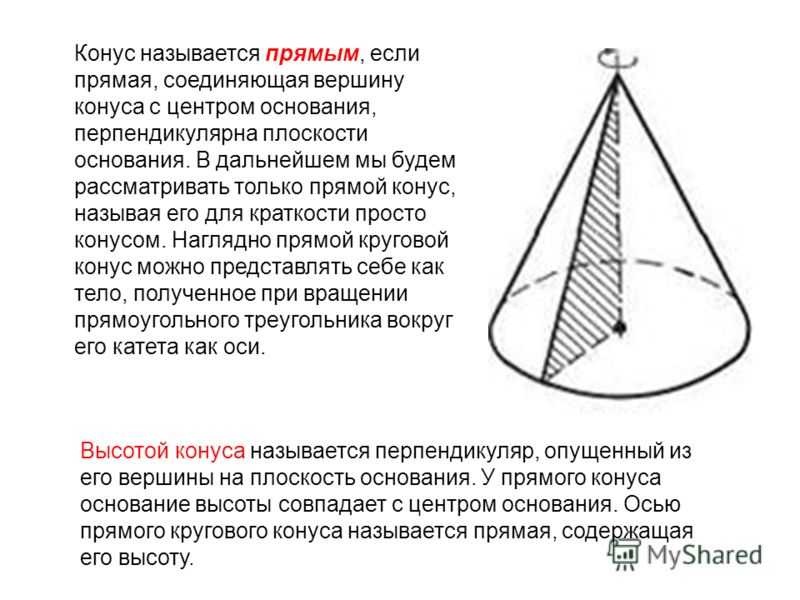
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом. Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.

5

Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 3). В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса (рис. 4). (рис. 3).(рис. 4)

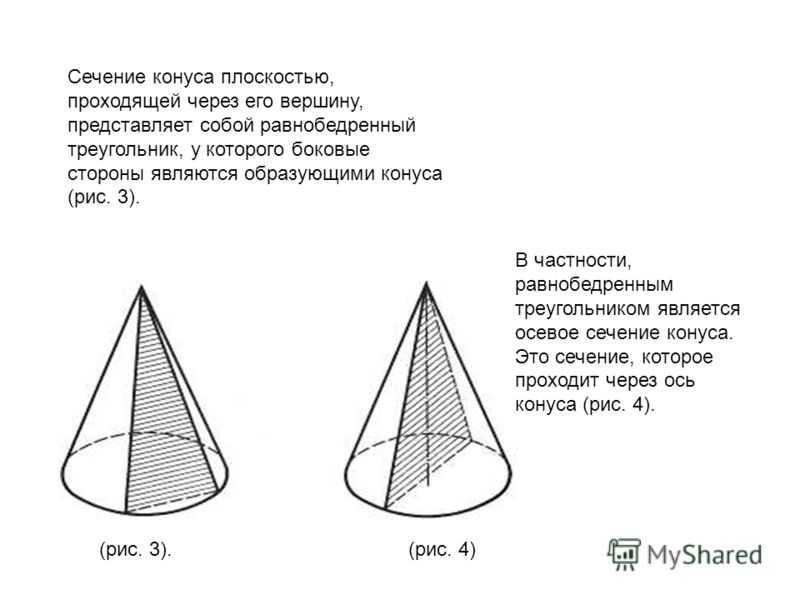
6

Усеченный конус Плоскость, перпендикулярная оси конуса, отсекает от него меньший конус. Оставшуюся часть называют усеченным конусом. Усеченный конус можно получить и как тело вращения. Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям. Круги O и O 1 — его основания, его образующие AA 1 равны между собой, прямая OO 1 — ось, отрезок OO 1 — высота. Его осевое сечение — равнобедренная трапеция.

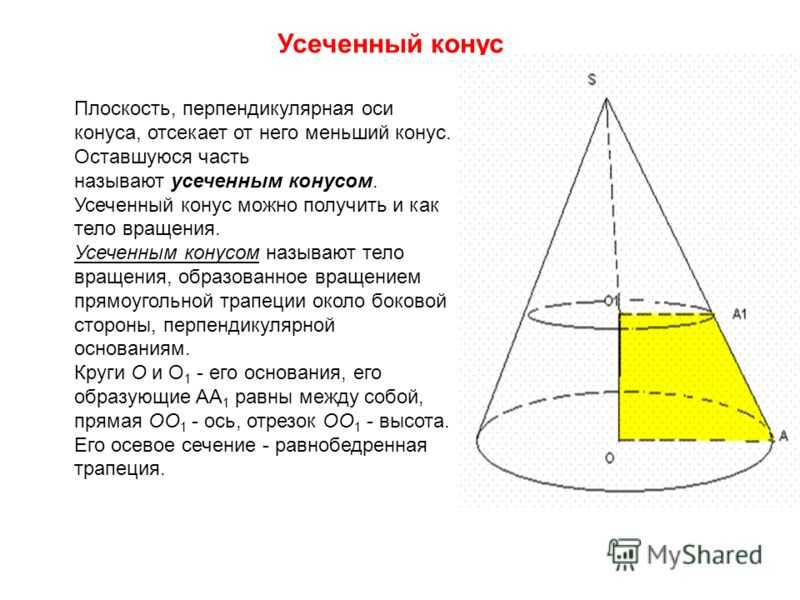
7

Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность — по окружности с центром на оси конуса. Доказательство. Пусть — плоскость, параллельная плоскости основания конуса и пересекающая конус (рис.5). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость с плоскостью основания, совмещает сечение конуса плоскостью с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса. Теорема доказана. (рис.5)

8

Площадь боковой поверхности усеченного конуса: $$S = \pi(R_{1} + R_{2}) \cdot l $$ Объем усеченного конуса: $$V = \frac{1}{3}\pi H(R^{2}_{1} + R_{1} \cdot R_{2} + R^{2}_{2})$$, где h — высота усеченного конуса; R 1,R 2 — радиусы верхнего и нижнего оснований; l — образующая.

9

Дополнительная информация о конусе 1.В геологии существует понятие «конус выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину. 2.В биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани. 3.«Конусами» называется семейство морских моллюсков подкласса переднежаберных. Раковина коническая (2–16 см), ярко окрашенная. Конусов свыше 500 видов. Живут в тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи. Раковины используются как украшения, сувениры.

10

Дополнительная информация о конусе 4.По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1 млн. жителей (чаще в южных странах). Этого бы не случалось, если бы везде были громоотводы, так как образуется конус безопасности. Чем выше громоотвод, тем больше объем такого конуса. Некоторые люди пытаются спрятаться от разрядов под деревом, но дерево не проводник, на нем заряды накапливаются и дерево может быть источником напряжения. 5.В физике встречается понятие «телесный угол». Это конусообразный угол, вырезанный в шаре. Единица измерения телесного угла – 1 стерадиан. 1 стерадиан – это телесный угол, квадрат радиуса которого равен площади части сферы, которую он вырезает. Если в этот угол поместить источник света в 1 канделу (1 свечу), то получим световой поток в 1 люмен. Свет от киноаппарата, прожектора распространяется в виде конуса.

Осевое сечение конуса и его площадь

Чтобы записать формулу площади осевого сечения конуса, необходимо сначала ознакомиться с самим сечением. Получается так: нужно взять секущую плоскость, расположить ее параллельно оси конуса. Затем необходимо разрезать конус плоскостью на две одинаковые части так, чтобы вершина фигуры попала в плоскость сечения.

Нетрудно представить, что в результате описанной операции получится равнобедренный треугольник. Равные стороны треугольника будут такими же, как длины образующих. А третья сторона будет равна диаметру основания.

Формула площади осевой части конуса (см рисунок выше) не сложна. Ему соответствует формула вычисления этого значения для описанного треугольника. Так как площадь треугольника равна произведению основания на высоту, которое нужно разделить пополам, то искомое равенство для осевого сечения будет иметь вид:

S = ч * г

Эта формула утверждает, что S в два раза больше площади прямоугольного треугольника, вращение которого было достигнуто конусом.

Врезка конуса и шестигранника

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку тела вращения и тела с наклонными гранями.

ПОСТАНОВКА ЗАДАНИЯ. Постройте врезку конуса и шестигранника.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

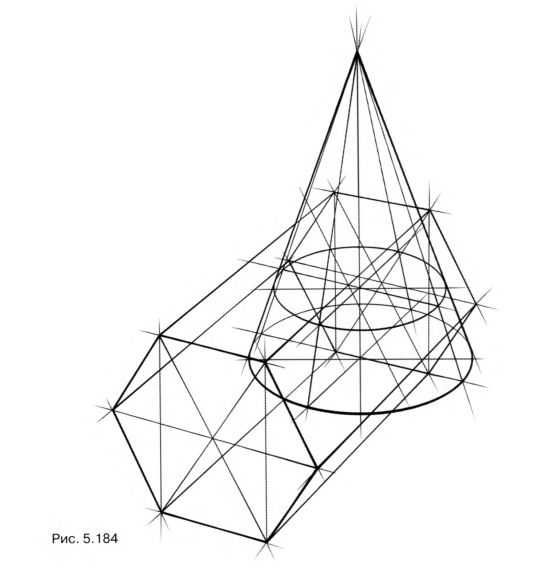
Изобразите вертикальный конус и горизонтальный шестигранник. Начните рисунок с куба (рис. 5.181). Его боковая грань послужит основой для построения основания шестигранника, а эллипс, вписанный в верхнее основание, поможет правильно определить раскрытие эллипса в основании конуса. Полученное изображение двух геометрических тел (рис. 5.182) может стать основой для создания разных связок. Представьте линию врезки. Сечение конуса верхней горизонтальной гранью призмы – окружность. Наклонная грань шестигранника рассекает конус по эллипсу. Осуществить такое построение вам поможет вспомогательная плоскость – шестиугольник на рис. 5.183.

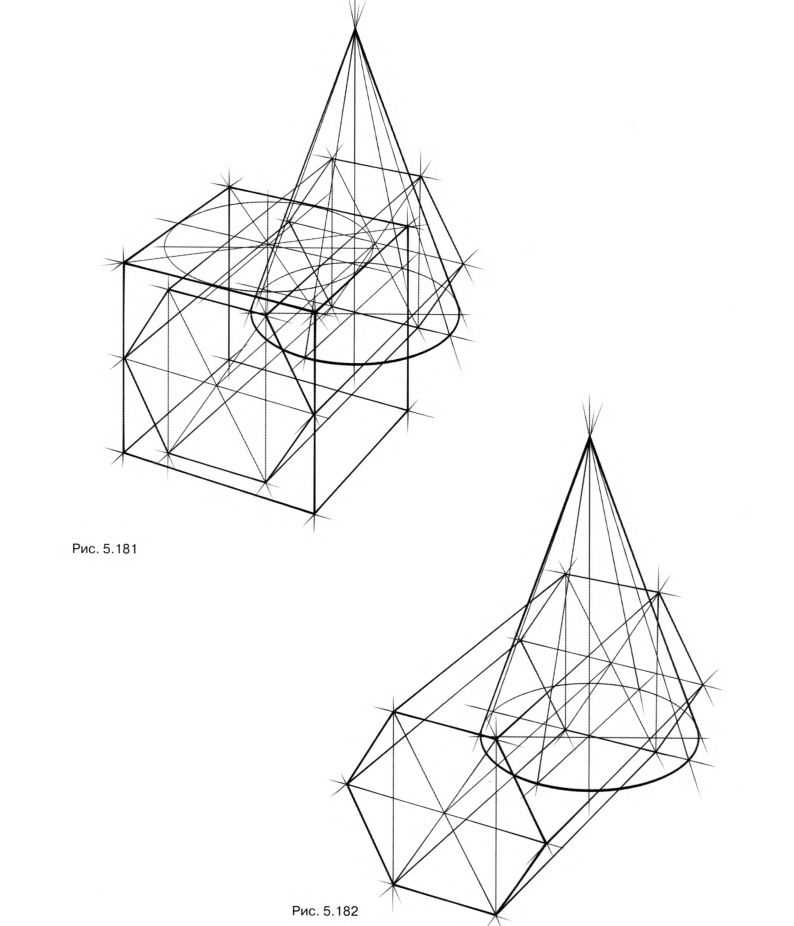
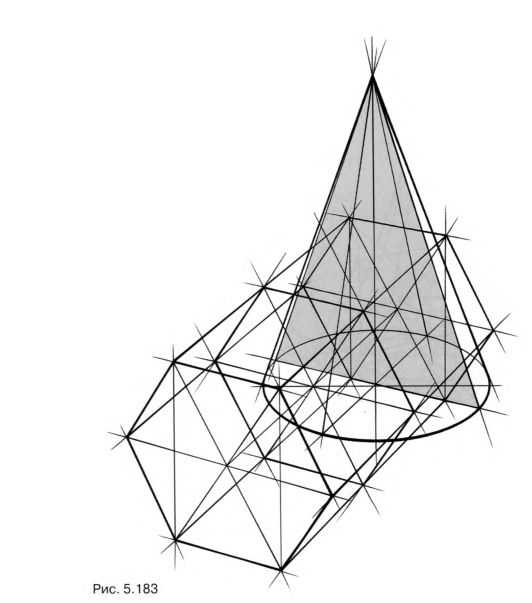
Она перпендикулярна плоскостям, рассекающим конус, и проходит через его вершину и центр окружности основания. Иначе можно сказать, что вспомогательная плоскость проходит через середину конуса, рассекает шестигранник и конус, образуя в сечении призмы – шестиугольник, а в сечении конуса – треугольник. Пересечение этих фигур определяет точки, необходимые для дальнейшего построения. Так, продлив верхнюю горизонтальную сторону шестиугольника, вы получите габариты и центр горизонтальной окружности сечения (рис. 5.184).

Продлив наклонную сторону шестиугольника, вы получите габариты наклонного эллипса сечения. На рис. 5.185 этот эллипс изображен полностью для пояснения построения, конус при этом можно продлить на столько насколько это нужно.

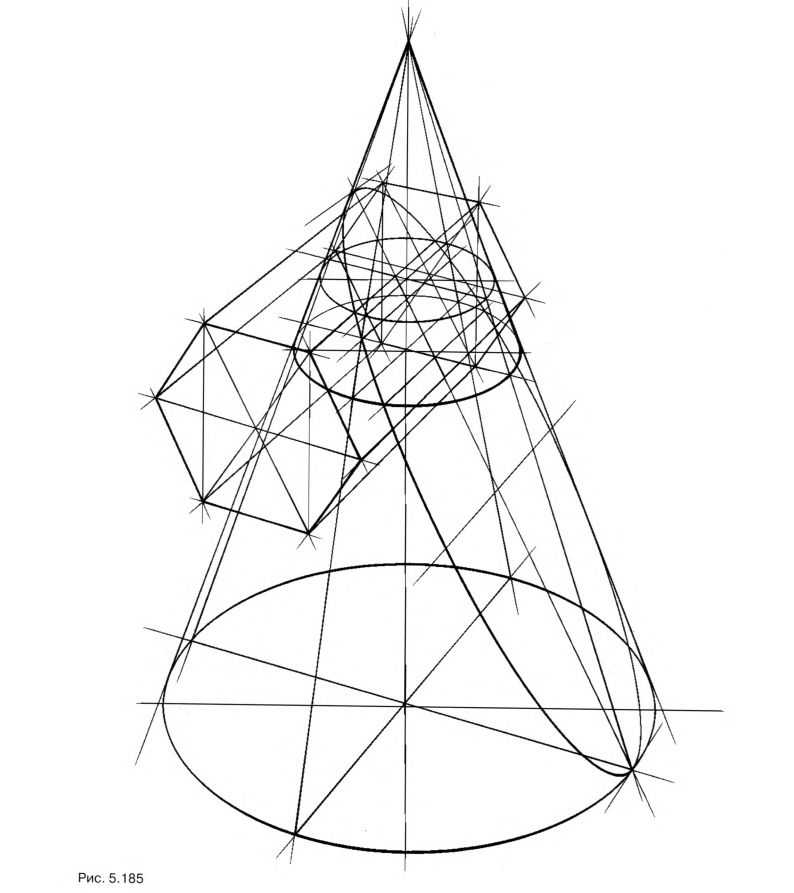
Вы в своей работе можете построить половину или только ту часть эллипса, которая является линией сечения. Изобразите линию пересечения шестигранника и конуса (рис. 5.186) и тонируйте связку (рис. 5.187).

Фундаментальная теория

Перед тем, как найти высоту конуса, необходимо разобраться с теорией.

Конус — фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.

Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.

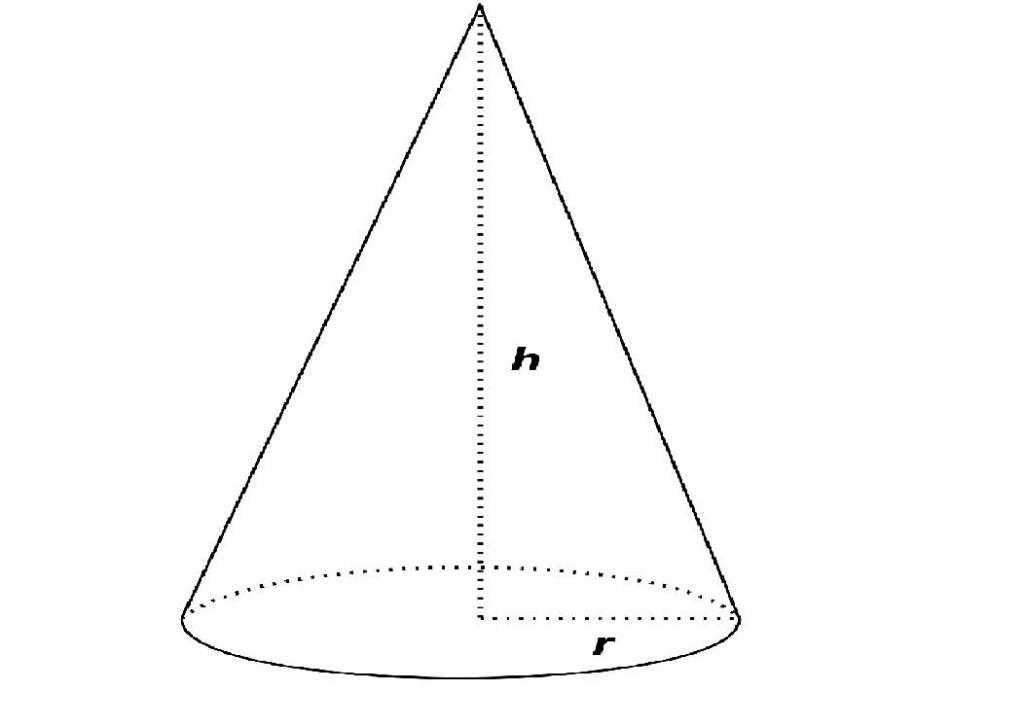
Ось — это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.

Если в основе лежит многоугольник, то объект является пирамидой.

Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.

Круговой конус

При все сечения конуса плоскостями становятся окружностями. Такой конус является фигурой вращения и называется прямым круговым конусом . Он может быть получен в результате вращения, например, прямой (образующей) вокруг оси аппликат (рис.4.44,б).

1. Конус является линейчатой поверхностью, поскольку может быть получен при помощи перемещения прямой.

2. Конус, образованный асимптотами гипербол, получающихся при пересечении гиперболоида плоскостями, проходящими через ось , называется асимптотическим конусом этого гиперболоида. На рис.4.44,в изображен асимптотический конус для однополостного и двуполостного гиперболоидов.

3. Конус (4.50) может быть получен из прямого кругового конуса (у которого ) в результате двух сжатий (растяжений) к координатным плоскостям и .

4. Начало канонической системы координат является центром симметрии конуса, координатные оси — осями симметрии конуса, координатные плоскости — плоскостями симметрии конуса.

В самом деле, если точка принадлежит конусу, то точки с координатами при любом выборе знаков также принадлежат конусу, поскольку их координаты удовлетворяют уравнению (4.50).

5. Рассмотрим сечение прямого кругового конуса плоскостями, не проходящими через его вершину, например, плоскостями , где — произвольная постоянная (параметр) — угловой коэффициент прямой в плоскости . Заметим, что образующие рассматриваемого конуса в плоскости описываются уравнением с угловым коэффициентом . Подставляя в уравнение конуса, получаем

Это уравнение проекции на координатную плоскость линии пересечения плоскости с конусом. Вычисляем инварианты

\tau\cdot\Delta=k^2-2 . По таблице 3.2 определяем, что рассматриваемое сечение, которое пересекает все образующие прямого кругового конуса, является эллипсом. При 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAVBAMAAADlb+D4AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAwAFBgwIcMaGw61tx0C5PF/kAAADbSURBVCjPY2DAD45D6Sasss4MDI7CQFoUXYIdIstq+ByLbHifAkQv4yJMWeaF66CyehNgsiUJcGklOais3QGYLLMEXJoJJutXkCEONZlZwgBNlklKffYSmL3sjQZosi9LWF7DXRXWuAlFlvltA1sBws1svRuQZVlerkxA8hGbL4os46KsCQhZti5Uk/Um8AqchsmyobvK7oDWhGkwH000gpqhcE8JLHuugGflBlhoFMBC8t27dw4gWTYGhjSovRVIIakE0QsEoTBXBWDGLxiI4op9PLLuUHoSFjkA6I4yBZZKaW0AAAAASUVORK5CYII=» style=»vertical-align: middle;» /> имеем . По таблице 3.2 определяем, что рассматриваемое сечение, которое параллельно двум образующим кругового конуса, является гиперболой. При имеем . По таблице 3.2 определяем, что рассматриваемое сечение, которое параллельно одной образующей кругового конуса, является параболой. Поскольку при аффинных преобразованиях тип линий не изменяется, такой же вывод можно сделать для произвольного конуса (4.50):

– сечение конуса плоскостью, пересекающей все его образующие, является эллипсом (рис.4.45,а);

– сечение конуса плоскостью, параллельной двум его образующим, является гиперболой (рис.4.45,б);

– сечение конуса плоскостью, параллельной одной его образующей, является параболой (рис.4.45,в).

6. Конические сечения могут быть взяты в качестве эквивалентных определений эллипса, гиперболы, параболы.

План-конспект урока геометрии в 11-м классе «Объем цилиндра»

Разделы: Математика

I. Вступительная часть.

Мы продолжаем встречи на уроках геометрии. Трудно не согласится со словами А.С. Пушкина «Вдохновение нужно в геометрии, как и в поэзии», ну а вас гуманитариев это чувство посещало уже не раз. И я желаю вам творческого вдохновения. И так в путь.

Как сказал мыслитель древности П. Рамус: «Геометрия это наука хорошо измерять». Мы продолжим сегодня измерять цилиндр и покажем, что целесообразно измерить в той или иной ситуации, и зачем это нужно делать.

II. Актуализация опорных знаний.

С элементами цилиндра мы уже знакомы, на столе у вас лежат тесты по названной теме. Он состоит из 10 заданий с выбором одного или нескольких правильных ответов из трех предложенных. Номер правильного ответа подчеркнуть ручкой. Исправления исключаются. Для работы с тестом выделяется 4 мин.

1. Какая фигура является основанием цилиндра:

а) окружность; б) круг; в) эллипс.

2. Назовите отрезок который является радиусом:

3. Укажите на рисунке образующую цилиндра:

4. Высота цилиндра это:

а) Расстояние между плоскостями его основания; б) отрезок, который соединяет две любые точки оснований; в) отрезок, который соединяет центр круга с любой точкой цилиндра.

5. Какая фигура является осью цилиндра?

6. Равносторонний цилиндр – это цилиндр, у которого:

а) образующая равна высоте; б) радиус основания равен высоте цилиндра; в) диаметр основания равен высоте цилиндра.

7. Масса тела вычисляется по формуле:

8. Буквой обозначают:

а) площадь; б) плотность; в) температуру.

9. Укажите номера правильных выражений:

10. Объем цилиндра вычисляется по формуле:

На экране вы видите кляч к тесту и критерий для самооценки своих знаний.

И поставьте оценку подпишите работы и сдайте.

III. Откроем тетради запишем: число, классная работа, тема урока «Объем цилиндра», и решим задачи.

При монтаже трубопровода по поверхности земли используются трубы размеры которой даны на рисунке. Размеры даны в см. Вычислить металла, который затратят на изготовление этой трубы. Проанализируем условие задачи и составим план решения.

Данное тело можно разбить на несколько цилиндров:

Запишите план решения этой задачи, а дома выполните вычисления.

Текст с рисунком на экране.

(фронтально) составим план решения задачи. Чтобы составить план решения проанализируем условие задачи:

При составлении плана решения задачи наши логические рассуждения запишем в обратном порядке:

Решение. (Самостоятельное решение)

Текст с рисунком на экране.

Для тренировки смекалки представьте себе такое вынужденное положение:

Необходимо, пользуясь только масштабной линейкой определить объем бутылки, которая частично наполнена жидкостью. Дно бутылки предполагается плоским. Выливать и доливать жидкость не разрешается.

V. Подведение итогов.

Давайте подведем итоги урока:

Тест с ответами: “Цилиндр”

1. Дан цилиндр, длина диаметра основания которого в два раза меньше длины образующей. Объем этого цилиндра равен 108п. Вычислите диаметр основания: а) 6 + б) 14 в) 12

2. Что представляет сечение цилиндра, проведенное плоскостью, перпендикулярно оси: а) овал б) круг + в) прямоугольник

3. Вычислите длину радиуса основания равностороннего цилиндра, площадь полной поверхности которого равна 24п: а) 48 б) 12 в) 2 +

4. Что представляет осевое сечение цилиндра: а) прямоугольник + б) треугольник в) овал

5. Объем цилиндра равен произведению площади … на высоту: а) стороны б) вершины в) основания +

6. Что представляет боковая поверхность цилиндра: а) треугольник б) прямоугольник + в) круг

7. Сечение, проходящее параллельно основаниям цилиндра, является: а) прямоугольником б) квадратом в) кругом +

8. Объем цилиндра равен 64π, а площадь боковой поверхности – 32π. Найдите площадь полной поверхности цилиндра, деленную на π: а) 64 + б) 72 в) 48

9. Цилиндр, осевым сечением которого является квадрат, называется: а) правильным круглым б) эллиптическим в) равносторонним +

10. Про прямые круговые цилиндры C1 и C2 известно, что у C1 радиус основания в два раза больше, чем у C2, но у C2 высота в три раза больше, чем у C1. Найдите отношение объёма цилиндра C2 к объёму C1: а) 1 б) 0,75 + в) 1,2

11. Если диаметр основания и образующая цилиндра равны друг другу, то осевым сечением является: а) квадрат + б) круг в) прямоугольник

12. В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 2,4 раза. Чему равен объем детали: а) 24 л б) 14 л + в) 12 л

13. Геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её: а) цилиндр + б) конус в) квадрат

14. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра: а) 1,20 б) 1,5 в) 1,25 +

15. Сечение, проходящее параллельно оси цилиндра, может быть: а) либо прямоугольником, либо квадратом + б) только квадратом в) только прямоугольником

16. В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого: а) 18 см б) 3 см + в) 9 см

17. Если диаметр основания и образующая цилиндра не равны друг другу, то осевым сечением является: а) квадрат б) круг в) прямоугольник +

18. В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали: а) 1100 см3 б) 1000 см3 + в) 100 см3

19. Вычислите длину высоты равностороннего цилиндра, площадь осевого сечения которого равна 25: а) 50 б) 12,5 в) 5 +

20. Пусть V, r, h соответственно объем, радиус и высота цилиндра. Найдите объем, если r=2√2 cм, h=3 см: а) 43π см3 б) 24π см3 + в) 31π см3

21. Сколько образующих можно провести в цилиндре: а) много + б) одну в) две

22. Радиус основания цилиндра равен 7, а высота – 10. Найдите площадь боковой поверхности цилиндра, деленную на π: а) 124 б) 140 + в) 104

23. Какой вид не может иметь сечение цилиндра: а) овал б) квадрат в) треугольник +

24. Шар вписан в цилиндр. Площадь поверхности шара равна 41. Найдите площадь полной поверхности цилиндра: а) 60 б) 61,5 + в) 55

25. Вращением какой геометрической фигуры можно получить цилиндр: а) прямоугольного треугольника вокруг гипотенузы б) прямоугольного треугольника вокруг катета в) прямоугольника вокруг одной из сторон +

26. Площадь боковой поверхности цилиндра равна 18π, а диаметр основания равен 9. Найдите высоту цилиндра: а) 4 б) 2 + в) 36

27. Площадь полной поверхности цилиндра: а) S=2п(r+h) + б) S= r(r+h) в) S=пr(r+h)

28. Поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей): а) поверхность основания цилиндра б) коническая поверхность в) цилиндрическая поверхность +

29. Площадь боковой поверхности цилиндра: а) S=пrh + б) S=2r в) S=r2

30. Отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка: а) сторона цилиндра б) высота цилиндра + в) вершина цилиндра

Элементы фигуры

Перед тем как привести формулу образующей конуса, следует пояснить, из каких элементов состоит рассматриваемая пространственная фигура, и какие геометрические понятия используются для ее описания.

Ориентируясь на предыдущий рисунок, можно сказать, что конус образован двумя поверхностями:

• конической, которая называется также боковой;
• плоской фигурой (круг на рисунке), которая называется основанием конуса.

В отличие от полиэдров, конус не имеет граней и ребер, однако у него имеется одна единственная вершина, которая сверху ограничивает коническую поверхность. На предыдущем рисунке вершина находится в начале координат.

Для рассматриваемой фигуры также используют понятия образующей и направляющей. Что такое образующая конуса, и что такое его направляющая. Начнем с определения последней. Направляющей является кривая, ограничивающая основание фигуры. Названа она так, поскольку вдоль нее движется образующая, описывая коническую поверхность. Направляющая часто называется директрисой.

Образующая — это прямой отрезок, который соединяет вершину фигуры и любую точку направляющей. Образующих у конуса бесконечное множество. Их совокупность определяет коническую поверхность. Образующую также называют генератрисой.

Уравнение конуса

Часто требуется при решении математических задач. Записывается в следующем виде:

где x0, y0,z0- координаты по соответствующим осям.

Таким образом, в данной статье были представлены основные сведения, которые могут понадобиться при решении задач на тему «Конус».

Составляющие конуса

Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.

Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.

Конус состоит из следующих элементов:

1. Круга, являющегося его основанием.
2. Боковой поверхности.
3. Точки, не лежащей в плоскости основания, называющейся вершиной конуса.
4. Отрезков, которые соединяют точки круга основания геометрического тела и его вершину.

Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.

Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.

Длина образующих в прямом конусе

Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.

То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:

l2 = r2+ h2 или l = √r2 + h2

где

• l – образующая;
• r – радиус;
• h – высота.

Образующая в наклонном конусе

Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.

Прежде всего необходимо знать высоту, длину оси и радиус основания.

Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:

r1= √k2 — h2

где

• r1 – это часть радиуса между осью и высотой;
• k – длина оси;
• h – высота.

В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r1), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:

R = r + r1

где

• R – катет треугольника, образованного высотой, образующей и частью диаметра основания;
• r – радиус основания;
• r1 – часть радиуса между осью и высотой.

Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:

l = √h2+ R2

или, не производя отдельно расчет R, объединить две формулы в одну:

l = √h2 + (r + r1)2.

Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу — использованию теоремы Пифагора.

Площадь поверхности

При изучении поверхности любой объемной фигуры удобно пользоваться ее разверткой на плоскость. Конус не является исключением. Для круглого конуса развертка показана ниже.

Мы видим, что развертка фигуры состоит из двух частей:

Круга, который образует основание конуса.
Сектора круга, являющегося конической поверхностью фигуры.

Площадь круга найти легко, и соответствующая формула известна каждому школьнику. Говоря о круговом секторе, заметим, что он является частью круга с радиусом g (длина генератрисы конуса). Длина дуги этого сектора равна длине окружности основания. Эти параметры позволяют однозначно определить его площадь. Соответствующая формула имеет вид:

S = pi*r2 + pi*r*g.

Первое и второе слагаемые в выражении — это конуса основания и боковой поверхности площади соответственно.

Если длина генератрисы g неизвестна, но дана высота h фигуры, тогда формулу можно переписать в виде:

S = pi*r2 + pi*r*√(r2 + h2).