Определение квадратного трехчлена

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .

Выполним чертеж:
Основные свойства функции :

Область определения: .

Область значений: .

Запись  обозначает: «любое действительное число, исключая ноль»

В точке  функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю справа.  При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось  является вертикальной асимптотой для графика гиперболы при .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы ,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: , то есть, если мы начнем уходить  по оси  влево (или вправо) на бесконечность, то  «игреки» стройным  шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .

Таким образом, ось  является горизонтальной асимптотой для графика функции, если «икс» стремится к плюс или минус бесконечности.

Функция  является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

График функции вида  () представляет собой две ветви гиперболы.

Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).

Если , то гипербола расположена во второй и четвертой координатных четвертях.

Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Пример 3

Построить правую ветвь гиперболы

Используем поточечный метод построения, при этом, значения  выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.

График квадратного трехчлена

Функция квадратного трехчлена называется квадратичной, а ее графиком является Парабола. Для того, чтобы ее построить, нужно решить квадратное уравнение, которое получается путем добавления знака “равно” и нуля в конце выражения. Мы подробно рассмотрели нахождение корней уравнения в отдельной публикации.

График имеет вершину:

Чтобы было понятнее, разберем алгоритм построения параболы на практических примерах.

Пример 1

Построим график квадратного трехчлена

Решение

Корнями уравнения являются -3 и -1. Т. е. Y принимает нулевые значения при X, равном двум этим числам. Другими словами, график пересекает ось абсцисс (Ox) в точках и.

Вершина параболы считается по формуле -b /2a. Так как коэффициент A – положительное число, следовательно, это будет ее минимум.
Мин. = -4 /(2 ⋅ 1) = -2

Полученное число – это значениеX, теперь подставляем его в нашу формулу и находим Y:
Y = (-2) 2 + 4 ⋅ (-2) + 3 = -1

Таким образом, вершина имеет координаты.

Остается только найти, в какой точке график пересекает ось ординат (0y). Для этого в формулу трехчлена вместо X подставляем число 0:
Y = (-0) 2 – 4 ⋅ 0 + 3 = 3

Следовательно, это точка с координатами.

Теперь у нас есть все необходимые данные, чтобы построить график.

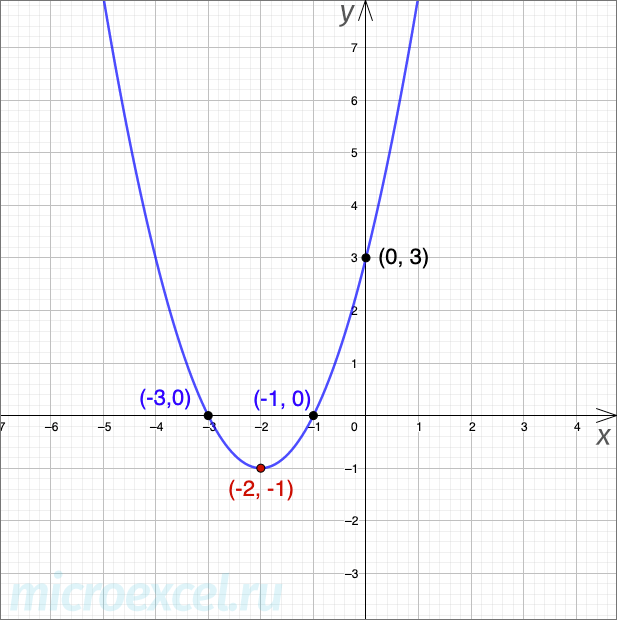
Примечание: Обратите внимание, что парабола – это симметричный график, т. е

если провести вертикальную линию через ее вершину, то правая часть будет зеркальным отражением левой (и наоборот).

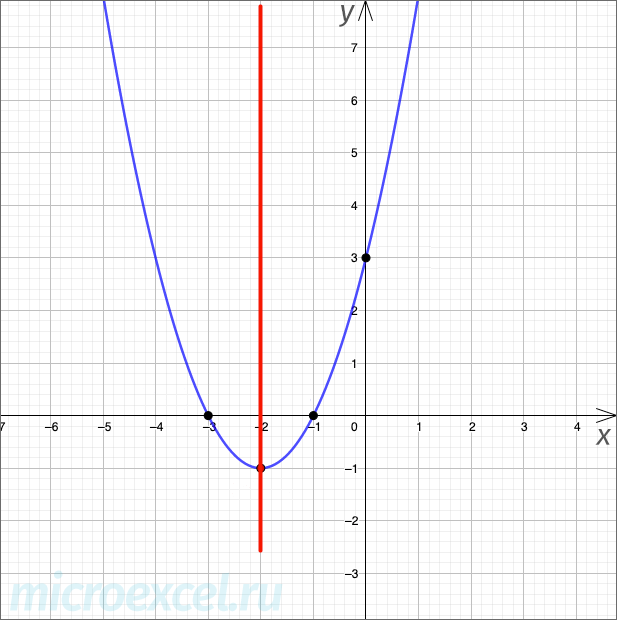
Пример 2

Построим параболу трехчлена

Решение

Уравнение имеет всего один корень. Следовательно, график не пересекает, а касается оси абсцисс в точке, которая одновременно является минимумом параболы (т. к. коэффициент A – положительный). Проверяем:
Мин. = 6 /(2 ⋅ 3) = 1 (это значение X)
Y = 3 ⋅ (1) 2 – 6 ⋅ 1 + 3 = 0

Теперь находим, в какой точке график пересекает ось Oy, подставив в формулу вместо X число 0:
Y = 3 ⋅ (0) 2 – 6 ⋅ 0 + 3 = 3

Значит, точка пересечения с осью ординат –

Строим параболу с учетом найденных точек:

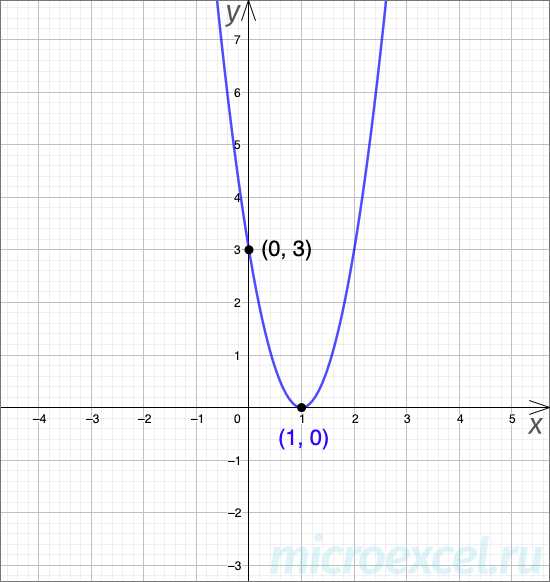
Пример 3

А так выглядит график квадратичной функции

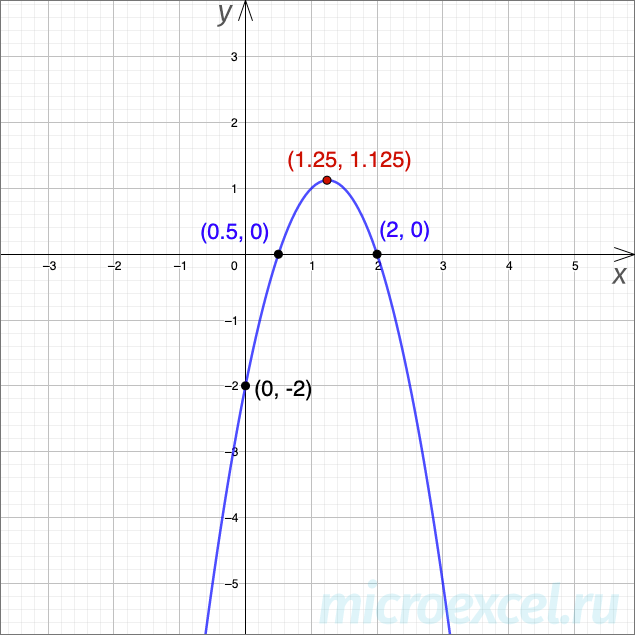
• Точки пересечения с осью Ox: и Так как A – отрицательное число, то максимум достигается в точке Пересечение с осью Oy – в точке

Публикации по теме:

• Факториал числа Показатель степени: определение и свойства Числа Фибоначчи Число Эйлера (e) Решение квадратных уравнений Определение логарифма, его свойства и график Степени натуральных чисел Формулы сокращенного умножения Свойства корней в степени n Производные логарифмов: формулы и примеры Производная функции: правила и формулы дифференцирования Нахождение производной степенной функции Логарифм деления (частного) или разность логарифмов Логарифм степени (коэффициент перед логарифмом) Логарифм корня (дробный коэффициент перед логарифмом) Логарифмическая функция Решение логарифмических неравенств Куб суммы: формула и примеры Куб разности: формула и примеры Сумма кубов: формула и примеры Разность кубов: формула и примеры Теорема Безу: нахождение остатка от деления многочлена на двучлен Обыкновенные (простые) дроби Правильные, неправильные и смешанные дроби Нахождение наибольшего общего делителя Основное свойство дроби Сокращение обыкновенных дробей Сложение обыкновенных дробей Вычитание обыкновенных дробей Нахождение дроби от числа и наоборот Понятие десятичной дроби Перевод десятичной дроби в обыкновенную Перевод обыкновенной дроби в десятичную Умножение десятичных дробей: правила, примеры Умножение обыкновенной дроби на десятичную: правило, примеры Сложение десятичных дробей: правила, примеры Вычитание десятичных дробей: правила, примеры Способы сравнения десятичных дробей Округление десятичных дробей: правила, примеры Сравнение модулей действительных чисел Модуль комплексного числа z: определение, свойства Решение уравнений с модулем Решение неравенств с модулем Что такое среднее арифметическое чисел: двух, трех, четырех и тд Алгебраическая сумма Правила раскрытия скобок с примерами Тождество и тождественные выражения Тождественные преобразования выражений Именные названия степеней тысячи Что такое линейная функция: определение, формула, график

Теперь находим, в какой точке график пересекает ось Oy, подставив в формулу вместо X число 0:
Y = 3 ⋅ (0) 2 – 6 ⋅ 0 + 3 = 3

Что такое квадратный трехчлен: определение, формула, график, примеры

В данной публикации мы рассмотрим, что такое квадратный трехчлен, а также приведем его формулу и разберем алгоритм построения графика (параболы). Представленная информация сопровождается практическими примерами для лучшего восприятия.

скрыть

Задания на соответствие графика и формулы функции.

Задания на соответствие графика и формулы функции легче и быстрее решаются с использованием свойств изученных функций, о которых было написано выше. Если график функции в задании изображен на клеточках, и указан масштаб координатных осей, то возможен второй способ решения, который я условно называю «по единичке». Способ заключается в том, что (x = 1) подставляем в приведенные формулы, вычисляем соответствующие значения (y). Затем на графиках находим точки с абсциссой (x = 1) и отмечаем их ординаты. Сравниваем отметки на графиках с вычислениями по формулам и делаем выводы. К сожалению, этот способ работает не всегда. В части задач отсутствуют клеточки, в некоторых масштаб таков, что на графике не видна точка с ординатой (y(1)), она расположена или слишком высоко для рисунка или слишком низко. Нередко бывает так, что значения (y(1)), вычисленные по разным формулам, совпадают. Приходится брать одно или несколько других значений (x), что затрудняет вычислительную часть и увеличивает временные затраты на это задание. Поэтому способ «по единичке» я рекомендую для проверки ответа или выбора из двух сомнительных вариантов.

Задачи, в которых приведены графики функций разных типов, я считаю самыми лёгкими в этом задании. Давайте рассмотрим несколько примеров, и вы в этом убедитесь.

Задача 1. Установите соответствие между графиками функций и формулами, которые их задают

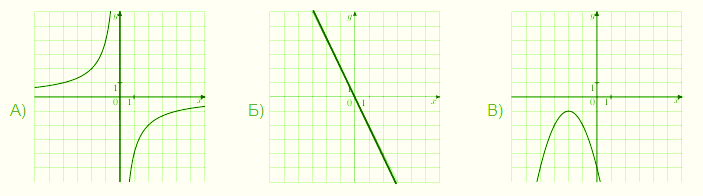
На рисунке всего один график прямая линия. Ищем среди формул ту, которая содержит (x) только в первой степени. Смотрим, чтобы в этой формуле не было квадрата и переменной в знаменателе. Такая формула только одна, это формула (3); y=-2x). Делаем вывод: графику Б) соответствует формула 3).

Среди формул только одна содержит (x^2) (формула 4), и только один график непрерывная кривая линия симметричная относительно вертикальной прямой, проведенной через её вершину. Это парабола – график В). Вывод: графику В) соответствует формула 4).

Остался один график с разрывом. Две отдельных ветви содержит график А) – гипербола. Но у нас две формулы с (x) в знаменателе. Придётся выбирать. На графике А) ветви гиперболы расположены во второй и четвёртой координатных четвертях, где знаки координат (x и y) не совпадают, поэтому перед дробью в формуле гиперболы должен быть знак минус. Но оказалось, что этой приметы недостаточно, так как минус есть в обеих формулах.

Ответы и решения некоторых задач временно скрыты. Это задачи для самостоятельного решения. Чтобы посмотреть ответы, воспользуйтесь соответствующими кнопками. Но предварительно попробуйте решить задачу самостоятельно.

Задача 2. Установите соответствие между функциями и их графиками.

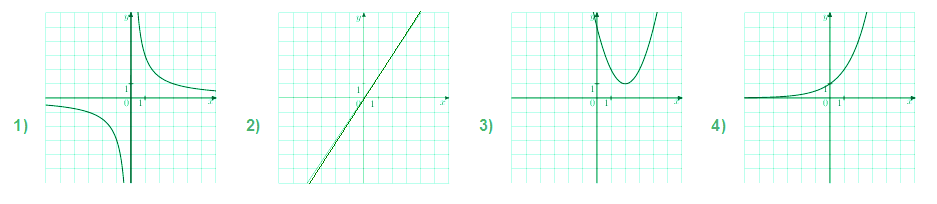
На графике 1) линия с разрывом, следовательно в формуле есть (x) в знаменателе. Вывод: графику 1) соответствует формула А).

Два оставшихся графика нелинейны, т. кривые линии. Формула Б) представляет собой квадратный трёхчлен. Следовательно, график должен быть параболой. Мы знаем, что парабола симметрична относительно линии, проходящей через вершину. График 3) обладает этим свойством, а на графике 4) такую линию провести невозможно. Вывод: формула Б) соответствует графику 3).

Замечение. Проверку ответа можно сделать «по единичке», т. задать какое-либо значение (x), подставить его в формулы, вычислить значения (y) и найти соответствующие точки на графике. Но решить задание в буквальном смысле по единичке, т. подставить (x = 1) в формулу Б), а затем найти на графиках 3) и 4) ординаты точек с абсциссой 1, не получится. Потому что во всех случаях будет (y = 2). Выбор не состоится.

Задача 3. Установите соответствие между графиками функций и формулами, которые их задают.

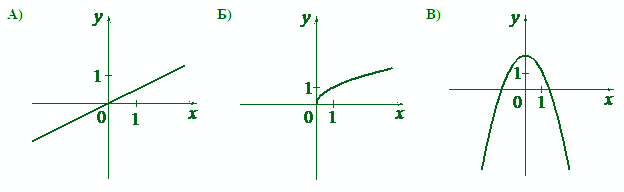
Координатные плоскости здесь представлены без клеточек. Проверить принадлежность точек не получится, выбираем только по внешнему виду графиков.

Прямая линия олна – А). Её формула 1) содержит просто (x). Симметричная кривая на графике В) – парабола. Формула 2) содержит (x^2). На среднем графике кривая линия похожа на перевёрнутую половинку параболы. Это график функции 3) квадратный корень.

Решение квадратного уравнения

Найти решение квадратного уравнения, если оно полное, достаточно тяжело. Нам поможет формула :

(а + b)2 = a2 + 2ab + b2

Напомним, что с ее помощью можно разложить на множители некоторые квадратные полиномы:

х2 + 8х + 16 = х2 + 2•4•х + 42 = (х + 4)2

Конечно, здесь нам повезло с квадратным трехчленом – его коэффициенты позволяли воспользоваться формулой квадрата суммы. Однако похожие преобразования можно выполнить и тогда, когда коэффициенты не такие удобные:

х2 + 8х + 20 = х2 + 8х + 16 + 4 =(х2 + 8х + 16) + 4 = (х2 + 2•4•х + 42) + 4 =

= (х + 4)2 + 4

Здесь мы разложили число 20 на сумму 16 + 4, чтобы можно было часть выражения «свернуть» формулой квадрата суммы. Такой прием можно применить вообще к любому квадратному трехчлену:

4х2 + 10х + 4 = (2х)2 + 2•2х•2,5 + 2,52 – 2,52 + 4 = (2х + 2,5)2 – 2,52 + 4 =

= (2х + 2,5)2 – 6,25 + 4 = (2х + 2,5)2 – 2,25

Здесь мы добавили к трехчлену слагаемое 2,52 и тут же его отняли. Оно было необходимо для получения формулы квадрата суммы.

Отметим, что подобное свертывание можно использовать для решения квадратного уравнения. Действительно, пусть дано уравнение

4х2 + 10х + 4 = 0

Выше мы уже преобразовали трехчлен, стоящий слева. Произведем замену:

(2х + 2,5)2 – 2,25 = 0

Имеем уравнение, очень похожее на неполное, где отсутствует коэффициент b. Попробуем его решить аналогичным путем:

Из этой записи мы получили два линейных уравнения:

2х + 2,5 = – 1,5 или 2х + 2,5 = 1,5

Решая их, находим два корня:

2х = – 1,5 – 2,5 или 2х = 1,5 – 2,5

2х = – 4 или 2х = – 1

х = – 2 или х = – 0,5

Аналогично можно решить и любое другое полное квадратное уравнение. Однако проще пользоваться специальными формулами, в которые надо подставлять значения коэффициентов a, b, с и получать корни квадратного уравнения. Выведем эти формулы.

Пусть есть уравнение

ах2 + bх + с = 0

Поделим обе части уравнения на коэффициент а:

Далее надо выделить квадрат суммы, что бы потом свернуть его по формуле сокращенного умножения:

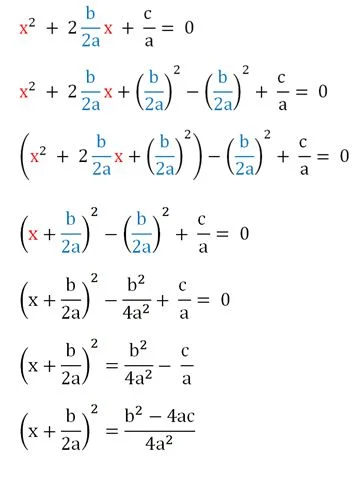
Далее обозначим числитель в правой части (b2 – 4ac) буквой D. Эту величину называют дискриминантом квадратного уравнения.

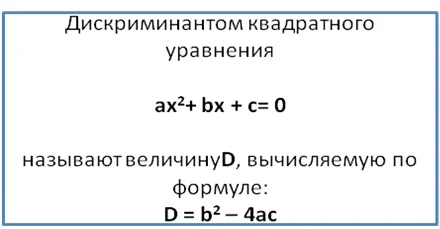
Перепишем уравнение с учетом этой замены:

Далее рассмотрим три случая:

1. D< 0. Если D отрицателен, то и вся дробь справа меньше нуля (так как в знаменателе стоит 4а2 – заведомо положительное число). Слева стоит квадрат выражения, а он никак не может оказаться отрицательным. В итоге имеем, что при отрицательном дискриминанте у уравнения отсутствуют корни.
2. D = 0. При таком варианте справа получается ноль:

Квадрат только одного числа равен нулю – самого нуля, поэтому

Итак, при нулевом дискриминанте у уравнения есть только один корень.

3. D> 0. В этом варианте дробь справа оказывается положительным числом, а потому у нее есть два квадратных корня. Решение будет выглядеть так:

Полученное выражение называют основной формулой корней квадратного уравнения.

Если дискриминант – положительное число, то уравнение существует два корня. Для вычисления первого из них надо в формуле квадратного уравнения вместо знака ± поставить минус, а для вычисления второго – знак плюс. Часто 1-ый корень обозначают как х₁, а 2-ой – как х₂. Заметим, что если D = 0, то при подстановке в основную формулу будет получаться один и тот же корень независимо от выбора знака плюс или минус.

Пример. Решите уравнение

2х2 – 5х – 3 = 0

Решение. Выпишем коэффициенты уравнения

a = 2

b = – 5

c = – 3

Вычислим значение дискриминанта:

D = b2 – 4ас = (– 5)2 – 4•2•(– 3) = 25 + 24 = 49

Так как он больше нуля, то должно получиться два корня. Их можно найти по основной формуле квадратного уравнения:

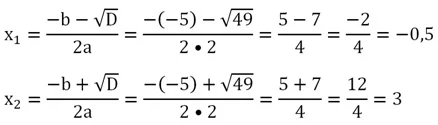
Ответ: – 0,5; 3

Пример. Найдите все корни уравнения

3х2 + 6х + 5 = 0

Решение. Найдем дискриминант:

D = b2 – 4ас = 62 – 4•3•5 = 36 – 60 = – 24

Дискриминант оказался отрицательным, значит, и корней у уравнения нет.

Ответ: нет корней.

Пример. Найдите значения х, при которых выполняется равенство

4х2 – 12х + 9 = 0

Решение. Вычислим дискриминант:

D = (– 12)2 – 4•4•9 = 144 – 144 = 0

Так как D = 0, существует лишь один корень:

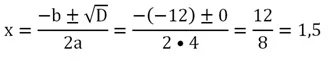
Ответ: 1,5

Пример. Найдите значения у, при которых справедливо равенство

2у2 + 4у + 9 = у2 + 11у + 3

Решение. На первый взгляд это уравнение не похоже на изучавшие до этого квадратные уравнения. Однако слагаемые, записанные справа, можно перенести влево, после чего можно будет привести подобные слагаемые:

2у2 + 4у + 9 = у2 + 11у + 3

2у2 + 4у+ 9–у2– 11у– 3 = 0

у2 – 7у + 6 = 0

Получили классическое квадратное уравнение, для которого можно рассчитать дискриминант: D = b2 – 4ас = (– 7)2 – 4•1•6 = 49 – 24 = 25

Найдем значения двух корней:

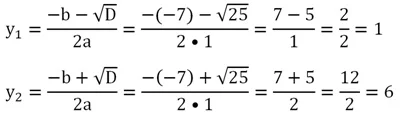
Ответ: 1; 6

Как строить параболу по квадратному уравнению

Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам

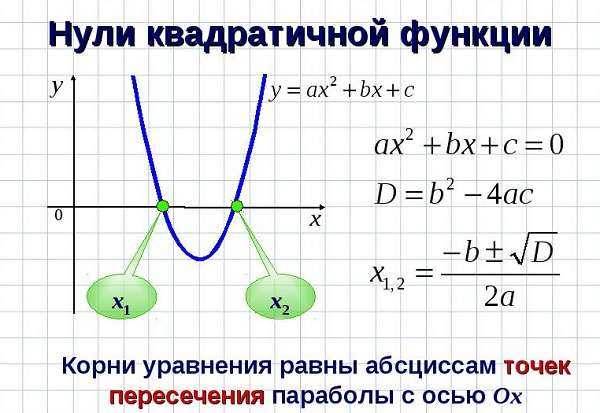
Анализируя выражения и уравнения, можно увидеть следующее:

1. Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
2. Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.

Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:

D = (b2 4 * a * c).

Для этого нужно приравнять выражение к нулю.

Наличие корней параболы зависит от результата:

• D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
• D = 0, то х1, 2 = -b / (2 * a),
• D ˂ 0, то нет точек пересечения с вектором ОХ.

Получаем алгоритм построения параболы:

• определить направление ветвей,
• найти координаты вершины,
• найти пересечение с осью ординат,
• найти пересечение с осью абсцисс.

Пример 1.

Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:

1. а = 1, следовательно, ветви направлены вверх,
2. координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
3. с осью ординат пересекается в значении у = 4,
4. найдем дискриминант: D = 25 — 16 = 9,
5. ищем корни:

• Х1 = (5 + 3) / 2 = 4, (4, 0),
• Х2 = (5 — 3) / 2 = 1, (1, 0).

По полученным точкам можно построить параболу.

Пример 2.

Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:

1. а = 3, следовательно, ветви направлены вверх,
2. координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
3. с осью у будет пересекаться в значении у = -1,
4. найдем дискриминант: D = 4 + 12 = 16. Значит корни:

• Х1 = (2 + 4) / 6 = 1, (1,0),
• Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).

По полученным точкам можно построить параболу.

Геометрический смысл параметра в уравнении параболы

Поясним геометрический смысл параметра в каноническом уравнении параболы. Подставляя в уравнение (3.51), получаем, т.е.. Следовательно, параметр равен половине длины хорды параболы, проходящей через ее фокус перпендикулярно оси параболы.

Фокальный параметр параболы, а также эллипса и гиперболы составляет половину длины струны, которая проходит через ее фокус перпендикулярно фокальной оси (см. Рис. 3.45, c). Из уравнения параболы в полярных координатах получаем, что параметр параболы совпадает с ее фокальным параметром.

• Параметр параболы характеризует ее форму. Чем больше, чем шире ветви параболы, чем ближе к нулю, тем уже ветви параболы (рис. 3.46).
• Уравнение (в) определяет параболу, которая лежит слева от оси ординат (рис. 3.47, а). Это уравнение сводится к каноническому изменением направления оси абсцисс (3.37). На рис. 3.47, а показаны заданная и каноническая системы координат .
• Уравнение определяет параболу с вершиной, ось которой параллельна оси абсцисс (рис. 3.47.6). Это уравнение сводится к каноническому с помощью параллельного переноса (3.36).

Уравнение также определяет параболу с вершиной, ось которой параллельна оси ординат (рис. 3.47, c). Это уравнение сводится к каноническому за счет параллельного переноса (3.36) и переименования осей координат (3.38). На рис. 3.47, б, в показаны заданные системы координат и канонические системы координат .

График квадратного трехчлена представляет собой параболу с вершиной в точке, ось которой параллельна оси ординат, ветви параболы направлены вверх (в) или вниз (в). Фактически, выделив полный квадрат, мы получим уравнение

что сводится к канонической форме, где, используя замену и .

Знак выбирается так, чтобы он совпадал со знаком основного коэффициента. Эта замена соответствует композиции: параллельный перенос (3.36) с помощью и, переименование осей координат (3.38), а в случае изменения направления оси координат (3.37). На рис. 3.48, а, б показаны указанные системы координат и канонические системы координат для случаев и соответственно.

Ось абсцисс канонической системы координат является осью симметрии параболы, поскольку изменение переменной на не меняет уравнение (3.51). Другими словами, координаты точки, принадлежащей параболе, и координаты точки, симметричной точке относительно оси абсцисс, удовлетворяют уравнению (3.S1). Оси канонической системы координат называются главными осями параболы.

Пример 3.22. Нарисуйте параболу в канонической системе координат. Найдите параметр фокуса, координаты фокуса и уравнение направляющей.

Решение. Строим параболу с учетом ее симметрии относительно оси абсцисс (рис. 3.49). При необходимости определяем координаты некоторых точек параболы. Например, подставив параболы в уравнение, мы получим. Следовательно, точки с координатами принадлежат параболе.

Сравнивая данное уравнение с каноническим (3.S1), определяем фокальный параметр:. Координаты фокуса, например… Составим уравнение директрисы, т.е.

Что называют квадратичной функцией

Запомните!

Квадратичная функция — это функция вида

y = ax2 + bx + c,

где

a

,

b

и

с

— заданные числа.

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит «x» — это «2», то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a», «b» и «с».

Квадратичная функция	Коэффициенты
y = 2×2 − 7x + 9	a = 2 b = −7 с = 9
y = 3×2 − 1	a = 3 b = 0 с = −1
y = −3×2 + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Запомните!

График квадратичной функции называют параболой.

Парабола выглядит следующим образом.

Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции.Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x2 −7x + 10».

1. Направление ветвей параболы
   Запомните!

   Если «a > 0», то ветви направлены вверх.

   Если «a », то ветви направлены вниз.

   В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.

2. Координаты вершины параболы
   Запомните!

   Чтобы найти «x0» (координата вершины по оси «Ox») нужно использовать формулу:

   Найдем «x0» для нашей функции «y = x2 −7x + 10».

   Теперь нам нужно найти «y0» (координату вершины по оси «Oy»). Для этого нужно подставить найденное значение «x0» в исходную функцию.Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».

   y0(3,5) = (3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 = −12,25 + 10 = −2,25

   Выпишем полученные координаты вершины параболы.

   (·) A (3,5; −2,25) — вершина параболы.

   Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси «Oy».

3. Нули функции

   Для начала давайте разберемся, что называют нулями функции.

   Запомните!

   Нули функции — это точки пересечения графика функции с осью «Ox» (осью абсцисс).

   Наглядно нули функции на графике выглядят так:

   Свое название нули функции получили из-за того, что у этих точек координата по оси «Oy» равна нулю.

   Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

   Запомните!

   Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо «y = 0».

   Подставим в заданную функцию «y = x2 −7x + 10» вместо «y = 0» и решим полученное квадратное уравнение относительно «x» .

   0 = x

   2

   −7x + 10

   x

   2

   −7x + 10 = 0

   x

   1;2

   =

   7 ± √49 − 4 · 1 · 10

   2 · 1

   x

   1;2

   =

   x

   1;2

   =

   x1 =	x2 =
   x1 =	x2 =
   x1 = 5	x2 = 2

   Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью «Ox». Назовем эти точки и выпишем их координаты.

   • (·) B (5; 0)
   • (·) C (2; 0)

   Отметим полученные точки («нули функции») на системе координат.

4. Дополнительные точки для построения графика

   Возьмем четыре произвольные числовые значения для «x». Целесообразно брать целые числовые значения на оси «Ox», которые наиболее близки к осисимметрии. Числа запишем в таблицу в порядке возрастания.

   Для каждого выбранного значения «x» рассчитаем «y».

   • y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 = 4
   • y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 = −2
   • y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 = −2
   • y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 = 4

   Запишем полученные результаты в таблицу.

   Отметим полученные точки графика на системе координат (зеленые точки).

   Теперь мы готовы построить график.На забудьте после построения подписать график функции.

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции.Только теперь запишем алгоритм построения коротко без подробностей.

Пусть требуется построить график функции «y = −3×2 − 6x − 4».

1. Направление ветвей параболы «

a = −3» — ветви параболы направлены вниз. Координаты вершины параболы

x0 = x0 = = = −1

y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1

(·) A (−1; −1)

— вершина параболы.

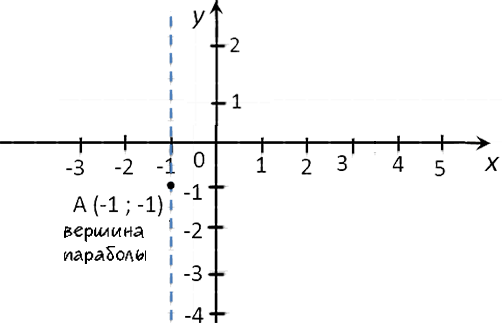Нули функции

Точки пересечения с осью «Ox» (y = 0).

0 = −3×2 − 6x − 4

−3×2 − 6x − 4 = 0 |·(−1)

3×2 + 6x + 4 = 0

x1;2 =

−6 ± √62 − 4 · 3 · 4

2 · 1

x1;2 = x1;2 =

Ответ: нет действительных корней.

Так как корней нет, значит, график функции не пересекает ось «Ox».

Вспомогательные точки для: «x = −3»; «x = −2»; «x = 0»; «x = 1». Подставим в исходную функцию «y = −3×2 − 6x − 4».

• y(−3) = −3 · (−3)2 − 6 · (−3) − 4 = −3 · 9 + 18 − 4 = −27 + 14 = −13
• y(−2) = −3 · (−2)2 − 6 · (−2) − 4 = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4
• y(0) = −3 · 02 − 6 · 0 − 4 = −4
• y(1) = −3 · 12 − 6 · 1 − 4 = −3 −6 − 4 = −13

x	−3	−2	1
y	−13	−4	−4	−13

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки «(−2; −4)» и «(0; −4)». Построим и подпишем график функции.

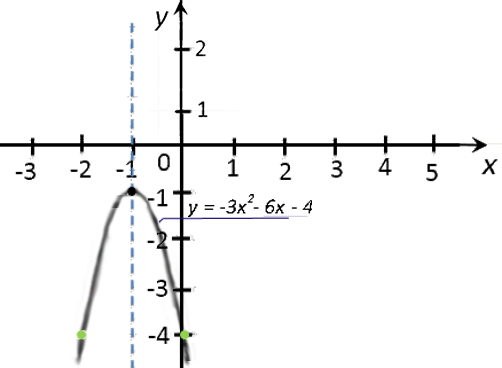
Изученные функции и их графики.

(y = x)

(y = x^2)

(y = 2x^2+4x-1)

К концу учебного года в 9-ом классе вы успели изучить следующие функции:

(y = kx+b) — линейная функция. Графиком является прямая линия. Коэффициент (k) задаёт тангенс угла наклона к оси (Ox). Если (k&gt;0), прямая наклонена под острым углом к оси, если (k&lt;0) – под тупым углом. При (k=0) формула приобретает вид (y = b), а график становится параллельным оси абсцисс (оси (Ox)). Коэффициент (b) «отвечает» за точку пересечения прямой с осью ординат (ось (Oy)).

Ещё подробнее повторить графики функций вы сможете, если перейдёте к сводной таблице и воспользуетесь помещенными там ссылками на другие статьи сайта и видео на youtube-канале Mathematichka.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

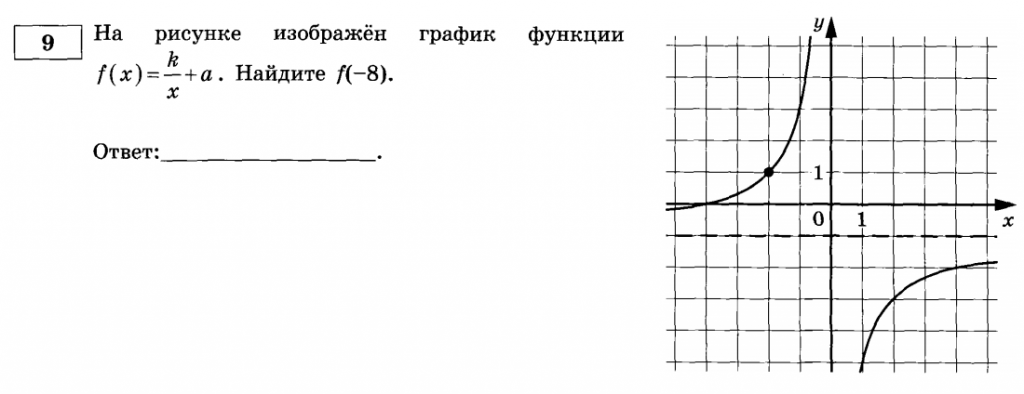
Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому. Пример:

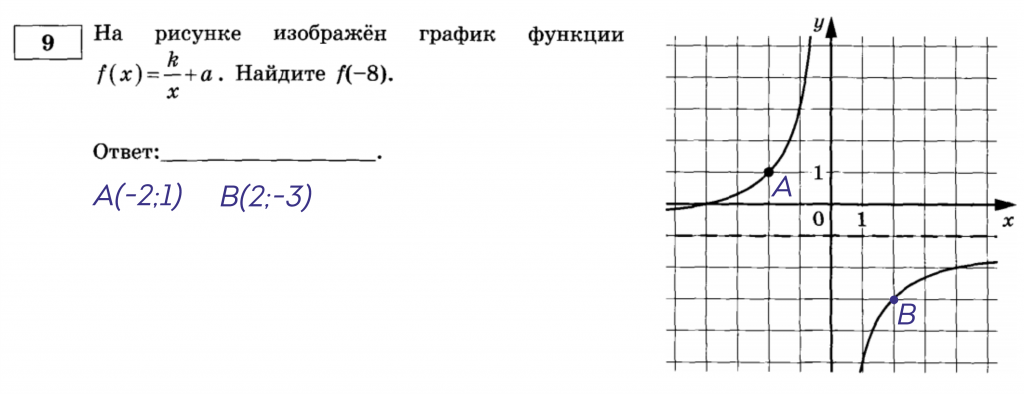
2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

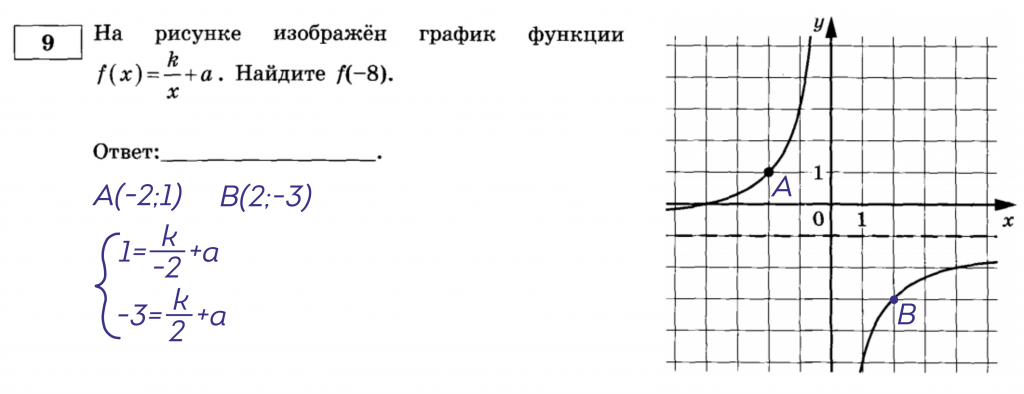
3. Решаем эту систему и получаем готовую формулу.

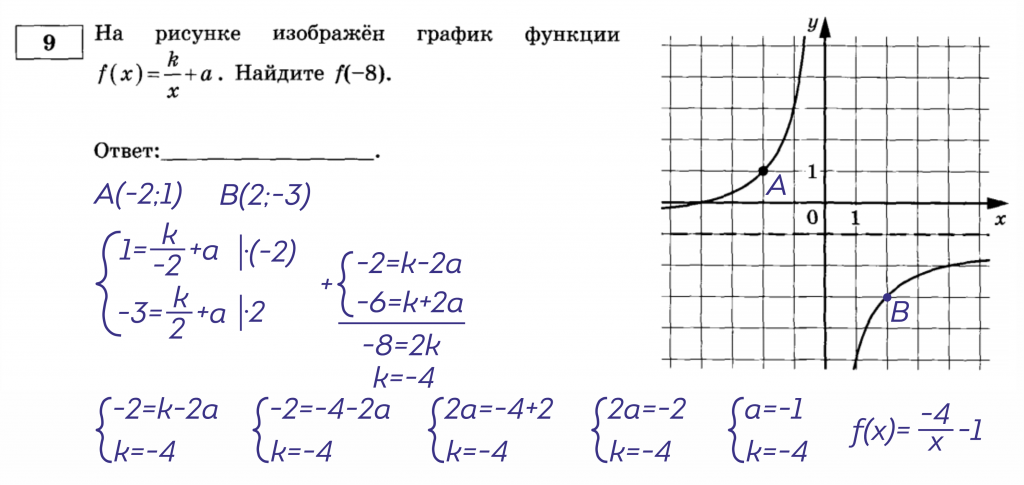
4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

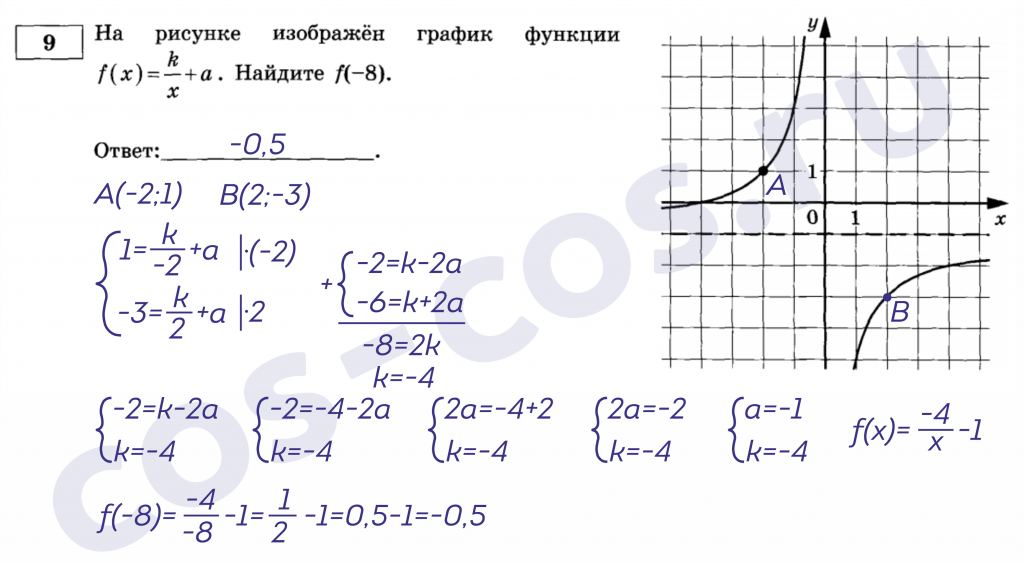
Давайте посмотрим метод еще раз на примере с логарифмической функцией.Пример:

График показательной функции

В данном параграфе я сразу рассмотрю экспоненциальную функцию , поскольку в задачах высшей математики в 95% случаев встречается именно экспонента.

Напоминаю, что  – это иррациональное число: , это потребуется при построении графика, который, собственно, я без церемоний и построю. Трёх точек, пожалуй, хватит:

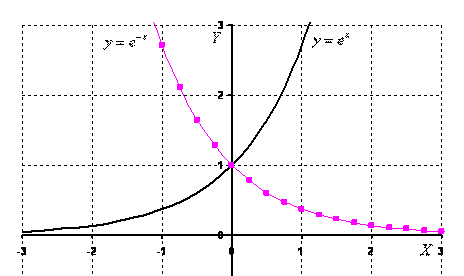
График функции  пока оставим в покое, о нём позже.

Основные свойства функции :

Область определения:  – любое «икс».

Область значений:

Обратите внимание, что ноль не включается в область значений. Экспонента – функция положительная, то есть для любого «икс» справедливо неравенство , а сам график экспоненты полностью расположен в верхней полуплоскости

Функция не ограничена сверху: , то есть, если мы начнем уходить по оси  вправо на плюс бесконечность, то соответствующие значения «игрек» стройным шагом будут тоже уходить вверх на  по оси  . Кстати, график экспоненциальной функции будет «взмывать» вверх на бесконечность очень быстро и круто, уже при   

Исследуем поведение функции на минус бесконечности: . Таким образом, ось  является горизонтальной асимптотой для графика функции , если Принципиально такой же вид имеет любая показательная функция , если . Функции , ,  будут отличаться только крутизной наклона графика, причем, чем больше основание, тем круче будет график.

Обратите внимание, что во всех случаях графики проходят через точку , то есть. Это значение должен знать даже «двоечник»

Теперь рассмотрим случай, когда основание . Снова пример с экспонентой  – на чертеже соответствующий график прочерчен малиновым цветом? Что произошло? Ничего особенного – та же самая экспонента, только она «развернулась в другую сторону». Об этой метаморфозе можно получить подробную информацию в статье Построение графиков с помощью геометрических преобразований.

Принципиально так же выглядят графики функций ,  и т. д.

Должен сказать, что второй случай встречается на практике реже, но он встречается, поэтому я счел нужным включить его в данную статью.