Конус - определение, основные свойства и элементы фигуры, формулы

Презентация к уроку по математике на тему «Цилиндр, конус и шар» в 6 классе по УМК А. Г. Мерзляк

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Цилиндр, конус, шар

Цель урока: сформировать представление о геометрических фигурах: цилиндре, конусе, шаре; сформировать умение применять формулу площади боковой поверхности цилиндра

Все определения и развертки фигур в тетрадь.В учебнике на стр. 155, рис. 56 внимательно изучить, в тетрадь записать площадь боковой поверхности цилиндра.

1.Какая из фигур лишняя? Почему?

Слово «цилиндр» произошло от греческого слова «кюлиндрос» означающего «валик», «каток».

Цилиндр в жизни

Цилиндр – это тело, образованное путем вращения прямоугольника

Основание цилиндраБоковая поверхность цилиндра

Слово «конус» произошло от греческого слова «конос», означающего сосновую шишку

Конус – это тело, образованное путем вращения прямоугольного треугольникаКонус – это тело, образованное путем вращения прямоугольного треугольника

Слово «шар» сначала имело значение «цвет, краска». В XVIII в. слово «шар» приобрело иной смысл и стало обозначать геометрическую фигуру.

Шар в жизниПри вращении полуокружности образуется поверхность шара – фигура, которую называют сферой

Домашнее задание:пар. 26, вопр. 1 – 12 стр.157,№ 770, № 773(применение формулы площади боковой поверхности цилиндра)

Курс повышения квалификации

Сейчас обучается 988 человек из 78 регионов

Курс профессиональной переподготовки

Сейчас обучается 672 человека из 75 регионов

Курс повышения квалификации

А как насчет трехмерных геометрических фигур?

Существуют также трехмерные формы, которые имеют не только длину и ширину, но также глубину или объем. Это формы, которые вы видите в реальном мире, такие как сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.

Трехмерные формы, естественно, более сложные, чем двухмерные, с дополнительное измерение — количество места, которое они занимают, а не только форма, — которое необходимо учитывать при расчете площади и периметра.

Математика, включающая двумерные фигуры, подобные приведенным выше, называется плоская геометрия, потому что она имеет дело с плоскостями или плоскими формами. Математика, включающая трехмерные формы, такие как сферы и кубы, называется сплошная геометрия, потому что она имеет дело с твердыми телами, другим словом для трехмерных форм.

2D-формы составляют 3D-фигуры, которые мы видим каждый день!

Усеченный геометрический объект

Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.

Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.

Способы построения

Можно выделить два основных способа построения усеченного круглого геометрического объекта:

из круглого прямого конуса;
с помощью трапеции.

В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной

Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр

Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.

Площадь поверхности

Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r 2 . Для боковой поверхности следует выполнить следующие действия:

Разрезать ее вдоль образующей и развернуть на плоскости.
Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую

В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:

S = S1 + S2 + Sb = pi*r1 2 + pi*r2 2 + pi*g*(r1 + r2).

Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.

Формула объема

Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:

V = 1/3*pi*r1 2 *H — 1/3*pi*r2 2 *(H-h).

Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:

V = 1/3*pi*h*(r1 2 + r2 2 + r1*r2).

Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:

V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).

Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.

Виды призм

Рассмотрим разновидности фигуры с треугольным основанием.

Прямая призма – боковые грани расположены под прямым углом к основаниям (т. е. перпендикулярны им). Высота такой фигуры равняется ее боковому ребру.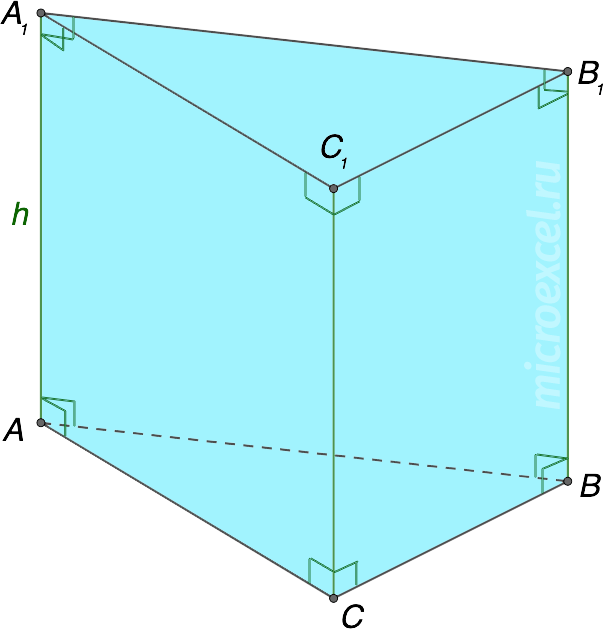Наклонная призма – боковые грани фигуры не перпендикулярны ее основаниям.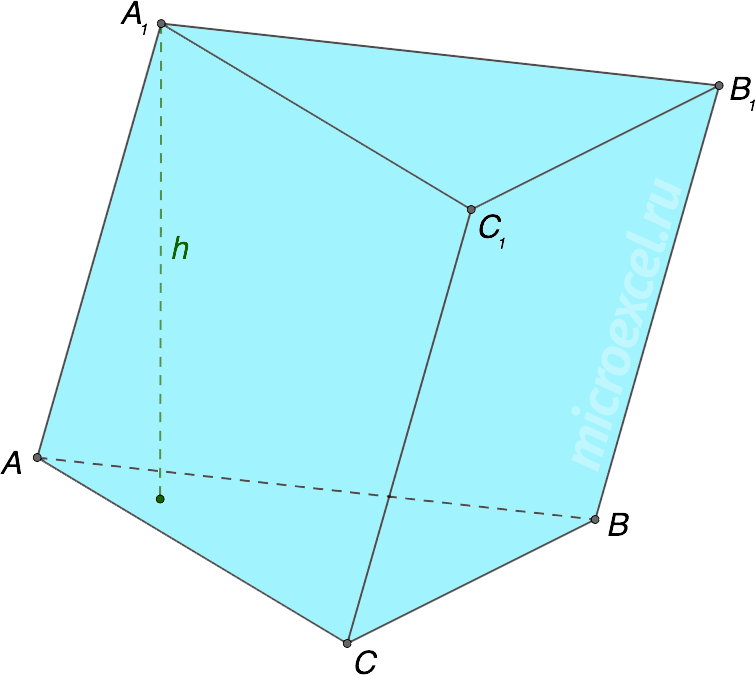Правильная призма – основаниями являются правильные многоугольники. Может быть прямой или наклонной.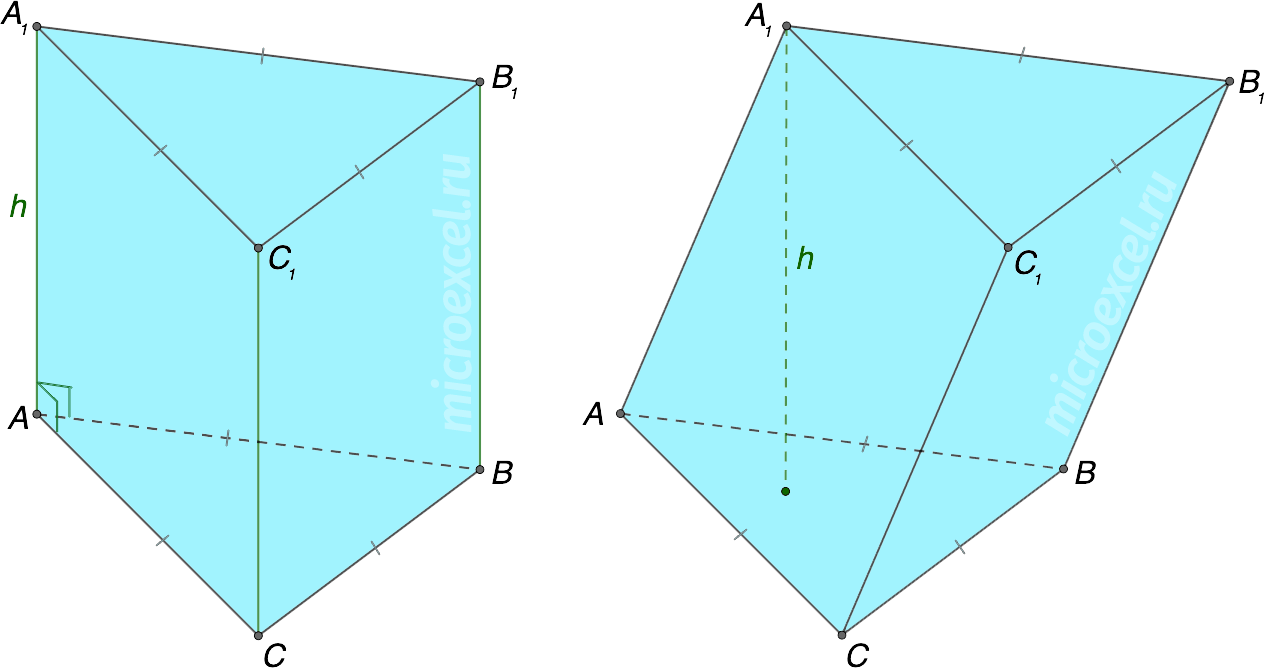Усеченная призма – часть фигуры, оставшаяся после пересечения ее плоскостью, не параллельной основаниям. Также может быть как прямой, так и наклонной.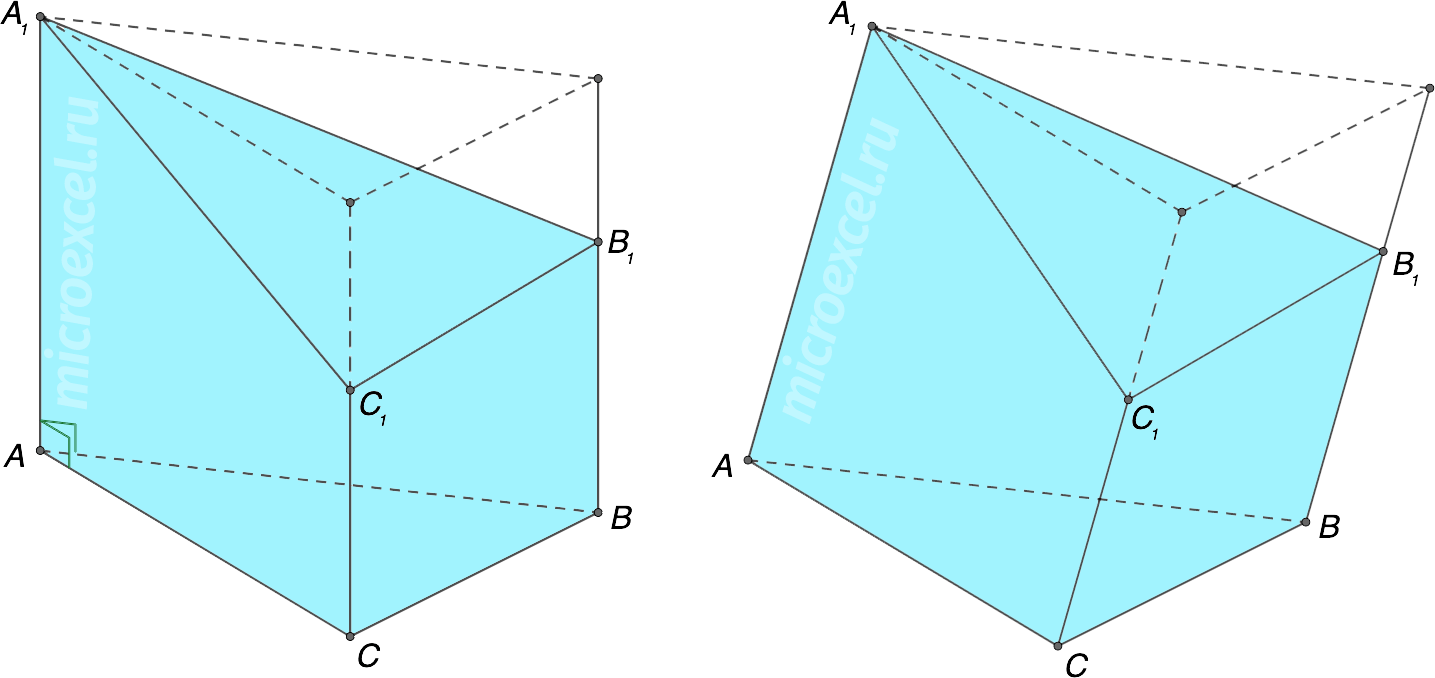

Публикации по теме:

Нахождение площади ромба: формула и примеры Нахождение площади трапеции: формула и примеры Нахождение площади параллелограмма: формула и примеры Нахождение площади эллипса: формула и пример Нахождение периметра прямоугольника: формула и задачи Нахождение периметра ромба: формула и задачи Нахождение периметра трапеции: формула и задачи Нахождение периметра параллелограмма: формула и задачи Теорема о сумме углов треугольника: формула и задачи Нахождение объема куба: формула и задачи Нахождение объема шара: формула и задачи Нахождение объема пирамиды: формула и задачи Нахождение площади правильного шестиугольника: формула и примеры Нахождение площади поверхности куба: формула и задачи Нахождение площади поверхности цилиндра: формула и задачи Нахождение радиуса шара: формула и примеры Нахождение радиуса круга: формула и примеры Нахождение радиуса цилиндра: формула и примеры Нахождение площади правильной призмы: формула и задачи Нахождение площади правильной пирамиды: формулы Формула Герона для треугольника Теорема Менелая: формулировка и пример с решением Теорема о внешнем угле треугольника: формулировка и задачи Теорема Фалеса: формулировка и пример решения задачи Геометрическая фигура: треугольник Свойства равнобедренного треугольника: теория и задача Свойства равностороннего треугольника: теория и пример задачи Определение и свойства биссектрисы угла треугольника Свойства биссектрисы равнобедренного треугольника Свойства биссектрисы прямоугольного треугольника Формулы для нахождения высоты треугольника Свойства высоты равнобедренного треугольника Свойства высоты прямоугольного треугольника Свойства высоты равностороннего треугольника Нахождение радиуса описанной вокруг треугольника окружности Что такое ромб: определение, свойства, признаки Нахождение радиуса вписанной в ромб окружности Что такое окружность: определение, свойства, формулы Что такое параллелограмм: определение, свойства, признаки Что такое трапеция: определение, виды, свойства Свойства равнобедренной (равнобокой) трапеции Что такое средняя линия треугольника Что такое шар (сфера): определение, свойства, формулы Нахождение площади шарового сегмента Что такое конус: определение, элементы, виды Основные свойства конуса Что такое усеченный конус: определение, основные элементы Что такое правильная пирамида: определение, виды, свойства Пирамида с перпендикулярным плоскости основания боковым ребром Что такое тетраэдр: определение, виды, формулы площади и объема

Примечание: свойства призмы представлены в отдельной публикации.

Врезка куба и конуса

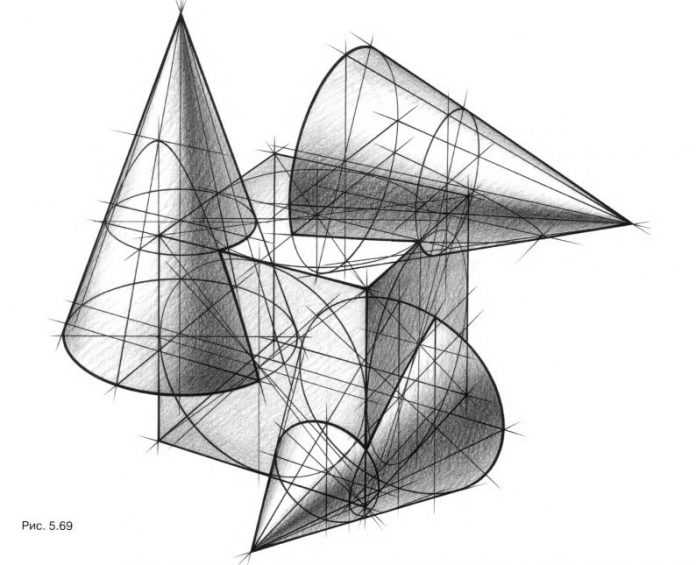
ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку куба и конуса. Оценить многообразие возможных связок куба и конуса, отработать приемы построения их врезок, научиться создавать на листе связки с гармоничными пропорциями.

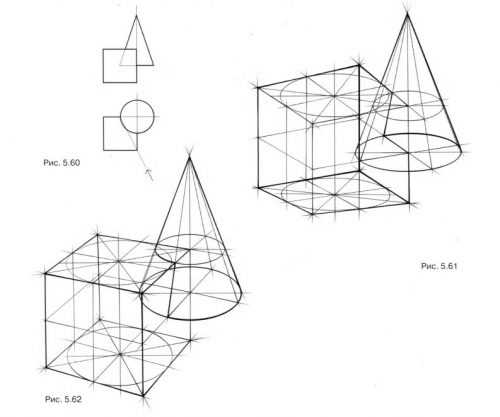
ПОСТАНОВКА ЗАДАНИЯ. Нарисуйте связки куба и конуса сначала по заданным ортогональным проекциям, а затем в произвольном положении по отношению друг к другу. Найдите наиболее красивые, гармоничные пропорции связок, изменяя положение линии пересечения геометрических тел.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ. Рассмотрите ортогональные проекции двух геометрических тел – куба и конуса – на рис. 5.60. Представьте взаимное положение тел. Изобразите в перспективе заданную связку куба и конуса с различным положением относительно линии горизонта (выше линии горизонта на рис. 5.61 и ниже линии горизонта на рис. 5.62).

Изобразите куб и конус в положении, представленном на рис. 5.63. Предложите несколько вариантов врезок, например, как на рис. 5.64 и 5.65. Тонируйте любую связку (рис. 5.66). Теперь, как и в предыдущих заданиях, попробуйте сделать подобное упражнение, увеличив количество геометрических тел. Связка тел – куба и трех конусов – предлагается на рис. 5.67. Постройте врезки, например, как это сделано на рис. 5.68. Легко тонируйте композицию (рис. 5.69).

Элементы конуса

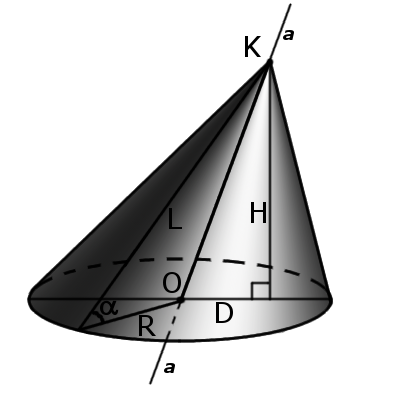
Определение. Вершиной конуса является точка (К), из которой выходят лучи. Определение. Основание конуса — это плоскость, образованная пересечением плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основания, как окружность, эллипс, гипербола и парабола. Определение Образующая конуса (L) — это любой отрезок, соединяющий вершину конуса с границей основания конуса. Образующая — это отрезок луча, выходящего из вершины конуса):

Л 2 = Р 2 + Н 2

Определение. Направляющая конуса – это кривая, описывающая контур основания конуса. Определение. Боковая поверхность конуса есть сумма всех образующих конуса. То есть поверхность, образованная движением образующей по направляющей конуса Определение Поверхность конуса состоит из боковой поверхности и основания конуса Определение Высота конуса (Н) – это отрезок, выходящий из вершине конуса и перпендикулярна основанию. Определение. Ось конуса (а) представляет собой прямую линию, проходящую через вершину конуса и центр основания конуса. Определение конусности (С) конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса это отношение разности диаметров сечений D и d усеченного конуса и расстояния между ними:

С =	Д	и С =	Д — д
ЧАС	час

где C — конусность, D — диаметр основания, d — диаметр меньшего основания, h — расстояние между основаниями.
Конусность характеризует остроту конуса, то есть угол наклона образующей к основанию конуса. Чем больше конусность, тем острее будет угол наклона угла конусности α:

α = 2 угл	Р
ЧАС

где R — радиус основания, H — высота конуса.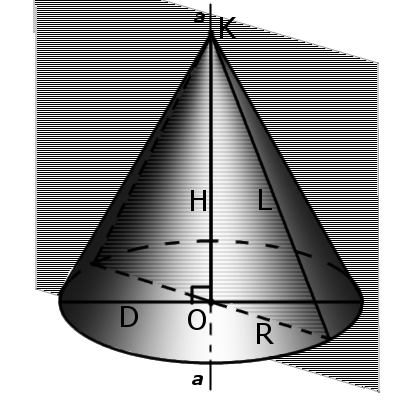
Определение: осевым сечением конуса называется сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, где стороны образованы образующими, а основание треугольника является диаметром основания конуса.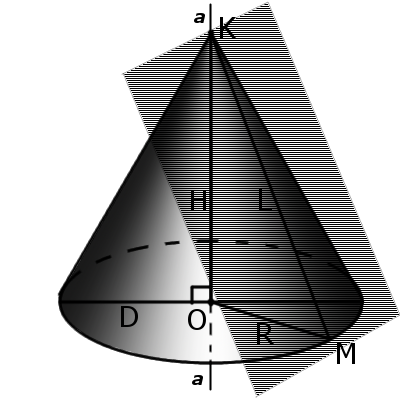
Определение: Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению конуса. Конус, покоящийся на окружности, эллипсе, гиперболе или параболе, называется круговым, эллиптическим, гиперболическим или параболическим конусом соответственно (последние два имеют бесконечный объем).
Определение: Прямой конус — это конус, ось которого перпендикулярна основанию. У такого конуса ось совпадает с высотой, а все образующие равны между собой Формула Объем круглого конуса:

В =	1	πHR2
3

где R — радиус основания, а H — высота конуса. Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:

Sb=πRL

Формула. Суммарная площадь поверхности (Sp) прямого кругового конуса по радиусу R и длине образующей L:

Sp = πRL + πR2

Определение: Наклонный (наклонный) конус – это конус, ось которого не перпендикулярна основанию. У такого конуса ось не совпадает с высотой Формула Объем любого конуса:

В =	1	Ш
3

где S — площадь основания, а H — высота конуса.
Определение. Усеченный конус — это часть конуса, расположенная между основанием конуса и плоскостью сечения, параллельной основанию. Формула. Объем усеченного конуса:

В =	1	(S2H-S1h)
3

где S1 и S2 — площади меньшего и большего основания соответственно, а H и h — расстояние от вершины конуса до центра нижнего и верхнего основания соответственно.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

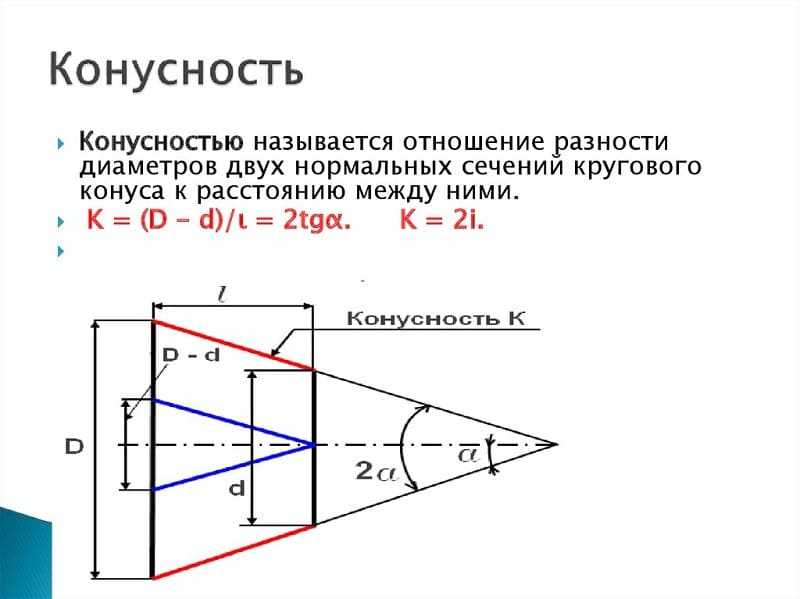
На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Понятие конуса

Построим на плос-ти α окруж-ть L с центром в точке О. Далее через О проведем перпендикуляр к α и отметим на нем точку Р. Если мы отрезками соединим точку Р с каждой точкой окруж-ти L, то получим поверх-ть, которая именуется конической поверхностью. При этом:

прямая ОР – это ось конической поверх-ти;
прямые, соединяющие Р с точками на окруж-ти L, именуются образующими конической поверх-ти;
сама точка Р – это вершина конической поверх-ти.

Объемное тело, ограниченное окруж-тью L и конической поверх-тью, именуется конусом. Соответственно вершина конической поверх-ти, её ось и образующие будут одновременно являться вершиной, осью и образующими конуса. Окруж-ть L – это основание конуса.

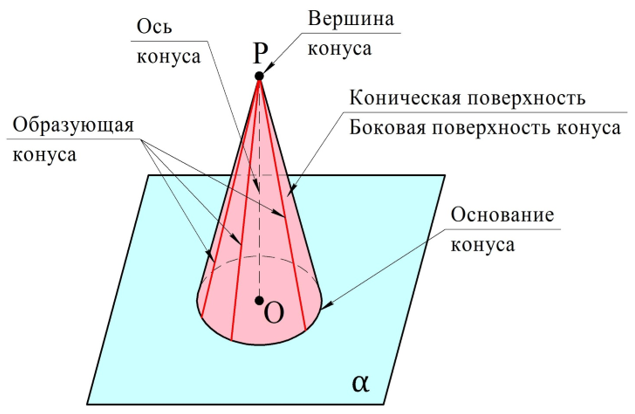
Ещё несколько терминов:

коническая поверх-ть конуса именуется его боковой поверх-тью;
если же к этой площади прибавить ещё и площадь основания, то в итоге получится полная площадь конуса;
отрезок ОР – это не только ось конуса, но и высота конуса.

Как и в случае с цилиндром, мы в данном случае рассматриваем особый случай конуса – прямой круговой конус. В более общем случае ось конуса может не быть перпендикуляром к плос-ти основания (так называемый косой конус). Также в его основании может находиться не окруж-ть, а другая плоская фигура.

В общем случае любая пирамида может рассматриваться как частный случай конуса. Однако в рамках школьного курса под конусом подразумевается исключительно прямой круговой конус, если только не обговорено иное.

Докажем важное утверждение:

Действительно, рассмотрим две произвольные образующие РА и РВ у конуса с вершиной Р, у которой О – центр основания:

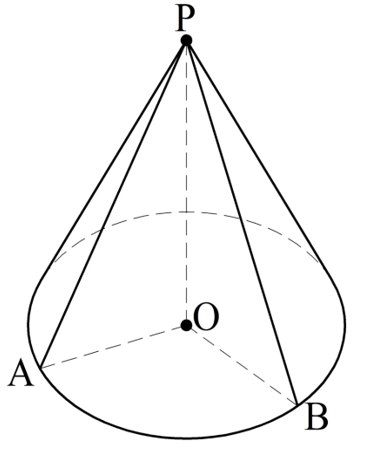
Так как ось ОР перпендикулярна основанию, то ∆РОА и ∆РОВ – прямоугольные. У них общий катет РО, а катеты АО и ОВ одинаковы как радиусы окруж-ти. Тогда ∆РОА и ∆РОВ равны, поэтому одинаковы и образующие РА и РВ, ч. т. д.

Заметим, что конус получается при вращении прямоугольного треуг-ка вокруг его катета. Так, на следующем рисунке конус получается при вращении ∆РОА с прямым углом О относительно катета РО:

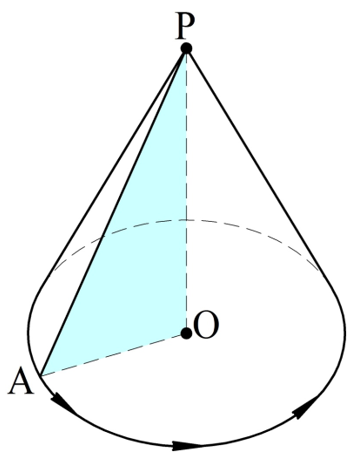
Если сечение конуса проходит через его ось, то оно именуется осевым сечением. Ясно, что это сечение будет являться треуг-ком, причем две его стороны – это образующие конуса, а третья сторона диаметр основания. Образующие конуса одинаковы, поэтому осевое сечение будет равнобедренным треуг-ком.

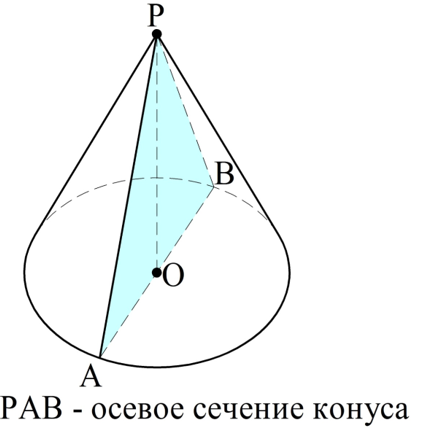
Теперь рассмотрим сечение, параллельное плос-ти основания. Пусть оно пересекает ось РО в какой-то точке О₁. Также пусть А₁ – точка пересечения образующей АР исходного конуса с секущей плос-тью α:

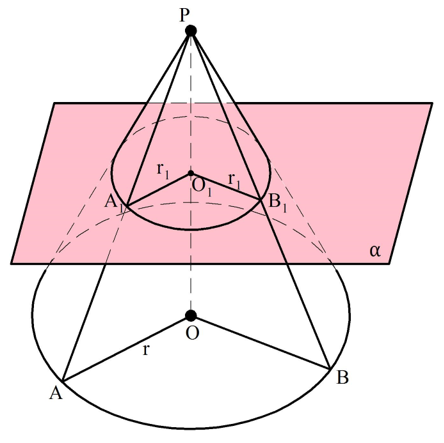
Заметим, что раз ось РО перпендикулярна основанию, то она также будет перпендикулярна и секущей плос-ти, ведь основание и плос-ть α параллельны. Тогда ∠РО₁А₁ будет прямым.

Теперь рассмотрим ∠РОА и ∠РО₁А₁. Они прямоугольные и у них есть общие угол ∠АРО. Значит, это подобные треуг-ки. Обозначим радиус ОА как r, а длину А₁О₁ как r₁. Тогда из подобия получаем:

Рассмотрим теперь другую образующую ВР, которая пересекает секущую плос-ть в точке В₁. Отрезки АО и ОВ одинаковы. Повторяя предыдущие рассуждения, легко доказать подобие ∆РОВ и ∆РО₁В₁, откуда можно вычислить длину О₁В₁:

Получили, что точки А₁и В₁ находятся на одинаковом расстоянии r₁ от точки О₁. Мы выбрали точки А и В произвольно, поэтому для любых двух точек, принадлежащих сечению конуса, можно утверждать, что они равноудалены от точки О₁. Это значит, что все точки сечения лежат на окруж-ти с центром в точке О₁ и радиусом r₁, то есть сечение имеет форму окруж-ти.

Как определить площадь боковой поверхности конуса? Для этого ее надо «разрезать» вдоль одной из образующих и развернуть на плос-ти. В результате получится круговой сектор.

Напомним, что площадь сектора может быть рассчитана по формуле

Теперь обозначим длину образующей буквой l, а радиус основания конуса как r. Тогда

Для вычисления полной площади конуса к боковой поверх-ти необходимо добавить ещё и площадь основания: