Основные сведения о геометрической фигуре цилиндр

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют Цилиндром вращения.

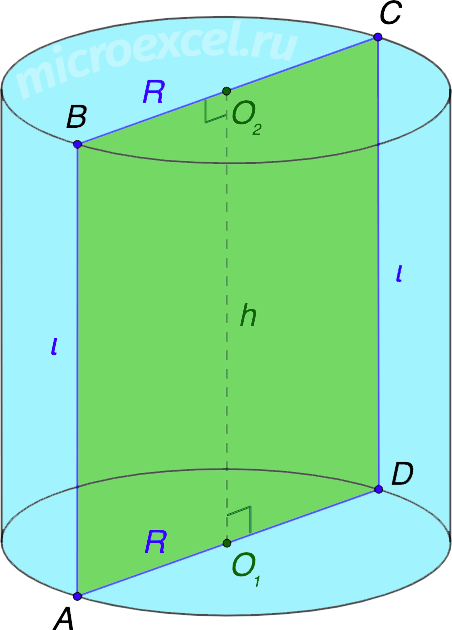
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.

Занятие предназначено для второго курса. Объяснения нового материала, очень хорошо преподнести с презентацией. Исторический материал, практические задачи, понятие цилиндра со всеми комплектующими, сечения цилиндра, площадь боковой и полной поверхности цилиндра, практическое применения цилиндра показано иллюстративно на слайдах. Проводя уроки с компьютерной поддержкой, можно использовать уже имеющиеся материалы (СD). Работа становится разнообразнее, красочней, эмоциональней. Но на таких уроках ученик остаётся в позиции объекта обучения. Современные технологии позволяют нам поставить ученика в позицию активно действующего и использующего свои знания и умения человека.

11 класс Самостоятельная работа по геометрии: «Цилиндр. Площадь поверхности цилиндра»

Поэтому такой цилиндр иногда называют цилиндром вращения.

06.06.2019 3:43:37

2019-06-06 03:43:37

Любые данныеЛюбые данные Любые данные

Площадь поперечного сечения

При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:S = πR 2

При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.

Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:

a 2 + b 2 = c 2

Из нее можно вывести такую формулу:

c = S*q*r*t*(a 2 + b 2 )

Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:

S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:

используется в тех случаях, когда сечение идет параллельно двум основаниям.

При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:

где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.

Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:

где 2а – значение хорды, расчета площади поперечного сечения.

Сечение цилиндра плоскостью

Построение сечения прямого кругового цилиндра аналогично построению сечения призмы, так как прямой круговой цилиндр можно рассматривать как прямую призму с бесчисленным количеством ребер — образующих цилиндра.

Выполнение чертежа начинают с построения трех проекций прямого кругового цилиндра. На поверхности цилиндра проводят несколько равномерно расположенных образующих, в данном примере двенадцать. Для этого горизонтальную проекцию основания делят на 12 равных частей. С помощью линий связи проводят фронтальные проекции образующих цилиндра (рисунок 186).

Из комплексного чертежа видно, что плоскость а» пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под углом к оси цилиндра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса (рисунок 186).

Фронтальная проекция фигуры сечения совпадает с фронтальным следом /» плоскости а». Горизонтальная проекция этой фигуры совпадает с горизонтальной проекцией основания цилиндра.

Профильная проекция фигуры сечения представляет собой проекцию части эллипса и может быть построена по нескольким точкам, которые строятся с помощью линий связи по горизонтальной и фронтальной проекциям фигуры сечения. Полученные таким образом профильные проекции точек фигуры сечения соединяют кривой по лекалу.

Действительный вид фигуры сечения получен на рисунке 186 способом перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой. Новая ось проекций 7г₂/тг₄ может быть проведена параллельно следу /» на произвольном расстоянии, но для упрощения построений она выполнена совпадающей с /». От оси л:₂/л:₄ откладывают отрезки 5″5 1У = 5’5_Х, 6″ 6 ,у = 6’6_Х, т. е. отрезки тип и т. д., так как расстояние от новой проекции этой точки до новой оси проекций равно расстоянию от прежней проекции этой точки до прежней оси проекций.

Развертка боковой поверхности усеченного цилиндра с основанием и фигурой сечения показана на рисунке 187.

Для построения развертки на горизонтальной прямой откладывают длину окружности основания, равную nd, и делят ее на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку nd, на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости а’, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки 7. 9, соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой 19 (сегмент), а фигуру нижнего основания цилиндра (окружность) соединяют с нижней частью развертки.

Изометрическую проекцию усеченного цилиндра строят следующим образом (рисунок 188).

Сначала строят изометрию нижнего основания (эллипс) и части верхнего основания — сегмента (часть эллипса). На диаметре окружности нижнего основания от центра откладывают отрезки а, бит. д., взятые с горизонтальной проекции основания (рисунок 186). Затем из намеченных точек проводят прямые, параллельные оси цилиндра до пересечения с осью эллипса.

Через полученные точки проводят прямые, параллельные оси у, и на них откладывают отрезки, взятые с действительного вида сечения. Полученные точки соединяют по лекалу. Заканчивают построение проведением очерковых образующих, касательных к основаниям эллипса.

Основные определения и свойства цилиндра

      Рассмотрим две   α   и   β   и произвольную   лежащую в плоскости   α   (рис. 1).

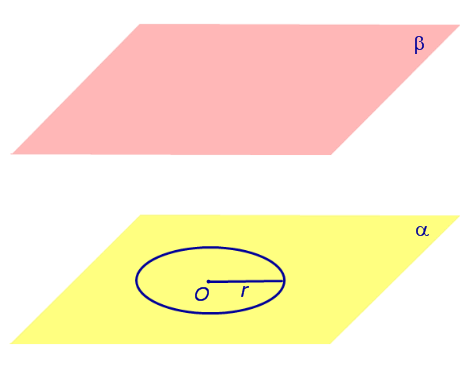
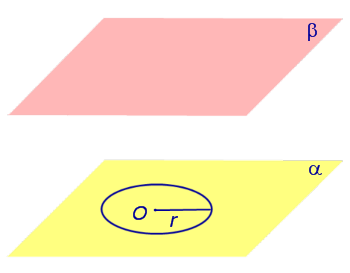
Рис.1

      Если из каждой точки окружности опустить   β,   то основания этих перпендикуляров образуют на плоскости   β   окружность радиуса   r,   центр   O₁   которой является основанием перпендикуляра, опущенного из точки   O   на плоскость   β   (рис.2).

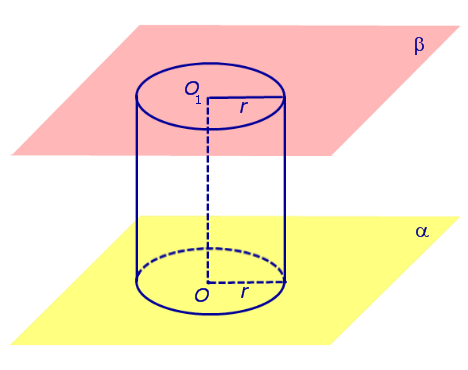
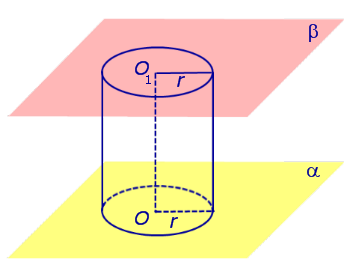
Рис.2

      Определение 1.

	Отрезок , опущенного из любой точки окружности с центром   O   на плоскость  β ,   который заключен между плоскостями   α   и   β ,   называют образующей цилиндра.
	Совокупность всех образующих цилиндра называют цилиндрической поверхностью.
	Фигуру, ограниченную цилиндрической поверхностью и плоскостями   α   и   β,   называют цилиндром.
	Отрезок   OO1   называют осью цилиндра .
	на плоскости   α   с центром в точке   O   называют радиусом цилиндра.
	α   и   β ,   называют высотой цилиндра.
	Круги с центрами   O   и   O1   на плоскостях   α   и   β ,   называют основаниями цилиндра.

      Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра. Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра.

      Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

     Замечание 3. Прямая   OO₁   является цилиндра, а середина отрезка   OO₁   является цилиндра.

Как найти высоту цилиндра

Рассмотрим варианты нахождения высоты фигуры, а также длины ее образующей (которая равна этой высоте).

Первым делом взглянем на формулу: \(V=\pi R^2\times H\), где V — объем цилиндра, R — радиус основания, H — высота фигуры.

Через эту формулу можем выразить высоту:

\(H=\frac V{\pi R^2}\)

Таким образом мы можем узнать H данного геометрического тела, если нам известен его объем и радиус. Если же вместо радиуса мы знаем диаметр, формула расчета будет выглядеть так:

\(H=\frac{4V}{D^2}\)

В случае, когда нам известен диаметр и площадь фигуры, мы так же можем найти высоту

Следует обратить внимание, что в зависимости от того, будет ли известна площадь боковой или полной поверхности, формула будет меняться

Для расчета S боковой поверхности (часть, ограниченная цилиндрической поверхностью) цилиндра мы используем формулу:

\(S=2\pi RH\)

выражаем H и получаем:

\(H=\frac S{2\pi R}\)

Если известна S полной поверхности (включает в себя площадь оснований фигуры), используем формулу:

\(S=2\pi R(H+R)=2\pi R\times H+2\pi R^2\)

выражаем H и получаем:

\(H=\frac{S-2\pi R^2}{2\pi R}\)

Для третьего способа нужно будет провести прямоугольное сечение, ширина которого должна будет совпадать с диаметрами оснований, а длина — с образующими цилиндра.

Таким образом, получается прямоугольный треугольник САВ. А так как высота равна образующей, мы можем вычислить ее по теореме Пифагора:

\(СВ^2=АС^2-АВ^2\)

\(H=СВ=\sqrt{АС^2-АВ^2}\)

Слайд 48Цилиндры Фараона — два загадочных предмета цилиндрической формы в руках некоторых

древнеегипетских изваяний. Среди специалистов-египтологов не существует единого мнения о происхождении данных предметов. В 1976 году в Закавказье Р.Добровольским и В.Ковтуном была обнаружена старинная эзотерическая рукопись под названием «Тайны Жизни и Смерти», в которой содержалась информация о Лунном и Солнечном цилиндрах, изготовленных из цинка и меди с определенным внутренним наполнением. По утверждению неизвестного автора Цилиндры Фараона использовались фараонами и жрецами Древнего Египта для укрепления жизненных сил и общения с богами. Цилиндры Фараона были воссозданы согласно древнему рецепту и затем в течение многих лет исследовались физиком Владимиром Ковтуном. В этих исследованиях принимали участие медики, физики, египтологи, экстрасенсы и парапсихологи. Результаты исследований поразили ученых. Оказалось, что Цилиндры Фараона обладают широчайшим спектром благотворного воздействия на организм человека.

Формула площади поверхности кругового цилиндра

S осн = 2 ⋅ π ⋅ r 2 S_{text{осн}}=2cdotpicdot r^2 Sосн​=2⋅π⋅r2

S бок = 2 ⋅ π ⋅ r ⋅ h S_{text{бок}}=2cdotpicdot rcdot h Sбок​=2⋅π⋅r⋅h

r r r — радиус круга (основания кругового цилиндра); h h h — высота этого цилиндра.

Сокращенно, это формулу можно записать так:

S = S осн + S бок = 2 ⋅ π ⋅ r 2 + 2 ⋅ π ⋅ r ⋅ h = 2 ⋅ π ⋅ r ⋅ ( r + h ) S=S_{text{осн}}+S_{text{бок}}=2cdotpicdot r^2+2cdotpicdot rcdot h=2cdotpicdot rcdot(r+h) S=Sосн​+Sбок​=2⋅π⋅r2+2⋅π⋅r⋅h=2⋅π⋅r⋅(r+h)

Пример

Радиус круга, лежащего в основании прямого кругового цилиндра, имеет длину 6 (см.). Высота цилиндра – 20 (см.). Найдите полную площадь его поверхности.

Решение:

r = 6 r=6 r=6 h = 20 h=20 h=20

По формуле:

S = 2 ⋅ π ⋅ r ⋅ ( r + h ) = 2 ⋅ π ⋅ 6 ⋅ ( 6 + 20 ) ≈ 979 , 68 S=2cdotpicdot rcdot(r+h)=2cdotpicdot 6cdot(6+20)approx979,68 S=2⋅π⋅r⋅(r+h)=2⋅π⋅6⋅(6+20)≈979,68 (см. кв.)

Ответ: 979,68 см. кв.

Слайд 42Винтовые линии бывают правовинтовые и левовинтовые.Предположим, что по винтовой линии движется

точка. Проекцией винтовой линии на плоскость, перпендикулярную кеё оси (будем называть осью винтовой линии ось цилиндра, на котором она расположена), будет, очевидно, окружность. Поэтому если смотреть на винтовую линию в направлении её оси, то будет казаться, что точка движется по окружности. Если точка движется по окружности по часовой стрелке, удаляясь от нас, то винтовая линия называется право- винтовой, если же она движется по часовой стрелке, приближаясь к нам, то винтовая линия называется левовин- товой. Правовинтовую и левовинтовую линии на одном итом же цилиндре с одинаковым углом подъёма совместить нельзя. На черт.1 у нас получилась левовинтовая линия; чтобы получить правовинтовую линию, нужно наматывать треугольник в противоположном направлении.

Цилиндр. Виды, объём цилиндра, площадь поверхности

Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.

Планиметрия – раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье – цилиндр.

Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже – коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец – знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.

Виды цилиндров

1. Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
2. Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
3. Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
4. Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
5. Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.

Сами прямые называют образующими цилиндрической поверхности.
Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости альфа, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость бета, которая будет параллельна плоскости альфа, то отрезки образующих, заключённые между плоскостями альфа и бета будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости бета, дают окружность, равную окружности, лежащей в плоскости альфа.

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях альфа и бета) называется цилиндром.
Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого – образующие, а две другие – отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: Sбок=2пRL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2пR(R+L).

Примеры и разбор решения заданий тренировочного модуля

Дан цилиндр.

Выберите значение площади его боковой поверхности

1. 60π
2. 192π
3. 120π
4. 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

Sполн=2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R2+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Задача

Осевое сечение цилиндра – квадрат со стороной 20 см. Найти высоту цилиндра, радиус цилиндра, ось цилиндра и площадь основания цилиндра.

Решение

Одна из сторон осевого сечения – образующая (она же равна оси цилиндра и она же равна высоте). Значит, высота и ось равны 20 см. Далее, вторая сторона осевого сечения – диаметр основания. Он равен 20 см, значит, радиус – 10 см. Наконец, площадь основания ищется по формуле

Итак, ребята, на этом уроке мы изучили, что такое цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения; площади поверхностей цилиндра.

Цилиндр

Стереометрия −
это раздел геометрии, в котором изучаются фигуры в пространстве. Основными
фигурами в пространстве являются точка, прямая и плоскость. В стереометрии
появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это
одно из немногих существенных отличий стереометрии от планиметрии, так как во
многих случаях задачи по стереометрии решаются путем рассмотрения различных
плоскостей, в которых выполняются планиметрические законы.

В окружающей нас
природе существует множество объектов, являющихся физическими моделями
указанной фигуры. Например, многие детали машин имеют форму цилиндра или
представляют собой некоторое их сочетание, а величественные колонны храмов и
соборов, выполненные в форме цилиндров, подчеркивают их гармонию и красоту.

Греч. −
кюлиндрос. Античный термин. В обиходе − свиток папируса, валик, каток
(глагол − крутить, катать).

У Евклида цилиндр
получается вращением прямоугольника. У Кавальери − движением образующей
(при произвольной направляющей − «цилиндрика»).

Цель данного
реферата рассмотреть геометрическое тело – цилиндр.

Для достижения
данной цели необходимо рассмотреть следующие задачи:

− дать
определения цилиндра;

−
рассмотреть элементы цилиндра;

− изучить
свойства цилиндра;

−
рассмотреть виды сечения цилиндра;

− вывести
формулу площади цилиндра;

− вывести
формулу объема цилиндра;

− решить
задачи с использованием цилиндра.

Тела вращения. Цилиндр

Вообще, произвольный цилиндр – это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями (основаниями цилиндра).

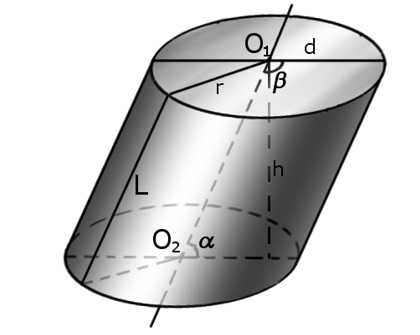
Цилиндрическая поверхность – поверхность, получаемая при движении прямой (образующей L) параллельно самой себе, вдоль плоской кривой направляющей.

Основания цилиндра – плоские фигуры, образованные пересечением цилиндрической поверхности с двумя плоскостями.

Форму таких цилиндров достаточно часто имеют детали различных механизмов.

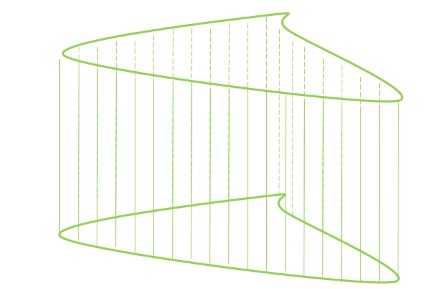
Цилиндрическая поверхность может быть и незамкнутой:

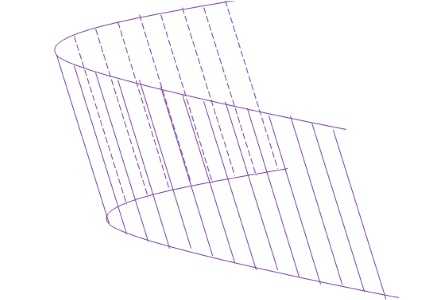
Призма – это тоже цилиндр (основание – многоугольник).

Объем цилиндра. Площадь боковой поверхности цилиндра.Площадь полной поверхности цилиндра

      Для цилиндра с   r   и   h   (рис. 5)

Рис.5

введем следующие обозначения

V	объем цилиндра
Sбок	площадь
Sполн	площадь
Sосн	площадь

      Тогда справедливы следующие формулы для вычисления объема, площади :

S_осн = πr2,

V = S_оснh = πr2h,

S_бок= 2πrh,

S_полн = 2πr2 + 2πrh == 2π(r + h).

      Замечание 7. Формула объема цилиндра   V = πr2h   может быть получена из

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Определение объёма фигуры

Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.

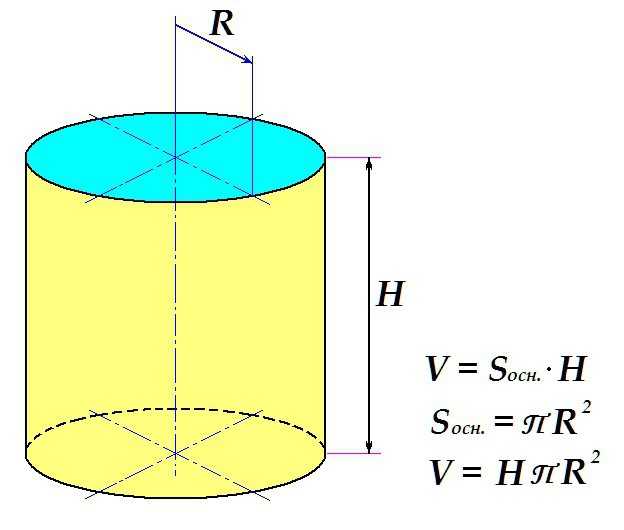
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.

Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.

Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.

Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.

Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.

Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними.

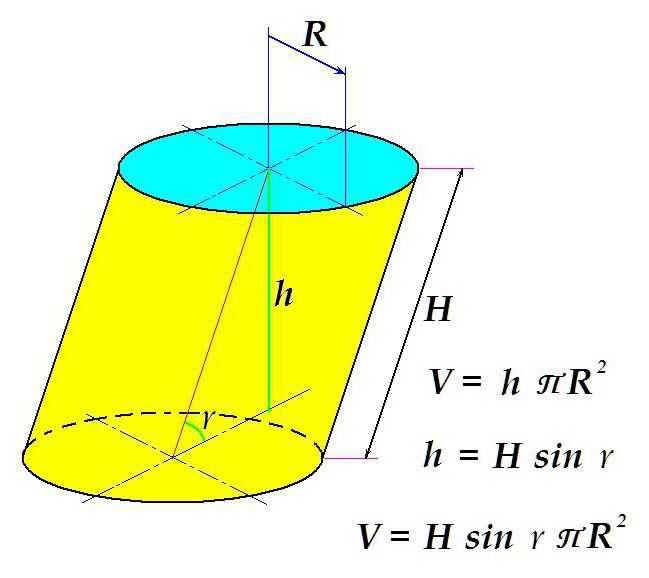
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.

Сечения цилиндра

Рис. 4. Ци­лин­дри­че­ская по­верх­ность и её об­ра­зу­ю­щие

Со­во­куп­ность па­рал­лель­ных пря­мых, со­еди­ня­ю­щих точки на окруж­но­стях, на­зы­ва­ет­ся ци­лин­дри­че­ской по­верх­но­стью, а сами пря­мые – об­ра­зу­ю­щи­ми ци­лин­дри­че­ской по­верх­но­сти (см. рис.4). И те­перь мы го­то­вы дать глав­ное опре­де­ле­ние урока.

Рис. 5. Кру­го­вой ци­линдр

Кру­го­вым ци­лин­дром на­зы­ва­ет­ся тело в про­стран­стве, огра­ни­чен­ное двумя кру­га­ми и ци­лин­дри­че­ской по­верх­но­стью (см. рис. 5).

Сразу ого­во­рим­ся, что это по­ня­тие можно обоб­щить, про­сто ци­линдр – это когда ос­но­ва­ния не круги. Но мы оста­но­вим­ся толь­ко на кру­го­вых, их и будем иметь в виду в даль­ней­шем.

Рис. 6. Ос­но­ва­ния и ра­ди­у­сы

Круги – ос­но­ва­ния ци­лин­дра. Ра­ди­ус каж­до­го из ос­но­ва­ний (они равны) – ра­ди­ус ци­лин­дра (см. рис. 6).

Рис. 7. Об­ра­зу­ю­щие ци­лин­дра

От­рез­ки об­ра­зу­ю­щих, за­клю­чен­ные между ос­но­ва­ни­я­ми, – об­ра­зу­ю­щие ци­лин­дра (см. рис. 7).

Рис. 8. Эл­лип­ти­че­ский ци­линдр

Само слово ци­линдр про­ис­хо­дит от гре­че­ско­го «ки­лин­дрос» – валик, каток. На­пом­ним, ци­линдр, ко­то­рый мы рас­смат­ри­ва­ем, еще на­зы­ва­ют кру­го­вым, так как в ос­но­ва­ни­ях лежат круги. Если рас­смот­реть дру­гую фи­гу­ру (на­при­мер, эл­липс), то по­лу­чит­ся эл­лип­ти­че­ский ци­линдр (см. рис. 8).

Рис. 9. Пря­мой ци­линдр

Если об­ра­зу­ю­щие пер­пен­ди­ку­ляр­ны ос­но­ва­ни­ям ци­лин­дра, такой ци­линдр на­зы­ва­ет­ся пря­мым (см. рис. 9).

В курсе школь­ной гео­мет­рии обыч­но рас­смат­ри­ва­ют­ся имен­но пря­мые кру­го­вые ци­лин­дры, при­чем по умол­ча­нию любой ци­линдр счи­та­ет­ся пря­мым кру­го­вым. По­го­во­рим о таких ци­лин­драх.

Рис. 10. Ось ци­лин­дра

От­ре­зок, со­еди­ня­ю­щий цен­тры ос­но­ва­ний та­ко­го ци­лин­дра, – ось ци­лин­дра (см. рис. 10).

Рис. 11. Вра­ще­ние пря­мо­уголь­ни­ка во­круг оси

Вра­щая пря­мо­уголь­ник во­круг этой оси, можно по­лу­чить наш ци­линдр (см. рис. 11).

Рис. 12. Вы­со­та

Вве­дем сле­ду­ю­щее опре­де­ле­ние. Вы­со­той ци­лин­дра на­зо­вем от­ре­зок, со­еди­ня­ю­щий точки его ос­но­ва­ний и пер­пен­ди­ку­ляр­ный ос­но­ва­ни­ям. Вы­со­той пря­мо­го кру­го­во­го ци­лин­дра яв­ля­ет­ся ось (или об­ра­зу­ю­щая) – все равно: они в пря­мом кру­го­вом ци­лин­дре равны (см. рис. 12).

Се­че­ния ци­лин­дра

Рис. 13. Пер­пен­ди­ку­ляр­ное се­че­ние ци­лин­дра

Далее рас­смот­рим пер­пен­ди­ку­ляр­ное се­че­ние та­ко­го ци­лин­дра (то есть се­че­ние, пер­пен­ди­ку­ляр­ное оси). Неслож­но по­нять, что, где бы мы его ни про­ве­ли, в се­че­нии будет такой же круг, что и в любом из ос­но­ва­ний (см. рис. 13).

Рис. 14. Осе­вое се­че­ние

Можно также рас­смот­реть се­че­ние, про­хо­дя­щее через ось ци­лин­дра. В этом слу­чае оно пред­став­ля­ет собой пря­мо­уголь­ник, одна сто­ро­на ко­то­ро­го равна об­ра­зу­ю­щей (или оси), а дру­гая яв­ля­ет­ся диа­мет­ром ос­но­ва­ния. Такое се­че­ние на­зы­ва­ют осе­вым. Имен­но вра­щая такое се­че­ние во­круг оси, мы и по­лу­ча­ем наш ци­линдр (см. рис. 14).

Рис. 15. Непер­пен­ди­ку­ляр­ное се­че­ние

На­ко­нец, можно го­во­рить и о непер­пен­ди­ку­ляр­ном се­че­нии: ведь ту же палку кол­ба­сы можно на­ре­зать не толь­ко пер­пен­ди­ку­ляр­но, но и под углом. В этом слу­чае се­че­ние по­лу­чит­ся в форме эл­лип­са, но об этих фи­гу­рах мы пока по­дроб­но го­во­рить не будем (см. рис. 15).

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся

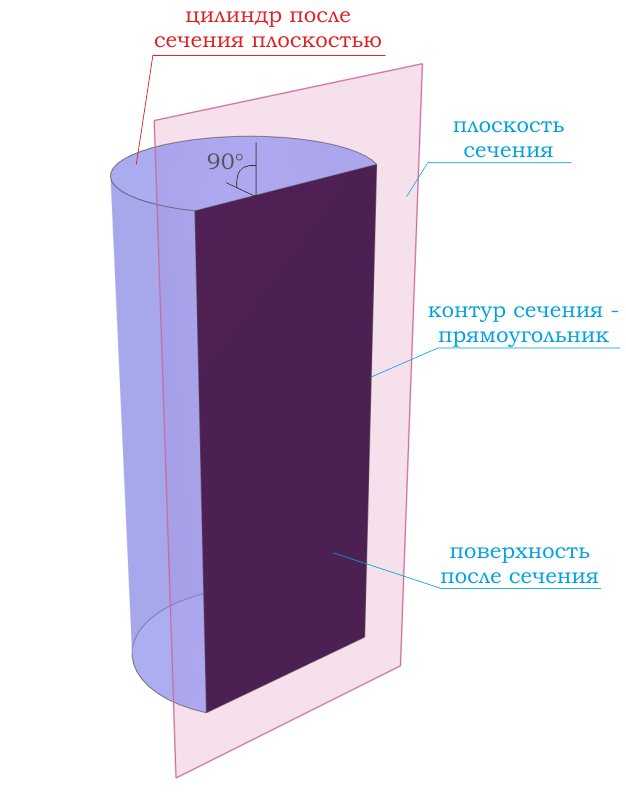
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура,

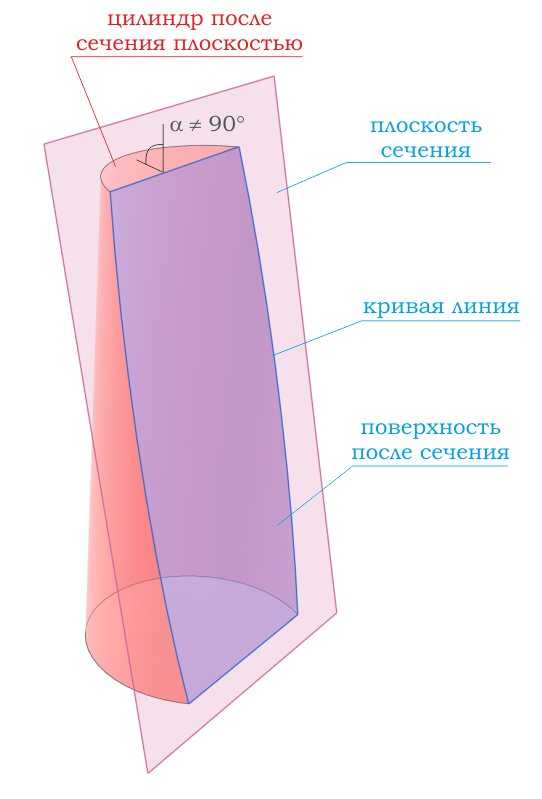
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет .

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается .

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде .

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

Способ расчета радиуса цилиндра:

через объем и высоту Через площадь боковой поверхности и высоту Через общую площадь поверхности и высоту Высота: Объем: Высота: Площадь боковой поверхности: Высота: Общая площадь:

Цилиндр – это геометрическое тело, полученное вращением прямоугольника вокруг его стороны. Цилиндр — это также тело, ограниченное цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями. Эта поверхность образуется, когда прямая линия движется параллельно самой себе. При этом выделенная точка на прямой движется по некоторой плоской кривой (направляющей). Эта прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где V — объем цилиндра, h — высота

Цилиндр – это геометрическое тело, полученное вращением прямоугольника вокруг его стороны. Цилиндр — это также тело, ограниченное цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями. Эта поверхность образуется, когда прямая линия движется параллельно самой себе. При этом выделенная точка на прямой движется по некоторой плоской кривой (направляющей). Эта прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb — площадь боковой поверхности, h — высота

Цилиндр – это геометрическое тело, полученное вращением прямоугольника вокруг его стороны. Цилиндр — это также тело, ограниченное цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями. Эта поверхность образуется, когда прямая линия движется параллельно самой себе. При этом выделенная точка на прямой движется по некоторой плоской кривой (направляющей). Эта прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра: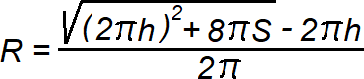
где S — общая площадь поверхности, h — высота

Как правильно штриховать цилиндр

В мастер-классе выше мы с вами увидели, как рисуется цилиндр в объеме, и как сделать этот цилиндр со штриховкой правильно. Теперь давайте более детально распишем, какой должна быть штриховка.

• Рефлекс – тон, похожий на полутень, располагается у краев предмета
• Блик – самая светлая часть рисунка, ее мы не трогаем карандашом, а наоборот, высветляем ластиком
• Полутень – основной тон в штриховке
• Светотень – распределение света и тени на рисунке

Представьте себе блик – яркое световое пятно на предмете. И вот этот свет от блика должен как-то расходиться по всей поверхности рисуемого вами предмета. Это и будет полутень.

Если вы сомневаетесь, в правильности своей работы, то вам нужно отойти на небольшое расстояние от рисунка и посмотреть на него со стороны. Как правило, при таком рассмотрении вы сразу заметите погрешности в объеме, тенях и пропорциях.

После нее, у вас будет гораздо меньше вопросов о штриховке и все получится уже с первого раза.

Цилиндр

Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:

• круглое;
• прямоугольное;
• эллиптическое.

Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.

Площадь круглого сечения рассчитывается по формуле:

S1 = pi*r2

Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:

S2 = 2*r*h

Определение объёма фигуры

Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.

Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.

Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.

Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.

Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.

Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.

Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними.

Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.

Заключение

На этом уроке мы узна­ли о ци­лин­дри­че­ской по­верх­но­сти, видах ци­лин­дра, эле­мен­тах ци­лин­дра и сход­стве ци­лин­дра с приз­мой.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/11-klass/btela-vraweniya-b/ponyatie-tsilindra

https://www.youtube.com/watch?v=eLv-lSek-60

https://www.youtube.com/watch?v=P7_5qWj2BZM

http://dok.opredelim.com/docs/index-7319.html

http://mypresentation.ru/download/125438_ponyatie_cilindra__prezentaciya_po_geometrii

http://fs1.ppt4web.ru/uploads/ppt/95242/50208d20656afdeb627a755fe2f9813e.ppt

http://mateshka.ru/matematika/tela-vrasheniya.html

http://math4school.ru/tela_vrashhenija.html#spr1301

http://www.stendzakaz.ru/images/school/k-geom/k-geom-30.jpg