Площадь поверхности цилиндра: как найти, формула

Область применения

Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:

1. Определение объемов емкостей.
2. Решение задач по сопротивлению материалов и электротехнике.
3. Расчет количества материалов при проектировании, строительстве и ремонте.
4. Ведение поливного земледелия.

Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью

Круг имеет ряд характеристик:

• радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
• диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
• длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).

Радиус цилиндра. Калькулятор

Автор Dominik Czernia, PhD

Отзыв от Bogna Szyk и Adena Benn

Последнее обновление: 20 ноября 2022 г.

• Что такое радиус формулы цилиндра?
• Как найти радиус цилиндра?
• Часто задаваемые вопросы

Этот калькулятор радиуса цилиндра быстро находит радиус правильного кругового цилиндра с восемью различными уравнениями . Вам нужно решить конкретную математическую задачу, но вы не знаете, как найти радиус цилиндра? Попробуйте ввести пару параметров и посмотрите, как просто работает этот калькулятор.

Существует множество различных способов оценки радиуса цилиндра. В следующем тексте мы представили восемь формул радиуса цилиндра, которые используются нашим калькулятором. В большинстве случаев вам понадобятся только два из следующих количеств:

• высота ;
• том ;
• самая длинная диагональ ;
• площадь основания ;
• площадь боковой поверхности ;
• общая площадь поверхности ; или
• отношение поверхности к объему .

Этот калькулятор радиуса цилиндра является удобным инструментом, который может вычислить параметры правильных круговых цилиндров . Под радиусом цилиндра мы подразумеваем радиус двух конгруэнтных окружностей, которые составляют оснований цилиндра. Вот почему этот тип цилиндра называется круговым .

Следует помнить, что слово цилиндр может соответствовать разным формам (обобщенный цилиндр). Однако обычно мы имеем в виду правильный круговой цилиндр. Цилиндр 9.0017 справа , когда одно из оснований лежит точно над другим. В противном случае цилиндр косой .

Этот калькулятор подготовлен для ответа на вопрос как найти радиус цилиндра . В другом нашем правом расчете цилиндров вы можете найти более общую информацию о цилиндрах. Обязательно проверьте это!

Какова формула радиуса цилиндра?

Для описания свойств цилиндра мы обычно используем радиус и высоту .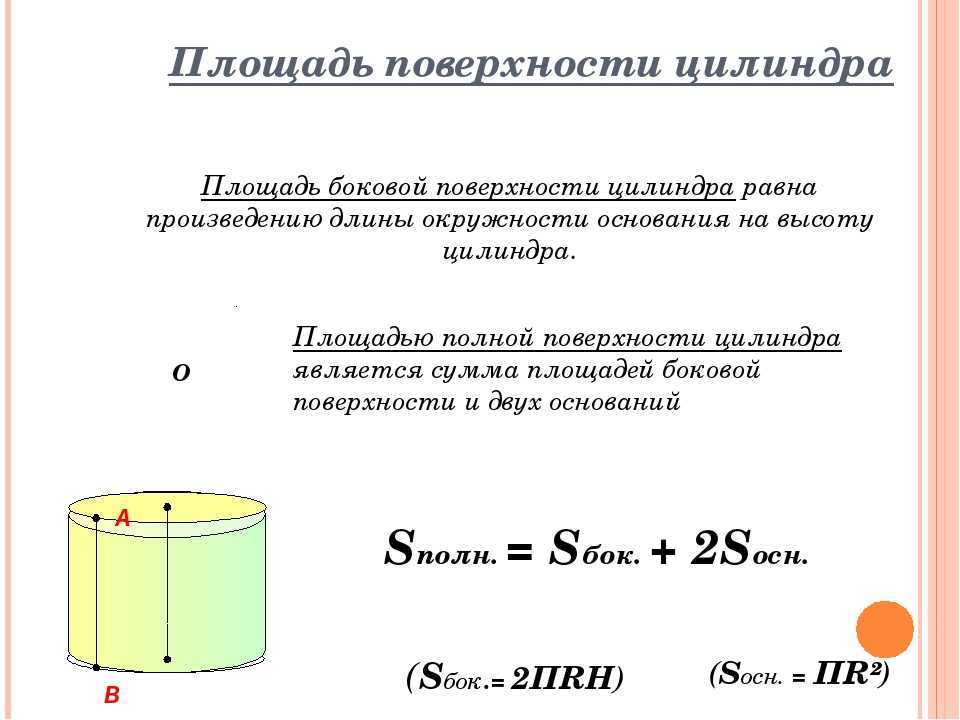

1. Объем цилиндра: ,
2. Площадь основания цилиндра: ,
3. Площадь боковой поверхности цилиндра: ,
4. Общая площадь поверхности цилиндра: ,
5. Наибольшая диагональ цилиндра: ,
6. Отношение площади поверхности к объему цилиндра:

Радиус цилиндра не всегда легко оценить. Однако с помощью нашего калькулятора радиуса цилиндра теперь вы можете быстро вычислить его с помощью следующих формул восьми радиусов цилиндра . Все они были получены непосредственно из приведенных выше уравнений.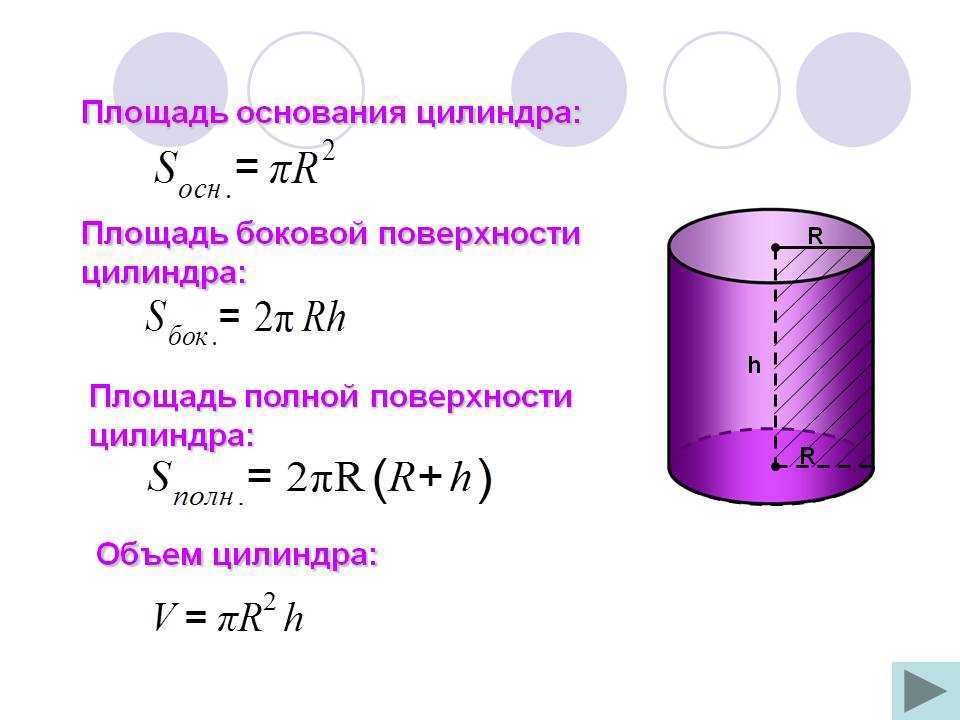

1. Учитывая высоту и объем : ;
2. Дано высоты и поперечной площади : ;
3. Учитывая высоту и общую площадь : ;
4. Учитывая высоту и диагональ : ;
5. Учитывая высоту и отношение площади поверхности к объему : ;
6. Учитывая объем и боковую площадь : ;
7. Учитывая базовую площадь : ; и
8. Даны боковой площади и общей площади : .

Вам нужно рассчитать еще один параметр цилиндра? Вам обязательно нужно проверить наш калькулятор площади поверхности цилиндра и калькулятор высоты цилиндра!

Как найти радиус цилиндра?

Калькулятор радиуса цилиндра является полезным инструментом, предназначенным для решения широкого круга различных задач.

1. Определите какие параметры цилиндра вам известны.
2. Введите значений выбранных величин.
3. Считать результат вычислений.

Разве это не просто? Кроме того, с помощью нашего калькулятора вы можете выбрать единицы измерения любого параметра, который вам нужен. Это может быть очень полезно во многих вычислениях! Если вы хотите узнать больше о преобразовании единиц измерения, обязательно ознакомьтесь с преобразователем длины и инструментом преобразования объема!

Как найти радиус цилиндра, зная его объем?

Чтобы определить радиус цилиндра по его объему, нужно также знать высоту (высоту) этого цилиндра:

1. Умножить высоту на .
2. Разделите объем на результат шага 1.
3. Извлеките квадратный корень из результата шага 2.
4. У вас есть радиус! Это было не так уж сложно, не так ли?

Как найти радиус, зная диаметр?

Чтобы определить радиус окружности (например, основания цилиндра), нужно диаметр разделить на . Например, если диаметр равен , то радиус равен .

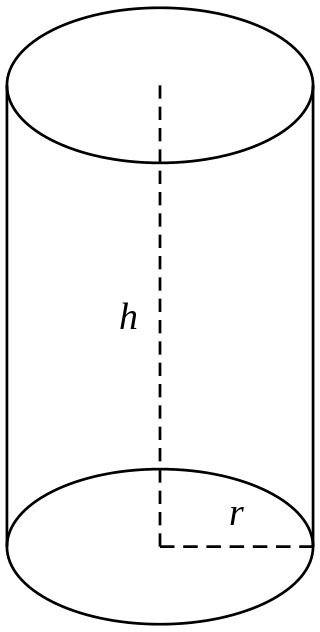
Каков радиус цилиндра?

Цилиндр — это твердое тело, имеющее два одинаковых круглых основания. Радиус цилиндра — это радиус основания этого цилиндра.

Доминик Черня, PhD

Высота (h)

Объем

Диагональный (D)

Свеча к объему к объему

Площади поверхности

Площадь базовой поверхности

Площадь боковой поверхности

Общая площадь поверхности

Радиус

Радиус (R)

Проверьте 21 Аналогичные геометрические калькуляторы

.

Площадь полушарияКубКуб Рассчитать: найти v, a, d… Еще 18

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
• Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
• Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
• Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
• Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
• Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
• Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
• Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
• Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
• Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.

Как вычислить площадь поверхности вращения, если линия задана в полярной системе координат?

Если кривая задана в полярных координатах уравнением , и функция   имеет непрерывную производную  на данном промежутке, то площадь поверхности, полученной вращением данной кривой вокруг полярной оси, рассчитывается по формуле , где  – угловые значения, соответствующие концам кривой.

В соответствии с геометрическим смыслом задачи подынтегральная функция , а это достигается только при условии  ( и  заведомо неотрицательны). Следовательно, необходимо рассматривать значения угла из диапазона , иными словами кривая должна располагаться выше полярной оси и её продолжения. Как видите, та же история, что и в двух предыдущих параграфах.

Пример 5

Вычислить площадь поверхности, образованной вращением кардиоиды  вокруг полярной оси.

Решение: график данной кривой можно посмотреть в Примере 6 урока о полярной системе координат. Кардиоида симметрична относительно полярной оси, поэтому рассматриваем её верхнюю половинку на промежутке  (что, собственно, обусловлено и вышесказанным замечанием).

Поверхность вращения будет напоминать яблочко.

Техника решения стандартна. Найдём производную по «фи»:

Составим и упростим корень: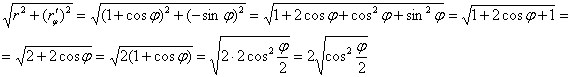
Надеюсь, с заштатными тригонометрическими формулами ни у кого не возникло затруднений.

Используем формулу: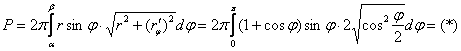

На промежутке , следовательно:  (о том, как правильно избавляться от корня, я подробно рассказал в статье Длина дуги кривой).

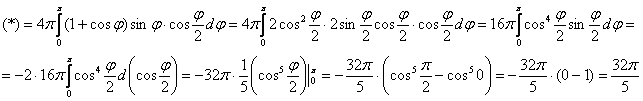Ответ:

Интересное и короткое задание для самостоятельного решения:

Пример 6

Вычислить площадь шарового пояса ,

Что такое шаровой пояс? Положите на стол круглый неочищенный апельсин и возьмите в руки нож. Сделайте два параллельных разреза, разделив тем самым фрукт на 3 части произвольных размеров. Теперь возьмите серединку, у которой сочная мякоть обнажилась с обеих сторон. Данное тело называется шаровым слоем, а ограничивающая её поверхность (оранжевая кожура) – шаровым поясом.

Читатели, хорошо знакомые с полярными координатами, легко представили чертёж задачи: уравнение  задаёт окружность с центром в полюсе радиуса , от которой лучи  отсекают меньшую дугу. Данная дуга вращается вокруг полярной оси и таким образом получается шаровой пояс.

Теперь можно с чистой совестью и лёгким сердцем съесть апельсинку, на этой вкусной ноте и завершим занятие, не портить же вам аппетит другими примерами =)

Решения и ответы:

Пример 2: Решение: вычислим площадь поверхности, образованной вращением верхней ветви  вокруг оси абсцисс. Используем формулу .В данном случае: ;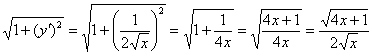Таким образом: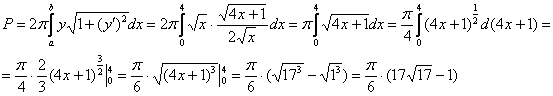Ответ

Пример 4: Решение: используем формулу . Первая арка циклоиды определена на отрезке .Найдём производные:Составим и упростим корень: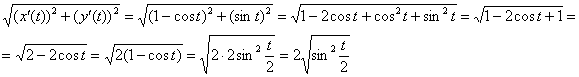Таким образом, площадь поверхности вращения: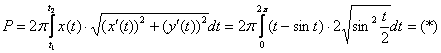На промежутке , поэтому 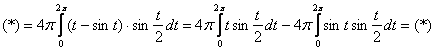Первый интеграл интегрируем по частям:Во втором интеграле используем тригонометрическую формулу .Ответ

Пример 6: Решение: используем формулу:Ответ

(Переход на главную страницу)

Как найти площадь круга и площадь поверхности цилиндра. Какую формулу вы используете?

Какова площадь круга?

Площадь определяется как объем пространства, занимаемый двумерной формой или поверхностью. Площадь измеряется путем взятия общего количества квадратов 1 на 1 единицу, которые могут поместиться в двумерную форму или поверхность.

Площадь круга может быть рассчитана с использованием следующей формулы:

Площадь круга

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍ A = Area of ​​Circle

π = 3.14 (rounded down) or 22/7

r = radius круга

‍

Пример задачи 1:

Найдите площадь круга, радиус которого равен 12 см.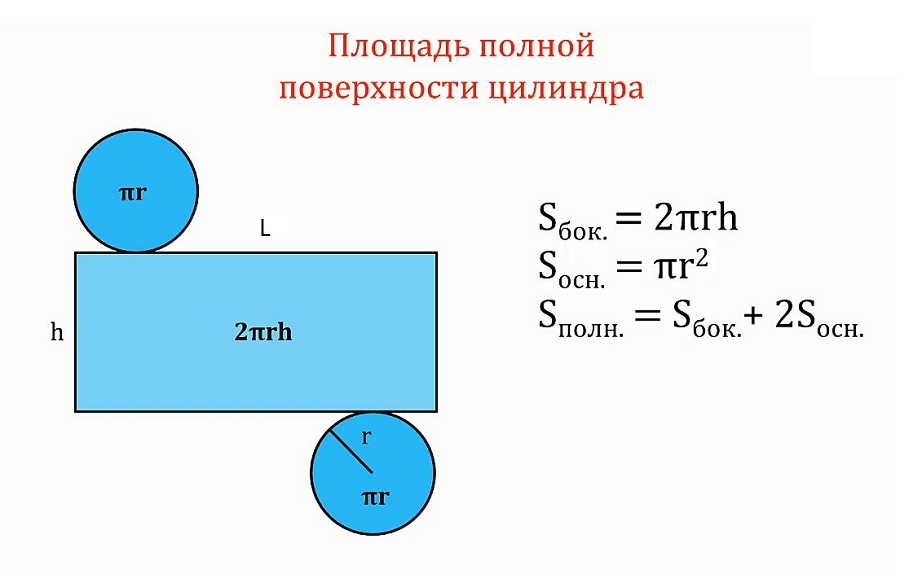

π.

Ответ:

Шаг 1 : Подставим радиус и π в формуле. Радиус равен 12, а π равно 3,14.

Шаг 2 : Упростите и запишите ответ в единицах измерения в квадрате.

Значит, площадь круга с радиусом 12 см равна 452,16 см в квадрате!

‍

Пример задачи 2:

Найдите площадь круга, диаметр которого равен 28 дюймам. Давайте на этот раз используем 22/7 для π .

Ответ:

Шаг 1 : Найдите радиус. Если диаметр 28 дюймов, то радиус равен 14. Это половина длины диаметра.

Шаг 2 : Подставим радиус и π в формулу. Радиус равен 12, а π равно 22/7.

Шаг 3: Просто рассчитайте площадь!

Итак, площадь круга диаметром 28 дюймов равна 616 дюймов в квадрате!

‍

Как площадь круга связана с нахождением площади поверхности цилиндра?

Площадь поверхности представляет собой сумму площадей всех поверхностей трехмерной фигуры.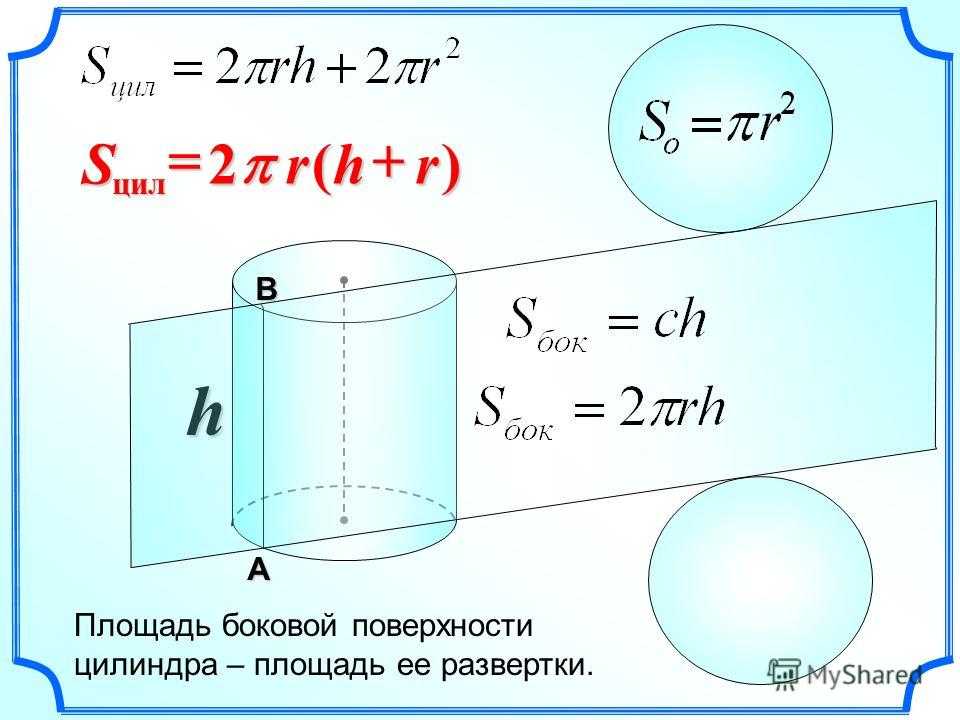

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

‍

В примере выше, в примере. фигура прямоугольной формы, которая на самом деле изогнута. Вам нужно будет найти площадь каждой части, а затем добавить сумму, чтобы получить площадь поверхности. В то время как для кругов используется нормальная формула площади круга, изогнутая прямоугольная фигура использует формулу длины окружности. Напомним, что площадь прямоугольника равна площади = длине х высоте, или A = l x h 9.0003

Как найти площадь поверхности цилиндра:

Площадь кругов   +   Площадь изогнутого прямоугольника  = Площадь поверхности                              

4 дюйма 6 дюймов

‍

Ответ:

Шаг 1 : Определите радиус и высоту.

r= 4 дюйма

h= 6 дюймов

Шаг 2: Подставьте значения в формулу.

‍

Шаг 3: Упрощение.

SA = 2 ((3,14 * 16) + 2 (3,14) (4) (6)

SA = 2 (3,14 * 16) + 2 (75,36)

SA = 2 (50,24) + 2 (75,36)

SA = 100,48 + 150,72

SA = 251,2 дюйма в квадрате

‍

Таким образом, площадь поверхности цилиндра с радиусом 4 дюйма и высотой 6 дюймов равна 251,2 дюйма в квадрате.

‍

Пример задачи 4. Цилиндр:

Найдите площадь поверхности этого цилиндра. Используйте 3,14 как π.

Ответ:

Шаг 1 : Определите радиус и высоту.

r= 5 см и h=9,5 см

‍

Шаг 2: Подставьте значения в формулу.

Шаг 3 : Упрощение.

«Компоненты» стереометрической фигуры

Цилиндр состоит из нескольких составляющих.

1. Цилиндрическая поверхность — это поверхность, которая образуется большим количеством параллельных прямых, проходящих через точки некоторой кривой.
2. Основания — это плоские фигуры, которые образованы пересечением ЦП с двумя параллельными плоскостями, ограничивающими цилиндр. Оснований у цилиндра два.
3. Боковой поверхностью называют часть ЦП, которая находится между основаниями.
4. И, наконец, высота — это отрезок, который высекается плоскостями оснований цилиндра на прямой, перпендикулярной им.

Примечание

Дополнительно можно измерить периметр S_бок. Для этого нужно длину окружности l сложить с высотой h и умножить данную сумму на 2.

Рассмотрим, как различаются типы рассматриваемой геометрической фигуры по форме. Цилиндр может быть:

1. Прямой. Его основания имеют центры симметрии, то есть являются кругами или эллипсами. При этом прямая между центрами перпендикулярна плоскостям оснований. Данная прямая называется осью цилиндра.
2. Косой. Его основания имеют центры симметрий, однако отрезок между ними не перпендикулярен плоскостям оснований.
3. Круговой. Имеет окружность в роли направляющей.
4. Прямой круговой. Его можно получить с помощью вращения прямоугольника вокруг одной из его сторон. Тогда эта сторона будет осью цилиндра и осью симметрии.
5. Равносторонний. Его диаметр равен высоте.
6. Эллиптический, гиперболический и параболический. Образованы соответственно эллипсами, гиперболами и параболами.
7. Усеченный. Геометрическое тело, которое отсекается от цилиндра плоскостью, не параллельной основанию.
8. Призма. Является разновидностью цилиндра, если имеет основание в виде многоугольника.

Объём стенки цилиндра

Чтобы посчитать объём стенки цилиндра

, то есть объём полого цилиндра, воспользуйтесь нашим очень удобным онлайн калькулятором:

Найти чему равен объём полого цилиндра

(Vст) можно зная (либо-либо):

• Высоту цилиндра h , внешний радиусr1 и внутренний радиусr2
• Высоту цилиндра h , внешний диаметрd1 и внутренний диаметрd2
• Высоту цилиндра h , внешний радиусr1 и толщину стенкиδ
• Высоту цилиндра h , внутренний радиусr2 и толщину стенкиδ
• Высоту цилиндра h , внешний диаметрd1 и толщину стенкиδ
• Высоту цилиндра h , внутренний диаметрd2 и толщину стенкиδ

Чему равен объём полого цилиндраVст

если:

Через радиусы или диаметры цилиндра

Vст = π ⋅ (r1² — r2²) ⋅ h , где r1

— внешний радиус,r2 — внутренний радиус , аh — высота

Vст = π ⋅ ((d1/2)² — (d2/2)²) ⋅ h , где d1

— внешний диаметр,d2 — внутренний диаметр, аh — высота

Через толщину стенки цилиндра

Vст = π ⋅ (d2 ⋅ δ + δ²) ⋅ h , где δ

— толщина стенки цилиндра,d2 — внутренний диаметр, аh — высота

Vст = π ⋅ ((d1 — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ

— толщина стенки цилиндра,d1 — внешний диаметр, аh — высота

Vст = π ⋅ ((2 ⋅ r1 — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ

— толщина стенки цилиндра,r1 — внешний радиус, аh — высота

ЭТО ИНТЕРЕСНО: Какая рабочая температура автомобильного генератора

Пример №1

К примеру, посчитаем каков объём металла в трубе, если её длинна 3 метра, внешний диаметр d1=5 см, а внутренний d2=4.5 см?

Vст = 3.14 ⋅ ((5/2)² — (4.5/2)²) ⋅ 300 = 3.14 ⋅ (6.25 — 5.0625) ⋅ 300 ≈ 1119 см³

Пример №2

Теперь посчитаем объём металла в этой же 3-х метровой трубе, но возьмём внутренний радиус r2 = 2.25 см и толщину стенки δ = 0.25 см (при этом у нас должен получится тот же ответ, что и в предыдущем примере):

Vст = 3.14 ⋅ (2 ⋅ 2.25 ⋅ 0.25 + 0.25²) ⋅ 300 = 3.14 ⋅ 1.1875 ⋅ 300 ≈ 1119 см³

Перевод объёма в массу

Объём цилиндра

Конвертер единиц объёма

Что такое цилиндр

Разработка инженерных чертежей зданий, сооружений, оборудования начинается с самых простых фигур геометрии

Цилиндры применяют повсеместно, что объясняет важность умения рассчитывать их основные параметры, в том числе площадь. Цилиндром также называют классический головной убор

Цилиндрическую форму имеют трубы, архитектурные компоненты зданий, посуда, разнообразные резервуары.

Использование в производстве продукции именно такой формы позволяет значительно сократить затраты. К примеру, на изготовление сосуда в виде цилиндра уходит меньше материала, чем на выпуск аналогичных товаров в форме параллелепипеда. Это объясняется разницей в величинах площади боковой поверхности материального тела.

Цилиндрические предметы удобнее держать в руках и размещать в местах хранения. По этой причине бутыли с жидкостями разного состава, которые используют в медицине, салонах красоты и других сферах, имеют цилиндрическую форму. Многие химические вещества, в том числе, газы, агрессивные среды, нефтепродукты, масла, транспортируют в цистернах в виде цилиндров. Это связано с отсутствием уязвимых мест и максимальной герметичностью подобных резервуаров. В цилиндрической емкости центр тяжести находится ниже, чем в контейнере прямоугольной формы, что обеспечивает стабильность положения заполненного резервуара. Кроме того, давление на стенки цилиндра с жидкостью или газом распределяется более равномерно.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Цилиндром называют некое тело в геометрии, внутренние границы которого обозначены цилиндрической поверхностью и парой плоскостей, расположенных параллельно относительно друг друга и пересекающих эту поверхность.

Разберем основные понятия, с которыми часто сталкиваются школьники в процессе решения геометрических задач. К примеру, материальное тело обладает некой поверхностью

Величину площади этой поверхности важно знать для проведения вычислений в теории и на практике

Цилиндрическая поверхность представляет собой такую поверхность, которая сформирована с помощью параллельных прямых и некой кривой, называемой направляющей.

Цилиндр обладает основаниями, которые можно измерить. Они являются плоскими геометрическими фигурами. Для того чтобы получить основания, необходимо пересечь цилиндрическую поверхность парой плоскостей, расположенных параллельно по отношению друг к другу. Тот участок поверхности, который разделяет плоскости цилиндрических оснований, обозначают за боковую поверхность цилиндра. Плоскости оснований цилиндра высекают в своем перпендикуляре некий отрезок, называемый высотой цилиндра.

Существуют следующие виды цилиндров:

1. Прямой цилиндр с основаниями в виде кругов или эллипсов. В этом случае цилиндрическая ось расположена между центральными точками симметрии и является перпендикуляром к основаниям.
2. Косой цилиндр отличается от прямого геометрического тела расположением оси, то есть данный отрезок не перпендикулярен цилиндрическим основаниям.
3. Круговой цилиндр имеет направляющую в виде окружности.
4. Прямой круговой цилиндр (цилиндр вращения) получают в результате вращательного движения прямоугольника относительно какой-то стороны.
5. Эллиптический, параболический, гиперболический цилиндры названы так по форме основания, которые имеют вид эллипсов, парабол, гипербол соответственно. В случае параболического и гиперболического цилиндров объем измеряется бесконечностью.
6. Призма представляет собой цилиндр с основанием, которое обладает формой многоугольника.
7. Равносторонний цилиндр является таким цилиндром вращения, в котором наблюдается равенство диаметра основания и цилиндрической высоты.

Примечание 1

При параллельном расположении плоскостей основания и направляющей цилиндра форма границы данного основания идентична направляющей кривой.

Для чего нужны расчеты параметров труб

В современном строительстве используются не только стальные или оцинкованные трубы. Выбор уже довольно широк — ПВХ, полиэтилен (ПНД и ПВД), полипропилен, металлопластк, гофрированная нержавейка. Они хороши тем, что имеют не такую большую массу, как стальные аналоги. Тем не менее, при транспортировке полимерных изделий в больших объемах знать их массу желательно — чтобы понять, какая машина нужна. Вес металлических труб еще важнее — доставку считают по тоннажу. Так что этот параметр желательно контролировать.

То, что нельзя измерить, можно рассчитать

Знать площадь наружной поверхности трубы надо для закупки краски и теплоизоляционных материалов. Красят только стальные изделия, ведь они подвержены коррозии в отличие от полимерных. Вот и приходится защищать поверхность от воздействия агрессивных сред. Используют их чаще для строительства заборов, каркасов для хозпостроек (гаражей, сараев, беседок, бытовок), так что условия эксплуатации — тяжелы, защита необходима, потому все каркасы требуют окраски. Вот тут и потребуется площадь окрашиваемой поверхности — наружная площадь трубы.

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью. Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

Рис.3

На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA1B1B .

Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .

Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).

Рис.4

Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

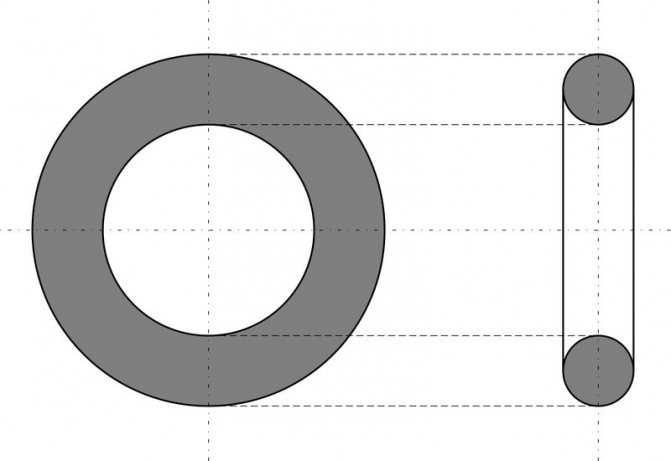
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».

Примеры задач

Задание №1.
Дан прямой цилиндр, площадь основания которого 12,56 см 2 . Необходимо вычислить полную площадь цилиндра, если его высота равна 3 см.

Решение. Необходимо воспользоваться формулой для полной площади кругового прямого цилиндра. Но в ней не хватает данных, а именно радиуса основания. Зато известна площадь круга. Из нее легко вычислить радиус.

Он оказывается равным квадратному корню из частного, которое получается от деления площади основания на пи. После деления 12,56 на 3,14 выходит 4. Квадратный корень из 4 — это 2. Поэтому радиус будет иметь именно такое значение.

Ответ: S пол = 50,24 см 2 .

Задание №2.
Цилиндр с радиусом 5 см пресечен плоскостью, параллельной оси. Расстояние от сечения до оси равно 3 см. Высота цилиндра — 4 см. Требуется найти площадь сечения.

Решение. Форма сечения — прямоугольная. Одна его сторона совпадает с высотой цилиндра, а другая равна хорде. Если первая величина известна, то вторую нужно найти.

Для этого следует сделать дополнительное построение. В основании проводим два отрезка. Оба они будут начинаться в центре окружности. Первая будет заканчиваться в центре хорды и равняться известному расстоянию до оси. Вторая — на конце хорды.

Получится прямоугольный треугольник. В нем известны гипотенуза и один из катетов. Гипотенуза совпадает с радиусом. Второй катет равен половине хорды. Неизвестный катет, умноженный на 2, даст искомую длину хорды. Вычислим его значение.

Для того чтобы найти неизвестный катет, потребуется возвести в квадрат гипотенузу и известный катет, вычесть из первого второе и извлечь квадратный корень. Квадраты равны 25 и 9. Их разность — 16. После извлечения квадратного корня остается 4. Это искомый катет.

Хорда будет равна 4 * 2 = 8 (см). Теперь можно вычислить площадь сечения: 8 * 4 = 32 (см 2).

Ответ: S сеч равна 32 см 2 .

Задание №3.
Необходимо вычислить площадь осевого сечения цилиндра. Известно, что в него вписан куб с ребром 10 см.

Решение. Осевое сечение цилиндра совпадает с прямоугольником, который проходит через четыре вершины куба и содержит диагонали его оснований. Сторона куба является образующей цилиндра, а диагональ основания совпадает с диаметром. Произведение этих двух величин даст площадь, которую нужно узнать в задаче.

Для поиска диаметра потребуется воспользоваться знанием того, что в основании куба — квадрат, а его диагональ образует равносторонний прямоугольный треугольник. Гипотенуза его является искомой диагональю фигуры.

Для ее расчета потребуется формула теоремы Пифагора. Нужно возвести в квадрат сторону куба, умножить ее на 2 и извлечь квадратный корень. Десять во второй степени — это сто. Умноженное на 2 — двести. Квадратный корень из 200 равен 10√2.

Сечение — это снова прямоугольник со сторонами 10 и 10√2. Его площадь легко сосчитать, перемножив эти значения.

Ответ. S сеч = 100√2 см 2 .

Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.

Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.

Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.

Цилиндр, его элементы и виды цилиндров

Наиболее распространенным видом цилиндра в геометрии является прямой круговой цилиндр. Введем его определение.

По определению понятно, почему в некоторых случаях эту фигуру называют цилиндром вращения.

На рисунке выше изображен цилиндр, который является результатом вращения прямоугольника АВСD вокруг оси, обозначенной О1О2. Поворот происходит на 180°. Аналогичный итог получаем, если повернуть ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.

Перечислим ключевые элементы цилиндра:

1. Основания цилиндра в виде пары идентичных по габаритам и площади круга с центральными точками, обозначенными за О1 и О2.
2. R определяет радиус, который имеют основания геометрической фигуры.
3. AD и BC являются диаметрами (d) оснований цилиндра.
4. O1O2 представляет собой ось симметрии рассматриваемого цилиндра, а также играет роль его высоты (h).
5. l (AB, CD) в виде образующих цилиндра являются сторонами прямоугольника ABCD, которые соответствуют высоте геометрической фигуры.

Представим изображение развертки цилиндра:

Заметим справедливость следующих соотношений:

• рассматриваемый прямоугольник имеет длину, равную длине окружности основания цилиндра ;
• ширина соответствует высоте (образующей) цилиндра.

Геометрическая фигура в виде цилиндра может обладать следующими видами сечений:

1. Осевое сечение имеет прямоугольную форму, сформировано при пересечении цилиндра плоскостью, которая пролегает через ее ось. На примере первого рисунка осевым сечением является АВСD. Определить площадь данного сечения легко, достаточно умножить высоту цилиндра на диаметр его основания.

2. Сечение в виде прямоугольника образуется в том случае, когда секущая плоскость не пересекает ось фигуры, но расположена перпендикулярно по отношению к основаниям цилиндра.

3. Сечение в виде аналогичного основаниям цилиндра круга образовано при условии параллельности секущей плоскости основаниям рассматриваемой фигуры. 

4. При пересечении цилиндра плоскостью, которая не является параллельной его основаниям и не пересекается с ними, образуется сечение в виде эллипса. 

5. Сечение в виде параболы и гиперболы сформировано путем пересечения секущей плоскости с одним из оснований цилиндра.

Рассмотрим основные виды цилиндров с примерами, которые часто встречаются на уроках в классе. Сначала разберемся с понятием прямого цилиндра.

Данная фигура обладает идентичными основаниями, расположенными симметрично и параллельно, в виде круга или эллипса. Отрезок, соединяющий точки симметрии оснований, является перпендикуляром к этим основаниям, осью симметрии и равен высоте фигуры.

Наклонный цилиндр обладает идентичными основаниями, которые расположены параллельно относительно друг друга. Отрезок, соединяющий точки симметрии, не перпендикулярен к основаниям фигуры.

Косой, или скошенный, цилиндр отличается расположением оснований. В данном случае они расположены не параллельно друг другу.

В круговом цилиндре основания имеют форму кругов.

Существуют также такие разновидности цилиндров:

• эллиптические;
• параболические;
• гиперболические.

Равносторонний цилиндр представляет собой прямой круговой цилиндр с основанием, диаметр которого соответствует высоте фигуры.

Заключение

В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.

Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе

И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей

Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.

У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.

Вершина и основание цилиндра являются окружностями, их легко определить.

Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .

Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).

После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.

Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.

Формула площади боковой поверхности цилиндра
S бок. = 2πrh