Трапеция, ее свойства, формулы площади, высоты, сторон

Послесловие

Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.

Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.

Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!

blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Доказательство свойств высоты равнобокой трапеции

Шаг 1

Рассмотрим равнобедренную трапецию ABCD (AB = CD). Из вершины B к основанию AD проводим высоту BH. Докажем, что точка H делит сторону AD на отрезки следующих длин:

Доказательство свойства высоты равнобедренной трапеции. Шаг 1

Шаг 2

Нарисуем высоту КА.

Рассмотрим четырехугольник NVSK, образовавшийся.

Поскольку все углы этого четырехугольника прямые по построению, NVSC является прямоугольником.

По свойству сторон прямоугольника:

Доказательство свойства высоты равнобедренной трапеции. Шаг 2

Шаг 3

Рассмотрим прямоугольные треугольники AHB и CKD.

АВ = CD — по условию;

HH = SK — как высота трапеции.

На основании подобия прямоугольных треугольников по катету и гипотенузе:

Из свойств подобных треугольников следует равенство сторон:

Доказательство свойства высоты равнобедренной трапеции. Шаг 3

Шаг 4

Рассмотрим сторону AD.

После строительства:

С учетом полученных ранее равенств (AH = KD, NK = BC) можно переписать последнюю формулу:

Отсюда:

Теперь найдем длину отрезка HD:

Так:

Таким образом, мы определили длины отрезков, образованных высотой равнобедренной трапеции, проведенной от вершины к большему основанию.

Итак, мы доказали свойства, которыми обладает высота равнобедренной трапеции.

Доказательство свойства высоты равнобедренной трапеции. Шаг 4

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Определение.

Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.

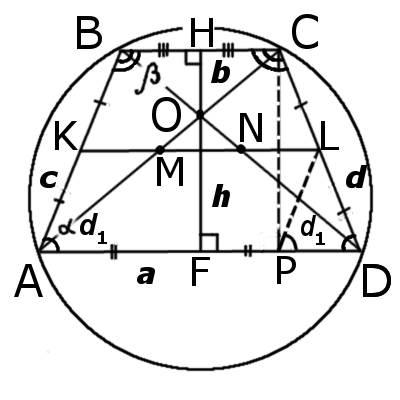Рис.1

Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны:

∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны:

AC = BD

3. Одинаковые углы между диагоналями и основаниями:

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

Основные свойства равнобедренной трапеции

1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:

AB = CD = m

3. Вокруг равнобедренной трапеции можно описать окружность

4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):

h = m

5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:

S_ABCD = h2

6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:

h2 = BC · AD

7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:

AC2 + BD2 = AB2 + CD2 + 2BC · AD

8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:

HF ┴ BC, HF ┴ AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

1. Формулы длины сторон через другие стороны, высоту и угол:

a = b + 2h ctg α = b + 2c cos α

b = a — 2h ctg α = a — 2c cos α

c =	h	=	a — b
sin α	2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d₁2 — c2	b =	d₁2 — c2	c = √d₁2 — ab
b	a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	— b b =	2S	— a
h	h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

1. Формула определения длины средней линии через основания, высоту и угол при основании:

m = a — h ctg α = b + h ctg α = a — √c2 — h2 = b + √c2 — h2

2. Формула средней линии трапеции через площадь и сторону:

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a — b	tg β	= c sin β
2

Диагонали равнобедренной трапеции

Диагонали равнобедренной трапеции равны:

d₁ = d₂

Формулы длины диагоналей равнобедренной трапеции:

1. Формула длины диагонали через стороны:

d₁ = √с2 + ab

2. Формулы длины диагонали по теореме косинусов:

d₁ = √a2 + c2 — 2ac cos α

d₁ = √b2 + c2 — 2bc cos β

3. Формула длины диагонали через высоту и среднюю линию:

d₁ = √h2 + m2

4. Формула длины диагонали через высоту и основания:

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√4c2 — (a — b)2
4

2. Формула площади через стороны и угол:

S = (b + c cos α) c sin α = (a — c cos α) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
sin α	sin β

4. Формула площади через основания и угол между основой и боковой стороной:

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = (a + b) · r = √ab·c = √ab·m

6. Формула площади через диагонали и угол между ними:

S =	d₁2	· sin γ	=	d₁2	· sin δ
2	2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Примеры задач

№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.

Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).

Теперь нужно воспользоваться подходящей формулой для площади:

S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм2). Задача решена.

Ответ: площадь трапеции равна 4,5 дм2.

№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.

Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.

Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.

Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.

Таким образом, площадь трапеции равна 5 * 4 = 20 см2.

Ответ: S = 20 см2.

№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.

Решение. Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).

Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.

S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см2).

Ответ: Искомая площадь равна 45 см2.

№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.

Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.

Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н₁, большей АОЕД — н₂.

Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:

(х + а₂) * н₁ = 1/5 (х + а₁) * н₂

или

н₁ /н₂ = (х + а₁) / (5(х + а₂)).

Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:

н₁ /н₂ = (х — а₂) / (а₁ — х).

В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а₁) / (5(х + а₂)) равно (х — а₂) / (а₁ — х).

Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.

В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.

Ответ: х = √ {(а₁2 + 5 а₂2 ) / 6}.

Как найти высоту прямоугольной трапеции?

Если трапеция — это четырехугольник, с двумя параллельными сторонами (основаниями) трапеции. То диагональ — это отрезок, который соединяющий две противоположные вершины углов трапеции (отрезок АС на рисунке). Если трапеция прямоугольная, с помощью диагонали, найдем величину высоты трапеции h.

Прямоугольной трапецией называется такая трапеция, где одна из боковых сторон перпендикулярна основаниям. В этом случае ее длина (АД) совпадает с высотой h.

Итак, рассмотрим прямоугольную трапецию ABCD, где AD — это высота, DC — это основание, AC — это диагональ. Воспользуемся теоремой Пифагора. Квадрат гипотенузы AC прямоугольного треугольника ADC равен сумме квадратов его катетов AB и BC.

Тогда можно записать:

AC² = AD² + DC².

AD — это катет треугольника, боковая сторона трапеции и, в то же время, ее высота. Ведь отрезок АД перпендикулярен основаниям. Его длина составит:

AD = √(AC² — DC²)

Итак, имеем формулу для вычисления высоты трапеции h = AD

Пример

Если длина основания прямоугольной трапеции(DC) равна 14 см, а диагональ (AC) составляет 15 см, для получения значения высоты(AD -боковой стороны) воспользуемся теоремой Пифагора.

Пусть х — это неизвестный катет прямоугольного треугольника(AD), тогда

AC² = AD² + DC² можно записать

15² = 14² + х²,

х = √(15²-14²) = √(225-196) = √29 см

Ответ: высота прямоугольной трапеции (АВ) составит √29 см, что приблизительно составит, 5.385 см

Задачи

№1. На определение углов при нижнем основании трапеции.

Условие.
Дана равнобедренная трапеция, боковая сторона которой 5 см. Ее основания равны 6 и 12 см. Требуется найти синус острого угла.

Решение.
Для удобства следует ввести обозначение. Пусть левая нижняя вершина будет А, все остальные по часовой стрелке: В, С, Д. Таким образом, нижнее основание будет обозначено АД, верхнее — ВС.

Нужно провести высоты из вершин В и С. Точки, которые укажут концы высот будут обозначены Н 1 и Н 2 , соответственно. Поскольку в фигуре ВСН 1 Н 2 все углы прямые, то она является прямоугольником. Это означает, что отрезок Н 1 Н 2 равен 6 см.

Теперь нужно рассмотреть два треугольника. Они равны, так как являются прямоугольными с одинаковыми гипотенузами и вертикальными катетами. Отсюда следует, что и меньшие катеты у них равны. Поэтому их можно определить как частное от разности. Последняя получится от вычитания из нижнего основания верхнего. Делиться оно будет на 2. То есть 12 — 6 нужно поделить на 2. АН 1 = Н 2 Д = 3 (см).

Теперь из теоремы Пифагора нужно найти высоту трапеции. Она необходима для нахождения синуса угла. ВН 1 = √(5 2 — 3 2) = 4 (см).

Воспользовавшись знанием о том, как находится синус острого угла в треугольнике с прямым углом, можно записать такое выражение: sin α= ВН 1 / АВ = 0,8.

Ответ.
Искомый синус равен 0,8.

№2. На нахождение высоты трапеции по известному тангенсу.

Условие.
У равнобедренной трапеции нужно вычислить высоту. Известно, что ее основания равны 15 и 28 см. Дан тангенс острого угла: 11/13.

Решение.
Обозначение вершин такое же, как в предыдущей задаче. Снова нужно провести две высоты из верхних углов. По аналогии с решением первой задачи нужно найти АН 1 = Н 2 Д, которые определятся как разность 28 и 15, деленная на два. После подсчетов получается: 6,5 см.

Поскольку тангенс — это отношение двух катетов, то можно записать такое равенство: tg α= АН 1 / ВН 1 . Причем это отношение равно 11/13 (по условию). Так как АН 1 известен, то можно вычислить высоту: ВН 1 = (11 * 6,5) / 13. Простые расчеты дают результат в 5,5 см.

Ответ.
Искомая высота равна 5,5 см.

№3. На вычисление высоты по известным диагоналям.

Условие.
О трапеции известно, что ее диагонали равны 13 и 3 см. Нужно узнать ее высоту, если сумма оснований составляет 14 см.

Решение.
Пусть обозначение фигуры будет таким же, как раньше. Предположим, что АС — меньшая диагональ. Из вершины С нужно провести искомую высоту и обозначить ее СН.

Теперь потребуется выполнить дополнительное построение. Из угла С нужно провести прямую, параллельную большей диагонали и найти точку ее пересечения с продолжением стороны АД. Это будет Д 1 . Получилась новая трапеция, внутри которой начерчен треугольник АСД 1 . Он-то и нужен для дальнейшего решения задачи.

Искомая высота окажется еще и ей же в треугольнике. Поэтому можно воспользоваться формулами, изученными в другой теме. Высота треугольника определяется как произведение числа 2 и площади, деленное на сторону, к которой она проведена. А сторона оказывается равна сумме оснований исходной трапеции. Это исходит из правила, по которому выполнено дополнительное построение.

В рассматриваемом треугольнике все стороны известны. Для удобства введем обозначения х = 3 см, у = 13 см, z = 14 см.

Теперь можно сосчитать площадь, воспользовавшись теоремой Герона. Полупериметр будет равен р = (х + у + z)/ 2 = (3 + 13 + 14) / 2 = 15 (см). Тогда формула для площади после подстановки значений будет выглядеть так: S = √(15 * (15 — 3) * (15 — 13) * (15 — 14)) = 6 √10 (см 2).

Ответ.
Высота равна 6√10 / 7 см.

№4. Для поиска высоты по сторонам.

Условие.
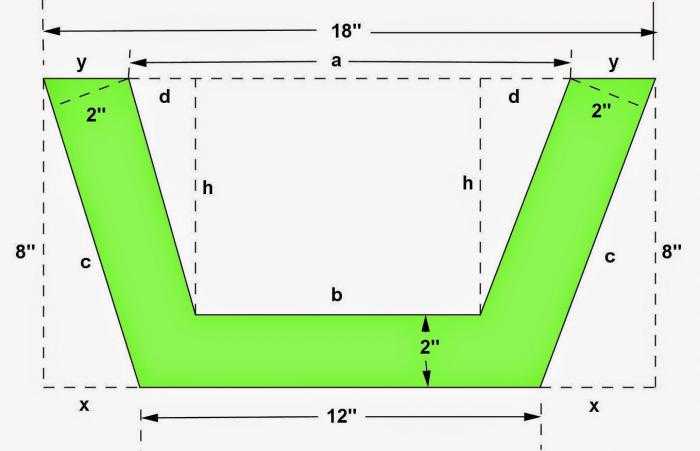
Дана трапеция, три стороны которой равны 10 см, а четвертая 24 см. Нужно узнать ее высоту.

Решение.
Поскольку фигура равнобедренная, то потребуется формула под номером 2. В нее нужно просто подставить все значения и сосчитать. Это будет выглядеть так:

н = √(10 2 — (10 — 24) 2 /4) = √51 (см).

Ответ.
н = √51 см.

Геометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?

Свойства диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства трапеции, достроенной до треугольника

совпадать с прямой линией, которая проходит через середины оснований

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, параллельного основаниям трапеции

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Свойства трапеций: определение и теорема

Трапеция

Четырехугольник, имеющий только одну пару параллельных сторон, называется трапецией .

Трапеция, у которой непараллельные стороны равны, равна равнобедренной трапеции .

Свойство трапеции, связанное с углами при основании

Теорема 1:

В равнобедренной трапеции каждая пара углов при основании конгруэнтна.

Дано: ABCD — трапеция, где AB∥CD.

Чтобы доказать: ∠ADC = ∠BCD и ∠BAD = ∠ABC

Доказательство:

Проведите перпендикулярные линии AE и BF между параллельными сторонами трапеции.

в ΔAED и ΔBFC,

AD = BC

AE = BF

omaEB = = 90 °

Если у двух прямоугольных треугольников гипотенузы равны по длине, а пара более коротких сторон равна по длине, то треугольники конгруэнтны.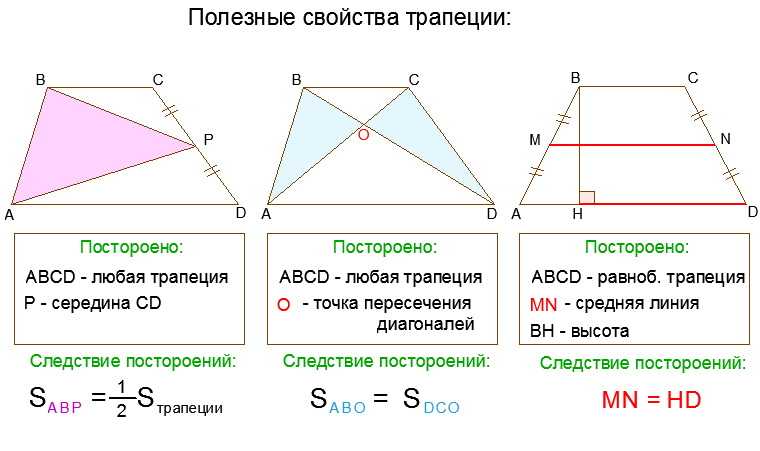

∴ ΔAED ≌ ΔBFC

Мы знаем, что соответствующие части конгруэнтных треугольников равны.

потряно РАД

∠BAD = ∠ABC

Следовательно, каждая пара углов при основании равнобедренной трапеции конгруэнтна.

Свойство трапеции, связанное с длиной диагоналей

Теорема 2:

Диагонали равнобедренной трапеции конгруэнтны.

Приведено: в трапециевии ABCD, AB∥CD и AD = BC

, чтобы доказать: AC = BD

Доказательство:

в ΔAdc и ΔBCD,

AD = BCESESIS ISOSCZESIOD].

CD = CD

Следовательно, ΔAed ≌ ΔBFC

Мы знаем, что соответствующие части конгруэнтных треурианцев равны.

Итак, AC = BD

Следовательно, диагонали равнобедренной трапеции равны.

Свойство трапеции, связанное с длиной диагоналей

Теорема 3:

В трапеции средний сегмент параллелен основаниям, а длина среднего сегмента равна половине суммы длин оснований.

Дано: В трапеции ABCD AB∥CD, X — середина AD, Y — середина BC.

Чтобы доказать: XY = 1/2 × (AB+CD)

Доказательство: Постройте BD так, чтобы середина BD проходила через XY.

В ΔADB X — это середина AD, а M — середина DB.

Итак, XM — это середина ΔADB.

Мы знаем, что отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и имеет длину, равную половине длины третьей стороны.

∴ XM ∥ AB и XM = 1/2 × AB …(1)

В ΔBCD Y — середина BC, а M — середина BD.

Итак, MY — это середина ΔBCD.

∴ MY ∥ CD и MY = 1/2 × CD …(2)

Поскольку XM ∥ AB и MY ∥ CD, то XY

Теперь XY=XM+MY

2 × AB + 1/2 × CD

XY = 1/2 × (AB+CD)

Воздушный змей

Воздушный змей — это два равных четырехугольника, четыре стороны которых можно сгруппировать в группы.

(или)

Параллелограмм также имеет две пары сторон одинаковой длины, но они противоположны друг другу в воздушном змее .

Только одна диагональ воздушного змея делит пополам другую диагональ.

Свойство воздушного змея, связанное с углом между диагоналями

Теорема:

Диагонали воздушного змея перпендикулярны.

Дано: В змее WXYZ, XY=YZ, WX=ZW

Доказать: XZ Ʇ WY

Доказательство: Проведите диагонали XZ и WY. Пусть диагонали пересекаются в O.

в ΔWxy и ΔWzy,

Wx = WZ

xy = zy

Wy = YW

δ ΔWxy ≌ ≌ ≌ wxy ≌. ΔWZY

Мы знаем, что соответствующие части конгруэнтных треугольников равны.

Итак, ∠XYW= ∠ZYW …(1)

в Δoxy и Δozy,

xy = ZY

OY = yo

δ Δoxy Δozy .

Применяем смекалку

Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.

Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.

Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.

Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.

Примеры задач на понятие средней линии трапеции

Пример 1

Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.

Решение.

Обозначим среднюю линию трапеции через $n$.

Сумма боковых сторон равна

Следовательно, так как периметр равен $52\ см$, сумма оснований равна

Значит, по теореме 1, получаем

Ответ:
$10\ см$.

Пример 2

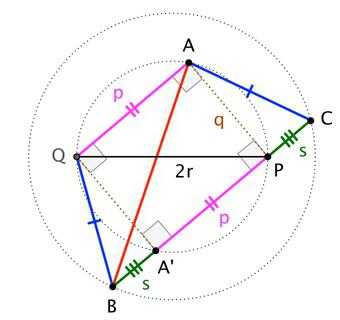
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.

Решение.

Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).

Рисунок 2.

Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем

Средняя линия трапеции равна полусумме
оснований. Она соединяет середины боковых сторон трапеции и всегда параллельна основаниям.

Если основания трапеции равны a и b, то средняя линия m равна
m=(a+b)/2.

Если известна площадь трапеции, то среднюю линию можно найти
и другим способом, разделив площадь трапеции S на высоту трапеции h:

То есть, средняя линия трапеции
m=S/h

Способов найти длину средней линии трапеции много. Выбор способа зависит от исходных данных.

Вот формулы длины средней линии трапеции
:

Чтобы найти среднюю линию трапеции, можно воспользоваться одной из пяти формул (выписывать их не буду, так как они уже есть в других ответах), но это только в тех случаях, когда известны нужные нам значения исходных данных.

На практике приходится решать много задач, когда данных недостаточно, а нужный размер нужно все таки найти.

Здесь есть такие варианты

пошаговым решением подвести все таки под формулу;

используя другие формулы, составить и решить необходимые уравнения.

нахождения длины середины трапеции методом подвода под нужную нам формулу
с помощью других знаний о геометрии и применяя при этом алгебраические уравнения:

Имеем равнобедренную трапецию, ее диагонали пересекаются под прямым углом, высота равна 9 см.

Делаем рисунок и видим, что в лоб эту задачу не решить (недостаточно данных)

Поэтому мы немного упростим и проведем высоту через точку пересечения диагоналей.

Это первый важный шаг, который ведет к быстрому решению.

обозначим высоту двумя неизвестными, увидим нужные нам равнобедренные треугольники со сторонами х
и у

и уже легко найдем сумму оснований
трапеции

она равна 2х+2у

И вот только теперь мы можем применить формулу где

и равна она х+у
а по условию задачи это длина высоты равная 9 см
.

И вот теперь мы вывели несколько моментов для равнобедренной трапеции, диагонали которой пересекаются под прямым углом

в таких трапециях

средняя линия всегда равна высоте

площадь всегда равна квадрату высоты
.

Средняя линия трапеции это отрезок, который соединяет середины боковых сторон трапеции.

Среднюю линию любой трапеции несложно найти, если пользоваться формулой:

m = (a + b)/2

m длина средней линии трапеции;

a, b длины оснований трапеции.

Итак, длина средней линии трапеции равна полусумме длин оснований
.

Основная формула для формулы средней линии трапеции:длина средней линии трапеции равна полусумме е оснований a и b: MN=(a+b)2.Доказательством этой формулы служит формула для средней линии треугольника.Любая трапеция может быть представлена после того как проведены из концов меньшего основания высоты на большее основание.Рассматриваются 2 полученных треугольника,и прямоугольник.После этого легко доказывается формула для средней линии трапеции.

Чтобы найти среднюю линию трапеции нам нужно знать величины оснований.

После того,как нашли эти величины или может быть они нам были известны,то складываем эти числа и просто делим пополам.

Это и будет средняя линия трапеции
.

Насколько я помню уроки школьной геометрии, для того, чтобы найти длину средней линии трапеции, нужно сложить длины оснований и разделить на два. Таким образом длина средней линии трапеции, равна полусумме оснований.

Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.

Послесловие

Похожие вопросы

Доказательство свойств высоты равнобокой трапеции

Шаг 1

Шаг 2

Шаг 3

Шаг 4

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Признаки равнобедренной трапеции

Основные свойства равнобедренной трапеции

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

Диагонали равнобедренной трапеции

Формулы длины диагоналей равнобедренной трапеции:

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

Окружность описанная вокруг трапеции

Примеры задач

Как найти высоту прямоугольной трапеции?

Пример

Задачи

Свойства диагоналей трапеции

Свойства трапеции, достроенной до треугольника

Свойства отрезка, параллельного основаниям трапеции

Свойства трапеций: определение и теорема

Трапеция

Свойство трапеции, связанное с углами при основании

Теорема 1:

Свойство трапеции, связанное с длиной диагоналей

Теорема 2:

Свойство трапеции, связанное с длиной диагоналей

Теорема 3:

Воздушный змей

Свойство воздушного змея, связанное с углом между диагоналями

Теорема:

Применяем смекалку

Примеры задач на понятие средней линии трапеции

Похожие записи:

Похожие записи: