Трапеция

Приложения

Храм Дендур в Метрополитен-музее в Нью-Йорке

Архитектура

В архитектуре это слово используется для обозначения симметричных дверей, окон и зданий, построенных шире у основания и сужающихся кверху в египетском стиле. Если они имеют прямые стороны и острые углы, их форма обычно представляет собой равнобедренные трапеции . Это был стандартный стиль для дверей и окон инков .

Геометрия

Задача о перекрещенных лестницах — это задача нахождения расстояния между параллельными сторонами прямой трапеции по длинам диагоналей и расстоянию от перпендикулярного катета до пересечения диагоналей.

Биология

Пример трапециевидной переднеспинки на молочайном жуке

В морфологии , таксономии и других описательных дисциплинах, в которых необходим термин для таких форм, такие термины, как трапециевидный или трапециевидный , обычно полезны при описании конкретных органов или форм.

Компьютерная инженерия

В вычислительной технике, особенно в цифровой логике и компьютерной архитектуре, трапеции обычно используются для обозначения мультиплексоров . Мультиплексоры — это логические элементы, которые выбирают между несколькими элементами и создают один выход на основе сигнала выбора. Типичные конструкции будут использовать трапеции без специального указания, что они являются мультиплексорами, поскольку они универсально эквивалентны.

Свойства

• Сумма углов, прилежащих к боковой стороне трапеции, равна (как сумма двух внутренних односторонних углов при параллельных прямых, содержащих основания трапеции, и секущей, содержащей боковую сторону).
• Средняя линия трапеции параллельна основаниям и равна их полусумме.
• Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
• Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен среднему гармоническому длин оснований трапеции.
• В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
• Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
• Если сумма углов при одном из оснований трапеции равна 90°, то продолжения боковых сторон пересекаются под прямым углом, а отрезок, соединяющий середины оснований, равен полуразности оснований.
• Диагонали трапеции делят её на 4 треугольника. Два из них, прилежащие к основаниям, подобны. Два других, прилежащие к боковым сторонам, являются равновеликими .
• Если отношение оснований равно , то отношение площадей треугольников, прилежащих к основаниям, равно .
• Высота трапеции определяется формулой:

где  — большее основание,  — меньшее основание, и  — боковые стороны.

Их можно выразить в явном виде:

Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами:

а при известных основаниях и диагоналях боковые стороны следующие:

Если же известна высота , то

Прямая Ньютона для трапеции совпадает с её средней линией.

Теорема о четырёх точках трапеции

Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.

Равнобедренная трапеция

Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий:

• прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции);
• высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований;
• углы при любом основании равны;
• сумма противоположных углов равна 180°;
• длины диагоналей равны;
• диагонали трапеции образовывали с одним и тем же основание равные углы;
• из каждой вершины одного основания другое основание было видно под одним и тем же углом;
• вокруг этой трапеции можно описать окружность;
• вершинами этой трапеции также являются вершины некоторого антипараллелограмма.

Кроме того

если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Если — равнобочная трапеция (, ), причём — диагональ трапеции, то .

Вписанная и описанная окружность

• Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
• В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
• Если трапецию можно вписать в окружность — то она равнобедренная.
• Радиус описанной окружности равнобедренной трапеции:[источник не указан 2872 дня]

где  — боковая сторона,  — бо́льшее основание,  — меньшее основание,  — диагонали равнобедренной трапеции.

Если , то в равнобедренную трапецию можно вписать окружность радиуса

Площадь

Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.

Примечание: Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:

или

Средняя линия разбивает фигуру на две трапеции, площади которых соотносятся как

Площадь трапеции равна произведению одной из боковых сторон на длину перпендикуляра, проведённого из середины другой боковой стороны к прямой, содержащей первую боковую сторону.

Формулы площади равнобедренной трапеции

Площадь равнобедренной трапеции:

где  — боковая сторона,  — бо́льшее основание,  — меньшее основание,  — угол между бо́льшим основанием и боковой стороной.

Площадь равнобедренной трапеции через её стороны

Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты:

В этом случае средняя линия совпадает по длине с высотой трапеции, т. е. .

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной
:

Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Площадь параллелограмма и трапеции

Правило. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

1. Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
2. Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
3. Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
4. Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
5. Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
6. Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.

Данный отрезок параллелен основаниям трапеции.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

илиLM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

• Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
• Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

• Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
• Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Симметрия

В заключение рассмотрим также такое важное геометрическое понятие, как симметрия

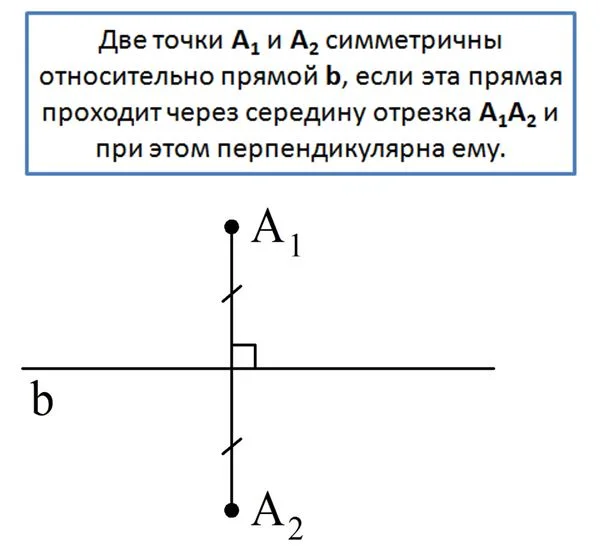
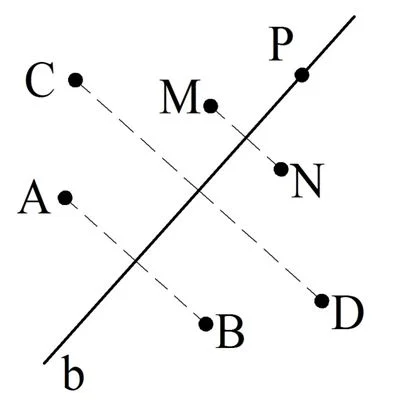
В случае, показанном на рисунке,А₁ и А₂ не лежат на b. Если же рассматривается точка, лежащая на b, то она считается симметричной самой себе. На рисунке пары точек А и B, C и D, M и N симметричны относительно b.Для точки же Р нельзя найти парную ей симметричную точку. Поэтому условно считается, что она симметрична сама себе.

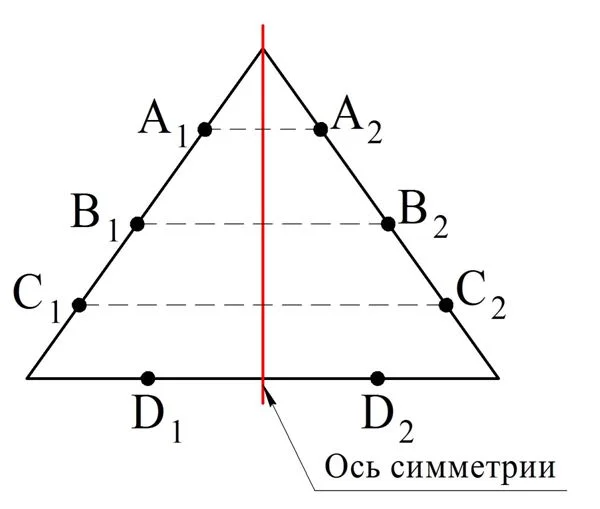
Теперь перейдем к такому понятию, как симметричная фигура.

В качестве иллюстрации приведем равнобедренный треуг-к. У него роль оси симметрии играет медиана, проведенная к основанию. Выберем на треугольнике произвольные точки А₁, В₁, С₁ и D₁. Далее отметим симметричные им относительно b точки, которые обозначим как А₂, В₂, С₂ и D₂. Видно, что они также принадлежат треугольнику:

Рассмотрим для иллюстрации и какую-нибудь несимметричную фигуру, например, треугольник с 3 разными сторонами:

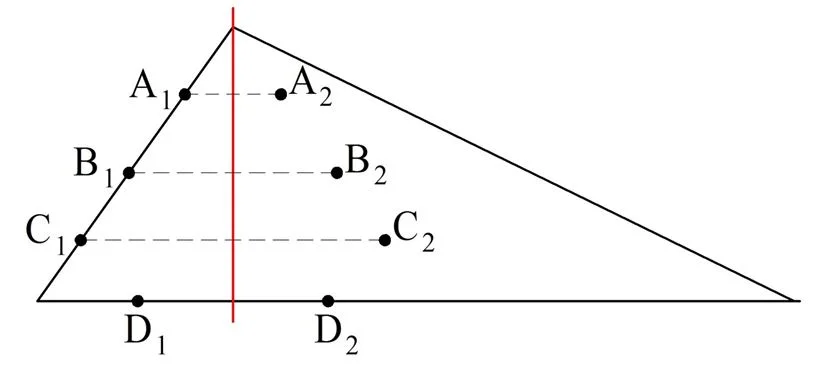
Видно, что например, для точка А₁ симметричная ей А₂ НЕ принадлежит треугольнику, поэтому красная линия НЕ является осью симметрии.

Осевая симметрия присуща и многим другим фигурам:

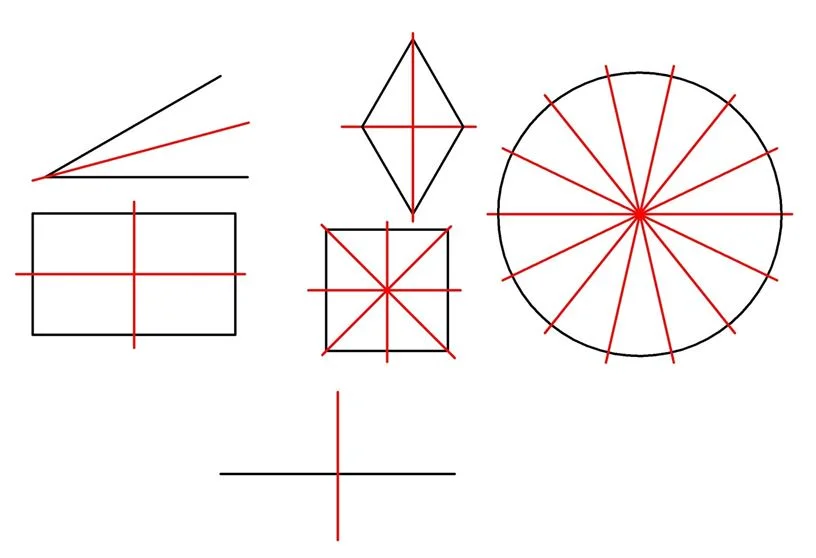
Обратите внимание, что осей симметрии фигуры может быть несколько. У ромба их две (это его диагонали), у квадрата уже четыре (помимо диагоналей добавляются ещё и линии, соединяющие середины его противоположных сторон), а у окружности их и вовсе бесконечно много, так как любой ее диаметр может играть эту роль

Возможен ещё один случай симметрии:

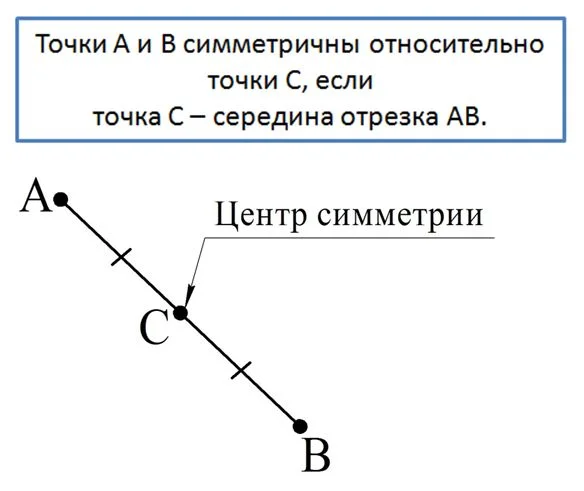
На приведенном рисунке С – это середина АВ, поэтому А и В симметричны, а точка С для них является центром симметрии.

Снова перейдем от отдельных точек к фигурам.

В частности, центральная симметрия присуща параллелограмму (его центром симметрии будет точка, в которой пересекаются его диагонали), а также окружность. Есть центральная симметрия и у любой прямой, причем в качестве центра симметрии фигуры можно выбрать любую точку, принадлежащую этой прямой:

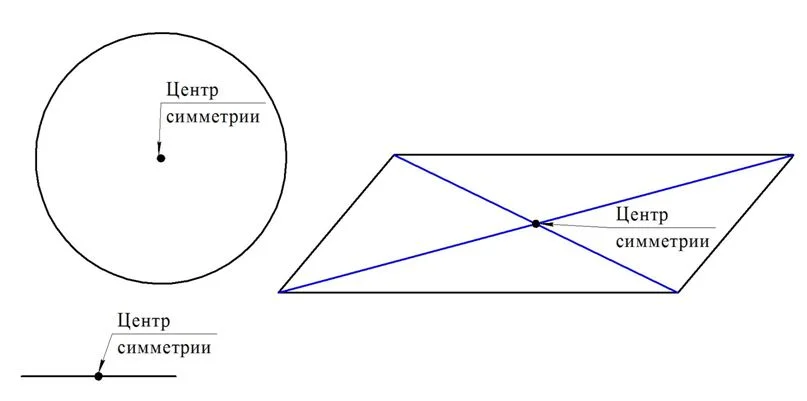
Симметрия – это не просто умозрительная геометрическая конструкция, она встречается и в реальной жизни. Например, листья многих деревьев обладают осевой симметрией, а зубчатое колесо – центральной симметрией. Интересно, что из 32 выделяемых в царстве животных типов у представителей 28 (это более 99% известных видов) можно выделить правую и левую половину, которые симметричны друг другу. Архитекторы и конструктора при проектировании зданий и машин стремятся придать им симметричную форму, так как в большинстве случаев именно такая форма оказывается оптимальной и экономичной.

Что такое равнобедренная трапеция?

Равнобедренная трапеция — это четырехугольник с двумя параллельными сторонами, из которых одна короче другой, и с двумя неравными боковыми сторонами. В равнобедренной трапеции дополнительно выполняется условие равенства углов между основанием и неравными боковыми сторонами.

У равнобедренной трапеции есть несколько характеристик, которые делают ее особенной:

• Основания равнобедренной трапеции — это параллельные стороны, одна из которых короче другой.
• Боковые стороны — это две стороны, не являющиеся основаниями, и они всегда равны между собой.
• Отрезок, соединяющий середины боковых сторон, называется медианой равнобедренной трапеции. Медиана параллельна основаниям и равна полусумме оснований.
• Равнобедренная трапеция имеет две оси симметрии — это медиана и высота.

Пример равнобедренной трапеции:

		Основания
		\
	/______\
Боковые стороны

Признаки и свойства средней линии трапеции

Теорема 1

Средняя линия трапеции равна половине сумм длины двух оснований

Доказательство

Для доказательства теоремы, которая показывает нам как найти среднюю линию трапеции, сначала посмотрим свойства трапеции.

Признак 1

Признак средней линии трапеции №1

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Формула 1

\(MN\;=\;\frac{BC+AD}2\), где MN — средняя линяя, BC, AD — основания трапеции, при условии MN\parallel AD\parallel BC

Признак 2

Признак средней линии трапеции №2

Средняя линяя трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции (рис.2)

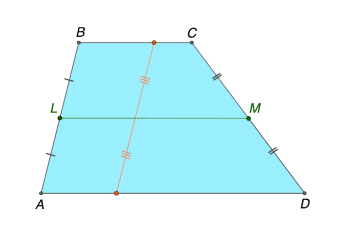
Признак 3

Признак средней линии трапеции №3

Средняя линяя трапеции делит ее на две трапеции, площадь которых соотносятся следующим образом:

Формула 2

\(\frac{S_{ABCD}}{S_{LBCM}}=\frac{4(BC\;+\;AD)}{3BC\;+\;AD}\)

Формула 3

\(\frac{S_{ABCD}}{S_{ALMD}}=\frac{4(BC\;+\;AD)}{3AD\;+\;BC}\)

Формула 4

\(\frac{S_{LBCM}}{S_{ALMD}}=\frac{3BC\;+\;AD}{3AD\;+\;BC}\)

Таким образом, доказательство данной теоремы основано на свойствах средней линии трапеции. И для ее доказательства нужно продлить нижнее основание AD и провести отрезок BK до пересечения этого отрезка с продленным нижнbм основанием. Из свойств трапеции следует, что образованные треугольники BMC и MKD равны, откуда следует, что MC = DK.

LM — средняя линяя треугольника BKA, следовательно, по определению средней линии треугольника \(LM\parallel AD\) и LM = 0.5AK, при этом AK = AD+DK.

Подставляя, получаем, что LM = 0.5*(AD+DK). Из свойства помним, что DK = BC, отсюда получаем LM = 0.5*(AD+BC), то есть средняя линия трапеции параллельна основаниям и равна их полусумме.

Что и требовалось доказать.

Рассмотрим существующие свойства трапеций, которые применимы для любого вида трапеций.

Свойство 1

Сумма углов трапеции, прилежащих к одной и той же боковой стороне в сумме дают всегда 180°.

Свойство 2

Средняя линяя трапеции параллельна ее основаниям и равна половине их суммы.

Свойство 3

Отрезок, который соединяет середины диагоналей трапеции, лежит на средней линии трапеции и равняется половине разности оснований (рис.3), где KL — отрезок, соединяющий середины диагоналей AC и BD, KL лежит на средней линии трапеции MN.

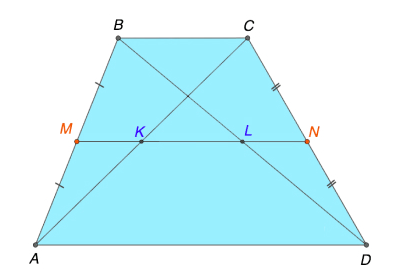
Свойство 4

Точки пересечения диагоналей трапеции, продолжений ее боковых сторон и середин оснований лежат на одной прямой (Рис.4), где DK — продолжение боковой стороны CD, AK — продолжение боковой стороны AB, E — середина основания BC, т.е. BE = EC, F — середина основания AD, т.е. AF = FD.

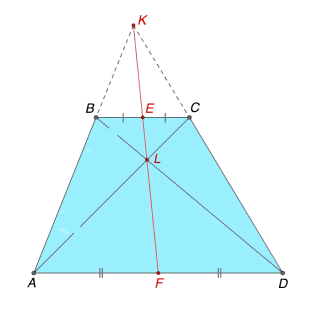
Свойство 5

Диагонали трапеции делят ее на 4 треугольника, два из которых (при основаниях) подобны, а два других (при боковых сторонах) равны по площади (рис.5).

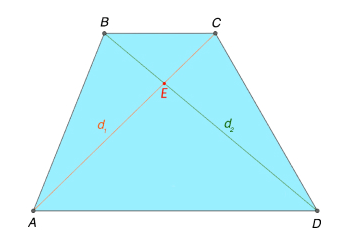
Свойство 6

Отрезок, проходящий через точку пересечения диагоналей трапеции параллельно ее основаниям, можно выразить через длины оснований (рис.6):

Формула 5

\(KL\;=\;\frac{2\ast AD\ast BC}{AD+BC}\)

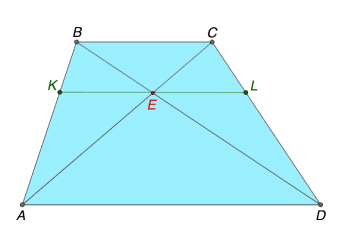
Свойство 7

Биссектрисы углов трапеции при одинаковой боковой стороне взаимно перпендикулярны (рис.7).

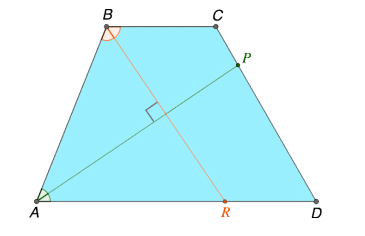
Свойство 8

В трапецию можно вписать окружность только в том случае, если сумма длин ее оснований равна сумме длин ее боковых сторон (рис.8).

Т.е. AD + BC = AB + CD

Радиус вписанной в трапецию окружности равен половине ее высоты: R = h/2.

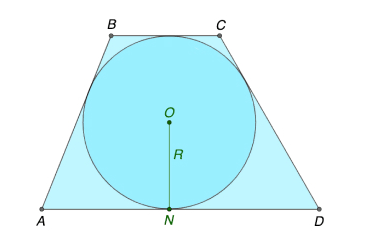
Шаги

1
По известным боковым сторонам и основаниям

1. 1
   Запишите формулу для вычисления периметра трапеции.
   Формула: P = T + B + L + R
2. 2
   В формулу подставьте известные длины сторон.
   Не используйте этот метод, если не даны значения всех четырех сторон.
   • Например, верхнее основание трапеции равно 2 см, нижнее основание равно 3 см, а каждая боковая сторона равна 1 см. В этом случае формула примет следующий вид: P = 2 + 3 + 1 + 1
     3
     Сложите длины сторон.
     Так вы найдете периметр трапеции.
     • В нашем примере: P = 2 + 3 + 1 + 1
       

       2
       По известным высоте, боковым сторонам и верхнему основанию

       1. 2
          Обозначьте каждую высоту.
          
       2. 3
          Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны. Не используйте этот метод, если не дано значение верхнего основания.
       3. 4
          Формула: a 2 + b 2 = c 2
       4. 5
          Боковую сторону трапеции подставьте вместо c
          6
          Возведите в квадрат известные значения.
          Затем при помощи вычитания обособьте переменную b
          7
          Извлеките квадратный корень, чтобы найти b .) Вы найдете основание первого прямоугольного треугольника. Напишите найденное значение под основанием соответствующего треугольника.
          
       5. В нашем примере: b 2 = 45
          8
          Найдите неизвестную сторону второго прямоугольного треугольника.
          Для этого запишите теорему Пифагора для второго треугольника и действуйте так, как описано выше. Если дана равнобедренная трапеция, у которой боковые стороны равны, то два прямоугольных треугольника являются равными, то есть любая сторона одного треугольника равна соответствующей стороне другого.
          
       6. Например, если вторая боковая сторона трапеции равна 7 см, то формула запишется так: a 2 + b 2 = c 2
          9
          Периметр любого многоугольника равен сумме всех его сторон: P = T + B + L + R
          

          3
          По известным высоте, основаниям и нижним углам

       7. 1
          Разбейте трапецию на прямоугольник и два прямоугольных треугольника.
          

          Если одна сторона трапеции перпендикулярна основаниям, вы не сможете получить два прямоугольных треугольника. В этом случае боковая сторона, перпендикулярная основаниям, равна высоте, а трапеция разбивается на прямоугольник и один прямоугольный треугольник.

Для этого из каждой вершины трапеции проведите высоту.

2
Обозначьте каждую высоту.

Например, высота трапеции равна 6 см. Из вершин трапеции проведите две высоты (к нижнему основанию). Возле каждой высоты напишите «6 см» (без кавычек).

Так как высоты являются противоположными сторонами прямоугольника, они равны.

3
Обозначьте среднюю часть нижнего основания (она является нижней стороной прямоугольника).

Например, если верхнее основание трапеции равно 6 см, то средняя часть нижнего основания также равна 6 см.

Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны.

4
Напишите функцию (формулу) синуса угла первого прямоугольного треугольника.
Функция: sin ⁡ θ = B H
5
В формулу синуса подставьте известные величины.
Вместо противоположной стороны подставьте высоту треугольника. Вы найдете гипотенузу, то есть боковую сторону трапеции.

• Например, если нижний угол трапеции равен 35 градусов, а высота треугольника равна 6 см, то формула запишется так: sin ⁡ (35) = 6 H
  6
  Найдите синус угла.
  Это делается при помощи научного калькулятора, а именно клавиши SIN. Найденное значение подставьте в формулу.
  • При помощи калькулятора вы найдете, что синус угла в 35 градусов приблизительно равен 0,5738. Таким образом, формула примет следующий вид: 0 , 5738 = 6 H
    7
    Найдите переменную H.
    Для этого каждую сторону уравнения (формулы) умножьте на Н, а затем каждую сторону уравнения разделите на синус угла. Или просто разделите высоту треугольника на синус угла.
    • В нашем примере: 0 , 5738 = 6 H
      8
      Найдите гипотенузу второго прямоугольного треугольника.
      Напишите функцию (формулу) синуса угла второго прямоугольного треугольника: sin ⁡ θ = B H
      9
      Запишите теорему Пифагора для первого прямоугольного треугольника.
      Формула: a 2 + b 2 = c 2
      10
      В формулу подставьте известные величины первого треугольника.
      Боковую сторону трапеции подставьте вместо c
      11
      Найдите b
      12
      Найдите основание второго прямоугольного треугольника.
      Для этого воспользуйтесь теоремой Пифагора (a 2 + b 2 = c 2
      13
      Сложите значения всех сторон трапеции.
      Периметр любого многоугольника равен сумме всех его сторон: P = T + B + L + R или треугольник 90-45-45) существуют формулы, при помощи которых можно найти неизвестные стороны без использования функции синуса или теоремы Пифагора.
      
    • Чтобы найти синус угла, воспользуйтесь научным калькулятором – введите угол, а затем нажмите клавишу SIN. Или используйте тригонометрические таблицы.
    • Калькулятор
    • Карандаш
    • Бумага

Этимология и трапеция против трапеции

Ошибка Хаттона в 1795 г.

Древнегреческий математик Евклид определил пять типов четырехугольников, четыре из которых имели два набора параллельных сторон (известные на английском языке как квадрат, прямоугольник, ромб и ромбоид), а последний не имел двух наборов параллельных сторон — τραπέζια ( буквально « трапеция»). стол», сам от τετράς ( tetrás ), «четыре» + πέζα ( péza ), «нога; конец, край, край»).

Два типа трапеций были введены Проклом (412–485 гг. Н.э.) в его комментарии к первой книге « Начал» Евклида :

• одна пара параллельных сторон – трапеция (τραπέζιον), разделенная на равнобедренные (равнобедренные) и разносторонние (неравнобедренные) трапеции
• нет параллельных сторон — трапеция ( τραπεζοειδή , trapezoeidé , буквально трапециевидный ( εἶδος означает «похожий»), точно так же, как кубовидный означает кубический , а ромбовидный означает ромбовидный )

Все европейские языки следуют структуре Прокла, как и английский до конца 18 века, пока влиятельный математический словарь, опубликованный Чарльзом Хаттоном в 1795 году, не поддержал без объяснения перестановку терминов. Эта ошибка была исправлена ​​в британском английском примерно в 1875 году, но сохранилась в американском английском до наших дней.

Тип	Изображение	Оригинальная терминология	Современная терминология
		Евклид (определение 22)	Прокл (Определения 30-34, цитируя Посидония)	Определение Евклида / Прокла	Британский английский (и европейские языки)	Американский английский
Параллелограмм		ῥόμβος (ромбы)	равносторонний, но не прямоугольный	Ромб	Трапецоид ( включительно)
	ῥομβοειδὲς (ромбоиды)	противоположные стороны и углы равны между собой, но не равносторонние и не прямые	Ромбовидный (в просторечии параллелограмм)
Непараллелограмм		τραπέζια (трапеция)	τραπέζιον ἰσοσκελὲς ( трапециевидные изоскелеты )	Две параллельные стороны и линия симметрии	Трапеция _	Трапеция ( эксклюзив )
	τραπέζιον σκαληνὸν ( трапеция ион скалинон)	Две параллельные стороны и отсутствие линии симметрии
	τραπέζοειδὲς ( трапециевидные )	Нет параллельных сторон	Трапецоид _	Трапеция _

В этой статье термин « трапеция » используется в том смысле, который распространен в США и Канаде. Форму часто называют неправильным четырехугольником.

8. Разные задачи на четырехугольники

При­мер 4. Через дан­ную точку внут­ри угла про­ве­ди­те пря­мую, от­ре­зок ко­то­рой, за­клю­чен­ный внут­ри этого угла, де­лил­ся бы дан­ной точ­кой по­по­лам.

Ре­ше­ние. Внут­ри угла с вер­ши­ной  дана точка . Изоб­ра­зим это на Рис. 20 со всеми эле­мен­та­ми, ко­то­рые по­на­до­бят­ся нам для ре­ше­ния за­да­чи.

Рис. 20

От­ло­жим от­ре­зок  из точки  через точку  так, чтобы , затем про­ве­дем от­рез­ки , по­лу­чим точки пе­ре­се­че­ния со сто­ро­на­ми угла  и  со­от­вет­ствен­но. Со­еди­ним эти точки пря­мой, она и будет ис­ко­мой. До­ка­жем это.

По­стро­ен­ная фи­гу­ра  яв­ля­ет­ся па­рал­ле­ло­грам­мом, т.к. по по­стро­е­нию имеет па­рал­лель­ные про­ти­во­по­лож­ные сто­ро­ны, от­рез­ки  яв­ля­ют­ся диа­го­на­ля­ми па­рал­ле­ло­грам­ма, сле­до­ва­тель­но, по его свой­ству точ­кой пе­ре­се­че­ния () де­лят­ся по­по­лам и , что и тре­бо­ва­лось по усло­вию за­да­чи.

Ответ. Ис­ко­мая пря­мая – .

При­мер 5. В пря­мо­уголь­ни­ке точка пе­ре­се­че­ния диа­го­на­лей от­сто­ит от мень­шей сто­ро­ны на 4 см даль­ше, чем от боль­шей сто­ро­ны. Пе­ри­метр пря­мо­уголь­ни­ка равен 56 см. Най­ди­те сто­ро­ны пря­мо­уголь­ни­ка.

Ре­ше­ние. Изоб­ра­зим Рис. 21.

Рис. 21

Опу­стим из точки пе­ре­се­че­ния диа­го­на­лей пер­пен­ди­ку­ля­ры на сто­ро­ны, длины ко­то­рых и будут рас­сто­я­ни­я­ми от точки пе­ре­се­че­ния диа­го­на­лей до сто­рон пря­мо­уголь­ни­ка. Обо­зна­чим от­ре­зок , тогда по усло­вию . По­сколь­ку  по­лу­ча­ем, что . Под­ста­вим это в фор­му­лу пе­ри­мет­ра пря­мо­уголь­ни­ка:

.

Ответ: .

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/povtorenie-teorii-i-reshenie-zadach

https://www.youtube.com/watch?v=axMe7L_01j0

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/83-test-po-geometrii-8-klass-tema-pryamougolnik-romb-kvadrat-variant-1.html

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/84-test-po-geometrii-8-klass-tema-pryamougolnik-romb-kvadrat-variant-2.html

http://festival.1september.ru/articles/416997/

Площадь равнобедренной трапеции

Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.

Равнобедренная трапеция

Найти площадь равнобедренной трапеции можно несколькими способами.

Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:

Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:

S = c * sin α * (a + c * cos α)

где а — верхнее основание, с — боковая сторона.

 Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:

S = c * sin α * (b – c * cos α)

Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:

S = ½ * (b2 – a2) * tg α

Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:

S = ½ * d2 * sin α

Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.

Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:

S = m * c * sin α

Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.

Круг в трапеции

Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:

S = 4r2 / sin α

Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):

S = D2 / sin α

Зная основания и угол, площадь равнобедренной трапеции вычисляется так:

S = a * b / sin α

(эта и последующие формулы верны только для трапеций с вписанной окружностью).

Трапеция в круге

Через основания и радиус окружности площадь ищется так:

S = r * (a + b)

Если известны только основания, то площадь считается по формуле:

Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:

Площадь прямоугольной трапеции

Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.

Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.

Прямоугольная трапеция

Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.

Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:

S = (a + b) * h / 2

В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:

S = (a + b) * c / 2

Другой способ рассчитать площадь — перемножить длину средней линии на высоту:

S = m * h

или на длину боковой перпендикулярной стороны:

S = m * c

Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:

S = ½ * d1 * d2 * sin α

Прямоугольная трапеция с перпендикулярными диагоналями

Если диагонали перпендикулярны, то формула упрощается до:

S = ½ * d1 * d2

Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

S = (a + b) * r

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:

S = (2r + c) * r

Если в трапецию вписана окружность, то площадь вычисляется так же:

S = 2m * r

где m — длина средней линии.