Параллелограмм

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

• Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
• Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
• Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
• Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
• Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
• Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d Площадь определить: S=h*(a+b)/2 Стороны и диагональ равнобокой трапеции: d² = ab+c²Радиус вписанной окружности: r = h/2

где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d1, d2 –диагонали, P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Как сформулировать и доказать утверждения о свойствах параллелограмма, теоремы о признаках данной фигуры

Параллелограммом называют четырёхугольник (фигура, что состоит из четырёх точек и отрезков, последовательно их соединяющих), у которого противоположные стороны попарно параллельны. Его свойства впервые детально изучали греческие математики Евклид и Пифагор. Конец эпохи Средневековья принёс людям полную теорию об этой фигуре.

…

История возникновения термина

О некоторых видах четырёхугольников, квадратов, прямоугольников, равносторонних и прямоугольных трапеций знали ещё давно.

Термин «параллелограмм» греческого происхождения, считают что его придумал Евклид (приблизительно 300 годов до нашей эры). Ещё известно, что эта фигура и её свойства были знакомы ученикам школы Пифагора, раньше их называли пифагорейцами.

В «Началах» Евклида приведена следующая теорема: в параллелограмме противоположные стороны равны, а диагонали разделяют его по половине. Но в данной книге не было написано о свойствах точки их сечения. Ещё этот учёный не упоминает о прямоугольнике и ромбе.

Полную теорию сделали только в конце Средневековья, а в книгах она появилась в семнадцатом столетии. Теоремы и свойства параллелограмма основывались на аксиомах Евклида.

Нужно сказать, что Евклид, как и большинство математиков того времени, для названия отрезка, который соединяет противоположные вершины четырёхугольника или прямоугольника, использовал другой термин — «диаметр». Это можно объяснить тем, что первые геометры свои мысли основывали на вписании круга в прямоугольник. В Средние века для названия приведённых отрезков использовали оба термина. Только в семнадцатом столетии «диагональ» стала общепринятой.

Доказательство признаков фигуры

На следующем рисунке изображён параллелограмм ABCD, где AB параллельно CD и AD параллельно BC:

Сумма любых двух соседних углов параллелограмма равна 180 градусам — это первая подсказка о том, как сформулировать и доказать утверждения о признаках параллелограмма.

На этом рисунке углы A и B фигуры ABCD есть внутренними односторонними углами для параллельных прямых AD и BC . Поэтому углы A + B равны 180 градусам. Аналогично это свойство можно привести для любой другой пары соседних (если вершины есть концами одной и той же стороны) углов.

Теорема признаков паралелограмма

• Теорема признаков параллелограмма гласит, что это выпуклый четырёхугольник. Исходя из предыдущего правила, угол А намного меньше 180 градусов, как и B, C, D, поэтому его называют опухлым четырёхугольником. Диагонали этой фигуры могут пересекаться.
• У параллелограмма противоположные стороны и углы равны.

Диагональ АС разбивает фигуру на два треугольника ABC и ADC. АС — общая сторона двоих треугольников и САD эквивалентен АСВ также с САВ и АСD. Тогда ∆АВС = ∆СDA, по стороне и двумя прилегающими углами. Это значит, что АВ=СD, BC=AD и B=D, как соответствующие элементы в различных треугольниках.

Теорема о диагоналях

• Периметр (сумма длин всех сторон четырёхугольника, которую обозначают буквой Р) параллелограмма эквивалентен 2 (АВ +ВС) или АВ + ВС + СD + DA.
• Теорема о диагоналях параллелограмма гласит, что точкой пересечения они делятся ровно пополовине.

По условию задачи O — это точка пересечения диагоналей AC и BD параллелограмма. AB эквивалентно BC, как противоположные, не имеющие своей общей вершины. CAD равен ACB также BDA и DBC, АD и BC секущими AC и B. D. Следуя дальше ∆АОD = ∆ COB, по стороне и двух прилегающих углах. Тогда, А = ОС, ВО = ОD, как соответствующие стороны разных треугольников.

На этом рисунке MN — это высота. Следуя за известным определением, из каждой вершины можно провести две высоты (BF и BT, которые приведены в соответствии к сторонам AD и CD).

Свойства параллелограмма с доказательствами 8 класса :

1. Две стороны равны и параллельны.
2. Противоположные стороны попарно равны.
3. Диагонали пересекаются и этой точкой делятся ровно пополам.
4. Противоположные углы попарно равны.

Теперь нужно вернуться к первому рисунку, чтобы до конца понять все признаки параллелограмма и доказательства любых признаков.

В нём AD = BC и AD || BC. Провели диагональ AC и получили ∆CAD и ∆ACB. CAD эквивалентен ВСА, как внутренние разносторонние углы при пересечениях прямых AD и BC секущей AC, ещё она является их общей стороной. Условия задачи говорят: AD=BC. Значит, что, ∆CAD=∆ACB, ACD = CAB. Из-за того, что они были созданы в таких условиях AB || CD, по признаку параллельных прямых.

Задачи на параллелограмм 8 класс онлайн-подготовка на Ростелеком Лицей

Повторение определения, свойств и признака параллелограмма

Сегодня мы основное внимание уделим задачам на параллелограмм

Определение. Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).

Рис. 1. Параллелограмм

Основные свойства параллелограмма:

Теорема. Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм.  параллелограмм.

Рис. 2. Первый признак параллелограмма

Рис. 3. Второй признак параллелограмма

Теорема. Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник – параллелограмм.  параллелограмм.

Теорема. Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм.  параллелограмм.

Рис. 4. Третий признак параллелограмма

Задачи на параллелограммы

Теперь рассмотрим решение задач с использованием определения, свойств и признаков параллелограмма.

Пример 1. В параллелограмме  проведены биссектрисы  и , которые пересекаются в точке . Найти .

Решение. Изобразим Рис. 5.

Рис. 5

Обозначим для удобства: . Следовательно,  поскольку  и  биссектрисы.

По теореме о сумме внутренних углов треугольника .

Вспомним свойство параллелограмма о сумме углов, прилежащих к одной стороне: . Тогда:

Ответ. .

Пример 2. Прямая , проведенная через середину  стороны  параллельно стороне  треугольника  пересекает третью его сторону в середине. Доказать, что  – это середина .

Доказательство. Изобразим Рис. 6 с дополнительными построениями: проведем .

Рис. 6

Рассмотрим четырехугольник :

 параллелограмм по определению. Тогда по свойству равенства противоположных сторон , но по условию еще известно, что , следовательно, .

Рассмотрим треугольники  и :

 по второму признаку равенства треугольников (по стороне и прилежащим углам).

Из равенства указанных треугольников следует равенство их соответствующих сторон, т.е., например, что . Это означает, что точка  является серединой стороны . Что и требовалось доказать.

Доказано.

3. Теорема Фалеса

Теорема Фалеса. Если параллельные прямые, которые пересекают стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство. Изобразим Рис. 7.

Рис. 7. Теорема Фалеса

Рассмотрим . В нем точка  – середина стороны , а прямая . Из предыдущего примера следует, что точка  делит сторону   на две равные части, т.е. . Равенство двух отрезков, ближайших к вершине угла доказано.

Доказано.

4. Пример задачи на применение теоремы Фалеса

Рассмотрим пример на доказанную теорему.

Пример 3. Дан отрезок , разделить его на три равные части.

Решение. Изобразим указанный отрезок на Рис. 8 и сделаем дополнительные построения: отложим три равных отрезка любой длины  вдоль одной прямой, не совпадающей с указанным в условии отрезком.

Рис. 8. Применение теоремы Фалеса

Соединим прямой точки  и , а затем проведем прямые, параллельные прямой , через точки  и : . Полученные при пересечении отрезка точки  и  будут делить отрезок  на три равных части по теореме Фалеса. Необходимое построение выполнено и задача решена.

Ответ: построено.

Методы, которые мы рассмотрели сегодня на примерах, демонстрирующих свойства и признаки параллелограмма, помогут нам в дальнейшем при работе с параллелограммами в более сложных случаях.

Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Narod.ru (Источник).
2. Фестиваль педагогических наук «Открытый урок» (Источник).

Домашнее задание

1. №  50 (г, д, е, ж, з, и), 51 (б, в, г, ж), 52 (б, в, е, ж). Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
2. В параллелограмме   см,  см, биссектрисы углов  и  пересекают сторону  в точках  и . Найдите длину отрезка .
3. Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен .
   Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.
4. ∗ Через середину  диагонали  параллелограмма  проведена прямая, которая пересекает стороны  и  в точках  и  соответственно. Докажите, что четырехугольник  параллелограмм.

5. Повторение: определение и свойства параллелограмма

На­пом­ним, что па­рал­ле­ло­грамм – это че­ты­рёх­уголь­ник, у ко­то­ро­го про­ти­во­по­лож­ные сто­ро­ны по­пар­но па­рал­лель­ны. То есть, если  – па­рал­ле­ло­грамм, то  (см. Рис. 1).

Рис. 1

Па­рал­ле­ло­грамм об­ла­да­ет целым рядом свойств: про­ти­во­по­лож­ные углы равны (), про­ти­во­по­лож­ные сто­ро­ны равны (). Кроме того, диа­го­на­ли па­рал­ле­ло­грам­ма в точке пе­ре­се­че­ния де­лят­ся по­по­лам, сумма углов, при­ле­жа­щих к любой сто­роне па­рал­ле­ло­грам­ма, равна  и т.д.

Но для того, чтобы поль­зо­вать­ся всеми этими свой­ства­ми, необ­хо­ди­мо быть аб­со­лют­но уве­рен­ны­ми в том, что рас­смат­ри­ва­е­мый че­ты­рёх­уголь­ник – па­рал­ле­ло­грамм. Для этого и су­ще­ству­ют при­зна­ки па­рал­ле­ло­грам­ма: то есть те факты, из ко­то­рых можно сде­лать од­но­знач­ный вывод, что че­ты­рёх­уголь­ник яв­ля­ет­ся па­рал­ле­ло­грам­мом. На преды­ду­щем уроке мы уже рас­смот­ре­ли два при­зна­ка. Сей­час рас­смот­рим тре­тий.

1. Определение и основные свойства параллелограмма

Нач­нем с того, что вспом­ним опре­де­ле­ние па­рал­ле­ло­грам­ма.

Опре­де­ле­ние. Па­рал­ле­ло­грамм – че­ты­рех­уголь­ник, у ко­то­ро­го каж­дые две про­ти­во­по­лож­ные сто­ро­ны па­рал­лель­ны (см. Рис. 1).

Рис. 1. Па­рал­ле­ло­грамм

Вспом­ним ос­нов­ные свой­ства па­рал­ле­ло­грам­ма:

Для того, чтобы иметь воз­мож­ность поль­зо­вать­ся всеми этими свой­ства­ми, необ­хо­ди­мо быть уве­рен­ным, что фи­гу­ра, о ко­то­рой идет речь, – па­рал­ле­ло­грамм. Для этого необ­хо­ди­мо знать такие факты, как при­зна­ки па­рал­ле­ло­грам­ма. Пер­вые два из них мы се­год­ня и рас­смот­рим.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
• Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
• Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
• Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
• Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
• Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
• Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
• Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c Площадь по стороне и высоте: S=(a*h)/2 Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r Площадь прямоугольного треугольника: S=(a*b)/2Стороны прямоугольного треугольника: c2=a2+b2 (Теорема Пифагора)

где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника) d1, d2 –диагонали, h -высота, проведенная к противоположной стороне, P-периметр, S-площадь, γ — угол между сторонами a и b r — радиус вписанной окружности, R — радиус описанной окружности

Свойства:

• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Сумма углов треугольника равна 180°:
• Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b|
• Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
• Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
• Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
• В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
• Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2=a2+b2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Признаки параллелограмма

Существует несколько признаков, которые позволяют доказать, что тот или иной четырехуг-к является параллелограммом. Рассмотрим первый из них.

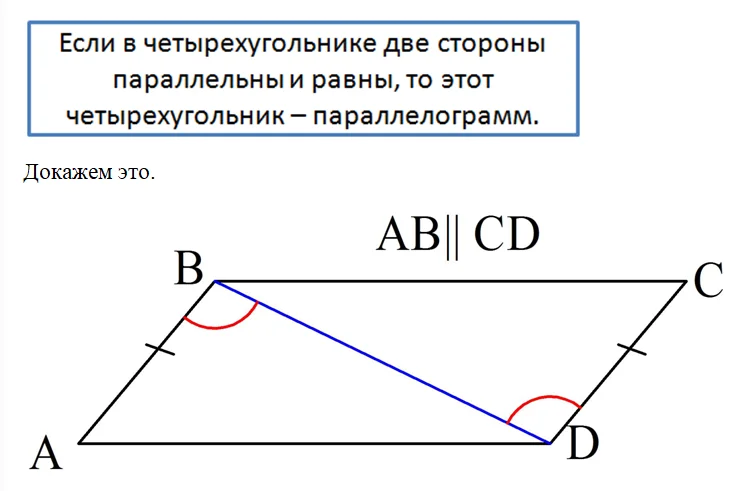
Пусть в четырехуг-ке параллельны и равны стороны АB и CD. Проведем диагональ ВD. Она окажется секущей для АВ и СD, поэтому накрест лежащие углы окажутся равными:

Сторона ВD – общая, а АВ = СD по условию. Тогда по 1-ому признаку равенства треуг-ков ∆АВD = ∆CВD. В свою очередь это означает, что

Они являются накрест лежащими уже при отрезках ВС и АD. Отсюда вытекает, что эти отрезки параллельны друг другу. В итоге в четырехуг-ке ABCD параллельными оказываются все противоположные стороны, поэтому он должен быть параллелограммом.

Задание. В параллелограмме АВCD смежные стороны различны, а∠А – острый. Из точек B и D опущены перпендикуляры ВК и DM на диагональ АС. Докажите, что фигура ВМDК – тоже параллелограмм.

Решение. Выполним построение по заданным условиям:

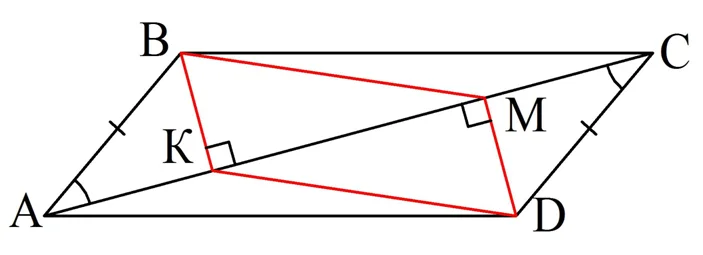
Необходимо доказать, что красная фигура – это параллелограмм. По выведенному нами признаку достаточно показать, что отрезки ВК и MD параллельны и равны. Их параллельность очевидна, ведь эти отрезки перпендикулярны к одной прямой (АС). Равенство отрезков можно доказать, рассмотрев ∆АВК и ∆СМD. Они являются прямоугольными, у них равны гипотенузы АВ и СD (как противоположные стороны в одном параллелограмме), а также

ведь это накрест лежащие углы при параллельных отрезках АВ и CD. В итоге получаем, что

Но тогда ВК = МD. В итоге, с учетом того, что ВК||МD, получаем, что ВМDК – это параллелограмм.

Следующая теорема позволяет определять, является ли фигура параллелограммом, только по длине ее сторон.

Для доказательства используем всё тот же прием: проведем в четырехуг-ке диагональ:

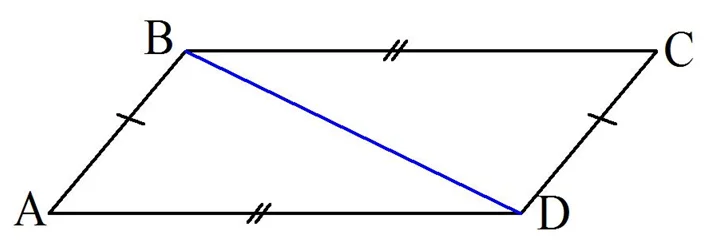
Мы снова получаем равенство треуг-ков

но на этот раз они равны по трем равным сторонам. Отсюда получаем равенство углов:

Из равенства этих углов, являющихся накрест лежащими, следует, что АВ||СDи ВС||АD. Это и значит, что АВСD– параллелограмм.

Задание. Середины смежных сторон параллелограмма соединили друг с другом отрезками. Докажите, что получившаяся таким образом фигура – параллелограмм.

Решение.

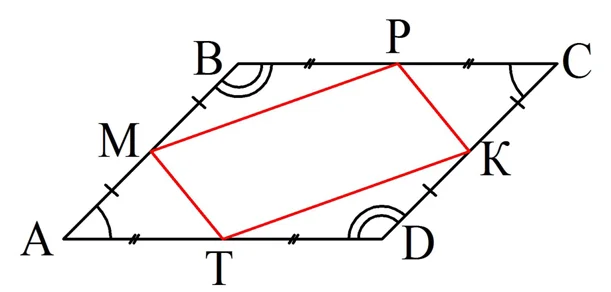
Обозначим середины сторон АВСD буквами М, Р, К и Т. Ясно, что

как противоположные стороны одного параллелограмма. Если отрезки равны, то равны и их половины, поэтому можно записать:

Теперь рассмотрим ∆АМТ и ∆СРК. Они равны, ведь у них одинаковы две стороны и угол, лежащий между ними:

Отсюда следует, что МТ = РК. Аналогично можно показать, что ∆МВР = ∆ТDК, из чего вытекает, что МР = ТК.

В итоге получаем, что у МРКТ противоположные стороны попарно равны. А это означает, что МРКТ – это параллелограмм.

Следующий признак параллелограмма связан с диагоналями.

Действительно, пусть в произвольном четырехуг-ке АВСD диагонали пересекаются в точке О, являющейся серединой диагоналей:

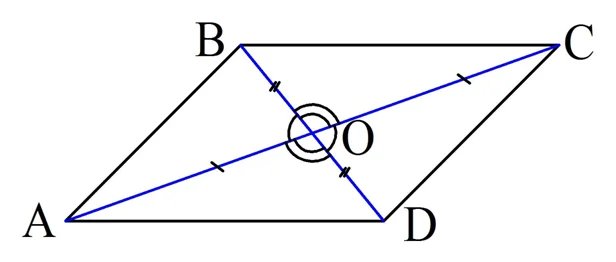
Тогда ВО = ОDи АО = ОС. Рассмотрим ∆АОВ и ∆СОD. ∠ВОА = ∠СОD, ведь это вертикальные углы. В итоге у этих треуг-ков равны две стороны, а также угол между ними. Следовательно, ∆АОВ = ∆СОD. Но отсюда следует, что

В итоге у АВСD противоположные стороны одинаковы. Значит, это параллелограмм.

Задание. О – точка, в которой пересекаются диагонали параллелограмма АВСD. М, Р, Н, К – середины отрезков АО, ВО, СО и DO соответственно. Докажите, что МРНК – это параллелограмм.

Решение.

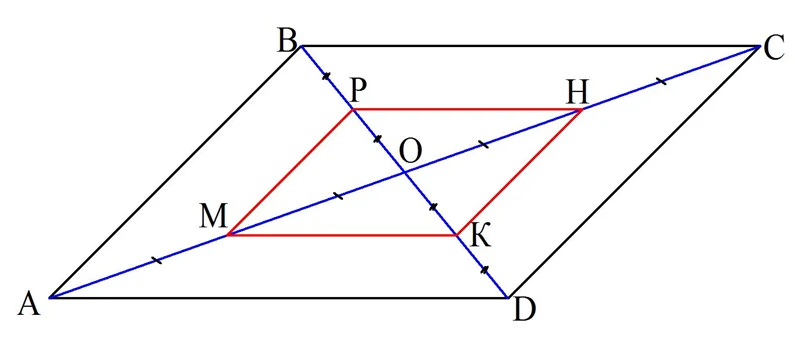
По свойству параллелограмма точка О делит их пополам, то есть на равные отрезки:

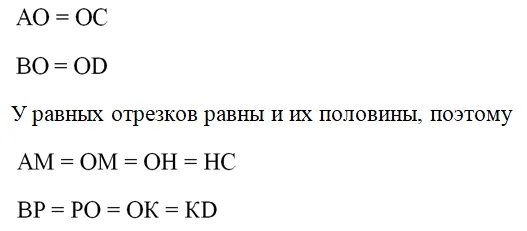
Заметим, что диагоналями МРНК являются отрезки РК и МН, причем они пересекаются в точке О. Так как

Можно сказать, что О – середина диагоналей РК и МН. Отсюда вытекает вывод, что МРНК – параллелограмм.

Признаки параллелограмма

Знаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первая особенность параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник является параллелограммом.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть ABCD — четырехугольник:

• АБ || CD
• АВ = CD

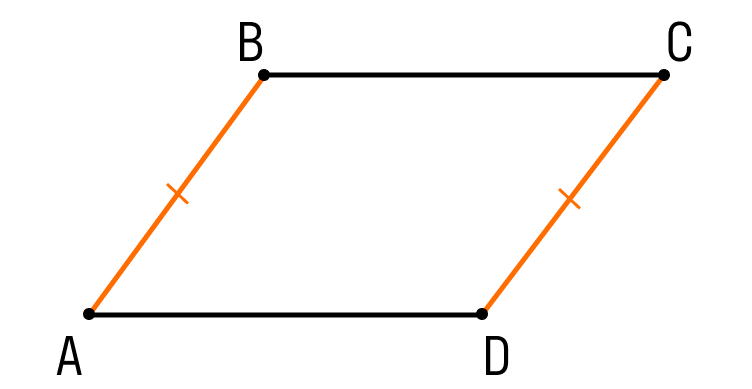
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Теперь мы видим одну пару параллельных сторон. Необходимо доказать, что вторая пара сторон также параллельна.

Шаг 2. Проведем диагональ. Получили два треугольника ABC и CDA, равных по первому признаку равенства, то есть по двум сторонам и углу между ними:

1. АС — общая строна;
2. По сонтию AB = CD;
3. ∠1 = ∠2 как внутренние диагональные углы при пересечении параллельных прямых AB и CD, пересекающих АС.

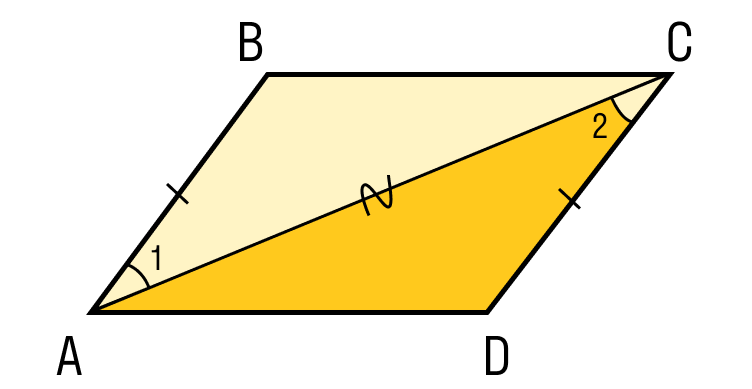
Шаг 3. Из чувствительных треугольников также следте:

∠3 = ∠4

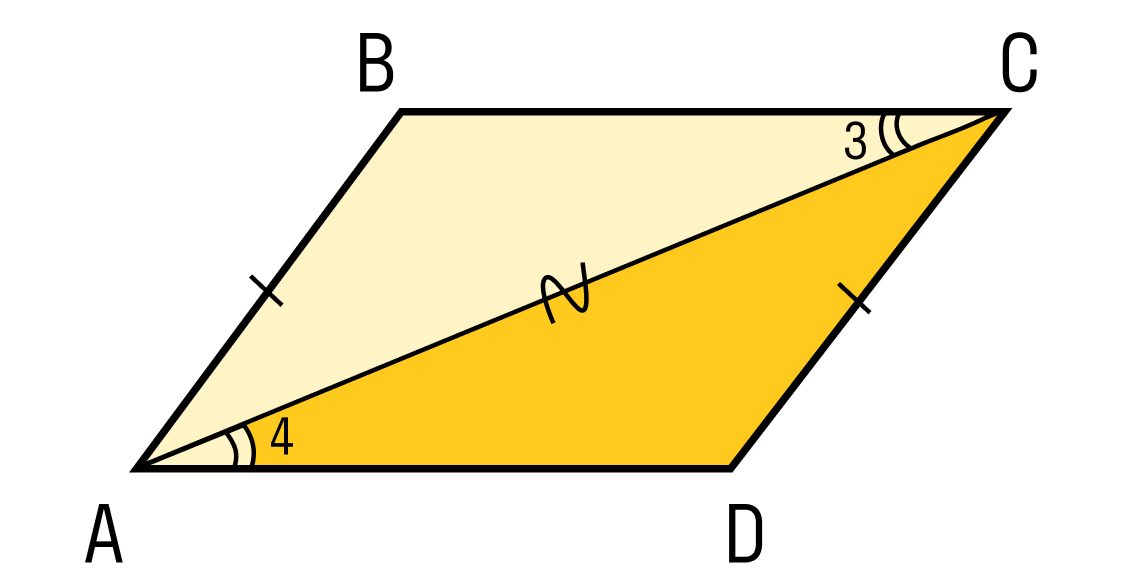
Эти углы также внутренне перекрываются для прямых CB и AD. А это признак параллельности прямых. Значит, КБ || AD и ABCD — параллелограммы.

Вот как быстро мы доказали первый признак.

Параллелограмм второго знака. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.

Докажем 2 признака параллелограмма:

Шаг 1. Пусть ABCD — четырехугольник:

• АВ = CD
• До н.э. = н.э

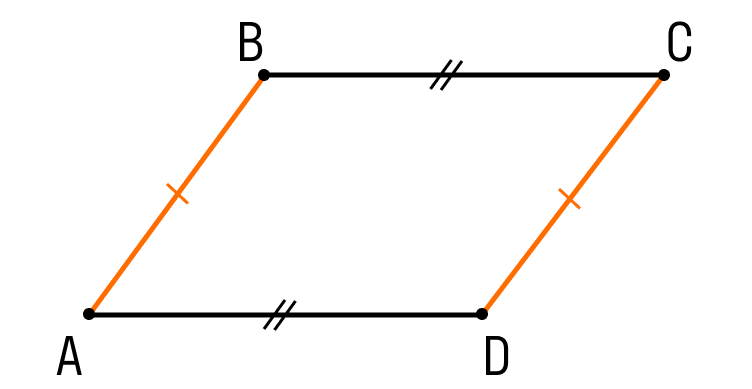
Шаг 2. Проведите диагональ AC и рассмотрите треугольники ABC и CDA:

• АС — общая строна;
• AB = CD по условиям;
• BC = AD в зависимости от условий.

Отсюда следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из чувствительных треугольников следа:

• ∠DCA = ∠BACА так как эти глы — накрест лежат при стронах BC и AD и диаганоли AC и между, строны BC и AD паралленны.
• ∠DAC = ∠BCAЭти углы — крест на ложе при стойках AB и CD и секущей AC. Следовательно, стороны AB и CD также параллельны. Значит, четыреугольника ABCD — параллелограмм, ЧТД.

Доказил второй зыгный.

Третий зызный параллелограмма. Если в четырехугольнике диагонали точки пересечения делятся пополам, то этот четырехугольник является параллелограммом.

Докажем 3 признака параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой О, то треугольник АОВ равен треугольнику COD по двум сторонам и углу между ними:

• СО = ОА;
• ДО = БО;
• углы между ними равны, как и вертикальные, поэтому угол АОВ равен углу COD.

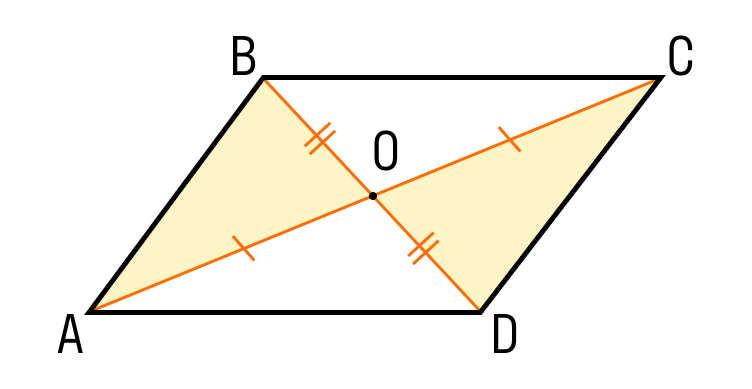
Шаг 2. Из чувствительных треугольников следе, что CD = AB.

Эти строки параллены CD || AB, на равенство углов лежания: ∠1 = ∠2 (следует из тонкости треугольников AOB и COD).

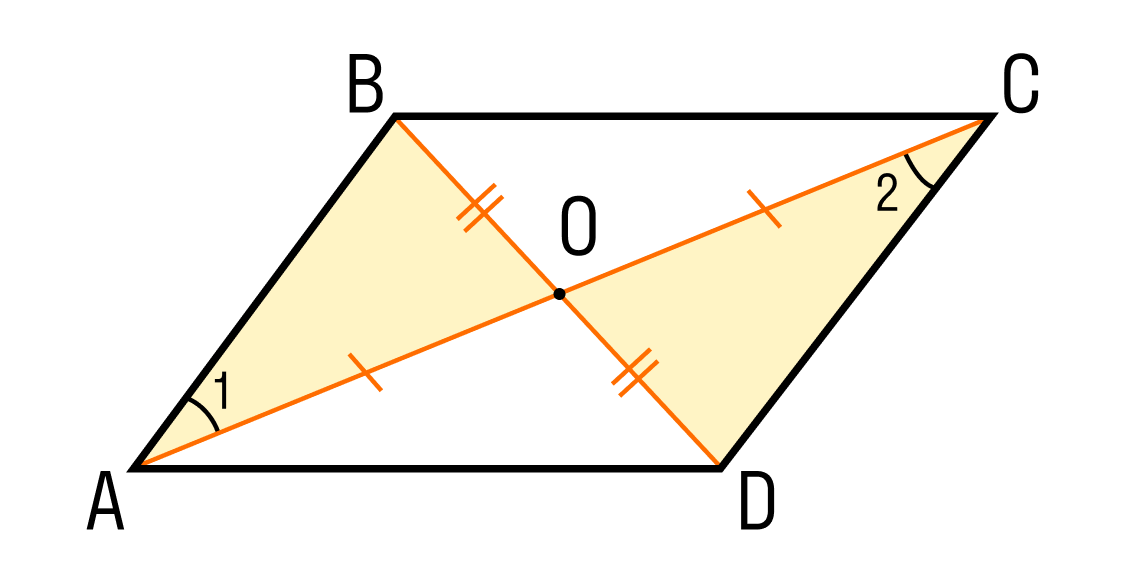
Итак, ABCD является параллелограммом по первому доказательству, которое мы доказали ранее. Что требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — знаки. Поскольку они совпадают, эти формулы можно использовать для определения параллелограмма. Но самое распространенное определение все же связано с параллелизмом противоположных сторон.

Что такое вершина и стороны угла?

Точка называется вершиной угла, лучи– сторонами угла. Обозначают строчными, заглавными буквами латиницы (отметив на сторонах дополнительные точки). Для письменного обозначенияиспользуется специальный знак ∠.

Записывается, читается:∠β – угол бета,∠BAС – угол BAС.

Углы равны, если при наложении они совпадают.

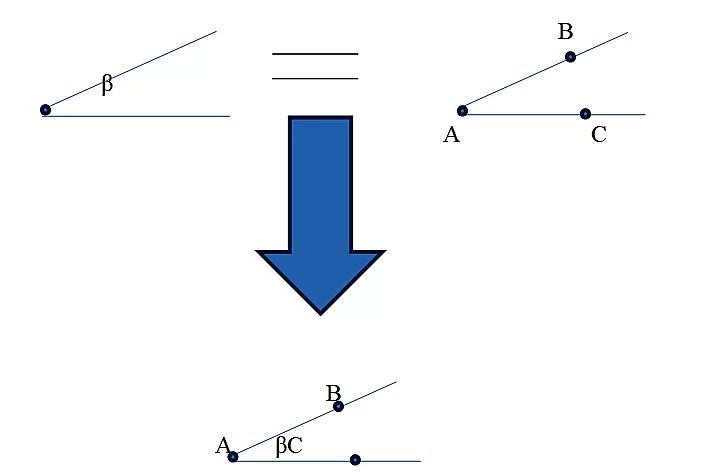
Мы наложили ∠BAС на ∠ β,при совмещении, у них совпали (полностью совместились) вершины, стороны углов. Значит ∠BAС=∠ β.

Бывают случаи, когда източки выходят два луча в противоположные стороны, образуя при этом прямую линию. Например:

Полученная фигура называется развернутым углом.

Развернутый угол – фигура, стороны которой, дополняя друг друга, создают прямую линию. Градусная мера угласоставляет 180 ˚.

Все углы принято измерять градусами. Градус–единица измерения углов, составляет 1/180 часть развернутого угла. Для письменного обозначения градуса используется специальный символ – ˚.

Получается, что∠ α=180 ˚.

Читается как: градусная мера развернутого угла альфа равна 180 градусам.

Если такой угол разделить пополам, то получим 2 равнозначных угла.

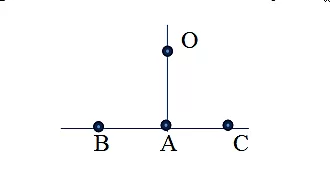
Рассмотрим развернутый ∠ВАС. Луч АО делит ∠ВАС пополам, чтобы узнать градусную меру полученных углов, необходимо градусную меру развернутого угла, поделить пополам (180:2=90). Получается, что ∠ОАС и ∠ВАО имеют градусную меру равную 90 ˚, называются прямыми углами.

Прямым углом называют половину развернутого угла, градусная мера которого составляет 90 ˚

Ну, а теперь, можете попросить у родителей чашку горячего чая. Ведь для изучения следующего определения, будем использовать вкусный, ароматный бублик.

Бублик – лакомство, знакомое с самого детства. Но вряд ли кто-то из вас задумывался какую форму имеет любимая выпечка? Если рассматриватьс геометрической точки зрения, то бублик представляетзамкнутую линию теста, все точки которой лежат на одинаковом расстоянии от центра изделия. В геометрии такая фигура называется окружностью.

Теорема Фалеса

Свойства параллелограмма помогают доказать одну из древнейших теорем планиметрии – теорему Фалеса. Она названа в честь философа, который считается родоначальником всей древнегреческой науки. Можно сказать, что Фалес – это самый ранний из всех ученых-геометров, чье имя дошло до наших дней. Сформулируем теорему Фалеса:

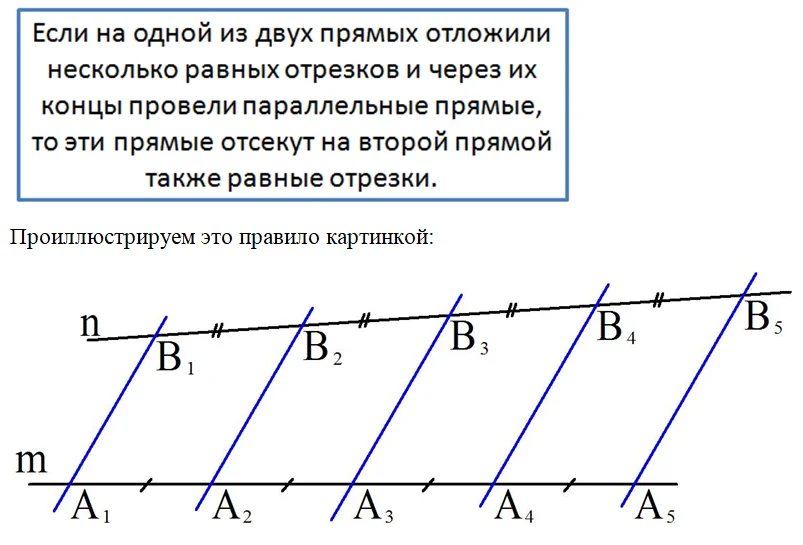
Здесь на прямой m отложили равные друг другу отрезки А₁А₂, А₂А₃,А₃А₄ и т.д.:

Далее через концы отрезков провели параллельные линии (показаны синим цветом), которые пересекли некоторую прямую n в точках В₁, В₂,В₃ и т.д. Теорема утверждает, что получившиеся при этом отрезки равны между собой:

Для доказательства теоремы нужно рассмотреть два случая. Сначала изучим ситуацию, когда прямые m и n параллельны друг другу:

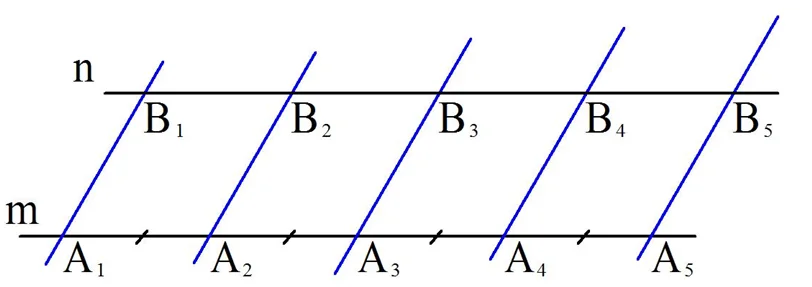
Рассмотрим четырехуг-к А₁В₁В₂А₂. Его противоположные стороны лежат на параллельных прямых:

Тогда этот четырехуг-к по определению оказывается параллелограммом, а в нем, как известно, противоположные стороны одинаковы, то есть

Однако отрезки А₁А₂, А₂А₃,А₃А₄ равны друг другу, следовательно, и равные им отрезки В₁В₂, В₂В₃, В₃В₄ и т. д. будут также равными, что мы и пытаемся доказать.

Более сложным является случай, когда исходные прямые m и n непараллельны друг другу:

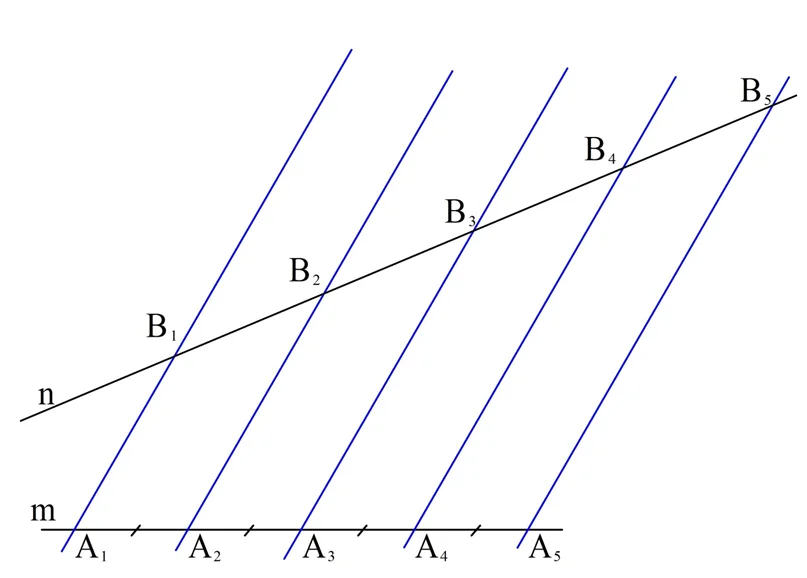
В этом случае проведем через В₁ отрезок В₁С₂, параллельный m. При этом точка С₂ будет лежать на прямой А₂В₂. Аналогично проведем отрезки В₂С₃, В₃С₄ и т. д. , каждый из которых будет параллельным прямой m:

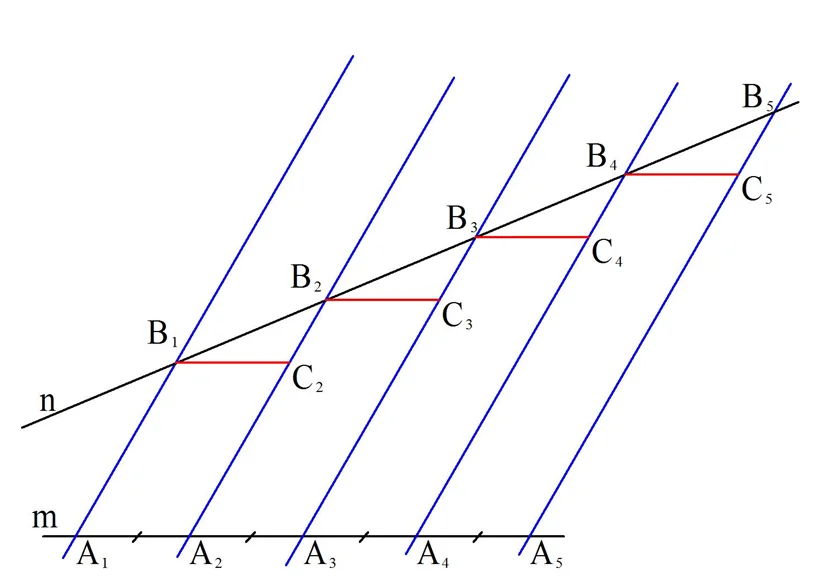
Рассмотрим фигуры А₁В₁С₂А₂, А₂В₂С₃А₃, А₃В₃С₄А₄ и т. д. Это четырехуг-ки, у каждого из которых противоположные стороны параллельны. Значит, все эти фигуры – параллелограммы. Но у него противоположные стороны одинаковы:

Далее заметим, что прямая n является секущей для параллельных прямых В₁С₂, В₂С₃, В₃С₄ и т.д. Это значит, что можно записать равенство углов:

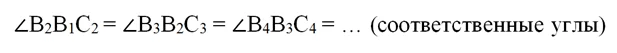
Эта же прямая является секущей для параллельных прямых А₁В₁, А₂В₂ и т. д., поэтому можно записать равенство углов:

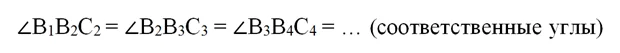
Наконец, рассмотрим треуг-ки ∆В₁В₂С₂, ∆В₂В₃С₃, ∆В₃В₄С₄. Только что мы выяснили, что у них есть по два равных угла. Но так как сумма углов в любом треуг-ке равна 180°, то и третьи углы у них также будут равными.

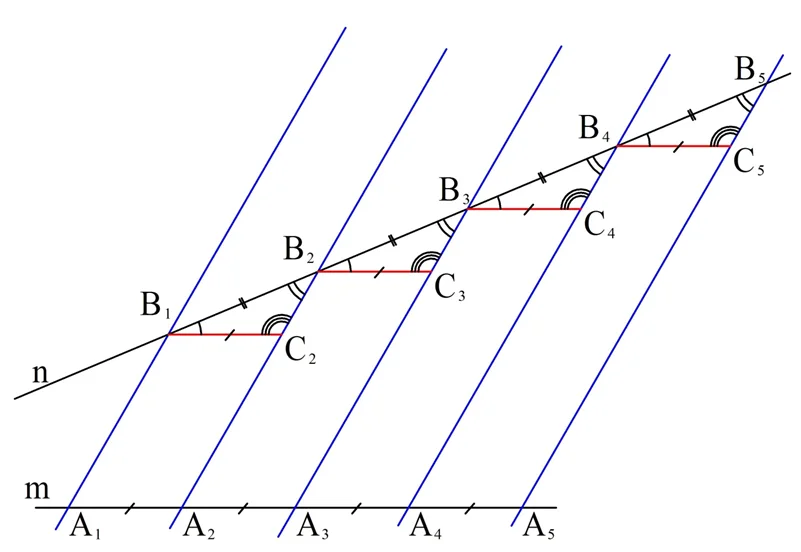
Но тогда эти треуг-ки оказываются равными друг другу, так как у них равны стороны В₁С₂, В₂С₃, В₃С₄ и т.д. Из равенства треуг-ков вытекает и равенство сторон:

Именно это равенство мы и пытались доказать.

Данная теорема может быть очень полезна при практических построениях. Пусть на клетчатом листке бумаги изображен такой треуг-к:

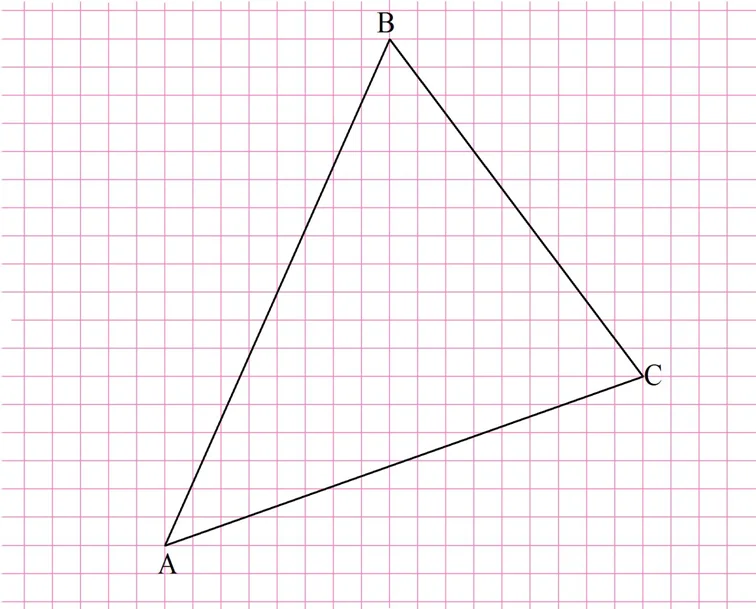
Предположим, требуется найти середину стороны АВ, а также разделить сторону ВС на три равные части. Для этого достаточно провести напротив этих сторон вертикальные линии, которые можно разделить на равные части буквально «по клеточкам». Далее надо просто провести уже горизонтальные линии, которые и разделят стороны АВ и ВС в нужных пропорциях:

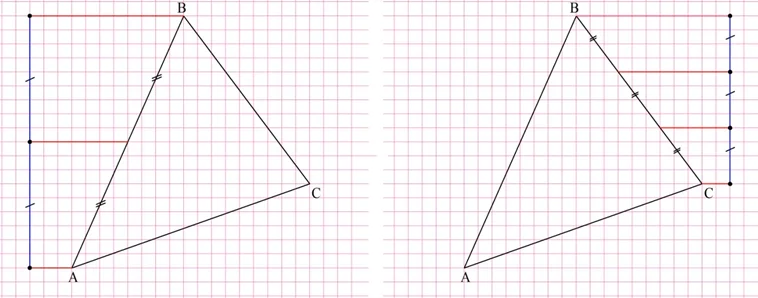
Итак, из этого урока мы узнали о понятии выпуклого четырехуг-ка и изучили один из его частных случаев – параллелограмм. В будущем мы познакомимся и с другими видами четырехуг-ков.

Периметр параллелограмма

Параллелограмм это геометрическая фигура имеющая четыре параллельные стороны, противоположных друг другу. В школьной программе все задания по решению параллелограмма, направлены на нахождение высоты, площади, диагонали и периметра. О них и пойдет речь.

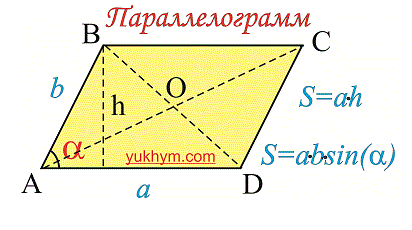Параллелограмм обладает свойствами, такими как:
В параллелограмме и углы и стороны, которые противоположны между собой одинаковы: АВ = CD, BC =AD. Так же как углы АВС = ADC и ВАD = BCD.
Диагонали проведенные из углов параллелограмма в месте пересечения разделятся на две одинаковые части. АО = ОС, ОВ = OD.
Сумма двух углов, одной стороны всегда 180 градусов.
углы: А + В = 1800, В + С = 1800, С + D =1800, A + D = 1800 .
Любая диагональ разделяет параллелограмм на две одинаковые фигуры (треугольник) как по площади так и по размеру.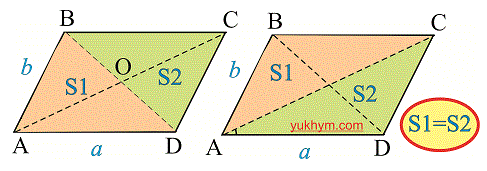

У параллелограмма есть несколько основных признаков.

Зачастую встречается такое интересное свойство как, сума диагоналей в квадрате одинакова с суммой сторон в квадрате.
АС2 + BD2 = (AB2 + BC2). AC2 + BD2 = 2 * (AB2 + BC2)

— Четырехугольная фигура с противоположными сторонами параллельными друг другу и есть параллелограмм. — Четырехугольная фигура имеющая одинаковые противоположные стороны, есть параллелограмм.

— Четырехугольная фигура имеющая одинаковые параллельные и противоположные стороны, есть параллелограмм.
— Когда встречающиеся диагонали четырехугольной фигуры в месте пересечения разделяются на равные части. Данная фигура является параллелограммом.

— Четырехугольная фигура в которой противоположные углы одинаковы называется параллелограммом.

1. Периметр параллелограмма находится по формуле

Р = 2 (а+b)

• что означает что периметр равняется двойной сумме сторон.
• Биссектриса параллелограмма

Из школьной программы помню определение которое засело в памяти на всю жизнь — Биссектриса это крыса, что ходит по углам и делит угол пополам. Если же говорить научным языком, то: Биссектрисы углов находящихся на одной стороне встречаются в точке пересечения под углом в 90 градусов.

Так же они могут совпадать и быть параллельны друг другу.
Так же в параллелограмме можно найти высоту, она обозначается в виде отрезка исходящего из угла к основанию, следовательно, от каждого угла их можно провести две.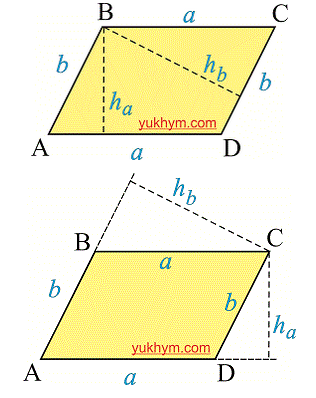

Площадь параллелограмма это произведение стороны и высоты приведенную к ней. Находится по формуле.

S = a * ha = b * hb

Есть еще один способ вычисления, но им не так часто пользуются в расчетах. Она звучит как площадь параллелограмма это произведение рядом лежащих сторон умноженный на синус угла находящегося между ними.

S = a * b * sin(?) = a * b * sin(?)

Все приведенные в данной статье формулы помогут Вам в решении различных задач по нахождению величин параллелограмма, это не сложно но очень интересно.