Как найти периметр квадрата, прямоугольника, параллелограмма, трапеции, ромба, эллипса, многоугольника

Прямоугольная и равнобедренная трапеция

Существует два частных вида трапеции, обладающих особыми свойствами. Первый из них – это прямоугольная трапеция. Она отличается тем, что один из ее углов равен 90°.

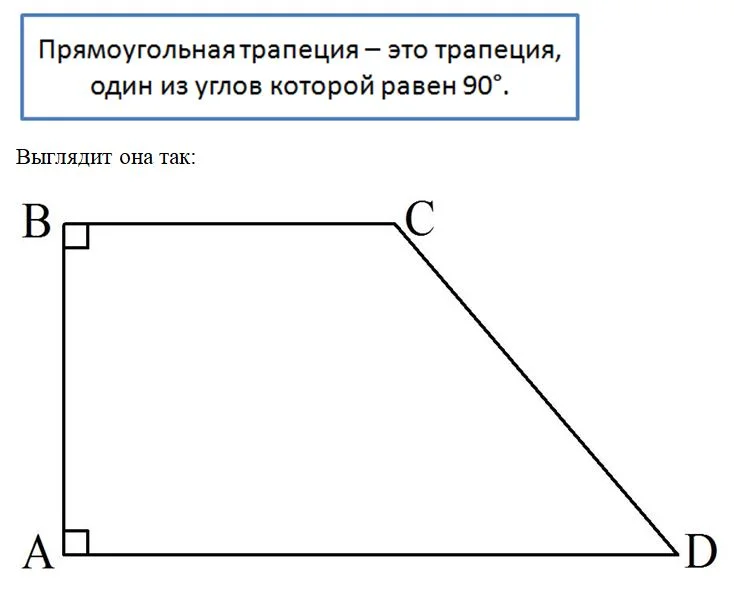
Здесь∠А = 90°. Легко догадаться, что на самом деле если у трапеции хоть один угол составляет 90°, то найдется и ещё один угол, также равный 90°. В данном случае это ∠В. Сумма ∠A и ∠D должна составлять 180°, ведь они односторонние. Именно поэтому из условия

Задание. Основания прямоугольной трапеции имеют длину 10 и 15 см, а один из углов составляет 45°. Вычислите длину ее наименьшей боковой стороны?

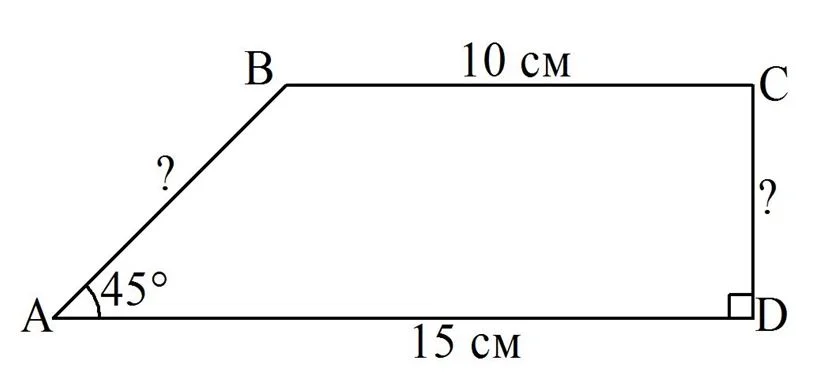
Решение:

Пусть основания заданной трапеции – это отрезки АD и ВС, ∠А = 45°, ∠D = ∠C = 90°. Опустим из точки В перпендикуляр ВН на АD:

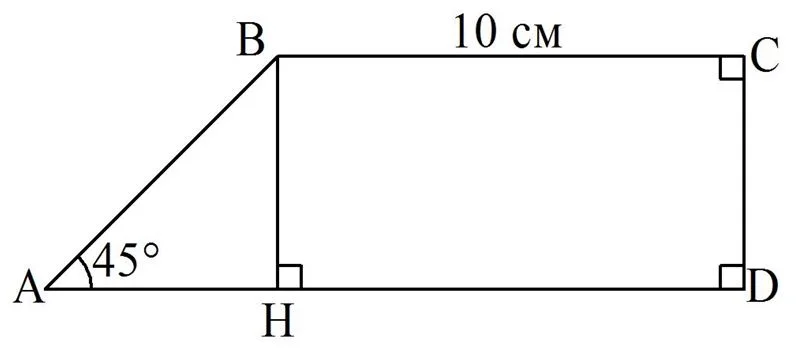
Очевидно, что ВН||CD, ведь эти отрезки перпендикулярны одной прямой АD. Получается, что в четырехуг-ке НВСD противоположные стороны попарно параллельны, то есть он является параллелограммом. Отсюда вытекает равенство его сторон:

Нашли СD, но является ли этот отрезок именно меньшей боковой стороной трапеции? Для ответа на этот вопрос вернемся к ∆АВН. В нем АВ – это гипотенуза, а потому она заведомо больше катета ВН, то есть больше 5 см. Значит, именно CD – это меньшая боковая сторона.

Ответ: 5 см.

Ещё один особый вид трапеции – равнобедренная трапеция. Она отличается тем, что у неё длины боковых сторон одинаковы.

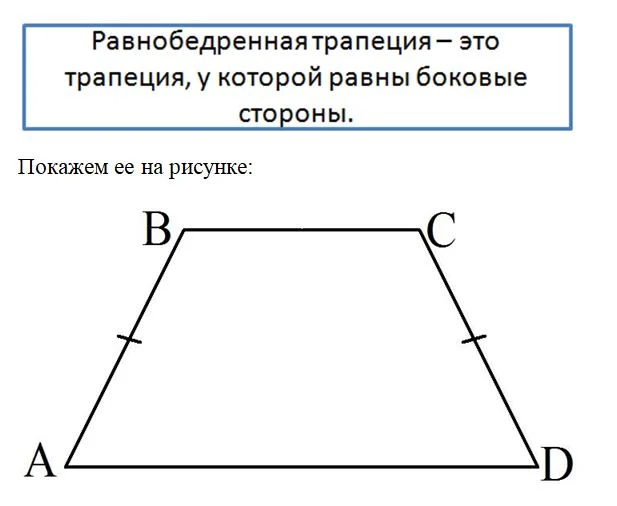
Равнобедренная трапеция обладает рядом интересных свойств. Начнем с того, что углы при каждом из ее оснований равны.

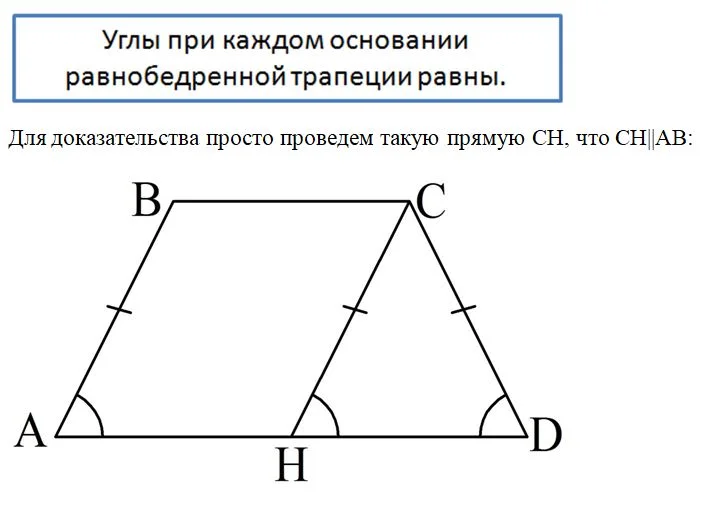
В итоге мы получили четырехуг-к АВСН, в котором АВ||CН, ВС||АН. Это значит, что он является параллелограммом, и тогда

Отсюда сразу же вытекает и второе свойство равнобедренной трапеции – у неё равные диагонали.

Доказывается этот факт с помощью :

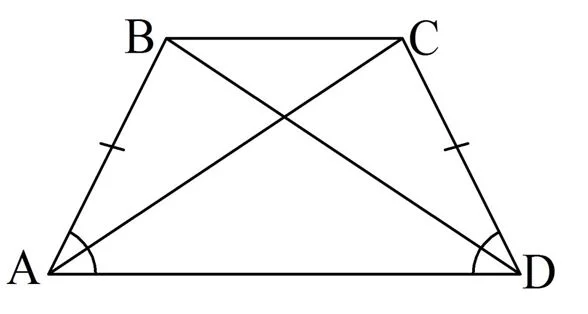
Действительно, треуг-ки ∆АВD и ∆АСD равны, ведь

Оказывается, есть признаки, которые позволяют определить, является ли трапеция равнобедренной. Сформулируем первый из них:

Для доказательства снова построим в трапеции АВСD такую прямую СН, что СН||АВ:

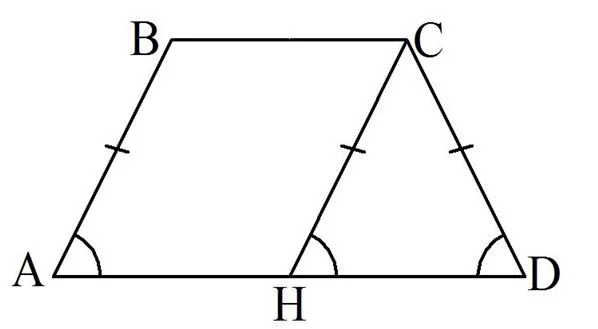
Тогда

Несколько сложнее доказать другую теорему:

Пусть в трапеции АВCD одинаковы диагонали ВD и АС. Для определенности будем считать, что большее основание – это АD. Опустим из точек В и С перпендикуляры ВЕ и СF на АD:

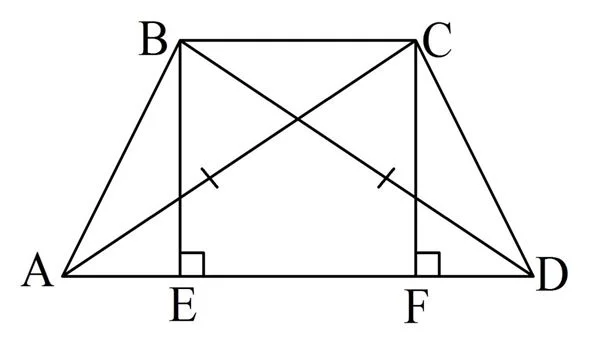
Ясно, что эти перпендикуляры параллельны друг другу, ведь они перпендикулярны третьей прямой. Тогда в ВСFЕ противоположные стороны параллельны, то есть эта фигура – параллелограмм. Отсюда вытекает, что

BE = CF

Далее рассмотрим ∆ВЕD и ∆АСF. Они оба являются прямоугольными, у них одинаковы гипотенузы (АС = ВD), а также и катеты ВЕ и СF. Значит, эти треуг-ки равны, следовательно,

Задание. Один из углов равнобедренной трапеции составляет 55°. Найдите все остальные углы этой трапеции.

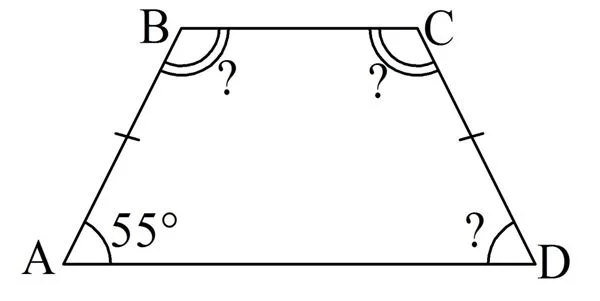
Решение. Проще всего найти ∠D, ведь углы при основании равнобедренной трапеции одинаковы:

Заметим одно важное обстоятельство. Если достроить равнобедренную трапецию до треугольника, продолжив ее боковые стороны, то получится равнобедренный треуг-к:

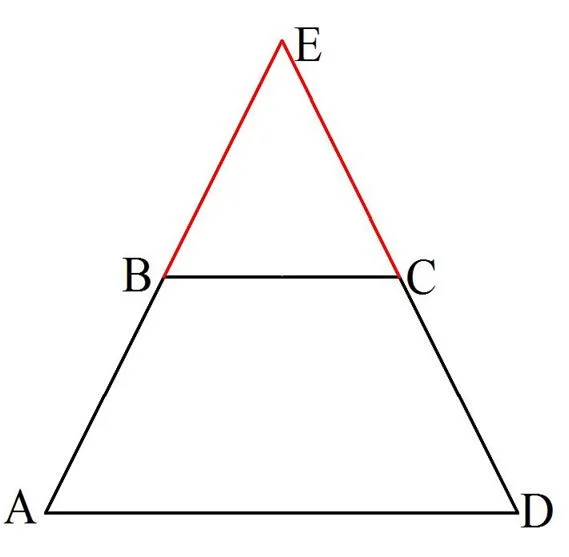
Действительно, если АВСD – равнобедренная трапеция, то

∠А = ∠D

Пусть продолжения боковых сторон пересеклись в некоторой точке Е. Тогда в ∆АЕD два угла, ∠А и ∠D, окажутся равными, следовательно, ∆АЕD– равнобедренный.

Математика – 3 класс. Прямоугольники

Что такое прямоугольник и квадрат

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2. Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.

PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Определим PABCD.

Пример:

Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см. Решение:

Нарисуем прямоугольник ABCD с исходными данными.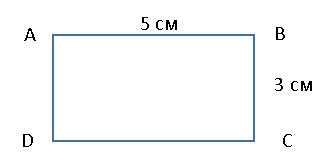

PABCD = 2 * (AB + BС)

Подставим в формулу наши данные:

PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: PABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

PABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

PABCD= 4 * AB

Пример:

Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата. Решение:

Нарисуем квадрат ABCD с исходными данными.

PABCD = 4 * AB

Подставим в формулу наши данные:

PABCD = 4 * 6 см = 24 см

Ответ: PABCD = 24 см.

Задачи на нахождение периметра прямоугольника

Измерь ширину и длину прямоугольников. Определи их периметр.

Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника. 3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора. 2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев. Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.). В вычислениях обозначается латинской буквой S.

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.

1. S AKMO = AK * KM
2. S AKMO= AK * KM = 7 см * 2 см = 14 см2.

Пример:

Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

Ответ: 14 см2.

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя. Пример:

В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

• S AВСО = AB * BC = AB * AB
• S AKMО = AK * KM = 8 см * 8 см = 64 см2

Пример:

Определи площадь квадрата AKMO со стороной 8 см.

Ответ: 64 см2.

Задачи на нахождение площади прямоугольника и квадрата:

1. Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Примеры задач

Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.

Задача №1:
Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.

Решение:
Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.

Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.

Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.

Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .

Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.

Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .

Задача №2:
Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.

Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.

Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).

Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).

Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) 5(х – а)(х + а) = (b + х)(b – х) 5(х 2 – а 2) = (b 2 – х 2) 6х 2 = b 2 + 5а 2 х = √(5а 2 + b 2)/6.

Таким образом, ОЕ = х = √(5а 2 + b 2)/6.

Шаги

1
По известным боковым сторонам и основаниям

1. 1
   Запишите формулу для вычисления периметра трапеции.
   Формула: P = T + B + L + R
2. 2
   В формулу подставьте известные длины сторон.
   Не используйте этот метод, если не даны значения всех четырех сторон.
   • Например, верхнее основание трапеции равно 2 см, нижнее основание равно 3 см, а каждая боковая сторона равна 1 см. В этом случае формула примет следующий вид: P = 2 + 3 + 1 + 1
     3
     Сложите длины сторон.
     Так вы найдете периметр трапеции.
     • В нашем примере: P = 2 + 3 + 1 + 1
       

       2
       По известным высоте, боковым сторонам и верхнему основанию

       1. 2
          Обозначьте каждую высоту.
          
       2. 3
          Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны. Не используйте этот метод, если не дано значение верхнего основания.
       3. 4
          Формула: a 2 + b 2 = c 2
       4. 5
          Боковую сторону трапеции подставьте вместо c
          6
          Возведите в квадрат известные значения.
          Затем при помощи вычитания обособьте переменную b
          7
          Извлеките квадратный корень, чтобы найти b .) Вы найдете основание первого прямоугольного треугольника. Напишите найденное значение под основанием соответствующего треугольника.
          
       5. В нашем примере: b 2 = 45
          8
          Найдите неизвестную сторону второго прямоугольного треугольника.
          Для этого запишите теорему Пифагора для второго треугольника и действуйте так, как описано выше. Если дана равнобедренная трапеция, у которой боковые стороны равны, то два прямоугольных треугольника являются равными, то есть любая сторона одного треугольника равна соответствующей стороне другого.
          
       6. Например, если вторая боковая сторона трапеции равна 7 см, то формула запишется так: a 2 + b 2 = c 2
          9
          Периметр любого многоугольника равен сумме всех его сторон: P = T + B + L + R
          

          3
          По известным высоте, основаниям и нижним углам

       7. 1
          Разбейте трапецию на прямоугольник и два прямоугольных треугольника.
          

          Если одна сторона трапеции перпендикулярна основаниям, вы не сможете получить два прямоугольных треугольника. В этом случае боковая сторона, перпендикулярная основаниям, равна высоте, а трапеция разбивается на прямоугольник и один прямоугольный треугольник.

Для этого из каждой вершины трапеции проведите высоту.

2
Обозначьте каждую высоту.

Например, высота трапеции равна 6 см. Из вершин трапеции проведите две высоты (к нижнему основанию). Возле каждой высоты напишите «6 см» (без кавычек).

Так как высоты являются противоположными сторонами прямоугольника, они равны.

3
Обозначьте среднюю часть нижнего основания (она является нижней стороной прямоугольника).

Например, если верхнее основание трапеции равно 6 см, то средняя часть нижнего основания также равна 6 см.

Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны.

4
Напишите функцию (формулу) синуса угла первого прямоугольного треугольника.
Функция: sin ⁡ θ = B H
5
В формулу синуса подставьте известные величины.
Вместо противоположной стороны подставьте высоту треугольника. Вы найдете гипотенузу, то есть боковую сторону трапеции.

• Например, если нижний угол трапеции равен 35 градусов, а высота треугольника равна 6 см, то формула запишется так: sin ⁡ (35) = 6 H
  6
  Найдите синус угла.
  Это делается при помощи научного калькулятора, а именно клавиши SIN. Найденное значение подставьте в формулу.
  • При помощи калькулятора вы найдете, что синус угла в 35 градусов приблизительно равен 0,5738. Таким образом, формула примет следующий вид: 0 , 5738 = 6 H
    7
    Найдите переменную H.
    Для этого каждую сторону уравнения (формулы) умножьте на Н, а затем каждую сторону уравнения разделите на синус угла. Или просто разделите высоту треугольника на синус угла.
    • В нашем примере: 0 , 5738 = 6 H
      8
      Найдите гипотенузу второго прямоугольного треугольника.
      Напишите функцию (формулу) синуса угла второго прямоугольного треугольника: sin ⁡ θ = B H
      9
      Запишите теорему Пифагора для первого прямоугольного треугольника.
      Формула: a 2 + b 2 = c 2
      10
      В формулу подставьте известные величины первого треугольника.
      Боковую сторону трапеции подставьте вместо c
      11
      Найдите b
      12
      Найдите основание второго прямоугольного треугольника.
      Для этого воспользуйтесь теоремой Пифагора (a 2 + b 2 = c 2
      13
      Сложите значения всех сторон трапеции.
      Периметр любого многоугольника равен сумме всех его сторон: P = T + B + L + R или треугольник 90-45-45) существуют формулы, при помощи которых можно найти неизвестные стороны без использования функции синуса или теоремы Пифагора.
      
    • Чтобы найти синус угла, воспользуйтесь научным калькулятором – введите угол, а затем нажмите клавишу SIN. Или используйте тригонометрические таблицы.
    • Калькулятор
    • Карандаш
    • Бумага

Найти периметр трапеции в задачах ЕГЭ

В задачах ЕГЭ вы найдете периметр трапеции. Например,

Задача 1

Около окружности описана трапеция, периметр которой равен 60. Найдите длину ее средней линии.

Решение:

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противолежащих сторон равны:

Где P_ABCD — периметр трапеции. В самом деле P_ABCD =AD+CB+DC+AB=2(DC+AB), а значит, DC+AB=P_ABCD /2

Средняя линия трапеции — это полусумма ее оснований, то есть MN=(DC+AB)/2=(P_ABCD /2)/2=P_ABCD /4 = 60/4=15 .

Ответ: 15.

Задача 2

Около окружности описана трапеция, периметр которой равен 44. Найдите длину ее средней линии.

Решение. Рассуждаем аналогично и получаем MN=(DC+AB)/2=(P_ABCD /2)/2=P_ABCD /4 = 44/4=11.

Ответ: 11.

То есть мы сами с вами вывели лайфхак для решения этой задачи:

И обратный лайфхак:

Применим наш лайфхак 1 к решению следующей задачи?

Около окружности описана трапеция, периметр которой равен 30. Найдите длину ее средней линии.

Ответ: 7,5.

Задача 4

Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 37, найдите радиус окружности.

Решение. Периметр трапеции равен: АD+DC+CB+AB=P_ABCD (1)

В трапецию можно вписать окружность, если суммы длин противоположных сторон равны. То есть, имеем: AD+CB=DC+AB (2)

С учетом (2) равенство (1) можно записать в виде: 2(АD+CB)=P_ABCD (3)

Теперь давайте посмотрим на вот такой рисунок:

Видно, что сторона AD=2R, где R — радиус окружности.

Тогда, AD+CB=2R+37, тогда равенство (3): 2(2R+37)=100.

Решаем уравнение, относительно R:

Ответ: 6,5

Задача 5

Из сборника ЕГЭ по математике профильный уровень 2020 год вариант 19 задание 6. Около окружности описана трапеция, периметр которой равен 28. Найдите длину ее средней линии. Решение: пользуясь лайфхаком, который мы вывели выше, вычисляем длину средней линии трепеции: делим периметр трапеции на 4. Получаем 28:4=7 Ответ: 7.

По высоте и основаниям

Проверьте вычисления, используя наш онлайн калькулятор. Десятичные дроби вводите через точку. Ориентируйтесь на обозначения на рисунке.

По высоте и средней линии

Если дана высота и средняя линяя трапеции, то ее площадь можно найти по формуле:

где  — средняя линия трапеции,

 — высота.

По известным основаниям и углам при основании

Если известны стороны трапеции , и углы при основании, то формула площади: Вы можете воспользоваться онлайн калькулятором:

По двум диагоналям и углу между ними

Если известны диагонали трапеции , и угол между ними, то формула площади трапеции: Если вам известны эти величины, то можно быстро найти площадь, используя наш калькулятор онлайн:

Площадь прямоугольной трапеции

Если известны основания прямоугольной трапеции , и угол у большего основания, то формула площади трапеции: Вывод формулы: действительно, для произвольной неравнобедренной и не прямоугольной трапеции площадь по известным основаниям и углам при основании определяется по формуле:. Если угол при основании равен 90 градусов (для прямоугольной трапеции) (пусть это угол ) то получим. По формулам приведения Тогда формула примет вид:, так как , то окончательно получается: Если вам известны эти величины, то можно быстро найти площадь, используя наш калькулятор онлайн:

Площадь равнобедренной трапеции

Площадь равнобедренной трапеции можно найти по любой из вышеприведенных формул, кроме формулы для прямоугольной трапеции, если ввести одинаковые значения для боковых сторон. Например, формула нахождения площади по известным сторонам, упростится и будет иметь вид:

Что такое периметр и площадь

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

• P= a*4
• P= a+a+a+a

Например, перед нами квадрат со стороной 10 см:

• P= 10*4
• P=40

Ответ: 40 см

• P= 10+10+10+10
• P=40

Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

• S= a*a
• S=a2

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

• S=10*10
• S= 100см2

Ответ: 100см2

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два. Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см:

• P= (6+2) * 2
• P= 16

Ответ: 16 см

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

S= a*b

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа:

1. S= 5*2
2. S=10см2

Ответ: 10 см2

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

• L = 2πr
• L= 2πd

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр:

• L= 2*3,14*3
• L=6π
• L=6*3.14
• L = 18.84 см
• Pк= 18,84 см

Ответ: 18.84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ. Площадь всегда измеряется в квадратных единицах (см2, м2, мм2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

Ромб

Следующая особенная фигура – это ромб. Дадим определение ромба:

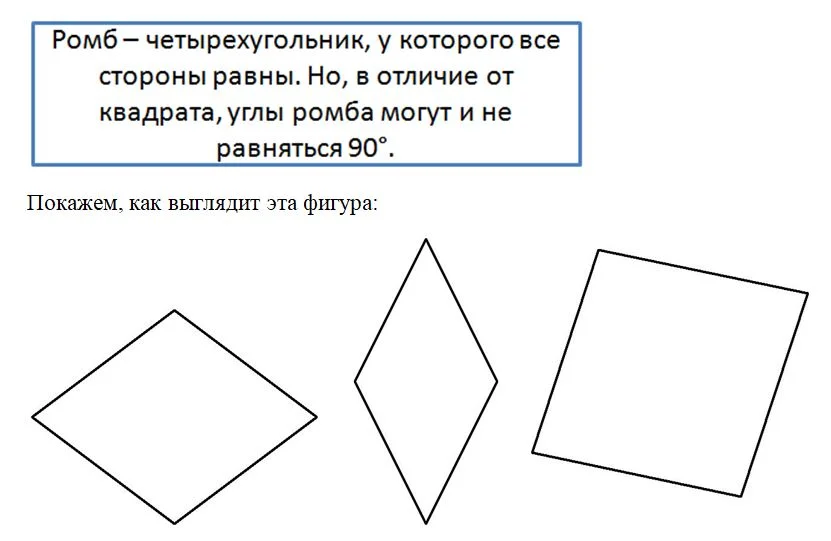
На рисунке видно, что ромб похож на параллелограмм, и это не случайно. Докажем, что любой ромб является частным случаем параллелограмма. Но прежде заметим, что обратное утверждение неверно – отнюдь не каждый параллелограмм является ромбом.

Для доказательства этого факта проведем диагональ ромба:

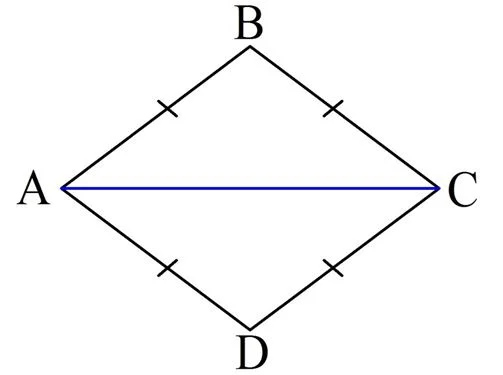
В результате получилось два треуг-ка: ∆АВС и ∆АСD. Можно заметить два факта. Во-первых, каждый из этих треуг-ков – равнобедренный, ведь стороны ромба равны. Тогда можно записать равенство углов:

Из равенства треуг-ков вытекает и равенство углов:

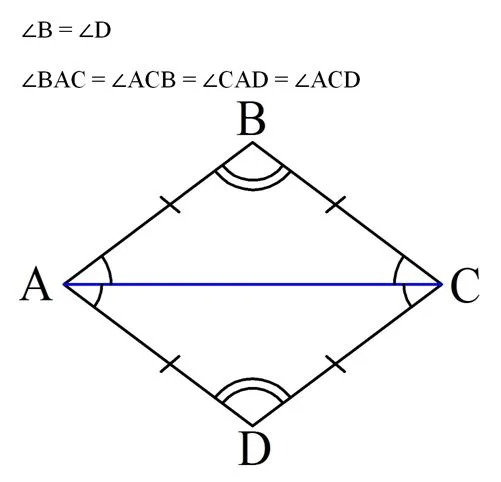
Тогда очевидно, что ∠А и ∠С также равны, ведь они состоят из двух равных углов:

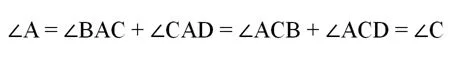
В итоге получается, что в ромбе противоположные углы одинаковы. Зная, что все 4 угла в сумме дают 360°, легко найдем сумму каких-нибудь двух смежных углов:

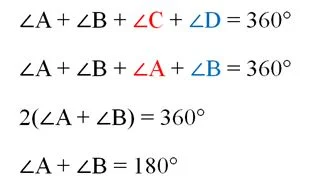
Итак, сумма смежных углов в ромбе равна 180°. Но эти углы можно рассматривать как односторонние. Если их сумма равна 180°, то и соответствующие прямые (в частности, ВС и АD) параллельны. Аналогично доказывается и то, что АВ||CD. Это и значит, что АВСD– параллелограмм.

Продолжим рассматривать построенный нами рисунок, но добавим в него ещё одну диагональ:

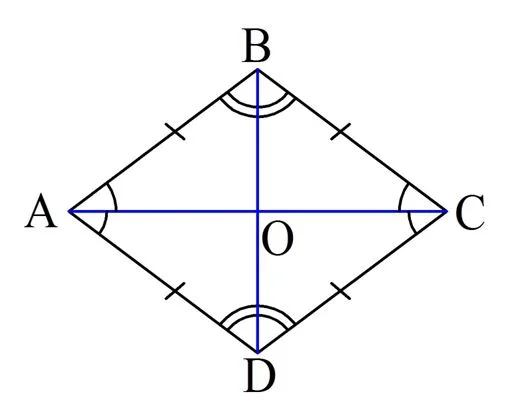
Во-первых, мы уже доказали следующее равенство

Из него вытекает, что диагональ АС является биссектрисой для∠А и ∠С. Аналогично и для диагонали ВD можно показать, что и она разбивает ∠В и ∠D пополам. Можно сформулировать следующее свойство ромба:

Далее рассмотрим ∆АВD. Он равнобедренный, а АО является биссектрисой, падающей на основание ВD. Но в равнобедренном треуг-ке такая биссектриса одновременно является высотой, то есть

Получается, что диагонали всякого ромба обязательно пересекаются под прямым углом.

Задание. Длина стороны ромба совпадает с длиной одной из его диагоналей. Определите углы этого ромба.

Решение. Построим рисунок по условию задачи:

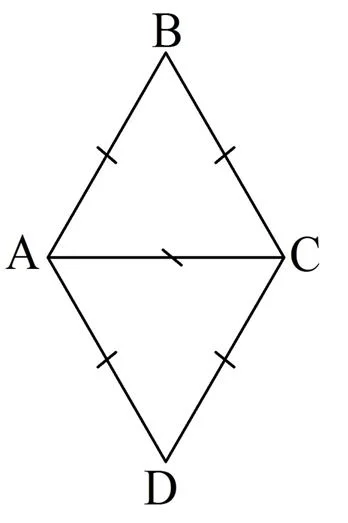
Легко заметить, что∆АВС и ∆АСD будут равносторонними. Однако все углы равностороннего треуг-ка равны 60°:

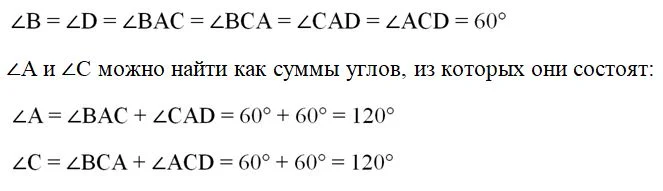
Итак, два угла ромба будут равны 60°, а другие два 120°.

Ответ: 60°; 120°.

Трапеция

(Переход к области трапеции или периметру трапеции)

Трапеция представляет собой 4-стороннюю плоскую форму с прямыми сторонами, имеющую , пару противоположных сторон, параллельных (отмечены стрелками ниже):

Трапеция		равнобедренная трапеция

трапеция:

	имеет пару параллельных сторон
	— это равнобедренной трапеции , когда она имеет равных углов с параллельной стороны
	называется « трапеция » в Великобритании (см. Ниже)

Играть с трапецией:

Параллельные стороны являются «основаниями»

Две другие стороны «ноги»

Расстояние (под прямым углом) от одной базы до другой называется «высотой»

Площадь
трапеции

Район представляет собой среднее значение двух базовых длин в раз больше высоты : Площадь = a + b 2 × ч

Пример: две базы трапеции имеют высоту 6 м и 4 м и высоту 3 м.Какова его площадь?

Площадь = 6 м + 4 м 2 × 3 м = 5 м × 3 м = 15 м 2

Инструмент Площадь многоугольника при рисовании полезен, когда вы можете нарисовать трапецию.

Периметр трапеции

Периметр — это расстояние по краям.

Периметр сумма всех сторон длины : Периметр = a + b + c + d

Пример: трапеция имеет длину стороны 5 см, 12 см, 4 см и 15 см, каков ее периметр?

Периметр = 5 см + 12 см + 4 см + 15 см = 36 см

медиана трапеции

Медиана (также называемая средней линией или средним сегментом) — это отрезок на полпути между двумя основаниями. Длина медианы — это средняя из двух базовых длин: m = a + b 2

Вы можете вычислить площадь, когда вы знаете медиану, это просто медиана, умноженная на высоту:

Площадь = MH

Трапеция

Трапеция (Великобритания: трапеция) представляет собой четырехугольник без параллельных сторон.

США и Великобритания поменяли свои определения, например:

	Трапеция	Трапеция
США:	пара параллельных сторон	НЕТ параллельных сторон
Великобритания:	НЕТ параллельных сторон	пара параллельных сторон

Несколько слов о трапеции и ее элементах

Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.

Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.

Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.

Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.

Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:

• высота, то есть отрезок, перпендикулярный обоим основаниям;
• средняя линия, которая имеет своими концами середины боковых сторон.

Примеры расчетов периметра трапеции

Рассмотрим несколько примеров расчета периметра трапеции:

1. Пример 1:

   Дана трапеция со сторонами a = 5 см, b = 7 см и основанием h = 4 см. Найдем периметр этой трапеции.

   Решение:

   Периметр трапеции можно найти, сложив длины всех сторон.

   Первое основание равно a = 5 см, второе основание равно b = 7 см.

   Боковые стороны равны h = 4 см.

   Тогда периметр трапеции равен:

   П = a + b + 2h = 5 + 7 + 2 × 4 = 5 + 7 + 8 = 20 см.

   Ответ: Периметр трапеции равен 20 см.

2. Пример 2:

   Дана трапеция со сторонами a = 9 см, b = 12 см и основанием h = 6 см. Найдем периметр этой трапеции.

   Решение:

   Периметр трапеции можно найти, сложив длины всех сторон.

   Первое основание равно a = 9 см, второе основание равно b = 12 см.

   Боковые стороны равны h = 6 см.

   Тогда периметр трапеции равен:

   П = a + b + 2h = 9 + 12 + 2 × 6 = 9 + 12 + 12 = 33 см.

   Ответ: Периметр трапеции равен 33 см.

3. Пример 3:

   Дана трапеция со сторонами a = 6 см, b = 10 см и основанием h = 8 см. Найдем периметр этой трапеции.

   Решение:

   Периметр трапеции можно найти, сложив длины всех сторон.

   Первое основание равно a = 6 см, второе основание равно b = 10 см.

   Боковые стороны равны h = 8 см.

   Тогда периметр трапеции равен:

   П = a + b + 2h = 6 + 10 + 2 × 8 = 6 + 10 + 16 = 32 см.

   Ответ: Периметр трапеции равен 32 см.

Таким образом, периметр трапеции находится путем сложения длин всех ее сторон.

Определение периметра прямоугольной трапеции

Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:

Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.

• опустим высоту из вершины С, высота CH = AB = 5см;
• исходя из рисунка 3, AH = BC = 7 см;
• HD = AD – AH = 10 – 7 = 3 см;
• далее для нахождения периметра, необходимо определить длину стороны СD, являющейся в равнобедренном треугольнике СHD гипотенузой. Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, таким образом, длина стороны СD = 5,83 см: CD = = 5,83 см;
• подставляя полученные значения в формулу, получим периметр равный 27,83 см: Периметр ABCD = 5+7+5,83+10 = 27,83 см.

Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же, для определения длины различных сторон трапеции могут помочь следующие формулы:

• формула расчета длины основания через среднюю линию;
• формулы длин сторон через высоту и угол при нижнем основании трапеции;
• формулы длин сторон трапеции через диагонали, высоту и угол между диагоналями;
• формулы длин сторон равнобедренной трапеции через площадь.

Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.

Решенные упражнения

Вопрос 1 — Значение x на изображении:

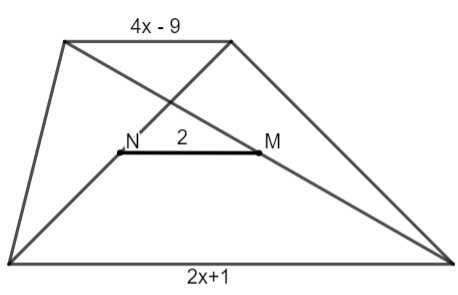
А) 2

Б) 2,5

В) 3

Г) 3,5

E) 4

разрешение

Альтернатива C

Анализируя приведенные значения, мы должны:

В = 2x + 1

б = 4х — 9

M_{а также} = 2

Вопрос 2 — Производитель рекомендует, чтобы на каждый м² кондиционируемой комнаты требовалось 800 BTUh, если в комнате находится до двух человек. К этому числу необходимо добавить 600 BTUh на каждого дополнительного человека, а также на каждое излучающее тепло электронное устройство в окружающей среде. Ниже приведены пять вариантов устройств от этого производителя и их соответствующие тепловые мощности:

Тип I: 10 500 БТЕ · ч

Тип II: 11 000 БТЕ / ч

Тип III: 11500 БТЕ · ч

Тип IV: 12 000 БТЕ / ч

Тип V: 12500 БТЕ · ч

Руководитель лаборатории должен купить устройство для акклиматизации окружающей среды. В нем будут два человека плюс центрифуга, излучающая тепло. Лаборатория имеет форму прямоугольной трапеции, размеры которой показаны на рисунке.

В целях экономии энергии супервайзер должен выбрать устройство с наименьшей теплоемкостью, которое соответствует потребностям лаборатории и рекомендациям производителя.

Выбор супервизора будет падать на устройство типа:

ТАМ

Б) II

В) III

Г) IV

E) V

разрешение

Альтернатива C

Рассчитывая площадь лаборатории, имеющую форму трапеции, мы должны:

Теперь мы знаем, что на каждый м² требуется 800 БТЕ / ч, и что, кроме того, поскольку в лаборатории есть электронное устройство, мы добавим к ответу 600 БТЕ / ч.

13,6 · 800 = 10.880

Примеры из реальной жизни

Платок

Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:

Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.

Откосы

К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде

Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.

Трапеция: определение и свойства

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны непараллельны. Одна из непараллельных сторон называется большей основой, а другая — меньшей основой. Стороны, соединяющие основания, называются боковыми сторонами. У трапеции также есть две пары углов: прямые углы между боковыми сторонами и один угол между большей основой и одной из боковых сторон.

Для трапеции можно найти площадь и периметр. Площадь трапеции можно найти с помощью следующей формулы:

площадь = ((большая основа + меньшая основа) * высота) / 2

Где высота — это перпендикуляр, опущенный от одной основы трапеции на другую основу. Величина высоты должна быть известна для того, чтобы найти площадь.

Периметр трапеции можно найти, сложив длины всех четырех сторон трапеции. Другая формула для нахождения периметра выглядит следующим образом:

периметр = большая основа + меньшая основа + боковая сторона1 + боковая сторона2

Теперь, зная определение и формулы для вычисления площади и периметра трапеции, можно легко решать задачи и находить значения этих параметров для разных трапеций.

Что такое трапеция и какие у нее стороны?

Трапеция — это геометрическая фигура, которая состоит из четырех сторон. У трапеции есть две параллельные стороны, которые называются основаниями, и две непараллельные стороны, которые называются боковыми сторонами. Одна из оснований обычно длиннее другой.

Какие у трапеции стороны? Основания трапеции обозначаются буквами «a» и «b», а боковые стороны — «c» и «d». Обычно боковые стороны не являются параллельными, но могут быть равными.

Формулы для нахождения площади и периметра трапеции могут быть использованы в решении задач по геометрии. Площадь трапеции можно найти по следующей формуле: S = (a + b) * h / 2, где «S» — площадь, «h» — высота трапеции.

Периметр трапеции можно найти по формуле: P = a + b + c + d, где «P» — периметр. В случае, когда стороны трапеции равны, формула упрощается и становится P = 2 * (a + c).

Таким образом, зная значения сторон трапеции и ее высоту, можно легко вычислить ее площадь и периметр с помощью соответствующих формул.

Какие свойства имеет трапеция?

Трапеция — это четырехугольник, у которого две параллельные стороны называются основаниями, а остальные две стороны называются боковыми сторонами. У трапеции есть несколько свойств, которые позволяют нам определить ее характеристики.

Первое свойство трапеции заключается в том, что сумма всех ее углов равна 360 градусов. Это означает, что если у нас есть информация о нескольких углах трапеции, мы можем легко определить остальные углы.

Второе свойство трапеции заключается в том, что боковые стороны трапеции равны по длине. Это означает, что если мы знаем длину одной боковой стороны, мы можем легко найти длину другой боковой стороны.

Третье свойство трапеции заключается в том, что высота трапеции — это перпендикуляр, опущенный из одного основания на другое основание. Если мы знаем длину высоты, мы можем легко найти площадь трапеции, используя соответствующую формулу.

Кроме того, для трапеции существуют формулы для вычисления ее площади и периметра. Площадь трапеции можно найти, умножив сумму длин оснований на высоту и разделив полученный результат на 2.

Периметр трапеции можно найти, сложив длины всех ее сторон. Для этого необходимо знать длины оснований и боковых сторон трапеции.