Как измерить угол
Для измерения углов используется транспортир:
Транспортир
Попробуем измерить угол \
Шаги для измерения угла \.
Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°
Далее попробуем измерить этот ∠AOC:
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°
что это такое в геометрии, формула с формулировкой, как найти, чему равна сумма
- Свойства и виды смежных углов в геометрии
- Как найти, чему равна сумма
- Примеры решения задач
Определение
Смежные углы — это два угла, у которых есть общая вершина и одна сторона, а две другие стороны являются продолжением друг друга и лежат на одной прямой.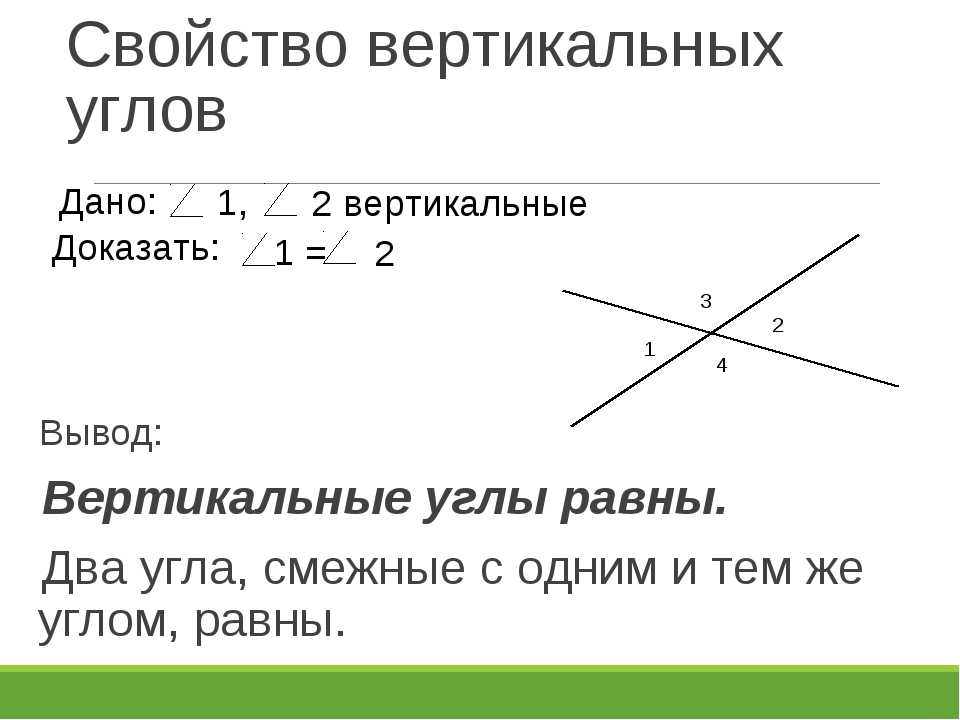
Если две прямые пересекаются, то они образуют две пары смежных углов: \(\angle1\) и \(\angle2\), \(\angle3\) и \(\angle4\), а также \(\angle1\) и \(\angle3\), \( \angle2\) и \(\angle4\). При этом объединение пар, которые обозначены обозначениями 1 и 4, 2 и 3, представляют из себя вертикальные углы, а значит — они равны. Поэтому рассматривать можно только одну из пар смежных углов, другая окажется идентична по всем показателям.
У смежных углов одинаковые синусы.
Для косинусов и тангенсов тоже распространяется равенство, но их значения противоположны по знаку.
Чтобы построить смежный угол уже заданному, требуется продлить одну из сторон существующего угла дальше вершины.
Примечание
В паре, если один угол тупой, то по правилу другой обязательно острый.
Если один из углов является прямым, то второй тоже прямой.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления)

Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Доказательство теоремы
Докажем следующую теорему о смежных углах:
Теорема: Если две прямые пересекаются, то смежные углы образуются смежными сторонами по разные стороны пересекающей прямой и равны между собой.
Доказательство:
- Пусть имеются две прямые AB и CD, пересекающиеся в точке O.
- Рассмотрим два смежных угла: угол AOC и угол BOD.
- Очевидно, что сторона AO является продолжением стороны BO, а сторона CO является продолжением стороны DO.
- Также, по условию пересечения прямых, угол AOC и угол BOD образованы внутри треугольника OBC (или OAB), и поэтому они между собой равны.
- Таким образом, смежные углы, образованные двумя пересекающимися прямыми, являются смежными сторонами по разные стороны пересекающей прямой и равны между собой. Теорема доказана.
Таким образом, мы доказали теорему о смежных углах и установили, что смежные углы, образованные пересекающимися прямыми, обладают определенными свойствами. Это позволяет использовать их при решении задач геометрии и конструировании фигур.
Значимость теоремы о смежных углах
Теорема о смежных углах — одно из основных положений геометрии, которое имеет огромную значимость для решения различных задач и построений в плоской геометрии. Она позволяет нам устанавливать взаимосвязь между углами при пересекающихся прямых и между углами при параллельных прямых.
Основная идея теоремы состоит в том, что при пересечении двух прямых углы, лежащие по одну сторону от пересекающей прямой и смежные с несмежными углами, равны между собой. Данное положение позволяет нам находить углы в сложных геометрических фигурах, а также доказывать их равенство или неравенство.
Одно из важных применений теоремы о смежных углах — доказательство параллельности прямых. Если мы знаем, что пара углов смежная и они равны, то можно заключить, что прямые, на которых эти углы лежат, параллельны.
Теорема о смежных углах используется также при решении задач на построение различных фигур. Зная значения некоторых углов, мы можем с использованием данной теоремы построить нужную нам фигуру или вычислить недостающие углы в уже построенной фигуре.
Также теорема о смежных углах находит свое применение в различных областях науки и техники. Ее используют математики, архитекторы, инженеры, дизайнеры при проектировании и построении сооружений, при создании компьютерных моделей и рендеринге изображений.
В целом, теорема о смежных углах имеет важное значение в геометрии и представляет собой одну из ключевых концепций, которую необходимо знать и применять при решении задач и построений в плоской геометрии
Смежные углы и их свойства
Смежные углы и их свойства.
Смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными и лежат на одной прямой.
Смежные углы (понятие и определение):
Смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными и лежат на одной прямой. Таким образом, вместе смежные углы составляют развёрнутый угол .
Рис. 1. Смежные углы
В свою очередь, развернутый угол – это угол, градусная мера которого равна 180°.
Поэтому сумма величин смежных углов составляет 180 градусов.
Из этого следует, что величина угла β, являющимся смежным для угла величиной α градусов, будет (180° – α) градусов.
Свойства смежных углов:
1. Сумма величин смежных углов равна 180 градусам.
2. При пересечении двух прямых образуются две пары смежных углов.
Рис. 2. Смежные углы
3. Угол, смежный с прямым углом, есть прямой угол . Такие углы равны между собой.
Рис. 3. Смежные углы
4. В паре смежных углов один угол всегда тупой, а другой – острый либо оба угла являются прямыми.
5. Синусы смежных углов равны.
6. Косинусы и тангенсы смежных углов равны по величине, но имеют противоположные знаки.
Примечание: Фото https://www.pexels.com, https://pixabay.com
- ← Тупоугольный треугольник, элементы, свойства, признаки и формулы
- Вертикальные углы и их свойства →
Востребованные технологии
- Концепция инновационного развития общественного производства – осуществления Второй индустриализации России на период 2017-2022 гг. (106 533)
- Экономика Второй индустриализации России (102 545)
- Программа искусственного интеллекта ЭЛИС (27 747)
- Метан, получение, свойства, химические реакции (24 179)
- Этилен (этен), получение, свойства, химические реакции (23 880)
- Природный газ, свойства, химический состав, добыча и применение (21 534)
- Крахмал, свойства, получение и применение (20 870)
- Пропилен (пропен), получение, свойства, химические реакции (19 941)
- Целлюлоза, свойства, получение и применение (19 728)
- Прямоугольный треугольник, свойства, признаки и формулы (18 986)
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя: – экономику Второй индустриализации России, – теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России, – организационный механизм осуществления Второй индустриализации России, – справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Треугольники
- Сумма углов любого треугольника равна 180° .
- Сторона треугольника меньше суммы двух других сторон данного треугольника. (неравенство треугольника)
- Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
- Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (1 признак равенства треугольников)
- Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. (2 признак равенства треугольников)
- Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. (3 признак равенства треугольников)
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. (1 признак подобия треугольников)
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны. (2 признак подобия треугольников)
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. (3 признак подобия треугольников)
- Напротив равных углов лежат равные стороны.
- Если два угла треугольника равны, то равны и противолежащие им стороны.
- Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне.
- Площадь треугольника равна полупроизведению двух сторон треугольника на синус угла между ними.
- Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, является медианой (то есть делит основание на две равные части) и высотой (перпендикулярна основанию).
- Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
- В прямоугольном треугольнике катет, лежащий напротив угла 30° равен половине гипотенузы.
- В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине этой гипотенузы.
- Площадь прямоугольного треугольника меньше произведения его катетов.
- Площадь прямоугольного треугольника равна половине произведения его катетов.
- Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. (теорема косинусов).
- Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
- Стороны треугольника пропорциональны синусам противолежащих углов. (теорема синусов)
- Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
- Один из углов треугольника всегда не превышает 60°.
- Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
- Биссектрисы треугольника пересекаются в центре его вписанной окружности.
Примеры применения теоремы о смежных углах
Теорема о смежных углах имеет множество применений в геометрии. Рассмотрим несколько примеров, демонстрирующих использование этой теоремы.
Пример 1:
Рассмотрим треугольник ABC, в котором угол A равен 70 градусов. Нам известно, что углы при основании треугольника равны друг другу. Найдем величину угла B.
По теореме о смежных углах, углы A и B являются смежными. Таким образом, сумма этих углов равна 180 градусов. Мы знаем, что угол A равен 70 градусов, следовательно, угол B будет равен 180 — 70 = 110 градусов.
Пример 2:
Рассмотрим две параллельные прямые AB и CD, пересекающиеся прямой EF. Нам нужно найти величину угла x.
По теореме о смежных углах, уголы 1 и x являются смежными, а также уголы 2 и x. Мы знаем, что угол 1 равен 70 градусов и угол 2 равен 110 градусов. Сумма углов 1 и x равна 180 градусов, поскольку они образуют прямую линию. Аналогично, сумма углов 2 и x равна 180 градусов.
Из этого следует, что угол x равен 180 — 70 = 110 градусов, а также 180 — 110 = 70 градусов.
Пример 3:
Рассмотрим два пересекающихся отрезка AB и CD. Нам нужно найти величину угла y.
По теореме о смежных углах, углы 1 и y являются смежными, а также углы 2 и y. Мы знаем, что угол 1 равен 30 градусов и угол 2 равен 150 градусов. Сумма углов 1 и y равна 180 градусов, поскольку они образуют прямую линию. Аналогично, сумма углов 2 и y равна 180 градусов.
Из этого следует, что угол y равен 180 — 30 = 150 градусов, а также 180 — 150 = 30 градусов.
Таким образом, теорема о смежных углах является полезным инструментом для нахождения величины углов в различных геометрических конструкциях.
Нахождение углов
Как найти углы в прямоугольном треугольнике
Углы в прямоугольном треугольнике возможно найти при помощи двух универсальных способов, которые обрисованы выше, либо с помощью тригонометрических функций — косинуса, синуса, котангенса, тангенса.
Тригонометрические функции
Если даются две стороны, то возможно найти угол по данному алгоритму:
- нужно определить, какими являются стороны в отношении к прямому углу (гипотенуза или катет) и углу, который следует найти (противолежащий\прилежащий катету);
- нужно найти тригонометрическую функцию, подходящую по смыслу решения задачи;
- нужно найти значение тригонометрической функции, подставив все значения сторон;
- нужно вычислить угол с помощью обратной функции (арккосинус, арксинус и др).
Понятие углов, виды углов
Обычно для названия углов используют три заглавные буквы. Ими обозначаются две точки, которые расположены на сторонах угла, а также вершины.
Посмотрите на рисунок:
Величина угла измеряется в градусах. Например, ∠AOB=24°.
Существует также другое определение угла.
Развернутым углом называется угол, при котором обе стороны угла располагаются на одной прямой (его стороны считаются дополнительными полупрямыми на одной прямой).
Посмотрите на рисунок развернутого угла:
Вершиной угла считается точка на данной прямой. Обычно в геометрии вершину угла называют точкой O. В математике угол обозначают обычно специальным знаком — . Если стороны угла подписать малыми латинскими буквами, то для точного определения угла записывают друг после друга буквы, которые соответствуют сторонам.
Если используется обозначение с помощью больших букв, то стороны угла будут иметь названия OB, OA. В данном случае у угла появляется обозначение из трех латинских букв, которые записаны друг за другом, с вершиной в центре — ∠AOB, ∠BOA. Используется также обозначение с помощью цифр. Используется в том случае, когда у углов нет названий, а также обозначений в виде букв.
Посмотрите на разные обозначения углов:
Угол может делить плоскость на две части. Если угол не является развернутым, тогда меньшая часть плоскости носит название внутренней области угла, большая часть называется внешней областью угла.
Посмотрите, какие части являются внешними, а какие внутренними:
Если развернутый угол разделяется на плоскости, любая из его частей является внутренней областью развернутого угла. Внутренняя область угла считается таким элементом, который служит для вторичного определения угла.
Определение смежных и вертикальных углов
Обратите внимание на рисунок ниже, на котором видно, что смежные углы являются дополнением друг друга до развернутого угла. Посмотрите на вертикальные углы:
Посмотрите на вертикальные углы:
В случае пересечения прямых формируются 4 пары смежных углов, а также 2 пары вертикальных углов.
Посмотрите на то, как это выглядит:
Бывает несколько видов углов:
- острый угол (менее 90°);
- тупой угол (более 90°);
- прямой угол (ровно 90°);
- развернутый угол (ровно 180°).
Посмотрите, как они выглядят:
Также стоит упомянуть о накрест лежащих углах. Накрест лежащими углами называются углы, которые расположены во внутренней области в разных сторонах от секущей (то есть накрест друг от друга).
Также вспомним соответственные углы. Это вид углов, которые образуются в случае пересечения двух параллельных прямых общей секущей.
Свойства вертикальных углов:
- вертикальные углы являются равными (∠AOC=∠BOD, ∠COD=∠AOB);
- биссектрисы вертикальных углов лежат на одной прямой.
Свойства смежных углов:
- сумма смежных углов равняется 180°;
- угол, который является смежным с прямым, является прямым; смежный с острым — является тупым; смежный с тупым — является острым;
- если два угла равны, то смежные тоже будут равны;
- чем больше угол, тем смежный меньше;
- биссектрисы смежных углов формируют прямой угол;
- если смежные равны, то они являются прямыми.
Геометрия. 7 класс
Конспект урока
Смежные и вертикальные углы. Аксиомы и теоремы
Перечень вопросов, рассматриваемых в теме:
- Понятие смежных и вертикальных углов
- Свойства смежных и вертикальных углов
- Отличие аксиомы от теоремы
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Свойства смежных углов:
- Сумма смежных углов равна 180 0 .
- Если два угла равны, то и смежные с ними углы равны.
- Угол, смежный с прямым углом, есть прямой угол.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны.
Аксиома– положение, принимаемое без доказательств.
Основная литература:
- Атанасян Л. С. Геометрия: 7 – 9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Погорелов А. В. Геометрия: 7 – 9 класс. // Погорелов А. В. – М.: Просвещение, 2017. – 224 с.
Теоретический материал для самостоятельного изучения
Давайте построим развёрнутый угол АОС и проведём в нём луч ОВ. В результате у нас получилось два угла ∠АОВ – острый угол и ∠ВОС– тупой угол. Стороны АО и ОС – продолжают друг друга, ВО– общая сторона. Углы АОВ и ВОС – это смежные углы. На основании этого сформулируем определение смежных углов.
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Обратите, внимание, что смежные углы АОВ и ВОС лежат на развёрнутом угле АОС. Отсюда можно сделать вывод: сумма смежных углов равна 180 о
Свойство смежных углов: сумма смежных углов равна 180 о .
Давайте докажем это свойство.
Доказательство. Пусть углы ∠АОВ и ∠ВОС – смежные, луч ОВ – проходит между сторонами развёрнутого угла ∠АОС. Поэтому, сумма углов ∠АОВ и ∠ВОС равна ∠АОС, а этот угол развёрнутый, он равен 180 о . Свойство доказано.
Укажем ещё одно свойство смежных углов.
Если два угла равны, то и смежные с ними углы равны.
Сейчас давайте вспомним определение прямого угла: угол, равный 90 0 , называется прямым углом. Опираясь на свойство суммы смежных углов, можно сделать вывод: угол, смежный с прямым углом, есть прямой угол.
Теперь построим две пересекающиеся прямые, АС и BD. Посмотрите, при пересечении прямых у нас получилось четыре угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ и ∠BОC.
Углы, которые не являются смежными:
∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов называются вертикальными углами.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны. Убедимся в справедливости этого свойства, докажем его.
Доказательство. Посмотрим на чертёж: пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1– смежные углы. Угол 2 одновременно является смежным с углом 1 и с углом 3. По свойству смежных углов
∠1+ ∠2= 180 0 и ∠3+ ∠2= 180 0 . Получаем, что ∠1+ ∠2= ∠3+ ∠2, значит, ∠1= ∠3. Углы ∠1 и ∠3 – вертикальные. Мы доказали справедливость этого свойства.
Свойства смежных и вертикальных углов, которые мы сегодня рассмотрели– в геометрии называются теоремами. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путём рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.
На предыдущих уроках вы познакомились с понятием аксиомы.
В чём же различие между аксиомой и теоремой? Ответ на этот вопрос таков: аксиома – положение, принимаемое без доказательств.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Используя чертёж, найдите угол ∠ВОК.
Ответ: ∠ВОК=____ 0
Решение. Воспользуемся свойством смежных углов: сумма смежных углов равна 180 0 . По условию задачи ∠АОК= 11 0 , то ∠ВОК+ ∠АОК= 180 0
∠ВОК+ 11 0 = 180 0
∠ВОК= 180 0 – 11 0 = 169 0 .
Ответ: ∠ВОК= 169 0
№2. Тип задания: единичный / множественный выбор.
Используя чертёж, найдите угол ∠AOD.
Варианты ответов:
- 112 0
- 64 0
- 116 0
- 68 0
Решение. На чертеже указано, что углы ∠СОЕ= ∠DOE. Значит, ∠COD= ∠СОЕ+ ∠DOE= 32 0 + 32 0 = 64 0 . ∠AOD смежный с углом ∠COD, по свойству смежных углов: ∠AOD= 180 0 –∠COD= 180 0 – 64 0 =116 0 .
№3. Тип задания: выделение цветом.
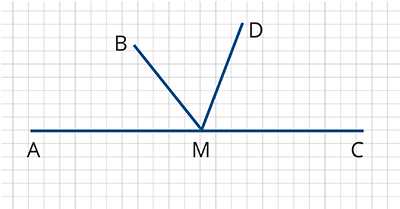
Используя чертёж, найдите градусную меру угла ∠BMD, если ∠AMD= 125 0 , ∠BMC= 115 0 .
Выделите верный ответ из списка:
60 0 ; 30 0 ; 75 0 ; 90 0
Решение. По чертежу можно увидеть, что ∠BМD является частью ∠AMD и ∠BMC. Рассмотрим ∠DMC и ∠AMD. Эти углы – смежные, т.е. их сумма равна 180 0 . Значит, зная градусную меру ∠AMD, мы сможем найти градусную меру ∠DMC= 180 0 –∠AMD= 180 0 -–125 0 = 55 0 . Теперь рассмотрим ∠BMC= ∠BMD+ ∠DMC. Мы знаем градусные меры ∠BMC и ∠DMC, значит, мы сможем найти градусную меру ∠BMD.
Свойства смежных углов:
1. сумма величин смежных углов равна 180 градусам.
2. пересечение двух прямых дает две пары смежных углов.
Рисунок 2. Смежные углы
3. угол, прилежащий к прямому углу, является прямым углом. Эти углы равны.
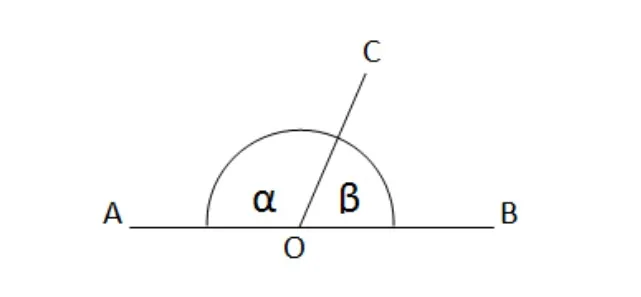
Рисунок 3: Смежные углы
4. в паре смежных углов один угол всегда тупой, а другой всегда острый, или оба угла прямые.
5. синус смежных углов равен.
6. значения косинуса и тангенса смежных углов равны, но имеют противоположные значения
Мы не продаем товары, технологии и т.д. производителям и изобретателям! Вы должны обращаться к ним напрямую!
Востребованные технологии
- Концепция инновационного развития общественного производства – осуществления Второй индустриализации России на период 2017-2022 гг. (107 491)
- Экономика Второй индустриализации России (104 204)
- Этилен (этен), получение, свойства, химические реакции (33 724)
- Программа искусственного интеллекта ЭЛИС (30 914)
- Метан, получение, свойства, химические реакции (28 563)
- Крахмал, свойства, получение и применение (28 332)
- Природный газ, свойства, химический состав, добыча и применение (27 902)
- Целлюлоза, свойства, получение и применение (26 992)
- Пропилен (пропен), получение, свойства, химические реакции (26 582)
- Прямоугольный треугольник, свойства, признаки и формулы (25 557)
О чём данный сайт?
Мы ведем переговоры с производителями и изобретателями отечественных инновационных технологий и даем рекомендации по их использованию.
Реализация второй индустриализации России базируется на качественно новом научном фундаменте (теория, методология и инструментарий), разработанном авторами.
Конечным результатом второй индустриализации России является рост благосостояния всех членов общества: рядовых граждан, предприятий и государства.
Вторая индустриализация России состоит из ряда научных, технических и других инновационных идей, проектов и разработок, которые могут быть широко применены в практике хозяйственной деятельности в краткосрочной перспективе (3-5 лет) и позволят обеспечить качественно новое, прогрессивное развитие общества в ближайшие 50-75 лет.
О Второй индустриализации
Страна, которая первой совершит этот сложный прорыв — Россия — займет лидирующее положение в мировом сообществе и останется недосягаемой для других стран на века.
Геометрия имеет немаловажное значение в нашей жизни. Ведь если посмотреть вокруг, то нетрудно заметить, что нас окружают различные геометрические фигуры
Мы встречаем их повсюду: на улице, в классе, дома, в парке, в спортзале, в школьной столовой, просто везде, куда бы мы ни пошли. Однако темой сегодняшнего урока является соседний уголь. Поэтому давайте осмотримся и попытаемся найти углы в этой среде. Если внимательно посмотреть из окна, то можно увидеть, что некоторые ветви образуют смежные углы, а в стенах ворот можно увидеть множество вертикальных углов. Приведите собственные примеры смежных углов, которые вы наблюдаете в своем окружении.
1. вот книга на столе на подставке для книг. Какой угол она образует? 2. Здесь вы видите студента, работающего на ноутбуке. Какой угол вы здесь видите? 3. под каким углом расположена рамка фотографии на основании? 4. как вы думаете, возможно ли, чтобы два смежных угла были равны?
Перед вами появляется геометрическая фигура. Что это за фигура, как она называется? Теперь назовите все смежные углы, которые вы видите в этой геометрической фигуре.
Геометрия. 7 класс
Конспект урока
Смежные и вертикальные углы. Аксиомы и теоремы
Перечень вопросов, рассматриваемых в теме:
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Свойства смежных углов:
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны.
Аксиома– положение, принимаемое без доказательств.
Теоретический материал для самостоятельного изучения
Давайте построим развёрнутый угол АОС и проведём в нём луч ОВ. В результате у нас получилось два угла ∠АОВ – острый угол и ∠ВОС– тупой угол. Стороны АО и ОС – продолжают друг друга, ВО– общая сторона. Углы АОВ и ВОС – это смежные углы. На основании этого сформулируем определение смежных углов.
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
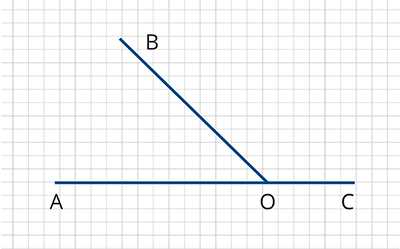
Давайте докажем это свойство.
Укажем ещё одно свойство смежных углов.
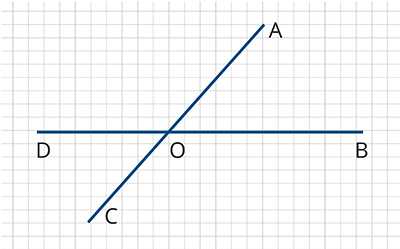
Теперь построим две пересекающиеся прямые, АС и BD. Посмотрите, при пересечении прямых у нас получилось четыре угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ и ∠BОC.
Углы, которые не являются смежными:
∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов называются вертикальными углами.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны. Убедимся в справедливости этого свойства, докажем его.
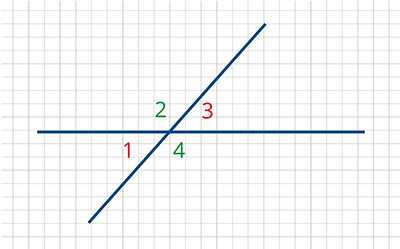
Доказательство. Посмотрим на чертёж: пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1– смежные углы. Угол 2 одновременно является смежным с углом 1 и с углом 3. По свойству смежных углов
Свойства смежных и вертикальных углов, которые мы сегодня рассмотрели– в геометрии называются теоремами. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путём рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.
На предыдущих уроках вы познакомились с понятием аксиомы.
В чём же различие между аксиомой и теоремой? Ответ на этот вопрос таков: аксиома – положение, принимаемое без доказательств.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Используя чертёж, найдите угол ∠ВОК.
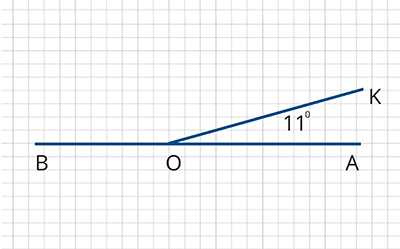
№2. Тип задания: единичный / множественный выбор.
Используя чертёж, найдите угол ∠AOD.
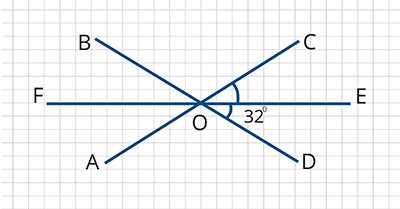
№3. Тип задания: выделение цветом.
Выделите верный ответ из списка:
60 0 ; 30 0 ; 75 0 ; 90 0
Интересный факт
Связь математики с музыкой«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»Г. НейгаузКазалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.Консонанс определяет приятное для слуха звучание струныВ основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .w = a : l ,где а — коэффициент, характеризующий физические свойства струны.
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Вычисление на онлайн-калькуляторе
Нахождение градусной меры смежных элементов обычно не вызывает проблем и относится к элементарным действиям при исследованиях различных треугольников, например, остроугольных или равнобедренных. Но при работе с нецелыми числами или в процессе обучения имеет смысл использовать так называемые онлайн-калькуляторы.
Это обычные интернет-сайты, содержащие встроенную программу для автоматических расчётов. Пользоваться ими сможет каждый, кто имеет компьютер или гаджет с установленным веб-обозревателем. Вся работа с сервисом сводится к загрузке его интернет-страницы и заполнения специальной формы, в которую вводятся исходные данные. Затем нажимается интерактивная кнопка и на дисплее появляется ответ.

Вычисление обычно занимает пару секунд, а появление ошибки исключено. Кроме этого, на сайтах, предлагающего такого рода услуги, содержится весь необходимый для расчётов теоретический материал. Поэтому даже слабо подготовленный по теме пользователь сможет понять, откуда и каким образом получился тот или иной ответ.
Из множества сервисов, существующих в русскоязычном сегменте всемирной сети, можно выделить следующие:
При этом пользователям предлагается ознакомиться с развёрнутым решением, то есть указан поэтапный расчёт. Для удобства на страницах даётся не только необходимая теория, но и ряд типовых примеров с подробным описанием действий.
Следует отметить, что указанные сервисы могут находить ответ для любой сложности математической задачи. Особенно востребованными становятся такие вычисления в инженерии, связанные с тригонометрическими функциями. Ведь для таких расчётов важны точность и время, что вполне могут обеспечить онлайн-калькуляторы.






























