Теорема синусов: формула и примеры решения задач

Теорема синуса, косинуса. Решение треугольников

Урок 57. Подготовка к ОГЭ по математике 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Конспект урока “Теорема синуса, косинуса. Решение треугольников”

· вспомнить формулировки и доказательства теорем синуса и косинуса;

· повторить, что значит «решить треугольник»

И начнём мы с вами с того, что вспомним формулировку теоремы синусов.

Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

Доказательство.

Расширенная теорема синусов.

Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.

Доказательство.

Что и требовалось доказать.

Теперь давайте вспомним теорему косинусов.

Теорема косинусов.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.

Доказательство.

Частным случаем теоремы косинусов является теорема Пифагора.

Давайте рассмотрим прямоугольный треугольник и запишем для него теорему косинусов.

Именно поэтому теорему косинусов называют обобщённой теоремой Пифагора.

Рассмотрим несколько примеров.

Рассмотрим ещё один пример.

Рассмотрим ещё один пример.

Теперь давайте вспомним, что значит решить треугольник.

Определение.

Решить треугольник – это значит найти все его элементы (три стороны и три угла) по каким-нибудь известным трём элементам, определяющим треугольник. К задачам такого плана относятся следующие задачи: решение треугольника по трём сторонам; решение треугольника по трём углам; решение треугольника по двум сторонам и углу между ними; решение треугольника по двум сторонам и углу, не лежащего между ними; решение треугольника по стороне и прилежащим к ней углам; решение треугольников по стороне и произвольным двум углам.

Рассмотрим каждый вид таких задач отдельно.

Начнём с решения треугольника по трём углам.

Запишем теорему синусов и косинусов и подумаем, с помощью какой из них можно решить треугольник.

Обе эти теоремы содержат длины сторон, поэтому зная только углы треугольника нельзя найти длины сторон треугольника. То есть зная только три угла, решить треугольник нельзя.

Попробуем теперь решить треугольник по трём сторонам.

Зная длины всех сторон треугольника, по теореме косинусов можно найти косинусы всех углов треугольника.

А, зная косинус угла, сам угол найти несложно.

Для этого можно воспользоваться либо калькулятором либо таблицами Брадиса.

Значит в этом случае решить треугольник можно с помощью теоремы косинусов.

Следующим мы рассмотрим решение треугольника по стороне и прилежащим к ней углам.

Сразу замечаем, что третий угол найти нетрудно, он равен разности 180 градусов и известных углов.

Запишем теорему синусов.

Из каждого равенства, мы можем найти сторону треугольника. Таким образом, зная длину одной стороны и величину двух прилежащих к ней углов, можно найти все остальные элементы треугольника, используя теорему синусов.

Нетрудно увидеть, что условие: углы прилежащие к стороне здесь не существенно. Поскольку даже если нам известны два любых угла треугольника, то мы всегда можем найти третий угол этого треугольника. Тогда можно сказать, что, зная одну сторону и два любых угла можно решить треугольник с помощью теоремы синусов.

Теперь давайте рассмотрим способ решения треугольника по двум сторонам и углу между ними.

Третью сторону можно найти с помощью теоремы косинусов.

А углы отыскать или с помощью теоремы косинусов, как мы это делали, когда решали треугольник по трём сторонам. Или с помощью теоремы синусов. То есть в таком случае можно решить треугольник используя или теорему синусов или теорему косинусов.

Теперь давайте посмотрим, а можно ли решить треугольник, если мы знаем две стороны и угол, который не лежит между ними. Да, можно. Для этого по теореме синусов надо найти второй угол треугольника, а затем и третий угол и по теореме косинусов найти третью сторону треугольника. То есть и в этом случае треугольник можно решить с помощью теоремы синусов и теоремы косинусов.

Итак, давайте обобщим.

Сегодня на уроке мы с вами вспомнили формулировки и доказательства теорем синуса и косинуса. Повторили, что значит решить треугольник.

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Задача 5-доказательство формулы площади параллелограмма через диагонали (первый способ)

До­ка­жи­те, что пло­щадь па­рал­ле­ло­грам­ма равна по­ло­вине про­из­ве­де­ния длин его диа­го­на­лей на синус угла между ними.

Дано: ABCD – па­рал­ле­ло­грамм (рис. 9)

До­ка­зать:

До­ка­за­тель­ство: пер­вый спо­соб:

Учтём, что угол α и угол  имеют один и тот же синус:

Пло­щадь тре­уголь­ни­ка АОВ (со­глас­но тео­ре­ме о пло­ща­ди тре­уголь­ни­ка):

Пло­щадь тре­уголь­ни­ка ВОС: 

Рис. 9. Ил­лю­стра­ция к за­да­че

Так как си­ну­сы равны, то и . Учи­ты­вая, что , а , мы до­ка­за­ли, что диа­го­на­ли па­рал­ле­ло­грам­ма делят его на 4 рав­но­ве­ли­ких тре­уголь­ни­ка.

По­это­му для на­хож­де­ния пло­ща­ди па­рал­ле­ло­грам­ма до­ста­точ­но найти пло­щадь од­но­го из тре­уголь­ни­ков и умно­жить на 4.

Так как , то

Что и тре­бо­ва­лось до­ка­зать.

А теперь внимание! Обсудим пользу этой теоремы

Понимаешь, теорема синусов – единственный разумный способ для нахождения радиуса описанной окружности.

Почему я так говорю? А ты вспомни сам: ну где ещё в формулах участвует \( \displaystyle R\)?! Возможно, правда, ты знаком с формулой \( \displaystyle S=\frac{abc}{4R}\), то есть \( \displaystyle R=\frac{abc}{4S}\quad\), но!

Давай – ка сравним:

Из теоремы синусов: \( \displaystyle R=\frac{a}{2\sin \angle A}\)

Из формулы площади: \( \displaystyle R=\frac{abc}{4S}\).

Чувствуешь разницу? В первой формуле нужно знать только одну сторону и один угол, а во второй формуле – все стороны, да ещё и площадь! Ну и какую формулу легче применить?

А кроме того, открою тебе маленький секрет: формула \( \displaystyle S=\frac{abc}{4R}\) как раз и доказывается именно с применением теоремы синусов.

Чтобы убедиться в этом, читай темы «Площадь круга», «Площадь треугольника и четырехугольника».

Итак, теорема синусов бывает полезна и для нахождения синуса какого – то угла, если известны две стороны и один угол.

Примеры задач

Задание 1 В треугольнике известна длина основания – 10 см, противолежащий основанию угол – 90°, а также, один из углов, прилегающих к нему – 45°. Найдите сторону напротив угла 45°.

Решение: Примем неизвестную сторону за x и применим теорему синусов:

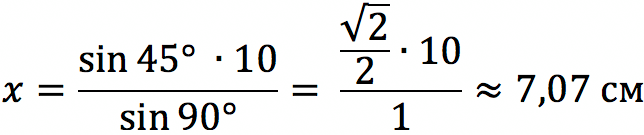
Задание 2 Гипотенуза и один из катетов прямоугольного треугольника равны, соответственно, 10 и 8 см. Найти угол, расположенный напротив данного катета.

Решение: Как мы знаем, в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. С учетом этого, соотношение сторон выглядит следующим образом:

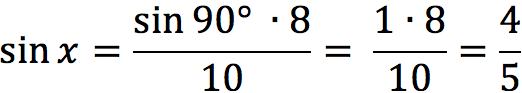
Значит x = arcsin (4/5) ≈ 53,1°.

Примеры задач

Задание 1
В треугольнике известна длина основания – 10 см, противолежащий основанию угол – 90°, а также, один из углов, прилегающих к нему – 45°. Найдите сторону напротив угла 45°.

Решение:
Примем неизвестную сторону за x и применим теорему синусов:

Следовательно:

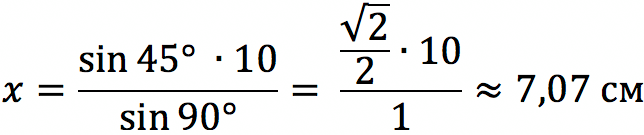
Задание 2
Гипотенуза и один из катетов прямоугольного треугольника равны, соответственно, 10 и 8 см. Найти угол, расположенный напротив данного катета.

Решение:
Как мы знаем, в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. С учетом этого, соотношение сторон выглядит следующим образом:

Следовательно:

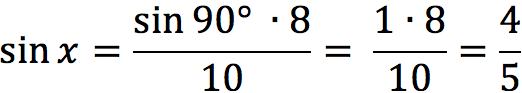
Задача 1 (решение треугольника для первого случая)

Дано: тре­уголь­ник ABC, a = 6, b =8,  (рис. 2)

Найти: углы , γ; сто­ро­ну с

Ре­ше­ние:

Вос­поль­зу­ем­ся тео­ре­мой си­ну­сов

Рис. 2. Ил­лю­стра­ция к за­да­че

Видим, что , сле­до­ва­тель­но, угол β су­ще­ству­ет и су­ще­ству­ет два угла.

Ри­су­нок 3 ил­лю­стри­ру­ет на­ли­чие двух углов β.

Рис. 3. Ил­лю­стра­ция к за­да­че

Тре­уголь­ник ABC (рис. 2) имеет опре­де­лён­ный ра­ди­ус опи­сан­ной окруж­но­сти.

По тео­ре­ме си­ну­сов:

Рас­смот­рим два слу­чая:

1.  (рис. 4) 

Тогда угол :

Сле­до­ва­тель­но, , 

Рис. 4. Ил­лю­стра­ция к за­да­че

Далее ис­поль­зу­ем тео­ре­му си­ну­сов:

Для пер­во­го слу­чая тре­уголь­ник решён.

Ответ: β , , 

Примеры задач

Задание 1
В треугольнике известны длины двух сторон – 5 и 9 см, а также, угол между ними – 60°. Найдите длину третьей стороны.

Решение:
Применим формулу теоремы, приняв известные стороны за B и C, а неизвестную за A:
A 2 = 5 2 + 9 2 – 2 ⋅ 5 ⋅ 9 ⋅ cos 60° = 25 + 81 – 45 = 61 см 2 . Следовательно, сторона

Задание 2
Самая большая сторона треугольника равна 26 см, а две другие – 16 и 18 см. Найдите угол между меньшими сторонами.

Решение:
Примем бОльшую сторону за A. Чтобы найти угол между сторонами B и C, воспользуемся следствием из теоремы:

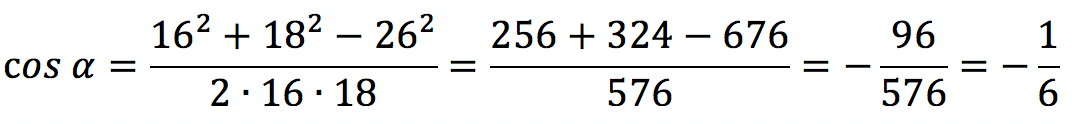
Следовательно, угол α = arccos (-1/6) ≈ 99,59°.

Публикации по теме:

• Нахождение площади квадрата: формула и примеры Нахождение площади прямоугольника: формула и пример Нахождение площади треугольника: формула и примеры Нахождение площади эллипса: формула и пример Нахождение площади выпуклого четырехугольника: формула и пример Нахождение периметра параллелограмма: формула и задачи Нахождение длины окружности: формула и задачи Теорема Пифагора для прямоугольного треугольника: формула и задачи Тригонометрические функции острого угла в прямоугольном треугольнике Нахождение объема конуса: формула и задачи Нахождение объема тетраэдра: формула и задачи Нахождение объема призмы: формула и задачи Нахождение площади поверхности конуса: формула и задачи Нахождение площади поверхности шара (сферы): формула и задачи Нахождение площади поверхности вписанного в цилиндр шара Теорема Чевы: формулировка и пример с решением Теорема Стюарта: формулировка и пример с решением Теорема о трех перпендикулярах Признаки равенства треугольников Признаки подобия треугольников Признаки равенства прямоугольных треугольников Определение и свойства медианы треугольника Определение и свойства медианы прямоугольного треугольника Определение и свойства медианы в равнобедренном треугольнике Свойства биссектрисы равностороннего треугольника Нахождение радиуса вписанной в треугольник окружности Что такое квадрат: определение и свойства Нахождение радиуса вписанной в квадрат окружности Что такое прямоугольник: определение, свойства, признаки, формулы Нахождение площади сектора круга Нахождение длины дуги сектора круга Нахождение высоты трапеции: формулы и примеры задач Нахождение высоты равнобедренной (равнобокой) трапеции Нахождение высоты прямоугольной трапеции Что такое средняя линия четырехугольника Нахождение радиуса описанной вокруг куба сферы (шара) Нахождение радиуса вписанного в куб шара Нахождение площади шарового сектора Нахождение объема шарового сектора Нахождение площади шарового слоя Нахождение объема усеченного конуса Что такое цилиндр: определение, элементы, виды, варианты сечения Что такое пирамида: определение, элементы, виды, варианты сечения Что такое призма: определение, элементы, виды, варианты сечения Основные свойства призмы Нахождение радиуса вписанного в цилиндр шара (сферы) Нахождение радиуса шара (сферы), вписанного в правильную пирамиду Нахождение радиуса сферы (шара), описанной около правильной пирамиды Что такое правильный многоугольник: определение, признаки, элементы, виды Что такое ломанная: определение, обозначение, элементы, виды, пример задачи

Задание 1
В треугольнике известны длины двух сторон – 5 и 9 см, а также, угол между ними – 60°. Найдите длину третьей стороны.

Примеры задач

Задание 1 В треугольнике известна длина основания – 10 см, противолежащий основанию угол – 90°, а также, один из углов, прилегающих к нему – 45°. Найдите сторону напротив угла 45°.

Решение: Примем неизвестную сторону за x и применим теорему синусов:

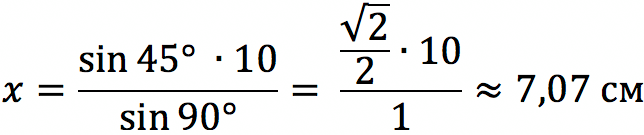
Задание 2 Гипотенуза и один из катетов прямоугольного треугольника равны, соответственно, 10 и 8 см. Найти угол, расположенный напротив данного катета.

Решение: Как мы знаем, в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. С учетом этого, соотношение сторон выглядит следующим образом:

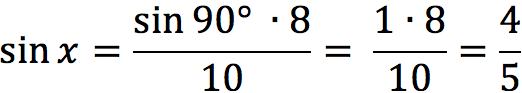
Значит x = arcsin (4/5) ≈ 53,1°.

Слайды и текст этой презентации

Слайд 21.Какие из следующих утверждений верны ?1) Если медиана и высота,

проведенные из одной вершины треугольника, не совпадают, то этот треугольник

не является равнобедренным.2) Если биссектриса треугольника делит противоположную сторону на равные отрезки, то этот треугольник равнобедренный.3) Если треугольник равносторонний, то длина любой его высоты равна длине любой его биссектрисы.4) Если треугольник равнобедренный, то наименьшей из сторон является его основание.

Слайд 32.Какие из следующих утверждений верны?
1) Каждая сторона треугольника меньше разности

двух других сторон.2) В равнобедренном треугольнике медиана является биссектрисой и

высотой.3) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.4) В треугольнике  АВС, для которого АВ = 3, ВС = 4, АС = 5 угол С  наименьший.

Слайд 43. Какие из следующих утверждений верны?
1) В треугольнике против меньшего

угла лежит большая сторона.2) Если один угол треугольника больше 1200, то

оба других его угла меньше 300.3) Если все стороны треугольника меньше 1, то и все его высоты меньше 1.4) Сумма острых углов прямоугольного треугольника не превосходит  900.

Слайд 54.Какие из следующих утверждений верны?
1) В треугольнике  , для которого

 , 

,  , сторона   ВС — наименьшая.2) В треугольнике, для которого  АВ = 4, ВС =5, АС= 6, угол  В — наибольший.3) Внешний угол треугольника больше каждого внутреннего угла.4) Треугольник со сторонами 1, 2, 3 не существует.

Слайд 65.Какие из следующих утверждений верны?1) Около всякого треугольника можно описать

не более одной окружности.2) В любой треугольник можно вписать не

более одной окружности.3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

Слайд 76. Выберите неверные утверждения

1) Если катет и гипотенуза прямоугольного треугольника

равны соответственно 6 и 10, то второй катет этого треугольника

равен 8.2) Любые два равнобедренных треугольника подобны.3)Любые два прямоугольных треугольника подобны.4) Треугольник ABC, у которого  АВ = 3, ВС = 4, АС = 5  , является тупоугольным.

Слайд 87. Выберите неверные утверждения
1) Квадрат любой стороны треугольника равен сумме

квадратов двух других сторон без удвоенного произведения этих сторон на

синус угла между ними.2) Любые два равносторонних треугольника подобны.3) Треугольник ABC, у которого АВ = 4, ВС=5,  АС = 6, является прямоугольным.4) В прямоугольном треугольнике квадрат гипотенузы не превосходит суммы квадратов катетов.

Слайд 98. Выберите неверные утверждения

1) Стороны треугольника пропорциональны синусам противолежащих углов.2)

Если угол одного треугольника равен углу другого треугольника, то такие

треугольники подобны.3) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без произведения этих сторон на косинус угла между ними.4) Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.

Слайд 109. Выберите неверные утверждения
1) Если в треугольнике два угла

равны, то он равнобедренный.2) В равнобедренном треугольнике отрезок, соединяющий любую

точку основания, отличную от вершины, с противоположной вершиной, меньше боковой стороны.3) В треугольнике против меньшей стороны лежит больший угол.4) Если в треугольнике два угла по 70°, то он тупоугольный.

Слайд 1110. Выберите неверные утверждения
1) Каждая сторона треугольника меньше суммы

Площадь треугольника меньше произведения двух его сторон.4) Площадь треугольника равна произведению его периметра на радиус вписанной окружности. 

Дистанционные курсы для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Онлайн-семинар о развитии управляющих функций мозга ребенка

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

В «Единой России» предложили ввести раздел безопасности детей в интернете в курс ОБЖ

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Пример использования теоремы

Итого, теорема о соотношениях между сторонами и углами треугольника сообщает: если есть пара сторон, в которой по значению одна сторона больше, то против большей стороны будет лежать больший по величине угол. Против меньшей — меньший. Ровно то же самое работает с парами углов. Если один из углов в паре больше, то сторона против большего угла больше. Против меньшего — меньше.    

А теперь, вооружившись новыми знаниями, вернемся к задачке из введения в урок, с треугольником $\bigtriangleup{ABC}$, про который известно, что $\angle{C}>\angle{A}>\angle{B}$. Как будет выглядеть неравенство сторон для треугольника $\bigtriangleup{ABC}$?

Перед тем, как дать ответ, загляните сюда!

Скрыть текст

Навыки на миллион. Как без рисунка определять буквенные обозначения противолежащих сторон и противолежащих сторонам углов? Что же, как обычно выручает геометрическая смекалка. Точка угла расположена не на прямой, где расположена противолежащая сторона. Поскольку у нас всего три точки и три отрезка, остаются две прочие точки, на которых построен отрезок, он же противолежащая сторона.

Смотрите, как это работает:

Например, как обозначается сторона, противолежащая углу $\angle{A}$? Точка $A$ «занята» углом, а точки $B$ и $C$ «свободны» (расположены в другой полуплоскости), следовательно противолежащая углу $\angle{A}$ сторона обозначается как $BC$.

Если «занята» точка $B$, то остаются точки $A$ и $C$ — сторона $AC$ противолежит углу $\angle{B}$. Если «занята» точка $C$, то остаются точки $A$ и $B$ — сторона $AB$ противолежит углу $\angle{C}$. Главное, держите порядок следствия точек при отрезках сторон строго так, как он задан. У нас порядок $ABC$, поэтому мы и записывали, скажем, противолежащую сторону для угла $C$ как $AB$, а не как $BA$. Не то чтобы что-то кардинально изменится, однако наука любит точность.

{"questions":,"answer":}}}]}

Теорема косинусов для треугольника — формулы, доказательство и решение задач

Треугольник является самой простой фигурой на плоскости, которая подробно рассматривается в классах общеобразовательных школ на уроках геометрии

Знание ее характеристик важно для понимания методов решения многих практических задач. Формулы для треугольника и теорема косинусов в частности являются математическим инструментом, позволяющим вычислять любые свойства фигуры

Геометрическая фигура

Прежде чем рассматривать теорему косинусов для треугольника и формулу, которая математически ее выражает, следует познакомиться с самим геометрическим объектом подробнее.

Треугольник представляет собой плоскую фигуру, которая состоит из двух типов элементов:

• трех отрезков, являющихся сторонами;
• трех вершин, образованных на пересечении отрезков и определяющих углы фигуры.

Если две стороны треугольника равны между собой и отличаются от третьей, его называют равнобедренным. Если все имеют одинаковую длину, речь идет о равностороннем объекте. Важным свойством любого треугольника является равенство суммы его трех углов 180°. Этот факт справедлив для всех типов фигуры на плоскости.

Важные линии

Для описания характеристик объекта в геометрии используют специальные линии. Основными из них являются:

• биссектриса — прямая, выходящая из произвольной вершины и делящая ее угол на 2 равные части;
• высота — перпендикуляр, который начинается на произвольной вершине и с противоположной стороной образует прямой угол;
• медиана — линия, которая делит на 2 одинаковые по площади части треугольник, пересекает противоположную сторону фигуры ровно посередине.

Для равносторонней фигуры все 3 типа линий совпадают друг с другом, для равнобедренного треугольника только для угла, образованного равными сторонами, они являются одинаковыми.

Основные законы

О треугольнике человечеству известно все, поскольку это самая простая геометрическая фигура. Кроме того, до настоящего времени дошли некоторые работы греческих мыслителей и даже древних египтян, которые были посвящены рассмотрению ее свойств. В общем случае можно назвать 3 основные теоремы, которые в полной мере описывают главные характеристики треугольника. К ним относятся:

Равенство площади фигуры половине произведения высоты на длину стороны, на которую она падает — ее принято называть основанием. Помимо этой формулы, существует еще одно выражение, которое позволяет получить тот же результат, но с использованием длин трех сторон и без проведения дополнительных геометрических построений.
Теорема синусов.

Теорема синусов. Доказательство

Тебе уже известно, что около каждого треугольника можно описать окружность. Мы это и сделаем. А потом проведём диаметр \( \displaystyle BO\).

Пусть этот диаметр пересекает окружность в точке \( \displaystyle K\). Давай рассмотрим \( \displaystyle \Delta BKC\).

Что же это за треугольник?

Ну, конечно же, прямоугольный, ведь в \( \displaystyle \Delta BKC\) угол \( \displaystyle C\) опирается на диаметр \( \displaystyle BK\quad\Rightarrow \quad\angle C=90{}^\circ \) (вспоминаем тему «Вписанный и центральный угол окружности»).

Но и кроме того, \( \displaystyle \angle K\) в \( \displaystyle \Delta BKC\) равен \( \displaystyle \angle A\) в \( \displaystyle \Delta ABC\), потому что эти углы опираются на одну дугу \( \displaystyle BC\) (опять вспоминаем ту же тему).

А теперь просто запишем выражение для синуса \( \displaystyle \angle K\) в прямоугольном \( \displaystyle \Delta BKC\) \( \displaystyle \sin \angle K=\frac{a}{BK}\).

Но ведь \( \displaystyle BK\) – диаметр \( \displaystyle \quad\Rightarrow\quad BK=2R\), и \( \displaystyle \sin \angle K=\frac{a}{2R}\).

Вспомним, что \( \displaystyle \angle K=\angle A\) и получим \( \displaystyle \sin \angle A=\frac{a}{2R}\quad\Rightarrow\quad \frac{a}{\sin \angle A}=2R\).

Вот и всё! Провели одну линию, рассмотрели один прямоугольный треугольник – и доказательство готово.

Но как же быть с углами \( \displaystyle B\) и \( \displaystyle C\)? – спросишь ты.

Да, точно также. Давай рассмотрим \( \displaystyle \angle B\).

Теперь проведём диаметр \( \displaystyle AO\) и соединим точки \( \displaystyle K\) и \( \displaystyle C\).

Как-то тут немного по-другому получается, ты заметил? \( \displaystyle \Delta AKC\), конечно, прямоугольный, так как \( \displaystyle \angle C\) опирается на диаметр \( \displaystyle AK\).

Но теперь \( \displaystyle \angle K+\angle B=180{}^\circ \), потому что четырехугольник \( \displaystyle ABCK\) – вписанный. (Надеюсь, ты ещё помнишь, что для угла \( \displaystyle A\) у нас было \( \displaystyle \angle A=\angle K\).) В чём же дело?

Ну, просто \( \displaystyle \angle B\) – тупой, поэтому и получилось такое различие. Но, к счастью, для теоремы синусов это различие не играет роли. Сейчас мы в этом убедимся.

Итак, запишем выражение для синуса \( \displaystyle \angle K\) в прямоугольном \( \displaystyle \Delta AKC\).

\( \displaystyle \sin \angle K=\frac{b}{AK}\); то есть \( \displaystyle \sin \angle K=\frac{b}{2R}\)

Но \( \displaystyle \angle B=180{}^\circ -\angle K\Rightarrow \sin \angle B=\sin \angle K\) (читаем или вспоминаем формулы приведения в тригонометрии.)

Значит, \( \displaystyle \sin \angle B=\frac{b}{2R}\quad\Rightarrow\quad \frac{b}{\sin \angle B}=2R\).

Ну вот, мы рассмотрели и острый, и тупой угол. Если ты все ещё беспокоишься об угле \( \displaystyle C\), то проделай все те же действия самостоятельно и убедись, что все получается.

Обрати внимание, что мы доказали «четверное равенство»