Как найти площадь поверхности призмы?

Объем правильной треугольной призмы

Общую формулу объема треугольной призмы, которая приведена в предыдущем разделе статьи, можно использовать для вычисления соответствующей величины для правильной треугольной призмы. Поскольку в ее основании лежит равносторонний треугольник, то его площадь равна:

Эту формулу может получить каждый, если вспомнит, что в равностороннем треугольнике все углы равны друг другу и составляют 60 o . Здесь символ a — это длина стороны треугольника.

Высота h является длиной ребра. Она никак не связана с основанием правильной призмы и может принимать произвольные значения. В итоге формула объема треугольной призмы правильного вида выглядит так:

Вычислив корень, можно переписать эту формулу так:

Таким образом, чтобы найти объем правильной призмы с треугольным основанием, необходимо возвести в квадрат сторону основания, умножить эту величину на высоту и полученное значение умножить на 0,433.

Призма

Определения:

1. Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
2. Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
3. Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
4. Боковая поверхность – объединение боковых граней.
5. Полная поверхность – объединение оснований и боковой поверхности.
6. Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
7. Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
8. Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
9. Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
10. Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
11. Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:

• Основания призмы являются равными многоугольниками.
• Боковые грани призмы являются параллелограммами.
• Боковые ребра призмы параллельны и равны.
• Объём призмы равен произведению её высоты на площадь основания:

где: S_осн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A₂B₂C₂D₂E₂).
• Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
• Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
• Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: S_сеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA₁или BB₁ и так далее).

Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: P_сеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:

• Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
• Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):

где: P_осн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = S_осн∙h = S_осн∙l.

Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

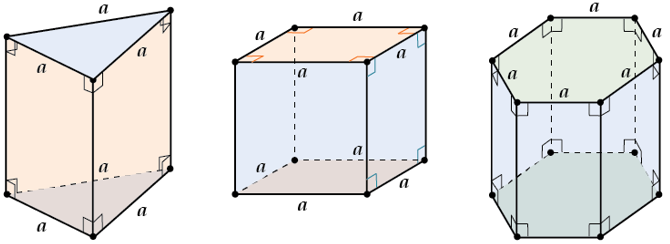
Свойства правильной призмы:

1. Основания правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной призмы являются равными прямоугольниками.
3. Боковые ребра правильной призмы равны между собой.
4. Правильная призма является прямой.

Призматические многогранники

Призматический многогранник — это обобщение призмы в пространствах размерности 4 и выше. n-мерный призматический многогранник конструируется из двух (n − 1)-мерных многогранников, перенесённых в следующую размерность.

Элементы призматического n-мерного многогранника удваиваются из элементов (n − 1)-мерного многогранника, затем создаются новые элементы следующего уровня.

Возьмём n-мерный многогранник с элементами fi{\displaystyle f_{i}} (i-мерная грань, i = 0, …, n). Призматический (n+1{\displaystyle n+1})-мерный многогранник будет иметь 2fi+f−1{\displaystyle 2f_{i}+f_{-1}} элементов размерности i (при f−1={\displaystyle f_{-1}=0}, fn=1{\displaystyle f_{n}=1}).

По размерностям:

• Берём многоугольник с n вершинами и n сторонами. Получим призму с 2n вершинами, 3n рёбрами и 2+n{\displaystyle 2+n} гранями.
• Берём многогранник с v вершинами, e рёбрами и f гранями. Получаем (4-мерную) призму с 2v вершинами, 2e+v{\displaystyle 2e+v} рёбрами, 2f+e{\displaystyle 2f+e} гранями и 2+f{\displaystyle 2+f} ячейками.
• Берём 4-мерный многогранник с v вершинами, e рёбрами, f гранями и c ячейками. Получаем (5-мерную) призму с 2v вершинами, 2e+v{\displaystyle 2e+v} рёбрами, 2f+e{\displaystyle 2f+e} (2-мерными) гранями, 2c+f{\displaystyle 2c+f} ячейками и 2+c{\displaystyle 2+c} гиперячейками.

Однородные призматические многогранники

Правильный n-многогранник, представленный символом Шлефли {p, q, …, t}, может образовать однородный призматический многогранник размерности (n + 1), представленный прямым произведением двух символов Шлефли: {p, q, …, t}×{}.

По размерностям:

• Призма из 0-мерного многогранника — это отрезок, представленный пустым символом Шлефли {}.
• Призма из 1-мерного многогранника — это прямоугольник, полученный из двух отрезков. Эта призма представляется как произведение символов Шлефли {}×{}. Если призма является квадратом, запись можно сократить: {}×{} = {4}.

  Пример: Квадрат, {}×{}, два параллельных отрезка, соединённые двумя другими отрезками, сторонами.

• многоугольная призма — это 3-мерная призма, полученная из двух многоугольников (один получен параллельным переносом другого), которые связаны прямоугольниками. Из правильного многоугольника {p} можно получить однородную n-угольную призму, представленную произведением {p}×{}. Если p = 4, призма становится кубом: {4}×{} = {4, 3}.

  Пример: Пятиугольная призма, {5}×{}, два параллельных пятиугольника связаны пятью прямоугольными сторонами.

• 4-мерная призма, полученная из двух многогранников (один получен параллельным переносом другого), со связывающими 3-мерными призматическими ячейками. Из правильного многогранника {p, q} можно получить однородную 4-мерную призму, представленную произведением {p, q}×{}. Если многогранник является кубом и стороны призмы тоже кубы, призма превращается в тессеракт: {4, 3}×{} = {4, 3, 3}.

  Пример: додекаэдральная призма, {5, 3}×{}, два параллельных додекаэдра, соединённых 12 пятиугольными призмами (сторонами).

• …

Призматические многогранники более высоких размерностей также существуют как прямые произведения двух любых многогранников. Размерность призматического многогранника равна произведению размерностей элементов произведения. Первый пример такого произведения существует в 4-мерном пространстве и называется дуопризмами, которые получаются произведением двух многоугольников. Правильные дуопризмы представляются символом {p}×{q}.

Семейство правильных призм

Многоугольник
Мозаика
Конфигурация	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	17.4.4	∞.4.4

Что собой представляет призма четырехугольная?

Очевидно, что прежде чем приводить формулу объема призмы четырехугольной, необходимо дать ясное определение этой геометрической фигуры. Под такой призмой понимают трехмерный многогранник, который ограничен двумя произвольными одинаковыми четырехугольниками, лежащими в параллельных плоскостях, и четырьмя параллелограммами.

Отмеченные параллельные друг другу четырехугольники называются основаниями фигуры, а четыре параллелограмма — это боковые стороны. Здесь следует пояснить, что параллелограммы также являются четырехугольниками, однако основания не всегда являются параллелограммами. Пример неправильного четырехугольника, который вполне может быть основанием призмы, показан ниже на рисунке.

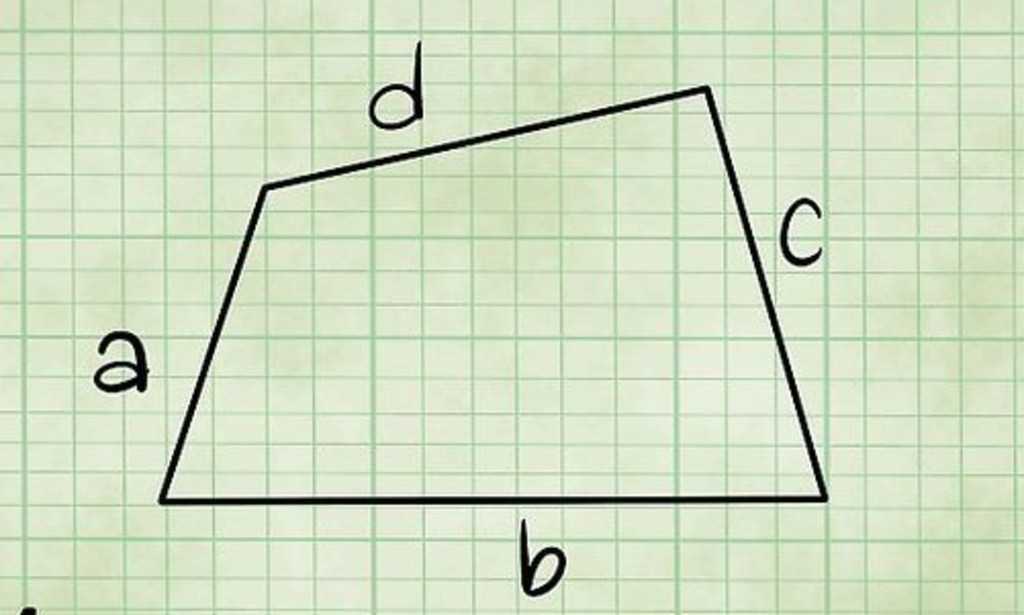
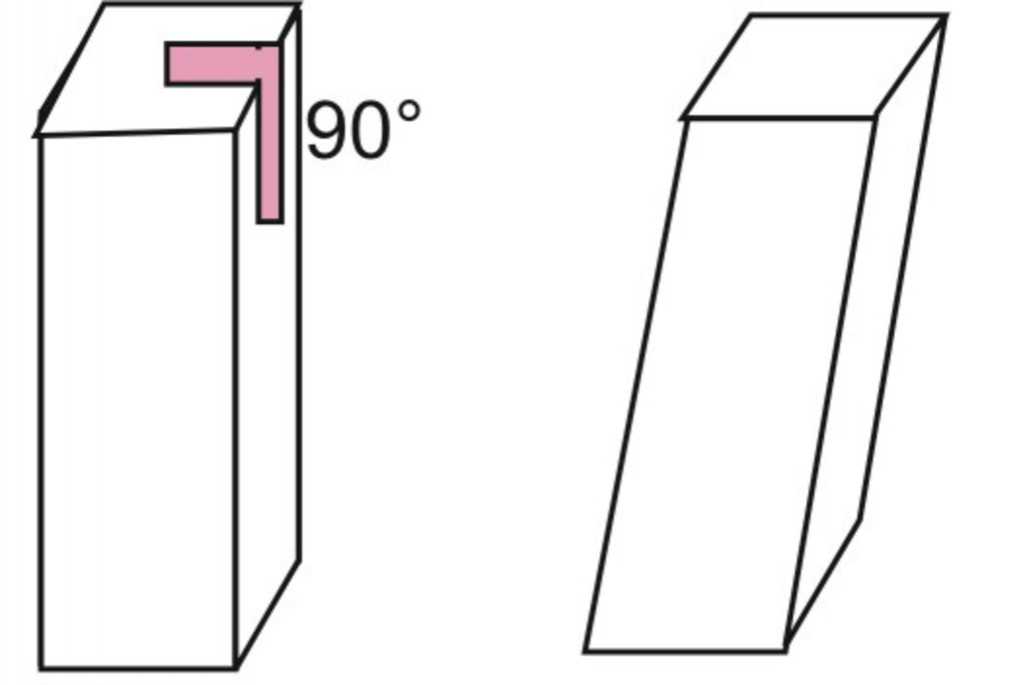
Любая четырехугольная призма состоит из 6 сторон, 8 вершин и 12 ребер. Существуют четырехугольные призмы разных видов. Например, фигура может быть наклонной или прямой, неправильной и правильной. Далее в статье покажем, как можно рассчитывать объем призмы четырехугольной с учетом ее вида.

Домашнее задание

А теперь давайте попробуем закрепить изученную тему с помощью решения задач.

Давайте нарисуем наклонную треугольную призму, у которой расстояние между ее ребрами будет равно: 3 см, 4 см и 5 см, а боковая поверхность этой призмы будет равна 60 см2. Имея такие параметры, найдите боковое ребро данной призмы.

А вы знаете, что геометрические фигуры постоянно окружают нас не только на уроках геометрии, но и в повседневной жизни встречаются предметы, которые напоминают ту или иную геометрическую фигуру.

У каждого дома, в школе или на работе имеется компьютер, системный блок которого имеет форму прямой призмы.

Если вы возьмете в руки простой карандаш, то вы увидите, что основной частью карандаша, является призма.

Идя по центральной улице города, мы видим, что у нас под ногами лежит плитка, которая имеет форму шестиугольной призмы.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

Определение. Призма— это многогранник, все вершины которого расположены в двух параллельных плоскостях, причем в этих же двух плоскостях лежат две грани призмы, представляющие собой равные многоугольники с соответственно параллельными сторонами, а все ребра, не лежащие в этих плоскостях, параллельны.

Две равные грани называются основаниями призмы (ABCDE, A 1 B 1 C 1 D 1 E 1).

Все остальные грани призмы называются боковыми гранями (AA 1 B 1 B, BB 1 C 1 C, CC 1 D 1 D, DD 1 E 1 E, EE 1 A 1 A).

Все боковые грани образуют боковую поверхность призмы.

Все боковые грани призмы являются параллелограммами.

Ребра, не лежащие в основаниях, называются боковыми ребрами призмы(AA 1, BB 1, CC 1, DD 1, EE 1).

Диагональю призмы называется отрезок, концами которого служат две вершины призмы, не лежащие на одной ее грани (АD 1).

Длина отрезка, соединяющего основания призмы и перпендикулярного одновременно обоим основаниям,называется высотой призмы.

Обозначение:ABCDE A 1 B 1 C 1 D 1 E 1. (Сначала в порядке обхода указывают вершины одного основания, а затем в том же порядке — вершины другого; концы каждого бокового ребра обозначают одинаковыми буквами, только вершины, лежащие в одном основании, обозначаются буквами без индекса, а в другом — с индексом)

Название призмы связывают с числом углов в фигуре, лежащей в ее основании, например, на рисунке 1 в основании лежит пятиугольник, поэтому призму называют пятиугольной призмой. Но т.к. у такой призмы 7 граней, то она семигранник (2 грани — основания призмы, 5 граней — параллелограммы, — ее боковые грани)

Среди прямых призм выделяется частный вид: правильные призмы.

Прямая призма называется правильной,если ее основания-правильные многоугольники.

У правильной призмы все боковые грани равные прямоугольники.Частным случаем призмы является параллелепипед.

Параллелепипед

Параллелепипед — это четырехугольная призма, в основании которой лежит параллелограмм (наклонный параллелепипед).Прямой параллелепипед — параллелепипед, у которого боковые ребра перпендикулярны плоскостям основания.

Прямоугольный параллелепипед — прямой параллелепипед, основанием которого является прямоугольник.

Свойства и теоремы:

Некоторые свойства параллелепипеда аналогичны известным свойствам параллелограмма.Прямоугольный параллелепипед, имеющий равные измерения, называются кубом.У куба все грани равные квадраты.Квадрат диагонали, равен сумме квадратов трех его измерений

,

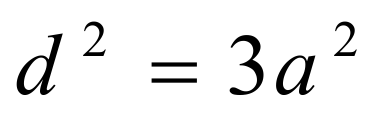где d — диагональ квадрата; a — сторона квадрата.

Представление о призме дают:

• различные архитектурные сооружения;
• детские игрушки;
• упаковочные коробки;
• дизайнерские предметы и т.д.

Площадь полной и боковой поверхности призмы

Площадь полной поверхности призмы называется сумма площадей всех ее гранейПлощадь боковой поверхности называется сумма площадей ее боковых гранейТ.к. основания призмы — равные многоугольник, то их площади равны. Поэтому

S полн = S бок + 2S осн,

где S полн— площадь полной поверхности,S бок -площадь боковой поверхности, S осн — площадь основания

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

S бок = P осн * h,

где S бок -площадь боковой поверхности прямой призмы,

P осн — периметр основания прямой призмы,

h — высота прямой призмы, равная боковому ребру.

Подготовка к единому госэкзамену вместе со «Школково» — залог вашего успеха!

Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь представлен весь необходимый материал, который поможет подготовиться к прохождению аттестационного испытания.

Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы, теоремы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня.

Базовая информация систематизирована и понятно изложена в разделе «Теоретическая справка». Если вы уже успели повторить необходимый материал, рекомендуем вам попрактиковаться в решении задач на нахождение площади и объема прямой призмы. В разделе «Каталог» представлена большая подборка упражнений различной степени сложности.

Попробуйте рассчитать площадь прямой и правильной призмы или прямо сейчас. Разберите любое задание. Если оно не вызвало сложностей, можете смело переходить к упражнениям экспертного уровня. А если определенные трудности все же возникли, рекомендуем вам регулярно готовиться к ЕГЭ в онлайн-режиме вместе с математическим порталом «Школково», и задачи по теме «Прямая и правильная призма» будут даваться вам легко.

Обновлено: 30.09.2019

103583

3. Задача 3

В ос­но­ва­нии пря­мой приз­мы лежит пря­мо­уголь­ный тре­уголь­ник с ка­те­та­ми  и . Бо­ко­вые ребра равны . Най­ди­те объ­е­мы приз­мы и ци­лин­дра, опи­сан­но­го около этой приз­мы. (См. рис. 7.)

Ре­ше­ние. Объем приз­мы на­хо­дит­ся сразу (см. рис. 8).

.

Для того чтобы найти объем ци­лин­дра, необ­хо­ди­мо знать ра­ди­ус его ос­но­ва­ния. Если ци­линдр опи­сан около приз­мы, то его ра­ди­у­сом будет ра­ди­ус окруж­но­сти, опи­сан­ной около ос­но­ва­ния приз­мы. Ос­но­ва­ни­ем приз­мы яв­ля­ет­ся пря­мо­уголь­ный тре­уголь­ник, тогда ра­ди­ус окруж­но­сти, опи­сан­ной около него, будет равен по­ло­вине ги­по­те­ну­зы.

По тео­ре­ме Пи­фа­го­ра ги­по­те­ну­за ос­но­ва­ния , а тогда ра­ди­ус опи­сан­ной окруж­но­сти равен  – это и есть ра­ди­ус ос­но­ва­ния ци­лин­дра. Вы­со­та у него такая же, как и у приз­мы.

Имеем: .

Ответ: .

Что такое призма

Самой популярной сферой применения призм является оптика. С помощью элементов такой геометрической формы инженеры проектируют оптические устройства и аппаратуру, к примеру, телескопы, бинокли, микроскопы, оборудование, предназначенное для фиксации изображений, генерируемых электроникой, и реализации широкого спектра функций, спектральная оптика, интерферометры, поляриметры и прочие измерители. Благодаря применению призм в технике, сконструированной на основе чувствительной оптики, получается менять направление излучения, осуществлять оборот и перенос изображений, дифференцировать лучевые пучки, формировать спектр, проводить разные исследования и анализы.

Призма представляет собой геометрическую фигуру с каким-то количеством граней, то есть является многогранником с равными двумя гранями в виде многоугольников, которые расположены в плоскостях, ориентированных параллельно друг относительно друга, и другими гранями в виде параллелограммов, обладающих едиными сторонами с данными многоугольниками.

В призме выделяют составные элементы. В качестве основных частей фигуры, которые часто встречаются при решении задач по геометрии, выделяют боковые грани, роль которых играют параллелограммы. Пара многоугольников, о которых идет речь в определении призмы, являются основаниями геометрической фигуры.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

В зависимости от вида многоугольника, расположенного в основании, формулируют наименование призмы, к примеру:

• если основание является треугольником, то призму называют треугольной;
• призма с четырехугольником в виде основания представляет собой четырехугольную призму;
• когда основание имеет вид пятиугольника, призма является пятиугольной.

Примечание 1

Призма напоминает геометрическую фигуру под названием цилиндр. В действительности призма является частным случаем некругового цилиндра.

Рассмотрим элементы призмы:

• основаниями называют пару граней в виде равных многоугольников, которые ориентированы параллельно друг другу;
• боковые грани представляют собой такие грани призмы, которые не являются основаниями;
• боковая поверхность объединяет боковые грани;
• полная поверхность объединяет основания и боковую поверхность;
• боковыми ребрами называют общие для граней с боков призмы стороны;
• высотой обозначают отрезок, с помощью которого соединены плоскости оснований геометрической фигуры и который является перпендикуляром к этим основаниям;
• диагональ представляет собой отрезок, с помощью которого соединены пара вершин геометрической фигуры, не имеющих общей грани;
• диагональная плоскость проходит через боковое ребро призмы и пересекает диагональ основания;
• диагональным сечением называют пересечение призмы с диагональной плоскостью, что сопровождается образованием параллелограмма, к примеру, ромба, прямоугольника, квадрата;
• перпендикулярное сечение представляет собой пересечение призмы с плоскостью, которая расположена перпендикулярно относительно бокового ребра этой призмы.

 

Особенности количества граней, вершин и ребер?

Четырехугольная призма основания — это многогранная фигура с двумя равными и параллельными основаниями и четырьмя прямоугольниками, являющимися боковыми гранями, соединяющими соответствующие стороны двух оснований..

Четырехугольную призму можно отличить от других типов призм, поскольку она имеет следующие элементы:

Основы (B)

Они представляют собой два многоугольника, образованных четырьмя сторонами (четырехугольником), которые равны и параллельны.

Лица (С)

Всего этот тип призмы имеет шесть граней:

• Четыре боковые грани, образованные прямоугольниками.
• Два лица, которые являются четырехугольниками, которые образуют основания.

Края: (A)

Это сегменты, где находятся две грани призмы, а именно:

• Края основания: это линия соединения между боковой гранью и основанием, всего их 8.
• Боковые ребра: это боковая соединительная линия между двумя гранями, всего их 4.

Число ребер многогранника также можно рассчитать с помощью теоремы Эйлера, если число вершин и граней известно; таким образом, для четырехугольной призмы она рассчитывается следующим образом:

Количество ребер = Количество граней + количество вершин — 2.

Количество ребер = 6 + 8 — 2.

Количество ребер = 12.

Элементы

Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).

В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:

Указанные выше цифры удовлетворяют этой формуле.

Площадь сферы

В предыдущих уроках мы уже узнали формулу для вычисления площади сферы, однако тогда мы ее не доказывали. Однако теперь мы можем ее доказать, используя формулу объема шара. Но сначала напомним саму формулу:

Впишем сферу в многогранник с n гранями. Ясно, что расстояние от граней этого многогранника до центра сферы равно радиусы сферы R. Далее построим пирамиды, чьи вершины находятся в центре сферы, а основания – это грани многогранника. Заметим, что такие пирамиды будут иметь одинаковые высоты длиной R.

Обозначим площади граней многогранника как S₁, S₂, S₃,…S_n. Тогда объемы пирамид, построенных на этих гранях, вычисляются так:

Заметим, что в сумме эти объемы дают объем всего многогранника, а сумма площадей S₁, S₂, S₃,…S_n – это площадь всей его поверхности. Тогда можно записать:

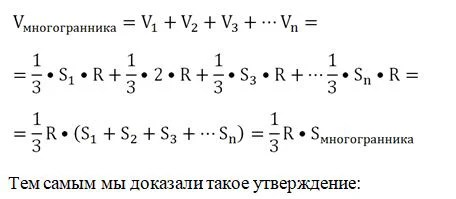
Теперь начнем неограниченно уменьшать размеры граней многогранника. Тогда число n будет расти, объем многогранника будет приближаться к объему шара, а площадь многогранника – к площади к сфере. Тогда и доказанное равенство можно будет записать так:

Задание. Необходимо изготовить закрытый сосуд с заранее заданным объемом V. Предлагается два варианта формы этого сосуда – шар и куб. Так как поверхность сосуда покрывается очень дорогой краской, то необходимо выбрать вариант с меньшей площадью поверхности. Какую форму для сосуда следует выбрать?

Решение. Обозначим радиус шара как R, а ребро куба как а. Тогда можно записать:

Теперь надо выяснить, какое из полученных значений больше. Для этого поделим площадь куба на площадь сферы. Если получится число, большее единицы, то площадь куба больше:

Получившееся число больше единицы, ведь 6 больше числа π, равного 3,1415926… Значит, и площадь куба больше, а потому необходимо выбрать сосуд, имеющий форму шара.

Ответ: шар.

Примечание. Более сложными математическими методами можно доказать, что если второй сосуд имеет не форму куба, а вообще любую форму, отличную от шара, то всё равно следует выбирать именно сосуд в форме шара. То есть из всех поверхностей, ограничивающих определенный объем, именно сфера имеет наименьшую площадь. Этот факт имеет и физическое следствие – капли дождя и мыльные пузыри стремятся принять форму шара, также как и любые жидкости, находящиеся в невесомости.

Итак, мы научились вычислять объемы таких тел, как конус, пирамида, шар, призма. Также помощью интегрирования можно находить объемы и ещё более сложных тел, если мы можем составить функцию, описывающую площадь их сечения.

Как найти площадь куба

h

Начертим отдельно основание призмы, т. е. треугольник АBС (рис. 307, а), и достроим его до прямоугольника, для чего через вершину В проведём прямую КМ || АС и из точек A и С опустим на эту прямую перпендикуляры АF и СЕ. Получим прямоугольник АСЕF. Проведя высоту ВD треугольника АBС, увидим, что прямоугольник АСЕF разбился на 4 прямоугольных треугольника. Причём \(\Delta\)ВСЕ = \(\Delta\)BCD и \(\Delta\)BAF = \(\Delta\)BAD. Значит, площадь прямоугольника АСЕF вдвое больше площади треугольника АBС, т. е. равна 2S.

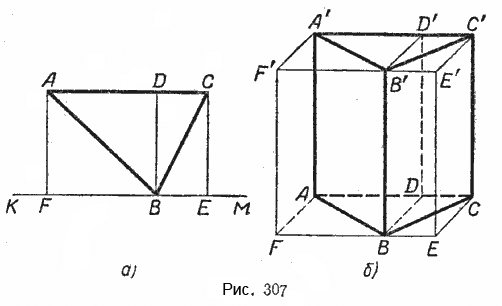
К данной призме с основанием АBС пристроим призмы с основаниями ВСЕ и BАF и высотой h
(рис. 307, б). Получим прямоугольный параллелепипед с основанием АСЕF.

Если этот параллелепипед рассечём плоскостью, проходящей через прямые BD и BB’, то увидим, что прямоугольный параллелепипед состоит из 4 призм с основаниями BCD, ВСЕ, BАD и BAF.

Призмы с основаниями BCD и ВСЕ могут быть совмещены, так как основания их равны (\(\Delta\)BCD = \(\Delta\)BСЕ) и также равны их боковые рёбра, являющиеся перпендикулярами к одной плоскости. Значит, объёмы этих призм равны. Также равны объёмы призм с основаниями BАD и BАF.

Таким образом, оказывается, что объём данной треугольной призмы с основанием АBС вдвое меньше объёма прямоугольного параллелепипеда с основанием АСЕF.

Нам известно, что объём прямоугольного параллелепипеда равен произведению площади его основания на высоту, т. е. в данном случае равен 2Sh
. Отсюда объём данной прямой треугольной призмы равен Sh
.

Объём прямой треугольной призмы равен произведению площади её основания на высоту.

2. Объём прямой многоугольной призмы.

h

Обозначив площади основания треугольных призм через S 1 , S 2 и S 3 , а объём данной многоугольной призмы через V, получим:

V = S 1 h
+ S 2 h
+ S 3 h
, или

V = (S 1 + S 2 + S 3)h
.

И окончательно: V = Sh
.

Таким же путём выводится формула объема прямой призмы, имеющей в основании любой многоугольник.

Значит, объём любой прямой призмы равен произведению площади её основания на высоту.

Задача № 1.Комбинация призмы и цилиндра

Условие: пусть в цилиндр вписана правильная треугольная призма. Необходимо определить отношение объёма призмы к объёму цилиндра (табл. 1).

Таблица 1. Комбинация призмы и цилиндра

Рисунок к задаче	Краткое условие
	Дано: Найти:  = ?

Решение:

1. Так как объём призмы и объём цилиндра вычисляется по формуле «площадь основания на высоту», а по условию задачи высота призмы и высота цилиндра одинаковы и равны h, то можно не делать пространственный чертёж, поэтому нарисуем только основание цилиндра и основание призмы  (табл. 1). Также обозначим сторону  за а, и  – радиус цилиндра за r. Таким образом, объём призмы – это площадь треугольника , умноженная на высоту.

2. Поскольку призма правильная – в основании лежит правильный треугольник – значит, объём призмы равен:

3. Объём цилиндра вычисляется по формуле:

4. Между а и r есть связь, поскольку r – это радиус окружности описанной вокруг равностороннего треугольника  и по формуле радиус равен:

Тогда а равно:

5. Напишем отношение объёма призмы к объёму цилиндра и подставим вместо а полученное ранее значение:

Неправильная четырехугольная призма

Этот тип призмы отличается тем, что ее основания не квадратные; Они могут иметь основания, состоящие из неравных сторон, и представлены пять случаев, когда:

к. Основания прямоугольные

Его поверхность образована двумя прямоугольными основаниями и четырьмя боковыми гранями, которые также являются прямоугольниками, все равны и параллельны.

Чтобы определить его общую площадь, вычисляется каждая площадь шести прямоугольников, которые его образуют, двух оснований, двух малых боковых поверхностей и двух больших боковых поверхностей:

Площадь = 2 (a_* б + а_*h + b_*час)

б. Основания — ромбы:

Его поверхность образована двумя ромбовидными основаниями и четырьмя прямоугольниками, которые являются боковыми гранями, для расчета его общей площади необходимо определить:

• Площадь основания (ромб) = (большая диагональ _* малая диагональ) ÷ 2.
• Боковая площадь = периметр основания _* height = 4 (стороны основания) * h

Таким образом, общая площадь составляет: A_Т = А_{боковая сторона} + 2А_{основание.}

c. Основания ромбовидные

Его поверхность образована двумя ромбовидными основаниями и четырьмя прямоугольниками, которые являются боковыми сторонами, его общая площадь определяется как:

• Площадь основания (ромбовидная) = основание _* относительная высота = B * h.
• Боковая площадь = периметр основания _* высота = 2 (сторона a + сторона b) _* час
• Итак, общая площадь: A_Т = А_{боковая сторона} + 2А_{основание.}

d. Основания трапециевидные

Его поверхность образована двумя основаниями в форме трапеций и четырьмя прямоугольниками, которые являются боковыми гранями, его общая площадь определяется как:

• Площадь основания (трапеция) = h _* .
• Боковая площадь = периметр основания _* высота = (a + b + c + d) * h
• Итак, общая площадь: A_Т = А_{боковая сторона} + 2А_{основание.}

а также. Основания трапециевидные

Его поверхность образована двумя основаниями трапециевидной формы и четырьмя прямоугольниками, которые представляют собой боковые грани, его общая площадь определяется как:

• Площадь основания (трапеция) = = (диагональ_{1 *} диагональ₂) ÷ 2.
• Боковая площадь = периметр основания _* height = 2 (сторона a _* сторона б * ч.
• Итак, общая площадь: A_Т = А_{боковая сторона} + 2А_{основание.}

Таким образом, чтобы определить площадь любой правильной четырехугольной призмы, необходимо только рассчитать площадь четырехугольника, который является основанием, его периметр и высоту, которую будет иметь призма, в общем, ее формула будет:

Площадь _Общее = 2_* Площадь_{основание} + Периметр_{основание *} высота = A = 2A_б + P_б* час

Для расчета объема призм этого типа используется та же формула:

Объем = Площадь_{основание*} высота = A_б* час

Шаровой сегмент

Когда плоскость проходит через шар, она рассекает его на две фигуры, которые именуются шаровым сегментом. Если из центра шара О провести радиус ОА длиной R в направлении плоскости сечения, который перпендикулярен этой плоскости, то он пересечет ее какой-то точке В. Длину отрезка АВ называют высотой шарового сегмента и обозначают буквой h:

Ясно, что при этом отрезок ОВ – это расстояние от секущей плоскости (или от основания сегмента) до центра шара, причем этот отрезок имеет длину R –h.

Можно считать, что шаровой сегмент, как и шар, получается при вращении дуги окружности вокруг оси Ох. Однако если сам шар при этом ограничен плоскостями x = R и х = – R, то сегмент ограничен другими плоскостями: х = R и х = R – h. Это значит, что его объем можно вычислить с помощью интеграла также, как и объем шара, отличаться будет лишь нижний предел интегрирования:

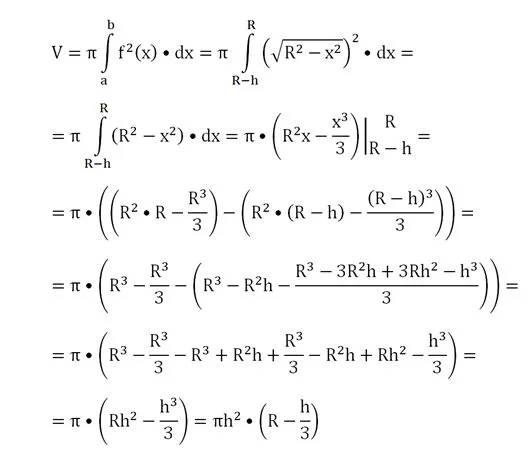
Заметим, что шар можно рассматривать как шаровой сегмент, чья высота вдвое больше его радиуса. И действительно, если в выведенную формулу мы подставим значение h = 2R, то получим уже известную нам формулу объема шара.

Задание. Найдите объем шарового сегмента высотой 6, если он отсечен от шара радиусом 15.

Решение. Используем выведенную формулу:

Задание. Диаметр шара разделили на три равных отрезка. Через концы этих отрезков провели секущие плоскости, перпендикулярные диаметру. Чему равен объем тела, заключенного между этими двумя плоскостями (оно называется шаровым слоем), если радиус шара обозначен буквой R?

Решение. Ясно, что для вычисления объема шарового слоя достаточно вычесть из объема шара объемы двух шаровых сегментов, образующихся при проведении секущих плоскостей. Так как они разделили диаметр на три одинаковых отрезка, то высота этих сегментов будет в три раза меньше диаметра шара:

Примеры задач с решениями

Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.

Задание 1.

В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?

Решение.

Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:

V₁ = ha² = 10a²

Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:

V₂ = h (2a)² = 4ha²

Поскольку V₁ = V₂, можно приравнять выражения:

10a² = 4ha²

После сокращения обеих частей уравнения на a² получается:

10 = 4h

В результате новый уровень песка составит h = 10 / 4 = 2,5 см.

Задание 2.

ABCDA₁B₁C₁D₁ правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.

Решение.

Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.

Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.

Длина любого ребра определяется через известную диагональ:

a = d / √2 = 6√2 / √2 = 6

Площадь полной поверхности находится по формуле для куба:

Sполн = 6a² = 6·6² = 216

Задание 3.

В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?

Решение.

Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.

Длина комнаты составляет a = √9 = 3 м.

Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².

Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.

Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.