Объем шара
Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.
Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h. Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров. Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:
0,5 Vsh = Vc − Vk
Объем конуса вычисляется по простой формуле:
Vk = 1/3 × So × h,
но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:
Vk = 1/3 × pi × R × R 2 = 1/3 pi × R 3
Объем цилиндра вычисляется по формуле:
Vc = pi × R 2 × h,
но считая, что высота цилиндра равна его радиусу, мы получаем:
Vc = pi × R 3 .
Используя эти формулы, Архимед получил:
0,5 Vsh = pi × R 3 — 1/3 pi × R 3 или Vsh = 4/3 pi × R 3
Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же
Vsh = 4/3 pi × R 3
Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.
Основные свойства сферы и шара
1. Все точки на сфере равноудалены от центра.
2. Любая часть сферы плоскостью является окружностью.
3. Любое сечение сферы плоскостью есть окружность.
4. Сфера имеет наибольший объем среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через две диаметрально противоположные точки можно провести много больших кругов для сферы или кругов для шара.
6. Через две точки, кроме диаметрально противоположных, можно провести только одну большую окружность для шара или одну большую окружность для шара.
7. Любые две большие окружности шара пересекаются по прямой, проходящей через центр шара, причем окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух сфер меньше суммы их радиусов и больше модуля разности их радиусов, то такие сферы пересекаются, и в плоскости пересечения образуется окружность.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение.Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула.Площадь внешней поверхности сегмента сферы с высотой h
через радиус сферы R:
S = 2π
Rh
Мы даем здесь очень простой, хотя и не совсем строгий вывод формулы для площади сферической поверхности; по своей идее он очень близок к методам интегрального исчисления. Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 412) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не плоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, например, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере).
Тогда, обозначая через площадь этого участка — основание «пирамиды», найдем ее объем как произведение одной трети высоты на площадь основания (высотой служит радиус шара):
Если теперь всю поверхность шара разложить на очень большое число N таких малых областей , тем самым объем шара на N объемов «пирамид», имеющих эти области своими основаниями, то весь объем представится суммой
где последняя сумма равна полной поверхности шара:
Итак, объем шара равен одной трети произведения его радиуса на площадь поверхности. Отсюда для площади поверхности имеем формулу
Последний результат формулируется так:
Площадь поверхности шара равна учетверенной площади его большого круга.
Приведенный вывод пригоден и для площади поверхности сектора шара (имеем в виду только основание, т. е. сферическую поверхность, или «шапочки»; см. рис. 409). И в этом случае объем сектора равен одной трети произведения радиуса шара на площадь его сферического основания:
откуда находим для площади шапочки формулу
Шаровым поясом (см. рис. 408) называют сферическую поверхность шарового слоя. Чтобы вычислить площадь поверхности шарового пояса, находим разность поверхностей двух сферических шапочек:
где — высота слоя. Итак, площадь поверхности шарового пояса для данного шара зависит только от высоты соответствующего слоя, но не от его положения на шаре.
Задача. Боковая поверхность конуса, описанного вокруг шара, имеет площадь, равную полуторной площади поверхности шара. Найти высоту конуса, если радиус шара равен .
Решение. Введем для удобства угол а между высотой и образующей конуса (рис. 413). Найдем для высоты, радиуса основания и образующей конуса выражения
Определение шара
Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее R R
R
— радиус этого шара.
В чем различие
Тогда возникает вопрос, а чем отличается шар от сферы кроме определения? Дело в том, что различия шара и сферы куда более размыты, нежели различия круга и окружности. Сфера так же имеет объем и площадь поверхности.
Пожалуй, кроме определения, разница заключается в том, что в задачах никогда не находят объем сферы. Как правило, ищут объем шара. Это не значит, что у сферы нет объема. Это трехмерная фигура, поэтому объем у нее есть.
Просто проводится аналогия с окружностью, у которой нет площади. Это не правило, но скорее традиция, которую нужно запомнить: в геометрии не приветствуется формулировка объем сферы.
Еще одно отличие, которое можно считать более или менее значимым: секущая плоскость сферы: окружность, которая не имеет внутреннего пространства, но имеет длину. Секущая плоскость шара: круг, который имеет площадь и не имеет длины окружности. Поэтому стоит быть аккуратным в формулировках задачи, чтобы не было ошибок из-за подобных мелочей.
Объём тела вращения: исходные данные и формулы
С помощью определённого интеграла можно вычислять не только площади плоских фигур,
но и объёмы тел, образованных вращением этих фигур вокруг осей координат.
Примеры таких тел — на рисунке ниже.
В задачах у нас есть криволинейные трапеции, которые вращаются вокруг оси или
вокруг оси . Для вычисления объёма тела, образованного вращением
криволинейной трапеции, нам понадобятся:
- число «пи» (3,14…);
- если кривая вращается вокруг оси — непосредственно данная в задаче функция («игрек»), задающая вращающуюся кривую, и определённый интеграл от квадрата «игрека»;
- если кривая вращается вокруг оси ) — «икс», выраженный из «игрека» — данной в задаче функции — и определённый интеграл от квадрата «икса»;
-
пределы интегрирования — a и b. Если кривая вращается вокруг оси , то это
значения на оси «иксов» крайних точек фигуры. Если же кривая вращается вокруг оси , то это
значения крайних точек фигуры на оси «игреков». Если фигура ограничена данными в задаче прямыми — то пределы найти совсем просто:
например, и
означает, что нижний и верхний пределы интегрирования равны соответственно 1 и 4. В более сложных случаях для
нахождения пределов интегрирования нужно найти точки пересечения линий, между которыми заключена вращающаяся кривая. Это делается
с помощью графика, который необходимо построить к каждой отдельно взятой задаче. На графике будут видны координаты
(абсциссы и ординаты) точек пересечения.
Итак, тело, которое образуется вращением вокруг оси криволинейной трапеции, ограниченной сверху
графиком функции , имеет объём
. (1)
Аналогично объём v тела, полученного вращением вокруг оси ординат
() криволинейной трапеции выражается формулой
. (2)

При вычислении площади плоской фигуры мы узнали, что площади некоторых фигур могут
быть найдены как разность двух интегралов, в которых подынтегральные функции — те функции, которые
ограничивают фигуру сверху и снизу. Похоже обстоит дело и с некоторыми телами вращения, объёмы которых
вычисляются как разность объёмов двух тел, такие случаи разобраны в примерах 3, 4 и 5.
Занимательные факты
Это интересно:
- У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
- Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
- Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.
Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.
Объем шара
Пришло время разобраться и с таким телом, как шар. Здесь можно использовать тот же метод интегрирования, что и в случае с конусом и пирамидой. Но можно поступить и иначе – использовать выведенную нами для тел вращения формулу
Шар как раз является телом вращения. Он получается при вращении полуокружности вокруг диаметра, на который эта дуга опирается.
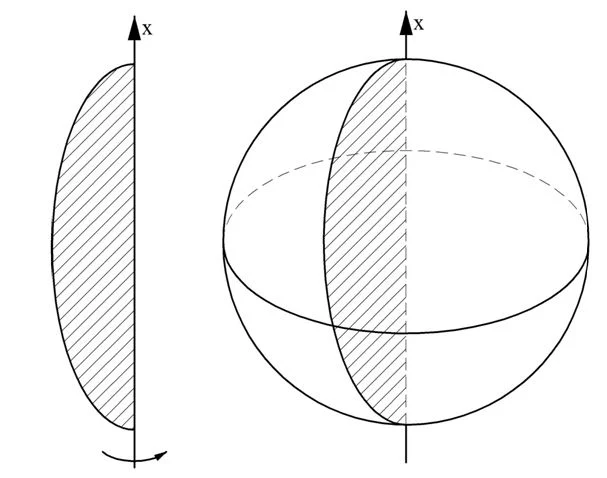
Напомним известное нам уравнение окружности, чей центр совпадает с началом координат:

Здесь надо уточнить, что если у получившейся функции впереди записан знак «+», то ее график соответствует полуокружности, находящейся над осью Ох. Если же используется знак «–», то получается уже нижняя полуокружность, расположенная под осью Ох:
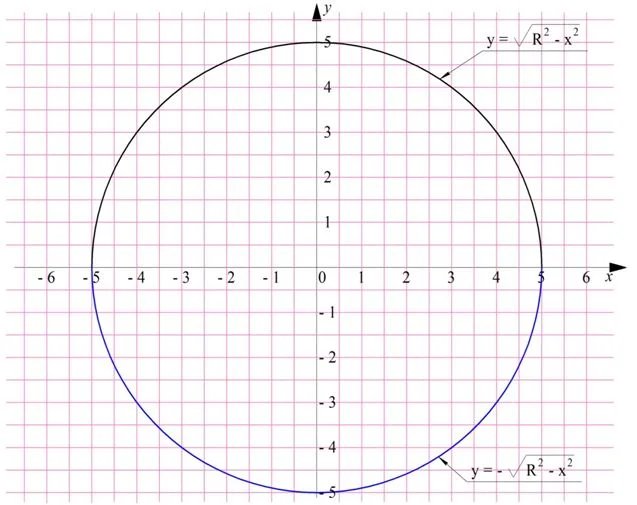
В принципе мы можем поворачивать любую из этих полуокружностей вокруг Ох, но мы выберем верхнюю полуокружность. Заметим, что эта дуга начинается в точке х = – R и заканчивается в точке х = R, эти числа будут пределами интегрирования. Тогда объем шара равен:
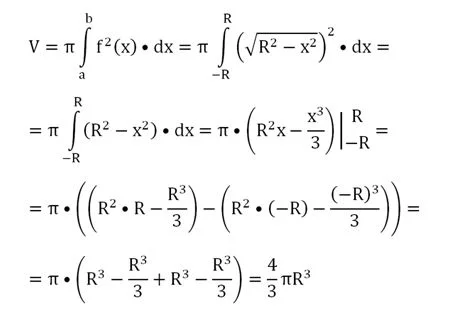

Задание. Найдите объем шара с радиусом 6.
Решение. Подставляем радиус из условия в формулу:
Задание. В цилиндр вписан шар. Во сколько раз объем цилиндра больше объема такого шара?
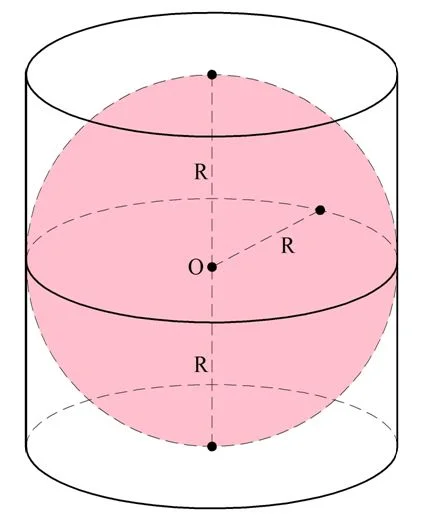
Решение. Ясно, что так как шар вписан в цилиндр, то радиусы этих тел одинаковы. Обозначим этот радиус как R. Также ясно, что раз шар касается оснований цилиндра, то расстояние между ними (то есть высота цилиндра) равно двум радиусам шара:

Секущая, хорда, секущая плоскость сферы и их свойства
Определение: секущая сферы – это прямая линия, которая пересекает сферу в двух точках. Точки пересечения называются точками прокалывания поверхности или точками входа и выхода на поверхность.
Определение Хорда сферы (сферы) – это отрезок, соединяющий две точки сферы (поверхность сферы) Определение Секущая плоскость – это плоскость, которая пересекает сферу.
Определение Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или сферы, при этом разрез образует большой круг и большой круг соответственно. Большой круг и большой круг имеют центр, совпадающий с центром сферы (сферы). Любая хорда, проходящая через центр сферы (сферы), является диаметром. Хорда – это отрезок секущей. Расстояние d от центра сферы до секущей всегда меньше радиуса сферы:
д < р
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
м < R
Сечение секущей плоскости на сфере всегда будет маленькой окружностью, а на сфере сечением будет маленькая окружность. Малый круг и малый круг имеют свои центры, не совпадающие с центром сферы (сферы). Радиус r такой окружности можно найти по формуле:
г = √R2 — м2,
где R — радиус сферы (сферы), м — расстояние от центра сферы до плоскости сечения. Определение Полусфера (полусфера) — это полусфера (сфера), образованная при разрезании ее диаметральной плоскостью.
Обобщения[править | править код]
Сечения других телправить | править код
Сфероидальный сегмент получается при отсечении части сфероида таким образом, что она обладает круговой симметрией (обладает осью вращения). Аналогичным образом определяют эллипсоидальный сегмент.
Сегмент гиперсферыправить | править код
Объём -мерного сегмента гиперсферы высотой и радиуса в -мерном евклидовом пространстве определяется по формуле
где (гамма-функция) задаётся выражением
Выражение для объёма можно переписать в терминах объёма единичного -мерного шара и гипергеометрической функции или регуляризованной неполной бета-функции как
Формула для площади поверхности может быть записана в терминах площади поверхности единичного -мерного шара как
где
Также справедливы следующие формулы: где
При
Было показано, что при и где — стандартное нормальное распределение.
Таблица кубатурник доски, сколько доски в кубе
Доска обрезная | Доска строганная
| Наименование | Размеры | Кол-во штук в одном м3 | Кол-во погонных метров в одном м3 |
| Доска обрезная / строганная | 25х100х2000 | 200 | 400 |
| Доска обрезная / строганная | 25х100х4000 | 100 | 400 |
| Доска обрезная / строганная | 25х100х6000 | 66 | 396 |
| Доска обрезная / строганная | 25х150х2000 | 133 | 266 |
| Доска обрезная / строганная | 25х150х4000 | 66 | 264 |
| Доска обрезная / строганная | 25х150х6000 | 44 | 264 |
| Доска обрезная / строганная | 25х200х2000 | 100 | 200 |
| Доска обрезная / строганная | 25х200х4000 | 50 | 200 |
| Доска обрезная / строганная | 25х200х6000 | 33 | 198 |
| Доска обрезная / строганная | 40х100х2000 | 125 | 250 |
| Доска обрезная / строганная | 40х100х4000 | 62 | 248 |
| Доска обрезная / строганная | 40х100х6000 | 41 | 246 |
| Доска обрезная / строганная | 40х150х2000 | 83 | 166 |
| Доска обрезная / строганная | 40х150х4000 | 41 | 164 |
| Доска обрезная / строганная | 40х150х6000 | 27 | 162 |
| Доска обрезная / строганная | 40х200х2000 | 62 | 124 |
| Доска обрезная / строганная | 40х200х4000 | 31 | 124 |
| Доска обрезная / строганная | 40х200х6000 | 20 | 120 |
| Доска обрезная / строганная | 50х100х2000 | 100 | 200 |
| Доска обрезная / строганная | 50х100х4000 | 50 | 200 |
| Доска обрезная / строганная | 50х100х6000 | 33 | 198 |
| Доска обрезная / строганная | 50х150х2000 | 66 | 132 |
| Доска обрезная / строганная | 50х150х4000 | 33 | 132 |
| Доска обрезная / строганная | 50х150х6000 | 22 | 132 |
| Доска обрезная / строганная | 50х200х2000 | 50 | 100 |
| Доска обрезная / строганная | 50х200х4000 | 25 | 100 |
| Доска обрезная / строганная | 50х200х6000 | 16 | 96 |
Как найти площадь сферы
Запомните!
Формула площади сферы:
S = 4π
R 2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа .
Зная определение степени,
можно записать формулу площади сферы следующим образом. S = 4π
R 2 =
4π
R · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
-
Вычислите площадь сферы, если её радиус равен
1 =
3 ·
=
=
/ (4 · 3)
= ) =
= ) =
= =
=88 = 1
- R 3 = 1
- R = 1 м
Важно!
Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.
Сфера и шар – это аналог круга и окружности в трехмерном пространстве. Стоит поговорить о каждой из этих фигур, выделить сходства и различия, а так же формулы, свойственные этим фигурам.
Большая часть геометрических построений производится в плоскости, но в старших классах начинают изучать трехмерные фигуры. Двухмерное пространство имеет только две характеристики: длину и ширину. В трехмерных областях добавляется высота. В математике 6 класса изучаются отдельные 3д фигуры.
На плоскости фигуру характеризовала площадь и периметр. В трехмерных объектах к ним прибавляется объем.
Рис. 1. Трехмерное пространство.
Кроме того, имеется ряд специфических свойств 3д фигур. Их может пересекать прямая и плоскость, могут имеется секущие плоскости, которые принимают формы других фигур.
Применение 3д фигур для составления задач значительно усложняет их, но в то же время делает куда более интересными. Приведем определения шара и сферы, после чего попробуем выделить различия этих фигур.
Формула объема шарового сегмента
О±ÃÂõü ôðýýþóþ ÃÂõûð üþöýþ òÃÂÃÂøÃÂûøÃÂàýõÃÂúþûÃÂúøüø ÃÂÿþÃÂþñðüø. ÃÂõÃÂòðàÃÂþÃÂüÃÂûð ÃÂðúþòð:
ÃÂûÃÂÃÂõÃÂýðÃÂøòýðàÃÂþÃÂüÃÂûð:
ÃÂÃÂþÃÂÃÂàÃÂþÃÂüÃÂûàüþöýþ ÿþûÃÂÃÂøÃÂàø÷ ÿõÃÂòþù, õÃÂûø øÃÂÿþûÃÂ÷þòðÃÂàÃÂòÃÂ÷àüõöôàRR, hh ø rr:
R=r2+h22âÂÂhR=frac{r^2+h^2}{2cdot h},
ÿþûÃÂÃÂðõüÃÂààÿþüþÃÂÃÂàÃÂõþÃÂõüàÃÂøÃÂðóþÃÂð ôûàÿÃÂÃÂüþÃÂóþûÃÂýþóþ ÃÂÃÂõÃÂóþûÃÂýøúð.
ÃÂøöõ ÿÃÂøòõôõýàÿÃÂøüõÃÂà÷ðôðàýð ýðÃÂþöôõýøõ þñÃÂõüþò ÃÂðÃÂþòþóþ ÃÂõóüõýÃÂð.
Определение сектора шара
Сектор шара (или шаровый сектор) – это часть шара, состоящая из шарового сегмента и конуса, вершиной которого является центр шара, а основанием – основание соответствующего сегмента. На рисунке ниже сектор закрашен оранжевым цветом.
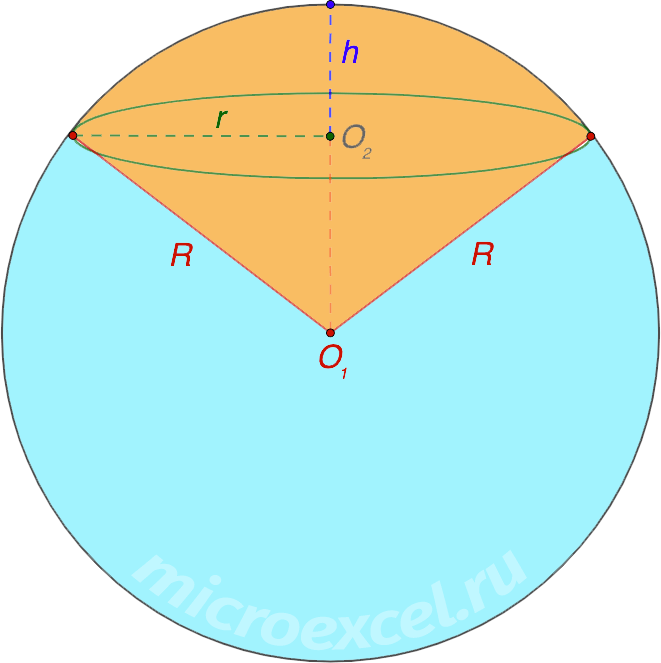
- R – радиус шара; R – радиус основания сегмента и конуса; H – высота сегмента; перпендикуляр от центра основания сегмента до точки на сфере.
Подставим формулы площади конуса и шарового сегмента:
Определение сектора шара
Свойства равнобедренной равнобокой трапеции.
10.09.2020 10:38:39
2020-09-10 10:38:39
Любые данныеЛюбые данныеЛюбые данныеЛюбые данные Любые данные
Длина и площадь
Окружность и круг — две фигуры, изучаемые в геометрии плоскости. Они имеют общую форму и определяются с помощью основных элементов — радиуса и центра. Длина окружности и площадь круга являются важными характеристиками этих фигур и вычисляются по определенным формулам.
Длина окружности можно вычислить с помощью формулы: L = 2πr, где L — длина окружности, r — радиус окружности. Радиус — это расстояние от центра окружности до любой точки на ней. Формула позволяет нам определить длину окружности, зная ее радиус. Таким образом, длина окружности выражается через число π (3,14) и умножается на радиус.
Площадь круга можно вычислить с помощью формулы: S = πr^2, где S — площадь круга, r — радиус круга. Площадь круга определяется как участок плоскости, ограниченный окружностью. Формула позволяет нам определить площадь круга, зная ее радиус. Площадь выражается через число π (3,14) и умножается на квадрат радиуса.
Теоретически окружность и круг неразрывно связаны друг с другом. Окружность — это граница круга, а круг — это фигура, заключенная внутри окружности. Однако, в геометрии плоскости, окружность и круг имеют разные характеристики и свойства, включая их длину и площадь. Понимание этих характеристик позволяет более глубоко изучать и использовать окружность и круг в различных областях науки и практики.
Расчет длины окружности
Окружность является геометрической фигурой, которая находится в плоскости и состоит из точек, равноудаленных от ее центра. Важнейшим параметром окружности является ее диаметр, который представляет собой максимальное расстояние между двумя точками на окружности, проходящими через ее центр.
Длина окружности может быть рассчитана по формуле, которая основана на теории геометрии и связана с радиусом окружности. Радиус представляет собой расстояние от центра окружности до любой точки на ее границе. Формула для расчета длины окружности выглядит следующим образом: L = 2πr, где L — длина окружности, π — математическая константа, примерное значение которой равно 3,14, а r — радиус окружности.
Размер длины окружности напрямую зависит от размера ее радиуса. Чем больше радиус, тем длиннее будет окружность, и наоборот. Точная длина окружности может быть рассчитана с высокой точностью при помощи математических функций или приближенно, используя значение π при округлении его до десятичных знаков.
Расчет площади круга
Геометрия изучает фигуры на плоскости, такие как круг. Круг — это геометрическая фигура, состоящая из всех точек на плоскости, которые находятся на одинаковом расстоянии от центра.
Основными понятиями, связанными с кругом, являются радиус и диаметр. Радиус — это расстояние от центра круга до любой точки его окружности, а диаметр — это удвоенный радиус.
Для расчета площади круга используется теория геометрии. Формула для расчета площади круга основана на длине его радиуса. Площадь круга равна произведению квадрата его радиуса на число π (пи).
Формула для расчета площади круга выглядит следующим образом: площадь = π * (радиус)^2. В данной формуле π — математическая константа, приблизительно равная 3.14159.
Для удобства расчетов площади круга можно использовать таблицу, где указывается значение радиуса и соответствующая площадь круга. Также можно воспользоваться онлайн-калькулятором для расчета площади круга, который автоматически выполнит необходимые математические операции.
Шар, сфера и их части
Введем следующие определения, относящиеся к шару, сфере и их частям.
Определение 1. Сферой с центром в точке O и радиусом r называется множество точек, расстояние до точки O которых равно r (рис. 1).
Определение 2. Сферой с центром в точке O и радиусом r называется множество точек, расстояние от которых до точки O не превышает r (рис. 1).
Рисунок 1
Таким образом, сфера с центром в точке O и радиусом r является поверхностью сферы с центром в точке O и радиусом r.
Примечание: Радиус сферы (радиус сферы) — это отрезок, соединяющий любую точку на сфере с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом сферы).
Определение 3. Сферический пояс (сферический пояс) – это часть сферы, заключенная между двумя параллельными плоскостями параллельных плоскостей (рис. 2).
Определение 4. Сферический слой – это часть сферы, заключенная между двумя параллельными плоскостями параллельных плоскостей (рис. 2).
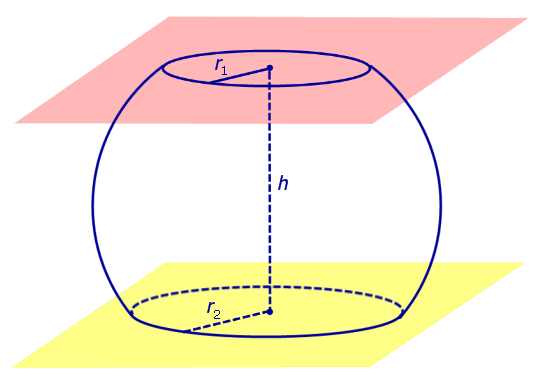
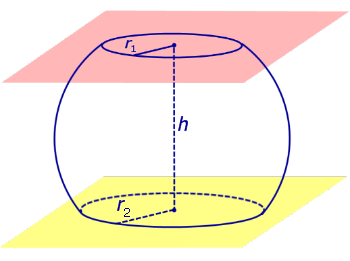
Рис.2
Окружности, ограничивающие сферический пояс, называются основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называется высотой сферического пояса.
Из определений 3 и 4 следует, что сферический слой ограничен сферическим поясом и двумя окружностями, плоскости которых параллельны и параллельны друг другу. Эти окружности называются основаниями сферического слоя.
Высота сферического слоя — это расстояние между плоскостями, расстояние между плоскостями оснований сферического слоя.
Определение 5. Сферическим сегментом называется каждая из двух частей, на которые шар делится секущей его плоскостью (рис. 3).
Определение 6. Каждая из двух частей, на которые шар делится секущей его плоскостью, называется сферическим сегментом (рис. 3).
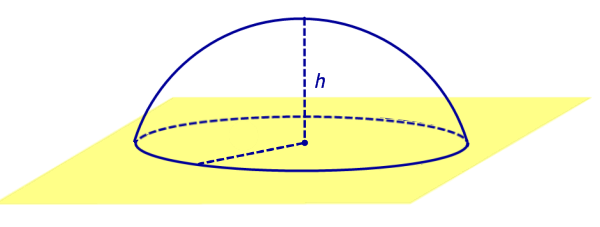

Рис.3
Из определений 3 и 5 следует, что сферический сегмент представляет собой сферический пояс, в котором одна из плоскостей основания касается сферы (рис. 4). Высота такого сферического пояса называется высотой сферического сегмента.
Соответственно сферический сегмент представляет собой сферический слой, в котором одна из плоскостей оснований касается шара (рис. 4). Высота такого сферического слоя называется высотой сферического сегмента.
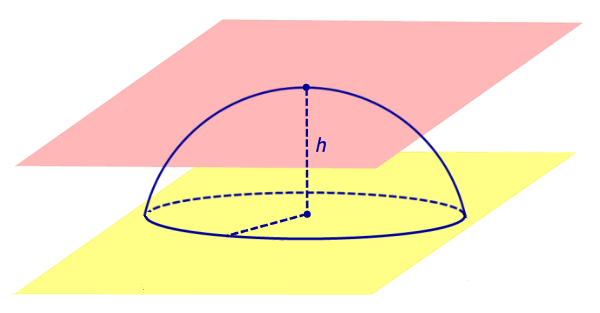
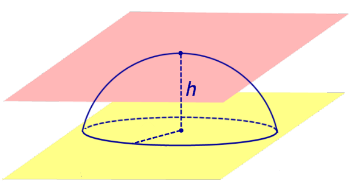
Рис.4
По той же причине всю сферу можно рассматривать как сферический пояс, где обе плоскости заземления соприкасаются со сферой (рис. 5). Следовательно, весь шар представляет собой сферический слой, где обе плоскости основания касаются шара (рис. 5).
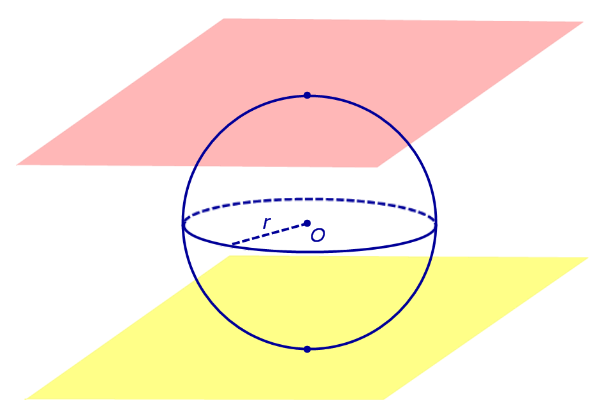
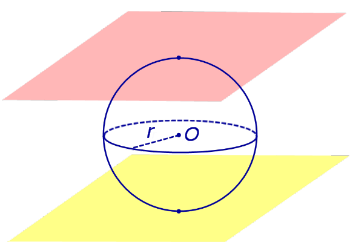
Рис.5
Определение 7. Сферическим сектором называется фигура, состоящая из всех отрезков, соединяющих точки сферического отрезка с центром сферы (рис. 6).
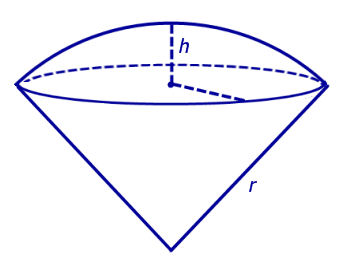
Рис. 6
Высота сферического сектора равна высоте его сферического сегмента .
Комментарий. Сферический сектор состоит из сферического сегмента и конуса с общим основанием. Вершина конуса является центром сферы.
Объем пирамиды
Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.
Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.
Далее построим сечение А1В1С1, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ1. Тогда ОМ1 – это координата х, характеризующая расположение сечения А1В1С1.
Осталось составить выражение для площади ∆А1В1С1. Так как АВ||A1B1, то ∠АВО и ∠А1В1О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А1В1О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что
Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ1В1. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому
Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:
Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S1, S2, S3…, которые в сумме составляют площадь многоугольника S.
Объем треугольных пирамид рассчитывается по выведенной нами формуле:


Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.
Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:
Задание. В кубе АВСDA1В1С1D1 отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С1EFC меньше объема куба?
Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:
Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?
Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.
Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.
Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А1В1С1, параллельное основанию.
Обозначим площадь нижнего основания пирамиды как S2, а площадь верхнего основания – как S1. Далее высоту усеченной пирамиды (отрезок ММ1) обозначим как h. Мы уже выяснили ранее, что основания АВС и А1В1С1 – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ1. Тогда можно записать:
Далее используем основное свойство пропорции:
Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:
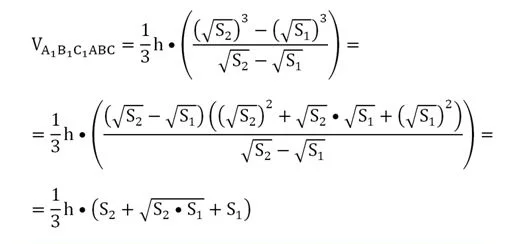

Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.
Сначала вычислим площади оснований:






























