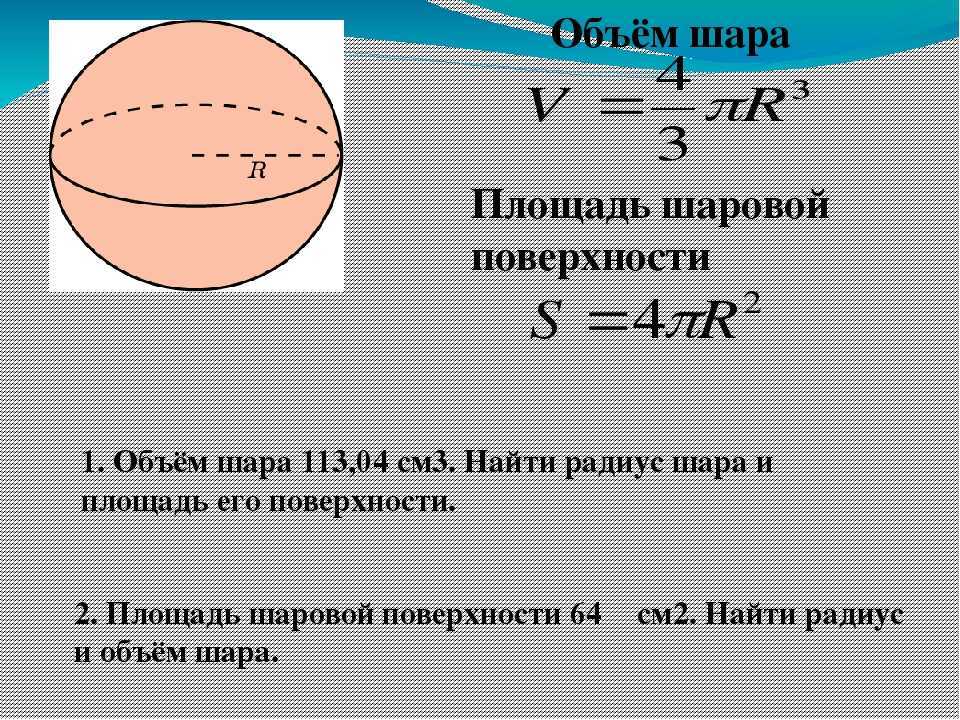
Введение понятия «шар»
Шар — это тело (рис. 3), ограниченное некой сферической поверхностью. Что за «сферическая поверхность», станет ясно из ее определения: это геометрическое место всех точек на поверхности, расстояние от которых до заданной точки (центра) не превышает некоего неотрицательного числа, называемого радиусом. Как видим, понятия круга и сферической поверхности аналогичны, только разнятся пространства, в которых они находятся. Если изобразить шар в двумерном пространстве, мы получаем круг, границей которого является окружность (у шара граница — сферическая поверхность). На рисунке мы видим сферическую поверхность с радиусами ОА = ОВ.
Примеры из жизни
Пушечные ядра
Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде
Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.
Воздушные шары
Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат
Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.
Объемы простых тел. Прямоугольный параллелепипед, Цилиндр, Пирамида, Конус, Сфера, Параллелепипед.
Объемы простых тел.Прямоугольный параллелепипед, Цилиндр,Пирамида, Конус, Сфера, Параллелепипед.
Объемы и площади поверхностей правильных тел.
Общая информация об объемах и площадях поверхностей правильных тел приведена в таблице.
Пример 1.Расчет объема прямоугольного бака.
Бак для воды имеет форму прямоугольного параллелепипеда длиной 1 м, шириной 65 см и высотой 30 см. Определить объем бака в м3, см3, литрах
Решение:
Объем прямоугольного параллелепипеда равен l*b*h
а)Vбака=1*0.65*03=0.195 м3
б) 1 м 315000 мм2=315000/100=3150 см2
1 м3=106 см3, значит, 0.195 м3=0.195*106=195000 см3
в) 1 литр=1000 см3, значит 195000 см3=195 л
Пример 2. Расчет объема и площади поверхности трапецеидальной призмы.
Вычислить объем и общую площадь поверхности призмы, показанной на рис.
Тело, показанное на рис. — это трапецеидальная призма.
Так как объем = площадь поперечного сечения * высота, то
V=1/2*(10+5)*4*20=30*20=600 cм3
Так как площадь поверхности вычисляется сложением суммы площадей двух трапеций и суммы площадей четырех прямоугольников, то
S=(2*30)+3(5*20)+(10*20)=560 см2
Пример 3. Расчет объема и общей площади поверхности правильной пирамиды.
Определить объем и общую площадь поверхности правильной пирамиды с квадратным основанием, показанной на рис., если ее высота равна 15 см.
Решение:
Так как объем пирамиды =1/3(площадь основания)*высота, то
V=1/3*(5*5)*15=125 см3
Общая площадь поверхности включает площадь квадратного основания и площади четырех равных треугольников.
Площадь треугольника ADE=1/2*основание*(высота грани).
Высоту грани АС можно найти по теореме Пифагора из треугольника АВС, где АВ=15 см, ВС=1/2*3=1.5 см, и АС2=AB2+BC2=225+2.25=227.25
AC=15.07 cм
Следовательно, площадь треугольника ADE
SADE=1/2*3*15.07=22.605 см2
Общая площадь пирамиды S=(3*3)+4*22.605=99.42 cм2.
Пример 4. Расчет объема и общей площади поверхности конуса.
Определить объем и общую площадь поверхности конуса радиусом 4 см и высотой 10 см.
Объем конуса V=1/3πr2h =1/3*π42*10=167.5см3
Общая площадь поверхности равна сумме площади конической поверхности и площади основания, т.е. S=πrl+πr2
Из рисунка видно, что длину образующей l можно найти по теореме Пифагора.
l2=102+42=116 см
l=10,8 cм
Следовательно, общая площадь поверхности равна
S=π*4*10.8)+(π*42=185.89 cм2
Пример 5. Расчет объема и общей площади поверхности призмы.
На рис. показан деревянный профиль. Найдем: а) его объем в м3
б) общую площадь его поверхности
Профиль представляет собой призму, поперечное сечение которой состоит из прямоугольника и полукруга. Поскольку радиус полукруга равен 6 см, диаметр равен 12 см.
Тогда размеры прямоугольника 12*11 см
Площадь поперечного сечения S.=(11*12)+1/2* π 62=188,52 см2
Поскольку объем деревянной детали равен произведению площади поперечного сечения на длину, то
a) V=188,52*200=37704 см3=37704 см3/106= 0,037704 м3
б) Общая площадь включает два торца (площадь каждого 188,52 см2), три прямоугольника и криволинейную поверхность (которая представляет собой полуцилиндр). Следовательно, общая площадь поверхности
S=(2*188,52)+2*(11*200)+(12*200)+1/2*(2π*6*200)=377,04+4400+2400+3768=10945,04 см2=1,094504 м2.
Пример 6. Расчет объема и общей площади поверхности сложного бойлера.
Бойлер состоит из цилиндрической секции длиной 9 м и диаметром 5 м, к одному концу которой присоединена полусферическая секция диаметром 5 м, а к другому концу — коническая секция высотой 3 м и диаметром основания 5 м. Вычислить объем бойлера и общую площадь его поверхности.
Vполусферы P =2/3*πr3 =2/3*π*2,53 =10,42 π м3
V цилиндра Q = π r2h=π*2,52*9=56,25 π м3
V конуса R =1/3 π r2=1/3*π*2,52*3=6,25π м 3
Общий объем бойлера V= 10,42 π м3+56,25 π м3+6,25π м 3=72,92π=228,97 м 3
S полусферы P. =2*(πr2)=2*π*2,52=12,5π м2
S бок. поверхности цилиндра Q. =2πrh=2*π*2,5*9=45π м2 (т.к. этот цилиндр представляет собой трубу без оснований)
Длина образующей конуса l рассчитывается по теореме Пифагора из треугольника ABC;
значит
l=(32+2,52)1/2=3,9 м.
S конуса R. =πrl=π*2,5*3,9=9,75 π м 2
Общая площадь поверхности бойлера
S= 12,5π+45π+9,75 π=67,25π=211,2 м 2
Мелкие нюансы
Если необходимо вычислить объем шара через его диаметр, помним о том, что радиус — это половина диаметра, и подставляем это значение в вышеуказанную формулу.
Также к формуле объема шара можно дойти через площадь его граничащей поверхности — сферы. Напомним, что площадь сферы вычисляется по формуле S = 4πr 2 , проинтегрировав которую, также придем к вышеуказанной формуле объема шара. Из этих же формул можно выразить радиус, если в условии задачи есть значение объема.
Шар
это геометрическое тело, образованное в результате вращения полукруга на оси своего диаметра.
Вычислить объем шара
Объем шара
можно вычислить по формуле:
R – радиус шара
V – объем шара
Найти объем шара радиусом сантиметров.
Для того чтобы вычислить объем шара формула используется следующая:
где – искомый объем шара, – , – радиус.
Таким образом, при радиусе сантиметров объем шара равен:
| V | 3,14 × 103 | = 4186,7 |
кубических сантиметров. |
В геометрии шар
определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара.
Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.
С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится вычислять объем шара
. Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары.
С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет вычислен
их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.
В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение.
Следует заметить, что при их расчете конструкторам требуется найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки.
Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.
Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений.
В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.
Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы.
Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.
Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка
Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий
Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.
Сфера — одно из простейших геометрических тел, в котором все точки ее поверхности находятся на одном и том же расстоянии от центра изображения. Расстояние от центра сферы до любой точки на ее поверхности называется радиусом.
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.
Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
- S = 4 * 3,14 * 10²;
- S мяча равна ≈ 1256 см².
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Объём шара и площадь сферы. Геометрия, 11 класс: уроки, тесты, задания.
1.
Отношение радиусов и объёмов двух шаров
Сложность:
лёгкое
1
2.
Шар, вписанный в куб
Сложность:
лёгкое
1
3.
Два шаровых сегмента
Сложность:
лёгкое
1
4.
Oбъём шарового сегмента по формуле
Сложность:
лёгкое
1
5.
Цилиндр, вписанный в шар
Сложность:
лёгкое
2
6.
Конус, вписанный в шар
Сложность:
лёгкое
1
7.
Вычисление объёма шара с использованием площади сферической поверхности
Сложность:
лёгкое
1
8.
Площадь сферы
Сложность:
лёгкое
2
9.
Объём шарового сегмента
Сложность:
среднее
3
10.
Шар касается плоскости
Сложность:
среднее
2
11.
Площадь поверхности шара, вписанного в цилиндр
Сложность:
среднее
2
12.
Cумма объёмов трёх шаров
Сложность:
среднее
2
13.
Шар, вписанный в конус
Сложность:
среднее
3
14.
Цилиндрическое отверстие в шаре
Сложность:
сложное
4
15.
Толщина плёнки мыльного пузыря
Сложность:
сложное
4
Шар и сфера
Круг — самая древняя геометрическая фигура, и античные ученые придавали ей сакральное значение. Круг — это символ нескончаемого времени и пространства, символ Вселенной и бытия. По мнению Пифагора, круг — прекраснейшая из фигур. В трехмерном пространстве окружность превращается в сферу, такую же идеальную, космическую и прекрасную, как и круг.
Сфера по-древнегречески означает «мяч». Сфера представляет собой поверхность, образованную бесконечным множеством точек, равноудаленных от центра фигуры. Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.
Части шара
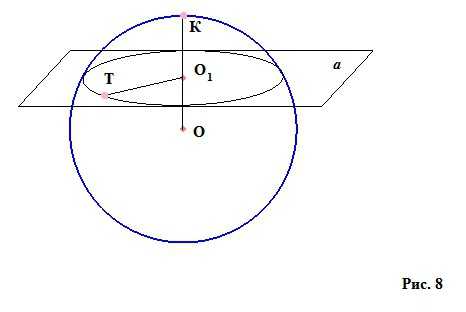
Если отсечь от сферы при помощи некоторой плоскости «кусочек» (рисунок 8), то он будет называться сферическим или шаровым сегментом. У него будет высота — перпендикуляр из центра секущей плоскости до сферической поверхности О 1 К. Точка К на сферической поверхности, в которую приходит высота, называется вершиной сферического сегмента. А малый круг с радиусом О 1 Т (в данном случае, согласно с рисунком, плоскость не прошла через центр сферы, но если сечение будет проходить через центр, то круг сечения будет большим), образованный при отсечении шарового сегмента, будет называться основанием нашего кусочка шара — сферического сегмента.
Если соединить каждую точку основания сферического сегмента с центром сферы, мы получим фигуру под названием «шаровой сектор».
Если через сферу проходят две плоскости, которые между собой параллельны, то та часть сферы, которая заключена между ними, называется шаровым слоем (рисунок 9, где изображена сфера с двумя плоскостями и отдельно — шаровой слой).
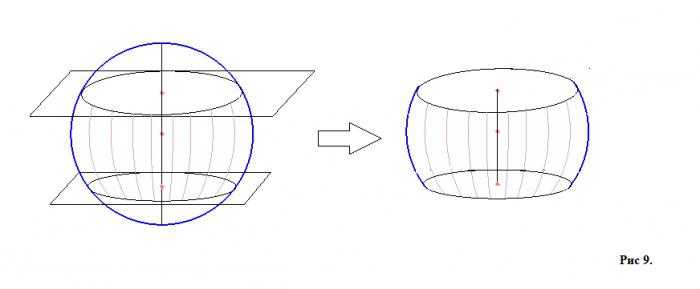
Поверхность (выделенная часть на рисунке 9 справа) этой части сферы называется поясом (снова для лучшего понимания можно провести аналогию с земным шаром, а именно с его климатическими поясами — арктическими, тропическими, умеренными и т. д.), а круги сечения будут основаниями шарового слоя. Высота слоя — часть диаметра, проведённого перпендикулярно к секущим плоскостям из центров оснований. Существует также понятие шаровой сферы. Она образуется в том случае, когда плоскости, которые параллельны друг другу, не пересекают сферу, а касаются ее в одной точке каждая.
Формулы исчисления объёма шара и площади его поверхности
Шар образуется при вращении вокруг неподвижного диаметра полукруга или круга. Для вычислений разных параметров данного объекта понадобится не так уж много данных.
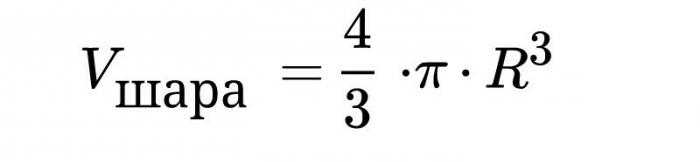
Объем шара, формула для исчисления которого указана выше, выведен посредством интегрирования. Разберемся по пунктам.
Рассматриваем круг в двумерной плоскости, ведь, как было сказано выше, именно круг лежит в основе построения шара. Используем лишь его четвертую часть (рисунок 10).
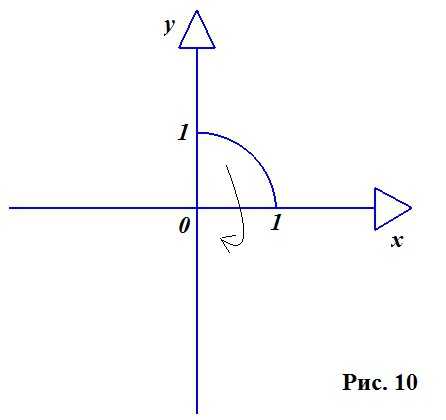
Берем круг с единичным радиусом и центром в начале координат. Уравнение такого круга выглядит следующим образом: Х 2 + У 2 = R 2 . Выражаем отсюда У: У 2 = R 2 — Х 2 .
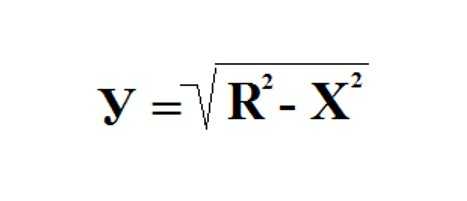
Обязательно отметим, что полученная функция неотрицательная, непрерывная и убывающая на отрезке Х (0; R), ведь значение Х в том случае, когда мы рассматриваем четверть круга, лежит от нуля до значения радиуса, то есть до единицы.
Следующее, что мы делаем, это вращаем нашу четверть круга вокруг оси абсцисс. В результате мы получим полушар. Чтобы определить его объём, прибегнем к методам интегрирования.
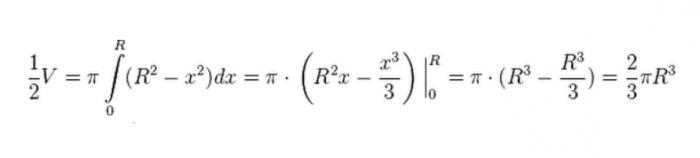
Так как это объём лишь полушара, увеличиваем результат в два раза, откуда получаем, что объем шара равен:
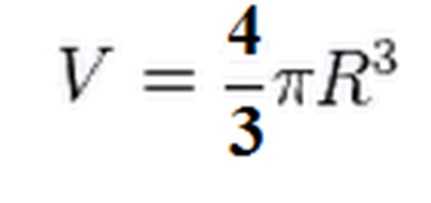
Формулы для нахождения объема шарового сегмента
Пояснения:
- В формулах ниже используется радиус шара (R) или радиус основания сегмента (r). Поэтому, если изначально дан их диаметр (d), то чтобы найти требуемый радиус, нужно соответствующий диаметр разделить на два.
- Число π округленно равняется до 3,14.
Чтобы найти объем (V) сегмента шара, необходимо знать радиус шара и высоту сегмента.
Через радиус основания сегмента и его высоту
Вычислить объем (V) шарового сегмента можно, зная его высоту и радиус основания (круга).
Данная формула получена следующим образом:
Радиус шара можно выразить через радиус основания сегмента и его высоту:
Таким образом, заменив R в первой формуле для расчета объема на выражение выше, получаем:
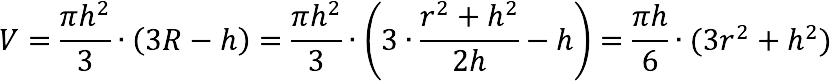
Касательная, касательная плоскость к сфере и их свойства
Определение.
Касательная к сфере
— это прямая, которая касается сферы только в одной точке.
Определение.
Касательная плоскость к сфере
— это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение.
Сегмент шара
— это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента
называют круг, который образовался в месте сечения. Высотой сегмента
h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула.
Площадь внешней поверхности сегмента сферы
с высотой h
через радиус сферы R:
S = 2π
Rh
где V – искомый объем шара
, π – 3,14 , R – радиус.
Таким образом, при радиусе 10 сантиметров объем шара
равен:
В геометрии шар
определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара. Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.
С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится вычислять объем шара
. Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары. С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет вычислен
их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.
В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение. Следует заметить, что при их расчете конструкторам требуется найти объем шара
(а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки. Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.
Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений. В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.
Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы. Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.
Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка
Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий. Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются
Прежде чем начать изучать понятие шара, что такое объём шара, рассматривать формулы исчисления его параметров, необходимо вспомнить о понятии круга, изучаемом ранее в курсе геометрии. Ведь большинство действий в трехмерном пространстве аналогичны или вытекают из двумерной геометрии с поправкой на появление третьей координаты и третьей степени.
Шар
Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.
Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.
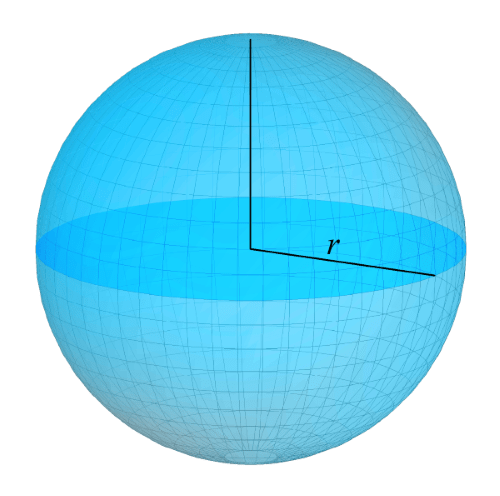Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.
В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.
Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.
Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.
Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.
Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.
Площади сферы и ее частей. Объемы шара и его частей
В следующей таблице приведены формулы для расчета объема сферы и объемов ее частей, а также площади сферы и площадей ее частей.
| Фигура | Рисунок | Формула | Описание |
| Прохладный | S = 4πr2,
где |
Диапазон пуль | |
| Мяч | где r — радиус шара. |
Объем мяча | |
| Сферический ремень | S = 2пр,
где Площадь сферического пояса не зависит от радиусов r1 и r2 ! |
Площадь сферического пояса | |
| Мяч команда | где r1, r2 — радиусы оснований сферического слоя, h – высота сферического слоя. |
Объем сферического слоя | |
| Сферический сегмент | S = 2пр,
где |
Площадь сферического сегмента | |
| Шаровой сегмент | где r — радиус шара, h – высота сферического сегмента. |
Объем сферического сегмента | |
| Сектор мяча | где r — радиус шара, h — высота сферического сектора. |
Объем сферического сектора |
| Прохладный |
|
Диапазон мяча: S = 4πr2, где |
| Мяч |
|
Объем мяча: где |
| Сферический ремень |
|
Площадь сферического пояса: S = 2пр, где Площадь сферического пояса не зависит от радиусов r1 и r2 ! |
| Мяч команда |
|
Объем шаровой кровати: где |
| Сферический сегмент |
|
Площадь сферического сегмента: S = 2пр, где |
| Шаровой сегмент |
|
Объем шарового сегмента: где |
| Сектор мяча |
|
Объем сектора сферы: где |
Решаем задачи вместе
Пример 1. Найти объём тела, образованного вращением вокруг оси
абсцисс () фигуры, ограниченной гиперболой
, осью абсцисс и прямыми
, .
Решение. Объём тела вращения найдём по формуле (1), в которой ,
а пределы интегрирования , . Применяем
. Постоянный множитель
выносим за знак интеграла. Получаем:
Пример 2. Найти объём шара радиуса R.
Решение. Рассмотрим шар как тело, получащееся при вращении вокруг оси абсцисс
полукруга радиуса R с центром в начале координат. Тогда в формуле (1) подынтегральная функция
запишется в виде ,
а пределами интегрирования служат -R и R. В вычислениях радиус R считается
константой (вместо него можно подставить любое значение для шара с любым радиусом). Применяем
. Следовательно,
Пример 3. Найти объём тела, образованного вращением вокруг оси
абсцисс () фигуры, заключённой между параболами
и
.
Решение. Представим искомый объём как разность объёмов тел, полученных вращением
вокруг оси абсцисс криволинейных трапеций и .
Объёмы этих тел найдём по формуле (1). В ней пределы интегрирования равны
и —
абсциссам точек B и D пересечения парабол. Эти точки и их абсциссы видны на графике.
Точно также — на графике — можно определить координаты точек пересечения линий из ваших задач. Только
для этого нужно построить график. Теперь можем найти объём тела, применяя
всё тот же табличный интеграл 7:
Пример 4. Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга (). Форму тора имеет, например, баранка).
Решение. Пусть круг вращается вокруг оси Ox (рис. 20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.
Уравнение окружности LBCD имеет вид
причём уравнение кривой BCD
а уравнение кривой BLD
Используя разность объёмов тел, получаем для объёма тора v выражение и
вычисляем интеграл:
Пример 5. Найти объём тела, образованного вращением вокруг оси
ординат () фигуры, ограниченной линиями
и
.
Решение. Представим искомый объём как разность объёмов тел, полученных вращением
вокруг оси ординат треугольника и
криволинейной трапеции .
Объёмы этих тел найдём по формуле (2). Пределами интегрирования служат
и —
ординаты точек O и B пересечения параболы и прямой, что видно на графике к этому примеру.
Таким образом, получаем объём тела:
Занимательные факты
Это интересно:
- У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
- Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
- Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.
Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара
, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади
применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма
может пригодиться и строительной бригаде, что делает ремонт
И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике
Но как быть, если не представляется возможным измерить объект?
Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара,
был Архимед
. Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.
Именно Архимед определил границы числа «пи»
и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.
Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.