Как найти площадь поверхности шара (сферы)

Трактовка значений

Это следует знать:

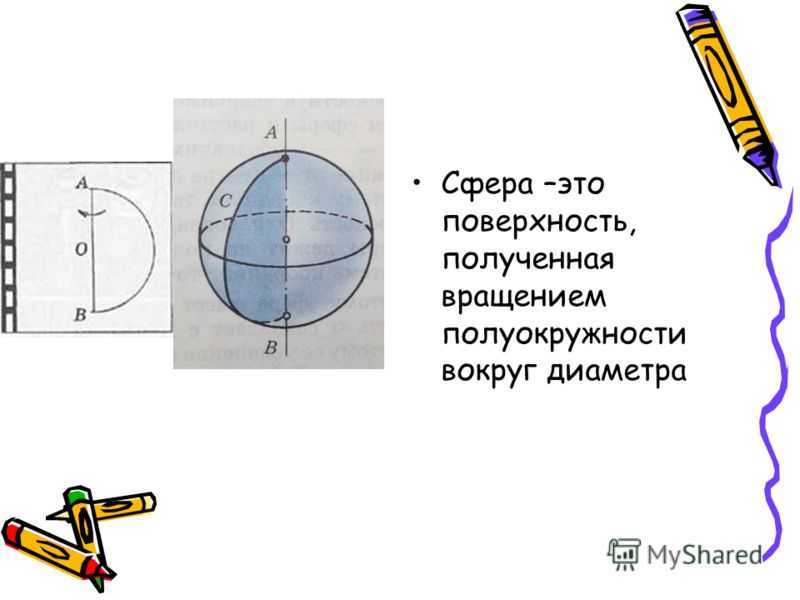
• Шар – это геометрический объект, который является результатом вращательных полукруговых движений вокруг центра. Каждая точка на поверхности сферы равноудалена от центра.
• Сфера не то же самое, что шар. Если это трехмерный объект и включает в себя внутреннее пространство, то сфера является лишь поверхностью этого объекта и имеет только собственную площадь. Иными словами, нельзя сказать, что сфера имеет такой-то объем, в отличие от шара.
• Число «пи» — это постоянное число, равное отношению длины окружности к ее диаметру. Сокращенно его обычно обозначают числом, равным 3,14. Но на самом деле после этих трех цифр идет больше тысячи!
• Радиус шара равен ½ диаметра. Точный диаметр можно рассчитать, используя несколько плоских и гладких предметов. Нужно просто зажать шарик между этими предметами, которые сдавливают шарик и располагаются перпендикулярно друг другу, а затем измерить получившийся диаметр.
• Квадратная степень обозначается как двойка и означает, что это число нужно умножить само на себя один раз. Если бы степень числа была в виде тройки, то надо было бы умножать само на себя дважды. Записав выражение на бумаге, можно понять, почему употребляется именно два и три, а не один и два.
• Объем — это значение, указывающее размер в пространстве, которое занимает объект. Объем шара зависит от его диаметра. Формула будет равна четырем третям, умноженным на число «пи» и снова умноженным на радиус.
• Площадь — это значение, указывающее размер поверхности объекта, но не внутреннего пространства.

Калькулятор

Сфера (шар) – замкнутая поверхность, геометрическое место точек равноудаленных от данной точки, являющейся центром сферы. Сфера является частным случаем эллипсоида, у которого все три полуоси одинаковые.

Отрезок, соединяющий центр сферы с ее точкой, а также его длина, называется радиусом; отрезок, соединяющий две точки шара – хордой; хорда, проходящая через центр сферы называется ее диаметром. Сечение сферы произвольной плоскостью есть круг.

У шара наименьшая площадь поверхности среди всех тел, замыкающих данный объем, и самый большой замкнутый объем при данной площади поверхности. По этой причине, сфера часто встречается в природе.

Площадь поверхности шара вычисляется по формуле

Поделиться в FacebookДобавить в TwitterДобавить в Telegram

Как найти площадь поверхности сегмента шара: формула, пример

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади шарового сегмента

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.

• Определение сегмента шара
• Формулы для нахождения площади сегмента шара
  • Площадь основания
  • Площадь сферической поверхности
  • Площадь полной поверхности
• Пример задачи

Определение сегмента шара

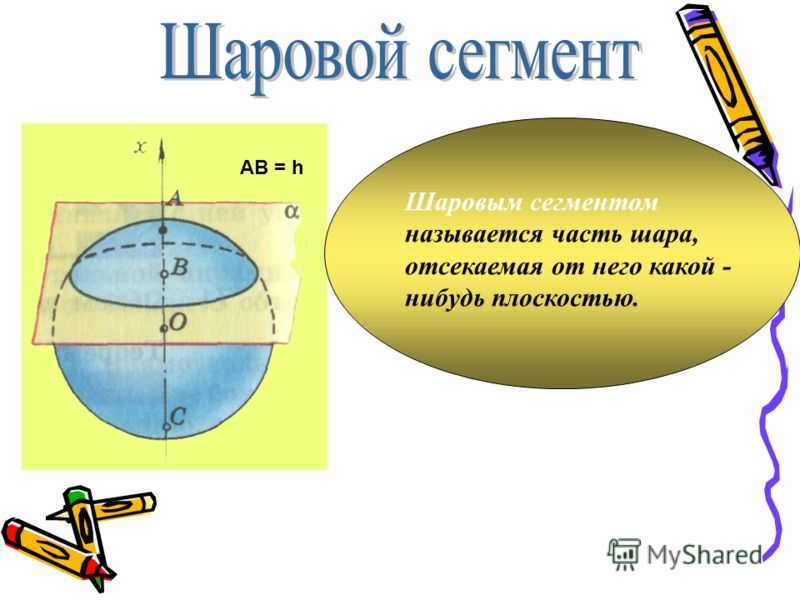
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью.

• R – радиус шара;
• r – радиус основания сегмента;
• h – высота сегмента; это длина перпендикуляра от центра его основания (точка O₂) до точки на поверхности шара.

Связь между радиусом основания сегмента, его высотой и радиусом шара:

Формулы для нахождения площади сегмента шара

Площадь основания

Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):

S_осн. = πr 2

Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.

Площадь сферической поверхности

Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.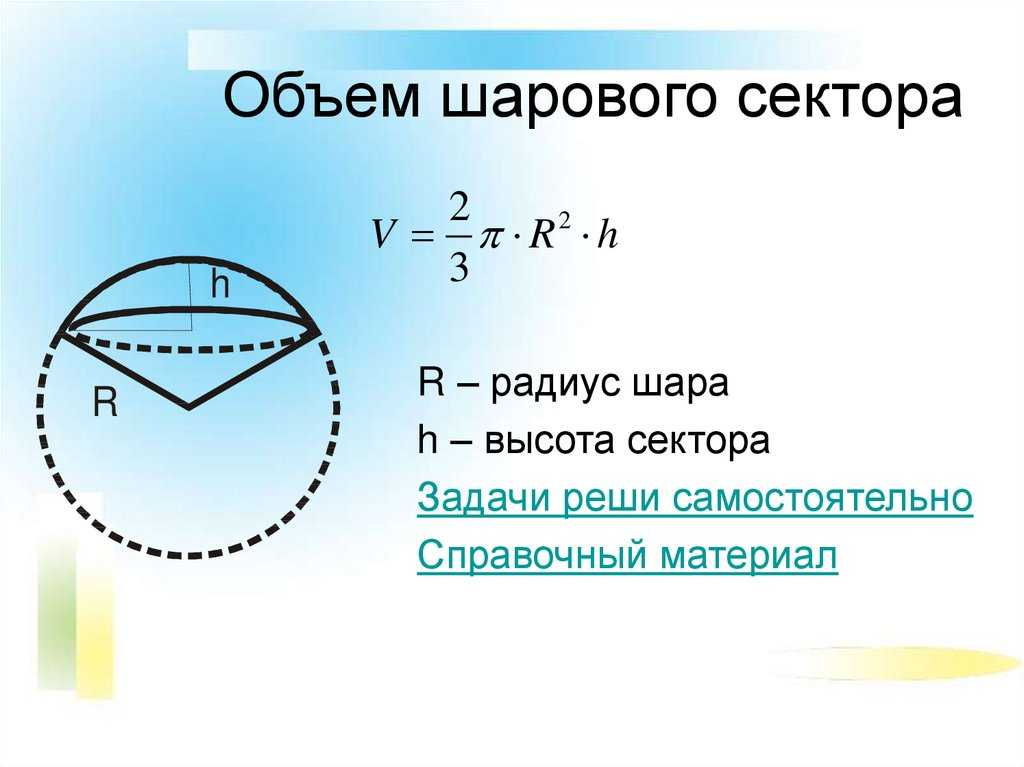

S_{сфер. пов.} = 2πRh

Площадь полной поверхности

Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.

S_полн. = S_осн. + S_{сфер. пов.} = π (2Rh + r 2)

Пример задачи

Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.

Решение

Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.

S_осн. = 3,14 ⋅ (4,7 см) 2 = 69,3626 см 2

S_{сфер. пов.} = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см 2

S_полн. = S_осн. + S _{сфер. пов.} = 69,3626 см 2 + 90,432 см 2 = 159,7946 см 2

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

В чем различие

Тогда возникает вопрос, а чем отличается шар от сферы кроме определения? Дело в том, что различия шара и сферы куда более размыты, нежели различия круга и окружности. Сфера так же имеет объем и площадь поверхности.

Пожалуй, кроме определения, разница заключается в том, что в задачах никогда не находят объем сферы. Как правило, ищут объем шара. Это не значит, что у сферы нет объема. Это трехмерная фигура, поэтому объем у нее есть.

Просто проводится аналогия с окружностью, у которой нет площади. Это не правило, но скорее традиция, которую нужно запомнить: в геометрии не приветствуется формулировка объем сферы.

Еще одно отличие, которое можно считать более или менее значимым: секущая плоскость сферы: окружность, которая не имеет внутреннего пространства, но имеет длину. Секущая плоскость шара: круг, который имеет площадь и не имеет длины окружности. Поэтому стоит быть аккуратным в формулировках задачи, чтобы не было ошибок из-за подобных мелочей.

Калькуляторстоимости

Решение контрольной от 300 рублей *

* Точная стоимость будет определена после загрузки задания для исполнителя

Привет.Я Настя из ИвГУ (это город Иваново).

«Сегодня от своего лица хочу поблагодарить этот сайт за помощь мне с учебой. Здесь я пользовалась не только материалами, но и нашла преподавателей которые решали мне задачи.

Если тебе нужно что-то сделать в универе, я сама рекомендую. А также пользуйся моей ссылкой и получай 300 руб. на счёт при регистрации.»

Пунктуация и орфография автора сохранены

Получить 300 руб. от Насти

Webmath — преподаватель со стажем более 5 лет выполнит учебную работу за вас

Договор

Строго соблюдаем условия договора от заказа до защиты

Наши авторы

10 000+ преподавателей и научных сотрудников

Гарантии

Точное соответствие ТЗ с бесплатными доработками

АкцияСкидка 25% на вашу работу + речь в подарок. Дарим вам 100₽ на первый заказ!

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются
, а в плоскости пересечения образуется круг.

Важные измерения

Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.

Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:

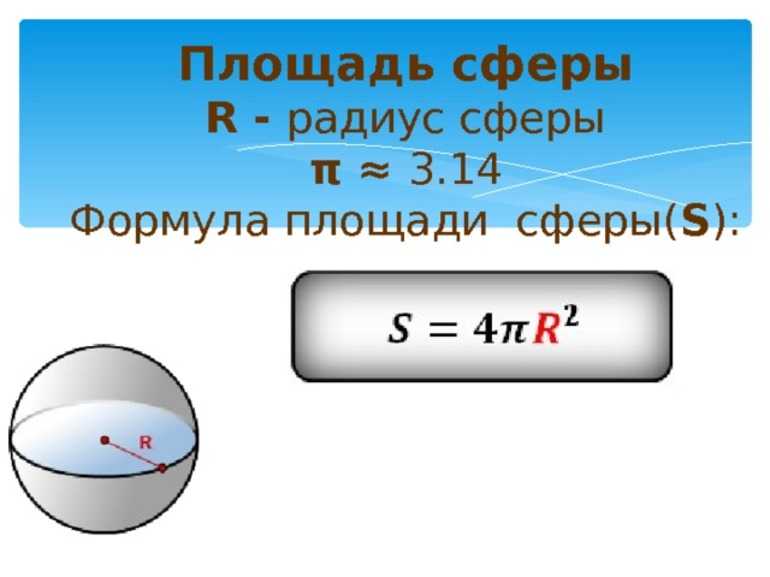
1. S = 4 * 3,14 * 10²;
2. S мяча равна ≈ 1256 см².

Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.

Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).

Объем шара

Формула для вычисления объема шара имеет вид:

где R — радиус шара.

Если нужно найти объем шарового сегмента — воспользуйтесь формулой:

V сег =πh 2 (R-h/3), h — высота шарового сегмента.

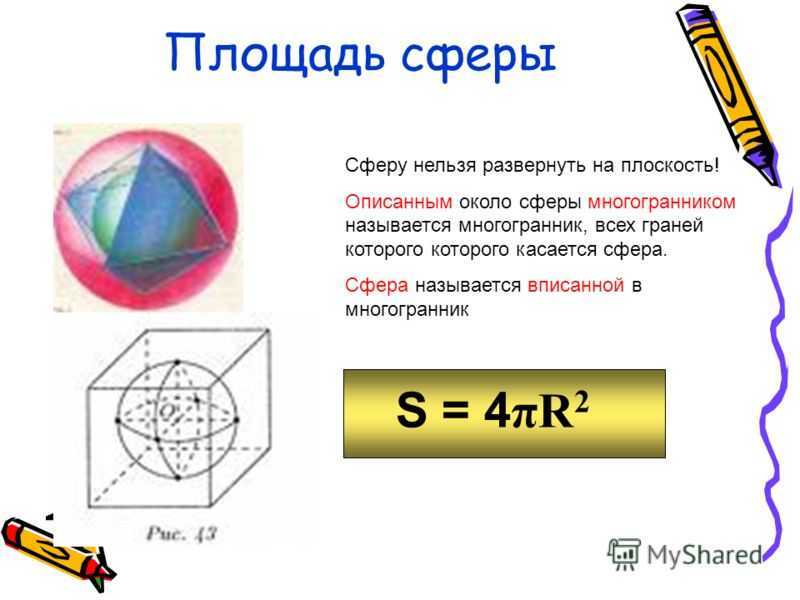
Площадь поверхности шара или сферы

Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):

где R — радиус сферы.

Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»

Определение.

Сфера
поверхность шара
центром сферы

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар
центром шара

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.
Радиус сферы (шара)
(R) — это расстояние от центра сферы (шара) O
к любой точке сферы (поверхности шара).

Определение.
Диаметр сферы (шара)
(D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула.
Объём шара
:

V =	4	π R 3 =	1	π D 3
3	6

Формула.
Площадь поверхности сферы
через радиус или диаметр:

S = 4π
R 2 = π
D 2

Одиннадцать свойств

В своей книге «Геометрия и воображение» Дэвид Гилберт и Стефан Кон-Фоссен описывают свойства сферы и обсуждают, однозначны ли такие характеристики. Несколько пунктов справедливы и для плоскости, которую можно представить как шар с бесконечным радиусом:

1. Точки на сфере находятся на одинаковом расстоянии от одной фиксированной, называемой центром. Можно сделать единственный вывод: это обычное определение и оно однозначно. А также отношение расстояний между двумя фиксированными точками является постоянным. И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
2. Контуры и плоские участки сферы являются кругами. Это однозначное свойство, которое определяет шар.
3. Сфера имеет постоянную ширину и обхват. Ширина поверхности — это расстояние между парами параллельных касательных плоскостей. Множество других замкнутых выпуклых поверхностей имеют постоянную ширину, например, тело Мейснера. Обхват поверхности — это окружность границы её ортогональной проекции на плоскость. Каждое из этих свойств подразумевает другое.
4. Все точки сферы омбилические. В любой точке поверхности вектор нормали расположен под прямым углом к ней, поскольку шар — это линии, выходящие из его центра. Пересечение плоскости, которая содержит нормаль с поверхностью, сформирует кривую — нормальное сечение. Любая замкнутая поверхность будет иметь как минимум четыре точки, называемых омбилическими. Для сферы кривизны всех нормальных сечений одинаковы, поэтому омбилической будет каждая точка.
5. У шара нет центра поверхности. Например, два центра, соответствующие минимальной и максимальной секционной кривизне, называются фокальными точками, а совокупность всех таких точек образует одноимённую поверхность. И только у шара она преобразуется в единую точку.
6. Все геодезические сферы являются замкнутыми кривыми. Для этой фигуры они большие круги. Многие другие поверхности разделяют это свойство.
7. Имеет наименьшую площадь при наибольшем объёме. Это определяет шар однозначно. Например, мыльный пузырь: его окружает фиксированный объём, поверхностное натяжение минимизирует площадь его поверхности для такого объёма. Конечно, пузырь не будет идеальным шаром, поскольку внешние силы, такие как гравитация, будут искажать его форму.
8. Сфера — единственная вложенная поверхность, у которой нет границы или сингулярностей с постоянной положительной средней кривизной.
9. Сфера имеет наименьшую общую среднюю кривизну среди всех выпуклых тел с заданной площадью поверхности.
10. Шар имеет постоянную гауссову кривизну. Это внутреннее свойство, которое определяется путём измерения длины и углов и не зависит от того, как поверхность встроена в пространство.

Резюме

И шар, и сфера являются абстрактными геометрическими объектами (геометрическими фигурами), задаваемыми через некоторое геометрическое место точек пространства — например, с помощью понятия центра шара/сферы и радиуса шара/сферы. Однако только шар является полноценным геометрическим телом, поскольку включает в себя не только описание ограничивающей его поверхности, но и всей той части пространства, что в себя эта поверхность заключает. С такой точки зрения сфера — лишь внешняя абстрактная граница (поверхность) задаваемого в пространстве шара.

Символ шара-глобальность шара Земли. Символ будущего, он отличается от креста тем, что последний олицетворяет собой страдание и человеческую смерть. В Древнем Египте впервые пришли к заключению, что земля шарообразна. Это предположение послужило основой для многочисленных размышлений о бессмертии земли и возможности бессмертия населяющих ее живых организмах.

Данная точка (О) называется центром сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы (R-радиус сферы). Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Очевидно, что диаметр сферы равен 2R.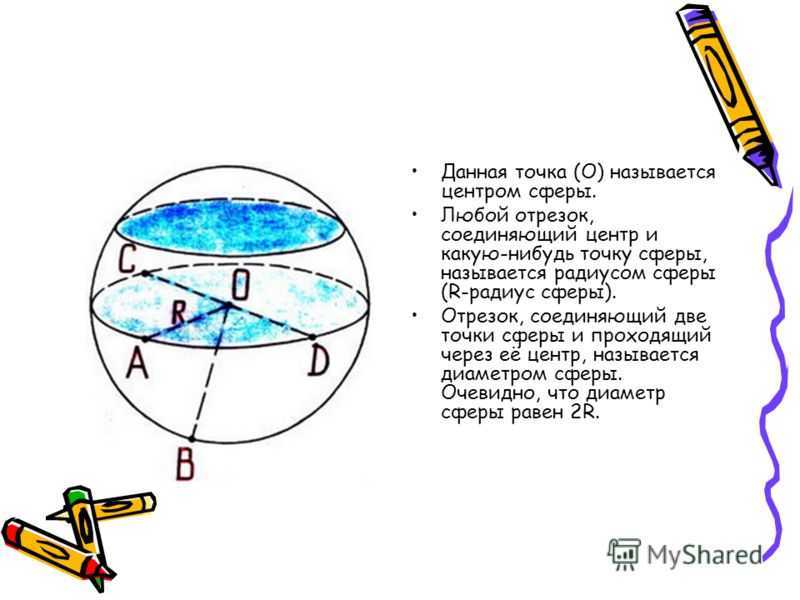

Определение шара Шар – это тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки (или фигура, ограниченная сферой). Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Шар

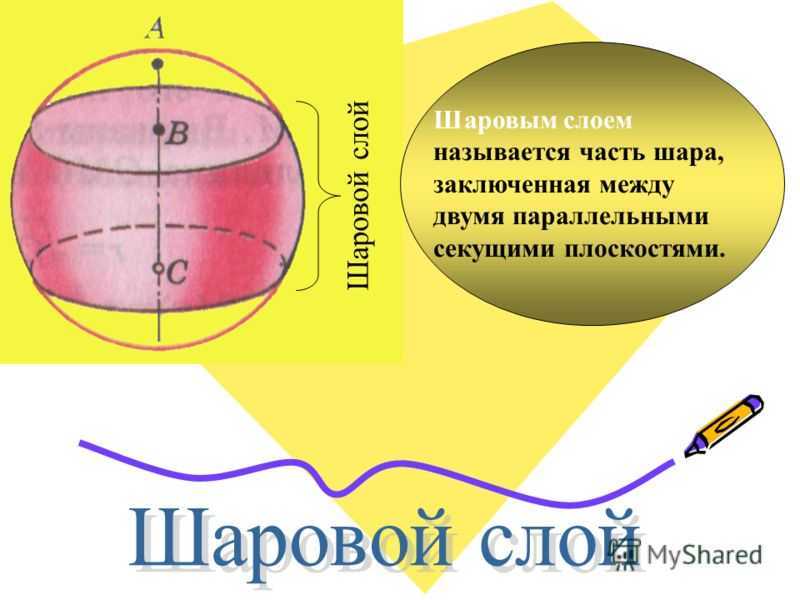
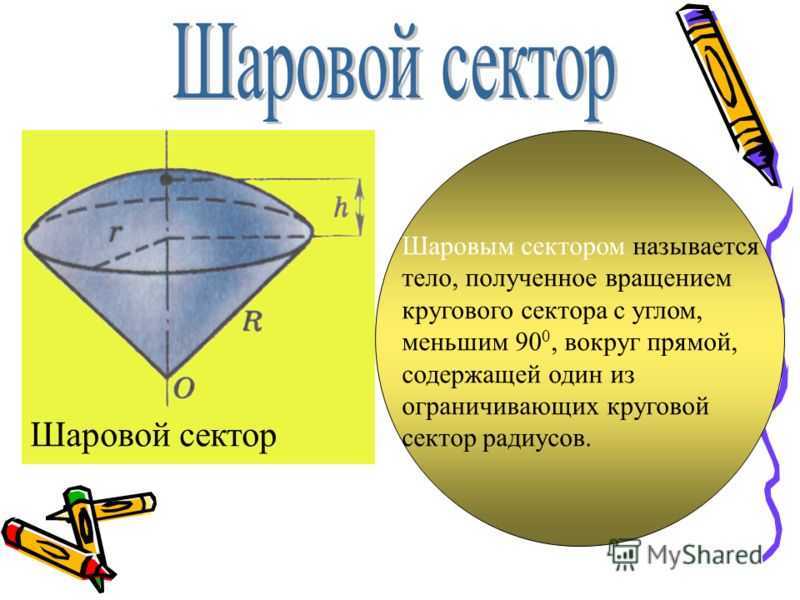
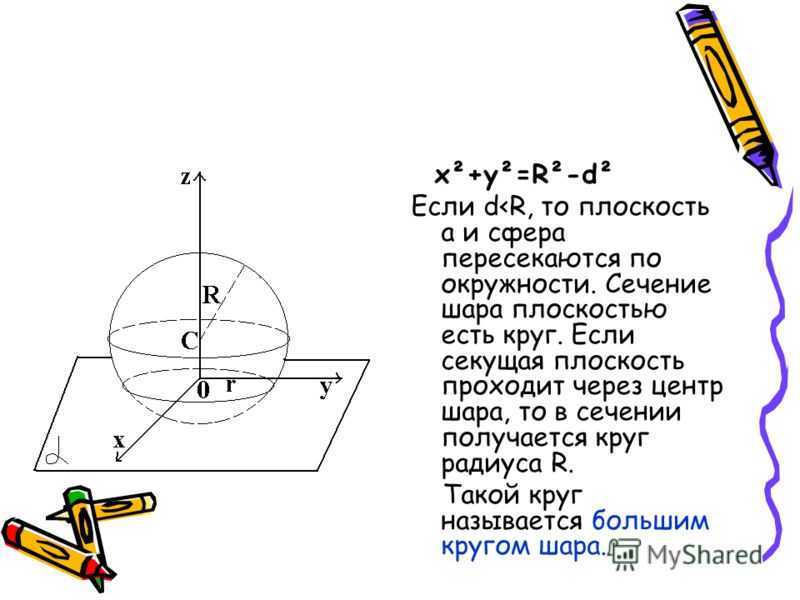
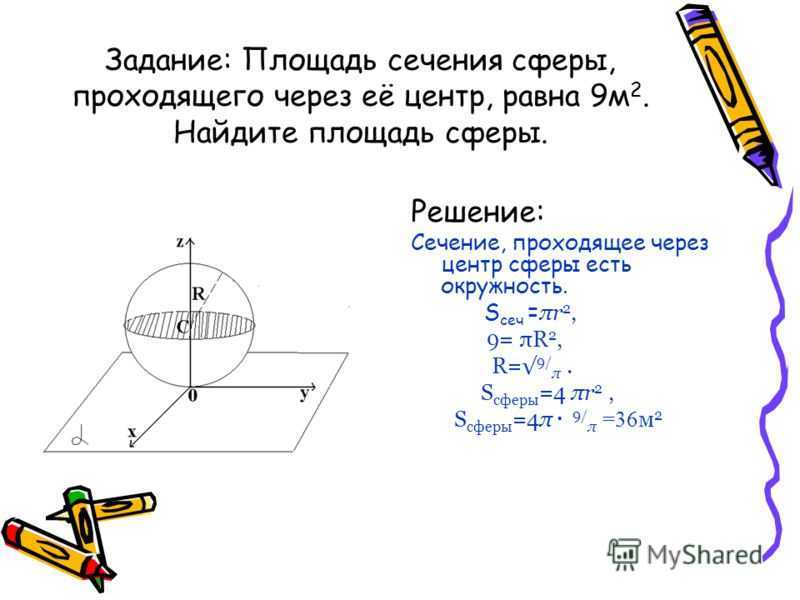
Плоскость,проходящая через центр шара,называется диаметральной плоскостью.Плоскость,проходящая через центр шара,называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью.Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью.

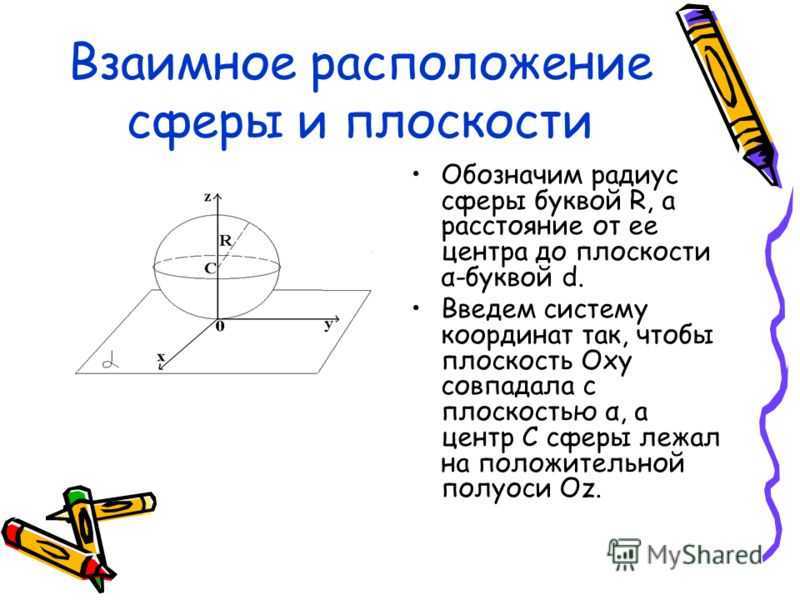
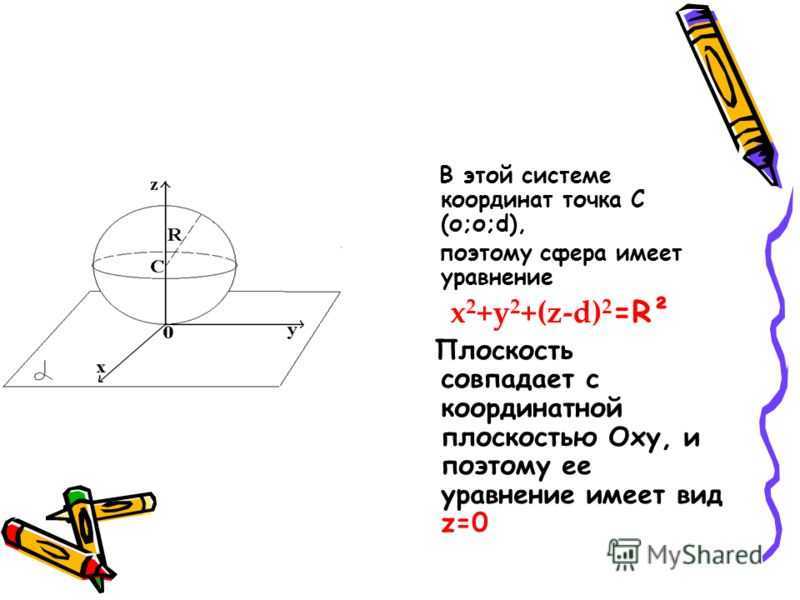
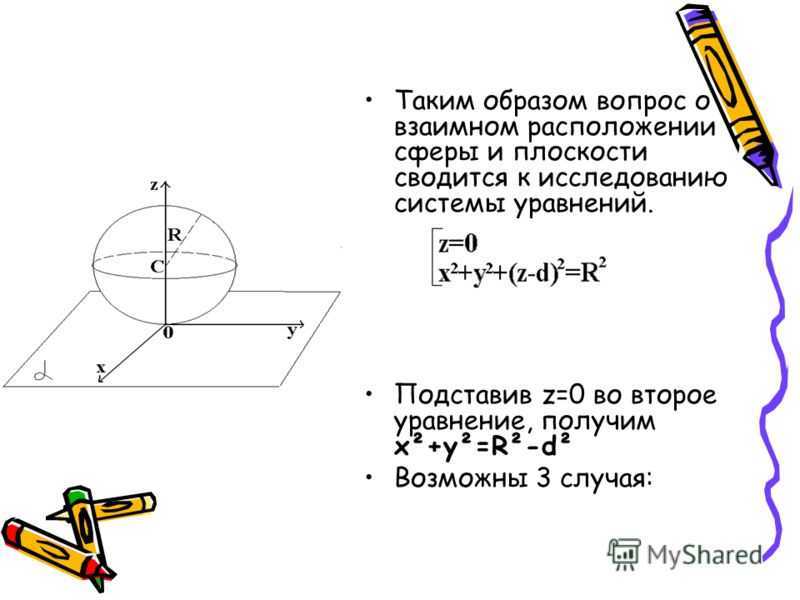
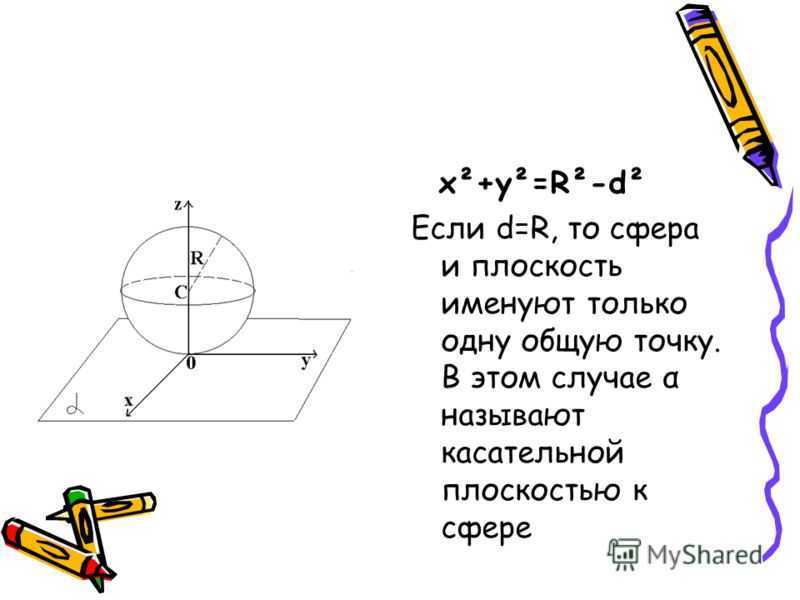
X²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.
R, то сфера и плоскость не имеют общих точек.»>
R, то сфера и плоскость не имеют общих точек.»>
R, то сфера и плоскость не имеют общих точек.» title=»x²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.»>
title=»x²+y²=R²-d² Если d>R, то сфера и плоскость не имеют общих точек.»>

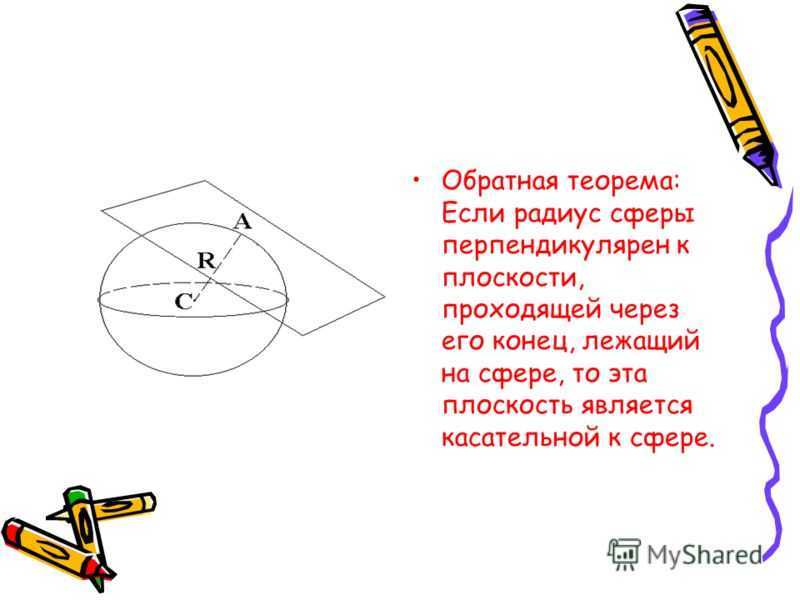
Касательная плоскость к сфере касательной плоскостью к сфереПлоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, точкой касания А плоскости и сферы.а их общая точка называется точкой касания А плоскости и сферы.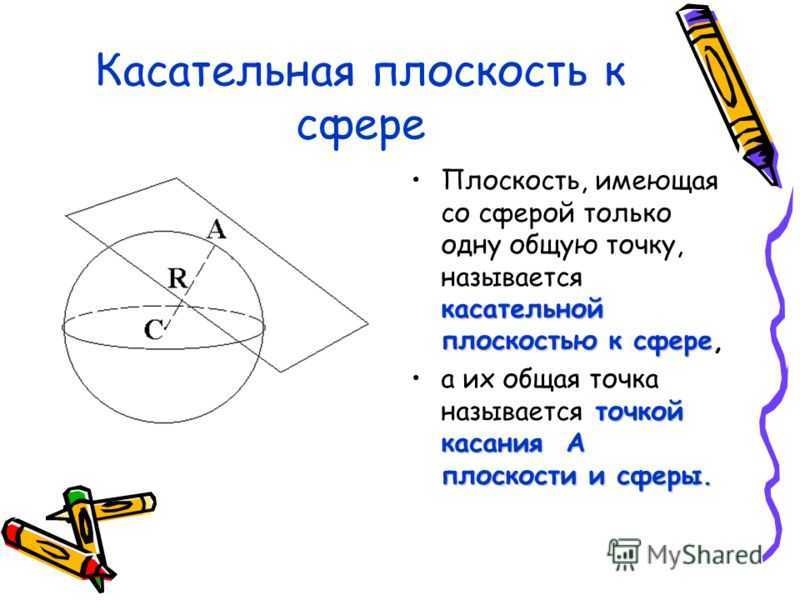

Теорема: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Доказательство: Рассмотрим плоскость α, касающуюся сферы с центром О в точке А. Докажем, что ОА перпендикулярен α. Предположим, что это не так. Тогда радиус ОА является наклонной к плоскости α, и, следовательно расстояние от центра сферы до плоскости меньше радиуса сферы. Поэтому сфера и плоскость пересекаются по окружности. Это противоречит тому, что-касательная, т.е. сфера и плоскость имеют только одну общую точку. Полученное противоречие доказывает, что ОА перпендикулярен α.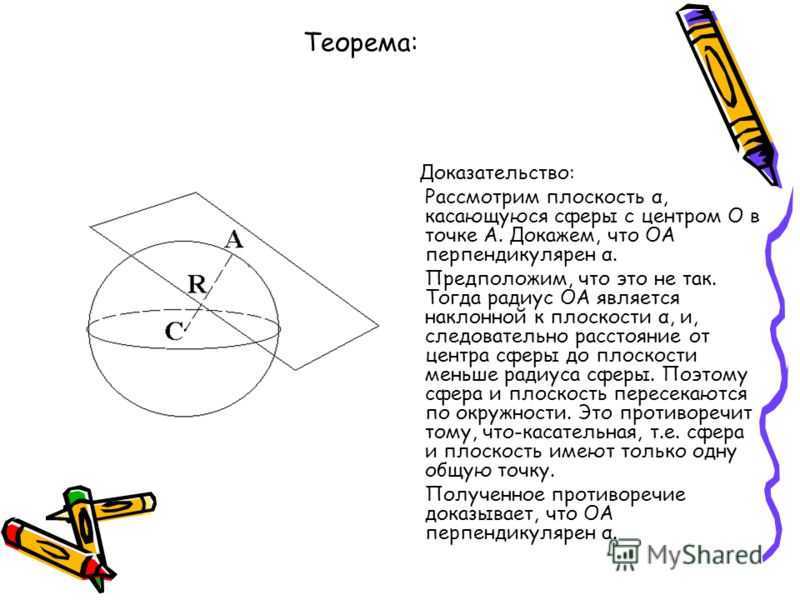

Определение.

Сфераповерхность шарацентром сферы

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шарцентром шара

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение.Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула.Объём шара:

V =	4	π R 3 =	1	π D 3
3	6

Формула.Площадь поверхности сферы через радиус или диаметр:

S = 4π
R 2 = π
D 2

Теория

Ликбез: Поверхность шара — сфера.

Площадь поверхности шара через радиус

Чему равна площадь поверхности шара Sпов, если его радиус r:

Sпов = 4⋅π⋅r² , где π ≈ 3.14…

Пример

Для примера посчитаем какая площадь поверхности у шара, если его радиус r = 3 см:

Sпов = 4 ⋅ 3.14 ⋅ 3² = 12.56 ⋅ 9 = 113.04 см²

Площадь поверхности шара через диаметр

Чему равна площадь поверхности шара Sпов, если его диаметр d?

Sпов = π⋅d² , где π ≈ 3.14…

Пример

Для примера посчитаем какая площадь поверхности у шара, если его диаметр d = 6 см:

Sпов = 3.14 ⋅ 6² = 3.14 ⋅ 36 = 113.04 см²

Пример

Для примера посчитаем чему равна площадь поверхности шара, имеющего длину окружности L = 10 см:

Sпов = 10² ⁄ 3.14 ≈ 31.85 см²

Занимательные факты

Это интересно:

1. У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
2. Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
3. Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.

Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.

Как найти площадь сферы

Запомните!

Формула площади сферы:

S = 4π
R 2

Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа .
Зная определение степени,
можно записать формулу площади сферы следующим образом. S = 4π
R 2 =
4π
R · R;

Закрепим полученные знания и решим задачу на площадь сферы.

Зубарева 6 класс. Номер 692(а)

Условие задачи:

• Вычислите площадь сферы, если её радиус равен
  
  1 =
  3 ·
  =
  =
  / (4 · 3)
  = ) =
  = ) =
  = =
  =

  88

  = 1

• R 3 = 1
• R = 1 м

Важно!

Уважаемые родители!

При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.

В 6 классе при решении такой задачи используйте метод перебора.

Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.

Определение.

Сфера
поверхность шара
центром сферы

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар
центром шара

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.
Радиус сферы (шара)
(R) — это расстояние от центра сферы (шара) O
к любой точке сферы (поверхности шара).

Определение.
Диаметр сферы (шара)
(D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула.
Объём шара
:

V =	4	π R 3 =	1	π D 3
3	6

Формула.
Площадь поверхности сферы
через радиус или диаметр:

S = 4π
R 2 = π
D 2