Шар, вписанный в цилиндр

Расчет объема шара и цилиндра

Объем шара

Объем шара можно вычислить по формуле:

V = 4/3 × π × r³,

где r – радиус шара, π ≈ 3,14.

Пример: Если радиус шара равен 5 см, то его объем будет:

V = 4/3 × 3,14 × 5³ ≈ 523,6 см³.

Объем цилиндра

Объем цилиндра можно найти по формуле:

V = π × r² × h,

где r – радиус основания цилиндра, h – его высота, π ≈ 3,14.

Пример: Если радиус основания цилиндра равен 6 см, а его высота 10 см, то его объем будет:

V = 3,14 × 6² × 10 ≈ 1130,4 см³.

Сравнение объемов шара и цилиндра

Если радиус шара и основания цилиндра равны, то объемы этих фигур будут отличаться в 2 раза. Если же высота цилиндра составит половину от радиуса его основания, то объемы шара и цилиндра будут равны при условии, что радиусы этих фигур также равны.

Сфера, шар, сегмент и сектор. Формулы и свойства

Определение.

Сфераповерхность шарацентром сферы

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шарцентром шара

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Объём шараПлощадь поверхности сферы

S = 4πR2 = πD2

Уравнение сферы

Уравнение сферы с радиусом R и центром в начале декартовой системе координат

x2 + y2 + z2 = R2

Уравнение сферы с радиусом R и центром в точке с координатами (x, y, z) в декартовой системе координат

(x — x)2 + (y — y)2 + (z — z)2 = R2

Параметрическое уравнение сферы с центром в точке

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

d < R

m < R

малая окружностьмалый круг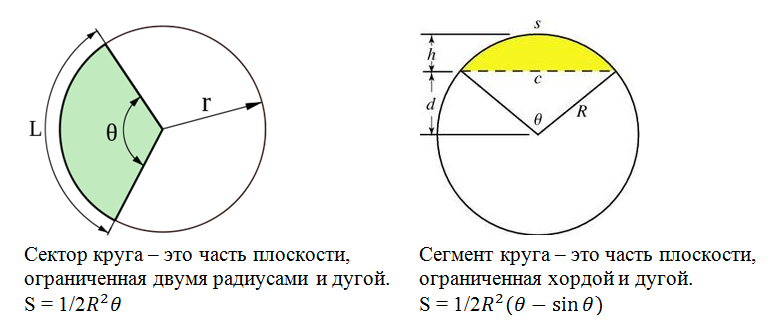

r = √R2 — m2,

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Сегмент шараОсновой сегментаВысотой сегментаПлощадь внешней поверхности сегмента сферы

S = 2πRh

Объём сегмента сферыСрез шараСекторомПлощадь поверхности сектора₁

S = πR(2h + √2hR — h2)

Объём сектора₁

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения.

Концентрическими сферами

Как вычислить радиус вписанного шара?

Формула радиуса вписанного шара

Для вычисления радиуса вписанного шара в цилиндр с известной высотой h и радиусом основания R применяется следующая формула:

Знак √ обозначает извлечение квадратного корня, а R и h — известные значения радиуса и высоты.

Пример вычисления радиуса вписанного шара

Для примера возьмем цилиндр с высотой 10 и радиусом основания 4. Вычислим радиус вписанного шара:

1. Запишем известные значения: R = 4, h = 10
2. Подставим значения в формулу: r = √(42 + 102) / 2 ≈ 5,9
3. Ответ: радиус вписанного шара ≈ 5,9

Таким образом, радиус вписанного шара в цилиндр с высотой 10 и радиусом основания 4 равен примерно 5,9.

Пирамида, вписанная в шар

Шар на­зы­ва­ют опи­сан­ным около пи­ра­ми­ды, если все вер­ши­ны пи­ра­ми­ды при­над­ле­жат по­верх­но­сти шара. Пи­ра­ми­ду в этом слу­чае на­зы­ва­ют впи­сан­ной в шар (рис. 1).

Рис. 1. Пи­ра­ми­да, впи­сан­ная в шар	Рис. 2. Пи­ра­ми­да, впи­сан­ная в шар

Неслож­но за­ме­тить, что вер­ши­ны ос­но­ва­ния пи­ра­ми­ды лежат в одной плос­ко­сти, зна­чит, они долж­ны при­над­ле­жать одной окруж­но­сти опи­сан­но­го шара. Таким об­ра­зом, необ­хо­ди­мым усло­ви­ем для того, чтобы впи­сать пи­ра­ми­ду в шар, яв­ля­ет­ся то, что мно­го­уголь­ник ос­но­ва­ния яв­ля­ет­ся впи­сан­ным (рис. 2).

До­ка­жем, что это яв­ля­ет­ся также и до­ста­точ­ным усло­ви­ем.

Формулы для нахождения площади вписанного шара

Формула Пикера

При вписанном шаре диаметр, равный стороне правильного многогранника, можно найти с помощью формулы Пикера:

где — длина стороны многогранника, — количество граней.

Формула Эйлера

Для любой трехмерной фигуры, включая цилиндр со вписанным шаром, существует формула Эйлера:

где — количество вершин, — количество ребер, — количество граней.

Для цилиндра с вписанным шаром вершины и ребра присутствуют только в основаниях цилиндра, поэтому мы можем упростить формулу:

Таким образом, формула Эйлера для цилиндра с вписанным шаром будет иметь вид:

Формула Герона

Для нахождения площади грани многогранника можно использовать формулу Герона:

где , , — длины сторон грани, — полупериметр грани.

Общая площадь цилиндра с вписанным шаром будет равна сумме площадей всех граней, а площадь вписанного шара можно найти по формуле:

где — диаметр вписанного шара, — радиус шара.

Решаем задачи вместе

Пример 1. Найти объём тела, образованного вращением вокруг оси
абсцисс () фигуры, ограниченной гиперболой
, осью абсцисс и прямыми
, .

Решение. Объём тела вращения найдём по формуле (1), в которой ,
а пределы интегрирования , . Применяем
. Постоянный множитель
выносим за знак интеграла. Получаем:

Пример 2. Найти объём шара радиуса R.

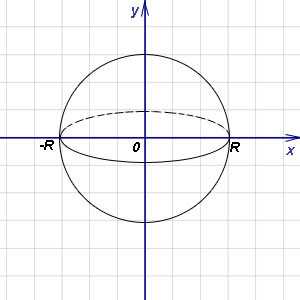
Решение. Рассмотрим шар как тело, получащееся при вращении вокруг оси абсцисс
полукруга радиуса R с центром в начале координат. Тогда в формуле (1) подынтегральная функция
запишется в виде ,
а пределами интегрирования служат -R и R. В вычислениях радиус R считается
константой (вместо него можно подставить любое значение для шара с любым радиусом). Применяем
. Следовательно,

Пример 3. Найти объём тела, образованного вращением вокруг оси
абсцисс () фигуры, заключённой между параболами
и
.

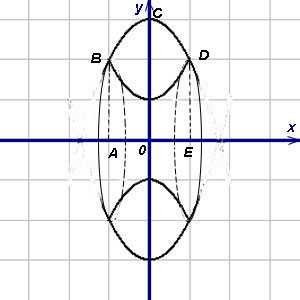
Решение. Представим искомый объём как разность объёмов тел, полученных вращением
вокруг оси абсцисс криволинейных трапеций и .
Объёмы этих тел найдём по формуле (1). В ней пределы интегрирования равны

и —
абсциссам точек B и D пересечения парабол. Эти точки и их абсциссы видны на графике.
Точно также — на графике — можно определить координаты точек пересечения линий из ваших задач. Только
для этого нужно построить график. Теперь можем найти объём тела, применяя
всё тот же табличный интеграл 7:

Пример 4. Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга (). Форму тора имеет, например, баранка).

Решение. Пусть круг вращается вокруг оси Ox (рис. 20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.

Уравнение окружности LBCD имеет вид

причём уравнение кривой BCD

а уравнение кривой BLD

Используя разность объёмов тел, получаем для объёма тора v выражение и
вычисляем интеграл:

Пример 5. Найти объём тела, образованного вращением вокруг оси
ординат () фигуры, ограниченной линиями
и
.

Решение. Представим искомый объём как разность объёмов тел, полученных вращением
вокруг оси ординат треугольника и
криволинейной трапеции .
Объёмы этих тел найдём по формуле (2). Пределами интегрирования служат

и —
ординаты точек O и B пересечения параболы и прямой, что видно на графике к этому примеру.
Таким образом, получаем объём тела:

Нахождение радиуса сферы/шара

Возле любого цилиндра можно описать шар (или, другими словами, вписать цилиндр в шар), но только один.

• Центром такой сферы будет центр цилиндра, в нашем случае это точка О.
• О1 и О2 — центры основания цилиндра.
• O1O2 – высота цилиндра (h).
• OO1 = OO2 = h/2.

Видно, что радиус описанной сферы (OE), половина высоты цилиндра (OO1) и радиус основания (O1E) образуют прямоугольный треугольник OO1E.

Используя теорему Пифагора, мы можем найти гипотенузу этого треугольника, которая также является радиусом сферы, описанной вокруг данного цилиндра:

Зная радиус сферы, можно вычислить площадь (S) поверхности и объем (V) сферы, ограниченной сферой:

• S = 4 ⋅ π ⋅ R2
• S = 4/3 ⋅ π ⋅ R3

Примечание: π округляется до 3,14.

Применение формулы

Рассмотрим на примере, как вычислить площадь круглого шара
, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.

Формула вычисления площади
применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.

Формула вычисления объёма
может пригодиться и строительной бригаде, что делает ремонт

И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике

Но как быть, если не представляется возможным измерить объект?
Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.

Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара,
был Архимед
. Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.

Именно Архимед определил границы числа «пи»
и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.

Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.

Шаровой сектор

Шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше полушара.

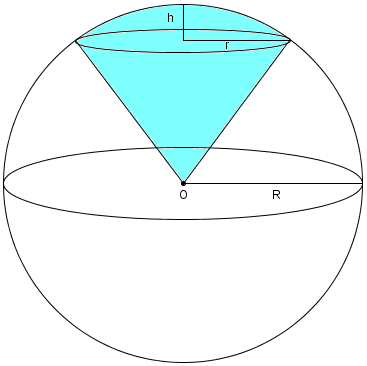
Поверхность шарового сектора складывается из кривых поверхностей шарового сегмента и конуса.

${S_{сектора}} = {S_{сегмента}} + {\operatorname{S} _{конуса}} $

${S_{сектора}} = 2\pi R{h} + \pi Rr$

${S_{сектора}} = \pi R\left( {2\left( {R — \sqrt {{R^2} — {r^2}} } \right) + r} \right)$

Объем шарового сектора равен объёму пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара.

\

Задача №3

Усло­вие: дана пра­виль­ная тре­уголь­ная приз­ма, сто­ро­на ос­но­ва­ния ко­то­рой равна 6. Из­вест­но, что в нее можно впи­сать шар и около нее можно опи­сать шар. Найти от­но­ше­ние их ра­ди­у­сов (рис. 12).

Рис. 12. Ил­лю­стра­ция к за­да­че 3

Ре­ше­ние

Нач­нем со впи­сан­но­го шара. Его ра­ди­ус сов­па­да­ет с ра­ди­у­сом окруж­но­сти, впи­сан­ной в тре­уголь­ник ос­но­ва­ния. Этот ра­ди­ус равен , то есть . Но тогда вы­со­та приз­мы равна .

Далее, центр опи­сан­но­го шара на­хо­дит­ся в се­ре­дине вы­со­ты, то есть рас­сто­я­ние от него до плос­ко­сти ос­но­ва­ния равно . Пусть центр этого шара , центр ос­но­ва­ния – . Тогда  (как ра­ди­ус опи­сан­ной окруж­но­сти, на­при­мер). И зна­чит,  по тео­ре­ме Пи­фа­го­ра.

Таким об­ра­зом, ис­ко­мое от­но­ше­ние равно .

Ответ: .

Сфера, вписанная в цилиндр

Определение 2. Сферой, вписанной в цилиндр, называется сфера, которая касается плоскостей обоих оснований цилиндра, причем каждая образующая цилиндра касается сферы (рис. 3).

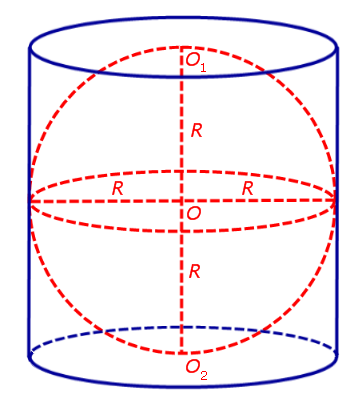
Рис.3

Определение 3. Если сфера вписана в цилиндр, то говорят, что цилиндр вписан около сферы.

Рисунок 3 показывает, что следующие два утверждения верны.

Утверждение 1. Вокруг любой сферы можно описать цилиндр.

Предложение 2. Шар можно вписать в цилиндр тогда и только тогда, когда высота цилиндра равна диаметру основания.

Комментарий. В случае, когда сферу можно вписать в цилиндр, радиус вписанной сферы равен радиусу основания цилиндра.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

AC^2+BC^2=AB^2

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике ABC с прямым углом C:

Для острого угла B: AC — противолежащий катет; ВС — соседняя ветвь.

Для острого угла A: BC — противолежащий катет; AC — соседняя нога.

1. Синус (sin) острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенс (tg) острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$сина$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$тга$	${√3}/{3}$	$1$	$√3$
$ctga$	$√3$	$1$	${√3}/{3}$

Признаки подобия между треугольниками:

1. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны.
2. Если две стороны треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.
3. Если три стороны треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) связаны друг с другом как коэффициент подобия k. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Практика: решить задание 8 и возможности подготовки к ЕГЭ по математике (профиль)

Способы вписать шар в цилиндр

Теперь давайте разберемся, как поместить сферу в цилиндр. В этом случае возможно несколько вариантов:

 Мяч касается основания и стороны цилиндра

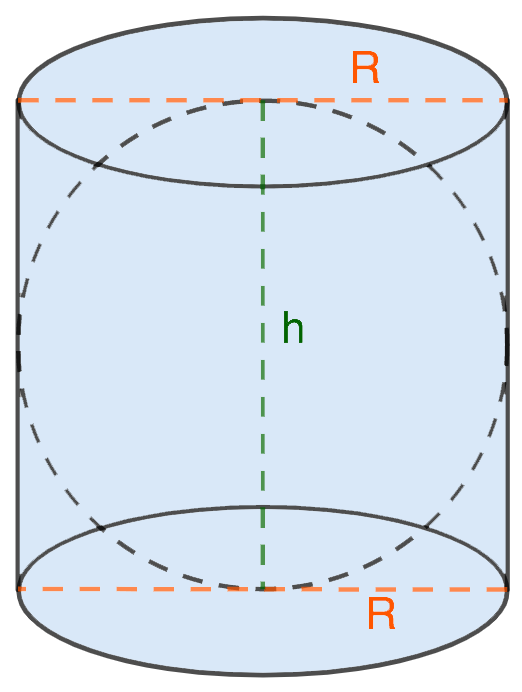
• радиус (диаметр) цилиндра является, в том числе, радиусом (диаметром) сферы;
• высота цилиндра равна диаметру шара.
•  Шарик касается только основания цилиндра

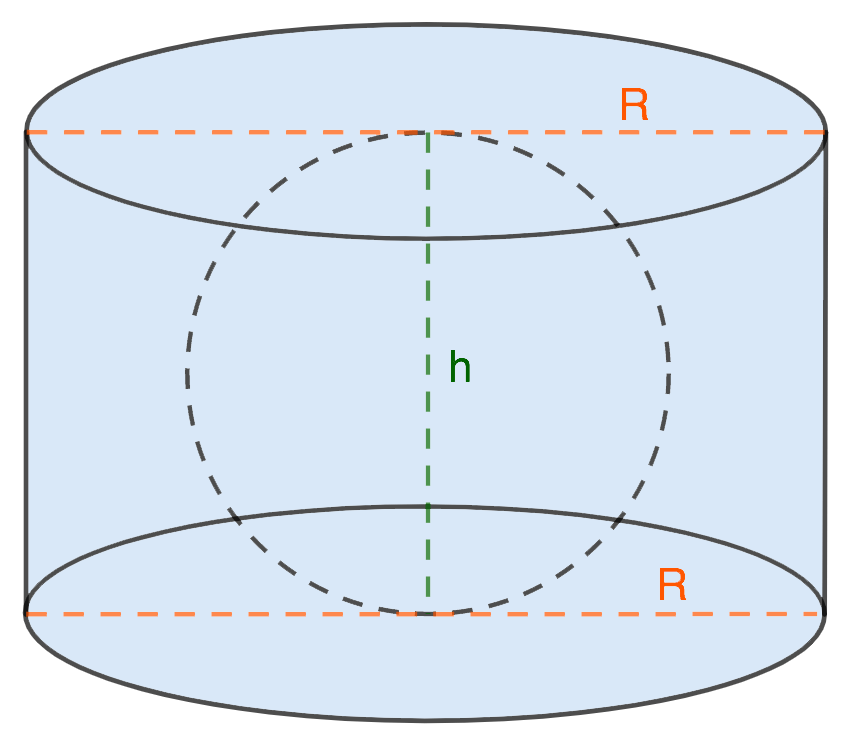
Радиус сферы равен половине высоты цилиндра, а диаметр равен полной высоте.

 Мяч касается только боковой стороны цилиндра

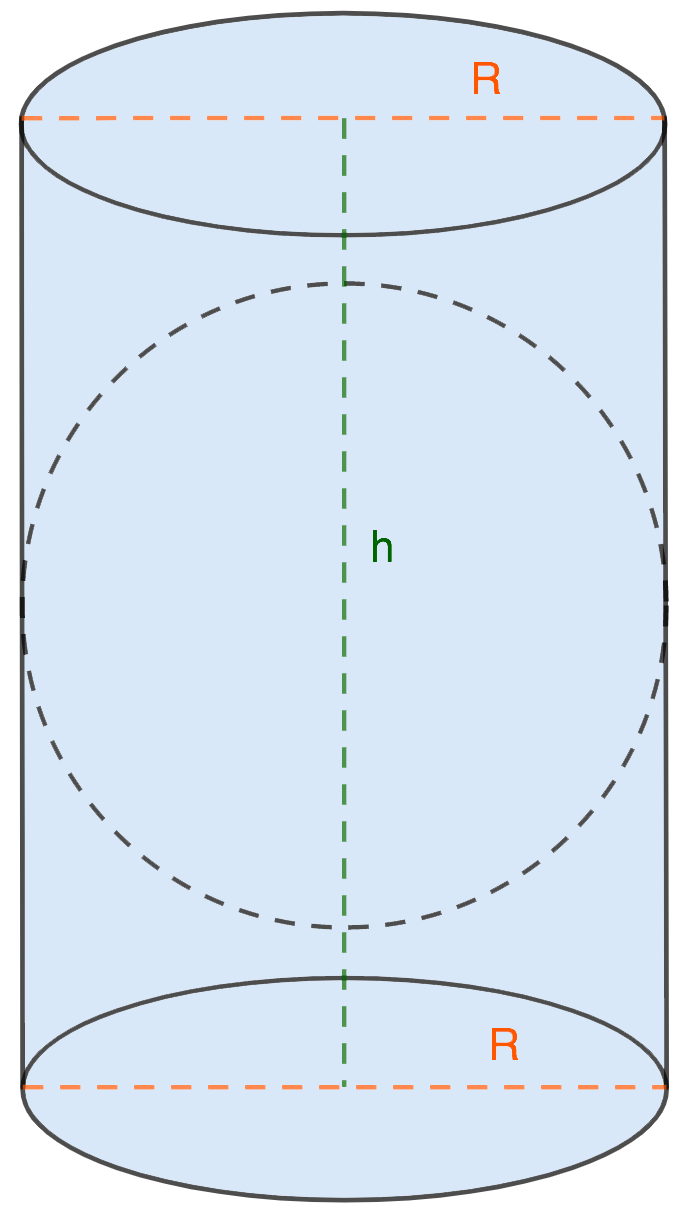
Радиус (диаметр) цилиндра равен радиусу (диаметру) шара.

Примечание: после выяснения радиуса или диаметра шара остается только воспользоваться формулой для расчета площади поверхности.

Прямой круговой цилиндр

Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью  и двумя параллельными плоскостями, пересекающими ее. Цилиндрическая поверхность образуется движением прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой, которая называется напрвляющей. Указанная прямая является образующей цилиндрической поверхности.

Цилиндр называется круговым, если его направляющая является окружностью.

Цилиндр называется прямым, если его образующая перпендикулярна основаниям.

Прямой круговой цилиндр определяется радиусом основания $R$ и образующей $L$, которая равна высоте цилиндра $H$.

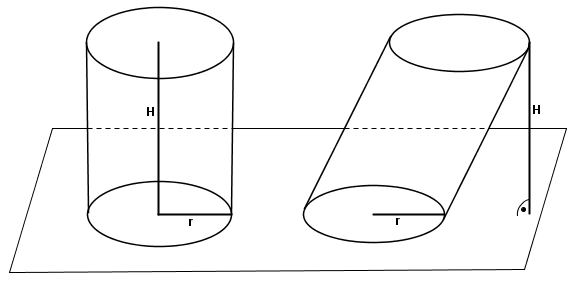
Пусть площадь боковой поверхности прямого кругового цилиндра $M$, площадь полной поверхности прямого кругового цилиндра $P$, объём прямого кругового цилиндра $V$:

$$ M = 2r\pi H,{\rm{   }}$$ 

$$ P = 2r\pi \left( {r + H} \right),{\rm{   }}$$ 

$$ V = {r^2}\pi H.$$

Вычисление объема тел вращения

Телом вращения называют тело, которое может быть получено вращением какой-то плоской фигуры относительно некоторой оси вращения. Например, цилиндр получают вращением прямоугольника вокруг одной из его сторон, а усеченный конус – вращением прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.

В задачах на вычисление объемов таких тел ось координат Ох уже задана естественным образом – это ось вращения тела. Ясно, что каждое сечение тела, перпендикулярное оси вращения, будет являться кругом.

Рассмотрим случай, когда вокруг оси Ох поворачивают график некоторой функции у = f(x), ограниченный прямыми х = а и у = b. Тогда получится тело, сечениями которого являются круги, причем их радиусы будут равны величине f(x). Напомним, что площадь круга вычисляют по формуле:

Рассмотрим, как на практике используется эта формула.

Задание. Объемное тело получено вращением ветви параболы

вокруг оси Ох. Оно ограничено плоскостями х = 0 и х = 4. Каков объем такой фигуры?

Решение. Здесь пределами интегрирования, то есть числами а и b, будут 0 и 4. Используем формулу для тела вращения:

Шар вписан в цилиндр: математические расчёты

Определение геометрических характеристик

Представим себе шар, радиус которого равен R. И цилиндр, в который этот шар вписан, высотой H и радиусом основания r. Чтобы определить площадь и диаметр, равные 111, необходимо знать математические характеристики этих фигур.

Шар имеет форму сферы и объем V = 4/3 * π * R^3, а его поверхность равна S = 4 * π * R^2.

Цилиндр – это фигура, состоящая из двух круговых оснований и боковой поверхности. Объем цилиндра V = π * r^2 * H, а его боковая поверхностьS = 2 * π * r * H.

Вычисление площади и диаметра

Для того чтобы найти площадь поверхности, равную 111, необходимо решить систему уравнений, в которой уравнение сферы приравнивается к уравнению боковой поверхности цилиндра. Отсюда можно получить диаметр и высоту цилиндра.

Для нахождения диаметра шара воспользуемся формулой диаметра d = 2 * R.

Если известны значения конкретного шара — R и H, то можно подставить их в формулы и найти соответствующие площадь и диаметр.

Например, при R = 4,5 и H = 3,7 см, диаметр шара будет d = 9 см, а площадь поверхности, равная 111, будет S = 99,41 см².

Таким образом, зная геометрические характеристики шара и цилиндра, можно вычислить их параметры и использовать для решения различных задач.

Задача №2

Усло­вие: найти ра­ди­ус шара, впи­сан­но­го в пра­виль­ную че­ты­рех­уголь­ную пи­ра­ми­ду , сто­ро­на ос­но­ва­ния ко­то­рой равна 10, а бо­ко­вое ребро – 13 (рис. 10). 

Рис. 10. Ил­лю­стра­ция к за­да­че 2	Рис. 11. Тре­уголь­ник

Ре­ше­ние

Пусть  – центр шара,  – центр ос­но­ва­ния,  – се­ре­ди­на ,  – се­ре­ди­на . В силу сфор­му­ли­ро­ван­но­го утвер­жде­ния  лежит на . Рас­смот­рим тре­уголь­ник . По усло­вию рас­сто­я­ния от точки  до ,  и  долж­ны быть рав­ны­ми – это и есть ра­ди­у­сы шара. Таким об­ра­зом,  – про­сто центр впи­сан­ной окруж­но­сти в тре­уголь­ник , ра­ди­ус этой окруж­но­сти и надо найти (рис. 11).

Оче­вид­но, ,  из тре­уголь­ни­ка  равно 12 (в силу тео­ре­мы Пи­фа­го­ра).

Тогда .

Зна­чит 

Ответ: .

В цилиндр вписан шар. Площадь поверхности шара равна 36π. Найдите площадь полной поверхности цилиндра. — вопрос №4593900

Лучший ответ по мнению автора

03. 01.22 Лучший ответ по мнению автора

Читать ответы

Читать ответы

Eleonora Gabrielyan

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

Решено

Найдите точку максимума функции y = (2x –3) cos x – 2sin x + 5 принадлежащую промежутку (0;П/2)

Решено

какая мощность (в ваттах) рассеивается на резисторе 5 Ом при протекании через него тока 2 А

Обсуждаем,эксперти,это ваша научный развити?!
https://docs.

Найдите количество способов покрасить все узлы прямоугольной сетки 2 × 6 в 2 цвета так, чтобы при её повороте на 180 градусов вокруг центра по часовой стрелке сетка перешла бы сама в себя

tga-? Если sina=-5/корень 26 и a пренадлежит (pi;3pi/2)

Разветвление: задача №4

Усло­вие: пра­виль­ная ше­сти­уголь­ная приз­ма впи­са­на в шар ра­ди­у­са 13. Вы­со­та приз­мы равна 24. Найти пло­щадь пол­ной по­верх­но­сти приз­мы (рис. 13).

Рис. 13. Ил­лю­стра­ция к за­да­че 4	Рис. 14. Ил­лю­стра­ция к за­да­че 4

Ре­ше­ние

Ра­зу­ме­ет­ся, до­ста­точ­но найти сто­ро­ну ос­но­ва­ния. Пусть  – центр шара,  – центр ос­но­ва­ния  приз­мы (рис. 14). Тогда , , а зна­чит,  по тео­ре­ме Пи­фа­го­ра.

Как из­вест­но, ра­ди­ус окруж­но­сти, опи­сан­ной около пра­виль­но­го ше­сти­уголь­ни­ка, равен его сто­роне. Зна­чит, сто­ро­на приз­мы – 5.

Най­дем пло­щадь ее бо­ко­вой по­верх­но­сти –  Ос­но­ва­ние приз­мы со­сто­ит из 6 рав­ных рав­но­сто­рон­них тре­уголь­ни­ков со сто­ро­ной 5 (и таких ос­но­ва­ний 2, итого, 12 тре­уголь­ни­ков). Зна­чит, сум­мар­ная пло­щадь ос­но­ва­ний равна .

Ответ: .

Калькулятор круглого цилиндра

Форма круглого цилиндра

r = радиус ч = высота В = объем L = площадь боковой поверхности T = площадь верхней поверхности B = площадь базовой поверхности

Калькулятор Использование

Этот онлайн-калькулятор рассчитает различные свойства цилиндра по двум известным значениям.

Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для обозначения порядка результатов, таких как футы, футы 2 или футы 3

Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм 3 , L в мм 2 , T в мм 2 , B в мм 2 и A в мм 2 .

Ниже приведены стандартные формулы для цилиндра. Расчеты основаны на алгебраических манипуляциях с этими стандартными формулами.

Формулы цилиндра через r и h:

• Рассчитать объем цилиндра:
• Рассчитайте площадь боковой поверхности цилиндра (только кривизну снаружи)**:
• Рассчитайте площадь верхней и нижней поверхности цилиндра (2
  круги):
• Общая площадь поверхности закрытого цилиндра:

** Расчетная площадь относится только к боковой поверхности внешней стенки цилиндра.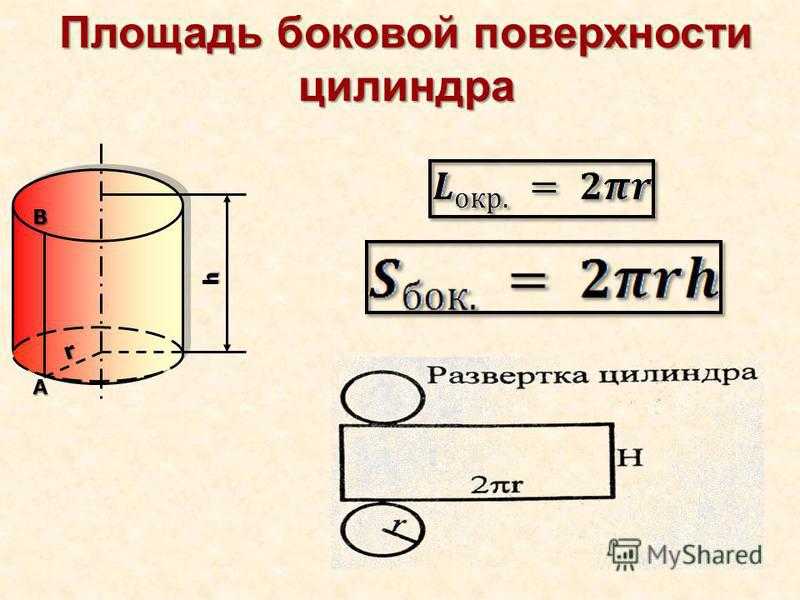

Вписанный в шар цилиндр

Рассмотрим комбинацию тел: шар и вписанный в шар цилиндр.

Цилиндр вписан в сферу, если окружности его оснований лежат на поверхности сферы. В этом случае также говорят, что сфера описана около цилиндра. Центр сферы лежит в центре оси цилиндра.

Как и при решении задач для сферы, вписанной в цилиндр, чаще всего рассматривают часть совокупности тел плоскостью, проходящей через ось цилиндра. Эта часть представляет собой вписанный в окружность прямоугольник, стороны которого равны высоте конуса и диаметру основания. Центр круга находится на пересечении диагоналей прямоугольника.

Рассмотрим пример такого осевого сечения. Здесь точка O — центр сферы, описанной вокруг цилиндра, BD — диаметр сферы, OD=R — радиус сферы, AB=H — образующая и высота цилиндра, AD — диаметр шарового цилиндра, FD=r — радиус цилиндра.

(как вписанные, так и центральные углы опираются на одну и ту же дугу AD).

Треугольник AOD равнобедренный (AO=OD=R), в нем OF=H/2 высота, медиана и биссектриса.

Треугольник OFD – прямоугольный треугольник. По теореме Пифагора получаем соотношение, связывающее радиус сферы с радиусом и высотой цилиндра, вписанного в сферу:

То же соотношение можно получить из прямоугольного треугольника ABD: по теореме Пифагора

Определение пересечения шара и цилиндра

Понятие пересечения шара и цилиндра

Пересечение шара и цилиндра возникает тогда, когда объемы этих геометрических фигур частично или полностью пересекаются друг с другом. Для определения этого пересечения необходимо знать радиус шара (r), радиус и высоту цилиндра.

Расчёт пересечения шара и цилиндра

Чтобы определить, пересекаются ли шар и цилиндр, необходимо рассчитать объем каждой фигуры.

Объем шара рассчитывается по формуле V = 4/3πr^3, а объем цилиндра — по формуле V = πr^2h.

Если объемы фигур пересекаются частично или полностью, то шар вписан в цилиндр, а их объемы можно вычислить по формуле V = πr^2h/2 + 4/3πr^3.

Если объемы фигур не пересекаются, то в шаре не может быть вписанного цилиндра.

Таким образом, для определения пересечения шара и цилиндра необходимо рассчитать объемы каждой фигуры и сравнить их. Если объемы пересекаются, то шар можно вписать в цилиндр.

Вычисление объема тела с помощью интеграла

Пусть у нас есть произвольная фигура, расположенная между двумя параллельными плоскостями:

Как найти ее объем? Поступим следующим образом. Проведем прямую, перпендикулярную этим плоскостям. Эта прямая будет осью координат х. Пусть одна из плоскостей пересекает эту ось в точке а, а другая – в точке b. Таким образом, на координатной прямой появляется отрезок . Далее разобьем этот отрезок на n равных отрезков, длина каждого из них будет равна величина ∆х. Обозначим концы этих отрезков как х, х₁, х₂…, х_n, причем точке х будет совпадать с точкой а, а точка х_n – с точкой b. Ниже показано такое построение для n = 10:

Далее через полученные точки проведем сечения, параллельные двум плоскостям, ограничивающим фигуру. Площадь сечения, проходящую через точку с номером i, обозначим как S(x_i). Эти плоскости рассекут тело на n других тел. Обозначим объем тела, заключенного между сечениями с площадями S(x_i) и S(x_i+1) как V(x_i). Можно приближенно считать, что эти тела имеют форму прямых цилиндров (напомним, что в общем случае цилиндром необязательно считается фигура, основанием которой является круг, основание может иметь и любую другую форму). Высота всех этих цилиндров будет равна величине ∆х. Тогда объем V(x_i) может быть приближенно рассчитан так:

Общий же объем исследуемой фигуры будет суммой объемов этих прямых цилиндров:

Здесь знак ∑ означает сумму i слагаемых, каждое из которых равно величине S(x_i)•∆х. Ясно, что чем больше мы возьмем число n, тем точнее будет полученная нами формула. Поэтому будет увеличивать число n до бесконечности, тогда приближенная формула станет точной:

В правой части стоит предел суммы бесконечного числа слагаемых. Мы уже сталкивались с такими пределами, когда изучали определенный интеграл в курсе алгебры. Так как х = a, а число х_n-1 при бесконечном увеличении n приближается к числу х_n, то есть к b, то можно записать следующее:

Здесь S(x) – это некоторая функция, которая устанавливает зависимость между площадью сечения объемной фигуры и координатой х, указывающей расположение этого сечения. Данная формула позволяет вычислять объем с помощью интеграла.

Итак, для вычисления объема тела необходимо:

1) выбрать в пространстве какую-то удобную ось координат Ох;

2) найти площадь произвольного сечения фигуры, проходящей перпендикулярно оси Ох через некоторую координату х;

3) найти значение чисел а и b – координат сечений, ограничивающих тело в пространстве;

4) выполнить интегрирование.

Понятно, что сразу понять, как используется эта формула, тяжело. Поэтому рассмотрим простой пример.

Задание. Фигура расположена в пространстве между двумя плоскостями, перпендикулярными оси Ох, причем координаты этих сечений равны 1 и 2. Каждое сечение фигуры с координатой х является квадратом, причем его сторона равна величине 1/х. Найдите объем тела.

Решение. В данной задаче ось Ох уже проведена. Известны и числа а и b – это 1 и 2, ведь именно плоскости, проходящие через точки х =1 и х = 2, ограничивают исследуемое тело. Теперь найдем площадь произвольного сечения с координатой х. Так как оно является квадратом со стороной 1/х, то его площадь будет квадратом этой стороны:

Области применения нахождения площади и диаметра вписанного шара

1. Геометрия

Вычисление площади и диаметра вписанного шара является важной задачей в геометрии. Эти параметры позволяют определить геометрические свойства фигур, которые могут быть использованы для решения разнообразных задач

2. Машиностроение и производственные технологии

Нахождение площади и диаметра вписанного шара имеет применение в машиностроении и производственных технологиях. Например, для вычисления объема гидравлического цилиндра, которые используются в производстве многих видов техники (например, налётного судна) и машин.

Также, знание площади и диаметра вписанного шара может быть полезно при проектировании металлических конструкций, таких как высокоэффективные балки и арки. В этом случае, вычисляя диаметр вписанного шара, можно подобрать наиболее оптимальный диаметр профиля.

3. Наука о материалах

Строительные материалы, обработка материалов и изготовление деталей требуют знания площади и диаметра вписанного шара. Это связано с тем, что форма материала или детали может быть использована в качестве ключевого фактора при определении свойств материала, таких как прочность и упругость.

4. Программирование и компьютерная графика

В программировании и компьютерной графике, знание площади и диаметра вписанного шара может быть использовано для создания цифровых моделей различных предметов и конструкций. Например, они могут быть использованы в программном обеспечении 3D-печати для создания точных копий объектов.

В результате, знание площади и диаметра вписанного шара имеет широкие области применения и используется в различных отраслях науки и техники.