Теоремы косинусов и синусов

Примеры решения задач

Задача 1

В треугольнике \(ABC\) сторона \(AB=10\), \(BC=12\). \(∠В=26°.\)

Найти \(АС.\)

Решение

\(b^2=a^2+c^2-2ac\;\cos\;\beta\)

Из этого \( b^2=12^2+10^2-2\times12\times10\;\cos\;26\;\frac\pi{180}=144+100-240(0.90)=28\)

Преобразуем \( \sqrt{28}=2\sqrt7.\)

Ответ: \(2\sqrt7.\)

Задача 2

В треугольнике \(ABC\),\( AC=3\), \(BC=5\), \(AB=6.\)

Найти \(cos ∠ACB.\)

Решение

\(AB^2=AC^2+BC^2-2AC\times BC\times\cos\;\angle ACB\)

Переставим члены уравнения и получим:

\(2AC\times BC\times\cos\;\angle ACB=AC^2+BC^2-AB^2\)

Поделим обе стороны 2AC\times BC и получаем cos ∠ACB:

\(\frac{AC^2+BC^2-AB^2}{2AC\times BC}=\frac{3^2+5^2-6^2}{2\times3\times5}=\frac{9+25-36}{30}=\frac{-2}{30}=-\frac1{15}\)

Ответ: \(-\frac1{15}.\)

Задача 3

В треугольнике \(ABC BC=\sqrt3\),\( AC=2\). \(∠ABC=60°\).

Найти \(sin ∠BAC\).

Решение

\(\frac{BC}{\sin\;\angle BAC}=2R=\frac{AC}{\sin\;\angle ABC}\)

Произведем перекрестное умножение:

\(\sin\;\angle BAC=\frac{BC}{AC}\sin\;\angle ABC=\frac{\sqrt3}2\times\frac{\displaystyle\sqrt3}{\displaystyle2}=\frac34\)

Ответ: \(\frac34.\)

Задача 4

В остроугольном треугольнике \(ABC\) \(BC=2\sqrt3\), \(AC=2\). \(∠ABC=30°.\)

Найти \(∠BAC\) в градусах.

Решение

\(\frac{BC}{\sin\;\angle BAC}=2R=\frac{AC}{\sin\;\angle ABC}\)

Произведем перекрестное умножение:

\(\sin\;\angle BAC=\frac{BC}{AC}\sin\;\angle ABC=\frac{2\sqrt3}2\times\frac{\displaystyle1}{\displaystyle2}=\frac{\sqrt3}2\)

В градусах получим: \(∠BAC=120°\) либо \(∠BAC=60°\).

Так как \(ABC\) остроугольный треугольник, то \(∠BAC<90°\).

Формулировка и доказательство следствия из теоремы синусов

Из тео­ре­мы си­ну­сов вы­те­ка­ет важ­ное след­ствие.

Рис. 2. Ил­лю­стра­ция к тео­ре­ме

 ,

где R – ра­ди­ус опи­сан­ной около тре­уголь­ни­ка окруж­но­сти (рис. 2).

Сле­до­ва­тель­но, мы по­лу­чи­ли три фор­му­лы ра­ди­у­са опи­сан­ной окруж­но­сти:

Но, по су­ще­ству, весь смысл след­ствия из тео­ре­мы си­ну­сов за­клю­чён в фор­му­ле:

Ра­ди­ус опи­сан­ной окруж­но­сти не за­ви­сит от угла α, β, γ. Удво­ен­ный ра­ди­ус опи­сан­ной окруж­но­сти равен от­но­ше­нию сто­ро­ны тре­уголь­ни­ка к си­ну­су про­ти­во­ле­жа­ще­го угла.

Для до­ка­за­тель­ства рас­смот­рим три слу­чая:

1. Угол  – ост­рый в тре­уголь­ни­ке АВС (рис. 3)

Рис. 3. Ил­лю­стра­ция к тео­ре­ме

Про­ве­дём диа­метр . В этом слу­чае точка А и точка  лежат в одной по­лу­плос­ко­сти от пря­мой ВС. Ис­поль­зу­ем тео­ре­му о впи­сан­ном угле и видим, что . Тре­уголь­ник        пря­мо­уголь­ный, в нём угол  равен 90, так как он опи­ра­ет­ся на диа­метр .

Для того чтобы найти катет a в тре­уголь­ни­ке , нужно ги­по­те­ну­зу В=2R (R – ра­ди­ус окруж­но­сти) умно­жить на синус про­ти­во­ле­жа­ще­го угла.

Сле­до­ва­тель­но

В пер­вом слу­чае тео­ре­ма до­ка­за­на.

2. Угол  – тупой в тре­уголь­ни­ке АВС (рис. 4)

Про­ве­дём диа­метр окруж­но­сти . Точки А и  по раз­ные сто­ро­ны от пря­мой ВС. Че­ты­рёх­уголь­ник  впи­сан в окруж­ность, и его свой­ство та­ко­во, что сумма про­ти­во­ле­жа­щих углов равна . Сле­до­ва­тель­но, =.

Вспом­ним дан­ное свой­ство впи­сан­но­го в окруж­ность че­ты­рёх­уголь­ни­ка (рис. 4):

=

Также мы знаем, что .

В тре­уголь­ни­ке  угол при вер­шине С равен 90, по­то­му что он опи­ра­ет­ся на диа­метр. Сле­до­ва­тель­но, катет а мы на­хо­дим таким об­ра­зом:           

Рис. 4. Ил­лю­стра­ция к тео­ре­ме

Сле­до­ва­тель­но

Во вто­ром слу­чае тео­ре­ма до­ка­за­на.

3. Угол  (рис. 5)

Рис. 5. Ил­лю­стра­ция к тео­ре­ме

В пря­мо­уголь­ни­ке АВС угол А пря­мой, а про­ти­во­по­лож­ная сто­ро­на , где R – это ра­ди­ус опи­сан­ной окруж­но­сти. Сле­до­ва­тель­но:

И в тре­тьем слу­чае тео­ре­ма до­ка­за­на.

Теорема косинусов

Теорема косинусов отлично помогает в решении треугольников. Решение треугольника — это нахождение всех его сторон и углов. Но если нам даны только стороны треугольника, как определить углы в нем? Вот тогда и приходит на помощь теорема косинусов. Это общий случай теоремы Пифагора, подходящий для треугольника с любым углом, не только с углом 90 0 .

Теорема и доказательство

Доказательство теоремы косинусов

Докажем теорему. Для этого нарисуем треугольник ABC и докажем, что:

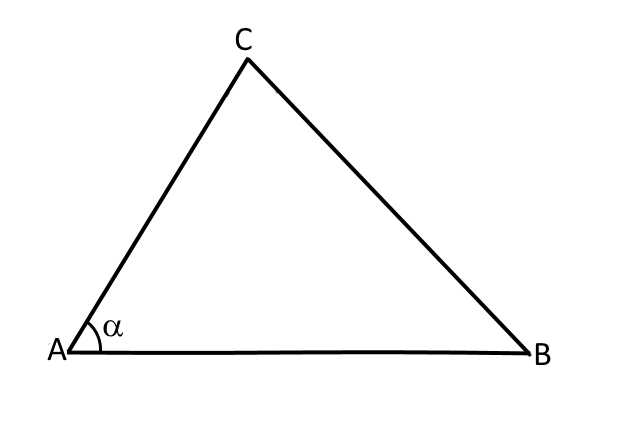
Если рассматривать стороны треугольника, как векторы, то будет справедливо равенство:

.

В теореме в квадрате, значит возведем векторное равенство в квадрат, получим:

Так как, , , а скалярное произведение векторов равно произведению их модулей на косинус угла между ними, то есть .

Подставим все в формулу (2):

Что и требовалось доказать.

Следствие теоремы косинусов

Проведем высоты :

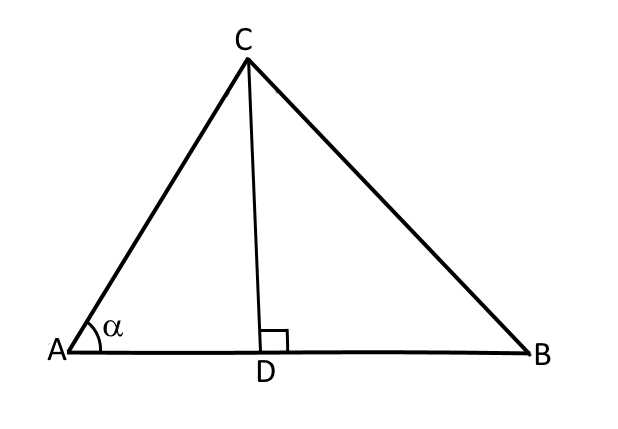
Обратим внимание, что. То есть — это проекция стороны на сторону треугольника

Если угол А острый, то , если угол А тупой, то косинус угла А будет отрицательным и

То есть из теоремы косинусов вытекает важное следствие:

Задачи на теорему косинусов

Задача 1

Найдите , если дано: , , .

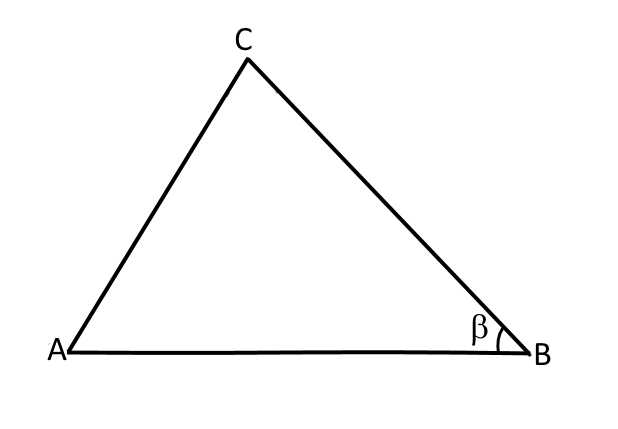
Решение: Так как нам известен угол между сторонами и и известна сторона — мы сможем найти сторону , если воспользуемся теоремой косинусов.

Из теоремы косинусов выразим сторону .

Обозначим

Получаем квадратное уравнение. Подставим в него значения и решим:

Тогда .

— не может быть длиной стороны треугольника.

Ответ: 12.

Задача 2

В треугольника ABC , , . Найдите

Решение: Нарисуем треугольник ABC. Это равнобедренный треугольник.

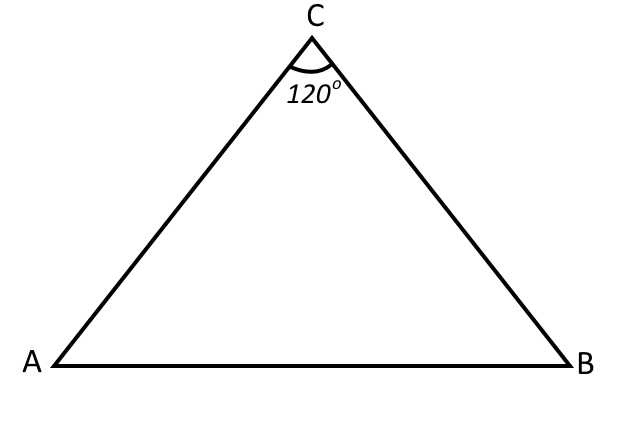
Запишем теорему косинусов для сторону так как нам дан угол между двумя другими сторонами:

Так как , то из формулы (1), получим:

Сделаем замену: :

,

перенесем в правую часть равенства и получим квадратное уравнение:

,

Так как , значит, .

Ответ: 6

Задача 3

Решите треугольник ABC, если известно, что , , .

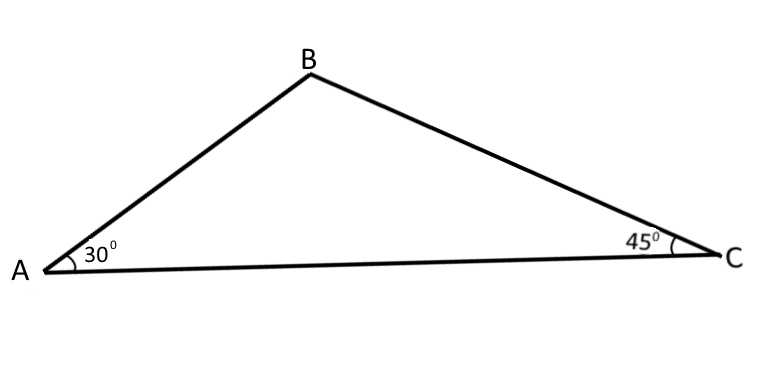
Решение: Решить треугольник — это значит, найти все его стороны и все углы. Нам два угла даны, значит, зная, что сумма всех углов в треугольнике равна получим:

.

Обозначим неизвестные стороны треугольника: , .

Выразим сторону треугольник по теореме косинусов:

Выразим сторону треугольника по теореме косинусов:

Решим уравнения (1) и (2) совместно, записав их в систему уравнений:

Сложим первое и второе уравнения системы и запишем получившееся уравнение вместо второго уравнения, получим:

Из второго уравнения выразим :

Итак, мы выразили из второго уравнения системы, теперь возьмем и подставим его в первое уравнение и сделаем необходимые преобразования.

, раскрываем скобки и умножим левую и правую части уравнения на 2:

Разделим левую и правую части уравнения на 2:

.

Получили квадратное уравнение. Решим его.

Тогда корни уравнения:

Оба значения подходят — они положительны. Находим, :

— отрицательное значение нам не подходит.

Таким образом, получаем следующие значения , .

Вы можете самостоятельно сделать проверку и убедиться в том, что данные значения верны.

Ответ: , .

Теорема косинусов для треугольника очень помогает в решении геометрических задач, однако некоторые задачи усложняются, если не знать еще одну теорему — синусов. Например, третью задачу мы могли решить гораздо проще — используя теорему синусов, с помощью которой мы бы довольно быстро получили тот же результат для . Однако, с ней мы бы получили лишь приближенное значение . Теорема косинусов дает нам точный результат. Однако, в дальнейшем, когда вы выучите две теоремы — рекомендуем решать задачи, используя их обе.

Соотношение отрезков и углов

Задачи на соотношение отрезков и угловых мер в рассматриваемой фигуре могут требовать либо качественный, либо количественный ответ. В первом случае следует провести определенное доказательство, опираясь на известные аксиомы и теоремы о сторонах треугольника и их следствия. Во втором же случае следует пользоваться формулами и выражениями, которые содержат тригонометрические функции. В действительности оба типа задач связаны между собой. Так, прежде чем использовать какую-либо формулу, следует доказать возможность ее применения в конкретной ситуации.

Большие и меньшие длины

Основная теорема о соотношении между элементами в рассматриваемом типе многоугольников гласит, что против большего угла лежит большая сторона. Ее доказательство провести несложно, если построить треугольник, например, тупоугольный. Из тупого провести отрезок к противоположной стороне таким образом, чтобы он образовывал новый равнобедренный треугольник внутри исходного. После этого следует воспользоваться тем свойством, что внешний угол треугольника всегда больше внутреннего.

Следуя условию равенства углов в построенном равнобедренном треугольнике, легко показать, что против тупого всегда находится самый длинный отрезок.

Обратно эта теорема также справедлива, то есть против большей стороны треугольника лежит больший угол. Ее справедливость понятна каждому школьнику на интуитивном уровне, а доказательство заключается в переборе возможных трех вариантов соотношения между отрезками (больше, меньше, равно) и в привлечении уже доказанной теоремы.

Рассмотренные теоремы приводят к двум важным следствиям:

1. Против равных сторон лежат равные углы, и наоборот. Следствие актуально для равносторонних и равнобедренных фигур.
2. Гипотенуза в треугольнике с прямым углом является самой длинной стороной, поскольку она лежит напротив самого большого угла.

Теоремы косинусов и синусов

Количественной характеристикой соотношения сторон и углов являются знаменитые формулы, содержащие зависимость длин отрезков и угловых мер. Первая из них называется теоремой косинусов. Соответствующая формула имеет вид:

c 2 = a 2 + b 2 — 2*a*b*cos.

Здесь величины a, b, c — это длины, C — угол напротив стороны c. Формула позволяет вычислить третью сторону по известным двум другим и углу между ними. Однако, возможности выражения шире, с его помощью можно посчитать всякий внутренний угол фигуры, если известны три ее стороны.

Следующая по счету, но не по важности теорема синусов. Ее математическое выражение записывается так:. a/sin (A) = b/sin (B) = c/sin.

a/sin (A) = b/sin (B) = c/sin.

Эти равенства говорят о том, что отношение стороны к синусу противоположного ей угла является постоянной характеристикой конкретного треугольника. Зная связь двух углов и стороны или двух отрезков и одного угла можно рассчитать все остальные характеристики фигуры. Следует запомнить, что для любого рассматриваемого типа многоугольников однозначное вычисление всех его свойств требует знания минимум трех элементов (кроме трех углов).

Прямоугольный треугольник

Этот особый случай следует рассмотреть подробнее. Каждый школьник знает знаменитую теорему, позволяющую сравнить соответствие отрезков друг другу в этом типе фигуры. Она гласит, что сумма квадратов катетов соответствует квадрату гипотенузы, и называется пифагоровой теоремой, то есть можно записать:

c 2 = a 2 + b 2 .

Работать с прямоугольными треугольниками удобно по одной простой причине: через их геометрические параметры вводятся в математику тригонометрические функции. Последние легко использовать при вычислении сторон и углов фигуры. Например, если фигура является не только прямоугольной, но и равнобедренной, то ее катеты равны, а углы напротив них составляют по 45 °. При этом любой из катетов всегда в 2 0,5 раза меньше гипотенузы:

sin (45 °) = a/c = ½ 0,5.

Это соотношение можно получить также из теоремы Пифагора.

Другая ситуация, когда один из острых углов равен 30 °. Для лежащего напротив него катета a можно записать следующее выражение:

sin (30 °) = ½ = a/c.

Иными словами, лежащий против 30 ° катет составляет ровно половину длины гипотенузы.

Следствия из теоремы

Доказательство:

∠А+∠В+∠=180°, ∠А+∠В=∠С=90°. Значит, ∠А<90°, ∠В<90°. Из этого следует, что АВ>ВС и АВ>АС. Гипотенуза АВ больше каждого из катетов. Следствие доказано.

Доказательство:

Пусть у ΔАВС ∠В=∠С. Докажем, что АС=АВ, применяя метод от противного. Предположим, что АВ>АС, тогда ∠С>∠В, что противоречит условию. Аналогично докажем, что АС не больше АВ. Значит, АВ=АС. Следствие доказано.

Равенство двух углов, как и равенство двух сторон, является признаком равнобедренного треугольника. Равными будут углы, лежащие напротив равных сторон. Если треугольник имеет этот признак, то такой треугольник — равнобедренный.

Архив записей

Архив записейВыберите месяц Ноябрь 2022  (1) Сентябрь 2022  (1) Январь 2022  (2) Сентябрь 2021  (1) Июль 2021  (1) Июнь 2021  (2) Май 2021  (1) Апрель 2021  (1) Март 2021  (1) Сентябрь 2020  (1) Август 2020  (2) Июль 2020  (2) Июнь 2020  (2) Декабрь 2019  (3) Ноябрь 2019  (4) Октябрь 2019  (3) Сентябрь 2019  (2) Май 2019  (1) Октябрь 2018  (1) Июнь 2018  (1) Апрель 2018  (1) Январь 2018  (1) Ноябрь 2017  (1) Октябрь 2017  (1) Сентябрь 2017  (2) Август 2017  (4) Июль 2017  (5) Июнь 2017  (4) Май 2017  (5) Апрель 2017  (2) Март 2017  (1) Февраль 2017  (1) Январь 2017  (3) Декабрь 2016  (1) Ноябрь 2016  (2) Октябрь 2016  (3) Сентябрь 2016  (4) Август 2016  (6) Июль 2016  (9) Июнь 2016  (4) Май 2016  (5) Апрель 2016  (6) Март 2016  (5) Февраль 2016  (8) Январь 2016  (8) Декабрь 2015  (9) Ноябрь 2015  (4) Июль 2015  (1) Март 2015  (1) Февраль 2015  (1) Январь 2015  (1) Июль 2014  (1) Июль 2013  (1) Март 2013  (2) Декабрь 2012  (1) Ноябрь 2012  (1) Сентябрь 2012  (3) Август 2012  (4) Июль 2012  (4) Июнь 2012  (4) Май 2012  (4) Апрель 2012  (5) Март 2012  (7) Февраль 2012  (8) Январь 2012  (7) Декабрь 2011  (5) Ноябрь 2011  (1)

Обобщение на евклидово пространство

Инжир. 10 — Тетраэдр: грани и двугранные углы.

Рассмотрим тетраэдр A ₁ A ₂ A ₃ A ₄ евклидова пространства. На рисунке 10 напротив представлены обозначения вершин, граней и углов тетраэдра:

• Sk{\ displaystyle \ mathrm {S} _ {k}}лицо напротив верха ;Вk {\ Displaystyle \ mathrm {А} _ {к} \}
• sk{\ displaystyle s_ {k}}поверхность ;Sk {\ Displaystyle \ mathrm {S} _ {к} \}
• Δk{\ displaystyle \ Delta _ {k}}плоскость , в которой погружена;Sk {\ Displaystyle \ mathrm {S} _ {к} \}
• θяj{\ displaystyle \ theta _ {ij}}двугранный угол .(Δя,Δj){\ displaystyle (\ Delta _ {i}, \ Delta _ {j})}

Затем поверхности и углы проверяют:

s42знак равноs12+s22+s32-2s1s2потому что⁡θ12-2s1s3потому что⁡θ13-2s2s3потому что⁡θ23.{\ displaystyle s_ {4} ^ {2} = s_ {1} ^ {2} + s_ {2} ^ {2} + s_ {3} ^ {2} -2s_ {1} s_ {2} \ cos \ theta _ {12} -2s_ {1} s_ {3} \ cos \ theta _ {13} -2s_ {2} s_ {3} \ cos \ theta _ {23}. \,}

Пример решения задачи

Известно, что стороны треугольника равны 6 см, 8 см и 10 см. Необходимо найти площадь этой фигуры.

Для решения задачи можно воспользоваться ресурсами интернета, которые предлагают множество сайтов, где с использованием онлайн-калькуляторов можно по известным данным найти нужную величину. Тем не менее представляет интерес решить эту задачу с использованием теоремы косинусов.

Площадь любого треугольника может быть вычислена так:

S = ½*a*h.

Здесь h — высота, проведенная к a. Известные стороны a = 6 см, b = 8 см, c = 10 см. Чтобы найти высоту h следует сначала рассчитать угол между a и c. Для этого можно применить закон косинусов:

β = arccos ((a 2 + c 2 — b 2 )/(2*a*c)) = arccos ((6 2 + 10 2 — 8 2 )/(2*6*10)) = 53,13 °.

Теперь, если рассмотреть треугольник, образованный высотой h, стороной c и частью стороны a, можно увидеть, что он является прямоугольным (c — гипотенуза). В нем h может быть найдена через синус угла β:

h = c*sin (β) = 10* sin (53,13 °) = 8 см.

Длина высоты h равна таковой для стороны b. Это означает, что исходный треугольник являлся прямоугольным (можно проверить через теорему Пифагора). Его площадь составляет:

S = ½*a*h = ½*a*b = ½*6*8 = 24 см 2 .

Таким образом, теорема косинусов является универсальным инструментом для решения геометрических задач с треугольниками. С помощью нее по трем известным параметрам можно найти все остальные характеристики фигуры, включая ее площадь.

Вычисление координат точки

Пусть есть некоторая точка А(х;у) с неотрицательной ординатой. Соединим ее с началом координат прямой, которая образует угол α с осью Ох. Посмотрим, как связаны координаты А со значением α.

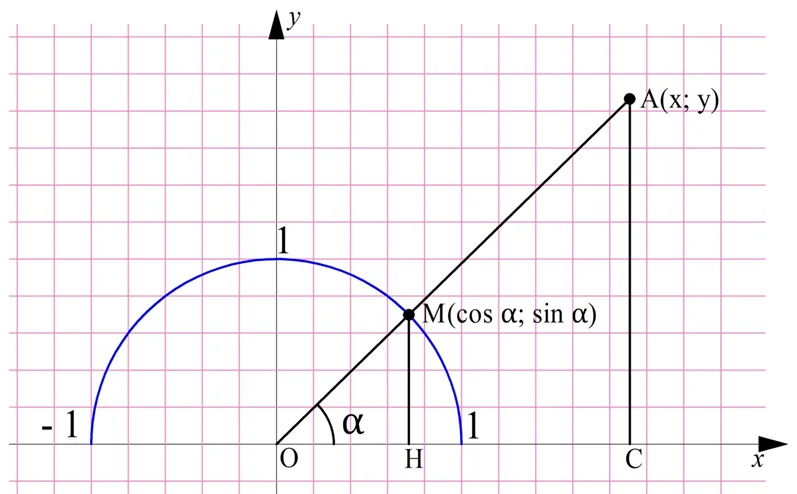
Пусть луч ОА пересечет единичную окружность в точке М. Опустим из М и А перпендикуляры на Ох, в точки Н и С соответственно. Теперь сравним ∆ОМН и ∆ОАС. Они прямоугольные, и у них есть одинаковый угол α, следовательно, они подобны. Коэффициент подобия можно найти, поделив ОА на ОМ, при этом учтем, что ОМ = 1, так как М лежит на единичной полуокружности:

Примечание. Данное доказательство не рассматривает частные случаи, когда точка А лежит непосредственно на осях Ох и Оу, и тогда подобные треугольники ∆ОМН и ∆ОАС построить не удается. Эти случаи можно рассмотреть отдельно и показать, что для них выведенные формулы также справедливы.

Задание. Точка А находится на расстоянии 3 от начала координат (точки О), причем луч ОА образует с осью Ох угол 135°. Найдите координаты точки А.

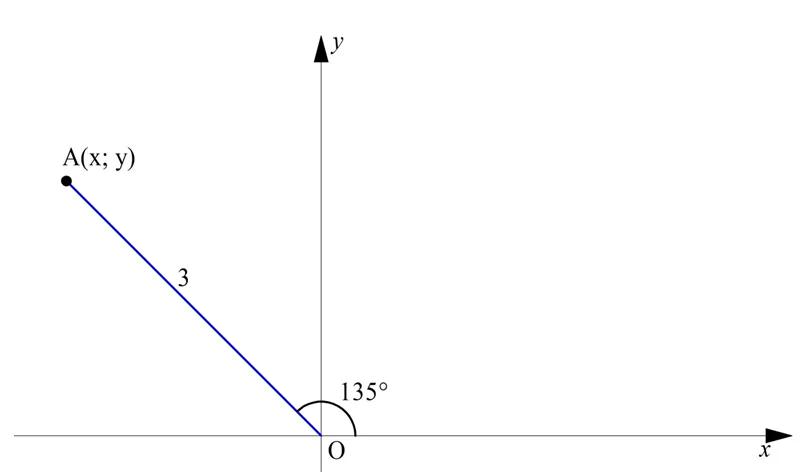
Решение. Используя выведенные формулы, мы можем записать:

Площадь параллелограмма

Из выведенной нами формулы площади треугольника вытекает и новая формула для площади параллелограмма. Пусть в параллелограмме нам известны смежные и угол между ними:

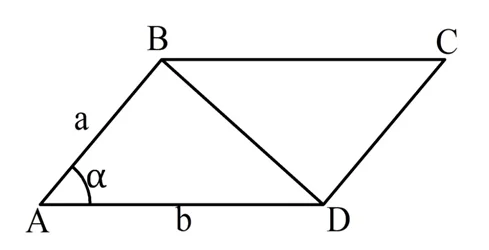
На рисунке смежные стороны АВ и AD обозначены буквами a и b, а угол между ними обозначен как α. Проведем диагональ BD. Площадь ∆ABD можно вычислить:

Задание. Стороны параллелограмма имеют длины 8 и 11 см, а один из углов параллелограмма равен 30°. Какова площадь этого параллелограмма?

Решение. Просто подставляем данные в формулу

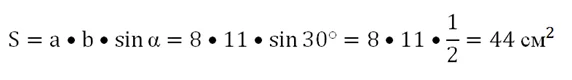
Ответ: 44 см2.

Задание. Известна площадь параллелограмма MNEF, одна из его сторон и угол:

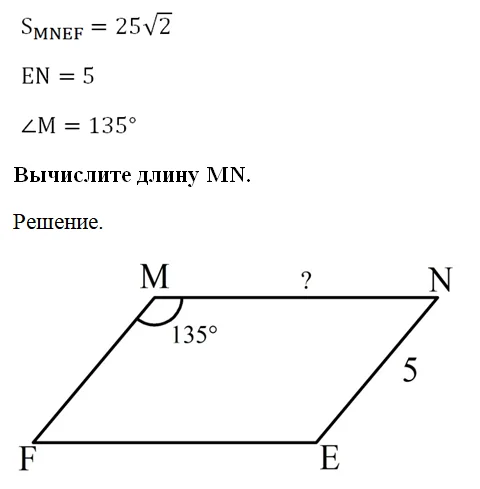
Так как противоположные стороны в параллелограмме одинаковы, то MF также имеет длину 5:

MF = NE = 5

Запишем формулу для площади и подставим в нее известные данные:

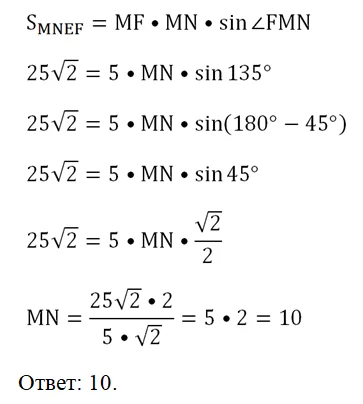
Примечания и ссылки

1. ↑ и
2. Паскаль Онво, Возможный подход к геометрии плоскости , Publibook ,2004 г. , стр.  41 год.
3. .
4. Произведения Евклида, пер. Ф. Пейрар, Париж (1819), тростник. Бланшар (1993). Для других изданий см. статьи об элементах .
5. Юсеф Гергур, «  Король Сарагосы аль-Мутаман ибн Худ и теорема Пифагора: ее источники и ее расширения  », LLULL , т.  28,2005 г., стр.  415-434 ( стр.  432 ).
6. Согласно , доказательство можно найти в KASHI (al) (1967): Miftam al-misab , al-Damardache, AS и al-Manfi al-Shikh, MM (Edit.), Le Каир, Дар аль-Китаб аль-Караби ли ат-тибака ва ан-Нашр, стр.  130-138 .
7. Смотрите это.
8. Например, см. ( In ) Roger B. Nelsen Proofs without Words II: More Exercises in Visual Thinking , MAA ,2000 г., стр.  9, а шире — статья «  Доказательство без слов  ».
9. , г. 11-2, стр.  265 .
10. (La) Н. Коперник, De Revolutionibus orbium coelestium , Книга I, гл. XII, § VII, стр.  20 и стр.  21 соответственно.
11. (in) Дэвид Юджин Смит , Справочник по математике , т.  1 , стр.  435.
12. Op. Cit. , стр.  17–20 , в Google Книгах .
13. (де) Антон фон Браунмюль , Vorlesungen über Geschichte der Trigonometrie ,1900 г. , стр.  53, примечание 1.
14. (in) Тони Филлипс, об университете Стоуни-Брук ,2006 г..
15. Жорж Достор, Элементы теории определителей: с применением к алгебре, тригонометрии и аналитической геометрии на плоскости и в пространстве, для использования в специальных классах математики , Париж, Готье-Виллар ,1877 г., 352  с. , стр. 251–252
16. (in) Дж. Р. Ли, «  Закон косинусов в тетраэдре  » , J. Korea Soc. Математика. Ed. Ser. B: Чистое приложение. Математика. , т.  4,1997 г., стр.  1-6Цитируется (в) Эриком В. Вайстейном , на MathWorld .

Что такое синус, косинус, тангенс и котангенс?

Тригонометрия в какой-то степени относится и к алгебре, и к геометрии. В этом уроке мы обсудим геометрическую часть тригонометрии.

А именно, нам понадобится прямоугольный треугольник. Это такой треугольник, в котором один из углов 90 градусов. Стороны, образующие прямой угол, называются катеты, для удобства обозначим их какими-нибудь буквами, например, \(a\) и \(b\). А гипотенузой называют сторону треугольника, лежащую напротив прямого угла, пусть она у нас будет \(c\). И обозначим острые углы в треугольнике за \(\alpha\) и \(\beta\).

С обозначениями закончили, без них изучать тригонометрию будет проблематично.

Подведение итогов урока

На дан­ном уроке мы рас­смот­ре­ли и  до­ка­за­ли тео­ре­му си­ну­сов и след­ствие из неё, а так же ре­ши­ли за­да­чу по этой теме.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/9-klass/sootnosheniya-mezhdu-storonami-i-uglami-treugolnika/teorema-sinusov

https://www.youtube.com/watch?v=KQbokFe6Dxs

https://www.youtube.com/watch?v=27ToPV10L6w

https://www.kursoteka.ru/teacher//index.cfm/getfile/2516/8249/4803

https://www.kursoteka.ru/teacher//index.cfm/getfile/2516/8249/4804

http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/28-test-po-geometrii-9-klass-tema-teorema-sinusov-variant-1.html