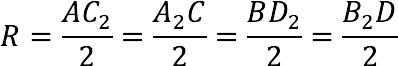Как найти радиус сферы вписанной в куб

Страница № 115.

Учебник: Геометрия. 11 кл.: Задачник для общеобразовательных учреждений с углуб. и профильным изучением математики / Е. В. Потоскуев, Л. И. Звавич. — 2-е изд., стереотип. — М.: Дрофа, 2004. — 240 с.: ил.

Страницы учебника:

, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , «115», , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

OCR-версия страницы из учебника (текст страницы, которая находится выше):

положение сферы и прямой, содержащей ребро основания пирамиды.

3.232. ^ Сторона основания правильной четырехугольной пирамиды MABCD равна 6, а боковое ребро — 5. Найдите радиус сферы, проходящей через вершины М, А и В, если центр сферы лежит на плоскости MCD.

3.233. «У Сфера касается всех ребер правильной четырехугольной пирамиды с боковым ребром 10 и ребром основания 8. Найдите радиус этой сферы.

Задачи к 19.6. Вписанные и описанные шары и сферы

Шар и сфера, описанные около куба и вписанные в него

3.234. (Устно.) Докажите, что можно описать шар около: а) прямоугольного параллелепипеда; б) правильной призмы;

в) прямой треугольной призмы; г) правильной пирамиды; д) правильного тетраэдра. Как найти центр этого шара?

3.235. Найдите радиус сферы, вписанной в куб с ребром а. Определите расстояние от центра этой сферы до грани, ребра и вершины куба.

3.236. В куб с ребром а вписан шар. Найдите радиус шара, касающегося данного шара и трех граней куба, имеющих общую вершину.

3.237. В куб с ребром а вписан шар. Найдите радиус шара, касающегося данного шара и плоскостей трех граней куба, имеющих общую вершину.

3.238. «У В куб с ребром а вписан шар. Найдите наименьший радиус шара, касающегося двух соседних граней куба и данного шара.

3.239. В куб ABCDA₁B₁C₁D₁ с ребром а помещены два касающихся друг друга шара. Один из них касается трех граней куба, имеющих общую вершину А, а другой — трех граней куба, имеющих общую вершину C_v Найдите радиусы шаров, если они равны между собой.

3.240. «У В куб AECDA₁B₁C₁D₁ с ребром а помещены два касающихся друг друга шара. Один из них касается трех граней

Страницы учебника:

Все учебники по геометрии:

Геометрия, 7 класс (В. В. Шлыков) 2011
Задачи к урокам геометрии, 7-11 классы. (Зив Б.Г.) 1998
Геометрия, 7—9 классы (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.) 2010
Геометрия, 7—9 класс (Шарыгин И. Ф.) 1997
Геометрия, 7—9 класс (А. В. Погорелов) 2001
Геометрия, 7—11 класс (Погорелов А. В.) 1995

Задачи к урокам геометрии, 7-11 классы. (Зив Б.Г.) 1998
Геометрия, 7—9 классы (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.) 2010
Геометрия, 7—9 класс (Шарыгин И. Ф.) 1997
Геометрия, 7—9 класс (А. В. Погорелов) 2001
Геометрия, 7—11 класс (Погорелов А. В.) 1995
Геометрия, 8 класс (Г.П. Бевз, В.Г. Бевз, н.Г. Владимирова) 2008

Задачи к урокам геометрии, 7-11 классы. (Зив Б.Г.) 1998
Геометрия, 7—11 класс (Погорелов А. В.) 1995
Геометрия, 10—11 класс (И. М. Смирнова, В. А. Смирнов) 2008
Геометрия, 10 класс (Е. В. Потоскуев, Л. И. Звавич) 2008
Геометрия, 10 класс. Задачник (Е. В. Потоскуев, Л. И. Звавич) 2004
Геометрия, 10 класс (А. Д. Александров, А. Л. Вернер, В. И. Рыжик) 1999
Геометрия, 10—11 классы (Калинин Л. Ю., Терёшин Д. А.) 2011
Геометрия, 10—11 класс (Шарыгин И. Ф.) 1999
Геометрия, 10—11 классы (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.) 2009

Задачи к урокам геометрии, 7-11 классы. (Зив Б.Г.) 1998
Геометрия, 7—11 класс (Погорелов А. В.) 1995
Геометрия, 10—11 класс (И. М. Смирнова, В. А. Смирнов) 2008
Геометрия, 10—11 классы (Калинин Л. Ю., Терёшин Д. А.) 2011
Геометрия, 10—11 класс (Шарыгин И. Ф.) 1999
Геометрия, 10—11 классы (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.) 2009
Геометрия, 11 класс. Задачник (Е. В. Потоскуев, Л. И. Звавич) 2004

В сферу радиуса R вписана правильная четырёхугольная призма, у которой диагональ наклонена к плоскости основания под углом а?

В сферу радиуса R вписана правильная четырёхугольная призма, у которой диагональ наклонена к плоскости основания под углом а.

Найдите боковую поверхность призмы.

На этой странице находится вопрос Найдите радиус сферы, вписанный в куб, диагональ которого равна 2корня из 3?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Примеры заданий из ЕГЭ

Они используются в части В, то есть там, где нужно выполнить развернутое решение задания. Просто выбрать ответ здесь не удастся. Поэтому придется знать формулы и уметь их применять в различных ситуациях.

Первая группа заданий.
В ней известна длина диагонали куба. Требуется вычислить его объем или узнать площадь поверхности.

К примеру, известная величина может быть равна единице. Тогда, чтобы узнать объем и площадь, нужно воспользоваться формулами № 1 и 3. Но в них идет речь о ребре, а дана диагональ. Потребуется записать еще одну формулу.

Если посмотреть на чертеж куба и проведенную в нем диагональ, то можно увидеть, что образуется прямоугольный треугольник. Один его катет совпадает с ребром, второй — с диагональю грани, а гипотенузой оказывается диагональ куба.

Тогда можно записать теорему Пифагора: квадрат гипотенузы (d 2) равен квадрату перового катета (а 2), сложенному с квадратом второго (а√2) 2 . После выполнения преобразований получается, что ребро куба а так связано с диагональю, что равно d, деленному на корень квадратный из 3.

Теперь можно начала узнать ребро, а потом подсчитать объем и площадь. В конкретной задаче а=1/√3=(√3)/3. Тогда объем получается равным (√3)/9. Площадь же — два.

Вторая группа заданий.
Обратная предыдущей, когда известны площадь или объем, а требуется вычислить значение диагонали куба.

Примером может служить задача, в которой известна площадь поверхности, и она равна 8. Необходимо будет воспользоваться формулой №3 и той зависимостью, которая выведена в предыдущей задаче.

Сначала потребуется узнать длину ребра. Она равна квадратному корню из частного S на 6. После подстановки известной величины а=√(8/6)=√(4/3). Теперь осталось вычислить диагональ куба, возведя это число в квадрат и умножив его на 3. Получится 2.

Третья группа заданий
содержит данные о диагонали грани куба. В них необходимо узнавать объем или площадь тела. Возможен также вариант, в котором потребуется вычислить диагональ самого куба. В таких задачах рассуждения идут тем же путем, который рассмотрен в предыдущих случаях.

Свойства

Радиус вписанной сферы куба представляет собой половину ребра куба, так как диаметр такой сферы точно совпадает с самим ребром. Поэтому чтобы найти ребро куба через радиус вписанной сферы, нужно умножить последний на два. (рис.2.2) a=2r

Найти площадь стороны куба можно как площадь квадрата, стороной которого является ребро куба. Тогда, вместо того чтобы возводить во вторую степень ребро, нужно возвести удвоенный радиус вписанной в куб сферы. Площадь боковой поверхности куба и площадь полной поверхности куба будут равны четырем и шести таким площадям соответственно, так как они представлены эти количеством граней куба. S=a^2=4r^2 S_(б.п.)=4S=16r^2 S_(п.п.)=6S=24r^2

Чтобы вычислить объем, необходимо возвести в куб ребро a или удвоенный радиус вписанной сферы. Таким образом, мы получим, что объем куба через радиус сферы, вписанной в него, равен кубу этого радиуса, умноженному на 8. V=a^3=8r^3

Периметр куба, как сумма длин всех ребер по одной стороне, равен произведению длины одного ребра и двенадцать. Периметр, выраженный через радиус вписанной окружности, равен 24 таким радиусам. P=12a=24r

Диагональ стороны куба, то есть диагональ квадрата, вычисляется как произведение ребра куба на корень из двух, в данном случае она будет выглядеть как произведение радиуса вписанной сферы на 2 корня из двух. d=a√2=2√2 r

Чтобы найти диагональ куба через радиус вписанной сферы, воспользуемся готовой формулой для диагонали куба через ребро и подставим вместо него удвоенный радиус. (рис.2.1.) D=a√3=2√3 r

Радиус окружности, описанной вокруг куба, равен половине диагонали, как видно из рисунка. Так как диагональ куба равна удвоенному произведению радиуса и корня из трех, то разделив это выражение на два, коэффициенты сократятся, и останется только радиус, умноженный на корень из трех. (рис.2.3.) R=D/2=(2√3 r)/2=√3 r

Окружность вписана в куб

Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.

Свойства куба:

1. В кубе $6$ граней и все они являются квадратами.

2. Противоположные грани попарно параллельны.

3. Все двугранные углы куба – прямые.

4. Диагонали равны.

5. Куб имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.

6. Диагональ куба в $√3$ раз больше его ребра

7. Диагональ грани куба в $√2$ раза больше длины ребра.

Пусть $а-$длина ребра куба, $d-$диагональ куба, тогда справедливы формулы:

Площадь полной поверхности: $S_=6а^2=2d^2$

Радиус сферы, описанной около куба: $R=/$

Радиус сферы, вписанной в куб: $r=/$

При увеличении всех линейных размеров куба в $k$ раз, его объём увеличится в $k^3$ раз.

При увеличении всех линейных размеров куба в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

1. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$-высота(она же боковое ребро);

$S_$-площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Формулы вычисления объема и площади поверхности правильной пирамиды.

$h_a$ — высота боковой грани (апофема)

В основании лежат правильные многоугольники, рассмотрим их площади:

Для равностороннего треугольника $S=√3>/$, где $а$ — длина стороны.
Квадрат $S=a^2$, где $а$ — сторона квадрата.

Задачи на нахождение объема составного многогранника:

Разделить составной многогранник на несколько параллелепипедов.
Найти объем каждого параллелепипеда.
Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Последние опубликованные вопросы

15,6÷7 Помогите срочно очень надо дана равнобедренная трапеция АBCД,с основаниями ВС и АД. ВС=8см АН=3см.ВН-высота, проведенная к основанию АД. Найти АД ПОЖАЛУЙСТА ПОМАГИТЕ5. В раннобокой транецни один из угиов раксн 120°, днагональ транеции обраитуст оснонанием угол 30°. найдите оснонаниня грансции, ссаи се божовая сторона ранна 8 гм. В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большое основание на отрезки 10см и 30см. Найдите основания трапецииа) 50 см и 20 смб) 30 см и 20 смв) 40 см и 10 смг)… ДАНО:∆ЕКРЕР=0,75СМУГОЛ Р=40°УГОЛ К =20°НаЙТИ; РК 80 баллов Через точку о, лежащую между параллельными плоскостями альфа и бета, проведены прямые l и m. Прямая l пересекает плоскости альфа и бета в точках d1 и d2 соответственно, прямая M – в точка… 5. 3 балла) Найди значение выражения: -6,3 +(-0,9) -5,7 помогите пожалуйста Длины оснований трапеции равны 14 и 22. Найдите длину отрезка, соединяющего середину ее диагоналей 5. На рисунке прямые а и b перпендикулярны, 21 = 1100 Найдите углы 2, 3 и 4.2помогите пожалуйста не понемаю пж гиометрия Найдите углы, образованные при пересечении двух прямых, если один из них равен 32° пжпж соч Найдите модуль вектора ⃗⃗ =1 3 − 2⃗ , где = 6 + 3 и ⃗ = −2 + 3 .
Предметы

Остальные предметы Скрыть

Наверх

К началу

Последние заданные вопросы в категории Геометрия

Геометрия 07.09.2023 06:48 26 Малявин Андрей.

Начертить треугольник ABC. Постройте его образ: а) при симметрии относительно его высоты, выходяще

Ответов: 1

Геометрия 07.09.2023 06:03 29 Маяковский Максим.

Найдите основание CF, изображенной на рисунке трапеции CDEF, если известно, что DO=9, DE= 15, OF=12

Ответов: 1

Геометрия 07.09.2023 05:45 19 Миронова Даша.

Угол A равнобедренного треугольника ABC с основанием BC равен 36 градусов ; BF − биссектриса треуг

Ответов: 1

Геометрия 07.09.2023 05:38 8 Писарева Софья.

Точка М середина отрезка АВ,МВ=4.3дм.Найдите длину отрезка АВ в милиметрах.

Ответов: 1

Геометрия 07.09.2023 05:38 21 Евдокимов Данила.

Площадь одной клетки равна 1.Найдите площадь закрашенной фигуры

Ответов: 1

Геометрия 07.09.2023 05:37 14 Жармагамбетов Тамерлан.

В равнобедренном треугольнике одна из сторон равна 9,а другая 20.Найти основание треугольника.

Ответов: 1

Геометрия 07.09.2023 05:35 29 Штонда Александр.

Решить пожалуйста срочно буду благодарен,

Ответов: 1

Геометрия 07.09.2023 05:34 5 Пикулев Сергей.

1.Даны три точки с координатами: F(8; 1; 0), E(0; 0; 4), K(0; 5; 1). а) Постройте их в декартовой

Ответов: 1

Геометрия 07.09.2023 05:34 11 Анна Бушмельова.

как найти третью сторону треугольника если известно что две стороны равны и известны и известен угол

Ответов: 2

Геометрия 07.09.2023 05:34 26 Кусакина Светлана.

Задача по геометрии 10 класс

Ответов: 1

Нахождение радиуса описанной вокруг куба сферы (шара)

В данной публикации мы рассмотрим, чему равняется радиус сферы (шара), описанной около куба, а также как его можно вычислить, если известна длина ребра куба.

Примечание: Напомним, что вокруг любого куба можно описать шар.

Для начала начертим рисунок.

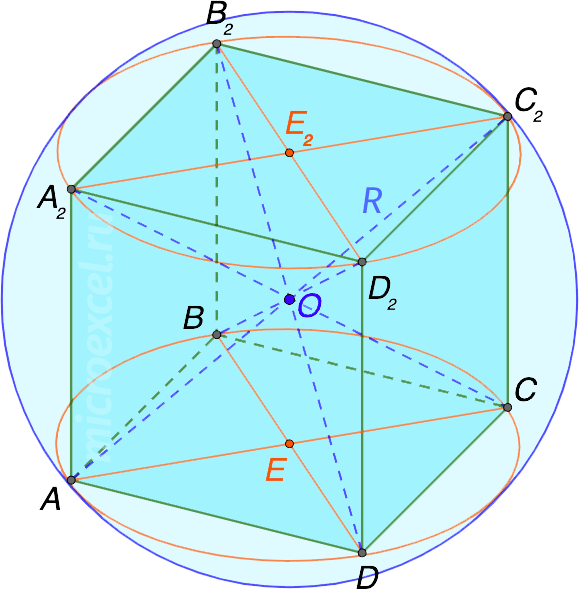
все 8 вершин куба касаются шара – это их общие точки;
центр шара – точка O, которая также является точкой пересечения диагоналей куба.

Радиус шара (R), описанного вокруг куба, равняется половине его диагонали, т.е.:

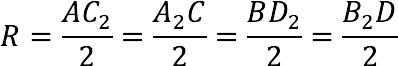
Примечание: все диагонали куба равны.

Чтобы было понятнее, выполним диагональное сечение, т.е. отсечем часть шара вместе со вписанным в него кубом по диагонали куба (линия отреза проходит через точку O).

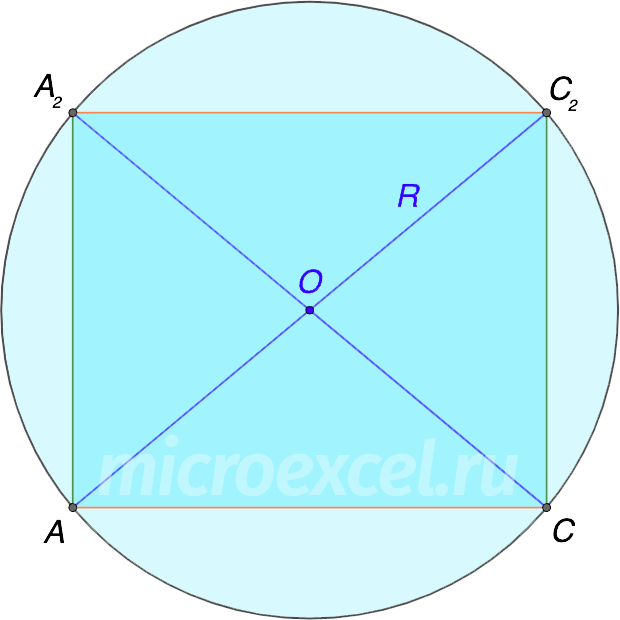
Таким образом, мы получим прямоугольник с описанной вокруг окружностью, радиус которой равняется половине диагонали прямоугольника.

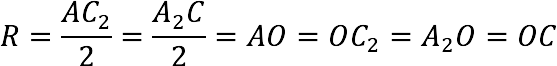
Примечание: Диагонали прямоугольника равны между собой и одновременно являются диагоналями куба.

Формула расчета радиуса описанного шара через ребро куба

Если известна длина ребра куба (примем ее за “a”), радиус описанного вокруг него шара (R) вычисляется следующим образом:

Нахождение радиуса вписанного в куб шара

В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.

Примечание: Напомним, что в любой куб можно вписать шар.

Для начала выполним чертеж.

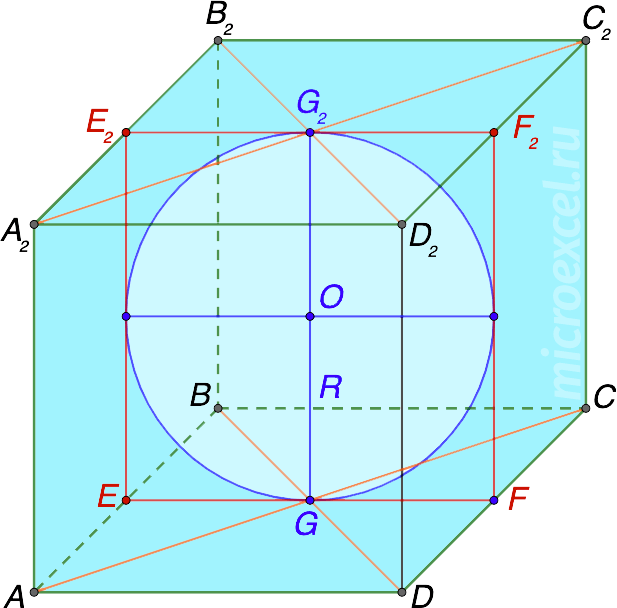
шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
центр шара – точка O, которая также является центром куба.

Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:

R = a/2, где “a” – ребро куба (является стороной его грани).

Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.

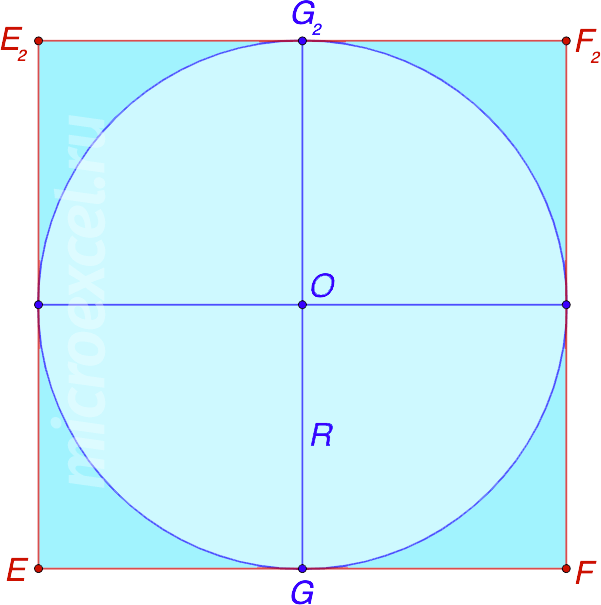
Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.

Радиус вписанного шара через диагональ куба

Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:

http://geleot.ru/education/math/geometry/calc/cube/radius_of_inscribed_sphere

Формула объема шара через его радиус

Объем шара вычисляется по следующей формуле:

Формула объема шара через радиус

V=43⋅π⋅R3V=frac{4}{3}cdotpicdot R^3V=34⋅π⋅R3

RRR — радиус данного шара.

Рассмотрим несколько примеров.

Задача 1

Шар вписан в куб, диагональ ddd которого равна 500 см.sqrt{500}text{ см.}5см. Найти объем шара.

Решение

d=500d=sqrt{500}d=5

Для начала необходимо определить длину стороны куба. Будем считать, что она равна aaa. Следовательно, диагональ куба, равна (исходя из теоремы Пифагора):

d=a2+a2+a2d=sqrt{a^2+a^2+a^2}d=a2+a2+a2

d=3⋅a2d=sqrt{3cdot a^2}d=3⋅a2

d=3⋅ad=sqrt{3}cdot ad=3⋅a

500=3⋅asqrt{500}=sqrt{3}cdot a5=3⋅a

a=5003a=sqrt{frac{500}{3}}a=35

a≈12.9aapprox12.9a≈12.9

Если в куб вписан шар, то его радиус равен половинке длины стороны этого куба. В результате имеем:

R=12⋅aR=frac{1}{2}cdot aR=21⋅a

R=12⋅12.9≈6.4R=frac{1}{2}cdot 12.9approx6.4R=21⋅12.9≈6.4

Заключительный этап — нахождение объема шара по формуле:

V=43⋅π⋅R3≈43⋅π⋅(6.4)3≈1097,5 см3V=frac{4}{3}cdotpicdot R^3approxfrac{4}{3}cdotpicdot (6.4)^3approx1097,5text{ см}^3V=34⋅π⋅R3≈34⋅π⋅(6.4)3≈197,5см3

Ответ

1097,5 см3.1097,5text{ см}^3.197,5см3.

🔮 В чем преимущество шарообразной формы?

Шарообразная форма имеет несколько преимуществ, которые делают ее полезной в различных областях:

Минимальная поверхность: шарообразная форма имеет минимальную поверхность в отношении своего объема. Это значит, что на единицу объема шара приходится меньше поверхности, чем на единицу объема других форм, что может быть полезно, например, для сокращения издержек при производстве.
Равномерность нагрузки: шарообразная форма имеет равномерное распределение нагрузки на поверхности, что позволяет ей лучше выдерживать внешнее давление.
Сферическая симметрия: шарообразная форма имеет сферическую симметрию, что означает, что она выглядит одинаково при любом повороте вокруг своей оси. Это может быть полезным, например, при проектировании оптических систем, таких как линзы и зеркала.
Простота: шарообразная форма является одной из самых простых геометрических форм, и ее параметры (радиус, диаметр, объем и т.д.) легко вычисляются.
Эстетика: шарообразная форма считается эстетичной и привлекательной для взгляда. Она широко используется в дизайне, искусстве и архитектуре для создания красивых и уникальных форм.

Немного теории о кубе

Этот многогранник относится сразу к прямым параллелепипедам и призмам. Он — частный случай того и другого. В основании куба лежит квадрат, и боковые ребра его равны стороне данного квадрата. Таким образом, все три измерения имеют одинаковые значения.

Все шесть граней куба представляют собой квадраты. Длина каждого из 12 ребер одинаковая.

В каждой из граней можно провести диагональ, длину которой легко найти по формуле Пифагора. Кроме того, сам куб имеет диагонали. Их всего четыре. Проводится диагональ куба так, чтобы начинаться из вершины нижнего основания. Конец этого отрезка оказывается в вершине верхнего основания, но так, чтобы не совпасть с диагональю квадрата.

Ответы на вопрос

Отвечает Федикович Вася.

Вписанный шар касается граней куба в их центрах. Расстояние между центрами противоположных граней куба — его высота, она равна ребру. Таким образом диаметр вписанного шара равен ребру куба.

Если ребро куба a, тогда диагональ грани a√2 и диагональ куба √(a^2 +2a^2)=a√3

14√3=a√3 => a=14

Радиус вписанного шара равен 7.

Отвечает Zhienbayev Nyrlan.

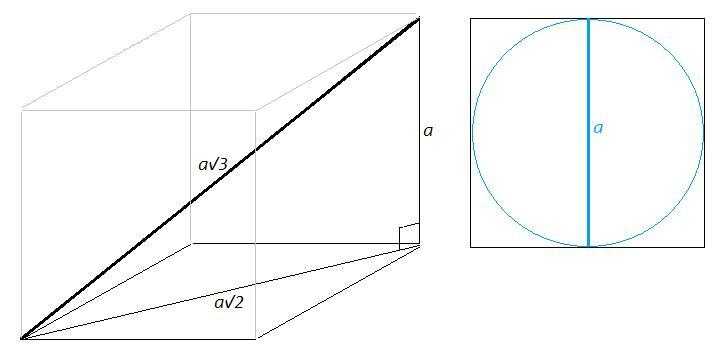
Для решения этой задачи нам понадобится найти связь между радиусом вписанного шара и диагональю куба.

Пусть r — радиус вписанного шара, и d — диагональ куба.

Рисунок представляет собой куб с вписанным шаром, а диагональ куба проходит через центр шара и соединяет противоположные вершины куба.

У нас есть два треугольника: прямоугольный треугольник с гипотенузой, равной диагонали куба, и равнобедренный треугольник с основанием, равным диаметру шара и высотой, равной радиусу шара.

Мы можем применить теорему Пифагора к прямоугольному треугольнику, чтобы найти длину половины диагонали куба:

(1/2) * d^2 = r^2 + r^2

d^2 = 4r^2

d = 2r * sqrt(2)

Также нам известно, что диагональ куба равна 14 * sqrt(3). Подставим это значение:

14 * sqrt(3) = 2r * sqrt(2)

Разделим обе части уравнения на 2 * sqrt(2):

7 * sqrt(3) = r * sqrt(2)

Теперь возводим обе части уравнения в квадрат:

147 = 2 * r^2

Теперь найдем радиус шара, выражая его из уравнения:

r^2 = 147 / 2

r = sqrt(147 / 2)

Таким образом, радиус шара равен sqrt(147 / 2), или можно упростить его дальше:

r = sqrt(73.5)

Таким образом, радиус шара равен sqrt(73.5).

Радиус сферы, вписанной в правильную n — угольную пирамиду

Задача. равна h , а длина равна a . Найти радиус

Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ … A_n и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).

Рис.7

Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем

(2)

В силу из формул (1) и (2) получаем

(3)

Поскольку

из формулы (3) получаем соотношение

Ответ.

Следствие 3. Радиус сферы, вписанной в с h и a, равен

Следствие 4. Радиус сферы, вписанной в с a, равен

Следствие 5. Радиус сферы, вписанной в с h и a, равен

Следствие 6. Радиус сферы, вписанной в с h и a, равен

Формулы вычисления радиуса цилиндра

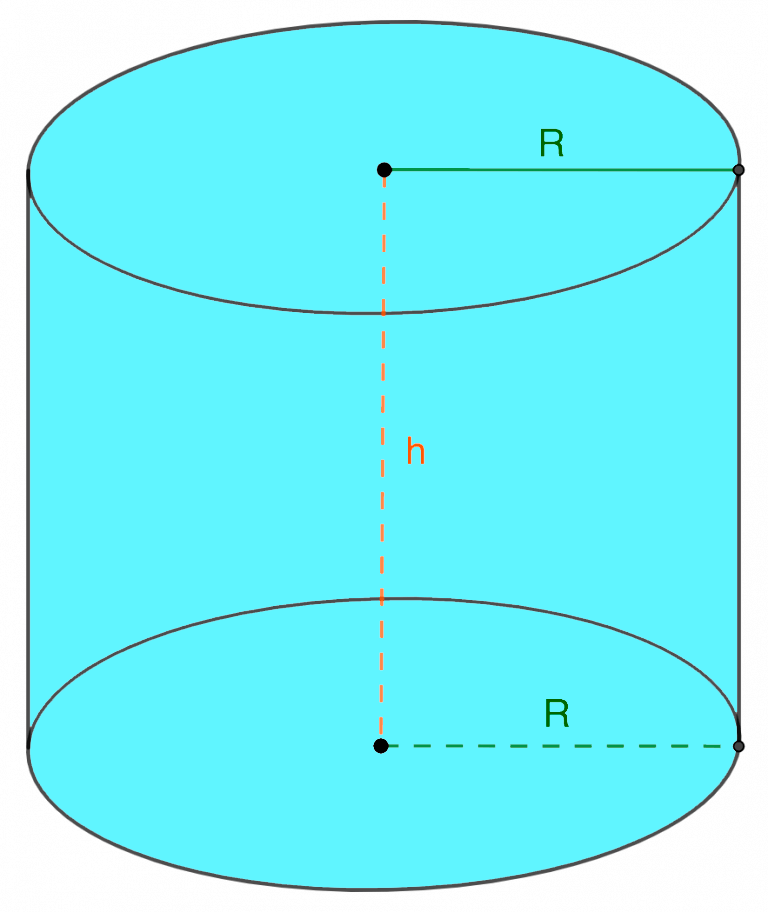
1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.

R – радиус основания цилиндра, т.е. окружности;
π – число, округленное значение которого равняется 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

3. Через полную площадь поверхности

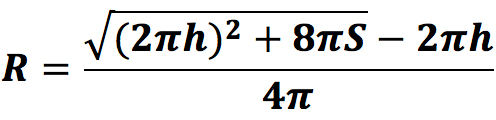
Данная формула получена следующим образом:

S – полная площадь поверхности фигуры, равная:

S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)

Возьмем первое выражение. Если перенести S в правую часть, получим:

2 π R 2 + 2 π Rh – S = 0

Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:

R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:

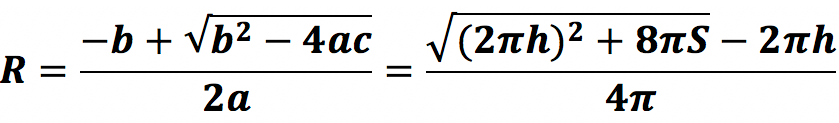
* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.

Нахождение радиуса вписанного в куб шара

Примечание: Напомним, что в любой куб можно вписать шар.

Для начала выполним чертеж.

шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
центр шара – точка O, которая также является центром куба.

Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:

R = a/2, где “a” – ребро куба (является стороной его грани).

Радиус вписанного шара через диагональ куба

Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:

Cube Formula — Что такое Cube Formula? Примеры

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.

Что такое формула куба?

Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.

Формула куба

Объем куба

Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.

Объем куба (на основе длины стороны) = a 3 кубических дюймов, где a – длина стороны куба
Объем куба (по диагонали) = (√3×d 3 )/9кубических дюймов, где d — длина диагонали куба

Боковая площадь куба

Боковая площадь куба равна сумме площадей всех боковых граней куба.

LSA куба = 4a 2

, где a — длина стороны.

Общая площадь куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a 2

, где a — длина стороны.

Диагональ куба

Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.

Диагональ куба = a√3

Давайте лучше разберемся с формулами куба на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры с использованием формулы куба

Пример 1: Найдите объем кубика Рубика длиной 4 дюйма. Решение:

Чтобы найти объем кубика Рубика: кубик Рубика0003

Длина стороны куба = 4 дюйма (дано)

Используя формулу куба, объем = с × с × с = с 3

Поместите значения,

объем = 4 × 4 × 4 = 4 3 = 64

Ответ: Объем кубика Рубика составляет 64 кубических дюйма.

Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба. Решение:

Чтобы найти диагональ куба:

Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)

Используя формулу куба,

диагональ = a√3

Поместите значения,

Диагональ = 64√3 = 110,848 дюйма

Ответ: Диагональ куба равна 110,848 дюйма

Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.

Решение:

Длина стороны куба, a = 25 дюймов

Используя формулу площади куба, а именно: A = 6a 2

Поместите значения,

A = 6 × 25 × 25 = 3750 квадратных дюймов

Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.

Как рассчитать диагональ куба по формуле куба?

Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .

Что такое s в формуле куба?

В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.

Как вывести формулу куба?

Чтобы вычислить объем по формуле куба,

Шаг 1: Рассмотрим любой квадратный лист бумаги.
Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s 2 ».
Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».

Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s 2 × s = s 3

Чтобы вывести формулу поверхности куба,

Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s 2 » (длина, умноженная на ширину).
Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s 2

Страница № 115.

OCR-версия страницы из учебника (текст страницы, которая находится выше):

В сферу радиуса R вписана правильная четырёхугольная призма, у которой диагональ наклонена к плоскости основания под углом а?

Примеры заданий из ЕГЭ

Свойства

Окружность вписана в куб

Свойства куба:

Прямоугольный параллелепипед

Пирамида

Последние опубликованные вопросы

Последние заданные вопросы в категории Геометрия

Нахождение радиуса описанной вокруг куба сферы (шара)

Нахождение радиуса вписанного в куб шара

Формула объема шара через его радиус

🔮 В чем преимущество шарообразной формы?

Немного теории о кубе

Ответы на вопрос

Радиус сферы, вписанной в правильную n — угольную пирамиду

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

2. Через площадь боковой поверхности

3. Через полную площадь поверхности

Нахождение радиуса вписанного в куб шара

Cube Formula — Что такое Cube Formula? Примеры

Что такое формула куба?

Формула куба

Примеры с использованием формулы куба

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Как рассчитать диагональ куба по формуле куба?

Что такое s в формуле куба?

Как вывести формулу куба?

Свойства

Похожие записи:

Похожие записи: