В четырехугольной пирамиде abcd вписана окружность

Правильный многогранник

Многогранник называется правильным, если его грани одинаковые правильные многоугольники. 

Существует пять различных многогранников.

Обозначения

Пусть $a$ длина ребра, $d$ число рёбер, выходящих из одной вершины, $k$ число сторон многоугольников, образующие грани многогранника, $s$ количество граней многогранника, $t$ число вершин, а $i$ общее число рёбер.

Эйлерова характеристика

$$s + t — i = 2$$

Справедливо и 

$$ks = dt = 2i.$$

Название	число граней	вид грани
тетраэдр	4	равносторонний треугольник
куб	6	квадрат
октаэдр	8	равносторонний треугольник
додекаэдр	12	правильный пятиугольник
икосаэдр	20	равносторонний треугольник

с	радиус описанной сферы	радиус вписанной сферы
4	$\frac{a}{4}\sqrt 6 $	$\frac{a}`12`\sqrt 6 $
6	$\frac{a}{2}\sqrt 3 $	$\frac{a}{2}$
8	$\frac{a}{2}\sqrt 2 $	$\frac{a}{6}\sqrt 6 $
12	$\frac{a}{4}\left( {1 + \sqrt 5 } \right)\sqrt 3 $	$\frac{a}{4}\sqrt {10 + \frac`22`{{\sqrt 5 }}} $
20	$\frac{a}{4}\sqrt {2\left( {5 + \sqrt 5 } \right)} $	$\frac{a}{{4\sqrt 3 }}\left( {3 + \sqrt 5 } \right)$

с	площадь	объём
4	${a^2}\sqrt 3 $	$\frac{{{a^3}}}`12`\sqrt 2 $
6	$6{a^2}$	${a^3}$
8	$2{a^2}\sqrt 3$	$\frac{{{a^3}}}{3}\sqrt 2 $
12	$3{a^2}\sqrt {25 + 10\sqrt 5 }$	$\frac{{{a^3}}}{4}\left( {15 + 7\sqrt 5 } \right)$
20	$5{a^2}\sqrt 3 $	$\frac{5}`12`{a^3}\left( {3 + \sqrt 5 } \right)$

SLIKA

Презентация на тему: » Правильная треугольная пирамида, вписанная в шар АQ = ВQ = CQ = SQ= R – радиус шара. AO = BO = CO = r – радиус круга, описанного около основания пирамиды.» — Транскрипт:

2

Правильная треугольная пирамида, вписанная в шар АQ = ВQ = CQ = SQ= R – радиус шара. AO = BO = CO = r – радиус круга, описанного около основания пирамиды. SO = H – высота пирамиды. SЕ = h – апофема пирамиды. P E T C A B R r H O S Q

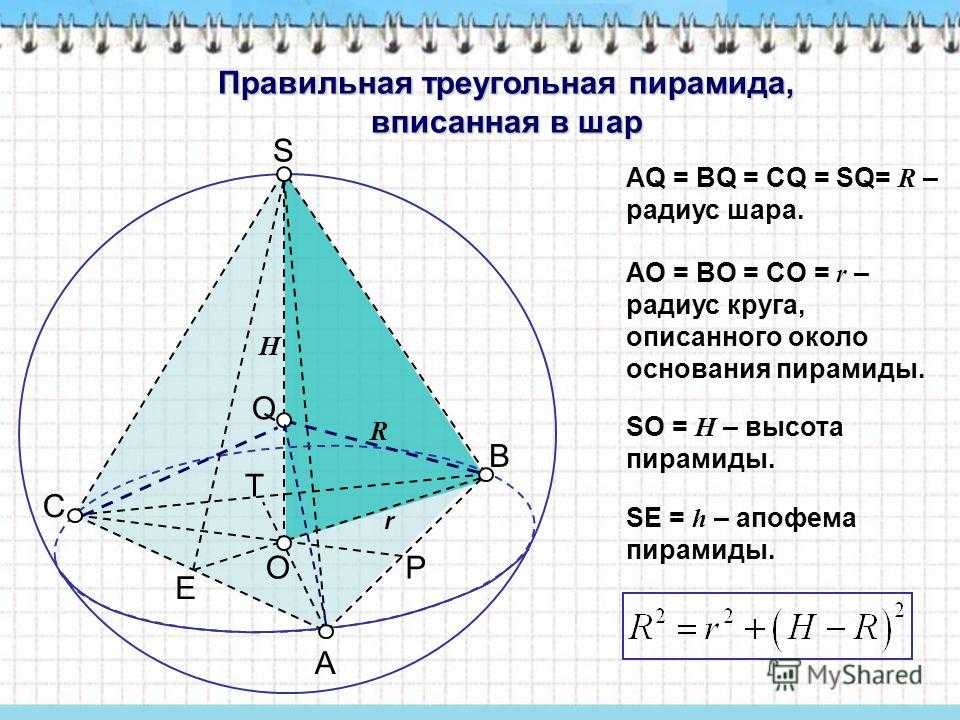
3

Правильная четырехугольная пирамида, вписанная в шар AQ = BQ = CQ = DQ = = SQ = R – радиус шара. AO = BO = CO = DO = r радиус круга, описанного около основания пирамиды. SO = H – высота пирамиды. SЕ = h – апофема пирамиды. P E D C A B R r H O S Q

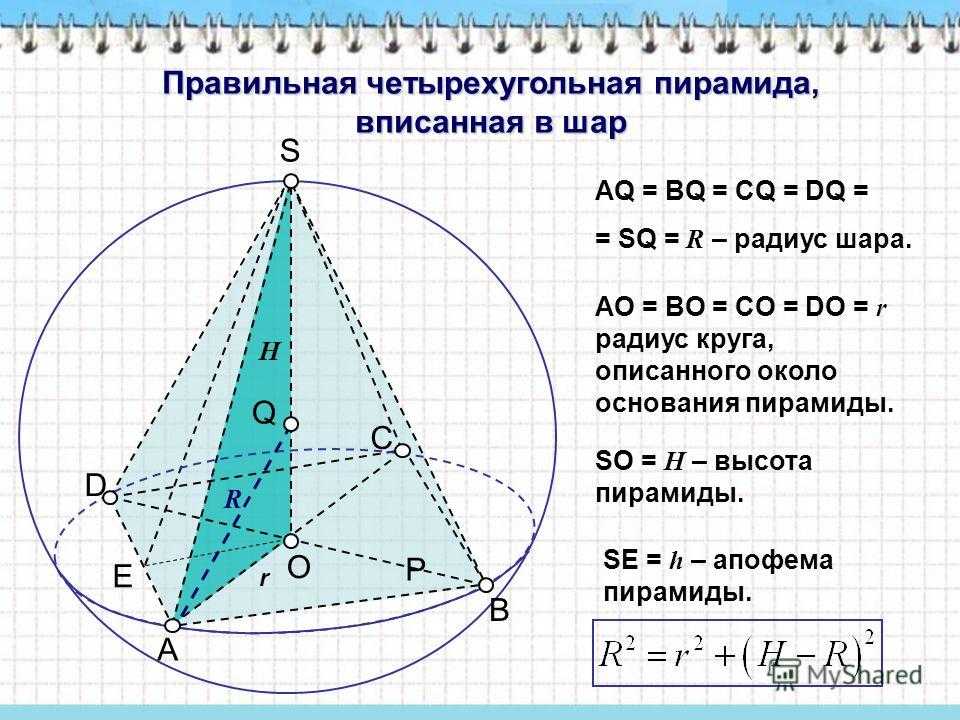
4

Треугольная пирамида описана около шара E 1 Q = OQ = TQ = R – радиус шара. EO = PO = r – радиус круга, вписанного в основание пирамиды. A B C O S P E Q E1E1 T r E1E1 E O Q S R R r r SO = H – высота пирамиды. R

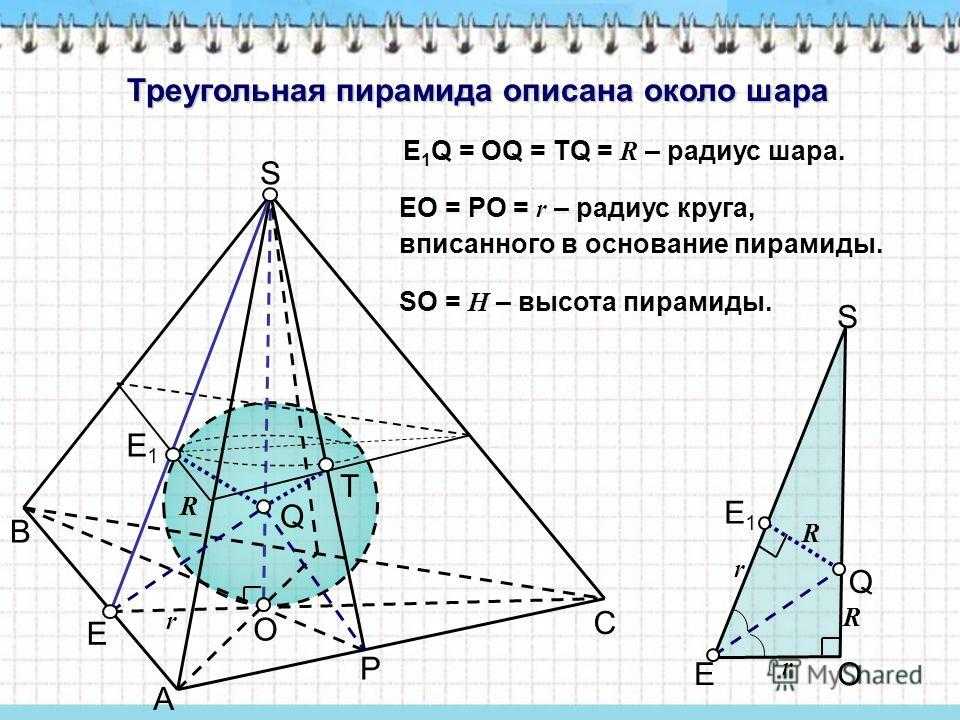
5

A B C O S D E Q E1E1 M P P1P1 Четырехугольная пирамида описана около шара E 1 Q = P 1 Q = OQ = R – радиус шара. EO = PO = r – радиус круга, вписанного в основание пирамиды. SO = H – высота пирамиды. R EP S E1E1 P1P1 O r

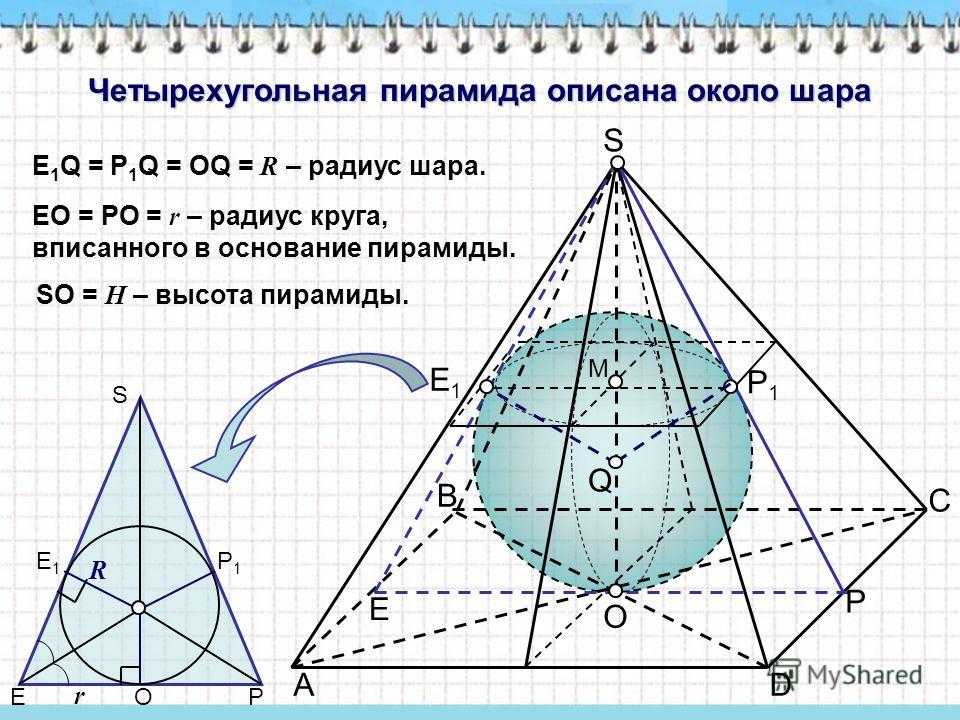
6

Задачи Шар вписан в пирамиду. Пирамида вписана в шар. Сфера вписана в конус. Куб вписан в конус. Шар вписан в конус.

7

A B C O S D P Q P1P1 В правильную четырехугольную пирамиду вписан шар, объем которого 32 /3. Найдите объем пирамиды, если её высота равна 6. Решение. 1) тогда 2) 3) SP 1 Q – прямоугольный, 4) SP 1 Q SOP ( Р 1 = О=90, S – общий), откуда 5) Тогда сторона основания пирамиды вдвое больше, и равна 6) Ответ:

8

В шар, объём которого, вписана правильная четырехугольная пирамида. Найдите объём пирамиды, если её боковое ребро равно, а высота больше радиуса шара. D C A B O S Q Решение. 1)тогда 2) Пусть OQ = x, тогда из AOQ выразим сторону АО: x 3) Составим теорему Пифагора для ASO: 5 5 Откуда находим OQ = 4. 4) Тогда SO = 5+4=9, 5) В основании пирамиды квадрат, со стороной a, равной 6) Ответ: и АО = 3. 2

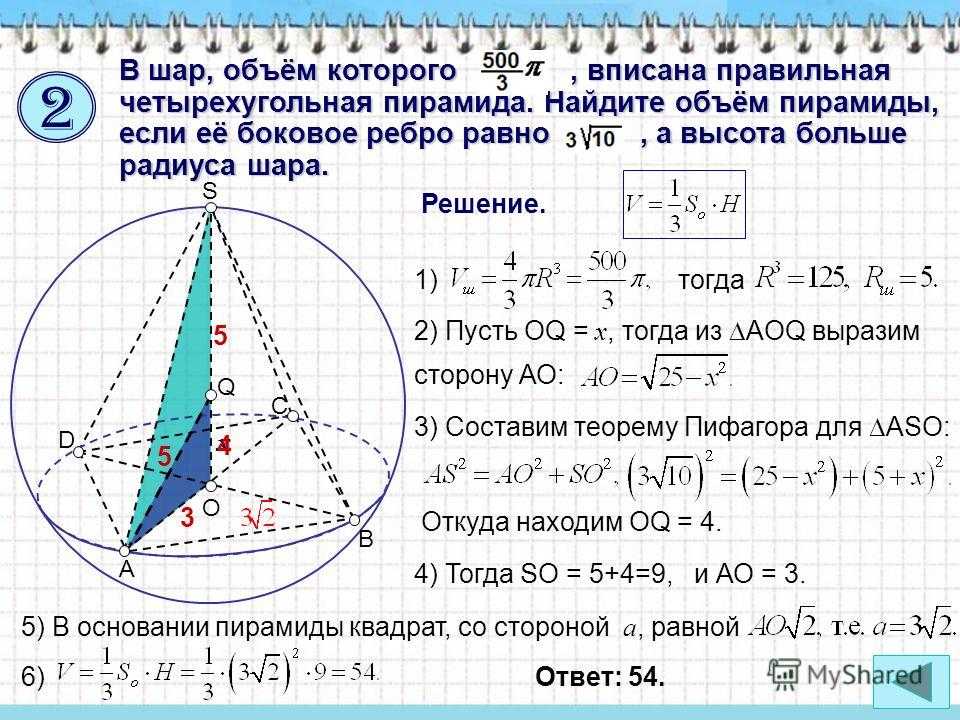
9

Площадь поверхности сферы, вписанной в конус, равна 100. Длина окружности, по которой сфера касается поверхности конуса, равна 6. Найдите радиус основания конуса. Решение. A B O S О1О1 РО2О2 1) C = 2 r = 6, тогда r = O 2 P = 3. 2) S сферы = 4 R 2 =100, тогда R = O 1 P = 5. 3) Из O 1 O 2 P по теореме Пифагора находим: 4) В O 1 PS отрезок РО 2 высота, проведенная из вершины прямого угла, значит 5) Найдем высоту конуса SO= SO 2 +O 2 O 1 +O 1 O = 2, = 11,25. 6) SО 2 Р SOВ ( О 2 = О=90, S – общий), откуда Ответ: ,

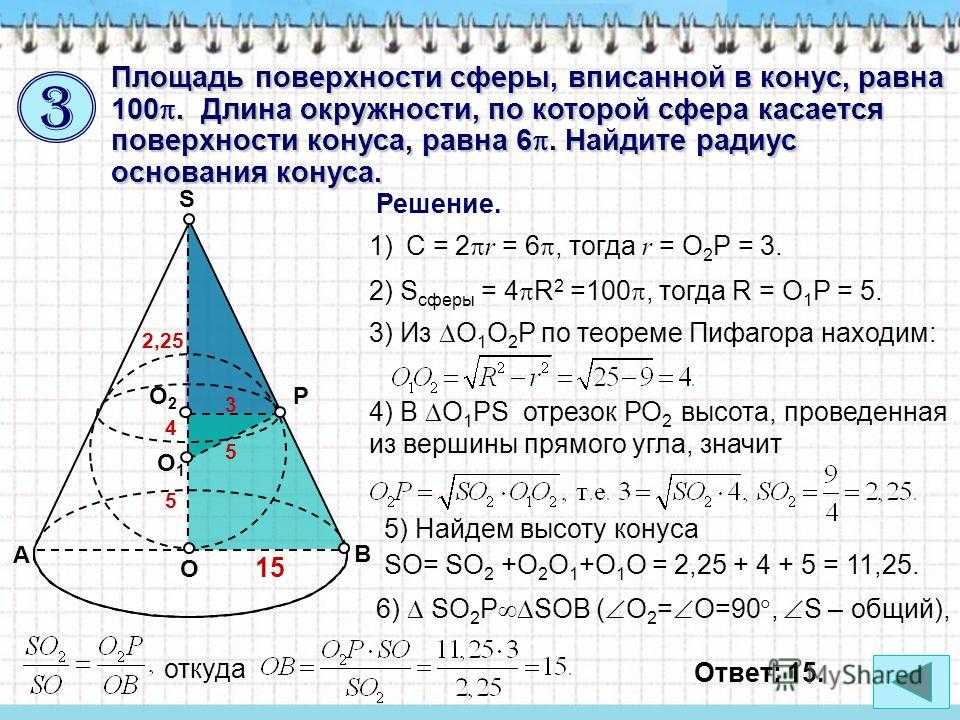
10

O S О1О1 Р Р1Р1 В конус с образующей 6 6 и высотой 12 вписан куб. Найдите объём куба. Решение. 2) a – сторона куба, тогда 3) Выразим через a: 4) SО 1 Р 1 SOР ( О 1 = О=90, S – общий), откуда a = 6. 1) Из прямоугольного SOP находим: 5) V куба = a 3 = 6 3 = 216. Ответ:

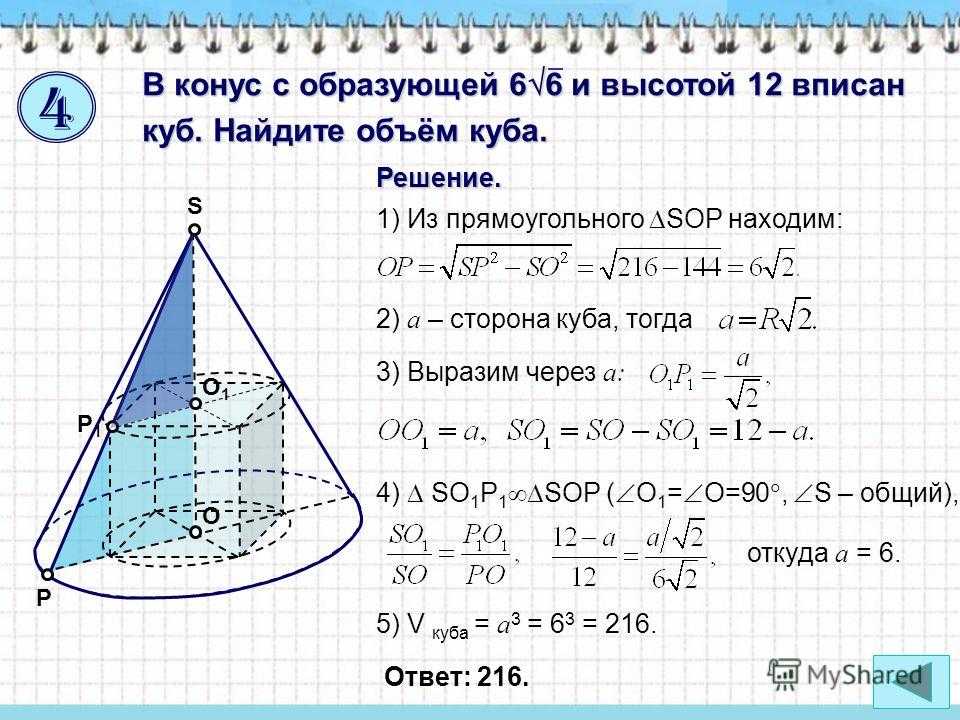
11

Площадь основания конуса равна площади поверхности вписанного в него шара. Найдите радиус шара, если образующая конуса равна 10. O S О1О1 Р Р1Р1 Решение. 1) Обозначим радиус шара r, а радиус основания конуса R. 2) По условию т.е. 3) SP 1 O 1 SOP ( Р 1 = О=90, S – общий), откуда SO 1 = 5, 5 5) Тогда коэффициент подобия треугольников k = ½. 2r2r 2r2r 10-2r откуда r = 3. 4) Заметим, что РР 1 = 2 r, SP 1 = 10 – 2 r, SO = 5+ r. Ответ: 3. r r 5

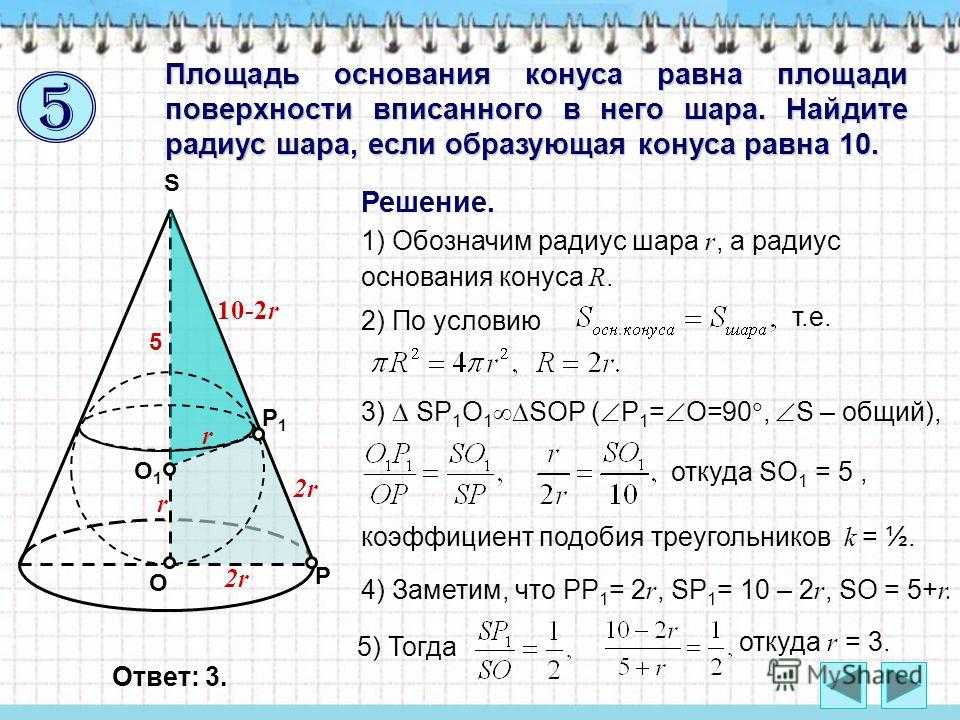
12

Ответ: Высота конуса равна 6, а объём равен 144. Найдите площадь полной поверхности куба, вписанного в конус Шар объём которого равен 32 /3, вписан в конус. Найдите высоту конуса, если радиус его основания равен Ответ:

13

Реши задачу и оформи решение либо на альбомном листе, либо в виде электронного документа (PowerPoint, Paint, Word и т.д.) Что нового вы узнали на уроке? Домашнее задание Рефлексия Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня? Чему вы научились? Какое у вас настроение в конце урока?

14

Использованные ресурсы 1. Готман Э.Г. Стереометрические задачи и методы их решения. М.: МЦНМО, с. 2. Гусев В. А., Литвиненко В. Н., Мордкович А. Г. Практикум по элементарной математике. Геометрия. М.: Просвещение, Комплект таблиц по стереометрии: Единый государственный экзамен 2001: Тестовые задания: Математика/С.В. Климин, Т.В. Стрункина, Е.И. Пантелеева и др.; М-во образования РФ. – М.: Просвещение, Для создания шаблона презентации использовалась картинка и шаблон с сайта Рисунки на слайдах 6, 12, 13 взяты с сайта: ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D 0%BB%D1%8B ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D 0%BB%D1%8B

2 ответа

Эту задачу можно довольно быстро решить при помощи подсчёта объёмов. Нам здесь известна площадь основания пирамиды и её высота. Отсюда легко находится объём. Далее, если соединить центр вписанного шара с вершинами, то получатся четыре пирамиды с одинаковыми высотами, равными радиусу шара. Если сложить объёмы этих пирамид, то получится объём всей пирамиды. Из этих соображений следует, что объём пирамиды равен $%frac13rS$%, где $%S$% — сумма площадей всех граней пирамиды. Её легко подсчитать, и отсюда сразу выражается $%r$%.

Этот способ быстро приводит к ответу, но его недостаток в том, что теория объёмов в курсе стереометрии изучается в самом конце, а задача этого типа может быть предложена раньше. Поэтому рассмотрим другой способ.

Пусть $%O$% — центр вписанного шара, а $%r$% — его радиус. Из соображений симметрии следует, что точка $%O$% лежит в плоскости, проходящей через высоту $%SA$% и середину $%K$% стороны $%BC$%. Треугольник $%SAK$% можно нарисовать на отдельном чертеже. Точка $%O$% лежит на биссектрисе угла при вершине $%K$%. Ясно, что $%AK=sqrt3$%, $%SK=2$%. Пусть $%O_1$% — проекция точки $%O$% на $%AK$%. Расстояние $%OO_1$% равно $%r$%, и теперь можно выразить расстояние $%O_1K$%. Для этого можно сначала найти котангенс угла $%OKO_1$%. Угол здесь равен 15 градусам, поскольку $%SKA$% равен 30 градусам. Это можно сделать через формулы половинного угла, но можно обойтись и без тригонометрии, применив свойство биссектрисы. Она делит сторону $%SA$% в отношении $%KS:KA=2:sqrt$%, то есть отрезки имеют длины $%2t$% и $%sqrt3t$%. В сумме они равны $%SA=1$%, откуда $%t=1/(2+sqrt3)$%, а сами отрезки равны $%2/(2+sqrt3)$% и $%sqrt3/(2+sqrt3)$%. Из подобия треугольников $%KOO_1$% и $%KLA$%, где $%L$% — основание биссектрисы, находим $%O_1K=r(KA:AL)=r(2+sqrt3)$%.3>

Теперь спроектируем точку $%O_1$% на прямую $%AB$% в плоскости основания пирамиды. Пусть $%O_2$% — основание опущенного перпендикуляра. Расстояние $%O_1O_2$% равно $%r$%, так как это расстояние от точки $%O$% до плоскости $%SAB$%. Действительно, прямая $%OO_1$% параллельна $%SA$%, а потому параллельна плоскости $%SAB$%. Расстояние от точки $%O$% до этой плоскости, равное $%r$%, равно расстоянию до этой же плоскости от точки $%O_1$%. Оно измеряется по перпендикуляру, но прямая $%O_1O_2$% перпендикулярна как $%AB$% (по построению), так и $%SA$% (поскольку $%O_1O_2$% лежит в основании пирамиды). Таким образом, $%O_1O_2=r$%, но при этом $%O_1O_2$% есть катет прямоугольного треугольника $%AO_1O_2$% с углом 30 градусов при вершине $%A$%. Из этого следует, что $%AO_1=2O_1O_2=2r$%.

Теперь можно составить уравнение: $%sqrt3=AK=AO_1+O_1K=2r+(2+sqrt3)r$%, откуда $$r=frac=frac.$$13>

«>

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

      Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду, все вершины которой лежат на сфере (рис. 1).

      Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.

Рис.1

      Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

      Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.

Рис.2

      На рисунке 2 изображена пирамида   SA1A2 … An ,   вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник   A1A2 … An   – основание пирамиды. Доказано.

      Теперь предположим, что около основания   A1A2 … An   пирамиды   SA1A2 … An   можно описать окружность. Докажем, что в этом случае около пирамиды   SA1A2 … An   можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника   A1A2 … An , символом   O’   и проведем прямую   p,   проходящую через точку   O’   и перпендикулярную к плоскости многоугольника   A1A2 … An   (рис. 3).

Рис.3

      Рассмотрим плоскость   β,   проходящую через середину отрезка   SAn   и перпендикулярную к этому отрезку. Если обозначить буквой   O   точку пересечения плоскости   β   с прямой   p,   то точка   O   и будет центром сферы, описанной около пирамиды   SA1A2 … An .   Для того, чтобы это доказать, рассмотрим следующий рисунок 4.

Рис.4

      Докажем, что точка   O   находится на одном и том же расстоянии от точек   S ,   A1 ,   A2 ,   …  ,   An .   Поскольку точка   O   лежит на серединном перпендикуляре к отрезку   SAn ,   то расстояния   OS   и   OAn   равны. С другой стороны, отрезки   OA1 ,   OA2 ,   …  ,   OAn   как гипотенузы в равных прямоугольных треугольниках   OO’A1 ,   OO’A2 ,   …  ,   OO’An .   (Треугольники   OO’A1 ,   OO’A2 ,   …  ,   OO’An   равны, так как у них катет   OO’   общий, а катеты O’A1 ,   O’A2 ,   … ,   O’An равны как радиусы окружности, описанной около многоугольника   A1A2 … An  ).

      Итак, мы доказали, что точка   O   находится на одном и том же расстоянии от всех вершин пирамиды   SA1A2 … An .   Отсюда вытекает, что точка   O   является центром сферы, описанной около пирамиды   SA1A2 … An .

      Для завершения доказательства теоремы остается лишь доказать, что плоскость   β   и прямая   p   действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость   β   и прямая   p   параллельны, а, значит, точка   S   лежит в плоскости   A1A2 … An ,   что противоречит определению пирамиды.

      Теорема доказана.

      Следствие 1. Около любой правильной пирамиды можно описать сферу.

      Следствие 2. Если у пирамиды все боковые ребра равны, то около нее можно описать сферу.

      Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. Посмотреть доказательство.

Формулы расчета радиуса шара (сферы)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

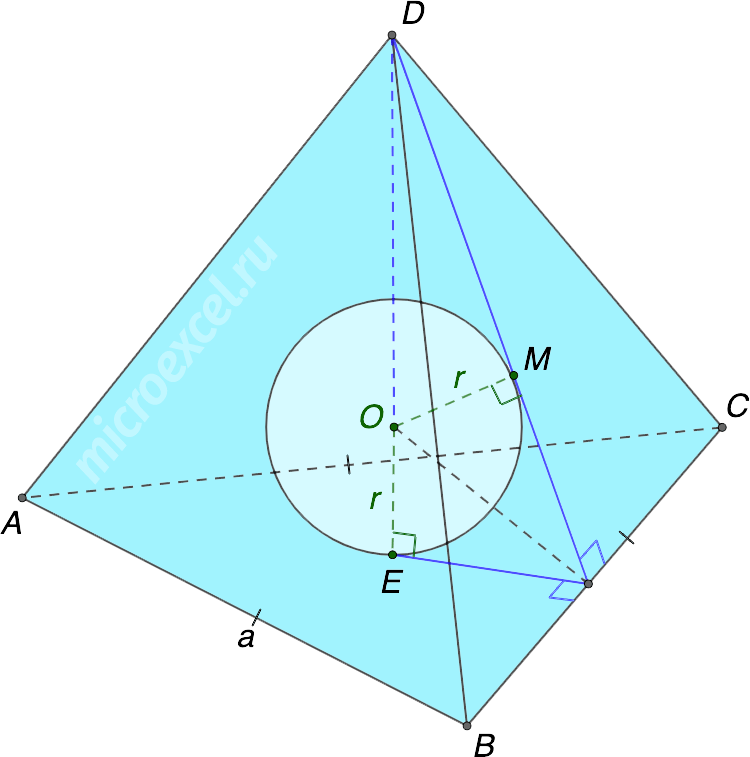
• a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;

Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:

Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:

Правильная четырехугольная пирамида

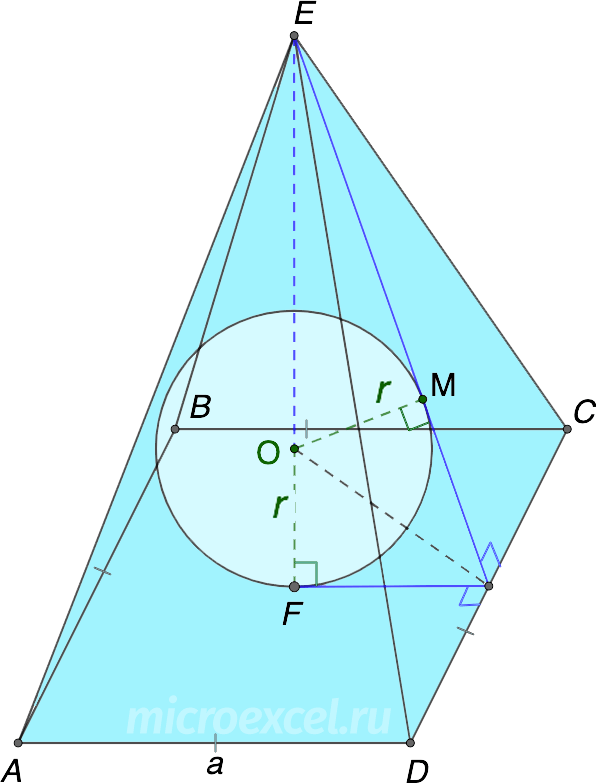
• a – ребро основания пирамиды, т.е. AB, BC, CD и AD;
• EF – высота пирамиды (h).

Радиус (r) вписанного шара/сферы рассчитывается так:

Правильная шестиугольная пирамида

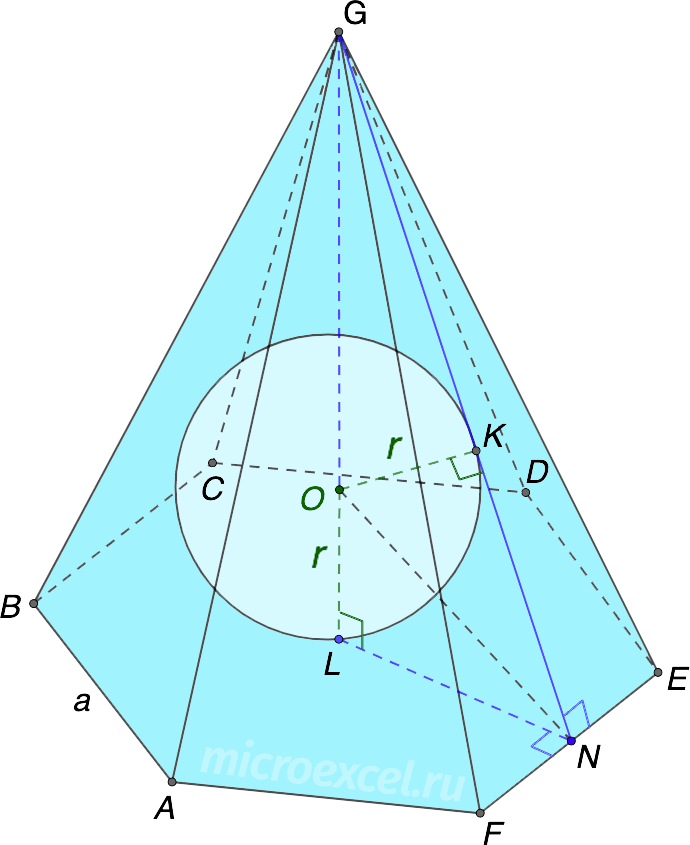
• a – ребро основания пирамиды, т.е. AB, BC, CD, DE, EF, AF;
• GL – высота пирамиды (h).

Радиус (r) вписанного шара/сферы вычисляется по формуле:

Формулы расчета радиуса шара (сферы)

Приведенная ниже информация относится только к обычным пирамидам. Формула нахождения радиуса зависит от типа фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На изображении:

• а — ребро основания пирамиды, т е это равные отрезки АВ, АС и ВС;
• DE – высота пирамиды (h).

Если известны значения этих величин, можно найти радиус (r) вписанного шара/сферы по формуле:

Частным случаем правильной треугольной пирамиды является правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:

Правильная четырехугольная пирамида

На изображении:

• а — ребро основания пирамиды, т е. АВ, ВС, CD и AD;
• EF – высота пирамиды (h).

Радиус (r) вписанного шара/сферы рассчитывается следующим образом:

Правильная шестиугольная пирамида

На изображении:

• а — ребро основания пирамиды, т.е. АВ, ВС, CD, DE, EF, AF;
• GL — высота пирамиды (h).

Радиус (r) вписанного шара/сферы рассчитывается по формуле:

Как найти радиус вписанного в правильную пирамиду шара (сферы): формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение радиуса шара (сферы), вписанного в правильную пирамиду

В данной публикации представлены формулы, с помощью которых можно найти радиус шара (сферы), вписанного в правильную пирамиду: треугольную, четырехугольную, шестиугольную и тетраэдр.

• Формулы расчета радиуса шара (сферы)
  • Правильная треугольная пирамида
  • Правильная четырехугольная пирамида
  • Правильная шестиугольная пирамида

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На рисунке:

• a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;
• DE – высота пирамиды (h).

Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:

Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:

Правильная четырехугольная пирамида

На рисунке:

• a – ребро основания пирамиды, т.е. AB, BC, CD и AD;

EF – высота пирамиды (h).

Радиус (r) вписанного шара/сферы рассчитывается так:

Правильная шестиугольная пирамида

На рисунке:

• a – ребро основания пирамиды, т. е. AB, BC, CD, DE, EF, AF;
• GL – высота пирамиды (h).

Радиус (r) вписанного шара/сферы вычисляется по формуле:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Шаровой слой.

Часть шара, заключенная между двумя параллельными секущими плоскостями, называется шаровым слоем. Отрезок перпендикуляра, заключенный между параллельными секущими плоскостями, называется высотой шарового слоя и шарового пояса.

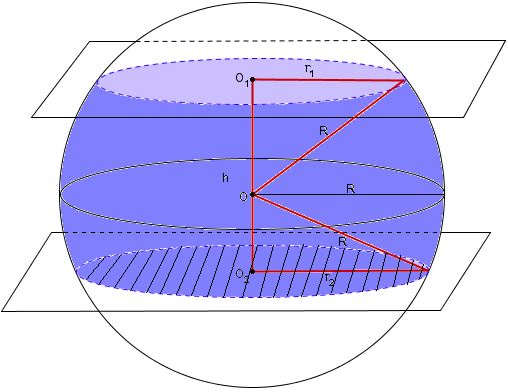
Площадь внешней поверхности шарового слоя

\

где $h$ − высота шарового слоя, $R$ − радиус шара.

Площадь полной поверхности шарового слоя

\

где $h$ − высота шарового слоя, $R$ − радиус шара, ${r_1^2,r_2^2}$ — радиусы оснований шарового слоя, а ${S_1},{S_2}$ — площади этих оснований.

Объём шарового слоя

\

где ${r_1^2,r_2^2}$ − радиусы оснований шарового слоя, $h$ − его высота.

Шар, вписанный в пирамиду

Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.

Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).

Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.

Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.

Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.

В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.

В треугольнике SOF применим свойство биссектрисы треугольника:

Из прямоугольного треугольника OO1F

При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.

Теперь найдем отношение объема пирамиды к площади ее поверхности:

Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:

Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны ).

В основании пирамиды SABC лежит правильный треугольник со стороной 2. Высота пирамиды SA=1. Найдите радиус шара вписанного в данную пирамиду..

задан 17 Дек ’13 16:41

Leva319 1.7k ● 1 ● 11 ● 54 77&#037 принятых

Тут в условии есть явное несоответствие. Если пирамида обозначена как $%SABCD$%, то в основании лежит не треугольник, а четырёхугольник.

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

http://www-formula.ru/2011-09-24-00-40-48

Радиус сферы, описанной около правильной n – угольной пирамиды

      Задача 1. Высота правильной n – угольной пирамиды равна   h ,   а длина ребра основания равна   a .   Найти радиус сферы, описанной около пирамиды.

      Решение. Рассмотрим правильную n – угольную пирамиду   SA1A2 … An   и обозначим буквой   O   центр описанной около пирамиды сферы, а символом   O’   – центр основания пирамиды. Проведем плоскость   SO’An   (рис. 5).

Рис.5

      Буквой   R   на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой   r   – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника   O’OAn   получаем

R2 = (h – R)2 + r2;

R2 = h2 – 2hR + R2 + r2;

2hR = h2 + r2.

      Следовательно,

(1)

      Поскольку

из формулы (1) получаем соотношение

(2)

      Ответ.

      Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой   h   и ребром основания   a ,   равен

      Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром   a ,   равен

      Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой   h   и ребром основания   a ,   равен

      Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой   h   и ребром основания   a ,   равен

Формулы расчета радиуса шара (сферы)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На рисунке:

• a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;
• DE – высота пирамиды (h).

Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:

Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:

Правильная четырехугольная пирамида

На рисунке:

• a – ребро основания пирамиды, т.е. AB, BC, CD и AD;
• EF – высота пирамиды (h).

Радиус (r) вписанного шара/сферы рассчитывается так:

Правильная шестиугольная пирамида

На рисунке:

• a – ребро основания пирамиды, т.е. AB, BC, CD, DE, EF, AF;
• GL – высота пирамиды (h).

Радиус (r) вписанного шара/сферы вычисляется по формуле: