Определение шара и сферы
Шар – это совокупность всех точек в трехмерном пространстве, которые находятся на расстоянии не больше заданного от точки, называемой центром шара (на рисунке ниже – это точка O). Другими словами, это совокупность точек, ограниченных сферой.
Шар образуется путем вращения круга вокруг своего диаметра (оси) на 180° или полукруга – на 360°.
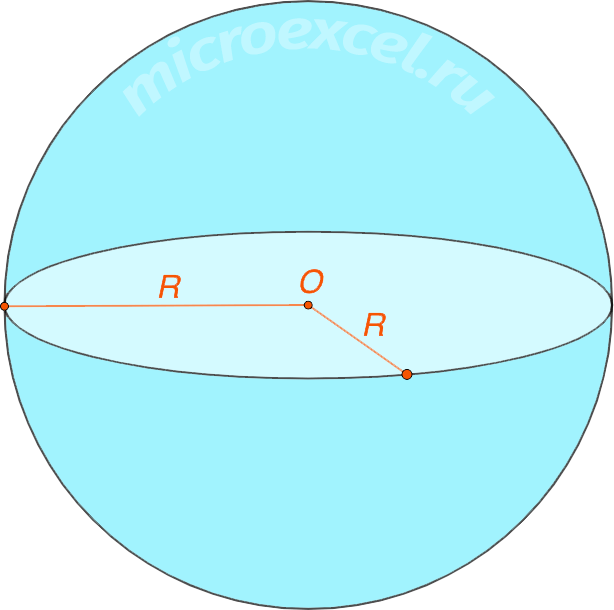
Сфера – это поверхность шара. Образуется путем вращения окружности вокруг своего диаметра на 180° или полуокружности – на 360°.
Различают два вида шаров:
- замкнутый – включает сферу;
- открытый – исключает сферу.
Радиус шара (сферы) – расстояние между центром и точками, лежащими на его поверхности. На рисунке выше обозначен буквой R.
Диаметр шара (сферы) – отрезок, проходящий через центр шара и соединяющие две противоположные точки на его поверхности. Совпадает с осью шара, обычно обозначается буквой d.
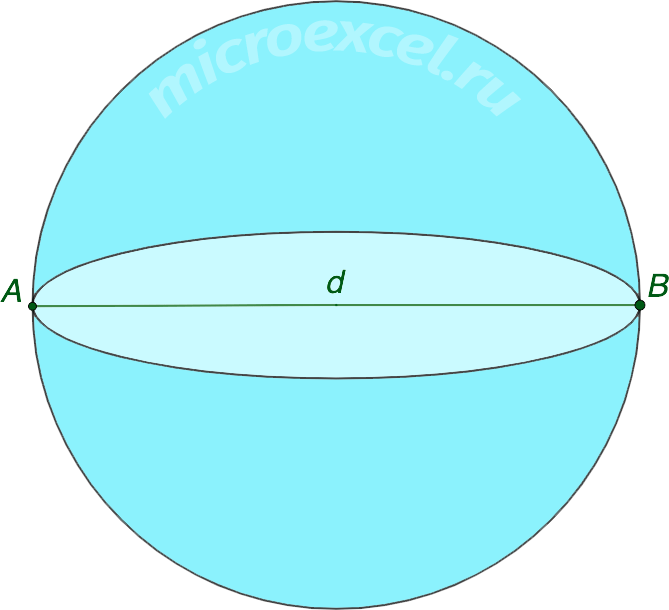
Полюсы шара (сферы) – точки A и B, расположенные на концах его диаметра.
Геометрия на сфереПравить
Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Большие окружности являются геодезическими линиями на сфере; любые две из них пересекаются в двух точках. Иными словами, большие круги сферы являются аналогами прямых на плоскости, расстояние между точками на сфере — длина дуги проходящего через них большого круга. Углу же между прямыми на плоскости соответствует двугранный угол между плоскостями больших кругов. Многие теоремы геометрии на плоскости справедливы и в сферической геометрии, существуют аналоги теоремы синусов, теоремы косинусов для сферических треугольников. В то же время, существует немало отличий, например, в сферическом треугольнике сумма углов всегда больше 180 градусов, к трём признакам равенства треугольников добавляется их равенство по трём углам, у сферического треугольника может быть два и даже три прямых угла — например, у сферического треугольника, образованного экватором и меридианами 0° и 90°.
Расстояние между двумя точками на сфере
Если даны сферические координаты двух точек, то расстояние между ними можно найти так:
Однако, если угол задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:
В этом случае и называются широтами, а и долготами.
Свойства шара и сферы
Любое сечение шара плоскостью является кругом.
Любое сечение сферы плоскостью является окружностью.
Все точки сферы равноудалены от ее центра.
Сфера имеет самый большой объем среди всех фигур в пространстве, имеющих одинаковую площадь поверхности.
Через две любые диаметрально противоположные точки (максимально отдаленные друг от друга точки на окружности) можно провести неограниченное количество кругов для шара или окружностей для сфер радиусом, равным радиусу шара/сферы.
Примечание: если точки не диаметрально противоположны, то провести можно только один круг (окружность).
Примеры решения задач
Задача 1
Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.
Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона , тогда
Ответ:
Задача 2
Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5
м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?
Решение:
Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны . Получим:
м2.
Теперь подсчитаем, сколько нам понадобится досок: .
Ответ: 108 досок.
Задача 3
Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.
Решение: иными словами — нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой — высотой. Определяем площадь по формуле:
.
Ответ: 8
Задача 4
Условие. Найти общую площадь пирамиды, если в его основании лежит равносторонний треугольник со стороной 4 см, а апофема имеет значение √3 см.
Решение. Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см2.
Для треугольника в основании получится такое значение площади: (42*√3) / 4 = 4√3 см2.
Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см2.
Ответ. 10√3 см2.
Задача 5
Условие. Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.
Решение. Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.
Первые расчеты просты и приводят к такому числу: 49 мм2. Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16)2) = √2985,9375 = 54,644 мм2. Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.
Получается: 49 + 4*54,644 = 267,576 мм2.
Ответ. Искомое значение 267,576 мм2.
Задача 6
Условие. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.
Решение. Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.
Придется вспомнить теорему Пифагора и рассмотреть прямоугольный треугольник. Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.
Искомая апофема (гипотенуза прямоугольного треугольника) равна √(32 + 42) = 5 (см).
Теперь можно вычислять искомую величину: ½*(4*6)*5+62 = 96 (см2).
Ответ. 96 см2.
Задача 7
Условие. Дана правильная шестиугольная пирамида. Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?
Решение. Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.
Первым делом вычисляется площадь основания по указанной выше формуле: (6*222) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см2.
Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.
Расчеты по формуле Герона: √(72*(72-22)*(72-61)2)=√435600=660 см2. Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см2. Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см2.
Ответ. Основания — 726√3 см2, боковой поверхности — 3960 см2, вся площадь — 5217 см2.
Радиус сферы, описанной около правильной n — угольной пирамиды
Задача 1. Высота — угольной пирамиды правильной равана h , а длина ребра остановки равана a . Найдите радиусную сферу, описанную вокруг пирамиды.
Решение. Возьмем правильную — угольную примиду SA1A2… An и обозначим центр сферы, описанной вокруг пирамиды, буквой O, а символом O’ – центр основания пирамиды. Проведем плоскость SO’An (рис. 5).
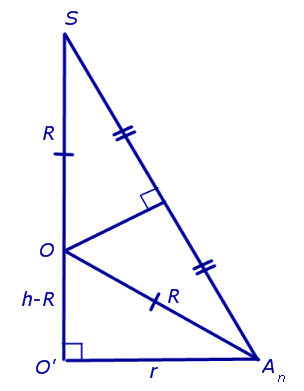
Рис. 5
Буква R на рисунке 5 обозначает радиус, описанный вокруг пирамиды сферы, а буква r – радиус, описанный вокруг основания пирамиды круга. По теореме Пифагора для треугольника O’OAn получаем
R2 = (h – R)2 + r2;
R2 = h2 – 2hR + R2 + r2;
2hR = h2 + r2.
Следовательно,
| (1) |
Потому что
— угол окружности выражается через сторону этого многоугольника по формуле радиуса, описанной вокруг правильного — угол окружности выражается через сторону этого многоугольника по формуле радиуса, описанной вокруг правильного
из форумы (1) получаем соотношение
| (2) |
Ответ
Следствие 3. Радиус сферы, описанной вокруг правильной треугольной пирамиды с высотой h и ребром основания a, равен
Следствие 4. Радиус сферы, спасительный около правильного тетраедра с ребром а , равенство
Следствие 5. Радиус сферы, описанной вокруг правильной прямоугольной пирамиды высотой h и ребром основания a, равен
Следствие 6. Радиус сферы, описанной вокруг правильной шестигранной пирамиды высотой h и ребром основания a, равен
1 ответ
Рассмотрим верхнюю грань куба с ребром $%a$%. Она вписана в равносторонний треугольник. Легко видеть, что половина его стороны складывается из двух величин. Одна из них равна $%\frac2$%, а другая равна $%\frac$%. Это значит, что длина стороны равна $%a(1+\frac2)$%.
Из условия задачи следует, что высота пирамиды в 3 раза больше радиуса описанной около основания окружности, то есть она равна $%2\sqrt3$%. Высота пирамиды, отсекаемой плоскостью верхнего основания куба, равна $%2\sqrt3-a$%. Из подобия двух правильных пирамид получается пропорция $%\frac=\frac2$% (отношение высот равно отношению сторон оснований). Решая линейное уравнение, находим $%a=\sqrt3-1$%.
отвечен 4 Янв ’15 0:30
объясните, пожалуйста, начало решения про величины, из которых складывается половина стороны ребра куба
Сделайте рисунок: квадрат, вписанный в правильный треугольник. Половина стороны треугольника, к которой примыкает квадрат, равна половине стороны квадрата + сторона квадрата, умноженная на $%\tan30^$%.
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Радиус сферы, описанной около правильной n — угольной пирамиды
Задача 1. Высота правильной n — угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, описанной около пирамиды.
Решение. Рассмотрим правильную n — угольную пирамиду SA1A2 . An и обозначим буквой O центр описанной около пирамиды сферы, а символом O’ – центр основания пирамиды. Проведем плоскость SO’An (рис. 5).
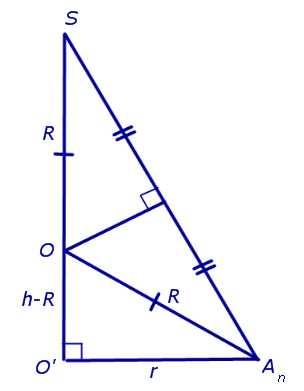
Буквой R на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой r – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника O’OAn получаем
| (1) |
из формулы (1) получаем соотношение
| (2) |
Ответ.
Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой h и ребром основания a , равен
Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром a , равен
Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой h и ребром основания a , равен
Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a , равен
ЛитератураПравить
Стоит остановиться на определении некоторых составляющих пирамиды.
У нее, как и у других многогранников, есть ребра. Они сходятся к одной точке, которая называется вершиной пирамиды. В ее основании может лежать произвольный многоугольник. Гранью называется геометрическая фигура, образованная одной из сторон основания и двумя ближайшими ребрами. В нашем случае это треугольник. Высотой пирамиды называется расстояние от плоскости, в которой лежит ее основание, до вершины многогранника. Для правильной пирамиды существует еще понятие апофемы — это перпендикуляр, опущенный из вершины пирамиды к её основанию.
Площадь поверхности шарового сектора
– радиус основания конуса = радиус сегмента
Формула площади поверхности шарового сектора, (S):

Апофема правильной пирамиды
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Тогда (displaystyle SK) – апофема данной пирамиды.
Пусть (displaystyle BC=4) – сторона основания правильной треугольной пирамиды.
В условии задачи дана площадь поверхности пирамиды.
Воспользуемся формулой для вычисления площади полной поверхности пирамиды.
Площадь полной поверхности пирамиды
Площадь полной поверхности пирамиды (displaystyle S ) равна
Площадь поверхности — аддитивная числовая характеристика поверхности.
Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды
Задача 2. Около — угольной прирамной паузы с высотой и ребром остановки проспанна шфера. Найдите отношение объемов пирамиды и сферы, ограниченной сферой, описанной вокруг пирамиды.
Решение. Объем шаракасается церезом его радиуса по формуле
Используя формулу (2), выразим объем сферы, ограниченной сферой, описанной вокруг пирамиды, через высоту и ребро основания пирамиды:
— угольной пирамиды находим по формулеОбъемлогир — угольной пирамиды находим по форумуОбъемпазол
Таким образом,
Ответ
Результат 7. Отношение объема правильной треугольной пирамиды высотой h и ребром основания a к объему сферы, ограниченной сферой, описанной вокруг этой пирамиды, равно
Следствие 8. Отношение воломы правильного тетраэдра с ребром к воему шару, ограниченного сферой, специальной около данного тетраэдра, раво
Результат 9. Отношение объема правильной четырехугольной пирамиды высотой h и ребром основания a к объему сферы, ограниченной сферой, описанной вокруг этой призмы, равно
Результат 10. Отношение объема правильной шестиугольной пирамиды высотой h и ребром основания a к объему сферы, ограниченной сферой, описанной вокруг этой призмы, равно
Сфера, вписанная в треугольную пирамиду.Формула для радиуса вписанной сферы
Утверждение 3. В любую треугольную пирамиду можно вписать шар.
Доказательство. Доказательство этого утверждения аналогично планиметрическому доказательству возможности вписания окружности в произвольный треугольник.
Действительно, пусть SABC — произвольный тетраэдр. Биссектриса внутреннего двугранного угла с ребром AC и биссектриса внутреннего двугранного угла с ребром AB пересекаются по прямой, проходящей через вершину A. Биссектриса внутреннего двугранного угла с ребром BC пересекает эту прямую в одной точке O , который является центром вписанной сферы (рис. 8).
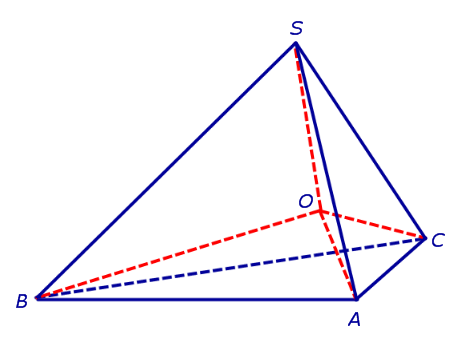
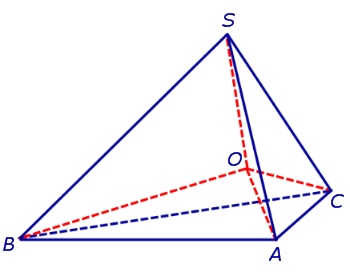
Рис. 8
Получим формулу, позволяющую вычислить радиус сферы, вписанной в тетраэдр SABC. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, а высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиус R сферы, вписанной в пирамиду SABC. Если обозначить площади граней тетраэдра SABC символами
SABC, SASC, SASB, SBSC ,
а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB — с условными обозначениями
ВАБК , В АСК , В АСБ , В БСК ,
то верны следующие равенства:
где символ Stot обозначает общую площадь поверхности пирамиды SABC.
Поэтому,
Замечание 2. Если в пирамиду можно вписать сферу (не обязательно треугольную), то, рассуждая аналогичным образом, можно получить следующую формулу для радиуса сферы, вписанной в пирамиду
где символы Vпир и Stot обозначают соответственно объем и площадь всей поверхности пирамиды.
Свойства и теоремы
Для фигуры характерны некоторые свойства. БР одинаковы, если нижняя сторона вписывается в сферу либо окружность так, что вершина приходится на центр. Другие особенности фигуры:
- Боковые рёбра и плоскость нижней стороны формируют равные углы.
- Если БР образуют с плоскостью одинаковые углы либо вблизи основания описывается окружность с вершиной в её центре, тогда все БР одинаковые.
- Если грани наклонены к плоскости основания под определённым углом, тогда площадь боковой поверхности (БП) пирамиды равна ½ произведения периметра нижней стороны на высоту грани.
При решении задач на сайтах онлайн либо из учебников по геометрии используются теоремы, которые связывают пирамиду с иными телами.
Для расчета нужной величины применяется калькулятор, подходящая формула, свойства многогранников. Учёные доказали, что вокруг пирамиды можно описать сферу, если в основании находится многоугольник с окружностью.
Центр сферы — точка, в которой пересекаются плоскости, проходящие через центральную часть ребер. Из теоремы вытекает, что около прямоугольной, квадратной и правильной пирамиды возможно описать сферу. В фигуру вписывается сфера, если биссекторные плоскости двугранных внутренних углов пересекаются в единой точке. Согласно другой теореме, конус вписан в пирамиду, если их вершины совпадают. Основание фигур и апофемы совпадают. Конус описывается вокруг пирамиды, если БР последней фигуры одинаковые.
Цилиндр находится внутри многоугольника, если любое его основание совмещено с окружностью. Цилиндр описан около пирамиды, если вершина последней фигуры находится на одном из его оснований. Другая его нижняя часть описана внизу пирамиды. Подобное действие возможно, если в основании пирамиды вписан многоугольник.
Для правильной пирамиды (нижняя сторона представлена в виде правильного многоугольника с вершиной в центре) характерны некоторые свойства: равенство БР, гранями являются равнобедренные конгруэнтные (равные) треугольники, внутрь и вокруг легко описывается и вписывается сфера. В последнем случае, когда центры сфер совпадают, сумма плоских углов равняется числу пи, а каждый — π/n, где n — количество сторон фигуры в основании.
Пирамида считается прямоугольной, если одно БР перпендикулярно нижней стороне. В таком случае ребро является высотой. В тетраэдре либо треугольной пирамиде любая грань принимается в качестве основания.
Дистанционные курсы для педагогов
Выдаём документы установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Студенты российских вузов смогут получить 1 млн рублей на создание стартапов
Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Курские власти перевели на дистант школьников в районах на границе с Украиной
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Минпросвещения России подготовит учителей для обучения детей из Донбасса
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы
Определение 2. Сферой, вписанной в пирамиду, называется сфера, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).
Рис.4
Определение 3. Если сфера вписана в пирамиду, то говорят, что пирамида вписана около сферы.
Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного смежными гранями пирамиды. По следствию 1 центр сферы, вписанной в пирамиду, должен находиться на пересечении биссектрис всех внутренних двугранных углов, образованных смежными гранями пирамиды.
Если в пирамиде нет точки, в которой пересекаются биссектрисы всех внутренних двугранных углов, образованных смежными гранями пирамиды, то в такую пирамиду нельзя вписать сферу.
Замечание 1. Чтобы проверить, вписывается ли сфера в пирамиду, достаточно проверить, есть ли пересечение биссектрис всех внутренних двугранных углов в основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.
Рассмотрим несколько типов пирамид, в которые можно вписать сферу.
Утверждение 2. Если пирамида SA1A2… An имеет перпендикуляр O, то основание, опущенное из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A1A2… An , а все боковые грани пирамиды наклонены под одинаковым углом к плоскости основания пирамиды, то в такую пирамиду можно вписать шар.
Доказательство. Пусть все боковые поверхности пирамиды наклонены к плоскости основания под углом φ, а высота пирамиды равна h. Рассмотрим, например, боковую поверхность SA1A2 и проведем в ней высоту SB (рис. 5).
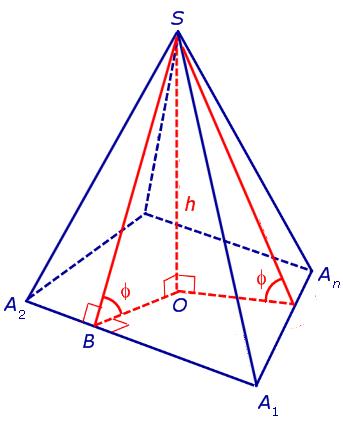
Рис.5
По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A1A2. Следовательно, угол SBO является линейным углом двугранного угла между боковой поверхностью SA1A2 и плоскостью основания пирамиды и равен φ. Биссектриса этого двугранного угла пересекает высоту пирамиды в точке О’ (рис. 6).
Рис. 6
Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле
OB знак равно час ctg φ .
Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле
Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, биссектрисы всех внутренних двугранных углов пересекаются у основания пирамиды в точке O’, являющейся центром сферы вписанный в пирамиду.
Доказательство утверждения 2 завершено.
Так как у любой правильной пирамиды все внутренние двугранные углы при основании равны, то верно
Следствие 2. В любую правильную пирамиду можно вписать сферу, а ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле
| (1) |
Радиус окружности описанной около основания правильной
Вопрос по геометрии:
радиус окружности, описанной около основания правильной треугольной пирамиды равен 3. Боковое ребро равно 5. Найдите высоту пирамиды.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Полиночка, все на чертеже. Так строится правильная треуголоная пирамида и только так. AO это радиус описанной окружности.SO находим по т.Пифагора SO^2=5^2=3^2=16, SO=4
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.






























