Как найти площадь полной поверхности правильного тетраэдра

Типы тетраэдров[]

Выделяют следующие специальные виды тетраэдров.

• Равногранный тетраэдр, у которого все грани — равные между собой треугольники.
• Ортоцентрический тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.
• Прямоугольный тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой.
• Правильный тетраэдр, у которого все грани — равносторонние треугольники.
• Каркасный тетраэдр — тетраэдр, отвечающий любому из следующих условий:
  • существует сфера, касающаяся всех ребер,
  • суммы длин скрещивающихся ребер равны,
  • суммы двугранных углов при противоположных ребрах равны,
  • окружности, вписанные в грани, попарно касаются,
  • все четырехугольники, получающиеся на развертке тетраэдра, — описанные,
  • перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
• Соразмерный тетраэдр, бивысоты которого равны.
• Инцентрический тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.

Пирамида и ее величины

Пирамида представляет собой многогранник и многоугольник. Особенности фигуры:

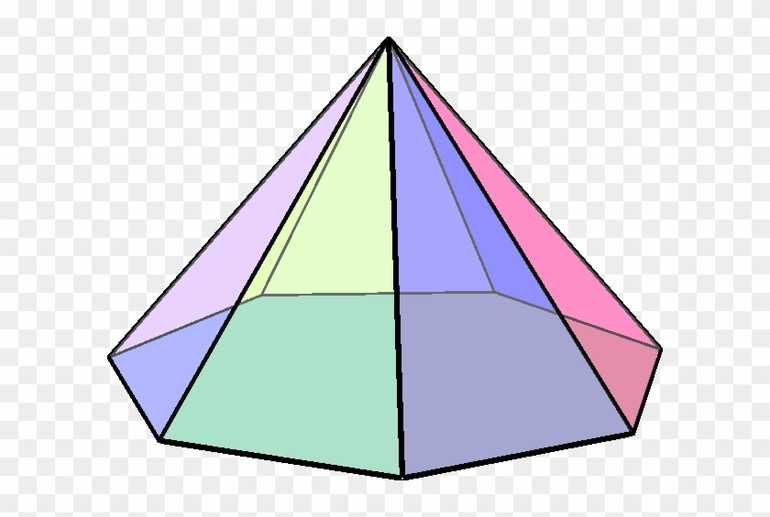
• Боковая поверхность равна сумме площадей граней;
• Высота — перпендикуляр от основания к вершине;
• Когда N — количество углов основания, пирамида называется N -угольной;
• Формула объема многогранника: V = 1/3·S·h;
• Формула площади всей поверхности: Sп = Sбоковых граней + Sоснования;
• Все сечения, включая диагональные, являются треугольниками.

Если пирамиду разделяет плоскость, параллельная нижней, она делит ее на две части. Причем верхняя пропорционально равна главной фигуре. Когда основанием является квадрат, геометрическое тело называется правильным. Гранями ее считаются равнобедренные треугольники.

Существует также такое понятие, как усеченная пирамида. Она получается только из правильной фигуры, если провести плоскость на противоположную от основания сторону, и убрать верхнюю часть. У данного тела отсутствует вершина, поскольку фактически она является квадратом , а не единичной точкой. Это не единственное отличие. К примеру, формулы, справедливые для классического формата, в данном случае неприемлемы.

Вариант развертки

Тетраэдр можно сделать самостоятельно. Бумага или картон – лучший вариант. Для сборки вам понадобится развертка бумаги — цельная деталь с линиями сгиба.

Древнегреческий философ Платон связывал тетраэдр с «земной» стихией огня, поэтому мы выбрали красный цвет для построения модели этого распространенного многогранника.

Обратите внимание, что это не единственный вариант свайпа. Для сборки модели можно скачать разработку в формате pdf и распечатать на листе формата А4:
— если вы собираетесь печатать на цветном принтере — цветное сканирование
— если вы собираетесь использовать для сборки цветной картон — отсканируйте

Для сборки модели можно скачать разработку в формате pdf и распечатать на листе формата А4:
— если вы собираетесь печатать на цветном принтере — цветное сканирование
— если вы собираетесь использовать для сборки цветной картон — отсканируйте

Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы тетраэдра определяется по формуле:

, где a — длина стороны.

Сфера может быть вписана внутрь тетраэдра.

Радиус вписанной сферы тетраэдра определяется по формуле:

Площадь поверхности тетраэдра

Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:

Объем тетраэдра определяется по следующей формуле:

Высота тетраэдра определяется по следующей формуле:

Расстояние до центра основания тетраэдра определяется по формуле:

Вариант развертки

Тетраэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка — единая деталь с линиями сгибов.

Древнегреческий философ Платон ассоциировал тетраэдр с «земным» элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.

Заметим, что это не единственный вариант развертки.

Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4: — если Вы предполагаете распечатать на цветном принтере — цветная развертка — если Вы предполагаете использовать для сборки цветной картон — развертка

Примеры решения задач

Задача 1

Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.

Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона , тогда

Ответ:

Задача 2

Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5
м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?

Решение:

Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны . Получим:
м2.

Теперь подсчитаем, сколько нам понадобится досок: .

Ответ: 108 досок.

Задача 3

Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Решение: иными словами — нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой — высотой. Определяем площадь по формуле:

.

Ответ: 8

Задача 4

Условие. Найти общую площадь пирамиды, если в его основании лежит равносторонний треугольник со стороной 4 см, а апофема имеет значение √3 см.

Решение. Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см2.

Для треугольника в основании получится такое значение площади: (42*√3) / 4 = 4√3 см2.

Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см2.

Ответ. 10√3 см2.

Задача 5

Условие. Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.

Решение. Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.

Первые расчеты просты и приводят к такому числу: 49 мм2. Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16)2) = √2985,9375 = 54,644 мм2. Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.

Получается: 49 + 4*54,644 = 267,576 мм2.

Ответ. Искомое значение 267,576 мм2.

Задача 6

Условие. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.

Решение. Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.

Придется вспомнить теорему Пифагора и рассмотреть прямоугольный треугольник. Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.

Искомая апофема (гипотенуза прямоугольного треугольника) равна √(32 + 42) = 5 (см).

Теперь можно вычислять искомую величину: ½*(4*6)*5+62 = 96 (см2).

Ответ. 96 см2.

Задача 7

Условие. Дана правильная шестиугольная пирамида. Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?

Решение. Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.

Первым делом вычисляется площадь основания по указанной выше формуле: (6*222) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см2.

Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.

Расчеты по формуле Герона: √(72*(72-22)*(72-61)2)=√435600=660 см2. Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см2. Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см2.

Ответ. Основания — 726√3 см2, боковой поверхности — 3960 см2, вся площадь — 5217 см2.

Объём тетраэдра

V = \frac16

\begin{vmatrix}
1 & x_1 & y_1 & z_1 \\
1 & x_2 & y_2 & z_2 \\
1 & x_3 & y_3 & z_3 \\
1 & x_4 & y_4 & z_4
\end{vmatrix} = \frac16 \begin{vmatrix}
x_2 — x_1 & y_2 — y_1& z_2 — z_1\\
x_3 — x_1 & y_3 — y_1& z_3 — z_1\\
x_4 — x_1 & y_4 — y_1& z_4 — z_1
\end{vmatrix},

V = \frac{1}{3}\ S H,

где S – площадь любой грани, а H – высота, опущенная на эту грань.

Объём тетраэдра через длины рёбер выражается с помощью определителя Кэли-Менгера :

288 \cdot V^2 =

0 & 1 & 1 & 1 & 1 \\
1 & 0 & d_{12}^2 & d_{13}^2 & d_{14}^2 \\
1 & d_{12}^2 & 0 & d_{23}^2 & d_{24}^2 \\
1 & d_{13}^2 & d_{23}^2 & 0 & d_{34}^2 \\
1 & d_{14}^2 & d_{24}^2 & d_{34}^2 & 0

\end{vmatrix}.

• Эта формула имеет плоский аналог для площади треугольника в виде варианта формулы Герона через аналогичный определитель.
• Объём тетраэдра через длины двух противоположных рёбер a
  и b
  , как скрещивающихся линий, которые удалены на расстояние h
  друг от друга и образуют друг с другом угол \phi , находится по формуле:

V = \frac{1}{6} ab h \sin \phi .

V = \frac{1}{3}\ abc \sqrt {D} ,

где
D=
\begin{vmatrix}

1 & \cos \gamma & \cos \beta \\
\cos \gamma & 1 & \cos \alpha \\
\cos \beta & \cos \alpha & 1
\end{vmatrix}.

Аналогом для плоскости последней формулы является формула площади треугольника через длины двух его сторон a
и b
, выходящих из одной вершины и образующих между собой угол \gamma :

S = \frac{1}{2}\ ab \sqrt {D} ,

где
D=
\begin{vmatrix}

1 & \cos \gamma \\
\cos \gamma & 1 \\
\end{vmatrix}.

Параллелепипед

Определение: Параллелепипед – это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед – это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для параллелепипеда. Однако, можно выделить несколько дополнительных свойств характерных для параллелепипеда.

Другие свойства и определения:

• Две грани параллелепипеда, не имеющие общего ребра, называются противолежащими, а имеющие общее ребро – смежными.
• Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
• Отрезок, соединяющий противолежащие вершины, называется диагональю параллелепипеда.
• Параллелепипед имеет шесть граней и все они – параллелограммы.
• Противоположные грани параллелепипеда попарно равны и параллельны.
• У параллелепипеда четыре диагонали; они все пересекаются в одной точке, и каждая из них делится этой точкой пополам.
• Если четыре боковые грани параллелепипеда – прямоугольники (а основания – произвольные параллелограммы), то он называется прямым (в этом случае, как и у прямой призмы, все боковые ребра перпендикулярны основаниям). Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда.
• Параллелепипед называется наклонным, если не все его боковые грани являются прямоугольниками.
• Объем прямого или наклонного параллелепипеда рассчитывается по общей формуле для объема призмы, т.е. равен произведению площади основания параллелепипеда на его высоту (V = S_осн∙h).
• Прямой параллелепипед, у которого все шесть граней – прямоугольники (т.е. кроме боковых граней еще и основания являются прямоугольниками), называется прямоугольным

  Диагональ прямоугольного параллелепипеда d и его рёбра a, b, c связаны соотношением:

  . Для прямоугольного параллелепипеда актуальны все свойства прямого параллелепипеда, а также:

d2 = a2 + b2 + c2.

• Прямоугольный параллелепипед, все грани которого являются равными квадратами, называется кубом. Помимо прочего, куб является правильной четырехугольной призмой, и вообще правильным многогранником. Для куба справедливы все свойства прямоугольного параллелепипеда и свойства правильных призм, а также:

  

  

  

  

  

  

  

  

  

  

  • Абсолютно все рёбра куба равны между собой.
  • Диагональ куба d и длина его ребра a связаны соотношением:

Из формулы для объема прямоугольного параллелепипеда можно получить следующую формулу для объема куба:

Как найти объем правильного тетраэдра?

Для того чтобы найти объем правильного тетраэдра, необходимо использовать определенную формулу. Тетраэдр является одной из плоских геометрических фигур, и его объем можно вычислить по формуле, которая основана на его геометрических характеристиках. Она учитывает длину ребра тетраэдра и его высоту.

Формула для расчета объема правильного тетраэдра выглядит следующим образом:

где V — объем тетраэдра, s — длина ребра.

Таким образом, если известна длина ребра правильного тетраэдра, то можно легко вычислить его объем по данной формуле. Если же длина ребра неизвестна, то перед расчетом объема необходимо сначала найти ее с помощью других геометрических свойств тетраэдра.

Таким образом, чтобы найти объем правильного тетраэдра, необходимо знать длину его ребра и использовать указанную формулу. Если длина ребра неизвестна, то необходимо сначала ее найти по другим геометрическим свойствам тетраэдра. Также следует учесть, что в формуле используется корень из 2, поэтому для точного вычисления объема необходимы высокая точность и правильность всех измерений и расчетов.

Тетраэдр.

Тетраэдр — это частный случай правильной треугольной пирамиды.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Медиана тетраэдра — это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).

Бимедиана тетраэдра — это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).

Высота тетраэдра — это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).

Как определить площадь сечения цилиндра, конуса, призмы и пирамиды? Формулы

На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.

Объемные фигуры

Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Вам будет интересно: Что значит слыть: толкование, синонимы

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.

Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).

Цилиндр

Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:

• круглое;
• прямоугольное;
• эллиптическое.

Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.

Площадь круглого сечения рассчитывается по формуле:

Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:

Сечения конуса

Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:

• круглое;
• эллиптическое;
• параболическое;
• гиперболическое;
• треугольное.

Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.

Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:

Определение геометрического тела

Такие понятия, как луч, отрезок, ломаная, кривая встречаются довольно часто в различных науках: математике, алгебре, физике и химии (траектория движения, графики и т.д.).

Все перечисленные фигуры можно представить как множество точек.

Любую фигуру в геометрии можно представить как множество точек, сгруппированных определенным образом.

Разберем понятие геометрического тела.

Представленный выше вариант определения геометрических тел не единственный. Иногда используют следующее определение: геометрическое тело — множество сгруппированных точек, из которых две любые точки образуют отрезок, не выходящий за границы тела.

Практические примеры

Задача. Найдите площадь поверхности треугольной пирамиды, у которой каждое ребро равно √3

Решение. Поскольку все ребра треугольной пирамиды равны — она является правильной. Площадь поверхности правильной треугольной пирамиды равна S = a 2 √3 . Тогда S = 3√3

Задача. Все ребра правильной треугольной пирамиды равны 4 см. Найдите объем пирамиды

Решение. Поскольку в правильной треугольной пирамиде высота пирамиды проецируется в центр основания, который одновременно является центром описанной окружности, то

AO = R = √3 / 3 a AO = 4√3 / 3

Таким образом, высота пирамиды OM может быть найдена из прямоугольного треугольника AOM

AO 2 + OM 2 = AM 2 OM 2 = AM 2 — AO 2 OM 2 = 4 2 — ( 4√3 / 3 ) 2 OM 2 = 16 — 16/3 OM = √(32/3) OM = 4√2 / √3

Объем пирамиды найдем по формуле V = 1/3 Sh При этом площадь основания найдем по формуле S = √3/4 a 2

V = 1/3 (√3 / 4 * 16 ) ( 4√2 / √3 ) V = 16√2 / 3

Ответ

Проверено экспертом

Центр вписанной окружности в равносторонний треугольник лежит на высоте (биссектрисе и медиане) и делит её в отношении 2/1 считая от вершины. ⇒ высота (7+7*2)=21 ед.

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера»

Равносторонний треугольник — треугольник, у которого все стороны равны.

Какие же особенные свойства присущи равностороннему треугольнику?

Равносторонний треугольник. Свойства

Свойство 1. В равностороннем треугольнике все углы равны между собой и равны .

Естественно, не правда ли? Три одинаковых угла, в сумме , значит, каждый по .

Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).

Почему так? А посмотрим-ка на равносторонний треугольник:

Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.

Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром! В равностороннем треугольнике оказалось не особенных линий, как во всяком обычном треугольнике, а всего три!

  Посоветуйте интересную книгу форум

Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.

Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной.

Уже должно быть очевидно, отчего так.

Посмотри на рисунок: точка – центр треугольника. Значит, – радиус описанной окружности (обозначили его ), а – радиус вписанной окружности (обозначим ).

Но ведь точка – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении , считая от вершины.

Поэтому , то есть .

Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.

Давай удостоверимся в этом.

Рассмотрим – он прямоугольный.

Равносторонний треугольник. Радиус описанной окружности

Мы уже выяснили, что точка – не только центр описанной окружности, но и точка пересечения медиан. Значит, .

Величину мы уже находили. Теперь подставляем:

Равносторонний треугольник. Радиус вписанной окружности

Это уже теперь должно быть совсем ясно

Ну вот, все основные сведения обсудили. Конечно, можно задавать сотни вопросов про всякие длины всяких отрезков в равностороннем треугольнике.

Но главное, что следует иметь в виду, решая задачки о равностороннем треугольнике, – это то, что все его углы известны – равны и все высоты являются и биссектрисами, и медианами, и серединными перпендикулярами.

Равносторонний треугольник. краткое изложение и основные формулы

Равносторонний треугольник — треугольник, у которого все стороны равны: .

В равностороннем треугольнике каждая медиана совпадает с биссектрисой и высотой, которые проведены из той же вершины Точки пересечения высот, биссектрис, медиан и серединных перпендикуляров равностороннего треугольника совпадают.

  С чем можно поесть сгущенку

Центры вписанной и описанной окружностей равностороннего треугольника совпадают: точка . В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной: .

В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны :

Высота=медиане=биссектрисе : Радиус описанной окружности : Радиус вписанной окружности : Площадь : Периметр :

Получить доступ к учебнику YouClever без ограничений можно кликнув по этой ссылке:

Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.

• Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
• Площадь треугольника равна произведению ПЕРИМЕТРА на радиус!
• Площадь треугольника равна произведению ПОЛУПЕРИМЕТРА на радиус вписанной окружности

Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.

Из формулы , где p — полупериметр, находим, что периметр описанного многоугольника равен отношению удвоенной площади к радиусу вписанной окружности:

Равносторонний треугольник вписан в окружность найти радиус Ссылка на основную публикацию