Объем пирамиды. все формулы. найти онлайн по формуле

ссылки

1. Биллштейн Р., Либескинд С. и Лотт Дж. У. (2013). Математика: проблемный подход для учителей базового образования. Лопес Матеос Эдиторес.
2. Fregoso, R.S. & Carrera, S.A. (2005). Математика 3. Редакция Прогресо.
3. Галлардо Г. & Пилар П. М. (2005). Математика 6. Редакция Прогресо.
4. Гутьеррес, С. Т. и Сиснерос, М. П. (2005). 3-й курс математики. Редакция Прогресо.
5. Кинси Л. и Мур Т. Э. (2006). Симметрия, форма и пространство: введение в математику через геометрию (иллюстрированный, перепечатанный ред.). Springer Science & Business Media.
6. Митчелл, C. (1999). Ослепительный дизайн Math Line (Иллюстрированный ред.). Scholastic Inc.
7. Р., М. П. (2005). Я рисую 6º. Редакция Прогресо.

Примеры решения задач

Задача 1

Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.

Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона , тогда

Ответ:

Задача 2

Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5
м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?

Решение:

Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны . Получим:
м2.

Теперь подсчитаем, сколько нам понадобится досок: .

Ответ: 108 досок.

Задача 3

Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Решение: иными словами — нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой — высотой. Определяем площадь по формуле:

.

Ответ: 8

Задача 4

Условие. Найти общую площадь пирамиды, если в его основании лежит равносторонний треугольник со стороной 4 см, а апофема имеет значение √3 см.

Решение. Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см2.

Для треугольника в основании получится такое значение площади: (42*√3) / 4 = 4√3 см2.

Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см2.

Ответ. 10√3 см2.

Задача 5

Условие. Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.

Решение. Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.

Первые расчеты просты и приводят к такому числу: 49 мм2. Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16)2) = √2985,9375 = 54,644 мм2. Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.

Получается: 49 + 4*54,644 = 267,576 мм2.

Ответ. Искомое значение 267,576 мм2.

Задача 6

Условие. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.

Решение. Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.

Придется вспомнить теорему Пифагора и рассмотреть прямоугольный треугольник. Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.

Искомая апофема (гипотенуза прямоугольного треугольника) равна √(32 + 42) = 5 (см).

Теперь можно вычислять искомую величину: ½*(4*6)*5+62 = 96 (см2).

Ответ. 96 см2.

Задача 7

Условие. Дана правильная шестиугольная пирамида. Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?

Решение. Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.

Первым делом вычисляется площадь основания по указанной выше формуле: (6*222) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см2.

Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.

Расчеты по формуле Герона: √(72*(72-22)*(72-61)2)=√435600=660 см2. Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см2. Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см2.

Ответ. Основания — 726√3 см2, боковой поверхности — 3960 см2, вся площадь — 5217 см2.

Свойства правильной треугольной пирамиды:

• боковые ребра правильной пирамиды равны
• все боковые грани правильной пирамиды являются равнобедренными треугольниками
• в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
• если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3  (пи делить на 3 или 60 градусов ).
• площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
• вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан

Формулы для правильной треугольной пирамиды

Формула объема правильной треугольной пирамиды:

где

V — объем правильной пирамиды, имеющей в основании правильный (равносторонний) треугольник
h — высота пирамиды
a — длина стороны основания пирамиды
R — радиус описанной окружности
r — радиус вписанной окружности

Поскольку правильная треугольная пирамида является частным случаем правильной пирамиды, то формулы, которые верны для правильной пирамиды, верны и для правильной треугольной — см. формулы для правильной пирамиды.

Примеры решения задач:

• Нахождение периметра правильной треугольной пирамиды 
• Вычисление объема 
• Нахождение площади поверхности   

Формулы объема и площади поверхности пирамиды с примерами расчета

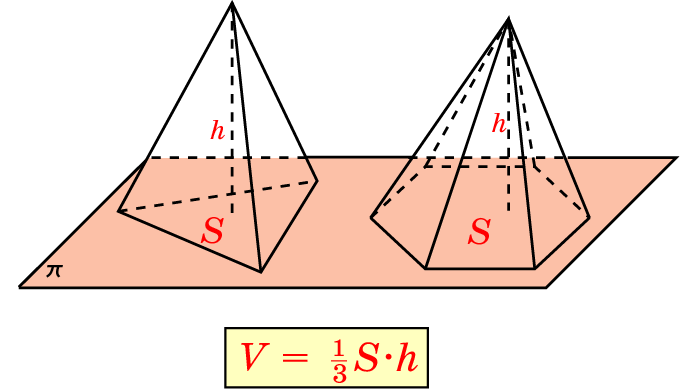
Вычислить объём можно с использованием следующей формулы.

V = (S * h) / 3,

где используются такие обозначения:

• V – объём;

• S – площадь основания;

• h – высота фигуры.

Полную площадь поверхности можно вычислить как сумму площадей основания и всех боковых треугольников.

Пример решения задачи

Если стороны основания составляют 3 см, а боковые рёбра — 4 см, то по теореме Пифагора можно определить высоту фигуры. 

Сначала по теореме Пифагора находят длину половины диагонали. Она будет равна корню квадратному из 18 (4,25 см), так как является диагональю квадрата. 

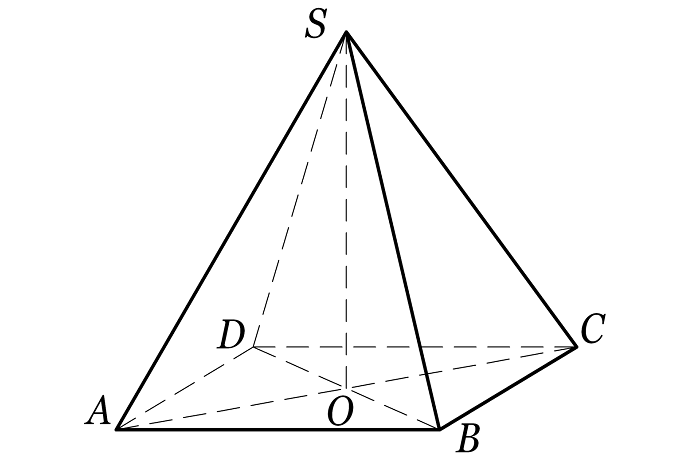
Здесь рассматривается четырехугольная пирамида.

По теореме Пифагора находим высоту. Она будет равна примерно 4,5 см.

Площадь основания составляет 3 * 3 = 9 кв. см. Нужно учесть, что это квадрат со стороной 3 см. Подставив значения в формулу для объёма, получим следующее.

V = (1 / 3) * 9 * 4,5 = 13,5 куб. см.

Для расчёта площади поверхности надо узнать площадь квадратного основания и треугольных боковых сторон. Для этого сначала по теореме Пифагора находят длину апофемы. Она будет равна 4,27 см. 

Каждая боковая сторона имеет площадь 12,81 кв. см, а основание — 9 кв. см. Сложив площади всех граней, получим 60,24 кв. см. Посчитать площадь поверхности можно, рассмотрев развертку фигуры.

Виды пирамид

1. Правильная пирамида – основанием фигуры является правильный многоугольник, а ее вершина проецируется в центр основания. Может быть треугольной, четырехугольной (на рисунке ниже), пятиугольной, шестиугольной и т.д.
2. Пирамида с боковым ребром, перпендикулярным основанию – одно из боковых ребер фигуры расположено под прямым углом к плоскости основания. В этом случае данное ребро является высотой пирамиды.
3. Усеченная пирамида – часть пирамиды, оставшаяся между ее основанием и параллельной этому основанию секущей плоскостью.
4. Тетраэдр – это треугольная пирамида, гранями которой являются 4 треугольника, каждый из которых может быть принят за основание. Является правильным (как на рисунке ниже) – если все ребра равны, т.е. все грани – это равносторонние треугольники.

Теория

Это интересно: Как оформлять реферат в школе по ГОСТу + образец титульного листа 2019

Для решения задач понадобится знать теоремы равнобедренного треугольника:

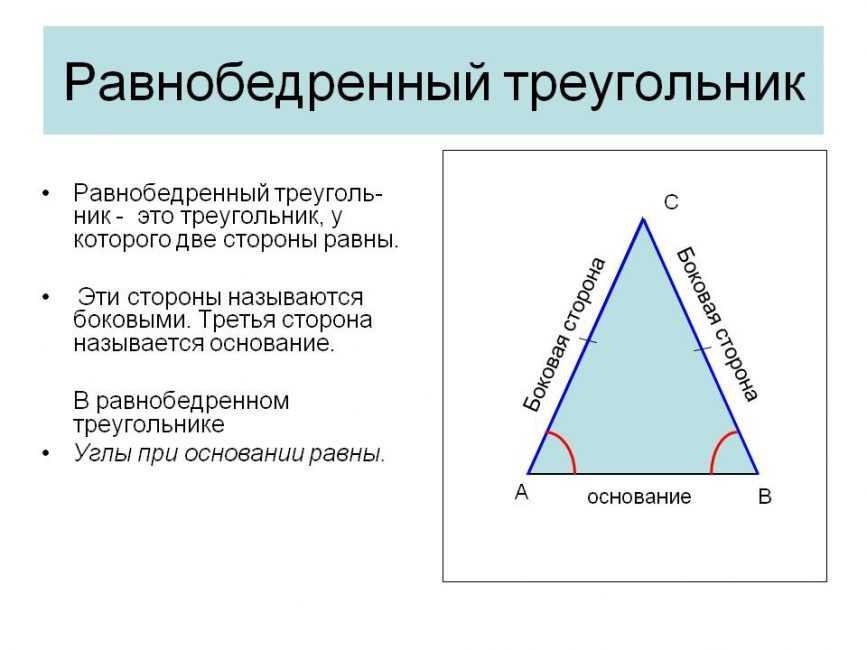
Равнобедренный треугольник

Основные свойства

1В правильную пирамиду можно вписать и описать сферу, так как при пересечении диагоналей, основание делится на равные части. Сферу нельзя вписать в любую фигуру.

2Площадь боковой поверхности – половина произведения периметра основания на апофему. Апофема есть на каждой грани, а не только на одной.

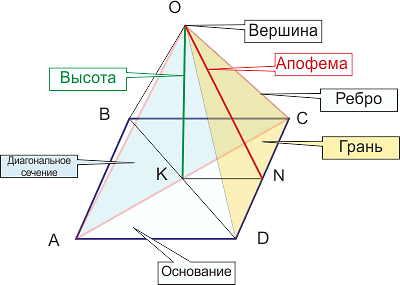
Пирамида

Четырехугольная пирамида

В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

Четырехугольная пирамида

Треугольная пирамида

В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.

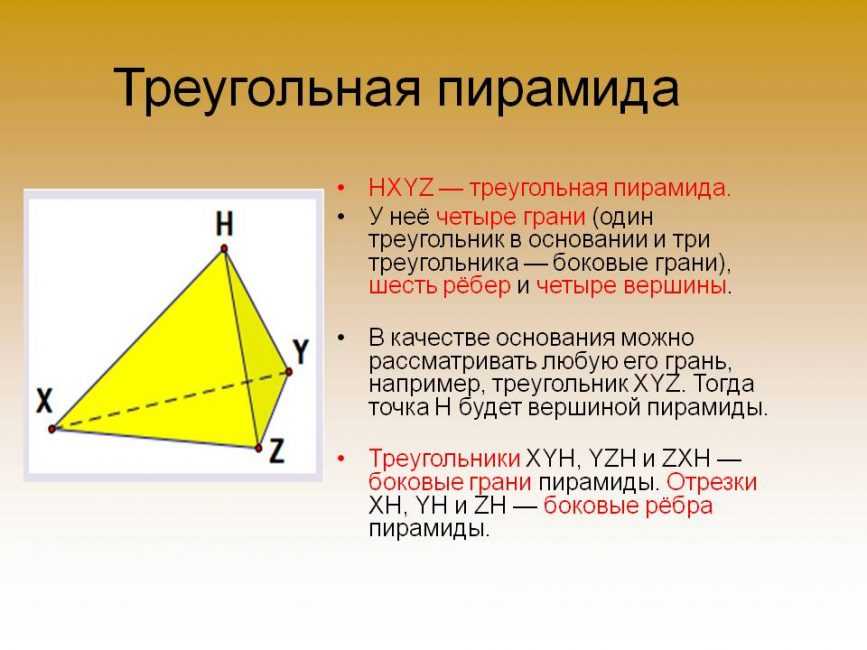
Треугольная пирамида

Необходимые знания для нахождения высоты

1Нужно понимать, что из себя представляют треугольники: свойства, формулы, определение. Большинство задач решается через треугольники (боковые грани).

2Понимать, что такое сечение и как оно влияет на геометрическую фигуру.

3Что такое правильные многоугольники: виды, свойства, формулы.

Когда теория закреплена, можно переходить к формулам.

Формулы для нахождения высоты

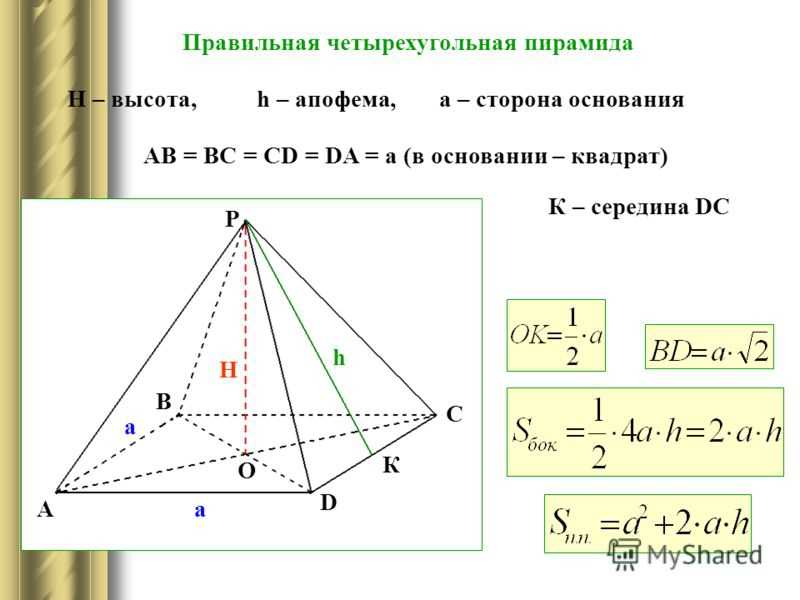
Формулы

Запомните, что маленькая буква h – это апофема, а большая H – высота.

В некоторых задачах, высоту можно найти через объем:

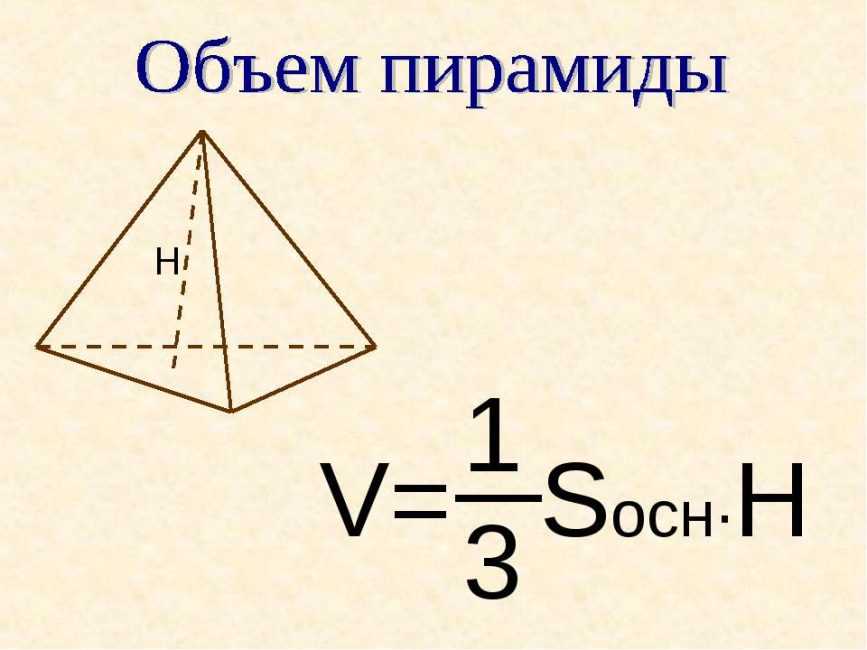
Объем пирамиды

Нахождение высоты в правильной пирамиде

Нахождение высоты в правильной пирамиде

Ниже будут представлены текстовые решения часто встречающихся задач.

Треугольная пирамида

Треугольная пирамида

Задача 1

В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.

DN – высота, следовательно, объем фигуры можно выразить по формуле:

DN = 3V/S основания = 3*12/4 = 9

Ответ: 9

Задача 2

DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.

Пользуясь формулой объема, получается:

DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6

Ответ: 6

Четырехугольная пирамида

Четырехугольная пирамида

Задача 1

Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.

ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:

OL = ½*12 = 6

Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:

MO ² = √ML ² — √OL ² = √100- √36 = √64

MO = 8

Задача 2

Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.

Найдем OL

В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).

Пользуясь теоремой Пифагора, находим OL:

OL² = √OC² — √LC² = √100 – √36 = √64 = 8

Задача 3

Ищем MO

Пользуясь той же теоремой, находим высоту:

MO² = √ML² – √OL² = 100 – 64 = 36

Ответ: 36

Задача 4

Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.

Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.

Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.

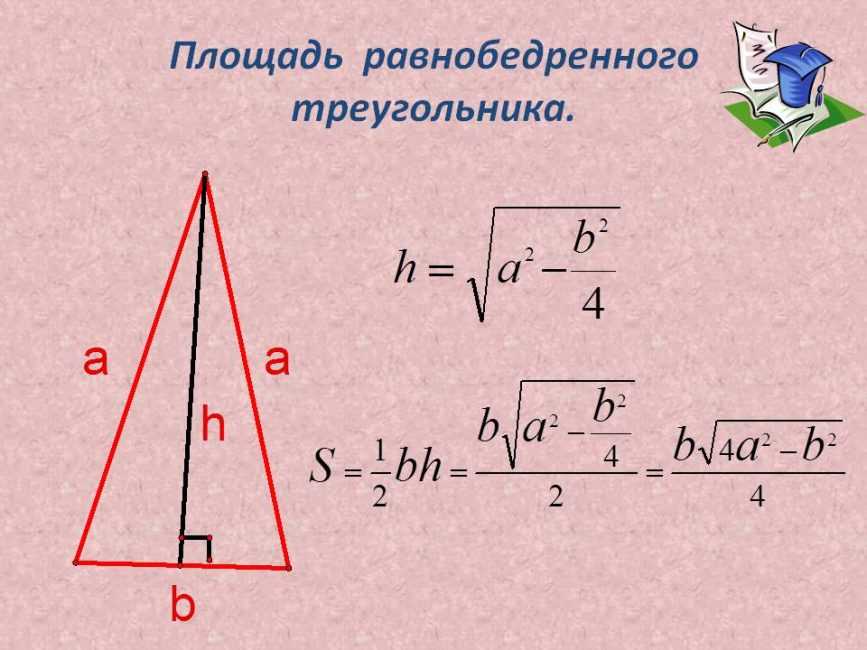
Площадь равнобедренного треугольника

36 = ½ * 4 *h

36 = 2h

H = 18

Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.

MO = ML – OL = 18 – 6 = 12

Ответ: 12

Тетраэдр

Частным случаем правильной треугольной пирамиды является тетраэдр.

Тетраэдр — это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.

У тетраэдра:

• Все грани равны
• 4 грани, 4 вершины и 6 ребер
• Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны

Медиана тетраэдра — это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего треугольника, противолежащего вершине)

Бимедиана тетраэдра — это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника, являющегося одной из граней тетраэдра)

Высота тетраэдра — это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является высотой, проведенной от любой грани, также совпадает с центром описанной окружности).

Тетраэдр обладает следующими свойствами:

• Все медианы и бимедианы тетраэдра пересекаются в одной точке
• Эта точка делит медианы в отношении 3:1, считая от вершины
• Эта точка делит бимедианы пополам

Современные пирамиды

Сегодня есть много сооружений, которые можно сравнить с пирамидами Египта.
Одна большая стеклянная пирамида находится в парижском Лувре.
Дворец мира и согласия представляет собой пирамиду высотой 62 метра в Астане (Казахстан).
Luxor Hotel Las Vegas, 30-этажная пирамида с более чем 4000 номерами, является домом для отеля Luxor.
Здание Словацкого радио находится в Братиславе в Словакии. Его форма представляет собой перевернутую (или перевернутую) пирамиду.

Для получения дополнительной информации перейдите по этой ссылке.)

cubic inches

cubic feet

cubic yards

us liquid gallons

us dry gallons

imp liquid gallons

barrels (oil)

cups

fluid ounces (UK)

fluid ounces (US)

pints (UK)

cubic meter

6.1 10^4

35.3

1.30^8

264.2

227

220

6.29

4227

3.52 10^4

3.38 10^4

1760

cubic decimeter

61.02

0.035

1.3 10^-3

0.264

0.227

0.22

0.006

4.23

35.2

33.8

1.76

cubic centimeter

0.061

3.5 10^-5

1.3 10^-6

2.64 10^-4

2.27 10^-4

2.2 10^-4

6.29 10^-6

4.2 10^-3

3.5 10^-2

3.34 10^-2

1.76 10^3

cubic millimeter

6.1 10^-5

3.5 10^-8

1.31 10^-9

2.64 10^-7

2.27 10^-7

2.2 10^-7

6.3 10^-9

4.2 10^-6

3.5 10^-5

3.4 10^-5

1.76 10^-6

hectoliters

6.1 10^3

3.53

0.13

26.4

22.7

22

0.63

423

3.5 10^3

3381

176

liters

61

3.5 10^-2

1.3 10^-3

0.26

0.23

0.22

6.3 10^-3

4.2

35.2

33.8

1.76

centiliters

0.61

3.5 10^-4

1.3 10^-5

2.6 10^-3

2.3 10^-3

2.2 10^-3

6.3 10^-5

4.2 10^-2

0.35

0.338

1.76 10^-2

milliliters

6.1 10^-2

3.5 10^-5

1.3 10^-6

2.6 10^-4

2.3 10^-4

2.2 10^-4

6.3 10^-6

4.2 10^-3

3.5 10^-2

3.4 10^-2

1.76 10^-3

cubic inches

1

5.79 10^-4

2.1 10^-5

4.3 10^-3

3.7 10^-3

3.6 10^-3

10-4

6.9 10^-2

0.58

0.55

2.9 10^-2

cubic feet

1728

1

0.037

7.48

6.43

6.23

0.18

119.7

997

958

49.8

cubic yards

4.7

104

27

1 202

173.6

168.2

4.8

3232

2.69

104

2.59

104

1345

us liquid gallons

231

0.134

4.95 10^-3

1

0.86

0.83

0.024

16

133.2

128

6.7

us dry gallons

268.8

0.156

5.76 10^-3

1.16

1

0.97

0.028

18.62

155

148.9

7.75

imp liquid gallons

277.4

0.16

5.9 10^-3

1.2

1.03

1

0.029

19.2

160

153.7

8

barrels (oil)

9702

5.61

0.21

42

36.1

35

1

672

5596

5376

279.8

cups

14.4

8.4 10^-3

3.1 10^-4

6.2 10^-2

5.4 10^-2

5.2 10^-2

1.5 10^-3

1

8.3

8

0.4

fluid ounces (UK)

1.73

10^-3

3.7 10^-5

7.5 10^-3

6.45 10^-3

6.25 10^-3

1.79 10^-4

0.12

1

0.96

5 10^-2

fluid ounces (US)

1.8 10^-3

3.87 10^-5

7.8 10^-3

6.7 10^-3

6.5 10^-3

1.89 10^-4

0.13

1.04

1

0.052

pints (UK)

34.7

0.02

7.4 10^-4

0.15

0.129

0.125

3.57

103

2.4

20

19.2

1

Полезные советы

• Если в задаче указан объем – ищите высоту через него.
• Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
• Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
• Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
• Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.

6.5 Total Score

Найти высоту в пирамиде

Достоверность информации

8.5

Актуальность информации

7.5

Раскрытие темы

8.5

Доступность применения

7

Удобство

8

ПЛЮСЫ

Благодаря доступной информации можно легко научиться решать задачи по геометрии

МИНУСЫ

Необходимы знания математики

 | 

Как поступить при вычислении площади боковой и полной поверхности?

Поскольку в основании лежит правильная фигура, то все грани пирамиды оказываются равными. Причем каждая из них является равнобедренным треугольником, поскольку боковые ребра равны. Тогда для того, чтобы вычислить боковую площадь пирамиды, потребуется формула, состоящая из суммы одинаковых одночленов. Число слагаемых определяется количеством сторон основания.

Площадь равнобедренного треугольника вычисляется по формуле, в которой половина произведения основания умножается на высоту. Эта высота в пирамиде называется апофемой. Ее обозначение — «А». Общая формула для площади боковой поверхности выглядит так:

S = ½ Р*А, где Р — периметр основания пирамиды.

Бывают ситуации, когда не известны стороны основания, но даны боковые ребра (в) и плоский угол при ее вершине (α). Тогда полагается использовать такую формулу, чтобы вычислить боковую площадь пирамиды:

S = n/2 * в2 sin α.

Часто задаваемые вопросы

1Как понять, что пирамида правильная, если в условии это не указано?

Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.

Зная определения и свойства, определить тип фигуры очень легко.

2Могут ли быть указаны в задании лишние данные?

Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.

3Обязательно ли оформлять высоту большой буквой H? Нужно ли выделять апофему?

Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой

Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении

4Как можно быстро изучить стереометрию?

Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.

4Как искать высоту, если известен объем?

Если выразить высоту через формулу объема, то получится следующее:

H = (3*V)/ S;

Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²

H = 3*70/30 = 7см

Объём пирамиды онлайн калькулятор

Онлайн калькулятор вычиселения объема пирамиды может вычислить объем пирамиды различными способами:

1. По площади основания и высоте для пирамиды любой формы,
2. По числу сторон и высоте для правильной пирамиды,
3. По стороне и высоте для треугольной, четырехугольной и шестиугольной пирамиды.

Объем пирамиды можно легко вычислить на этом онлайн калькуляторе.
Вы получите ответ в развернутом виде шаг за шагом. Тем самым усвоете материал по данной теме.

• Калькулятор
• Инструкция
• Теория
• История
• Сообщить о проблеме

В основании правильной треугольной пирамиды лежит равносторонний треугольник.Формула объема пирамиды:

где a — длина одной из сторон основания,h — высота пирамиды.

Решение:

V =

=

=

0.722

Ответ: Объём правильной треугольной пирамиды с длиной стороны основания a = 1 и высотой h = 5 равен 0.722

Многогранник, у которого одна грань многоугольник, а все остальные грани — треугольники с общей вершиной, называется пирамидой.
Многоугольная грань пирамиды называется ее основанием, треугольные грани с общей вершиной — боковыми гранями, а их общая вершина — вершиной пирамиды.

Как рассчитать площадь? формулы

Рассмотрим правильную шестиугольную пирамиду. Быть приспособленным к каждой стороне шестиугольника. Тогда A соответствует мере основания каждого треугольника пирамиды и, следовательно, краям основания.

Площадь многоугольника представляет собой произведение периметра (суммы сторон) на апофему основания, разделенную на два. В случае шестиугольника это будет 3 * A * APb.

Можно заметить, что площадь правильной гексагональной пирамиды в шесть раз превышает площадь каждого треугольника пирамиды плюс площадь основания. Как упоминалось ранее, высота каждого треугольника соответствует апофеме пирамиды, AP.

Следовательно, площадь каждого треугольника пирамиды определяется как A * AP / 2. Таким образом, площадь правильной гексагональной пирамиды равна 3 * A * (APb + AP), где A — край основания, APb — апофем основания, а AP — апофем пирамиды..

Расчет в неправильных гексагональных пирамидах

В случае неправильной гексагональной пирамиды не существует прямой формулы для расчета площади, как в предыдущем случае. Это потому, что каждый треугольник пирамиды будет иметь различную площадь.

В этом случае площадь каждого треугольника должна рассчитываться отдельно и площадь основания. Тогда площадь пирамиды будет суммой всех площадей, рассчитанных ранее.