Все способы нахождения площади параллелограмма

Параллелограмм и окружность

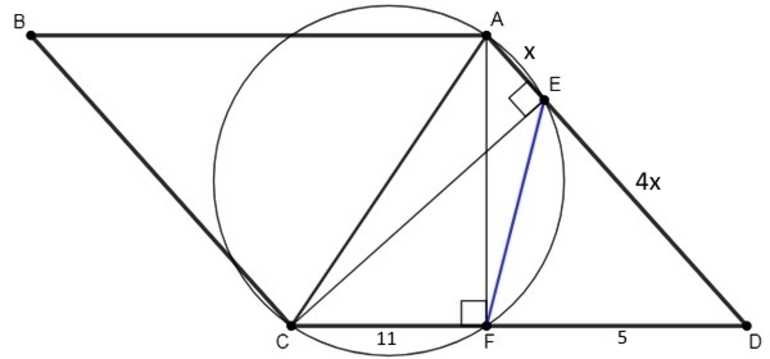
Существуют определенный тип задач, в которых речь идет о параллелограмме и окружности. Всего бывает два варианта: вписанная и описанная окружности. Следует отметить, что не всегда это возможно. Существуют определенные условия, при которых возможны такие операции

Кроме того, следует обратить особое внимание на дополнительные свойства, которые появляются при комбинации данных фигур. Можно не только чередовать комбинации, но и использовать одновременно.

Для решения сложного типа задач и выполнения расчетов, в некоторых случаях рекомендуется применять вписанные и описанные окружности. Например, при проектировании деталей, необходимо полностью подогнать ее размеры, поскольку они должны быть правильной формы. При помощи окружности (вписанной или описанной) можно выявить ряд дефектов, которые могут привести к некорректной работе механизма.

Круг и прямоугольник

Главное условие: любой четырехугольник можно вписать в окружность, когда сумма его двух противоположных углов составляет 180 градусов. У параллелограмма есть одно свойство: сумма углов, которые прилегают к любой из вершин, составляет 180 градусов. Кроме того, сумма всех его углов составляет 360, а, следовательно, сумму противоположных углов составляет 360 — 180 = 180 (градусов).

Однако при попытке описать около него окружность ничего не выйдет, поскольку есть одно свойство: противоположные углы у него равны. Ими могут быть тупые и острые. Сумма градусной меры тупых углов будет больше 180, а острых — меньше. Когда противоположные углы будут равны 90, то значит их сумма составит 180. В этом случае нужно рассматривать частный случай — прямоугольник

Появляется очень важное свойство: диагонали прямоугольника пересекаются и точкой пересечения (центром окружности) делятся пополам, а также являются диаметрами окружности.

Ромб и квадрат

В параллелограмм также можно вписать окружность. Однако для этого необходимо выполнение определенного условия. Оно заключается в следующем: суммы противолежащих сторон параллелограмма должны быть равны. Нужно отметить, что это выполняется только для ромба и квадрата.

Ромбом называется параллелограмм, стороны которого равны, а углы не равны 90 градусов. Квадрат — геометрическая фигура, у которой все стороны и углы равны. Из последнего определения можно найти значение градусной меры одного угла: 360 / 4 = 90. Последняя фигура является частным случаем ромба. Радиус окружности находится с помощью формулы: r = S / p = 0,5 * H. В этом соотношении переменные S, p и H — площадь, полупериметр и высота соответственно. Для нахождения S можно воспользоваться такими соотношениями:

• Известны длина стороны (а) и высота (H): S = a * H.
• Через диагонали d1 и d2: S = d1 * d2 / 2.

Полупериметром фигуры называется половина от значения ее периметра. Соотношение записывается таким образом: p = P / 2 = 4 * a.

Таким образом, знать основные свойства и признаки параллелограмма необходимо, поскольку от этого может зависеть не только качество сдачи экзаменов, решения задач, но и проектирование различных деталей.

Свойства параллелограмма

Геометрическая фигура – ​​это любое множество точек. Каждая фигура имеет свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Мы рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем, чему равна сумма углов параллелограмма, и другие особенности этой фигуры. Вот они:

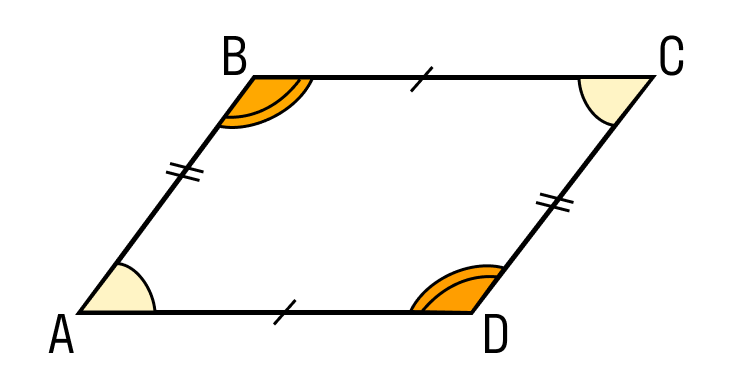
1. Противоположные стороны параллелограмма равны.
   ABCD — параллелограмм, поэтому AB = DC, BC = AD.
2. Противолежащие углы параллелограмма равны.
   ABCD — параллелограмм, то есть ∠A = ∠C, ∠B = ∠D.
3. Диагонали параллелограмма в точке пересечения делятся пополам.
   ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, следовательно, BO = OD, AO = OC.
4. Диагональ делит параллелограмм на два равных треугольника.
   ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA.
5. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180 градусам.
   ABCD — параллелограмм, поэтому ∠A + ∠D = 180°.
6. В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d12 + d22 = 2 × (a2 + b2).

А теперь докажем теорему, основанную на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

Диагонали любого выпуклого четырехугольника пересекаются. Все, что мы знаем о точке их пересечения, это то, что она лежит внутри четырехугольника.

Если провести обе диагонали в параллелограмме, то точка пересечения разделит их пополам. Убедись в том, что:

1. AB = CD как противоположные стороны параллелограмма.
2. ∠1 = ∠2 как на крест лежащие углы при пересекении секущей AC пралленых прямомятых AB и CD; ∠3 = ∠4 как перпендикулярные углы при пересечении секущих BD, параллельных прямым AB и CD.
3. Следовательно, треугольник АОВ равен треугольнику COD по второму признаку равенства треугольников, т е по стороне и прилежащим к его углам, из чего следует:
   • СО = АО
   • БО = ДЕЛАТЬ

Теория доказана. Наши предположения вроно.

Противоположные (или противоположные) стороны параллелограмма равны.

• АВ = CD
• До н.э. = н.э

Противоположные углы параллелограмма равны.

• ∠АВС = ∠АЦП
• ∠ПЛОХОЕ = ∠BCD

Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

Для рисунка выше: α + β = 180°.

Любая из двух диагоналей параллелограмма делит его на два равных треугольника.

△ABC = △ADC

Диагонали параллелограмма в точке пересечения делятся пополам.

• АЭ = ЕС
• БЭ = ЭД

Свойство 6

Точка пересецения диагоналей параллегормы (также называемой центром симметрии) одновременно является точкой пересецения его средних линий.

Средняя линия четырехугольника – это отрезок, соединяющий середины его противоположных сторон.

В данном случае средние линии — это отрезки FM и EN.

Свойство 7

Угол между двумя высотами параллелограмма равен его острому углу.

• BL – высота, отнесенная в сторону CD
• BK – высота, пройденная в сторону AD
• ∠КБЛ = ∠НАЗАД

Свойство 8

Биссектрисы углов параллелограмма, прилежащие к одной стороне, взаимно перпендикулярны (т е расположены под углом 90° друг к другу).

• AP – биссектриса ∠BAD
• BR – биссектриса ∠ABC
• AP перпендикулярно BR

Свойство 9

Биссектрисы двух противоположных углов параллелограмма параллельны.

Углы ABC и ADC противоположны. Их биссектрисы параленные, т.е. БР || ДП.

Важные свойства параллелограмма

Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны. Он обладает рядом свойств, которые позволяют решать различные задачи по его изучению и использованию.

Одно из важных свойств параллелограмма связано с его углами. Сумма углов параллелограмма всегда равна 180 градусам. Это позволяет устанавливать связи между внутренними и внешними углами, а также решать задачи на нахождение углов параллелограмма по известным данным.

Еще одно важное свойство параллелограмма связано с его диагоналями. Диагонали параллелограмма делят его на две равные части

Это означает, что общая площадь параллелограмма можно найти, умножив длину одной из его сторон на высоту, опущенную на эту сторону. Формула для вычисления площади параллелограмма S=а * h, где S — площадь, а — длина одной из сторон, h — высота, опущенная на эту сторону.

Еще одно важное свойство параллелограмма связано с его сторонами. Противоположные стороны параллелограмма равны по длине и параллельны

Это позволяет устанавливать связи между данными о длинах сторон и решать задачи на нахождение неизвестных сторон параллелограмма.

Таким образом, знание важных свойств позволяет успешно решать задачи, связанные с определением углов, сторон и площади параллелограмма. Это основополагающие знания при изучении геометрии и решении прикладных задач.

Противоположные стороны равны и параллельны

Параллелограмм — это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. У такой фигуры есть некоторые особенности, включая способы нахождения ее площади.

Площадь параллелограмма можно найти несколькими способами. Один из них — умножить длину одной из сторон на высоту, проведенную к этой стороне. Другой способ — умножить длины двух соседних сторон на синус угла между ними. Третий способ — использовать формулу, в которой нужно умножить длины двух соседних сторон на синус угла между ними и на половину суммы этих сторон.

Для нахождения площади параллелограмма также можно использовать формулу, в которой нужно умножить длину одной из сторон на длину высоты, опущенной на эту сторону из противоположного угла. Кроме того, площадь параллелограмма можно найти, составив таблицу со значениями длин сторон и углов и применив подходящую вычислительную формулу.

Важно запомнить, что при решении задач на нахождение площади параллелограмма необходимо учитывать, что противоположные стороны этой фигуры параллельны и равны друг другу. Используя соответствующие формулы и методы, можно легко найти площадь параллелограмма и успешно решать задачи из этой области геометрии

Противоположные углы равны

В геометрии существует базовая теорема, утверждающая, что в параллелограмме противоположные углы равны. Противоположные углы — это углы, лежащие по разные стороны от прямой, соединяющей противоположные вершины параллелограмма. Эта теорема является одним из основных свойств параллелограмма.

Знание того, что противоположные углы параллелограмма равны, позволяет нам находить площадь этой фигуры. Площадь параллелограмма определяется как произведение длины одной из его сторон на высоту, проведенную к этой стороне. Высота параллелограмма — это расстояние между параллельными сторонами.

Применяя эту теорему, мы можем найти площадь параллелограмма, зная длины его сторон и длину проведенной к одной из сторон высоты. Для этого нужно умножить длину одной из сторон на длину высоты, или воспользоваться формулой: площадь = a * h, где a — длина одной из сторон, h — высота параллелограмма.

Таким образом, зная, что противоположные углы параллелограмма равны, мы можем легко найти площадь этой фигуры, используя соответствующую формулу или связанные с ней вычисления.

Площадь произвольного треугольника

Перейдем к более сложному случаю, когда необходимо подсчитать площадь произвольного треугольника, не являющегося прямоугольным. Предположим, надо найти площадь произвольного ∆АВС. Опустим из А на сторону ВС высоту АН:

В результате мы получили два прямоугольных треуг-ка, ∆АВН и ∆АCН. Мы уже знаем, как найти их площади:

Общая площадь всего ∆АВС равна сумме площадей ∆АВН и ∆АСН. Запишем ее и вынесем общий множитель АН/2 за скобки:

В скобках стоит сумма ВН + НС. Но ведь эта сумма равна длине стороны ВС! Тогда окончательно формулу можно записать в виде:

Получили, что для вычисления площади произвольного треугольника надо сначала умножить его высоту на сторону, на которую она падает, а далее поделить результат на 2. Однако для полного доказательства этого факта надо рассмотреть особый случай, когда высота в треуг-ке падает не на сторону, а на ее продолжение (такая ситуация возникает в тупоугольном треуг-ке):

На рисунке снова получились всё те же прямоугольные треуг-ки ∆АСН и ∆АВН. Запишем формулы их площади:

Отличие в том, что на этот раз площадь АВС можно вычислить не как сумму, а как разницу этих площадей:

Итак, можно сформулировать следующее правило:

Примечание. Часто сторону, на которую опущена высота, называют основанием треуг-ка.

Задание. Вычислите площадь ∆АВС, если сторона АВ имеет длину 7, а высота СН равна 4.

Решение. В данной задаче на сторону длиной 7 падает высота длиной 4. Надо просто подставить эти числа в формулу:

Задание. Докажите, что медиана треуг-ка разбивает его на два равновеликих треуг-ка.

Решение.

Пусть в ∆АВС проведена медиана СМ. Требуется доказать, что

Важно заметить, что СН будет являться высотой не только для ∆АВС, но также и для ∆СВМ и ∆САМ. Обозначим СН как h, а АВ как а

Тогда мы можем найти длины отрезков ВМ и АМ, ведь медиана делит сторону АВ пополам:

Получили одно и то же значение, то есть площади треуг-ков равны.

В рассмотренной задаче мы использовали тот факт, что у нескольких треуг-ков может быть общая высота. Общая высота используется и в многих других геометрических задачах.

Задание. Предложите способ, как разделить треуг-к, показанный на рисунке, на три равновеликих треуг-ка:

Чтобы треуг-ки были равновелики, достаточно, чтобы у них была общая высота, а основания, на которые эта высота падает, были бы равны друг другу. Поэтому можно просто поделить нижнюю сторону на три одинаковых отрезка (длиной по 7 клеток) и соединить концы полученных отрезков с противоположной вершиной:

Красной линией здесь показаны границы треуг-ков, а штриховой – их общая высота СН. Вычислить площадь каждого из треуг-ков можно по следующим формулам:

Но отрезки BD, DE и EA одинаковы (по 7 клеточек), поэтому одинаковы будут и площади:

Заметим, что необязательно делить на три одинаковых отрезка именно нижнюю сторону. Допустимы и два других варианта решения:

Но и это не единственные решения задачи. Попробуйте самостоятельно предложить ещё несколько вариантов.

Формула площади треуг-ка показывает, что между длинами высот и сторон есть взаимосвязь.

Задание.В ∆РЕТ РЕ = 72, ЕТ = 45. Высота ТН имеет длину 40. Найдите высоту РМ.

Решение.

Зная ТН и РЕ, мы сможем найти площадь треуг-ка:

Теперь запишем эту формулу площади в ином виде, когда используется высота МР и сторона ЕТ

Величину S_РЕТ мы только что вычислили, а длина ЕТ известна из условия, поэтому можно подставить их в формулу:

Пример задачи

Пример 1

Найти площадь равностороннего треугольника, если длина его стороны равняется $a.$

Решение.

Так как треугольник равносторонний, то все его углы равняются ${60}^0$.

Тогда, по теореме $4$, имеем

Ответ:
$\frac{a^2\sqrt{3}}{4}$.

Заметим, что результат этой задачи можно применять при нахождении площади любого равностороннего треугольника с данной стороной.

Формула для площади параллелограмма

Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону.

Доказательство

Если параллелограмм — прямоугольник, то равенство выполнено по теореме о площади прямоугольника. Далее считаем, что углы параллелограмма не прямые.

Пусть в параллелограмме $ABCD$ угол $\angle BAD$ острый и $AD > AB$. Иначе переименуем вершины. Тогда высота $BH$ из вершины $B$ на прямую $AD$ падает на сторону $AD$, так как катет $AH$ короче гипотенузы $AB$, а $AB

Сравним площадь параллелограмма $ABCD$ и площадь прямоугольника $HBCK$. Площадь параллелограмма больше на площадь $\triangle ABH$, но меньше на на площадь $\triangle DCK$. Так как эти треугольники равны, то и их площади равны. Значит, площадь параллелограмма равна площади прямоугольника со сторонами длиной в сторону и высоту параллелограмма.

Формула для площади параллелограмма через стороны и синус

Площадь параллелограмма равна произведению соседних сторон на синус угла между ними.

Доказательство

Высота параллелограмма $ABCD$, опущенная на сторону $AB$ равна произведению отрезка $BC$ на синус угла $\angle ABC$. Осталось применить предыдущее утверждение.

Формула для площади параллелограмма через диагонали

Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Доказательство

Пусть диагонали параллелограмма $ABCD$ пересекаются в точке $O$ под углом $\alpha$. Тогда $AO=OC$ и $BO=OD$ по свойству параллелограмма. Синусы углов, в сумме дающих $180^\circ$ равны, $\angle AOB = \angle COD = 180^\circ — \angle BOC = 180^\circ — \angle AOD$. Значит, синусы углов при пересечении диагоналей равны $\sin \alpha$.

$S_{ABCD}=S_{\triangle AOB} + S_{\triangle BOC} + S_{\triangle COD} + S_{\triangle AOD}$

по аксиоме измерения площади. Применяем формулу площади треугольника $S_{ABC} = \dfrac{1}{2} \cdot AB \cdot BC \sin \angle ABC$ для этих треугольников и углов при пересечении диагоналей. Стороны каждого равны половинам диагоналей, синусы также равны. Следовательно, площади всех четырёх треугольников равны $S = \dfrac{1}{2} \cdot \dfrac{AC}{2} \cdot \dfrac{BD}{2} \cdot \sin \alpha = \dfrac{AC \cdot BD}{8} \sin \alpha$. Суммируя всё вышесказанное, получаем

$S_{ABCD} = 4S = 4 \cdot \dfrac{AC \cdot BD}{8} \sin \alpha = \dfrac{AC \cdot BD \cdot \sin \alpha}{2}$

Прежде чем узнать, как найти площадь параллелограмма, нам необходимо вспомнить, что такое параллелограмм и что называется его высотой. Параллелограмм – четырехугольник, противолежащие стороны которого попарно параллельны (лежат на параллельных прямых). Перпендикуляр, проведенный из произвольной точки противоположной стороны к прямой, содержащей эту сторону называется высотой параллелограмма.

Квадрат, прямоугольник и ромб – это частные случаи параллелограмма.

Площадь параллелограмма обозначается как (S).

Как сформулировать и доказать утверждения о свойствах параллелограмма, теоремы о признаках данной фигуры

Параллелограммом называют четырёхугольник (фигура, что состоит из четырёх точек и отрезков, последовательно их соединяющих), у которого противоположные стороны попарно параллельны. Его свойства впервые детально изучали греческие математики Евклид и Пифагор. Конец эпохи Средневековья принёс людям полную теорию об этой фигуре.

…

История возникновения термина

О некоторых видах четырёхугольников, квадратов, прямоугольников, равносторонних и прямоугольных трапеций знали ещё давно.

Термин «параллелограмм» греческого происхождения, считают что его придумал Евклид (приблизительно 300 годов до нашей эры). Ещё известно, что эта фигура и её свойства были знакомы ученикам школы Пифагора, раньше их называли пифагорейцами.

В «Началах» Евклида приведена следующая теорема: в параллелограмме противоположные стороны равны, а диагонали разделяют его по половине. Но в данной книге не было написано о свойствах точки их сечения. Ещё этот учёный не упоминает о прямоугольнике и ромбе.

Полную теорию сделали только в конце Средневековья, а в книгах она появилась в семнадцатом столетии. Теоремы и свойства параллелограмма основывались на аксиомах Евклида.

Нужно сказать, что Евклид, как и большинство математиков того времени, для названия отрезка, который соединяет противоположные вершины четырёхугольника или прямоугольника, использовал другой термин — «диаметр». Это можно объяснить тем, что первые геометры свои мысли основывали на вписании круга в прямоугольник. В Средние века для названия приведённых отрезков использовали оба термина. Только в семнадцатом столетии «диагональ» стала общепринятой.

Доказательство признаков фигуры

На следующем рисунке изображён параллелограмм ABCD, где AB параллельно CD и AD параллельно BC:

Сумма любых двух соседних углов параллелограмма равна 180 градусам — это первая подсказка о том, как сформулировать и доказать утверждения о признаках параллелограмма.

На этом рисунке углы A и B фигуры ABCD есть внутренними односторонними углами для параллельных прямых AD и BC . Поэтому углы A + B равны 180 градусам. Аналогично это свойство можно привести для любой другой пары соседних (если вершины есть концами одной и той же стороны) углов.

Теорема признаков паралелограмма

• Теорема признаков параллелограмма гласит, что это выпуклый четырёхугольник. Исходя из предыдущего правила, угол А намного меньше 180 градусов, как и B, C, D, поэтому его называют опухлым четырёхугольником. Диагонали этой фигуры могут пересекаться.
• У параллелограмма противоположные стороны и углы равны.

Диагональ АС разбивает фигуру на два треугольника ABC и ADC. АС — общая сторона двоих треугольников и САD эквивалентен АСВ также с САВ и АСD. Тогда ∆АВС = ∆СDA, по стороне и двумя прилегающими углами. Это значит, что АВ=СD, BC=AD и B=D, как соответствующие элементы в различных треугольниках.

Теорема о диагоналях

• Периметр (сумма длин всех сторон четырёхугольника, которую обозначают буквой Р) параллелограмма эквивалентен 2 (АВ +ВС) или АВ + ВС + СD + DA.
• Теорема о диагоналях параллелограмма гласит, что точкой пересечения они делятся ровно пополовине.

По условию задачи O — это точка пересечения диагоналей AC и BD параллелограмма. AB эквивалентно BC, как противоположные, не имеющие своей общей вершины. CAD равен ACB также BDA и DBC, АD и BC секущими AC и B. D. Следуя дальше ∆АОD = ∆ COB, по стороне и двух прилегающих углах. Тогда, А = ОС, ВО = ОD, как соответствующие стороны разных треугольников.

На этом рисунке MN — это высота. Следуя за известным определением, из каждой вершины можно провести две высоты (BF и BT, которые приведены в соответствии к сторонам AD и CD).

Свойства параллелограмма с доказательствами 8 класса :

1. Две стороны равны и параллельны.
2. Противоположные стороны попарно равны.
3. Диагонали пересекаются и этой точкой делятся ровно пополам.
4. Противоположные углы попарно равны.

Теперь нужно вернуться к первому рисунку, чтобы до конца понять все признаки параллелограмма и доказательства любых признаков.

В нём AD = BC и AD || BC. Провели диагональ AC и получили ∆CAD и ∆ACB. CAD эквивалентен ВСА, как внутренние разносторонние углы при пересечениях прямых AD и BC секущей AC, ещё она является их общей стороной. Условия задачи говорят: AD=BC. Значит, что, ∆CAD=∆ACB, ACD = CAB. Из-за того, что они были созданы в таких условиях AB || CD, по признаку параллельных прямых.

Теоремы параллелограмма

Все существующие теоремы доказывают свойства параллелограмма и исходят из определения о том, что это четырехугольник с противоположно расположенными параллельными сторонами.

Основные теоремы доказывают, что:

• параллелограммом является выпуклый четырехугольник;
• противоположные стороны попарно равны;
• углы, являющиеся противоположными, попарно равны;
• точка пересечения диагоналей разделает их пополам.

Параллелограммом является выпуклый четырехугольник

Многоугольник признается выпуклым при условии отсутствия продления до прямой хотя бы одной из сторон, а все оставшиеся стороны будут располагаться по одну сторону от этой прямой.

Пусть дан параллелограмм MNPK, сторона MN противоположна PK, а MK противоположна NP. Следовательно, исходя из определения, следует вывод о том, что MN || PK, а MK || NP.

Параллельные отрезки общих точек соприкосновения не имеют. Следовательно, PK находится со стороной MN по одну сторону. Отрезок NP соединяет точку N отрезка MN с точкой P отрезка PK. Противоположный отрезок MK соединяет оставшиеся две точки отрезков, что дает право утверждать о нахождении отрезков NP и MK по одну сторону от прямой MN. Исходя из всего вышесказанного, можно сделать вывод о том, что три стороны PK, NP и MK располагаются по одну сторону от отрезка MN.

Аналогичный алгоритм доказательства предположения о нахождении трех других сторон по одну сторону относительно остальных.

Противоположные стороны и углы попарно равны

Имеется четырехугольник MNPK, у которого MK=NP, MN=PK, ∠NMK=∠NPK, ∠MNP=∠MKP.

Параллелограмм — это, как мы знаем, четырехугольник. Следовательно, имеет 2 диагонали. Зная о том, что это выпуклая фигура, делаем вывод о делении фигуры на два треугольника. В нашем случае образовались треугольники MNP и MKP.

У треугольников имеется общее — сторона MP. ∠NPM=∠PMK, а ∠NMP=∠MPK, так как накрест лежащие углы, пересекая параллельные прямые, равны.

Следовательно, ΔMNP=ΔMKP, так как одна общая сторона и два равных смежных угла. Отсюда NP=MK, MN=PK.

∠NMP=∠NMP+∠PMK

∠NPK=∠NPM+∠MPK

∠NPM=∠PMK и ∠NMP=∠MPK

Из равенств следует, что ∠NMK=∠NPK.

Таким образом, теорема о равенстве противоположных углов и сторон доказана.

Точка пересечения диагоналей разделяет их пополам

Зная, что параллелограмм представляет собой выпуклый четырёхугольник, можно сказать о наличии двух пересекающихся диагоналей.

Есть четырехугольник MNPK с диагоналями NK и PM, пересекающимися в точке O. Возьмем два полученных треугольника MNO и PKO.

Из свойства противоположно лежащих сторон параллелограмма следует равенство MN=PK. Угол MNO и угол OKP — накрест лежащие, следовательно, они равны. Аналогично, два других угла — NMO и OPK — являются равными. Делаем вывод о равенстве треугольников MNO и PKO по стороне и двум углам.

Из рисунка видно, что углы MON и KOP вертикальные, а значит, они равны.

Зная о равенстве образовавшихся треугольников, можно утверждать и о равенстве всех соответствующих элементов. Сторона MO равна стороне PO, как и сторона NO=OK. Каждая из пар вместе представляет собой диагональ параллелограмма.

Таким образом, теорема о делении диагоналей пополам доказана.

Признаки параллелограмма

Существует несколько признаков, которые позволяют доказать, что тот или иной четырехуг-к является параллелограммом. Рассмотрим первый из них.

Пусть в четырехуг-ке параллельны и равны стороны АB и CD. Проведем диагональ ВD. Она окажется секущей для АВ и СD, поэтому накрест лежащие углы окажутся равными:

Сторона ВD – общая, а АВ = СD по условию. Тогда по 1-ому признаку равенства треуг-ков ∆АВD = ∆CВD. В свою очередь это означает, что

Они являются накрест лежащими уже при отрезках ВС и АD. Отсюда вытекает, что эти отрезки параллельны друг другу. В итоге в четырехуг-ке ABCD параллельными оказываются все противоположные стороны, поэтому он должен быть параллелограммом.

Задание. В параллелограмме АВCD смежные стороны различны, а∠А – острый. Из точек B и D опущены перпендикуляры ВК и DM на диагональ АС. Докажите, что фигура ВМDК – тоже параллелограмм.

Решение. Выполним построение по заданным условиям:

Необходимо доказать, что красная фигура – это параллелограмм. По выведенному нами признаку достаточно показать, что отрезки ВК и MD параллельны и равны. Их параллельность очевидна, ведь эти отрезки перпендикулярны к одной прямой (АС). Равенство отрезков можно доказать, рассмотрев ∆АВК и ∆СМD. Они являются прямоугольными, у них равны гипотенузы АВ и СD (как противоположные стороны в одном параллелограмме), а также

ведь это накрест лежащие углы при параллельных отрезках АВ и CD. В итоге получаем, что

Но тогда ВК = МD. В итоге, с учетом того, что ВК||МD, получаем, что ВМDК – это параллелограмм.

Следующая теорема позволяет определять, является ли фигура параллелограммом, только по длине ее сторон.

Для доказательства используем всё тот же прием: проведем в четырехуг-ке диагональ:

Мы снова получаем равенство треуг-ков

но на этот раз они равны по трем равным сторонам. Отсюда получаем равенство углов:

Из равенства этих углов, являющихся накрест лежащими, следует, что АВ||СDи ВС||АD. Это и значит, что АВСD– параллелограмм.

Задание. Середины смежных сторон параллелограмма соединили друг с другом отрезками. Докажите, что получившаяся таким образом фигура – параллелограмм.

Решение.

Обозначим середины сторон АВСD буквами М, Р, К и Т. Ясно, что

как противоположные стороны одного параллелограмма. Если отрезки равны, то равны и их половины, поэтому можно записать:

Теперь рассмотрим ∆АМТ и ∆СРК. Они равны, ведь у них одинаковы две стороны и угол, лежащий между ними:

Отсюда следует, что МТ = РК. Аналогично можно показать, что ∆МВР = ∆ТDК, из чего вытекает, что МР = ТК.

В итоге получаем, что у МРКТ противоположные стороны попарно равны. А это означает, что МРКТ – это параллелограмм.

Следующий признак параллелограмма связан с диагоналями.

Действительно, пусть в произвольном четырехуг-ке АВСD диагонали пересекаются в точке О, являющейся серединой диагоналей:

Тогда ВО = ОDи АО = ОС. Рассмотрим ∆АОВ и ∆СОD. ∠ВОА = ∠СОD, ведь это вертикальные углы. В итоге у этих треуг-ков равны две стороны, а также угол между ними. Следовательно, ∆АОВ = ∆СОD. Но отсюда следует, что

В итоге у АВСD противоположные стороны одинаковы. Значит, это параллелограмм.

Задание. О – точка, в которой пересекаются диагонали параллелограмма АВСD. М, Р, Н, К – середины отрезков АО, ВО, СО и DO соответственно. Докажите, что МРНК – это параллелограмм.

Решение.

По свойству параллелограмма точка О делит их пополам, то есть на равные отрезки:

Заметим, что диагоналями МРНК являются отрезки РК и МН, причем они пересекаются в точке О. Так как

Можно сказать, что О – середина диагоналей РК и МН. Отсюда вытекает вывод, что МРНК – параллелограмм.

Пример 1

Рассмотрим пример нахождения площади параллелограмма. Дано, что длина его стороны равна 5 см, а высота, опущенная на эту сторону, равна 3 см. Найдем площадь параллелограмма по формуле.

Сначала найдем основание параллелограмма, равное длине одной стороны. Так как сторона равна 5 см, основание также будет равно 5 см.

Теперь найдем угол, образованный этим основанием и высотой. Пользуясь теоремой косинусов, найдем этот угол. Зная длину стороны и высоты, можно найти косинус угла, а затем сам угол.

Далее, воспользуемся формулой для нахождения площади параллелограмма: S = a * h * sin(угол), где a — основание, h — высота, угол — угол между основанием и высотой.

Подставляя значения в формулу, получаем: S = 5 см * 3 см * sin(угол). Таким образом, площадь параллелограмма составляет S = 15 см² * sin(угол).

В результате, для полного вычисления площади параллелограмма нам необходимо знать значение синуса угла, а также ориентацию параллелограмма (вектор, диагональ).

Задача на расчет площади параллелограмма

Ученикам на уроке геометрии была поставлена задача на расчет площади параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны. Основание параллелограмма — это одна из его сторон, а высота — это расстояние между основанием и его параллельной стороной.

Для решения задачи ученикам было предложено использовать формулу для расчета площади параллелограмма. Эта формула основана на применении векторов: площадь параллелограмма равна модулю векторного произведения его сторон.

Также для решения задачи ученикам было дано знание о том, что диагональ параллелограмма делит его на два равных треугольника. При этом, высота параллелограмма является высотой треугольника, проведенной к основанию треугольника, а основание треугольника равно любой стороне параллелограмма.

Для расчета площади параллелограмма по формуле, ученикам было необходимо знать длину основания и высоту параллелограмма, а также угол между основанием и одной из его сторон.

Используя полученные знания о понятии параллелограмма, его основании, диагонали, формуле расчета площади и векторах, ученики успешно решали задачу на расчет площади параллелограмма.

Решение задачи и расчет площади

Для расчета площади параллелограмма необходимо знать его основание и высоту. Основание параллелограмма – это одна из его сторон, на которую опирается высота. Высота параллелограмма – это отрезок, проведенный из вершины параллелограмма к основанию под прямым углом.

Расчет площади параллелограмма основан на формуле, которая связывает его основание и высоту. Формула площади параллелограмма выглядит следующим образом: S = a × h, где S – площадь, a – длина основания, h – высота.

Чтобы решить задачу на расчет площади параллелограмма, необходимо знать значения основания и высоты. По условию задачи могут быть даны значения углов параллелограмма или длины сторон. В таком случае, для определения основания и высоты можно воспользоваться связью основания и углов, а также применить векторное представление площади параллелограмма.

Для решения задачи на расчет площади параллелограмма можно использовать следующий алгоритм:

1. Определить основание и высоту параллелограмма.
2. Рассчитать площадь параллелограмма по формуле S = a × h.
3. Дать ответ на вопрос задачи, используя расчитанную площадь.

Таким образом, для решения задачи на расчет площади параллелограмма необходимо использовать формулу, связывающую основание и высоту, а также учитывать дополнительные условия задачи, такие как значения углов параллелограмма или длины сторон. Решение задачи позволит нам определить площадь параллелограмма, что является важным при работе с геометрическими фигурами.