Площадь поверхности куба

Куб и его свойства

В настоящее время видеоуроки нельзя просматривать или распространять среди студентов.

Чтобы получить доступ к этому и другим видеоурокам из комплекта, добавьте его в свой личный кабинет через покупку в каталоге.

Конспект урока “Куб и его свойства”

На предыдущем уроке мы узнали о таких многогранниках, как Прямоугольный параллелограмм..

Решив задачу со спичками, мы получили геометрическую фигуру под названием пирамида.

Перед этим вас познакомят и с другими многогранниками. Теперь вернемся к параллелепипеду.

Таким образом, поверхность параллелепипеда состоит из шести прямоугольников. Эти прямоугольники называются лица параллелограмм.

Обратите внимание, что два соседних прямоугольника имеют общую сторону, которую мы называем край прямоугольного параллелепипеда. Концы ребер называются вершины прямоугольного параллелепипеда

Таким образом, прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин.

Обратите внимание, что хотя многогранники различны, поверхность каждого многогранника состоит из правильных многоугольников, которые мы называем гранями многогранника. Два соседних правильных многоугольника имеют общую сторону – ребро многогранника

Концы ребер являются вершинами многогранника.

Этот многогранник называется октаэдр. Он имеет 8 ребер, которые являются треугольниками, 12 граней и 6 вершин.

Куб – это прямоугольный параллелограмм, у которого все ребра равны

Обратите внимание, что мы рисуем пунктирные линии для граней куба, которые не видны. Это дает полное представление о фигуре и ее положении относительно нас

Все грани куба – равные квадраты. Поверхность куба состоит из 6 равных квадратов. Убедитесь, что грани напротив друг друга не имеют общих ребер. Эти называются напротив.

лицакоторые имеют общее ребро, называются прилегающая территория.

Теперь давайте проведем небольшой эксперимент. Возьмите коробку, имеющую форму куба. Мы раскрываем его, затем разрезаем вдоль четырех вертикальных ребер, а затем разворачиваем.

Форма, которую мы имеем, называется Разворачивание куба.. Он состоит из 6 равных квадратов.

Фигуры ниже также являются взрывающимися кубами.

Используя каждую из разверток, вы можете сделать модель куба. Для этого выполните следующие действия. Нарисуйте чертеж куба на листе бумаги. Выключите его. Согните его вдоль секций, соответствующих граням куба, и склейте.

Теперь нарисуйте отрезок, который соединит самые удаленные вершины куба. Мы называем эти вершины противоположными вершинами.

Отрезок, соединяющий две противоположные вершины куба, называется диагональю куба.

Теперь давайте решим несколько задач.

Проблема первая. Определите, какой кубик мы получим из данной сборки.

Давайте представим, какие грани куба являются смежными, то есть имеют общее ребро, и сравним с предложенными вариантами, чтобы найти правильный. Для этого нам удобнее всего сравнивать лица, которые отличаются в зависимости от рисунка на них

Обратите внимание на лицо с желтым треугольником и лицо с зеленым треугольником. Конечно, при сборке куба эти грани будут примыкать друг к другу

Следовательно, при различных поворотах куба возможны четыре варианта взаимного расположения этих граней.

Давайте теперь сравним четыре предложенных варианта. Сразу видно, что первый вариант неверен. Второй вариант неверен. Конечно, третий вариант также неверен. Однако вариант четыре является правильным, поскольку грани, на которых изображены треугольники, правильные. В этом случае на верхней поверхности должен быть синий круг. Это правильно.

Таким образом, мы выяснили, что из данного расширения получится куб с числом 4.

Вы можете решить эту проблему другим способом. Вы можете нарисовать этот контур на бумаге. Удобнее это делать на листе бумаги с квадратами, тогда вам не придется пользоваться линейкой, чтобы соблюсти размеры куба. Вы просто посчитаете количество квадратов, которое вам необходимо.

Затем вам нужно будет раскрасить и вырезать нарисованный контур. Затем скатайте его в кубик и склейте. После этого вы можете легко сравнить полученный куб с любым из предложенных вариантов и выбрать подходящий.

Вторая задача. Модель куба с длиной ребра 4 см была окрашена серой краской и разрезана вдоль ребра на кубики с длиной ребра 1 см. Сколько кубиков получилось: а) окрашенных по трем граням; б) окрашенных по двум граням?

Третья проблема. На рисунке показан скелет куба. Затем нарисуйте видимые грани так, чтобы на куб можно было смотреть: a) сверху слева; b) снизу справа.

Проблема четвертая .. Фигура, показанная на рисунке, состоит из пяти кубиков. Какой формы фигура, если смотреть на нее: a) спереди; b) слева; c) сверху?

Что такое файл cookie и другие похожие технологии

Файл cookie представляет собой небольшой текстовый файл, сохраняемый на вашем компьютере, смартфоне или другом устройстве, которое Вы используете для посещения интернет-сайтов.

Некоторые посещаемые Вами страницы могут также собирать информацию, используя пиксельные тэги и веб-маяки, представляющие собой электронные изображения, называемые одно-пиксельными (1×1) или пустыми GIF-изображениями.

Файлы cookie могут размещаться на вашем устройстве нами («собственные» файлы cookie) или другими операторами (файлы cookie «третьих лиц»).

Мы используем два вида файлов cookie на сайте: «cookie сессии» и «постоянные cookie». Cookie сессии — это временные файлы, которые остаются на устройстве пока вы не покинете сайт. Постоянные cookie остаются на устройстве в течение длительного времени или пока вы вручную не удалите их (как долго cookie останется на вашем устройстве будет зависеть от продолжительности или «времени жизни» конкретного файла и настройки вашего браузера).

как найти диагональ куба,если известна только полная площадь поверхности ?

Пусть площадь поверхности х.
тогда площадь грани х\6
тогда сторона ребро куба корень (х\6)
диагональ равна утроенный квадрат стороны, то есть 3·(х\6) = х\2
Удачи))

берете грань за х тогда площадь будет x^3 находите х а дальше и треугольника диагональ

По теореме пифагора.
Диагональ — гипотенуза
Ширина и длина у куба — катеты и они одинаковы.
И формула гипотенуза в квадрате=высота в квадрате + ширина в квадрате.
Ну площадь поверхности куба — квадрат же.
Ну вот к примеру — площадь — 16
Значит высота=ширина=4
Значит диагональ равна х^2=4^2+4^2
И равна корень из 32

я думаю, что для начала надо узнать площадь одной стороны, т. к. сторон шесть и они все равны, то и общую площадь надо поделить на шесть. дальше узнать длину грани, то есть корень квадратный и т. д.

Как найти площадь поверхности куба

Все материалы по математике для старших классов

← Предыдущая 1 2 Следующая →

Справка по математике для средней школы »
Геометрия »
Твердая геометрия »
Кубики »
Как найти площадь поверхности куба

Какова площадь поверхности куба со стороной 15?

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти площадь поверхности куба, мы должны подсчитать количество граней поверхности и сложить площади каждой из них.

В кубе 6 граней, каждая из которых представляет собой квадрат с одинаковыми длинами сторон.

В этом примере длины сторон равны 15, поэтому площадь каждого квадрата будет

Затем мы умножаем это число на 6, количество граней куба, чтобы получить

Наш ответ для площади поверхности: .

Сообщить об ошибке

Какова площадь поверхности куба со стороной ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь поверхности куба, мы должны подсчитать количество граней поверхности и сложить площади каждой из них. В кубе есть грани, каждая из которых представляет собой квадрат с одинаковыми длинами сторон. В этом примере длина стороны равна .

Площадь квадрата определяется уравнением . Используя нашу длину стороны, мы можем найти площадь одной грани куба.

Затем мы умножаем это число на число граней куба, чтобы найти общую площадь поверхности.

Наш ответ для площади поверхности .

Сообщить об ошибке

Если площадь поверхности куба равна 96, какова длина одной стороны куба?

Возможные ответы:

Правильный ответ:

4

Пояснение:

Площадь поверхности куба = 6a 2 , где a — длина стороны каждого ребра куба. Иными словами, поскольку все стороны куба равны, а — это просто длина одной стороны куба.

У нас есть 96 = 6a 2  → a 2 = 16, так что это площадь одной грани куба.

Решив, мы получим √16, поэтому a = 4

Сообщить об ошибке

Какова площадь поверхности куба с длиной стороны ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь поверхности куба, используйте формулу .

Сообщить об ошибке

Какова площадь поверхности в дюймах прямоугольной призмы длиной , шириной и высотой ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь поверхности прямоугольной призмы, используйте формулу .

Однако все единицы измерения должны быть одинаковыми. Все единицы измерения этой задачи указаны в дюймах, за исключением .

Преобразование в дюймы.

Теперь мы можем подставить известные значения в формулу площади поверхности, чтобы рассчитать площадь поверхности прямоугольной призмы.

Если вы вычислили площадь поверхности равной , тогда вы использовали формулу объема прямоугольной призмы, которая равна ; это неправильно.

Сообщить об ошибке

Какова площадь поверхности куба с диагональю ?

Возможные ответы:

Правильный ответ:

Объяснение:

Для решения этой задачи необходимо знать несколько фактов.

Изменить порядок решения для .

Теперь найдите площадь куба по формуле .

Сообщить об ошибке

Эта фигура представляет собой куб с одной гранью площадью 16 в 2 .

Какова площадь поверхности куба (в 2 )?

Возможные ответы:

Правильный ответ:

Объяснение:

Площадь поверхности куба равна сумме площадей каждой грани. Поскольку у куба 6 граней, площадь поверхности всего куба равна .

Сообщить об ошибке

Куб имеет высоту 4 фута.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь поверхности куба, возведите в квадрат длину одного ребра и умножьте результат на шесть:

Сообщить об ошибке

Длина стороны определенного куба . Какова площадь поверхности этого куба?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти поверхность куба, используйте стандартное уравнение: 

, где  обозначает длину стороны.

Подставьте данное значение для , чтобы найти ответ:

Сообщить об ошибке

Сара упаковывает подарок на день рождения.

Возможные ответы:

Правильный ответ:

Объяснение:

Помните, .

Для куба:

Таким образом .

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Квадрат, свойства и формулы, площадь и периметр

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат (понятие, определение), диагональ квадрата:

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат – это четырехугольник, имеющий равные стороны и углы.

Все углы квадрата прямые. Каждый из них прямой и равен 90°.

Таким образом, все квадраты отличаются друг от друга только длиной стороны.

Рис. 2. Квадрат и диагонали квадрата

Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.

Квадрат является одновременно частным случаем других фигур: параллелограмма, ромба и прямоугольника. Поэтому квадрату присущи все свойства параллелограмма, ромба и прямоугольника .

Квадрат – это равносторонний прямоугольник.

Квадрат – это ромб с прямыми углами.

Свойства квадрата:

1. Длины всех сторон равны.

2. Противоположные стороны квадрата параллельны.

3. Все углы квадрата прямые. Каждый из них равен 90°.

4. Сумма углов квадрата равна 360 градусам.

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.

5. Диагонали квадрата равны между собой.

6. Диагонали квадрата взаимно перпендикулярны.

7. Диагонали квадрата точкой пересечения делятся пополам.

8. Угол между диагональю и стороной квадрата равен 45 градусам.

9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.

10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.

Обе диагонали делят квадрат на 4 равных равнобедренных прямоугольных треугольника .

11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.

Формулы квадрата. Площадь квадрата. Периметр квадрата:

Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.

Формула диагонали квадрата:

, , , , .

Формула радиуса вписанной окружности квадрата:

Радиус вписанной окружности квадрата равен половине его стороны.

.

Формула радиуса описанной окружности квадрата:

.

Формула периметра квадрата:

, , .

Формула площади квадрата:

, , , , .

Вычисление объемов фигур

Радиус первого шара в \(5\) раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади поверхности первого шара?

Площадь поверхности шара радиуса \(R\) ищется по формуле \(S=4\pi R^2\) . Следовательно, площадь поверхности первого шара относится к площади поверхности второго шара как \ Так как радиус первого шара больше радиуса второго шара в 5 раз, то \(R_1=5R_2\) . Следовательно, \ Следовательно, площадь поверхности первого шара в 25 раз больше площади поверхности второго, значит, площадь поверхности второго в 25 раз меньше.

Даны два конуса. Радиус второго конуса в \(3\) раза больше радиуса первого конуса, а высота второго конуса в \(6\) раз меньше высоты первого конуса. Найдите объем первого конуса, если объем второго конуса равен \(18\) .

Объем конуса с высотой \(h\) и радиусом основания \(R\) вычисляется по формуле \(V=\frac13\pi R^2h\) . Следовательно, объем первого конуса относится к объему второго конуса как \ Так как радиус второго в 3 раза больше радиуса первого, то \(R_2=3R_1\) . Так как высота второго в 6 раз меньше высоты первого, то \(h_1=6h_2\) . Следовательно, \

Даны два конуса: \(K_1\) и \(K_2\) . Площадь полной поверхности \(K_1\) относится к площади полной поверхности \(K_2\) как \(4:1\) . Известно, что радиус \(K_1\) в 4 раза больше образующей \(K_1\) и в 2 раза больше радиуса \(K_2\) . Найдите отношение образующей \(K_2\) к образующей \(K_1\) .

Площадь полной поверхности конуса с образующей \(l\) и радиусом основания \(R\) ищется по формуле \(S=\pi R (R+l)\) . Тогда площадь полной поверхности \(K_1\) относится к площади полной поверхности \(K_2\) как \ Из условия следует, что \(R_1=4l_1\) , \(R_2=\frac12R_1=2l_1\) , следовательно, \

Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в \(343\) раза больше объема второго шара?

Объем шара радиуса \(R\) ищется по формуле \(V=\dfrac43 \pi R^3\) . Следовательно, объем первого шара относится к объему второго как \=7.\] Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.

Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.

Пусть буквы \(a\) , \(b\) и \(c\) обозначают высоту, ширину и длину соответственно. Объем прямоугольного параллелепипеда ищется по формуле \(V=abc\) . Следовательно, объем первого параллелепипеда относится к объему второго как \ Из условия следует, что \(a_1=7a_2\) , \(b_2=2b_1\) , \(c_1=3c_2\) . Тогда \

Площадь боковой поверхности первого цилиндра равна \(16\) . Найдите площадь боковой поверхности второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты первого цилиндра.

Площадь боковой поверхности цилиндра с высотой \(H\) и радиусом основания \(R\) ищется по формуле \(S=2\pi RH\) . Тогда площадь бок. поверхности первого цилиндра относится к площади бок. поверхности второго как \ Из условия следует, что \(R_2=4R_1\) , \(H_1=5H_2\) , значит, \ Следовательно, \

Площадь боковой поверхности первого конуса относится к площади боковой поверхности второго конуса как \(3:7\) . Найдите отношение образующей первого конуса к образующей второго конуса, если радиус первого конуса относится к радиусу второго как \(15:7\) .

Площадь боковой поверхности конуса с образующей \(l\) и радиусом основания \(R\) ищется по формуле \(S=\pi Rl\) . Тогда площадь бок. поверхности первого конуса относится к площади бок. поверхности второго как \ Так как радиус первого конуса относится к радиусу второго как \(15:7\) , то есть \(\frac=\frac7\) , то \

Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.

Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

Примечание: куб является частным случаем параллелепипеда или призмы.

Формула площади поверхности куба

П»Ã¾ÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð â ÃÂÃÂþ ÃÂÃÂüüð ÿûþÃÂðôõù òÃÂõàõóþ óÃÂðýõù:

S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6

ÃÂûþÃÂðôàúðöôþù óÃÂðýø þôøýðúþòð, ÃÂþ õÃÂÃÂÃÂ:

S1=S2=S3=S4=S5=S6=Sâ²S_1=S_2=S_3=S_4=S_5=S_6=SâÂÂ

Sâ²Sâ â ÿûþÃÂðôàûÃÂñþù óÃÂðýø úÃÂñð.

âþóôð ÿþûýðàÿûþÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð ÷ðÿøÃÂõÃÂÃÂàúðú:

àðÃÂÃÂüþÃÂÃÂøü ýð ÿÃÂøüõÃÂðàÃÂð÷ýÃÂõ ÃÂÿþÃÂþñàòÃÂÃÂøÃÂûõýøàÿþûýþù ÿûþÃÂðôø ÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð.

ÃÂûþÃÂðôàúðöôþù óÃÂðýø úÃÂñð òÃÂÃÂøÃÂûÃÂõÃÂÃÂàúðú ÿûþÃÂðôàúòðôÃÂðÃÂð, ÃÂþ ÃÂÃÂþÃÂþýþù ÃÂõñÃÂð úÃÂñð ÿþ ÃÂþÃÂüÃÂûõ:

Sâ²=aâÂÂa=a2SâÂÂ=acdot a=a^2

aa â ÃÂÃÂþÃÂþýð úÃÂñð.

ÃÂÃÂÃÂÃÂôð, þúþýÃÂðÃÂõûÃÂýþ ÿûþÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð:

ÃÂþ ÃÂõþÃÂõüõ ÃÂøÃÂðóþÃÂð, ôøðóþýðûàúÃÂñð ÃÂòÃÂ÷ðýýð àôûøýþù õóþ ÃÂõñÃÂð ÿþ ÃÂþÃÂüÃÂûõ:

d2=a2+a2+a2d^2=a^2+a^2+a^2d2=3âÂÂa2d^2=3cdot a^2d=3âÂÂad=sqrt{3}cdot a

ÃÂÃÂÃÂÃÂôð:

a=d3a=frac{d}{sqrt{3}}

ÃÂþôÃÂÃÂðòøü ò ÃÂþÃÂüÃÂûàôûàÿûþÃÂðôø:

S=6âÂÂa2=6âÂÂ(d3)2=2âÂÂd2S=6cdot a^2=6cdotBig(frac{d}{sqrt{3}}Big)^2=2cdot d^2

ÃÂþ ÃÂõþÃÂõüõ ÃÂøÃÂðóþÃÂð, ôøðóþýðûàúòðôÃÂðÃÂð ll ÃÂòÃÂ÷ðýýð àõóþ ÃÂÃÂþÃÂþýþù aa:

l2=a2+a2l^2=a^2+a^2l2=2âÂÂa2l^2=2cdot a^2l=2âÂÂal=sqrt{2}cdot a

âþóôð ÃÂÃÂþÃÂþýð úòðôÃÂðÃÂð:

a=l2a=frac{l}{sqrt{2}}

ÃÂþôÃÂÃÂðòûÃÂõü ò ÃÂþÃÂüÃÂûàôûàÿûþÃÂðôø ø ÿþûÃÂÃÂðõü:

S=6âÂÂa2=3âÂÂl2S=6cdot a^2=3cdot l^2

àð÷ñõÃÂõü ñþûõõ ÃÂûþöýÃÂõ ÿÃÂøüõÃÂÃÂ.

Теория

Площадь поверхности куба через ребро

Чему равна площадь поверхности куба S_пов, если длина его ребра a:

S_пов = 6 ⋅ a²

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если он имеет длину рёбер a = 5 см :

S_пов = 6 ⋅ 5² = 6 ⋅ 25 = 150 см²

Площадь поверхности куба через диагональ

Чему равна площадь поверхности куба S_пов, если длина диагонали этого куба d:

S_пов = 2 ⋅ d²

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если длина диагонали у него d = 3 м:

S_пов = 2 ⋅ 3² = 2 ⋅ 9 = 18 м² = 180 000 см²

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если его объём V_куба = 8 см³:

S_пов = 6 ⋅ 3√8² = 6 ⋅3√64 = 6 ⋅ 4 = 24 см²

Как связан куб с другими фигурами и телами?

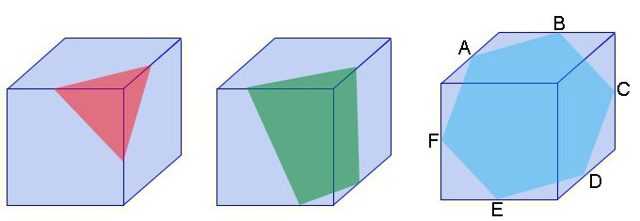
Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше.

Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником.

Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.

Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.

В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.

Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.

Примеры задач с решениями

Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.

Задание 1.

В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?

Решение.

Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:

V₁ = ha² = 10a²

Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:

V₂ = h (2a)² = 4ha²

Поскольку V₁ = V₂, можно приравнять выражения:

10a² = 4ha²

После сокращения обеих частей уравнения на a² получается:

10 = 4h

В результате новый уровень песка составит h = 10 / 4 = 2,5 см.

Задание 2.

ABCDA₁B₁C₁D₁ правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.

Решение.

Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.

Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.

Длина любого ребра определяется через известную диагональ:

a = d / √2 = 6√2 / √2 = 6

Площадь полной поверхности находится по формуле для куба:

Sполн = 6a² = 6·6² = 216

Задание 3.

В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?

Решение.

Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.

Длина комнаты составляет a = √9 = 3 м.

Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².

Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.

Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.

Площадь куба | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Площадь куба, она же площадь полной поверхности куба, равна увеличенной в шесть раз площади одной его грани. Так как площадь куба зависит только от ребра, зная ее, можно легко вычислить ребро и затем все остальные параметры куба.
S_(п.п.)=6a^2
a=√(S_(п.п.)/6)

Соответственно, площадь стороны куба – одной его грани, будет равна площади полной поверхности разделенной на шесть, а площадь боковой поверхности, состоящей из четырех граней, — двум третям площади полной поверхности куба.
S=S_(п.п.)/6
S_(б.п.)=2/3 S_(п.п.)

Для того чтобы найти объем куба, необходимо его ребро возвести в третью степень. Используя полученную формулу ребра куба через площадь полной поверхности, получим, что объем куба равен одной шестой квадратного корня из площади куба в третьей степени, деленной на шесть.
V=a^3=(√(S_(п.п.)/6))^3=1/6 √(〖S_(п.п.)〗^3/6)

Периметр куба можно найти, умножив ребро куба на 12. Если подставить вместо ребра квадратный корень через площадь куба, то получим следующую формулу для периметра куба:
P=12a=12√(S_(п.п.)/6)

Диагональ одной стороны куба является по определению диагональю квадрата, которая вычисляется как произведение стороны квадрата на корень из двух. Так как ребро куба является стороной этого квадрата, то диагональ будет равна квадратному корню из площади, деленной на 3.
d=a√2=√(S_(п.п.)/3)

Чтобы рассчитать диагональ куба, необходимо провести дополнительное построение на чертеже, соединяющее ребро куба и одну из вершин диагонали в прямоугольный треугольник. Это дает возможность воспользоваться теоремой Пифагора и вычислить диагональ куба через площадь, подставив формулу вместо ребра куба. (рис.2.1)
a^2+d^2=D^2
D^2=a^2+2a^2
D^2=3a^2
D=a√3=√(S_(п.п.)/2)

Радиус сферы, вписанной в куб, по определению равен половине ребра куба или половине квадратного корня из площади куба, деленной на шесть. (рис. 2.2)
r=a/2=1/2 √(S_(п.п.)/6)

Радиус сферы, описанной вокруг куба, представлен половиной диагонали куба, которая равна площади полной поверхности куба, деленной на два, под корнем. (рис.2.3)
R=D/2=1/2 √(S_(п.п.)/6)

Как найти площадь куба по объему без формул: шаг за шагом решение задачи

Если нужно найти площадь куба по его объему, то можно использовать не только формулы, но и простые математические выкладки. Чтобы решить эту задачу, следует понимать, что куб состоит из 6 квадратов. Их площади равны между собой и находятся по формуле S=a^2, где a — длина стороны квадрата.

Таким образом, чтобы найти площадь куба, нужно найти длину стороны квадрата, а для этого необходимо извлечь кубический корень из объема куба. Формула для этого: a = V^(1/3), где V — объем куба.

Далее, чтобы найти площадь куба, нужно возвести длину стороны квадрата в квадрат и умножить на 6: S = 6a^2.

Давайте рассмотрим пример. Пусть объем куба равен 27 кубическим единицам. Тогда, чтобы найти длину стороны куба, извлекаем из объема кубический корень: a = 3 см.

Формула вычисления площади куба

1. Через длину ребра

Площадь (S) поверхности куба равна произведению числа 6 на квадрат длины ребра.

S = 6 ⋅ а2

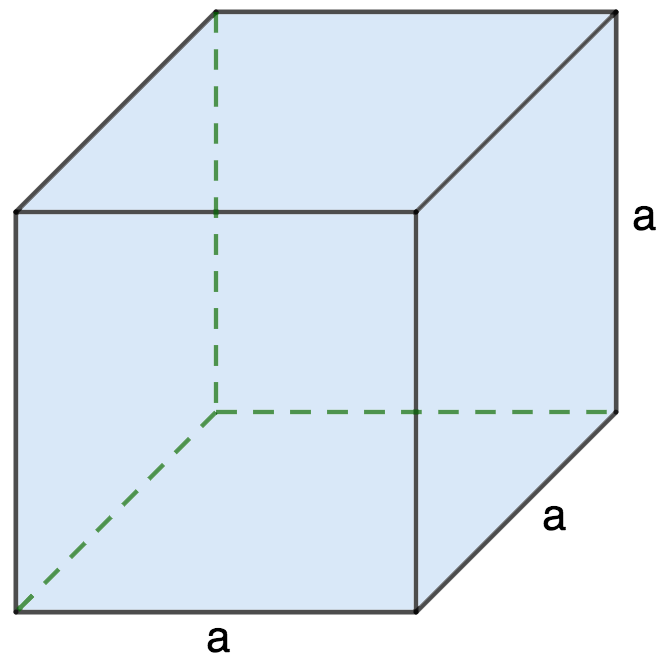
Эта формула выводится следующим образом:

• Куб — это правильная геометрическая фигура, грани которой — равные квадраты со стороной а (он же — ребро куба).
• Площадь каждой грани рассчитывается следующим образом: S = a ⋅ a = a2.
• Всего у куба 6 граней, значит, площадь поверхности равна шести площадям грани: S = 6 ⋅ a2.

2. Через длину диагонали грани

Сторону любой грани куба (ребра) можно вычислить через длину диагонали по формуле: a=d/√2.

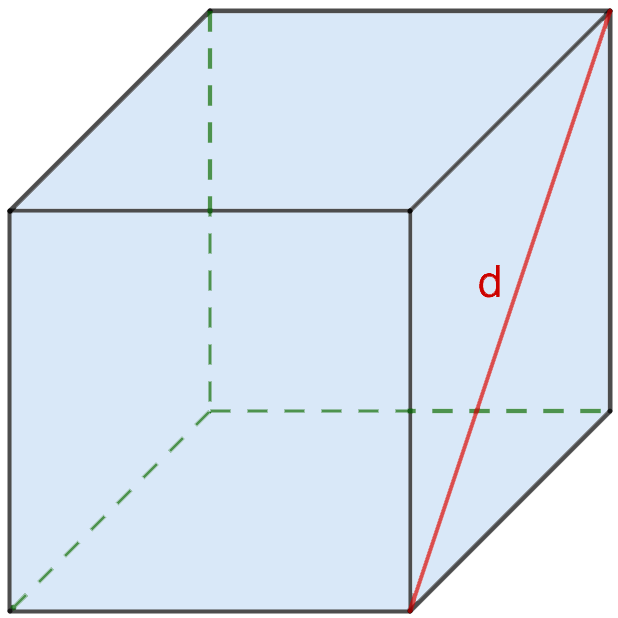
Это означает, что вы можете рассчитать площадь поверхности фигуры следующим образом:

S = 6 ⋅ (д/√2)2

Cookie файлы бывают различных типов:

Необходимые. Эти файлы нужны для обеспечения правильной работы сайта, использования его функций. Отключение использования таких файлов приведет к падению производительности сайта, невозможности использовать его компоненты и сервисы.

Файлы cookie, относящиеся к производительности, эффективности и аналитике. Данные файлы позволяют анализировать взаимодействие посетителей с сайтом, оптимизировать содержание сайта, измерять эффективность рекламных кампаний, предоставляя информацию о количестве посетителей сайта, времени его использования, возникающих ошибках.

Рекламные файлы cookie определяют, какие сайты Вы посещали и как часто, какие ссылки Вы выбирали, что позволяет показывать Вам рекламные объявления, которые заинтересуют именно Вас.

Электронная почта. Мы также можем использовать технологии, позволяющие отслеживать, открывали ли вы, прочитали или переадресовывали определенные сообщения, отправленные нами на вашу электронную почту. Это необходимо, чтобы сделать наши средства коммуникации более полезными для пользователя. Если вы не желаете, чтобы мы получали сведения об этом, вам нужно аннулировать подписку посредством ссылки «Отписаться» («Unsubscribe»), находящейся внизу соответствующей электронной рассылки.

Сторонние веб-сервисы. Иногда на данном сайте мы используем сторонние веб-сервисы. Например, для отображения тех или иных элементов (изображения, видео, презентации и т. п.), организации опросов и т. п. Как и в случае с кнопками доступа к социальным сетям, мы не можем препятствовать сбору этими сайтами или внешними доменами информации о том, как вы используете содержание сайта.

Задачи на нахождение площади куба

Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 40 и высота равна 15.

Площадь поверхности складывается из площади основания и площади четырех боковых граней: Высоту боковой грани найдем по теореме Пифагора: Тогда площадь поверхности пирамиды:

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 2, 4, 3 и двух площадей прямоугольников со сторонами 2, 1:

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 3, 4 и двух площадей квадратов со стороной 2:

Там же «квадраты» со сторонами 2 и 3.

Мы вычитаем, только боковые грани из большого прямоугольного параллелепипеда — это как раз квадраты со сторонами 2 и 2.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 2, 3, 5 и площади двух прямоугольников со сторонами 1, 2:

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 5, 4, 1 и двух прямоугольников со сторонами 1 и 2, уменьшенной на площадь двух квадратов со стороной 2:

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 3, 5, 7 и двух прямоугольников со сторонами 1 и 5, уменьшенной на площадь двух прямоугольников со сторонами 1 и 3:

Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 4, 3, 6 и двух прямоугольников со сторонами 2 и 3, уменьшенной на площадь двух прямоугольников со сторонами 3 и 2:

Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 5, 5, 6 и двух прямоугольников со сторонами 2 и 5, уменьшенной на площадь двух прямоугольников со сторонами 2 и 3:

Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?

Наш образовательный портал предлагает выстроить занятия по-новому. Переходя от простого к сложному, выпускники смогут определить непонятные для себя темы и улучшить собственные знания.

Весь базовый материал по теме «Вычисление площадей и объемов фигур» собран в разделе «Теоретическая справка». Освежив в памяти эту информацию, учащиеся смогут попрактиковаться в решении задач. Большая подборка упражнений как простого, так и экспертного уровня представлена в разделе «Каталог». База заданий регулярно дополняется.

Решать задачи на вычисление объемов фигур или на построение сечения геометрических фигур школьники могут в режиме онлайн. Функционал образовательного сайта «Школково» позволяет сохранять упражнения в разделе «Избранное». Благодаря этому учащиеся смогут вернуться к задаче необходимое количество раз и обсудить ход ее решения со школьным учителем или репетитором.

Понимание связи между площадью и объемом куба

Понимание связи между площадью и объемом куба важно при решении задач, связанных с геометрией и физикой. Площадь куба — это сумма площадей его граней, а объем — это произведение длины, ширины и высоты

Очевидно, что при увеличении длины, ширины и высоты куба, его объем будет увеличиваться гораздо быстрее, чем площадь его граней. И наоборот, при увеличении площади граней, объем куба будет увеличиваться медленнее.

Таким образом, понимание связи между площадью и объемом куба позволяет более осознанно подходить к решению задач, например, при нахождении размеров куба по заданному объему или при определении объема куба по его площади граней.

Важно также помнить, что площадь и объем куба могут быть использованы для расчета других параметров, например, длины его диагонали или радиуса вписанной сферы