Основное свойство пропорции: определение и применение

Прямая пропорциональность

Сначала рассмотрим несколько примеров.

Пример:

Пусть буква х обозначает в годах возраст сына, а буква у — возраст отца и пусть в данный момент сыну один год, а отцу 25 лет.

Составим таблицу значений х и соответствующих им значений буквы у. В третьей строке этой таблицы выпишем значения отношения :

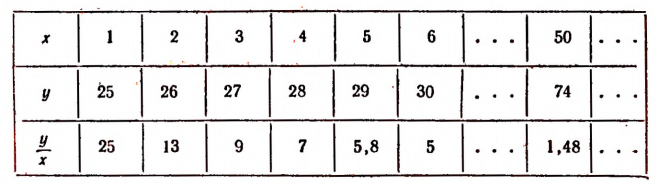
В этом примере отношение (отношение возраста отца к возрасту сына) не остается неизменным. Оно с течением времени убывает.

Пример:

Пусть буква х обозначает в сантиметрах длину стороны квадрата, а буква у — площадь квадрата в квадратных сантиметрах.

Составим таблицу, подобную предыдущей.

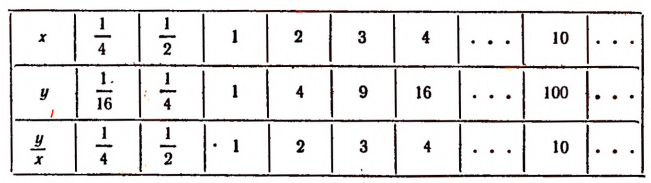
Отношение и здесь не остается неизменным. Оно возрастает при возрастании х.

Пример:

Пусть буква х обозначает в кубических сантиметрах объем ртути при температуре 0°, а буква у — вес этой ртути в граммах. Известно, что 1 куб. см ртути при температуре 0° весит 13,6 г.

Опять составим таблицу значений х, у и .

Этот третий пример существенно отличается от двух предыдущих. Здесь отношение сохраняет неизменное значение.

Определение:

Две величины у и х называются прямо пропорциональными (или просто пропорциональными), если при всех их возможных изменениях отношение остается равным одному и тому же числу и если при х = 0 значение у также равно нулю.

Значит, вес ртути и объем ртути при постоянной температура являются величинами пропорциональными.

Возраст отца и возраст сына не пропорциональны.

Также не пропорциональны сторона квадрата и его площадь.

Пусть изменяющиеся величины у и х пропорциональны. Тогда отношение будет равно некоторому постоянному числу.

Обозначая это постоянное число буквой k, получим:

или

Следовательно, если величины у и х пропорциональны и отношение равно k, то у выражается в зависимости от х формулой

Число k называется коэффициентом пропорциональности (величины у по отношению к величине х).

Теперь докажем обратное положение. Пусть

где k — постоянное число.

Отсюда следует, что при х = 0 и у = 0 и что А это и означает, что величины у и х пропорциональны.

Из того что следует, что , или что Отсюда можно сделать следующий вывод:

Если коэффициентом пропорциональности величины у по отношению к величине х служит постоянное число k, то коэффициентом пропорциональности величины х по отношению к величине у будет служить число .

Приведем еще один пример пропорциональных величин. Путь s, пройденный при равномерном движении, пропорционален. времени t, т. е.

Здесь постоянное число v есть коэффициент пропорциональности величины s по отношению к величине t (v есть скорость равномерного движения).

Сделаем еще два замечания.

Замечание:

Если имеется два ряда чисел:

и

и если

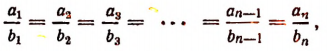
то числа одного из этих рядов называются пропорциональными числам другого ряда.

Замечание:

Если имеются только два постоянных числа а и b, то бессмысленно говорить о них, что они пропорциональны или не пропорциональны.

В этом случае можно интересоваться либо характером этих чисел, либо их разностью, либо их отношением и т. д.

В заключение решим две простые задачи на пропорциональные величины.

Задача:

На карте в масштабе расстояние между двумя пунктами равно 42,5 см. Определить, чему равно это расстояние на карте в масштабе

Решение:

Длина на карте прямо пропорциональна масштабу. Поэтому.

Задача:

С помощью непосредственного измерения установили, что при повышении температуры рельса на 24°С его длина увеличивается на 1,5 мм. Требуется вычислениями определить изменение длины рельса при понижении его температуры на 40°С. (Считать изменение длины рельса величиной, прямо пропорциональной изменению температуры.)

Решение:

Обозначив искомое изменение (в мм) буквой х, получим:

откуда

т. е. при понижении температуры рельса на 40°С его длина сократится на 2,5 мм.

Пропорция в дизайне

Пропорция это одно из основных свойств дизайна, которое позволяет создать визуальное равновесие и гармонию в композиции. Дизайнеры используют пропорцию для разделения пространства и создания иерархии элементов.

Пропорция может быть выражена числами или отношениями между различными элементами в дизайне. Она может быть применена к различным аспектам дизайна, таким как размеры и расположение объектов, цвета и шаблоны.

Пропорция может быть использована для создания различных эффектов и настроений в дизайне. Например, пропорция золотого сечения (отношение двух величин, в котором отношение большей величины к меньшей равно отношению суммы обеих величин к большей величине) может создавать визуальную гармонию и привлекательность.

Пропорция также может быть использована для создания различных композиционных структур, таких как сетки и сетки с асимметричным расположением элементов. Эти структуры могут быть использованы для создания удобной и эффективной навигации по дизайну или для подчеркивания ключевых элементов.

Пропорция может быть использована для создания баланса и визуальной стабильности в дизайне. Она может помочь улавливать взгляд зрителя и создавать удобную и понятную структуру.

Важно помнить, что пропорция является инструментом, а не жестким правилом. В дизайне нет жестких правил, и правила пропорции можно нарушать с целью достижения определенного эффекта или выражения идеи

Примеры пропорции в дизайне:
Пример
Описание

Золотое сечение
Разделение объекта или композиции на две части, пропорции которых соответствуют золотому сечению.

Сетки
Расположение элементов в дизайне с использованием сеток, создающих определенные пропорции и отношения.

Фибоначчиева последовательность
Использование числовых пропорций, основанных на Фибоначчиевой последовательности, для создания визуального баланса и гармонии.

Соотношение сторон
Использование определенного соотношения сторон (например, 1:1 или 4:3) для создания определенной формы или композиции.

Пропорция является важным инструментом в дизайне, который позволяет создавать гармоничные и визуально привлекательные композиции. Она может быть использована для создания баланса, иерархии и эффектных структур в дизайне.

алгебраическое предварительное исчисление — прямо отрицательно пропорциональна и обратно пропорциональна?

Задавать вопрос

спросил 1 год, 3 месяца назад

Изменено
1 год, 3 месяца назад

Просмотрено
448 раз

$\begingroup$

Если у меня есть пропорциональность
$$x\propto-y$$
Это предполагает, что x увеличивается с $-y$, и поскольку присутствует отрицательный символ, это будет означать, что чем ниже значение $y$, тем выше значение $x$… так можно ли считать это прямо пропорциональным?

Похоже, что оно отличается от $x\propto\frac{1}y$, так что я полагаю, что оно не обратно пропорционально?

Прямая связь $y$ с $x$ звучит неправильно, если ее называют прямо пропорциональной, так как же именно называется отрицательная пропорциональность, если не то же самое, что и обратно пропорциональная?

Спасибо.

• алгебра-предварительное исчисление
• терминология

2

$\begingroup$

МАТЕМАТИКА

21. Пропорции

Отношения 3,6 : 1,2 и 6,3 : 2,1 равны, так как значения частных равны 3. Поэтому можно записать равенство 3,6 : 1,2 = 6,3 : 2,1, или = .

Равенство двух отношений называют пропорцией.

С помощью букв пропорцию записывают так: a : b — с : d или .

Эти записи читают так: «Отношение а к b равно отношению с к d» или «а так относится к Ь, как с относится к d».

В пропорции = 21 или a : b = с : d, числа a и d называют крайними членами, а числа b и с — средними членами пропорции. В дальнейшем будем считать, что все члены пропорции отличны от нуля: а ≠ 0, b ≠ 0, с ≠ 0, d ≠ 0.

В пропорции найдем произведение её крайних и произведение её средних членов. Получим 3,6 • 2,1 = 7,56; 1,2 • 6,3 = 7,56. Значит, 3,6 • 2,1 = 1,2 • 6,3.

B верной пропорции произведение крайних членов равно произведению средних.

Верно и обратное утверждение:

Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.

Это свойство называют основным свойством пропорции.

Пропорция 20 : 16 = 5 : 4 верна, так как 20 • 4 = 16 • 5 = 80.

Поменяем местами в этой пропорции средние члены. Получим новую пропорцию: 20 : 5 = 16 : 4. Она тоже верна, так как при такой перестановке произведение крайних и произведение средних членов не изменилось. Эти произведения не изменятся, если в пропорции 20 : 5 = 16 : 4 поменять местами крайние члены.

Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.

Используя основное свойство пропорции, можно найти её неизвестный член, если все остальные члены известны.

Пример 1. Найдём в пропорции 0,5 : a = 2 : 13 неизвестный средний член а.

Решение. Используя основное свойство пропорции, получим а • 2 = = 0,5 • 13. Отсюда .

Пример 2. Решим уравнение .

Решение. Используя основное свойство пропорции, получим 8,75 • 0,75 = . Отсюда x = . Представим в виде десятичной дроби 3,75 и сократим выражение на 0,75, имеем х = ; х = 1,75.

Вопросы для самопроверки

• Что такое пропорция?
• Как называются числа х и у в пропорции х : а = b : у?
• Как называются числа m и n в пропорции а : m = п : b?
• Сформулируйте основное свойство пропорции.
• Какие перестановки членов пропорции снова приводят к верным пропорциям?
• Останется ли пропорция верной, если поменять местами какой-нибудь средний её член с одним из крайних? Приведите пример.
• Останется ли пропорция верной, если оба средних члена поменять местами с крайними членами? Проверьте ваш ответ на пропорции 3 : 4 = 9 : 12.

Выполните упражнения

760. Запишите пропорцию:

• а) 5 так относится к 3, как 2 относится к 1,2;
• б) 0,9 так относится к , как 45 относится к 16;
• в) отношение к 0,1 равно отношению 14 к 4,9.

Проверьте полученные пропорции, определяя отношения чисел.

761. Из каких отношений 0,6 : 5; 4,2 : 7; : 6,25 можно составить верную пропорцию?

762. Прочитайте пропорции и проверьте, верные ли они, используя основное свойство пропорции:

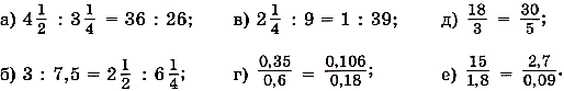
763. Решите уравнение:

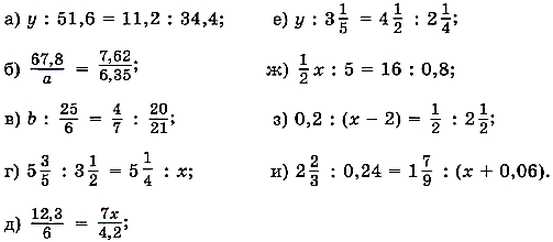
764. Переставив средние или крайние члены пропорции, составьте три новые верные пропорции из пропорции:

765. Используя верное равенство 4 • 9 = 0,2 • 180, составьте четыре верные пропорции.

766. Вычислите устно:

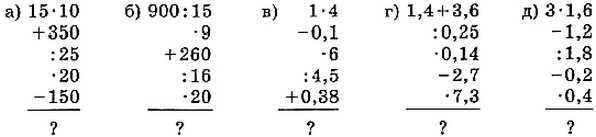
767. Какой знак действия надо подставить вместо *, чтобы получилось верное равенство:

768. Найдите отношение величин:

• а) 1,5 м и 30 см;
• б) 1 кг и 250 г;
• в) 1 ч и 15 мин;
• г) 50 см2 и 1 дм2.

769. числа равны этого числа. Какое это число?

770. Какое число надо прибавить к числителю и знаменателю дроби , чтобы получить дробь ?

771. Какие из фигур (рис. 33) являются развёртками:

• а) четырёхугольной призмы;
• б) треугольной призмы;
• в) треугольной пирамиды?

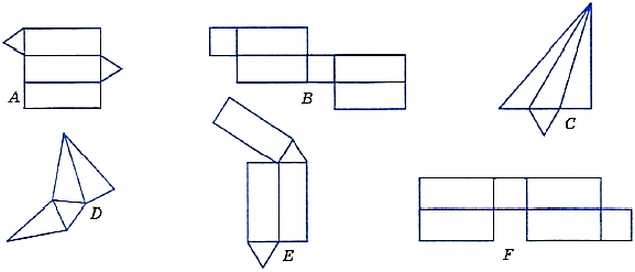
Рис. 33

772. Из ружья сделано 50 выстрелов, при этом 5 пуль пролетели мимо цели. Определите процент попаданий.

773. Угол А равен 30°, а угол В равен 50°. Какую часть от угла В составляет угол А? Во сколько раз угол В больше угла А?

774. Бригаде было дано задание собрать 280 ц винограда. Она собрала 350 ц. На сколько процентов бригада перевыполнила задание? На сколько процентов бригада выполнила задание?

775. В парке посадили клёны и дубы, причём на каждые 4 клёна приходится один дуб. Сколько процентов от всех посаженных деревьев составляют клёны? Сколько всего посадили деревьев в парке, если клёнов посадили 480?

776. Верна ли пропорция:

• а) 2,04 : 0,6 = 2,72 : 0,8;
• б) 0,0112 : 0,28 = 0,204 : 0,51?

777. Решите уравнение:

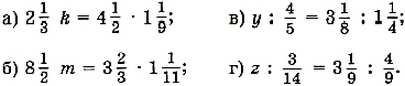
778. Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?

779. Через 2 ч после выхода со станции А тепловоз увеличил скорость на 12 км/ч и через 5 ч после начала движения прибыл в пункт назначения В. Какова была скорость тепловоза в начале пути, если расстояние от А до В равно 261 км?

780. Если к неизвестного числа прибавить 0,8, то получится 1,2. Найдите неизвестное число.

781. Выполните действия:

• а) (3,2 : 4 + 4 : 3,2) • 4,8;
• б) (385,7 : 0,19 — 30) • 0,2 — (35,7 • 3,29 + 2,547).

Пропорция.

Поскольку 3,6 : 0,9 = 4 и 1,2 : 0,3 = 4, то верно и равенство 3,6 : 0,9 = 1,2 : 0,3, которое называют пропорцией (от лат. ргороrtio — «соизмеримость»).

Если соотношение а : b равно соотношению с : d, то тождество а : b = с:d называют пропорцией.

Пропорцию можно выразить также в виде:

Приведённые записи читают: «соотношение а к b равно соотношению с к d или «а соотносится к b, как с соотносится к d».

В пропорции 3,6 : 0,9 = 1,2 : 0,3 числа 3,6 и 0,3 — крайние члены, числа 0,9 и 1,2 — средние члены. Рассмотрим произведение крайних и средних членов 3,6•0,3 = 0,9 • 1,2

Это определяется так:

если , то ad = bc

Главную особенность пропорции еще именуют правилом креста. Следуя главной особенности пропорции, можно рассчитать ее неизвестный член, если все остальные члены определены.

Чтобы определить неизвестный крайний член пропорции, необходимо произведение средних членов пропорции поделить на известный крайний член.

Чтобы определить неизвестный средний член пропорции, необходимо произведение крайних членов пропорции поделить на известный средний член. Или обобщенно можно сформулировать так: чтобы вычислить неизвестный член пропорции, следует перемножить диагональ с обоими известными членами, а далее поделить на оставшееся известное значение.

Правильна и следующая формулировка: если а, b, с и d числа отличные от нуля, то для них верно:

если

эта особенность называется свойством обращения пропорции.

Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны. Это свойство перестановки крайних и средних членов пропорции.

Если

Так же на практике пользуются правилом увеличения и уменьшения пропорции.

Если

Если

Обратим внимание, что составление пропорций — ещё один способ решения задач на проценты. Олово производят из минерала, который называют касситеритом

Сколько тонн олова получат из 25 т касситерита, если он содержит 78 % олова?

Олово производят из минерала, который называют касситеритом. Сколько тонн олова получат из 25 т касситерита, если он содержит 78 % олова?

Решив 25•78 = 100х мы находим, что х = 19,5т.

Пропорциональность может быть прямой и обратной.

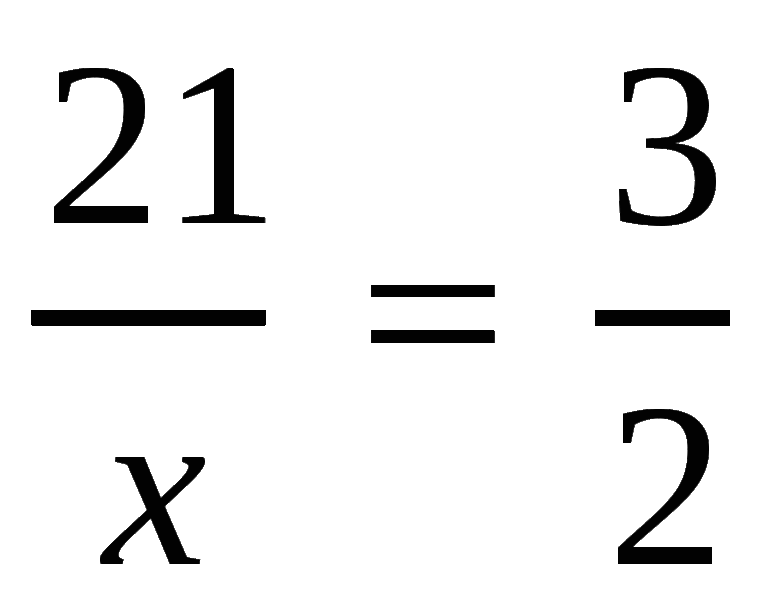
среда, 4 июля 2018 г.

Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.

Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.

Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.

Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.

Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…

А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.

Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.

Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».

Правило встречается в следующих упражнениях:

6 класс

Номер 607, Мерзляк, Полонский, Якир, Учебник

Номер 623, Мерзляк, Полонский, Якир, Учебник

Номер 686, Мерзляк, Полонский, Якир, Учебник

Номер 688, Мерзляк, Полонский, Якир, Учебник

Номер 823, Мерзляк, Полонский, Якир, Учебник

Номер 1154, Мерзляк, Полонский, Якир, Учебник

Задание 787, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1313, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1501, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1528, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 405, Мерзляк, Полонский, Якир, Учебник

Номер 406, Мерзляк, Полонский, Якир, Учебник

Теория

a/b = c/X или, другими словами, a относится к b так же как c относится к X – это геометрическая пропорция, которая позволяет выяснить как одно число относится к другому, если известно, как третье относится к четвёртому. Например, с помощью геометрической пропорции можно посчитать процент от числа.

Пример

Мы положили в банк 4000 рублей под 5% годовых и хотим выяснить сколько в рублях составят эти пять процентов. Мы понимаем, что 4000 – это 100%, а сколько 5% –?

Геометрическая пропорция в данном случаи будет выглядеть так: 100/5=4000/X

X = (4000*5)/100 = 200

Ответ: 5% от 4000 рублей составляет 200 рублей

Что такое пропорция: определение, элементы, основное свойство

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Что такое пропорция: определение, элементы, основное свойство

В данной публикации мы рассмотрим, что такое пропорция, из каких элементов она состоит, а также разберем основное свойство пропорции вместе с практическим примером.

• Определение пропорции
• Основное свойства пропорции

Определение пропорции

Пропорция – это равенство двух или более отношений чисел.

Допустим, у нас есть два равных отношения:

Если между этими отношениями поставить знак “равно”, то получится пропорция:

Элементы пропорции

• крайние – выделены красными кружками;

• средние – обведены зелеными цветом.

Основное свойства пропорции

В любой верно составленной пропорции произведение крайних элементов равняется произведению средних.

Т.е. a · d = b · c.

Чтобы было проще запомнить, используется так называемое “правило крестика”, т.е. перемножение накрест лежащих элементов.

Пример

Проверим основное свойство и правило на пропорции ниже:

Оба отношения дают результат, равный одному и тому же числу (двум), следовательно, пропорция верна.

Значит мы можем перемножить ее элементы, пользуясь “правилом крестика”:

Получаем:12 · 15 = 6 · 30 или 180 = 180

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Золотое сечение[]

Основная статья: Золотое сечение

(Рис.2) Cхема пропорциональных отрезков золотого сечения

‎Золотое сечение (золотая пропорция, гармоническое деление, деление в крайнем и среднем отношении) — соотношение числовых величин в математике и искусстве: отношение суммы двух величин к большей из них равно отношению большей величины к меньшей

Отношение частей в этой пропорции выражается квадратичной иррациональностью

φ=5+12≈1,6180339887…{\displaystyle \varphi ={\frac {{\sqrt {5}}+1}{2}}\approx 1{,}6180339887\dots }

Т. е. (см.Рис.2) равенство вида (a + b):a = a : b, или, в других обозначениях, равенство a+ba=ab=ϕ{\displaystyle \!{\frac {a+b}{a}}={\frac {a}{b}}=\phi } (часто читается как: «(a + b) относится к a так же, как a относится к b»). Если (a + b):a = a : b, то (a + b) и b называют крайними, а a — средними членами пропорции.

Золотое сечение в отличие от пропорции содержит произведение определённых значений средних членов (вместо c·d имеем a·a или a·c = a·a). Не любое деление отрезка даёт среднее сечение. Например, деление отрезка на части, выраженных рациональными числами или на равные части, не даёт золотого сечения.

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, называл это отношение «божественной пропорцией». Термин «золотое сечение» (goldener Schnitt) был введён в обиход Мартином Омом в 1835 году.

Золотое сечение и иррациональность

Золотое сечение в пятиконечной звезде

φ{\displaystyle \varphi } — иррациональное алгебраическое число, положительное решение квадратного уравнения

φ2=φ+1.{\displaystyle \varphi ^{2}=\varphi +1.}

φ{\displaystyle \varphi } представляется в виде бесконечной цепочки квадратных корней:

φ=1+1+1+1+….{\displaystyle \varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+…}}}}}}}}.}

φ{\displaystyle \varphi \;} представляется в виде бесконечной цепной дроби

φ=1+11+11+11+⋯,{\displaystyle \varphi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\,\cdots }}}}}},}

подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом, φ=limn→∞Fn+1Fn{\displaystyle \varphi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}}.

Построение золотого сечения

В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны φ{\displaystyle \varphi }).

Геометрическое построение. Золотое сечение отрезка AB{\displaystyle AB} можно построить следующим образом: в точке B{\displaystyle B} восстанавливают перпендикуляр к AB{\displaystyle AB}, откладывают на нём отрезок BC{\displaystyle BC}, равный половине AB{\displaystyle AB}, на отрезке AC{\displaystyle AC} откладывают отрезок AD{\displaystyle AD}, равный AC−CB{\displaystyle AC-CB}, и наконец, на отрезке AB{\displaystyle AB} откладывают отрезок AE{\displaystyle AE}, равный AD{\displaystyle AD}. Тогда

φ=|AB||AE|=|AE||EB|.{\displaystyle \varphi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|EB|}}.}

Уравнения с пропорцией

Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:

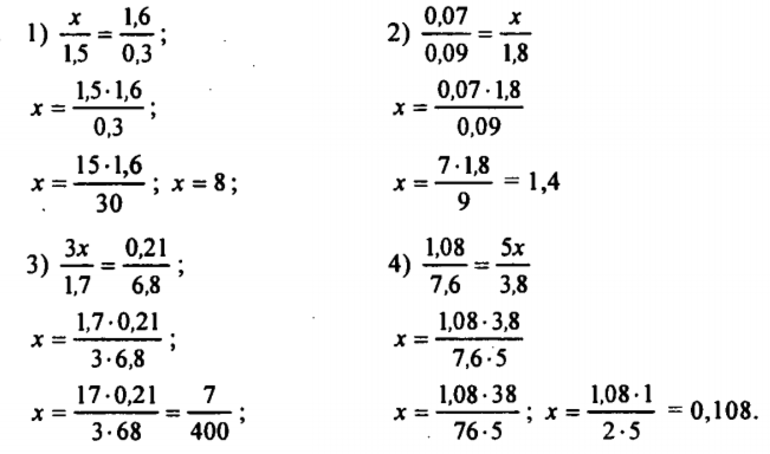
Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.

Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:

1. Два корня, когда D > 0: р1 = (-b — ^(½)) / 2a и р2 = (-b + ^(½)) / 2a.
2. При D равном 0 (один): р = (-b) / 2a.
3. Если D 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.

Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.