Комплексные логарифмы
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида ex для любого произвольного комплексного числа x, при этом используется бесконечный ряд с комплексным x. Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x, для которого ex = 0, и оказывается, что e2πi = 1 = e. Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то ez = ez+2nπi для всех комплексных z и целых n.
Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i4 = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.
Подстановка пределов интегрирования
График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x).
Натуральный логарифм — это логарифм по основанию , где e {\displaystyle e}
— иррациональная константа, равная приблизительно 2,72. Он обозначается как ln x {\displaystyle \ln x}
, log e x {\displaystyle \log _{e}x}
или иногда просто log x {\displaystyle \log x}
, если основание e {\displaystyle e}
подразумевается . Другими словами, натуральный логарифм числа x — это показатель степени , в которую нужно возвести число e, чтобы получить x. Это определение можно расширить и на комплексные числа .
ln e = 1 {\displaystyle \ln e=1}
e 1 = e {\displaystyle e^{1}=e}
ln 1 = 0 {\displaystyle \ln 1=0}
e 0 = 1 {\displaystyle e^{0}=1}
Натуральный логарифм может быть также определён геометрически для любого положительного вещественного числа a как площадь под кривой y = 1 x {\displaystyle y={\frac {1}{x}}}
на промежутке {\displaystyle }
. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется данный логарифм, объясняет происхождение названия «натуральный».
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции , что приводит к тождествам:
e ln a = a (a > 0) ; {\displaystyle e^{\ln a}=a\quad (a>0);}
ln e a = a (a > 0) . {\displaystyle \ln e^{a}=a\quad (a>0).}
Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
ln x y = ln x + ln y . {\displaystyle \ln xy=\ln x+\ln y.}
E = lim(1+1/N), при N → ∞.
С точностью 17 знаков число e равно 2.71828182845904512.
6. Логарифм.
6.1. Определение функции логарифм
Y = Log b (x).
Логарифм показывает в какую степень надо возвести число — основание логарифма (b), чтобы
получить заданное число (X). Функция логарифм определена для X больше нуля.
Например: Log 10 (100) = 2.
Y = Log 10 (x) .
Обозначается Log(x): Log(x) = Log 10 (x).
Пример использования десятичного логарифма — децибел .
Y = Log 2 (x).
Обозначается Lg(x): Lg(x) = Log 2 (X)
6.5. Натуральный логарифм
Y = Log e (x) .
Обозначается Ln(x): Ln(x) = Log e (X)
Натуральный логарифм — обратная функция к экспоненциальной функции exp (X).
Пример:
Log 2 (8) = Log 10 (8)/Log 10 (2) =
0.903089986991943552 / 0.301029995663981184 = 3
7. Формулы полезные в жизни
Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича .
Разрешается использовать материалы сайта при условии установки активной ссылки на источник.
Как рассчитать логарифм по основанию, отличному от 10
Excel предоставляет функцию LOG для рассчета логарифма по основанию 10. Однако, если необходимо рассчитать логарифм по основанию, отличному от 10, то следует использовать формулу, базирующуюся на свойствах логарифма.
Если необходимо рассчитать логарифм числа a по основанию b, то формула будет выглядеть следующим образом:
LOGb a = LOG a / LOG b
Сначала рассчитывается логарифм числа a, затем логарифм основания b. Затем, логарифм числа a делится на логарифм основания b.
Используем данную формулу и функции Excel для рассчета логарифма по основанию 2:
| Число (a) | Логарифм по основанию 2 |
|---|---|
| 8 | =LOG(8)/LOG(2) |
| 16 | =LOG(16)/LOG(2) |
| 32 | =LOG(32)/LOG(2) |
Результат можно округлить до нужного количества знаков после запятой, используя функцию округления ROUND.
Интересные сведения
Логарифмы (особенно натуральные и десятичные) широко применимы почти во всех сферах деятельности.
Например, в теории простых чисел, количество простых чисел в интервале от 0 до n будет равно приблизительно: , при этом s-ое простое число приблизительно будет равно .
В математическом анализе, как мы уже убедились ранее, натуральные логарифмы встречаются сплошь и рядом, при этом они объединяют тригонометрические и логарифмические функции при помощи интегралов, например интеграл от тангенса:
.
В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е зачастую отражает темп роста экспоненциальных величин.
В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти натуральное число N понадобится битов.
В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.
В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее процессы, которые математически можно описать только при помощи логарифмирования.
В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.
Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.
Натуральный логарифм Функция y=ln x ее свойства
https://youtube.com/watch?v=e_MZrekT1-0
Доказательство основного свойства натурального логарифма
Таблица-шпаргалка логарифмов: десятичных, по основанию 2
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
Ниже представлена таблица логарифмов (по основанию 2, 10 и числу e), которую можно использовать для выполнения быстрых расчетов, а также, проверки своих знаний.
| x | log10x | log2x | logex |
| — | — | — | |
| 0+ | — ∞ | — ∞ | — ∞ |
| -4 | -13.287712 | -9.210340 | |
| 0.001 | -3 | -6.907755 | |
| 0.01 | -2 | -6.643856 | -4.605170 |
| -1 | -3.321928 | -2.302585 | |
| 1 | |||
| 2 | 1 | 0.693147 | |
| 3 | 0.477121 | 1.584963 | |
| 4 | 0.602060 | 2 | 1.386294 |
| 5 | 2.321928 | 1.609438 | |
| 6 | 0.778151 | 2.584963 | |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 3 | 2.079442 | |
| 9 | 0.954243 | 3.169925 | |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 4.321928 | 2.995732 | |
| 30 | 1.477121 | 4.906891 | |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 5.643856 | 3.912023 | |
| 60 | 1.778151 | 5.906991 | |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 6.321928 | 4.382027 | |
| 90 | 1.954243 | 6.491853 | |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 7.643856 | 5.298317 | |
| 300 | 2.477121 | 8.228819 | |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 8.965784 | 6.214608 | |
| 600 | 2.778151 | 9.228819 | |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 9.643856 | 6.684612 | |
| 900 | 2.954243 | 9.813781 | |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 9.210340 |
microexcel.ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Какие формулы необходимы для сдачи ЕГЭ по профильной математике?
Помимо очевидного, что для сдачи профиля нужно уметь складывать, вычитать и умножать, необходимы еще некоторые знания. Все это проходится в течение школы, но повторить или заполнить пробелы перед экзаменом нужно обязательно. Вот, что пригодится:
- Формулы сокращенного умножения;
- Арифметическая и геометрическая прогрессии;
- Вероятность;
- Свойства степеней;
- Свойства логарифмов;
- Тригонометрия;
- Производные;
- Первообразные.
Список внушительный, но вполне реальный, чтобы его выучить. Для того, чтобы лишний раз не гуглить в интернете «формулы для ЕГЭ по математике профильный уровень», приложим их ниже. А начнем по порядку из списка выше.
Формулы сокращённого умножения
Первые в нашем списке – формулы сокращенного умножения – нужны для решения задания №9 из профильного уровня. Вам встретятся задачи на преобразование выражений, поэтому умение это делать будет вознаграждено баллами.
Вот то, что будет вашим спасательным кругом:
Есть те, которые знать не обязательно. Но чем большими знаниями вы будете обладать, тем легче вам будет на экзамене. Вот они:
Умея применять эти формулы для ЕГЭ по математике, профильный уровень вам уже будет решить легче. Но это далеко не все, что нужно знать, чтобы получить сто баллов за ЕГЭ.
Арифметическая и геометрическая прогрессии
Для задания №19 нужно знание арифметической и геометрической прогрессии. Прикладываем формулы для ЕГЭ по математике, профильный уровень которой невозможен без их знания:
Вероятность
Вероятность встречается в задании №4, а ведь в самом начале обычно ставят легкие задания. Тем не менее, придется применять знания, которые представлены ниже:
Перейдем к свойствам степеней, ведь в них тоже есть, что запомнить.
Свойства степеней
Эти свойства нужно знать и для того, чтобы решить «базу», так что гуманитарии тоже могут обратить внимание на это:
Как вы видите, запоминать не очень много, зато формулы не самые простые. Но есть еще сложнее, и сейчас узнаем, какие они.
Формулы логарифмов лучше всего начать с их определения:
Теперь перейдем к более сложному:
Тригонометрия
Тригонометрические уравнения встречаются в задании №13. Для того, чтобы заработать баллы, нужно знать это:
Но это еще не все. Есть такая вещь, как основное тригонометрическое тождество. Вот оно:
Формулы двойного угла:
Формулы суммы и разности аргументов:
Преобразование суммы и разности в произведение:
Формулы половинного аргумента:
На этом с тригонометрией все.
Производные
Начнем с основных правил дифференцирования:
Уравнение касательной:
Производные элементарных функций:
Закончим эту статью первообразными.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
- Десятичный a, где основанием служит число 10.
- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Как посчитать логарифм
Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма \(log_{a}(b)\) существует только при положительных значениях основания \(a\) и аргумента \(b\). И, кроме этого, на основание накладывается условие, что оно не должно быть равно \(1\).
Почему так? Это следует из определения показательной функции. Показательная функция не может быть равна \(0\) и не может быть меньше \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д
Так как (вспоминайте определение отрицательной степени):
Теперь давайте разберем общий алгоритм вычисления логарифмов:
- Во-первых, постарайтесь представить основание и аргумент под логарифмом в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
- Разобраться, в какую степень \(x\) нужно возвести основание, чтобы получить аргумент. Когда у вас и там, и там степени с одинаковым основанием, посчитать значение логарифма становится проще.
- \(x\) и будет искомым значением логарифма.
Разберем на примерах.
Пример 1Посчитать логарифм от \(9\) по основанию \(3\): \(\quad log_{3}(9)=?\)
- Сначала представим аргумент и основание в виде степеней тройки:
$$ 3=3^1, \qquad 9=3^2;$$
$$log_{3}(9)=log_{3^1}(3^2);$$ - Теперь надо разобраться в какую степень \(x\) нужно возвести \(3^1\), чтобы получить \(3^2\)
$$ (3^1)^x=3^2, $$
$$ 3^{1*x}=3^2, $$
$$ 1*x=2,$$
$$ x=2.$$ - Вот мы и решили:
$$log_{3}(9)=2.$$
Пример 2Вычислить логарифм от \(\frac{1}{125}\) по основанию \(5\): \(\quad log_{5}(\frac{1}{125})=?\)
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1, \qquad \frac{1}{125}=\frac{1}{5^3}=5^{-3};$$
$$log_{5}(\frac{1}{125})=log_{5^1}(5^{-3});$$ - В какую степень \(x\) надо возвести \(5^1\), чтобы получить \(5^{-3}\):
$$ (5^1)^x=5^{-3}, $$
$$ 5^{1*x}=5^{-3},$$
$$1*x=-3,$$
$$x=-3.$$ - Получили ответ:
$$ log_{5}(\frac{1}{125})=-3.$$
Пример 3Вычислить логарифм от \(4\) по основанию \(64\): \(\quad log_{64}(4)=?\)
- Представим аргумент и основание в виде степени двойки:
$$ 64=2^6, \qquad 4=2^2;$$
$$log_{64}(4)=log_{2^6}(2^2);$$ - В какую степень \(x\) надо возвести \(2^6\), чтобы получить \(2^{2}\):
$$ (2^6)^x=2^{2}, $$
$$ 2^{6*x}=2^{2},$$
$$6*x=2,$$
$$x=\frac{2}{6}=\frac{1}{3}.$$ - Получили ответ:
$$ log_{64}(4)=\frac{1}{3}.$$
Пример 4Вычислить логарифм от \(1\) по основанию \(8\): \(\quad log_{8}(1)=?\)
- Представим аргумент и основание в виде степени двойки. Напоминаю, что любое число в нулевой степени равно единице:
$$ 8=2^3 \qquad 1=2^0;$$
$$log_{8}(1)=log_{2^3}(2^0);$$ - В какую степень \(x\) надо возвести \(2^3\), чтобы получить \(2^{0}\):
$$ (2^3)^x=2^{0}, $$
$$ 2^{3*x}=2^{0},$$
$$3*x=0,$$
$$x=\frac{0}{3}=0.$$ - Получили ответ:
$$ log_{8}(1)=0.$$
Пример 5Вычислить логарифм от \(15\) по основанию \(5\): \(\quad log_{5}(15)=?\)
Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 \qquad 15= ???;$$
\(15\) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$
Внимание!
Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\)? Это довольно просто – нужно разложить \(a\) на простые множители.
\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.
Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) нельзя представить в виде степени какого-нибудь числа.
Что такое логарифм
Степень, в которую нужно возвести основание, чтобы получить заданное число, называется логарифмом этого числа по соответствующему основанию.
Для нахождения логарифма необходимо знать два фактора: основание и число.
Примеры:
Логарифм 8 по основанию 2 = log 2 (8) = 3Объяснение: 2 3 = 8
Поскольку 2 нужно возвести в степень 3, чтобы получить 8, таким образом, логарифм 8 по основанию 2 равен 3.
Логарифм 81 по основанию 9 = log 9 (81) = 2,Объяснение: 9 2 = 81Поскольку 9 нужно возвести в степень 2, чтобы получить 81, Таким образом, логарифм 81 по основанию 9 равен 2.
Примечание. Экспоненциальная функция является полной противоположностью логарифмической функции. Когда значение многократно умножается, говорят, что оно растет экспоненциально, тогда как когда значение многократно делится, говорят, что оно растет логарифмически.
Что такое О(log n)
O(log N) означает, что время растет линейно, а N растет экспоненциально. Таким образом, если для вычисления 10 элементов требуется 1 секунда, для 100 нужно будет 2 секунды, для 1000 элементов — 3 и так далее.
Бинарный поиск — как раз пример алгоритма. Его структура данных — отсортированный массив из n элементов (что означает n — количество).
Другой пример — быстрая сортировка, когда каждый раз мы делим массив на две части и каждый раз требуется O(N)время, чтобы найти опорный элемент. Следовательно, это N O(log N).
Логарифмическое умножение — просто умора
Сколько времени займёт четырёхкратный рост? Конечно, можно просто взять ln(4). Но это слишком просто, мы пойдём другим путём.
Можно представить четырёхкратный рост как удвоение (требующее ln(2) единиц времени) и затем снова удвоение (требующее ещё ln(2) единиц времени):
Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)
Интересно. Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?
ln(a*b) = ln(a) + ln(b)
Логарифм от A, умноженного на B, есть log(A) + log(B). Это отношение сразу обретает смысл, если оперировать в терминах роста.
Если вас интересует 30-кратный рост, вы можете подождать ln(30) за один присест, либо же подождать ln(3) Для утроения, и затем ещё ln(10) для удесятирения. Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).
Что на счёт деления? В частности, ln(5/3) означает: сколько времени понадобится для того, чтобы вырасти в 5 раз, и затем получить 1/3 от этого?
Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,
ln(5/3) = ln(5) – ln(3)
Сие означает: дайте вырасти в 5 раз, и затем «вернитесь во времени» к той отметке, где останется всего треть от того количества, так что у вас получится 5/3 рост. В общем получается
ln(a/b) = ln(a) – ln(b)
Я надеюсь, что странная арифметика логарифмов начинает обретать для вас смысл: умножение показателей роста становится сложением единиц времени роста, а деление превращается в вычитание единиц времени. Не надо запоминать правила, попробуйте осознать их.
40.500. Логарифмические уравнения
Логарифмом числа $ b $ по основанию $ a(c=log_{a}b) $ называется такой показатель степени $ c $, в которую нужно возвести $ a $, чтобы получить $ b $ (то есть $ a^{c}=b $). При этом задаются ограничения: $ a>0, \; a \neq 1, \; b>0$. Значение $ c $ логарифма может быть любым.
Вычислите:
$ log_{3}27, \; log_{\frac {1}{3}}27 $
1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27.
$ 3=log_{3}27 $
2. При возведении $ \big(\frac{1}{3} \big)^{-3}=27 $ значит, $ -3=log_{\frac{1}{3}}27 $
Ответ: 3; -3.
Помня об ограничениях, построим по точкам графики логарифмической функция в разных случаях.
Пусть $ y=log_{2}x $. Подставим вместо $ x $ разные числа и определим соответствующие значения переменной $ y $.
Отметим координаты точек на плоскости и соединим их плавной линией.
Легко заметить, что функция все время возрастает. Такое поведение характерно для всех логарифмических функций с основанием больше единицы.
Пусть теперь $ y=log_{\frac{1}{2}}x $. Составим таблицу значений для этого случая.
Тогда график функции будет выглядеть следующим образом.
Все логарифмические функции с основанием от 0 до 1 убывают на всей области определения.
Графики всех логарифмических функций проходят через точку с координатами (1;0).
Особыми знаками принято обозначать логарифмы с основанием десять $ log_{10}a=lga $ и логарифмы с натуральным основанием $ e \approx 2.72 \; log_{e} \; a=In \; a $.
Свойства логарифмов
Для упрощения вычислений при работе с логарифмами полезно знать и уметь использовать основные свойства.
| Правило | Формула |
| Логарифм 1 по любому основанию равен 0. | $log_{a}1=0$ |
| Логарифм числа по равному ему основанию равен 1. | $log_{a}a=1$ |
| Основное логарифмическое тождество. При разведении основание в степень логарифма получается подлогарифмическое выражение. | $a^{log_{a}b}=b$ |
| Логарифм произведения равен сумме логарифмов. | $log_{a}bc=log_{a}b+log_{a}c$ |
| Логарифм частного равен разности логарифмов. | $log_{a} \frac{b}{c}=log_{a}b-log_{a}c$ |
| Показатель степени можно выносить из подлогарифмического выражения за знак логарифма. | $log_{a}b^{p}=plog_{a}b$ |
| Показатель степени можно выносить из основания логарифма, возводя его в -1 степень. | $log_{a^{a}}b=\frac{1}{q}log_{a}b$ |
| Можно представить логарифмов в виде частного логарифмов с новым основанием. |
$log_{a}b=\frac {log_{c}b}{log_{c}a}$ |
| Если поменять местами подлогарифмическое выражение и основание логарифма, получится логарифм, обратный исходному. | $log_{a}b=\frac {1}{log_{b}a}$ |
Используем рассмотренные свойства для решения некоторых задач.
Пример 2
Вычислите $ log_{5}3125 $
1. Представим $ 3125=5^{5} $.
2. Вынесем степень из—под знака логарифма:
$ log_{5}3125=log_{5}5^{5}=5log_{5}5 $
3. Логарифм числа по равному ему основанию равен 1:
$ 5log_{5}5=5 $
Ответ: 5.
Пример 3
Вычислите $ 5^{2+log_{5}3} $
1. Воспользуемся свойством степеней:
$ 5^{2+log_{5}3}=5^{2} \cdot 5^{log_{5}3} $
2. Используем основное логарифмическое тождество:
$ 5^{2} \cdot 5^{log_{5}3}=25 \cdot 3=75 $
Ответ: 75.
Пример 4
Вычислите $ lg125+lg8 $
1. Воспользуемся формулой для суммы логарифмов:
$ lg125+lg8=lg1000 $
2. Представим 1000 = 103 и вынесем 3 за знак логарифма:
$ lg1000=lg10^{3}=3lg10 $
3. Воспользуемся тем, что $ lg10=1 $.
Ответ: 3.
Пример 5
Вычислить $ log_{36}84-log_{36}14 $.
1. Воспользуемся формулой для частного логарифмов:
$ log_{36}84-log_{36}14=log_{36}6 $
2. Преобразуем основание логарифма 36 = 62 и вынесем, «перевернув», вынесем показатель:
$ log_{36}6=log_{6^{2}}6= \frac {1}{2}log_{6}6 $
3. Воспользуемся тем, что $ log_{6}6=1 $
Ответ: 0,5.
Пример 6
Вычислите $ \frac {lg8+lg18}{2lg2+lg3} $.
1. Применим в числителе формулу для сумы логарифмов:
$ \frac {lg8+lg18}{2lg2+lg3}=\frac {lg144}{2lg2+lg3} $
2. В знаменателе внесем 2 под знак логарифма:
$ 2lg2=lg2^{2}=lg4 $
3. Воспользуемся формулой суммы логарифмов для знаменателя:
$ \frac {lg144}{lg4+lg3}=\frac {lg144}{lg12} $
4. Перейдем от частного к логарифму с основанием 12:
$ \frac {lg144}{lg12}=log_{12}144 $
5. Представим 144 = 122, вынесем степень за знак логарифма и воспользуемся соотношением $ log_{12}12=1 $
$ log_{12}144=log_{12}12^{2}=2log_{12}12=2 $
Ответ: 2.
Кроме выражений с числами, на экзамене могут встретиться выражения, содержащие переменные. В этом случае можно использовать те же формулы и правила.
Пример 7
Вычислите $ log_{125}\frac {a^{2} \cdot a}{a^{3}} $
1. Преобразуем отдельно подлогарифмическое выражение:
$ \frac {a^{2} \cdot a}{a^{3}}=a^{2+1-3}=a^{0}=1 $
2. Логарифм 1 по любому основанию равен 0:
$ log_{125}1=0 $
Ответ: 0.
ПрочитаноОтметь, если полностью прочитал текст
Понятие логарифма
Великий ученый Пьер-Симон Лаплас говорил, что изобретение логарифмов продлило жизнь астрономов вдвое, ведь с их помощью астрономические расчеты, которые ранее занимали несколько месяцев, стало возможно выполнять за считанные дни. Что же представляют собой логарифмы и как они так сильно упрощают вычисления? Для ответа на этот вопрос сначала следует вспомнить показательные уравнения.
Рассмотрим простейшее показательное уравнение 2х = 4. Так как 22 =4, то, очевидно, оно имеет единственный корень, равный 2. Найти его можно не только аналитически, но и графически:
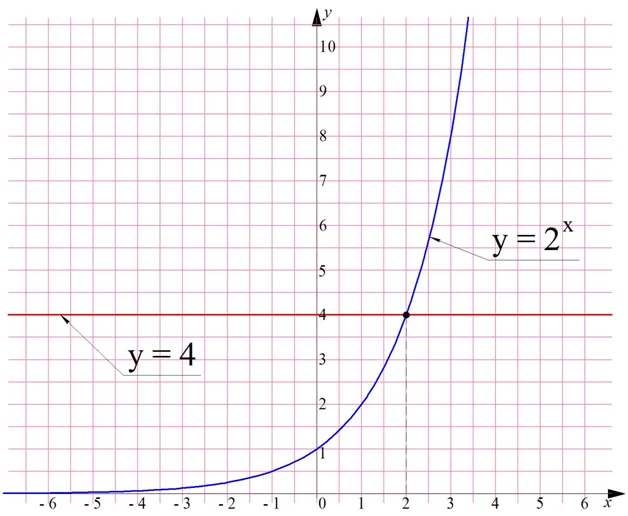
Далее посмотрим на уравнение 2х = 8. Так как восьмерка – это двойка в кубе (23 = 8), то единственным корнем ур-ния будет число 3. Также проиллюстрируем это с помощью графика:
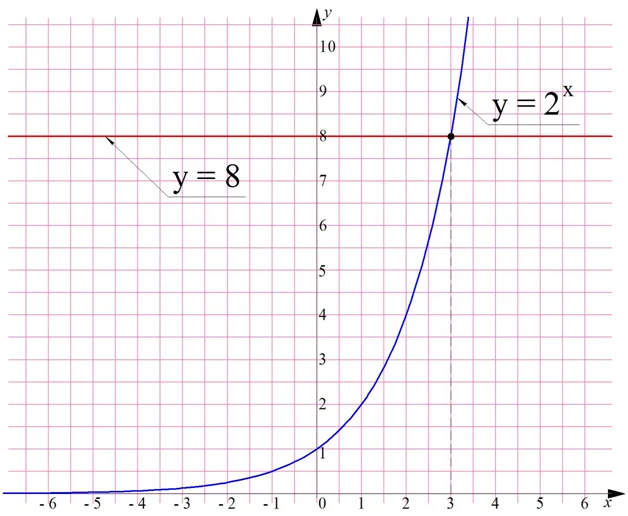
Однако если мы попытаемся решить уравнение 2х = 6, то мы столкнемся с проблемами. Представить шестерку как какую-то степень двойки не получается. Графический метод показывает, что у этого ур-ния есть единственный корень, который лежит между числами 2 и 3, но точно определить его значение не получается:
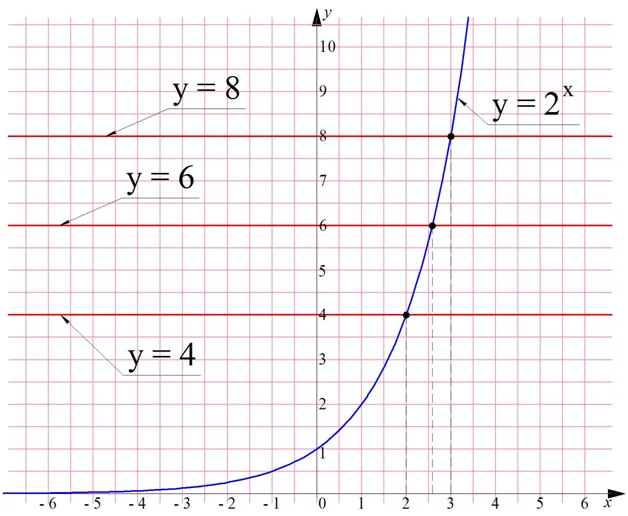
Можно доказать (мы не будем этого делать), что искомый нами корень невозможно выразить с помощью дробей и даже корней n-ой степени. Поэтому возникает необходимость ввести какое-то новое обозначение, чтобы записывать корни таких уравнений. Математики придумали для такого числа обозначение log2 6, которое читается как «логарифм шести по основанию два».
Рассмотрим теперь более общий случай. Пусть есть некоторое ур-ние
Если число b положительно, то уравнение имеет корень, и при том единственный. Для его обозначения используется запись logab. Покажем, как графически показать значение величины logab. Для этого надо построить показательную функцию у = ах и горизонтальную линию у = b. Они пересекутся в единственной точке (если b положительно). Абсцисса (координата х) этой точки и будет равна logab:
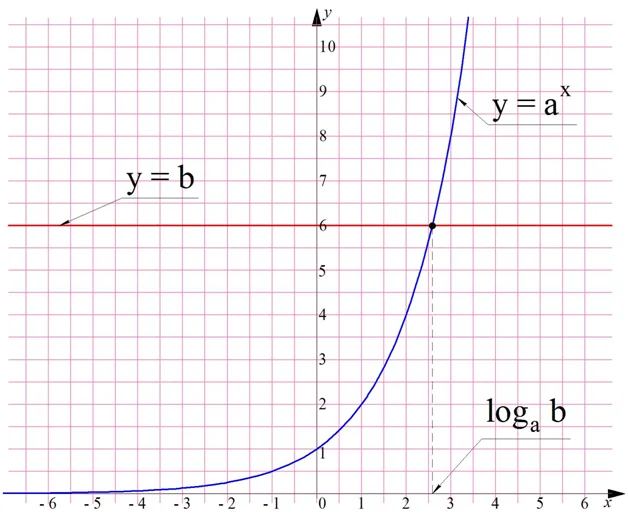
Дадим строгое определение логарифма:

Задание. Какое число является решением показательного уравнения

Задача. Слиток радиоактивного изотопа, чей период полураспада (его обозначают буквой Т) составляет 10 минут, имеет начальную массу (m), равную 1 кг. Через сколько минут его вес уменьшится до 300 грамм (0,3 кг)? Масса радиоактивного изотопа изменяется по закону
m(t) = m•2–t/T
Решение. Подставим исходные данные в формулу, и получим уравнение с неизвестной величиной t:
0,2 = 1•2–t/10
0,3 = 2–t/10
Получили простейшее показательное уравнение, однако его левую часть (число 0,3) нельзя представить как степень двойки. Однако с помощью определения логарифма мы можем записать, что
– t/10 = log2 0,3
Умножаем ур-ние на (– 10) и получаем:
t = – 10 log2 0,3
С помощью калькулятора или компьютера можно узнать, что
log2 0,3 ≈ – 1,737
Тогда искомое нами время примерно равно
t = – 10 log2 0,3 ≈ – 10•(– 1,737) ≈ 17,37 минут ≈ 17 минут 22 секунды
Ответ: – 10 log2 0,3 минут ≈ 17 минут 22 секунды.
Из задачи видно, что с логарифмы используются и при решении некоторых практических задач.
Иногда бывает удобнее использовать иное определение, которое по своей сути почти не отличается от первого:

Вычислим для примера несколько простейших логарифмов:
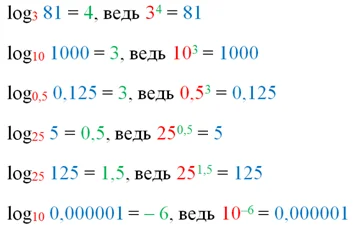
Что такое логарифм
Пожалуй, для большинства из нас логарифмы – самый «страшный» раздел математики. Как их считать? В каких сферах применять? И вообще, зачем свойства логарифмов нужны за пределами страниц учебника?

Что такое логарифм
Логарифм – это функция, обратная возведению в степень. Иначе говоря, он позволяет понять, в какую степень нужно возвести одно число, чтобы получить другое.
В переводе на язык математики, это выглядит следующим образом:
logaB=x, Ax=B
Таким образом, чтобы рассчитать число В, число А необходимо возвести в степень х.
Чтобы стало понятнее, стоит обратиться к примеру с числами: необходимо вычислить степень, в которую требуется возвести число 2, чтобы получилось 8. Для тех, кто помнит таблицу степеней двойки, сразу очевидно, что 2³ = 8. Иными словами, число 2 необходимо возвести в третью степень. Путем этих нехитрых вычислений получилось найти логарифм числа 8 по основанию 2:
Log28 = 3, так как 23 = 8
Начиная знакомство с логарифмами, многие путают основание и степень. Чтобы быстрее запомнить, что есть что, нужно держать в голове следующее правило: основание у логарифма, как и у возведения в степень, находится внизу.
Узнай, какие ИТ — профессии входят в ТОП-30 с доходом от 210 000 ₽/мес
Павел Симонов
Исполнительный директор Geekbrains
Команда GeekBrains совместно с международными специалистами по развитию карьеры
подготовили материалы, которые помогут вам начать путь к профессии мечты.
Подборка содержит только самые востребованные и высокооплачиваемые специальности и направления в
IT-сфере. 86% наших учеников с помощью данных материалов определились с карьерной целью на ближайшее
будущее!
Скачивайте и используйте уже сегодня:
Павел Симонов
Исполнительный директор Geekbrains
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ бесплатных нейросетей для упрощения работы и увеличения заработка
Только проверенные нейросети с доступом из России и свободным использованием
ТОП-100 площадок для поиска работы от GeekBrains
Список проверенных ресурсов реальных вакансий с доходом от 210 000 ₽
Получить подборку бесплатно
pdf 3,7mb
doc 1,7mb
Уже скачали 22321
В общем виде запись logAB читается как «логарифм В по основанию А». Число А, которое необходимо возвести в некую степень, – это основание логарифма.
Чтобы закрепить в памяти структуру записи логарифмов, стоит проанализировать математические выражения из списка, приведенного ниже, и понять, что они означают:
- log39 = 2
- log464 = 3
- log5625 = 4
- log7343 = 3
- log10100 = 2
- log2128 = 7
- log20,25 = −2
- log625125 = 0,75
В математике чаще всего используются десятичные и натуральные логарифмы.
Десятичный логарифм (lg), как следует из названия, имеет в основании число 10. То есть, вычисляя подобные выражения, необходимо определить, в какую степень требуется возвести 10, чтобы получилось желаемое число.
lg100 = log10100 = 2, поскольку 102 = 100
Основание натуральных логарифмов (ln) – число Эйлера (е = 2,71828)
В математике число «е» по важности схоже с числом Пи в геометрии. Логарифмы по основанию е часто используются для решения разнообразных математических задач
logeB=lnB



























