Все про куб для егэ

Что такое точный куб в математике

Точный куб является частным случаем правильного многогранника и представляет собой трехмерный объект, состоящий из шести квадратных граней равного размера, пересекающихся под прямым углом.

Одним из наиболее заметных свойств точного куба является то, что все его грани, ребра и вершины являются симметричными друг относительно друга. Это свойство позволяет использовать точный куб в качестве простой и надежной геометрической модели для решения различных задач в науке и технике.

Примерами применения точного куба могут быть создание трехмерных моделей в компьютерной графике и архитектуре, расчет объема и веса кубических предметов в промышленности, а также изучение геометрии и математической логики в школах и университетах.

Как нарисовать куб в перспективе

1 этап – намечаем куб, его высоту и ширину

Карандашом НВ намечаем высоту и ширину нашего куба

Обращаем внимание на то, чтобы справа у нас было немного больше расстояние, чем слева. Высота и ширина у куба должны быть примерно равны

Также обозначаем переднюю грань нашего куба, где левая сторона у нас чуть-чуть больше, чем правая. Правая сторона куба должна вмещаться в левую сторону по ширине, примерно в полтора раза. Также, намечаем, условно, где у нас будет располагаться крышка нашего куба.

В данном случае, высота крышки куба будет равняться, примерно почтив два раза должна вкладываться она в правую сторону нашего куба, чуть-чуть меньше, чем в два раза.

2 этап – рисуем стороны наклона куба

Далее, мы показываем наклоны сторон у куба

Обращаем внимание на то, что правая сторона куба меньше, и уходит в перспективу, поэтому, углы наклона будут гораздо более резкими и линии направлены больше вверх, чем слева

Также, обращаем внимание на то, чтобы все линии у нас сходились в одну точку. То есть, линии, которые у нас направлены вправо, они должны в итоге в конце, если их дальше и дальше проводить, они должны сойтись в одной точке

Точно также и с левой стороны. Также обращаем внимание на то, что нижняя плоскость от основания куба имеет более резкие наклоны, чем верхняя часть.

3 этап – рисуем линии куба и крышку в перспективе

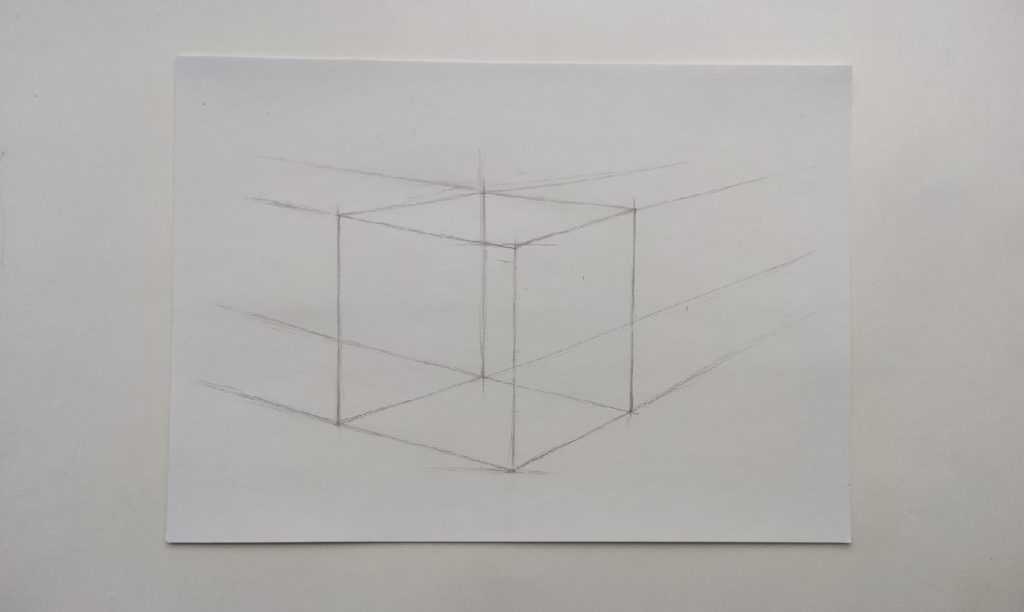
Куб мы должны видеть насквозь, поэтому мы рисуем дно нашего куба. Таким образом, мы из левого нижнего угла и из правого нижнего угла выводим линии. Они точно также должны уходить в перспективу. То есть, линии, которые у нас направлены влево, они уходят в левую точку, и линии, которые у нас направлены вправо, они уходят в правую точку.

Таким образом, мы находим самую дальнюю грань нашего куба, которую мы не видим. Она нужна нам для того, чтобы увидеть, где у нас заканчивается угол на крышке куба сверху.

После этого, мы, когда нашли эту точку, мы поднимаем вверх вертикальную линию и находим дальнюю невидимую нам грань куба. Точно также, опираясь на эту грань и имея размер нашей крышки, мы намечаем нашу крышку.

Точно также обращаем внимание на то, чтобы все линии уходили в перспективу

Далее, подтираем все лишние линии. Затем, карандашом НВ, либо 2В мы делаем штриховку. Правую сторону мы делаем самой темной. На нее мы накладываем штриховку сначала диагональными штрихами, а затем вертикальными

Обращаем внимание на то, что тон у нас расположен именно в левом углу верхнем. То есть, сторона нашего тона сверху темнее, снизу становится чуть-чуть светлее

Точно также, просто диагональной штриховкой мы проходимся по левой стороне куба, а крышку мы оставляем полностью белой. Далее, карандашом 2В, либо 4В мы еще сильнее уточняем переднюю грань нашего куба. То есть, мы делаем ее самой яркой. Далее, точно также подчеркиваем основание и верхнюю сторону куба. А дальние линии крышки мы оставляем светлыми.

Таким образом, получаем заштрихованный рисунок куба карандашом поэтапно для начинающих.

Примеры задач

Задание 1
Вычислите объем куба, если его ребро равняется 5 см.

Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .

Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.

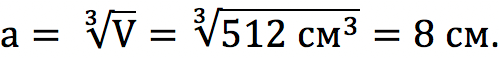
Решение:
Пусть ребро куба – это A. Выведем его длину из формулы расчета объема:

Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.

Решение:
Применим формулу, в которой используется диагональ грани:

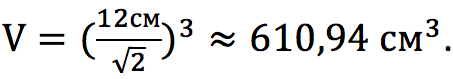
Публикации по теме:

• Нахождение площади квадрата: формула и примеры Нахождение площади прямоугольника: формула и пример Нахождение площади треугольника: формула и примеры Нахождение площади круга: формула и примеры Нахождение площади ромба: формула и примеры Нахождение площади трапеции: формула и примеры Нахождение площади параллелограмма: формула и примеры Нахождение площади эллипса: формула и пример Нахождение площади выпуклого четырехугольника: формула и пример Нахождение периметра квадрата: формула и задачи Нахождение периметра треугольника: формула и задачи Нахождение периметра прямоугольника: формула и задачи Нахождение периметра трапеции: формула и задачи Нахождение периметра параллелограмма: формула и задачи Нахождение длины окружности: формула и задачи Теорема Пифагора для прямоугольного треугольника: формула и задачи Теорема косинусов для треугольника: формула и задачи Теорема синусов для треугольника: формула и задачи Теорема о сумме углов треугольника: формула и задачи Тригонометрические функции острого угла в прямоугольном треугольнике Нахождение объема конуса: формула и задачи Нахождение объема цилиндра: формула и задачи Нахождение объема шара: формула и задачи Нахождение площади правильного шестиугольника: формула и примеры Нахождение объема тетраэдра: формула и задачи Нахождение объема призмы: формула и задачи Нахождение объема параллелепипеда: формула и задачи Нахождение площади поверхности цилиндра: формула и задачи Нахождение площади поверхности конуса: формула и задачи Нахождение площади поверхности шара (сферы): формула и задачи Нахождение площади поверхности вписанного в цилиндр шара Нахождение радиуса шара: формула и примеры Нахождение радиуса цилиндра: формула и примеры Нахождение площади прямоугольного параллелепипеда: формула и пример Нахождение площади правильной пирамиды: формулы Формула Герона для треугольника Теорема Менелая: формулировка и пример с решением Теорема о внешнем угле треугольника: формулировка и задачи Теорема Чевы: формулировка и пример с решением Теорема Стюарта: формулировка и пример с решением Теорема о трех перпендикулярах Теорема Фалеса: формулировка и пример решения задачи Геометрическая фигура: треугольник Признаки равенства треугольников Признаки подобия треугольников Признаки равенства прямоугольных треугольников Свойства прямоугольного треугольника Свойства равнобедренного треугольника: теория и задача Определение и свойства медианы треугольника Определение и свойства медианы прямоугольного треугольника

Куб – это правильный многогранник, все грани которого являются квадратами.

Формулы объема и площади поверхности. Призма, пирамида — материалы для подготовки к ЕГЭ по Математике

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

1. Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
2. Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

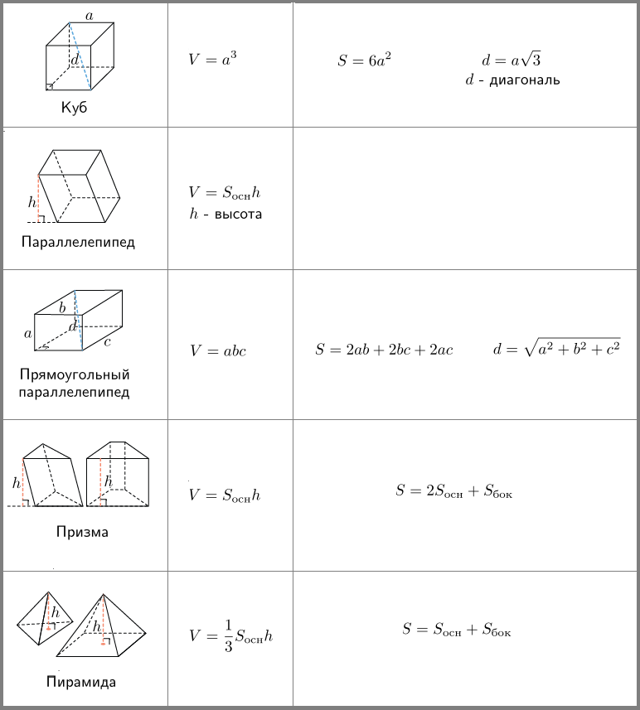
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Иногда в задаче  надо посчитать площадь поверхности куба или призмы.

Напомним, что площадь поверхности многогранника — это сумма площадей всех его граней.

В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в раз.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Что такое куб: определение, свойства, формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Что такое куб: определение, свойства, формулы

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

• Определение куба
• Свойства куба
  • Свойство 1
  • Свойство 2
  • Свойство 3
• Формулы для куба
  • Диагональ
  • Диагональ грани
  • Площадь полной поверхности
  • Периметр ребер
  • Объем
  • Радиус описанного вокруг шара
  • Радиус вписанного шара

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

• Вершины куба – это точки, являющиеся вершинами его граней.Всего их 8: A, B, C, D, A₁, B₁, C₁ и D₁.
• Ребра куба – это стороны его граней.Всего их 12: AB, BC, CD, AD, AA₁, BB₁ , CC₁, DD₁, A₁B₁, B₁C₁, C₁D₁ и A₁D₁.
• Грани куба – это квадраты, из которого состоит фигура.Всего их 6: ABCD, A₁B₁C₁D₁, AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.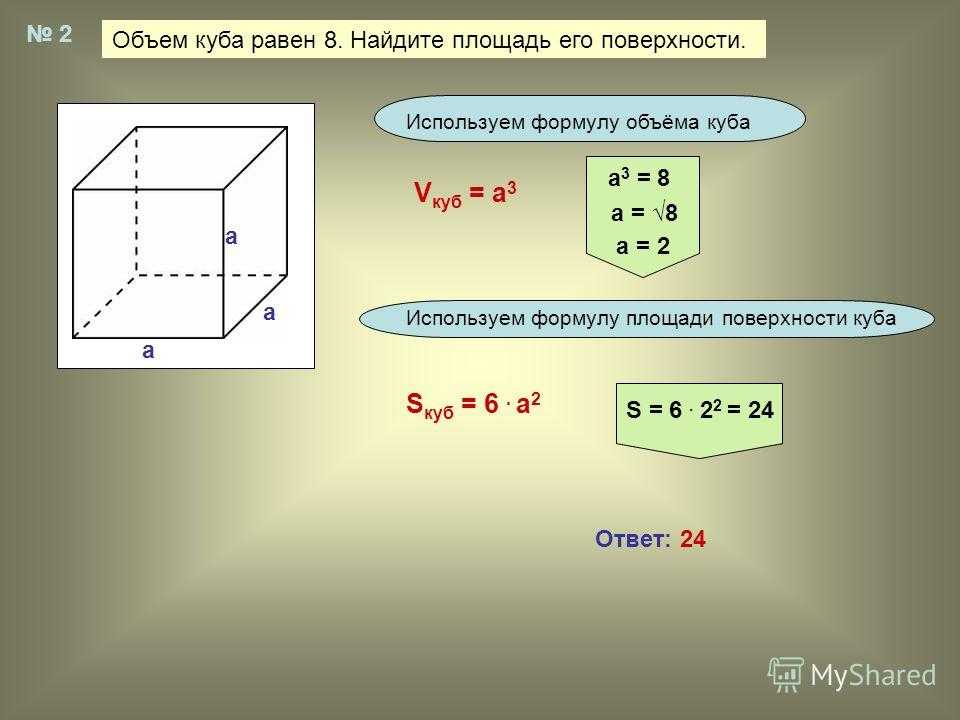

• ABCD || A₁B₁C₁D₁
• AA₁B₁B || CC₁D₁D
• BB₁C₁C || AA1D₁D

Свойство 2

Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

• AC₁ = BD₁ = A₁C = B₁D (диагонали куба).
• О – точка пересечения диагоналей:AO = OC₁ = BO = OD₁ = A₁O = OC = B₁O = OD.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

• a – ребро куба;
• d – диагональ куба или его грани.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Примеры использования куба

Куб в алгебре имеет множество применений и используется в различных областях науки и техники. Рассмотрим некоторые из них:

1. Геометрия: куб является одним из платонических тел, и его свойства активно изучаются в геометрии. Куб имеет 6 граней, 12 ребер и 8 вершин. Также известно, что диагональ любой грани куба равна его ребру.
2. Арифметика: куб числа a обозначается как a^3 и представляет собой результат умножения числа a на себя два раза: a^3 = a * a * a. Например, куб числа 3 равен 27 (3^3 = 3 * 3 * 3 = 27).
3. Алгебра: куб используется при решении уравнений и систем уравнений, а также при факторизации. Например, для факторизации выражения a^3 — b^3 можно использовать формулу разности кубов: a^3 — b^3 = (a — b)(a^2 + ab + b^2).
4. Физика: куб может быть использован для моделирования трехмерных объектов и систем. Например, в механике куб может быть использован для моделирования твердых тел, а в физике жидкостей — для моделирования контейнеров и емкостей.
5. Программирование: в компьютерной графике и 3D-моделировании куб используется для создания и отображения трехмерных объектов. Куб также может быть использован для хранения данных в виде трехмерного массива.

Это лишь некоторые из множества примеров использования куба в различных областях. Куб имеет множество свойств и применений, которые делают его важным элементом в алгебре и других науках.

Cube Formula — Что такое Cube Formula? Примеры

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.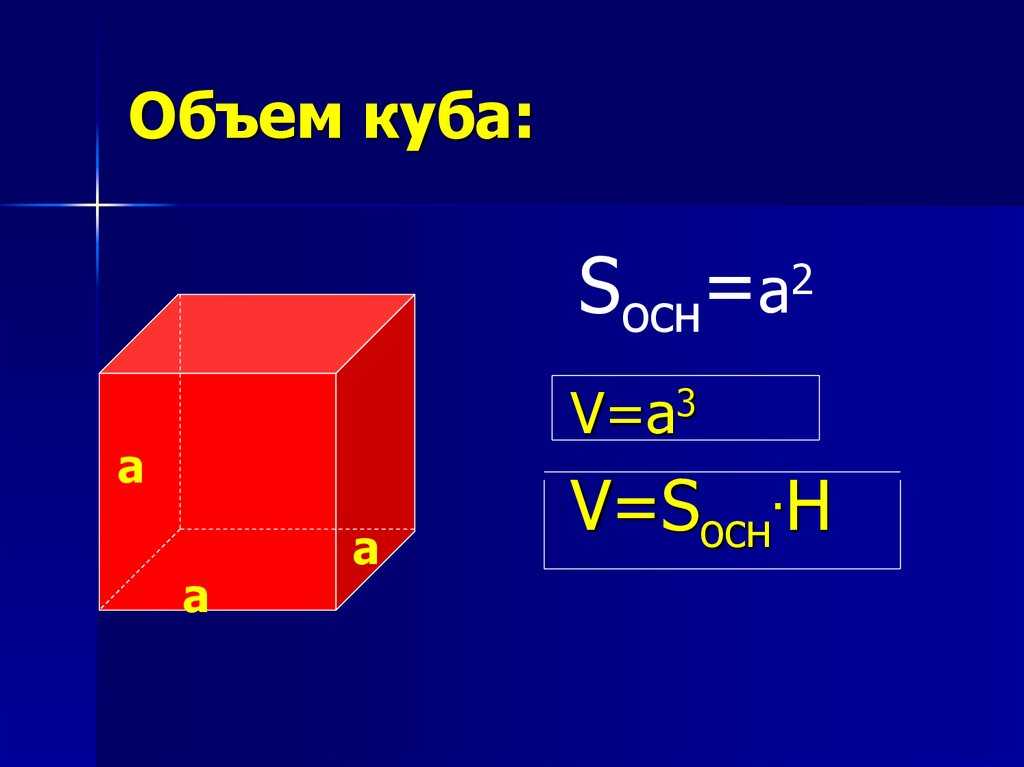

Что такое формула куба?

Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.

Формула куба

Объем куба

Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.

• Объем куба (на основе длины стороны) = a 3  кубических дюймов, где a – длина стороны куба
• Объем куба (по диагонали) = (√3×d 3 )/9кубических дюймов, где d — длина диагонали куба

Боковая площадь куба

Боковая площадь куба равна сумме площадей всех боковых граней куба.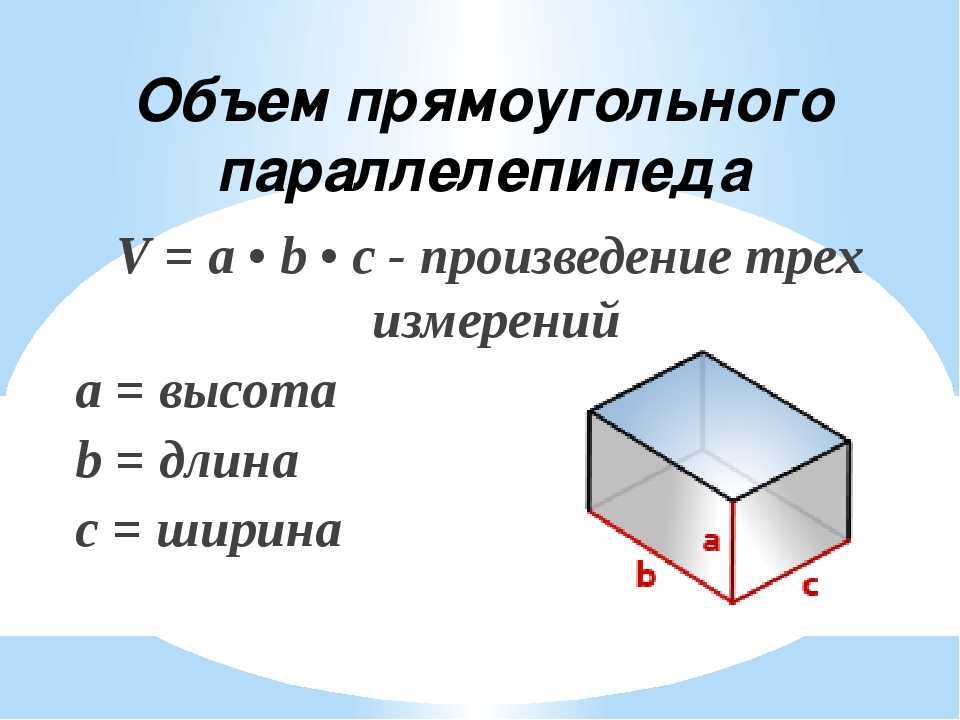

LSA куба = 4a 2

, где a — длина стороны.

Общая площадь куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a 2

, где a — длина стороны.

Диагональ куба

Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.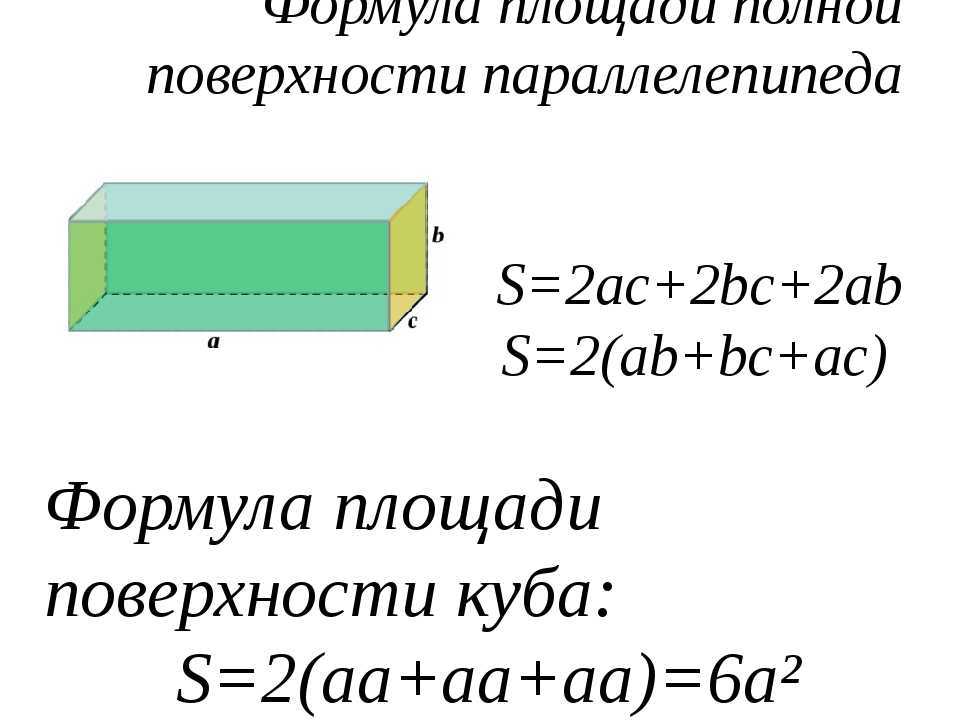

Диагональ куба = a√3

Давайте лучше разберемся с формулами куба на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры с использованием формулы куба

Пример 1: Найдите объем кубика Рубика длиной 4 дюйма. Решение:

Чтобы найти объем кубика Рубика: кубик Рубика0003

Длина стороны куба = 4 дюйма (дано)

Используя формулу куба, объем = с × с × с = с 3

Поместите значения,

объем = 4 × 4 × 4 = 4 3  = 64

Ответ: Объем кубика Рубика составляет 64 кубических дюйма.

Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба. Решение: 

Чтобы найти диагональ куба:

Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)

Используя формулу куба,

диагональ = a√3 

Поместите значения,

Диагональ = 64√3 = 110,848 дюйма

Ответ: Диагональ куба равна 110,848 дюйма

Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.

Решение:

Длина стороны куба, a = 25 дюймов 

Используя формулу площади куба, а именно: A = 6a 2

Поместите значения,

A = 6 × 25 × 25 = 3750 квадратных дюймов

Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.

Как рассчитать диагональ куба по формуле куба?

Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .

Что такое s в формуле куба?

В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.

Как вывести формулу куба?

Чтобы вычислить объем по формуле куба,

• Шаг 1: Рассмотрим любой квадратный лист бумаги.
• Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s 2 ».
• Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».

Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s 2  × s = s 3

Чтобы вывести формулу поверхности куба,

• Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
• Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s 2 » (длина, умноженная на ширину).
• Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s 2

Технический рисунок

Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз. Им пользуются в тех случаях, когда нужно быстро и наглядно показать на бумаге форму предмета. Обычно в этом возникает необходимость при конструировании, изобретательстве и рационализации, а также при обучении чтению чертежей, когда с помощью технического рисунка нужно пояснить форму детали, представленной на чертеже.

Выполняя технический рисунок, придерживаются правил построения аксонометрических проекций: под теми же углами располагают оси, так же сокращают размеры по осям, соблюдают форму эллипсов и последовательность построения.

Лучший ответ:

У куба всего 6 граней. И они все одинаковые, в виде квадрата. Две боковые слева и справа, верхняя и нижняя, передняя и задняя. Для наглядности посмотрите на два рисунка ниже. На рис 2 изображен куб, где показаны все основные части: грань, ребро, вершина.На рис 1 изображен параллелипипед , где показаны цветом противоположные грани. Не забываем, что у куба все 6 граней одинаковые, а значит, они равны!

более месяца назад

Лучшее из галереи за : неделю   месяц   все время

Вы можете из нескольких рисунков создать анимацию (или целый мультфильм!). Для этого нарисуйте несколько последовательных кадров и нажмите кнопку Просмотр анимации.

Элементы куба

Основными элементами многогранника являются грани, ребра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название страницы.

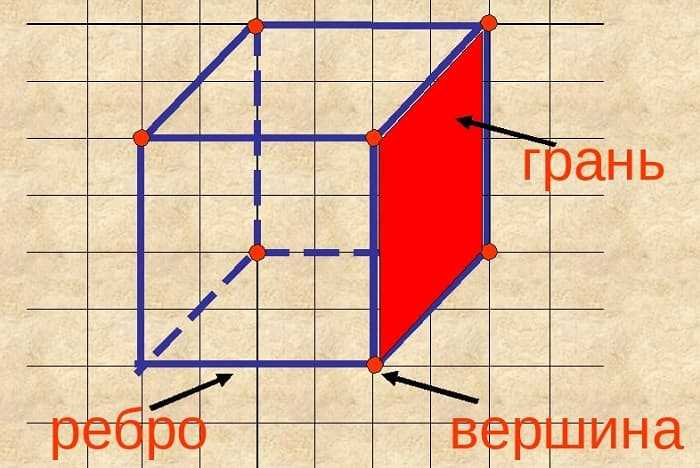
Интересно, сколько граней у куба и какие у них функции? Всего ребер шесть. Два из них, параллельные друг другу, считаются основаниями, остальные — боковыми.

Грани куба представляют собой пары перпендикуляров, являются квадратами и равны друг другу.

Ребро

Линии, где пересекаются стороны, называются ребрами.

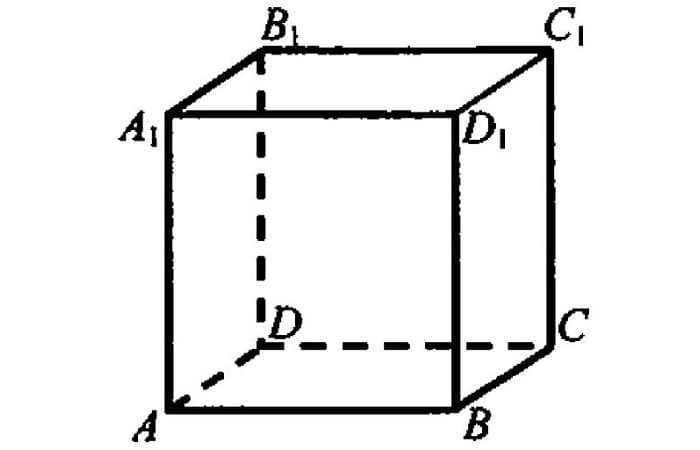
Не все учащиеся могут ответить, сколько ребер у куба. Их двенадцать. Они одинаковой длины. Те из них, которые имеют общий конец, располагают под прямым углом к ​​одному из двух других.

Ребра могут пересекаться в вершине, быть параллельными. Ребра, не лежащие на одной грани, скошены.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

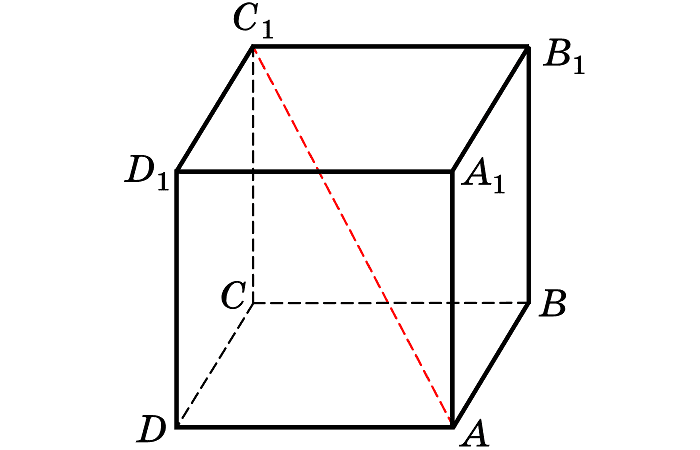
Центром грани считается точка пересечения диагоналей грани — точка, равноудаленная от всех углов и сторон квадрата. Это центр симметрии лица.

Центр куба

Точкой пересечения диагоналей куба является его центр — точка, равноудаленная от всех углов, ребер и сторон многогранника.

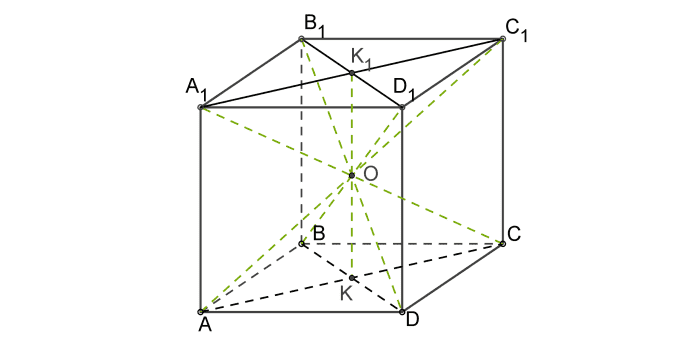
Это центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей с ортогональной (под прямым углом) симметрией. К ним относятся: диагонали куба и прямые линии, проходящие через центр параллельно краям.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

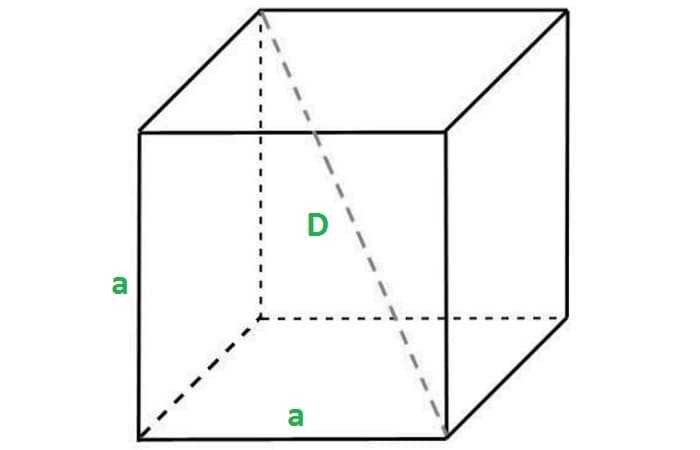
Учитывая, что ребра куба имеют равные размеры a, мы можем найти длину диагонали:

Формула доказывается с помощью дважды примененной теоремы Пифагора.

Диагональ куба является одной из осей симметрии.

Все диагонали в кубе равны между собой, а точка пересечения делится пополам.

Понятие о диметрической прямоугольной проекции

Расположение осей диметрической проекции и способ их построения приведены на рис. 3.19. Ось z проводят вертикально, ось х – под углом около 7° к горизонтали, а ось у образует с горизонталью угол приблизительно в 41° (рис. 3.19, а). Построить оси можно, пользуясь линейкой и циркулем. Для этого из точки О откладывают по горизонтали вправо и влево по восемь равных делений (рис. 3.19, б). Из крайних точек восставляют перпендикуляры. Высота их равна: для перпендикуляра к оси х – одному делению, для перпендикуляра к оси у – семи делениям. Крайние точки перпендикуляров соединяют с точкой О.

Рис. 3.19. Расположение осей диметрической проекции

При вычерчивании диметрической проекции, как и при построении фронтальной, размеры по оси у сокращают в 2 раза, а по осям х и z откладывают без сокращений.

На рис. 3.20 показана диметрическая проекция куба с вписанными в его грани окружностями. Как видно из этого рисунка, окружности в диметрической проекции изображаются эллипсами.

Рис. 3.20. Диметрические проекции окружностей, вписанных в грани куба

Формула вычисления объема куба

1. Через длину ребра

Объем (V) куба равняется произведению его длины на ширину на высоту. Т. к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.

V = a ⋅ a ⋅ a = a 3

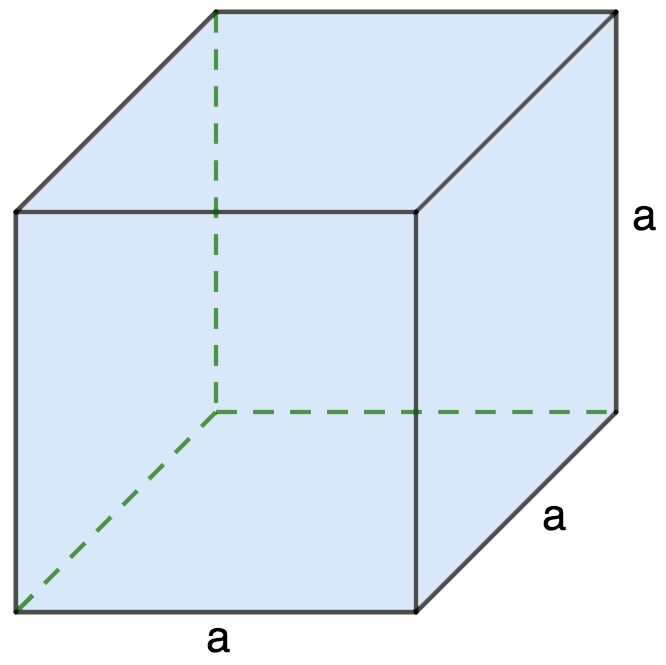
2. Через длину диагонали грани

Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: A=d/√ 2 .

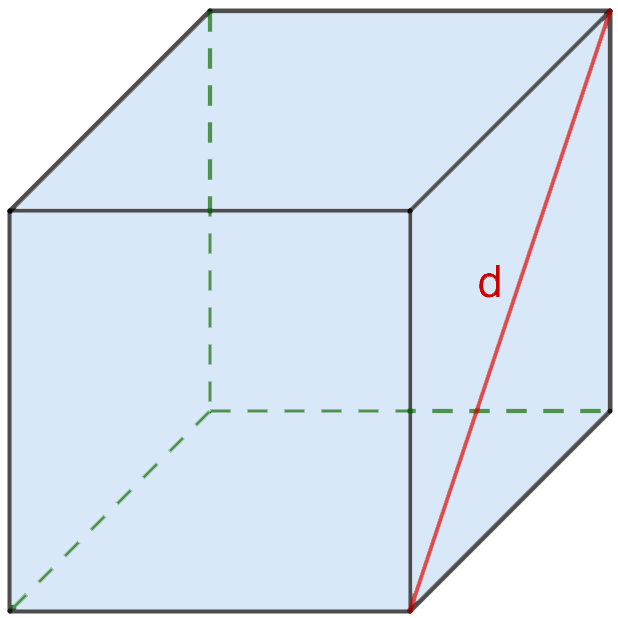
Следовательно, вычислить объем куба можно так:

Объем (V) куба равняется произведению его длины на ширину на высоту. Т. к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.

Определение куба

Периметр ребер.

22.03.2017 10:59:51

2017-03-22 10:59:51

Любые данныеЛюбые данныеЛюбые данныеЛюбые данные Любые данные

Формула куба – объяснение, свойства и примеры решения

Нас окружают разные предметы, которые состоят из разных геометрических форм. Подумайте о детской игре с кубиками, игральными костями или кубиком льда. Что вы замечаете общего среди всего этого? Все они имеют форму куба, не так ли? В этой статье мы изучим, что такое куб? Объем формулы куба, площадь формулы куба, площадь поверхности формулы куба. Некоторыми из распространенных примеров кубика являются кубик льда, игральные кости, кубик Рубика.

Введение. Что такое куб?

Куб — это трехмерная фигура, состоящая из граней квадратной формы одинакового размера.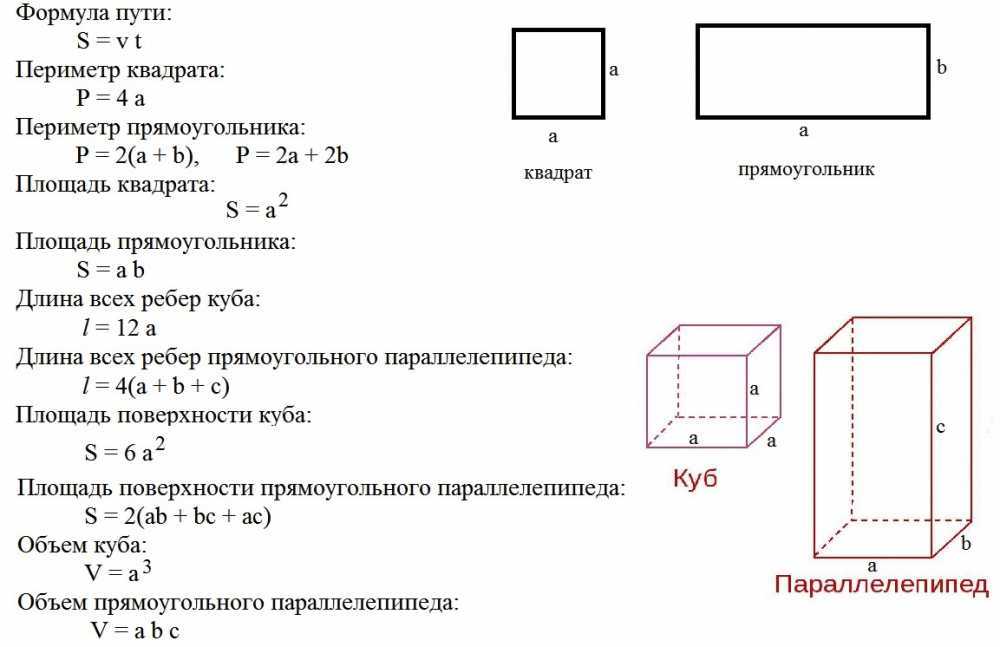

На приведенном ниже рисунке изображен куб, где l — длина, b — ширина, h — высота, и l = b = h. Длина, ширина и высота представляют ребра куба. И когда три ребра встречаются в точке, это называется вершиной.

(Изображение будет загружено в ближайшее время)

Свойства куба

1.  Все грани куба имеют квадратную форму.

2. Все грани и ребра равны.

3. Углы куба прямые.

4. Каждая из граней встречается с четырьмя соседними гранями.

5. Каждая из вершин встречается с тремя гранями и тремя ребрами.

6. Ребра, противоположные друг другу, параллельны и также равны.

7. Все 12 диагоналей на поверхности имеют площадь одинаковой величины

8. Все 4 внутренние диагонали равны

Например, куб имеет шесть граней. Следовательно, площадь его поверхности будет равна сумме площадей всех шести граней.

В основном площадь поверхности можно классифицировать как:

Площадь изогнутой поверхности объекта – это площадь всех криволинейных поверхностей объекта.

Боковая поверхность предмета – это площадь всех граней предмета, за исключением площади его основания и вершины. Для куба площадь боковой поверхности будет равна сумме площадей четырех сторон, то есть умноженной на 4 стороны.

Площадь боковой поверхности = 4 × (край) 2

902

Куб — это трехмерный объект, поэтому пространство, занимаемое кубом, будет трехмерным.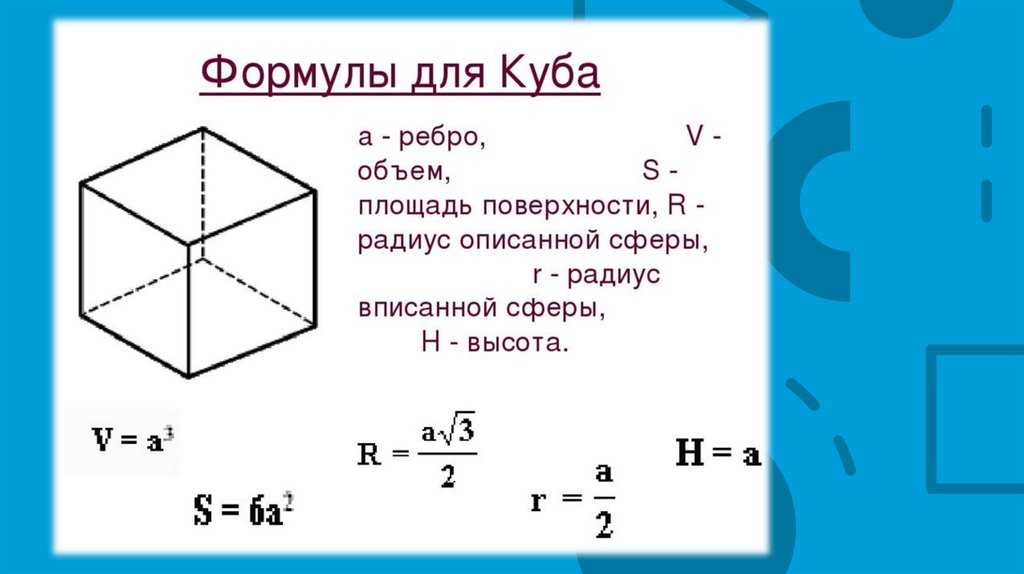

Куб ограничен шестью квадратными гранями, поэтому площадь поверхности будет вычисляться путем сложения площадей всех шести квадратных граней. Следовательно, площадь поверхности куба по формуле равна 9.0003

Площадь поверхности куба = 6 (сторона) 2

Внутренняя часть полого объекта может быть заполнена воздухом или какой-либо жидкостью, которая принимает форму объекта. В таких случаях объем вещества, который может вместить внутренность предмета, называется вместимостью полого предмета. Таким образом, мы можем сказать, что объем объекта — это мера занимаемого им пространства, а вместимость объекта — это объем вещества, которое может вместить его внутренность.

А объем куба — это занимаемое им пространство. Объем формулы куба будет рассчитан как:

Volume = (side) 3

Length of Diagonal of Face of the Cube = √2(edge)

Длина диагонала из куба = √3 (Edge)

3

3

3

3 9000

Периметр = 12 (ребро)

Решаемые примеры

Пример 1. Найдите площадь поверхности куба, длина стороны которого равна 7 см.

Решение:

Указанная длина = края = 7 см

Ум.

        = 6 × 49

        =  294 см 2

Пример 2: Сторона кубического ящика равна 9 м. Найдите объем кубического ящика.

Решение:

DED, сторона = A = 9m

по формуле объема A Cube, мы знаем, что

V = A 3 11963

9

v = 3 1113

9

v = 3 1113

9

v = 3 1113

V = 3 111996469

v = 3 11996469

v = 3 113

V = 3 x 9 x 9

V = 729 кв.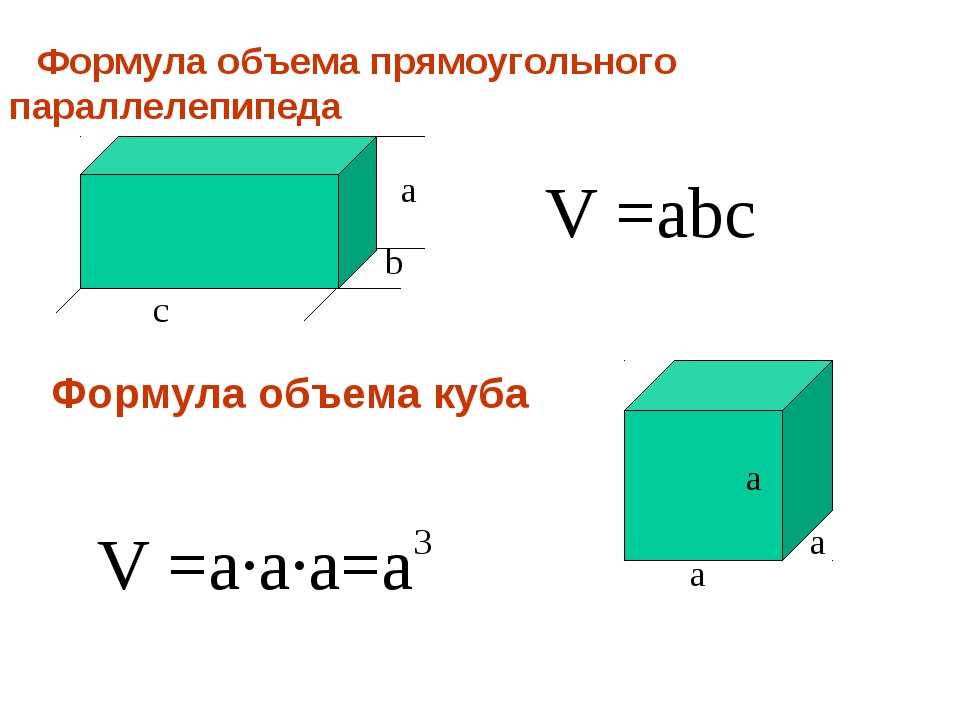

2

Значение кубов в математике

Кубы — это трехмерные квадраты, которые многие считают символом геометрического совершенства. С какой стороны на него ни посмотри, он выглядит одинаково. Это часть геометрии в математике и чрезвычайно важна как глава. Понимание этого является ключом к пониманию других связанных концепций. Учащиеся должны быть внимательны при изучении кубиков, так как из этой главы возникнет много вопросов. Они могут перейти к формуле куба — объяснение, свойства и примеры решений и подробно разобраться в этом. На этой странице Веданту каждая концепция упрощена для понимания учеником.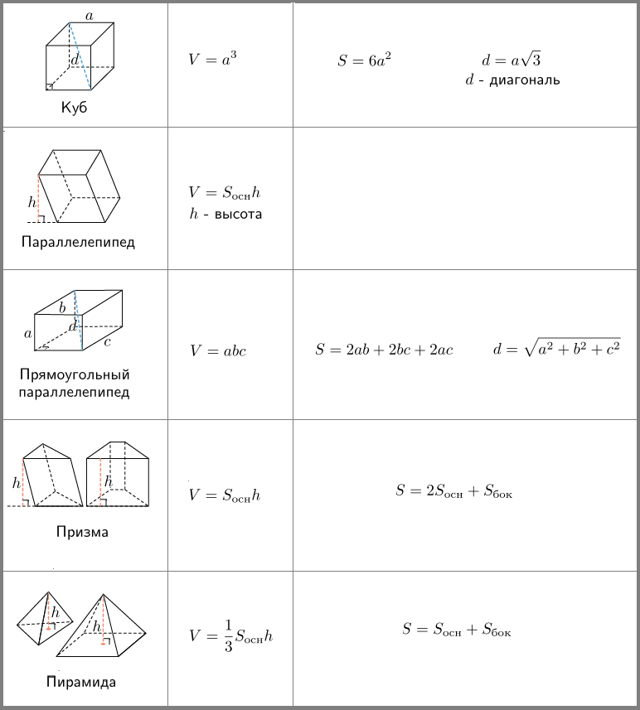

Формула объема цилиндра

Объем цилиндра можно вычислить, зная его высоту H и площадь основания:

V = Sосн ⋅ H = πR 2 H

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.

Любой цилиндр характеризуется высотой h (осевой линией) и радиусом r (см. рисунок). Именно эти характеристики используются в Формулах цилиндра при вычислении объема, площади поверхности и площади боковой поверхности.

Цилиндр формулы

Цилиндр – это геометрическая фигура, полученная вращением прямоугольника вокруг одной из его сторон. У каждого цилиндра есть 2 одинаковых основания (верхнее и нижнее) и боковая поверхность.

Любой цилиндр характеризуется высотой h (осевой линией) и радиусом r (см. рисунок). Именно эти характеристики используются в Формулах цилиндра при вычислении объема, площади поверхности и площади боковой поверхности.

Высота цилиндра (осевая линия) – это перпендикуляр, проведенный от верхнего основания к нижнему.

Радиус цилиндра – это радиус его основания.

Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.

Формула площади боковой поверхности цилиндра

Именно эти характеристики используются в формулах цилиндра при вычислении объема, площади поверхности и площади боковой поверхности.

16.02.2017 7:19:33

2017-02-16 07:19:33

Любые данныеЛюбые данные Любые данные Любые данные

Вычисляем длину секций

Здесь нам поможет знание о том, что полный оборот внутри круга — это 360 градусов.

Так как во внутреннем треугольнике все стороны равны, то это равносторонний треугольник. А раз так, то углы в нём равны 60 градусов. Добавим сюда по два прямых угла по 90 градусов из прямоугольников:

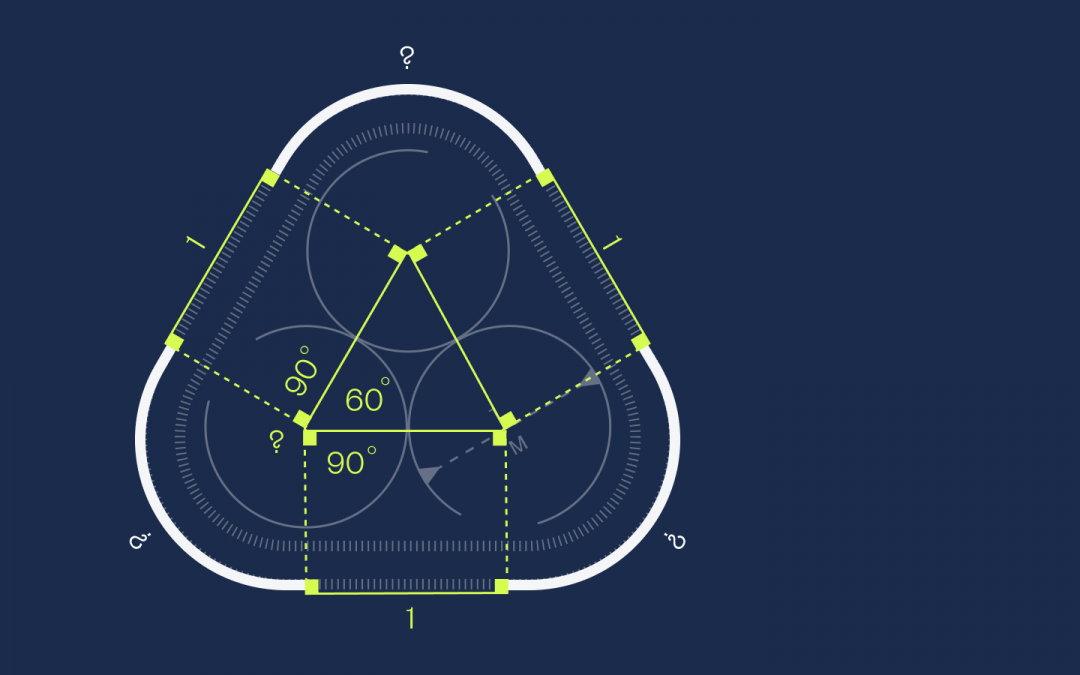
Решаем уравнение: 90 + 60 + 90 + X = 360 → X = 120 градусов.

Но 120 градусов — это ровно треть круга, а у нас таких частей как раз три:

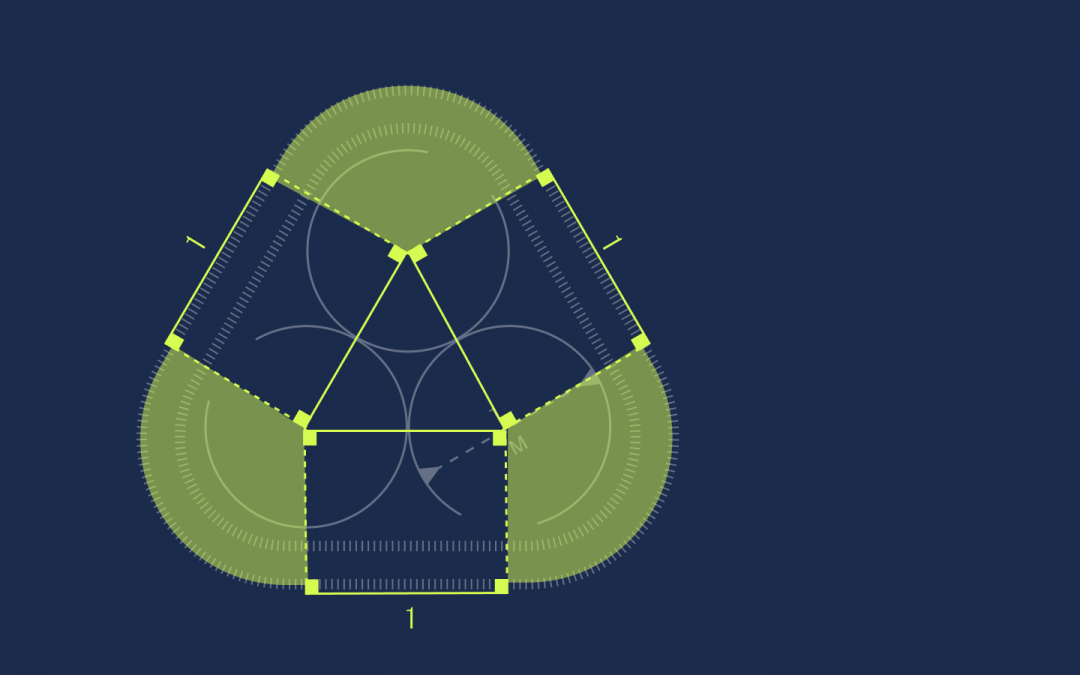
Это значит, что из них можно составить один целый круг. При этом мы знаем, что у этого круга радиус 0,5, а диаметр тогда равен единице. Этого достаточно, чтобы посчитать длину окружности: L = π × d → L = 3,14.

Складываем это число с длинами трёх отрезков и получаем полную длину: 3 + π

Объем и поверхностная площадь куба

Куб — это геометрическое тело, у которого все шесть граней являются квадратами и все его углы прямые. Имея сторону куба, мы можем вычислить его объем и поверхностную площадь.

Объем куба вычисляется по формуле:

где V — объем куба, a — длина стороны куба.

Поверхностная площадь куба

Поверхностная площадь куба вычисляется по формуле:

где S — поверхностная площадь куба, a — длина стороны куба.

Таким образом, чтобы найти объем куба, нужно возвести длину его стороны в куб и для нахождения поверхностной площади умножить длину стороны на себя и затем умножить на 6.

Например, если длина стороны куба равна 5 см, то:

• Объем куба = 5³ = 125 см³
• Поверхностная площадь куба = 6 * 5² = 150 см²

Свойства куба

1. В куб можно вписать тетраэдр так, чтобы все четыре вершины тетраэдра лежали на четырех вершинах куба, а все шесть ребер тетраэдра будут лежать на шести гранях куба и ребра будут равны диагонали грани куба.

2. В куб можно вписать правильный шестиугольник так, что все шесть вершин лежат в центрах граней куба.

Куб, параллелепипед. Видео (1 час 53 минуты)

Это видео – один из вебинаров нашей Программы подготовки к профильному ЕГЭ по математике.  Вся программа – это: 

• 3 вебинара в неделю c Алексеем Шевчуком до самой даты экзамена;
• проверка домашних работ по каждому вебинару;
• майский марафон “Год за месяц”, где мы повторим все темы ЕГЭ, то есть “упакуем” ваши знания, чтобы получить максимум на ЕГЭ.

НЕ ПРОПУСТИ!

Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.

На вебинарах все будет еще понятнее. Шорткаты, лайфхаки, разбор “капканов” – все там.

Регистрируйся здесь и приходи!

Если слишком сложно, просто посмотри на картинку.

Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?

Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.

Смотри, запоминай и не путай!

Та грань, на которую опущена высота, называется основанием.

• Все грани параллелепипеда – параллелограммы.
• Противоположные грани параллелепипеда параллельны и равны.

Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, асмежные

Точка пересечения диагоналей называется центром параллелепипеда.

НРАВИТСЯ УЧЕБНИК?

Его автор, Алексей Шевчук, ведет курсы подготовки к ЕГЭ по математике и информатике.

Приходи, научишься решать задачи любой сложности с самого нуля. Шаг за шагом.

До 3990 руб / месяц, 3 раза в неделю по 2 часа.

Вот так:

Это такая обувная коробка:

У прямоугольного параллелепипеда все грани – прямоугольники.

Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.

Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.

Смотри:

( displaystyle Delta BAD) – прямоугольный, поэтому

( displaystyle B{{D}^{2}}=A{{B}^{2}}+A{{D}^{2}}={{b}^{2}}+{{c}^{2}})

( displaystyle Delta BD{{D}_{1}}) – тоже прямоугольный!

Поэтому

( displaystyle B{{D}_{1}}^{2}=B{{D}^{2}}+D{{D}_{1}}^{2}),

Подставим:

( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}})

Вывели формулу.

Все ребра куба равны.

Кстати, заметь, что куб – частный вид прямоугольного параллелепипеда.

Поэтому для диагонали куба действует формула, которую мы получили для прямоугольного параллелепипеда.

( displaystyle {{d}^{2}}={{a}^{2}}+{{a}^{2}}+{{a}^{2}}),

То есть

( displaystyle d=asqrt{3})

Давай убедимся в пользе этой формулы.

Представь, что у тебя задача: «Диагональ куба равна ( displaystyle 5sqrt{3}). Найти полную поверхность».

Решим ее.

Пользуясь нашей формулой: ( displaystyle d=asqrt{3}), мы узнали, что ( displaystyle 5sqrt{3}=asqrt{3} ), то есть ( displaystyle a=5).

Значит полная поверхность – шесть площадей квадратов со стороной ( displaystyle a) -равна:

( displaystyle S=6cdot {{a}^{2}}=6cdot 25=150).

Видишь, как быстро? И ты применяй!

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Координаты вершин куба

1.

Координаты вершин куба со стороной a и вершиной D в начале декартовой системы координат так, что ребра этой вершины лежат на осях координат

A(a, 0, 0), B(a, a, 0), C(0, a, 0), D(0, 0, 0), E(a, 0, a), F(a, a, a), G(0, a, a), H(0, 0, a).

2.

Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что ребра куба параллельны осям координат:

A(a, –a, –a),B(a, a, –a),C(-a, a, –a),D(-a, –a, –a),E(a, –a, a),F(a, a, a),G(-a, a, a),H(-a, –a, a).

Определение. Единичный куб – это куб, у которого длина ребер равна единице.

Сумма длин всех рёбер равна:

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Как находить сторону точного куба по объёму

Для того чтобы найти сторону точного куба по заданному объёму, необходимо выполнить следующие шаги:

1. Определить значение объёма куба.
2. Найти кубический корень из значения объёма куба. Это и будет стороной точного куба.

Например, если известен объём точного куба и он равен 125 м3, то необходимо найти кубический корень из 125. Найденное значение будет равно 5, так как 5*5*5=125. Следовательно, сторона точного куба равна 5 м.

Также можно воспользоваться формулой для вычисления объёма куба, если известна его сторона:

V = a3

где V — объём куба, a — сторона точного куба.

Таким образом, если известна сторона точного куба, можно легко вычислить его объём, а если известен объём, то можно найти сторону точного куба.