Вписанные и описанные пирамиды: примеры. пирамида

Свойства правильной пирамиды

1. все боковые ребра правильной пирамиды равны;

2. боковые грани являются равными равнобедренными треугольниками.

Доказательство этих свойств приведем на примере правильной четырехугольной пирамиды.

Дано: РАВСD – правильная четырехугольная пирамида,

АВСD – квадрат,

РО – высота пирамиды.

Доказать:

1. РА = РВ = РС = РD

2. ∆АВР = ∆ВCР =∆СDР =∆DAP См. Рис. 4.

Рис. 4

Доказательство.

РО – высота пирамиды. То есть, прямая РО перпендикулярна плоскости АВС, а значит, и прямым АО, ВО, СО и DО, лежащим в ней. Значит, треугольники РОА, РОВ, РОС, РОD – прямоугольные.

Рассмотрим квадрат АВСD. Из свойств квадрата следует, что АО = ВО = СО = DО.

Тогда у прямоугольных треугольников РОА, РОВ, РОС, РОD катет РО – общий и катеты АО, ВО, СО и DО равны, значит, эти треугольники равны по двум катетам. Из равенства треугольников вытекает равенство отрезков, РА = РВ = РС = РD. Пункт 1 доказан.

Отрезки АВ и ВС равны, так как являются сторонами одного квадрата, РА = РВ = РС.  Значит, треугольники АВР и ВCР – равнобедренные и равны по трем сторонам.

Аналогичным образом получаем, что треугольники АВР, ВCР, СDР, DAP равнобедренны и равны, что и требовалось доказать в пункте 2.

Объем пирамиды

Объем пирамиды — это объем пространства, заполненного пирамидой. Он вычисляется с помощью определенных формул, которые зависят от параметров пирамиды.

Для правильной пирамиды, объем можно вычислить по формуле:

V = (1/3) * S * h

где V — объем пирамиды, S — площадь основания пирамиды, а h — высота пирамиды.

Если пирамида не является правильной, то при вычислении объема нужно знать еще дополнительные параметры пирамиды, такие как площадь боковой поверхности или углы между боковыми гранями.

Объем пирамиды можно представить также как количество кубических единиц, которые могут поместиться внутри пирамиды.

Размеры объема пирамиды могут быть выражены в кубических единицах измерения, таких как кубический метр (м³), кубический сантиметр (см³) или кубический дециметр (дм³).

Свойства правильной пирамиды

1. Вершина пирамиды равноудалена от всех углов основания.

2. Все боковые ребра равны.

3. Все боковые ребра наклонены под одинаковыми углами к основанию.

4. Апофемы всех боковых граней равны.

5. Площади всех боковых граней равны.

6. Все грани имеют одинаковые двугранные (плоские) углы.

7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.

8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.

9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n
, где n
— это количество углов в основании пирамиды.

Определение пирамиды

Пирамида – это многогранник, у которого одна грань называется основанием, а все остальные грани – боковыми. Основание пирамиды может быть любой плоской фигурой: треугольником, прямоугольником, кругом и т.д.

Наиболее распространенную пирамиду можно представить как правильную пирамиду с основанием в форме многоугольника и равными боковыми гранями, которые пересекаются в одной точке – вершине пирамиды.

В пирамиде можно выделить несколько основных элементов:

1. Вершина пирамиды;
2. Основание пирамиды;
3. Боковые грани пирамиды;
4. Высота пирамиды;
5. Ребро пирамиды;
6. Радиус основания пирамиды;
7. Площадь основания пирамиды;
8. Объем пирамиды.

Также пирамиды могут быть различных типов, включая тетраэдр, гексагональную пирамиду, пирамиду с отверстием и другие.

Свойства пирамиды

Пирамида — это геометрическое тело, имеющее плоское многоугольную основание и вершину, которая находится выше основания и соединена с ним ребрами. Рассмотрим основные свойства пирамиды.

1. Основание пирамиды: Основание пирамиды представляет собой плоскую фигуру, которая может быть любым многоугольником. Часто встречаются пирамиды с основанием, которое является треугольником, прямоугольником или правильным многоугольником.
2. Вершина пирамиды: Вершина пирамиды находится выше основания и соединяется с ним ребрами. Вершина является общей точкой для всех боковых граней пирамиды.
3. Боковые грани: Боковыми гранями пирамиды называются треугольные плоскости, которые соединяют вершину пирамиды с ее основанием.
4. Высота пирамиды: Высотой пирамиды называется расстояние между ее вершиной и плоскостью основания. Высота пирамиды может быть перпендикулярна плоскости основания либо может образовывать любой угол с плоскостью основания.
5. Объем пирамиды: Объем пирамиды можно вычислить по формуле: V = (1/3) * S * h, где S — площадь основания пирамиды, h — высота пирамиды.
6. Площадь поверхности пирамиды: Площадь поверхности пирамиды равна сумме площадей ее основания и боковых граней. Для вычисления площади поверхности пирамиды можно использовать формулу, учитывая площадь основания и периметр основания.

Изучая эти свойства пирамиды, можно получить более глубокое представление об этом геометрическом теле и использовать его в различных математических задачах.

Основные свойства

Правильная пирамида обладает множеством свойств,
которые присущи только ей. Перечислим их:

1. Основа – фигура правильной формы.
2. Ребра пирамиды, ограничивающие боковые элементы, имеют равные числовые значения.
3. Боковые элементы – равнобедренные треугольники.
4. Основание высоты фигуры попадает в центр многоугольника, при этом он одновременно является центральной точкой вписанной и описанной .
5. Все боковые рёбра наклонены к плоскости основы под одинаковым углом.
6. Все боковые поверхности имеют одинаковый угол наклона по отношению к основе.

Благодаря всем перечисленным свойствам, выполнение вычислений элементов намного упрощается

Исходя из приведенных свойств, обращаем внимание на два признака:

1. В том случае, когда многоугольник вписывается в окружность, боковые грани будут иметь с основой равные углы.
2. При описании окружности около многоугольника, все рёбра пирамиды, исходящие из вершины, будут иметь равную длину и равные углы с основой.

В основе лежит квадрат

Правильная четырёхугольная пирамида – многогранник, у которого в основе лежит квадрат.

У неё четыре боковых грани, которые по своему виду являются равнобедренными.

На плоскости квадрат изображают , но основываются на всех свойствах правильного четырёхугольника.

К примеру, если необходимо связать сторону квадрата с его диагональю, то используют следующую формулу: диагональ равна произведению стороны квадрата на корень квадратный из двух.

В основе лежит правильный треугольник

Правильная треугольная пирамида – многогранник, в основании которого лежит правильный 3-угольник.

Если основание является правильным треугольником, а боковые рёбра равны ребрам основания, то такая фигура называется тетраэдром.

Все грани тетраэдра являются равносторонними 3-угольниками. В данном случае необходимо знать некоторые моменты и не тратить на них время при вычислениях:

• угол наклона ребер к любому основанию равен 60 градусов;
• величина всех внутренних граней также составляет 60 градусов;
• любая грань может выступить основанием;
• , проведённые внутри фигуры, это равные элементы.

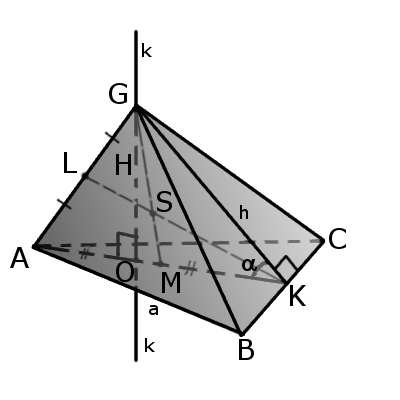
Радиус сферы, описанной около правильной n — угольной пирамиды

      Задача 1. равна   h ,   а длина равна   a .   Найти радиус сферы, описанной около пирамиды.

      Решение. Рассмотрим правильную n — угольную пирамиду   SA₁A₂ … A_n   и обозначим буквой   O   центр описанной около пирамиды сферы, а символом   O’   – центр основания пирамиды. Проведем плоскость   SO’A_n   (рис. 5).

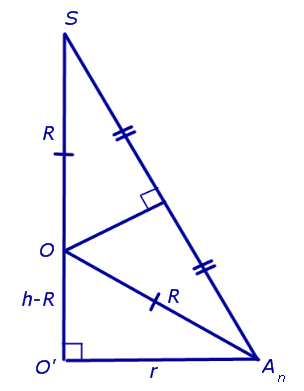
Рис.5

      Буквой   R   на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой   r   – радиус описанной около основания пирамиды окружности. По для треугольника   O’OA_n   получаем

R2 = (h – R)2 + r2;

R2 = h2 – 2hR + R2 + r2;

2hR = h2 + r2.

      Следовательно,

(1)

      Поскольку

из формулы (1) получаем соотношение

(2)

      Ответ.

      Следствие 3. Радиус сферы, описанной около с   h   и   a ,   равен

      Следствие 4. Радиус сферы, описанной около с   a ,   равен

      Следствие 5. Радиус сферы, описанной около с   h   и   a ,   равен

      Следствие 6. Радиус сферы, описанной около с   h   и   a ,   равен

Примеры применения пирамид в математике и повседневной жизни

• Пирамиды используются в геометрии для решения различных задач. Например, с помощью формулы для объема пирамиды можно найти объем конкретной фигуры и применить его в строительстве или архитектуре.
• Пирамиды также применяются в геодезии для определения высоты объектов. Составляются треугольники, а одна из сторон является горизонтальной линией. С помощью формул и вычислений можно определить высоту объекта.
• В повседневной жизни пирамиды встречаются в виде пирамидальных упаковок, например, для продуктов или подарков. Такая форма упаковки позволяет экономить место и обеспечивает устойчивость.
• В зоологии некоторые организмы имеют форму пирамиды. Например, пирамидальное строение можно встретить у некоторых видов муравьев, термитов и других насекомых.

Свойства пирамиды

Среди свойств, которыми обладает многоугольник в виде пирамиды, можно отметить следующие:

1. В случае равенства всех боковых ребер фигуры вокруг ее основания можно описать круг, центр которого совпадет с центром основания пирамиды. Кроме того, через эту точку пройдет перпендикуляр, который опустили из вершины многоугольника.
2. Равенство всех ребер пирамиды говорит о том, что они расположены под равными углами к плоскости основания.
3. Равенство боковых ребер будет соблюдаться в том случае, когда ими образованы равные углы с плоскостью основания, либо имеется возможность описать вокруг основания многоугольника круг.
4. При наклоне боковых граней к плоскости основания под одинаковым углом можно вписать круг в основание пирамиды. При этом проекция вершины пирамиды будет совпадать с центральной точкой данной окружности.
5. Равенство апофем боковых граней пирамиды возможно в том случае, когда углы наклона боковых граней к основанию равны.

Свойства правильной пирамиды

Правильную пирамиду характеризуют следующие особенности:

• вершина такой геометрической фигуры расположена на одинаковом расстоянии от всех углов основания;
• равенство всех боковых ребер;
• равенство углов наклона всех боковых ребер к плоскости основания;
• равенство апофем всех боковых граней;
• равенство площадей, которыми обладают все боковые грани;
• для всех граней характерно наличие одинаковых двугранных или плоских углов;
• вокруг такой пирамиды можно описать сферу, центром которой будет являться точка пересечения перпендикуляров, пересекающих середину ребер геометрической фигуры;
• в данный многоугольник можно вписать сферу с центром в точке, в которой пересекаются биссектрисы, выходящие из угла, разделяющего ребро и основание;
• при совпадении центра вписанной сферы с центральной точкой описанной сферы сумма плоских углов при вершине равна π (числу «пи», или 180-ти градусам), или наоборот, один угол соответствует π/n, где n является количеством углов в основании пирамиды.

Определение

К примеру, Эвклид определял ее как телесную фигуру, состоящую из плоскостей, которые, начиная от одной, сходятся в определенной точке.

Герон представил более точную формулировку. Он настаивал на том, что это фигура, которая имеет основание и плоскости в виде треугольников, сходящиеся в одной точке.

Опираясь на современное толкование, пирамиду представляют, как пространственный многогранник, состоящий из определённого k-угольника и k плоских фигур треугольной формы, имеющую одну общую точку.

Разберемся более подробно, из каких элементов она состоит:

• k-угольник считают основой фигуры;
• фигуры 3-угольной формы выступают гранями боковой части;
• верхняя часть, из которой берут начало боковые элементы, называют вершиной;
• все отрезки, соединяющие вершину, называют рёбрами;
• если из вершины на плоскость фигуры опустить прямую под углом в 90 градусов, то её часть, заключенная во внутреннем пространстве — высота пирамиды;
• в любом боковом элементе к стороне нашего многогранника можно провести перпендикуляр, называемый апофемой.

Число рёбер вычисляется по формуле 2*k, где k – количество сторон k-угольника. Сколько граней у такого многогранника, как пирамида, можно определить посредством выражения k+1.

Важно! Пирамидой правильной формы называют стереометрическую фигуру, плоскость основы которой является k-угольник с равными сторонами.

Свойства пирамиды

Пирамида с равным боковыми ребрами

Все углы между боковыми ребрами и основанием пирамиды равны.

Свойство 2

Вокруг основания пирамиды можно описать окружность, центр которой будет совпадать с проекцией вершины на ее основание.

• Точка F– проекция вершины E на основание ABCD; одновременно является центром этого основания.
• R– радиус описанной окружности.

Боковые грани пирамиды наклонены к основанию под одинаковым углом

Примечание: для перечисленных выше свойств верны и обратные формулировки. Например, для Свойства 1: если все углы между боковыми ребрами и плоскостью основания пирамиды равны, значит эти ребра имеют одинаковую длину.

Правильная пирамида

Определение 2

Пирамида, в основании которой лежит правильный многоугольник и высота пирамиды падает в его центр называется правильной пирамидой (рис. 3).

Правильная пирамида»>Рисунок 3. Правильная пирамида

Введем и докажем свойство правильной пирамиды.

Теорема 1

Все боковые грани правильной пирамиды являются равнобедренными треугольниками, которые равны между собой.

Доказательство.

Рассмотрим правильную $n-$угольную пирамиду с вершиной $S$ высотой $h=SO$. Опишем вокруг основания окружность (рис. 4).

Рисунок 4.

Рассмотрим треугольник $SOA$. По теореме Пифагора, получим

Очевидно, что так будет определяться любое боковое ребро. Следовательно, все боковые ребра равны между собой, то есть все боковые грани — равнобедренные треугольники. Докажем, что они равны между собой. Так как основание — правильный многоугольник, то основания всех боковых граней равны между собой. Следовательно, все боковые грани равны по III признаку равенства треугольников.

Теорема доказана.

Введем теперь следующее определение, связанное с понятием правильной пирамиды.

Определение 3

Апофемой правильной пирамиды называется высота её боковой грани.

Очевидно, что по теореме 1 все апофемы равны между собой.

Теорема 2

Площадь боковой поверхности правильной пирамиды определяется как произведение полупериметра основания на апофему.

Доказательство.

Обозначим сторону основания $n-$угольной пирамиды через $a$, а апофему через $d$. Следовательно, площадь боковой грани равна

Так как, по теореме 1, все боковые стороны равны, то

Теорема доказана.

Угол между боковыми гранями пирамиды

Пирамида — многогранник, у которого одна из граней (основание) является многоугольником, а оставшиеся грани (боковые грани) — треугольниками, имеющими общую вершину (вершину пирамиды).

Угол между боковыми гранями пирамиды — это угол между двумя соседними боковыми гранями пирамиды в вершине пирамиды. Данный угол зависит от формы пирамиды и может быть различным.

Чтобы найти угол между боковыми гранями пирамиды, можно использовать следующую формулу:

угол = arccos((a^2 + b^2 — c^2) / (2ab))

где a и b — длины сторон треугольника, образованного боковыми гранями пирамиды, и c — длина основания пирамиды.

Для угла между боковыми гранями пирамиды можно использовать тригонометрические функции, такие как арккосинус, чтобы найти значение угла.

Понятие пирамиды

Определение 1

Геометрическая фигура, образованная многоугольником и точкой, не лежащей в плоскости, содержащей этот многоугольник, соединенной со всеми вершинами многоугольника называется пирамидой (рис. 1).

Рисунок 1. Пирамида

Многоугольник, из которого составлена пирамида, называется основанием пирамиды, получаемые при соединение с точкой треугольники — боковыми гранями пирамиды, стороны треугольников — сторонами пирамиды, а общая для всех треугольников точка — вершиной пирамиды.

В зависимости от количества углов в основании пирамиды ее можно назвать треугольной, четырехугольной и так далее (рис. 2).

Рисунок 2.

Замечание 1

Отметим, что тетраэдр является частным случаем треугольной пирамиды.

Основные свойства

Правильная пирамида обладает множеством свойств, которые присущи только ей. Перечислим их:

1. Основа – фигура правильной формы.
2. Ребра пирамиды, ограничивающие боковые элементы, имеют равные числовые значения.
3. Боковые элементы – равнобедренные треугольники.
4. Основание высоты фигуры попадает в центр многоугольника, при этом он одновременно является центральной точкой вписанной и описанной окружностей.
5. Все боковые рёбра наклонены к плоскости основы под одинаковым углом.
6. Все боковые поверхности имеют одинаковый угол наклона по отношению к основе.

Благодаря всем перечисленным свойствам, выполнение вычислений элементов намного упрощается

Исходя из приведенных свойств, обращаем внимание на два признака:

1. В том случае, когда многоугольник вписывается в окружность, боковые грани будут иметь с основой равные углы.
2. При описании окружности около многоугольника, все рёбра пирамиды, исходящие из вершины, будут иметь равную длину и равные углы с основой.

В основе лежит квадрат

Правильная четырёхугольная пирамида – многогранник, у которого в основе лежит квадрат.

У неё четыре боковых грани, которые по своему виду являются равнобедренными.

На плоскости квадрат изображают параллелограммом, но основываются на всех свойствах правильного четырёхугольника.

К примеру, если необходимо связать сторону квадрата с его диагональю, то используют следующую формулу: диагональ равна произведению стороны квадрата на корень квадратный из двух.

В основе лежит правильный треугольник

Правильная треугольная пирамида – многогранник, в основании которого лежит правильный 3-угольник.

Если основание является правильным треугольником, а боковые рёбра равны ребрам основания, то такая фигура называется тетраэдром.

Все грани тетраэдра являются равносторонними 3-угольниками. В данном случае необходимо знать некоторые моменты и не тратить на них время при вычислениях:

• угол наклона ребер к любому основанию равен 60 градусов,
• величина всех внутренних углов граней также составляет 60 градусов,
• любая грань может выступить основанием,
• высоты, проведённые внутри фигуры, это равные элементы.

Определение

Определений пирамиды можно встретить достаточно много. Начиная еще с древних времен, она пользовалась большой популярностью.

К примеру, Эвклид определял ее как телесную фигуру, состоящую из плоскостей, которые, начиная от одной, сходятся в определенной точке.

Герон представил более точную формулировку. Он настаивал на том, что это фигура, которая имеет основание и плоскости в виде треугольников,
сходящиеся в одной точке.

Опираясь на современное толкование, пирамиду представляют, как пространственный многогранник, состоящий из определённого k-угольника и k плоских фигур треугольной формы, имеющую одну общую точку.

Разберемся более подробно, из каких элементов она состоит:

• k-угольник считают основой фигуры;
• фигуры 3-угольной формы выступают гранями боковой части;
• верхняя часть, из которой берут начало боковые элементы, называют вершиной;
• все отрезки, соединяющие вершину, называют рёбрами;
• если из вершины на плоскость фигуры опустить прямую под углом в 90 градусов, то её часть, заключенная во внутреннем пространстве — высота пирамиды;
• в любом боковом элементе к стороне нашего многогранника можно провести перпендикуляр, называемый апофемой.

Число рёбер вычисляется по формуле 2*k, где k – количество сторон k-угольника. Сколько граней у такого многогранника, как пирамида, можно определить посредством выражения k+1.

Важно!
Пирамидой правильной формы называют стереометрическую фигуру, плоскость основы которой является k-угольник с равными сторонами

Свойства пирамиды

Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).

Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.

Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.

Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.

Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.

Правильная пирамида

Пирамида называется правильной, если:

• ее основание – правильный многоугольник;
• отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.

Пояснение на примере правильной четырехугольной пирамиды

Рассмотрим правильную четырехугольную пирамиду PABCD (рис. 3).

Р – вершина пирамиды. Основание пирамиды АВСD – правильный четырехугольник, то есть квадрат. Точка О, точка пересечения диагоналей, является центром квадрата. Значит, РО – это высота пирамиды.

Рис. 3

Пояснение: в правильном n-угольнике центр вписанной и центр описанной окружности совпадает. Этот центр и называется центром многоугольника. Иногда говорят, что вершина проектируется в центр.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой и обозначается hа.

Сечения многогранника

В любом многограннике различают несколько видов сечения плоскостью. Зачастую в школьном курсе геометрии работают с двумя:

• осевое,
• параллельное основе.

Осевое сечение получают при пересечении плоскостью многогранника, которая проходит через вершину, боковые рёбра и ось. В данном случае осью является высота, проведённая из вершины. Секущая плоскость ограничивается линиями пересечения со всеми гранями, в результате получаем треугольник.

Внимание! В правильной пирамиде осевым сечением является равнобедренный треугольник. Если секущая плоскость проходит параллельно основанию, то в результате получаем второй вариант

В этом случае имеем в разрезе фигуру, подобную основе

Если секущая плоскость проходит параллельно основанию, то в результате получаем второй вариант. В этом случае имеем в разрезе фигуру, подобную основе.

К примеру, если в основании лежит квадрат, то сечение параллельно основе также будет квадратом, только меньших размеров.

При решении задач при таком условии используют признаки и свойства подобия фигур, основанные на теореме Фалеса. В первую очередь необходимо определить коэффициент подобия.

Если плоскость проведена параллельно основе, и она отсекает верхнюю часть многогранника, то в нижней части получают правильную усеченную пирамиду. Тогда говорят, что основы усеченного многогранника являются подобными многоугольниками. В этом случае боковые грани являются равнобокими трапециями. Осевым сечением также является равнобокая трапеция.

Для того чтобы определить высоту усеченного многогранника, необходимо провести высоту в осевом сечении, то есть в трапеции.

Высота пирамиды

Высота пирамиды — это вертикальное расстояние от вершины пирамиды до её основания. В зависимости от формы основания пирамиды, расчет высоты может выполняться по-разному.

Для пирамид с правильным многоугольным основанием (равносторонний треугольник, квадрат, правильный пятиугольник и т.д.) высота пирамиды может быть вычислена по следующей формуле:

h = (√3 / 2) * a

где h — высота пирамиды, а a — длина стороны основания.

Если же основание пирамиды не является правильным многоугольником, то формула для вычисления высоты будет отличаться. В этом случае можно использовать теорему Пифагора или другие геометрические методы для определения высоты пирамиды.

Зная высоту пирамиды, можно вычислить объём пирамиды по формуле:

V = (1 / 3) * S * h

где V — объём пирамиды, S — площадь основания, а h — высота пирамиды.

Связь пирамиды с цилиндром

Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.

Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.

Усеченная пирамида (пирамидальная призма)

Треугольная пирамида (четырехгранник)

В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.

Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол
.

Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника
(GM).

Бимедианой
называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).

Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.

Наклонная пирамида

Прямоугольная пирамида

Определение.
Остроугольная пирамида
— это пирамида в которой апофема больше половины длины стороны основания.

Определение.
Тупоугольная пирамида
— это пирамида в которой апофема меньше половины длины стороны основания.

Определение.
Правильный тетраэдр
— четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.

Определение.
Прямоугольный тетраэдр
называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол
и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.

Определение.
Равногранный тетраэдр
называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.

Определение.
Ортоцентричный тетраэдр
называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.

Определение.
Звездная пирамида
называется многогранник у которого основой является звезда.

Бипирамида

С понятием пирамида учащиеся сталкиваются еще задолго до изучения геометрии. Виной всему знаменитые великие египетские чудеса света. Поэтому, начиная изучение этого замечательного многогранника, большинство учеников уже наглядно представляют ее себе. Все вышеупомянутые достопримечательности имеют правильную форму. Что такое правильная пирамида
, и какие свойства она имеет и пойдет речь дальше.

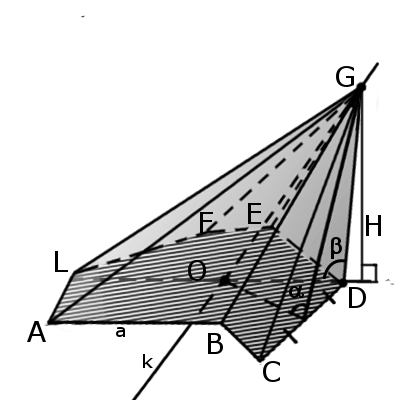
Усеченная пирамида

Определение 4

Если через обычную пирамиду провести плоскость, параллельную её основанию, то фигура, образованная между этой плоскостью и плоскостью основания называется усеченной пирамидой (рис. 5).

Рисунок 5. Усеченная пирамида

Боковыми гранями усеченной пирамиды являются трапеции.

Теорема 3

Площадь боковой поверхности правильной усеченной пирамиды определяется как произведение суммы полупериметров оснований на апофему.

Доказательство.

Обозначим стороны оснований $n-$угольной пирамиды через $a\ и\ b$ соответственно, а апофему через $d$. Следовательно, площадь боковой грани равна

Так как все боковые стороны равны, то

Теорема доказана.

Сечения многогранника

В любом многограннике различают несколько видов сечения
плоскостью. Зачастую в школьном курсе геометрии работают с двумя:

• осевое;
• параллельное основе.

Осевое сечение получают при пересечении плоскостью многогранника, которая проходит через вершину, боковые рёбра и ось. В данном случае осью является высота, проведённая из вершины. Секущая плоскость ограничивается линиями пересечения со всеми гранями, в результате получаем треугольник.

Внимание!
В правильной пирамиде осевым сечением является равнобедренный треугольник. Если секущая плоскость проходит параллельно основанию, то в результате получаем второй вариант

В этом случае имеем в разрезе фигуру, подобную основе

Если секущая плоскость проходит параллельно основанию, то в результате получаем второй вариант. В этом случае имеем в разрезе фигуру, подобную основе.

К примеру, если в основании лежит квадрат, то сечение параллельно основе также будет квадратом, только меньших размеров.

При решении задач при таком условии используют признаки и свойства подобия фигур, основанные на теореме Фалеса
. В первую очередь необходимо определить коэффициент подобия.

Если плоскость проведена параллельно основе, и она отсекает верхнюю часть многогранника, то в нижней части получают правильную усеченную пирамиду. Тогда говорят, что основы усеченного многогранника являются подобными многоугольниками. В этом случае боковые грани являются равнобокими трапециями. Осевым сечением также является равнобокая .

Для того чтобы определить высоту усеченного многогранника, необходимо провести высоту в осевом сечении, то есть в трапеции.

Итоги урока

Итак, мы рассмотрели, что такое пирамида, что такое правильная пирамида, доказали теорему о боковой поверхности правильной пирамиды. На следующем уроке мы познакомимся с усечённой пирамидой.

ИСТОЧИК

http://interneturok.ru/ru/school/geometry/10-klass/mnogogranniki/piramida-pravilnaya-piramida

http://zazdoc.ru/docs/2800/index-2129972.html

http://fmklass.ru/math.php?id=48626399be5d8

http://ppt4web.ru/mkhk/piramida1.html

http://pandia.ru/text/78/287/91594.php

http://matematikalegko.ru/piramidi/pravilnye-piramidy-ploshhad-poverxnosti.html

http://www.otbet.ru/book/class-10/geometria/uchebnik-glazkov-yu-a-testy-po-geometrii/