Правильные и неправильные фигуры
Мы выяснили, что такое основание фигуры. Тем не менее, до того как начать обсуждение формулы площади основания пирамиды, следует дать определение правильных и неправильных фигур этого класса.
Каждый школьник знает, что любой плоский многоугольник имеет геометрический центр. Если многоугольник изготовить из однородного материала, то геометрический центр совпадет с центром масс. Например, геометрический центр прямоугольника — это точка, где его диагонали пересекаются, для треугольника он находится в точке пересечения медиан. Концепция геометрического центра связана с понятиями правильной и неправильной пирамиды.
Выше было упомянуто о вершине пирамиды. Она соответствует точке, где пересекаются все треугольные боковые грани фигуры. Если из вершины опустить перпендикуляр к основанию, то длина полученного отрезка будет соответствовать расстоянию от вершины до основания. Этот отрезок называется высотой фигуры.
Если высота пересекает многоугольник в его геометрическом центре, то пирамида называется прямой. Если основанием прямой пирамиды будет многоугольник, имеющий стороны одинаковой длины и равные между собой углы, то пирамида называется правильной. Соответственно, если какое-либо из названных условий не выполняется, то говорят о неправильной пирамиде.
Согласно описанной классификации, пирамида Хеопса является правильной четырехугольной, имеющей в основании квадрат.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одном основании цилиндра, а основание пирамиды вписано в другое основание цилиндра. Цилиндр можно описать вокруг пирамиды, если вокруг основания пирамиды можно описать окружность.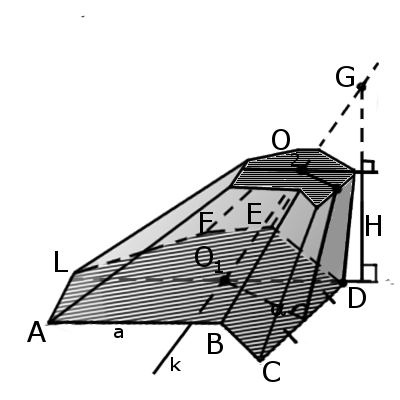
Определение: Усеченная пирамида (пирамидальная призма) – это многогранник, который расположен между основанием пирамиды и секущей плоскостью, параллельной основанию. Таким образом, пирамида имеет большое основание и меньшее основание, подобное большему. Боковые грани — трапеции. 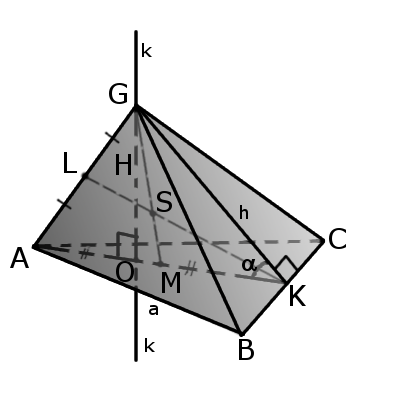
Определение Треугольная пирамида (тетраэдр) – это пирамида, у которой три грани и основание представляют собой произвольные треугольники. Тетраэдр имеет четыре грани, четыре вершины и шесть ребер, причем два ребра не имеют общих вершин, но не касаются друг друга. Каждая вершина состоит из трех граней и ребер, образующих трехгранный угол. Отрезок, соединяющий вершину тетраэдра с центром противоположной грани, называется медианой тетраэдра (GM) Бимедиана – это отрезок, соединяющий середины противоположных ребер, не соприкасающихся (KL) Все бимедианы и медианы тетраэдра пересекаются в одной точке (S). В этом случае бимедианы делятся пополам, а медианы в соотношении 3:1 сверху.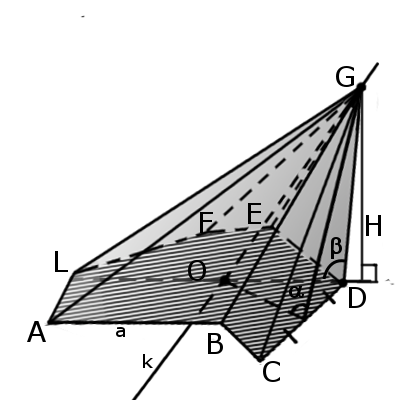
Определение Наклонная пирамида — это пирамида, одна из граней которой образует тупой угол (β) с основанием.
Определение Прямоугольной пирамидой называется пирамида, у которой одна из боковых граней перпендикулярна основанию. Определение Остроугольной пирамидой называется пирамида, у которой апофема составляет более половины длины стороны основания. Определение.
Тупой пирамидой называется пирамида, у которой апофема меньше половины длины стороны основания Определение Правильный тетраэдр — это тетраэдр, все четыре грани которого представляют собой равносторонние треугольники. Это один из пяти правильных многоугольников. В правильном тетраэдре все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение Прямоугольный тетраэдр — это тетраэдр с прямым углом между тремя ребрами в вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол, причем грани — прямоугольные треугольники, а основание — произвольный треугольник. Апофема любой грани равна половине стороны основания, на которое падает апофема. Определение Равногранным тетраэдром называется тетраэдр, боковые грани которого равны между собой, а основание представляет собой правильный треугольник. В таком тетраэдре грани равнобедренные треугольники Определение Ортоцентрическим тетраэдром называется тетраэдр, у которого все высоты (перпендикуляры), опущенные от вершины к противоположной грани, пересекаются в одной точке Определение Звездчатой пирамидой называется многогранник, основание которого равно звезда.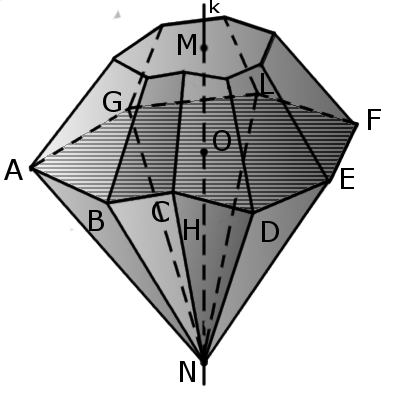
Определение Бипирамида – это многогранник, состоящий из двух различных пирамид (пирамиды также могут быть отсечены), имеющих общее основание, а вершины находятся по разные стороны от плоскости основания.
Как определить площадь сечения цилиндра, конуса, призмы и пирамиды? Формулы
На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.
Вам будет интересно: Что значит слыть: толкование, синонимы
Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.
Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.
Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
Примеры решения задач
Задача 1
Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.
Решение: пирамида правильная и треугольная, значит, основание равнобедренный треугольник. Тогда площадь основания пирамиды находится по формуле: Затем мы получаем страницу
Отвечать:
Задача 2
Строитель решил построить здание в виде правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?
Решение:
Вычислите площадь основания правильной шестиугольной пирамиды. Для этого используем формулу: Заменяем в ней значение страницы. Мы получаем:
м2.
Теперь посчитаем, сколько досок нам понадобится:
.
Ответ: 108 досок.
Задача 3
Основание пирамиды представляет собой прямоугольный равнобедренный треугольник, катет которого равен 4. Найдите площадь основания пирамиды.
Решение: Другими словами, нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то одна сторона будет основанием треугольника, а другая высотой. Определяем площадь по формуле:.
Ответ: 8
Площадь усеченной пирамиды
Усеченная пирамида – это многогранник, образованный пирамидой и ее сечением, параллельным основанию.
Формула площади боковой поверхности усеченной пирамиды очень проста. Площадь равна произведению половины суммы периметров оснований и апофемы:
Рассмотрим пример вычисления площади боковой поверхности усеченной пирамиды.
Дана правильная квадратная пирамида. Длина основания b = 5 см, c = 3 см. Апофема а = 4 см. Найдите площадь боковой поверхности фигуры.
Сначала найдите периметр оснований. В большей базе это будет равно:
В меньшей базе:
Рассчитаем площадь:
Таким образом, используя простые формулы, мы нашли площадь усеченной пирамиды.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.2. Все боковые ребра равны.3. Все боковые ребра наклонены под одинаковым углом к основанию.4. Апотемы всех боковых поверхностей равны.5. Площади всех боковых поверхностей равны.6. Все грани имеют одинаковые двугранные (плоские) углы.7. Вокруг пирамиды можно описать сферу. Центром описываемой сферы будет точка пересечения перпендикуляров, проходящих через середины ребер.8. Сферу можно вписать в пирамиду. Центром вписанной сферы будет пересечение биссектрис, исходящих из угла между краем и основанием.9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π, или, наоборот, угол равен π/n, где n — число углов при основании пирамида.
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, причем центр основания совпадает с центром окружности. Также перпендикуляр, падающий сверху, проходит через центр основания (окружности). Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами. Боковые грани равны, если они образуют равные углы с плоскостью основания или если можно описать окружность вокруг основания пирамиды Если боковые грани наклонены к плоскости основания под углом, то в основание можно вписать окружность пирамиды, а вершина пирамиды проецируется в середину.Если боковые поверхности наклонены к плоскости основания под одним углом, то апофемы боковых поверхностей равны.
Боковая поверхность пирамиды через периметр и апофему
Боковая поверхность правильной пирамиды в этом случае определяется по формуле:
$S_b = frac12 cdot P cdot c$, где
$P$ — периметр основания пирамиды;
$c$ — это апофема пирамиды.
В этом случае периметр правильного многоугольника можно определить по формуле:
$P = a cdot n$, где
$a$ — длина стороны многоугольника;
$n$ — количество страниц.
Вычислим боковую поверхность через апофему и периметр на примере четырехугольной пирамиды.
Пример 2
Задача
Дана правильная пирамида с квадратом в основании, сторона которого равна $5$ см. Апофема пирамиды составляет $9$ см. Вычислите площадь боковой поверхности.
Решение:
Вычислите периметр основания. Для квадрата периметр равен стороне, умноженной на 4:
$P_{main} = 4 cdot a^2 = 20$ см
Теперь рассчитаем площадь боковой поверхности:
$S_b = frac12 cdot 20 cdot 9 = $90 кв.см.
Примеры задач с решением
Задача
Дано
Правильный тетраэдр MABC с вершиной М. Высота основания AK=3 см.
∠MAB=∠MAC=∠MBA=∠MBC=∠MAB=∠MCA=∠MCB=45°. Необходимо вычислить площадь пирамиды MABC.
Решение
В основании правильного тетраэдра лежит равносторонний треугольник с известной длиной высоты. Применим свойство правильного треугольника, состоящее в следующем:
\(h=\frac{\sqrt3}2a\)
Преобразуем данное выражение так, чтобы вывести формулу стороны a:
\(a=\frac h{\frac{\sqrt3}2}\)
Теперь найдем a:
\(a=\frac3{\frac{\sqrt3}2}=\frac{3\times2}{\sqrt3}=\frac6{\sqrt3}\)
Подставим полученное выражение в формулу нахождения площади основания правильного многогранника с тремя боковыми гранями:
\(S_{осн}=\frac{\sqrt3}4\times\left(\frac6{\sqrt3}\right)^2=\frac{\sqrt3}4\times\frac{6^2}{\sqrt3^2}=\frac{36\sqrt3}{4\times3}=3\sqrt3\)
Далее необходимо найти площадь боковых граней тетраэдра. Для этого произведем вычисление высоты MK. Так как угол между гранью и основанием пирамиды равен 45°, то ∠OKM=45°, следовательно:
\(\frac{OK}{MK}=\cos\left(45^\circ\right)=\frac{\sqrt2}2\)
По свойству правильного треугольника, отрезок OK равен радиусу вписанной в ΔABC окружности.
Найдем ее по соответствующей формуле:
\(OK=r=\frac{\sqrt3}6a=\frac{\sqrt3}6\times\frac6{\sqrt3}=\frac{6\sqrt3}{6\sqrt3}=1\)
Подставим найденную величину в отношение ОК к МК:
\(\frac{OK}{MK}=\frac{\sqrt2}2\)
\(\frac1{MK}=\frac{\sqrt2}2\)
Из данной пропорции выведем выражение, по которому можно определить длину высоты MK:
\(MK=\frac2{\sqrt2}\)
Теперь, когда известны основание и высота равнобедренного треугольника, составляющего боковую грань пирамиды MABC, подставим значения в классическую формулу нахождения площади треугольника:
\(S_{бок}=\frac12ah=\frac12\times\frac6{\sqrt3}\times\frac2{\sqrt2}=\frac{1\times6\times2}{2\times\sqrt3\times\sqrt2}=\frac{12}{2\sqrt6}=\frac6{\sqrt6}\)
Суммируем площадь основания и боковых граней пирамиды:
\(S_{MABC}=3\sqrt3+3\times6\sqrt6=3\sqrt3+18\sqrt6\)
Примеры решения задач
Задача 1
Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.
Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона , тогда
Ответ:
Задача 2
Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5
м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?
Решение:
Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны . Получим:
м2.
Теперь подсчитаем, сколько нам понадобится досок: .
Ответ: 108 досок.
Задача 3
Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.
Решение: иными словами — нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой — высотой. Определяем площадь по формуле:
.
Ответ: 8
Задача 4
Условие. Найти общую площадь пирамиды, если в его основании лежит равносторонний треугольник со стороной 4 см, а апофема имеет значение √3 см.
Решение. Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см2.
Для треугольника в основании получится такое значение площади: (42*√3) / 4 = 4√3 см2.
Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см2.
Ответ. 10√3 см2.
Задача 5
Условие. Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.
Решение. Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.
Первые расчеты просты и приводят к такому числу: 49 мм2. Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16)2) = √2985,9375 = 54,644 мм2. Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.
Получается: 49 + 4*54,644 = 267,576 мм2.
Ответ. Искомое значение 267,576 мм2.
Задача 6
Условие. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.
Решение. Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.
Придется вспомнить теорему Пифагора и рассмотреть прямоугольный треугольник. Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.
Искомая апофема (гипотенуза прямоугольного треугольника) равна √(32 + 42) = 5 (см).
Теперь можно вычислять искомую величину: ½*(4*6)*5+62 = 96 (см2).
Ответ. 96 см2.
Задача 7
Условие. Дана правильная шестиугольная пирамида. Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?
Решение. Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.
Первым делом вычисляется площадь основания по указанной выше формуле: (6*222) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см2.
Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.
Расчеты по формуле Герона: √(72*(72-22)*(72-61)2)=√435600=660 см2. Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см2. Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см2.
Ответ. Основания — 726√3 см2, боковой поверхности — 3960 см2, вся площадь — 5217 см2.
Теорема о площади боковой поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему:
Для доказательства выберем правильную треугольную пирамиду.
Дано: РАВС – правильная треугольная пирамида.
АВ = ВС = АС.
РО – высота.
Доказать: . См. Рис. 5.
Рис. 5
Доказательство.
РАВС – правильная треугольная пирамида. То есть АВ = АС = ВС. Пусть О – центр треугольника АВС, тогда РО – это высота пирамиды. В основании пирамиды лежит равносторонний треугольник АВС. Заметим, что .
Треугольники РАВ, РВC, РСА – равные равнобедренные треугольники (по свойству). У треугольной пирамиды три боковые грани: РАВ, РВC, РСА. Значит, площадь боковой поверхности пирамиды равна:
Sбок = 3SРАВ
Теорема доказана.
Свойства правильной пирамиды
1. все боковые ребра правильной пирамиды равны;
2. боковые грани являются равными равнобедренными треугольниками.
Доказательство этих свойств приведем на примере правильной четырехугольной пирамиды.
Дано: РАВСD – правильная четырехугольная пирамида,
АВСD – квадрат,
РО – высота пирамиды.
Доказать:
1. РА = РВ = РС = РD
2. ∆АВР = ∆ВCР =∆СDР =∆DAP См. Рис. 4.
Рис. 4
Доказательство.
РО – высота пирамиды. То есть, прямая РО перпендикулярна плоскости АВС, а значит, и прямым АО, ВО, СО и DО, лежащим в ней. Значит, треугольники РОА, РОВ, РОС, РОD – прямоугольные.
Рассмотрим квадрат АВСD. Из свойств квадрата следует, что АО = ВО = СО = DО.
Тогда у прямоугольных треугольников РОА, РОВ, РОС, РОD катет РО – общий и катеты АО, ВО, СО и DО равны, значит, эти треугольники равны по двум катетам. Из равенства треугольников вытекает равенство отрезков, РА = РВ = РС = РD. Пункт 1 доказан.
Отрезки АВ и ВС равны, так как являются сторонами одного квадрата, РА = РВ = РС. Значит, треугольники АВР и ВCР – равнобедренные и равны по трем сторонам.
Аналогичным образом получаем, что треугольники АВР, ВCР, СDР, DAP равнобедренны и равны, что и требовалось доказать в пункте 2.
Вычисление площади боковых граней и полной поверхности
Боковые грани правильной треугольной пирамиды представлены тремя равнобедренными треугольниками. Выведем формулу расчета площади каждого из них из классического способа вычисления площади треугольника:
\(S=\frac12ah\)
Здесь переменная a обозначает основание треугольника, h — его высоту.
Теперь выполним подстановку выражения, с помощью которого находится высота треугольника с одинаковыми бедрами, и получим уравнение определения площади равнобедренного треугольника:
\((3)\;S_{бок}=\frac{a\sqrt{b^2-\frac{a^2}4}}2\)
В этом случае b — это боковые ребра треугольника, равные между собой.
Подставим в выражение (1) формулы (2) и (3) и получим уравнение, с помощью которого рассчитывается площадь полной поверхности правильного тетраэдра:
\(S=\frac{\sqrt3}4a^2+\frac32\times a\sqrt{b^2-\frac{a^2}4}\)
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) всей поверхности пирамиды равна сумме площадей боковой поверхности и основания.
Полный = Страница. + Соч.
Боковая поверхность правильной пирамиды представляет собой равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
1. По длине основания (а) и высоте (h):
2. Через основание (а) и сторону (б):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
| Квадрат | Формула |
| база | |
| боковая поверхность | |
| полный | |
L (апофема) — перпендикулярная линия, проведенная от вершины пирамиды к краю основания. Апофема пирамиды – это высота (h) боковой поверхности.
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Квадрат | Формула |
| база | Сосн. = a2″заказ данных=»Sосн. = a2″>Sбаза = а2 |
| боковая поверхность | Страница = 2al»data-order=»Sбок. = 2aL»>Страница = 2aL |
| полный | Полный = a2 + 2aL» data-order=»Sполн. = a2 + 2aL»>Полный = a2 + 2aL |
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник
| Формула | |
| база | |
| боковая поверхность | Страница = 3al»data-order=»Sбок. = 3aL»>Страница = 3aL |
| полный | |
Вычисление площади правильной треугольной пирамиды
Определение
Правильная треугольная пирамида (тетраэдр) — это многогранник, в основании которого лежит правильный треугольник со сторонами a и боковыми гранями в виде равнобедренных треугольников с основанием a и сторонами b.
Площадь поверхности такой фигуры складывается из площадей основания многогранника и трех боковых граней. В записи на математический язык это выглядит так:
\((1)\;S=S_{осн}+3\times S_{бок}\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Правильная пирамида
Пирамида называется правильной, если:
- ее основание – правильный многоугольник;
- отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Пояснение на примере правильной четырехугольной пирамиды
Рассмотрим правильную четырехугольную пирамиду PABCD (рис. 3).
Р – вершина пирамиды. Основание пирамиды АВСD – правильный четырехугольник, то есть квадрат. Точка О, точка пересечения диагоналей, является центром квадрата. Значит, РО – это высота пирамиды.
Рис. 3
Пояснение: в правильном n-угольнике центр вписанной и центр описанной окружности совпадает. Этот центр и называется центром многоугольника. Иногда говорят, что вершина проектируется в центр.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой и обозначается hа.
Что представляет собой пирамида?
Ответ на этот вопрос не так очевиден, как многие могут подумать. Когда люди слышат слово «пирамида», в их воображении возникает огромное каменное сооружение египетских фараонов. Однако это лишь частный случай фигур этого класса.
С точки зрения точной науки геометрии пирамида — это фигура в пространстве, образованная n-угольником, каждый из углов которого соединен с одной точкой. Эта точка не должна находиться в плоскости n-угольника. Здесь n — целое число, равное количеству вершин (сторон) плоского многоугольника. Для наглядного представления описываемого рисунка приведем фотографию.

Вот набор различных пирамид. Верхний левый называется треугольным, потому что основание представляет собой треугольник. Нижняя правая пирамида называется восьмиугольником.
Это изображение позволяет нам сделать некоторые выводы относительно пирамид. Во-первых, стороны, соединяющие n-угольник с вершиной фигуры, являются треугольниками. Во-вторых, количество сторон любой пирамиды равно n + 1 (n-угольник и n треугольников), n-угольник называется основанием, а треугольники — сторонами. В-третьих, видно, что увеличение сторон основания приближает пирамиду по форме к конусу. Этот факт позволяет рассматривать конус как пирамиду с бесконечным числом сторон.
Задача 1
Радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м, высота пирамиды равна 4 м. Найдите площадь боковой поверхности пирамиды.
Дано: правильная четырехугольная пирамида АВСD,
АВСD – квадрат,
r = 3 м,
РО – высота пирамиды,
РО = 4 м.
Найти: Sбок . См. Рис. 6.
Рис. 6
Решение.
По доказанной теореме, .
Найдем сначала сторону основания АВ. Нам известно, что радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м.
Тогда, м.
Найдем периметр квадрата АВСD со стороной 6 м:
Рассмотрим треугольник BCD. Пусть М – середина стороны DC. Так как О – середина BD, то (м).
Треугольник DPC – равнобедренный. М – середина DC. То есть, РМ – медиана, а значит, и высота в треугольнике DPC. Тогда РМ – апофема пирамиды.
РО – высота пирамиды. Тогда, прямая РО перпендикулярна плоскости АВС, а значит, и прямой ОМ, лежащей в ней. Найдем апофему РМ из прямоугольного треугольника РОМ.
(м).
Теперь можем найти боковую поверхность пирамиды:
Ответ: 60 м2.
Итоги урока
Итак, мы рассмотрели, что такое пирамида, что такое правильная пирамида, доказали теорему о боковой поверхности правильной пирамиды. На следующем уроке мы познакомимся с усечённой пирамидой.
ИСТОЧИК
http://interneturok.ru/ru/school/geometry/10-klass/mnogogranniki/piramida-pravilnaya-piramida
http://zazdoc.ru/docs/2800/index-2129972.html
http://fmklass.ru/math.php?id=48626399be5d8
http://ppt4web.ru/mkhk/piramida1.html
http://pandia.ru/text/78/287/91594.php
http://matematikalegko.ru/piramidi/pravilnye-piramidy-ploshhad-poverxnosti.html
http://www.otbet.ru/book/class-10/geometria/uchebnik-glazkov-yu-a-testy-po-geometrii/






























