Как вычислить площадь квадрата

Задачи на площадь фигуры на координатной плоскости.

Чем отличаются задачи этого типа от предыдущих? Почти ни чем. Координатная плоскость — та же самая сетка. Только линии этой сетки
пронумеровали, а затем стерли, а на фигуре написали на каких линиях были расположены её вершины. Когда? Еще в 17-ом веке. Зачем?
Чтобы как-то, хотя бы условно, изображать большие и несоразмерные фигуры, которые не помещаются на рисунке в нормальном масштабе.

Из этих соображений, следуют два способа решения задач:Первый, самый надежный, — выучить понятия и формулы из раздела «Декартовы
координаты на плоскости и в пространстве». Второй, самый простой для тех, кто разобрался с предыдущей задачей, —
восстановить сетку.

Решение вторым способом более очевидное. Теоретически так можно решать любую задачу на координатную плоскость, но это может
оказаться значительно медленнее, чем первым способом, и потребовать «немеряного количества» бумаги. (Иначе не надо было бы
изобретать координаты.) Поэтому здесь мы рассмотрим те задачи, для которых решение восстановлением сетки достаточно быстрое и
компактное, а затем еще раз вернемся к понятию координатной плоскости в следующем разделе.

Задача 13

Найдите площадь четырёхугольника, вершины которого имеют координаты (3, 2), (7, 6), (7, 8), (3, 6).

Решение.

Оси координат — это линии сетки, с которых начинается нумерация. Ось Ox — нулевая горизонтальная линия, ось Oy — нулевая вертикальная линия. Запись «координаты (3, 2)» означает, что точка находится на 3-ей вертикальной линии сетки и на второй горизонтальной, аналогично «координаты (7, 6)» — на 7-ой вертикальной и 6-ой горизонтальной, и т. д. Рисуем нужное количество линий на заданном чертеже. Результат на рисунке слева. Видно, что этот рисунок очень похож на рисунок к условию предыдущей задачи. А, если не обращать внимания на оси, то абсолютно тот же (это потому, что для примера я специально выбрала задачу с той же самой трапецией). Значит решать можно любым из представленных выше четырёх способов. Например, разбиваем трапецию на два прямоугольных треугольника и вычисляем:S1 = 4×2/2 = 4. S2 = 4×4/2 = 8. S = S1 + S2 = 4 + 8 = 12.

Ответ: 12

Следующую задачу постарайтесь сначала решить самостоятельно, а затем проверьте своё решение.

Задача 14

Найдите площадь четырехугольника, вершины которого имеют координаты (4, 2), (8, 4), (6, 8), (2, 6).

Решение

На рисунке в условии задачи пунктиром показаны отрезки линий сетки, которые проходят через вершины четырёхугольника (здесь это 2-я, 4-я, 6-я и 8-я линии как по вертикали, так и по горизонтали). Дорисовываем весь участок сетки в окрестности заданной фигуры. Решаем задачу так, как если бы она была задана на клеточках, без координатных осей. У нашего четырёхугольника нет сторон, лежащих на линиях сетки, поэтому выберем третий метод из предыдущего раздела — метод «вырезания». Строим внешний прямоугольник, стороны которого проходят по сетке через вершины заданного. Прямым подсчетом клеточек убеждаемся в том, что красная линия на чертеже ограничивает квадрат со стороной 6 единиц, значит его площадь равна S_кв = 36 ед.2, а четыре зеленых прямоугольных треугольника равны между собой и имеют катеты 2 ед. и 4 ед., площадь каждого из них равна 2×4/2 = 4. Следовательно, искомая площадь желтого четырехугольника равна S = 36 − 4×4 = 20.

Ответ: 20

Замечания:
1) По рисунку видно, и равенством зеленых треугольников подтверждается, что заданный четырёхугольник тоже квадрат. Но нам здесь это даже не потребовалось.
2) В качестве упражнения на развитие воображения попробуйте найти эту площадь вторым методом из предыдущего раздела — методом разрезания желтого квадрата по линиям сетки на простые части.

Продолжение:Задачи на понятие координатной плоскости.Задачи на вектора.

Перейдите по стрелке, чтобы найти ссылки на другие задачи ЕГЭ по математике.

Что такое площадь

Площадь является математической величиной, с помощью которой измеряют размер поверхности.

Площадь обозначают, используя математический знак S.

Перечислим популярные единицы измерения площади, которые часто встречаются в задачах:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

• квадратный метр \((м^{2})\);
• сантиметр в квадрате \((см^{2})\);
• квадратный миллиметр \((мм^{2})\);
• километр в квадрате \((км^{2})\);
• ар (а);
• гектар (га).

Такая величина, как площадь характеризуется следующими свойствами:

• положительность (при вычислении площади какой-либо фигуры или поверхности получается в любом случае число со знаком плюс, величина не может иметь отрицательное значение);
• нормировка (для определения площади предусмотрены стандартизированные единицы измерения);
• если геометрические фигуры идентичны, то такие фигуры обладают равными площадями;
• площадь совокупности пары фигур без учета единых точек, расположенных во внутреннем пространстве, соответствует сумме площадей.

Формулы для треугольников

Имеется несколько формул площади треугольника. Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.

При известности всех трёх сторон — a, b, c, широко применяется формула, названная в честь Герона — математика из Древней Греции: S = √(p*(p — a)*(p — b)*(p — c)). Величина p — это половина от периметра треугольника (полупериметр). Чтобы его рассчитать, необходимо суммировать все стороны и разделить сумму на два: (a + b + c)/2.

Для ещё одной формулы требуются следующие данные:

• длина двух соприкасающихся в одной вершине сторон — a и b;
• градус угла, который образуют эти стороны.

Тогда расчёт можно произвести таким способом: S = ½ * a * b * sin γ. Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.

Когда два треугольника являются подобными (подобие означает, что у них равны углы и стороны пропорциональны), то отношение их площадей соответствует отношению возведённых в квадрат сторон. Такое отношение сторон для них (например, AB: A (1) B (1)) именуется коэффициентом подобия (k). Поэтому отношение площадей равняется коэффициенту подобия в квадрате.

Если в треугольнике даны все стороны, тогда, кроме формулы Герона, есть возможность воспользоваться ещё одним способом. Он основан на том, что можно вписать любой треугольник в круг. Зная такую величину, радиус окружности и три стороны треугольника, производится расчёт: S = (a * b * c) / 4 R.

https://youtube.com/watch?v=aXyKgX6RAqw

Площадь квадрата

Из известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

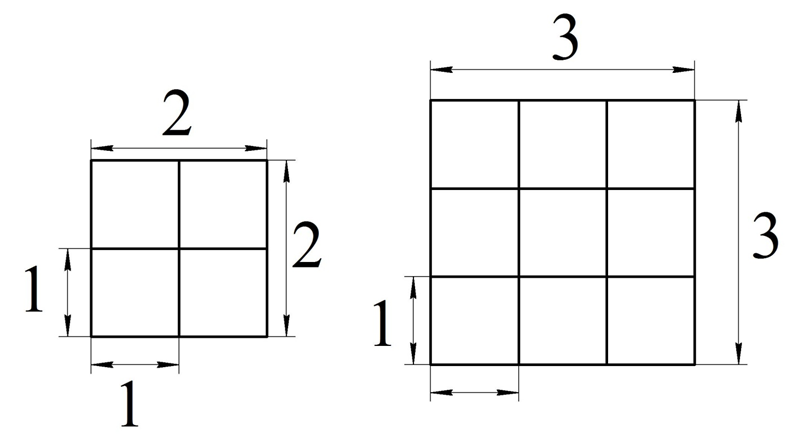
Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– ) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

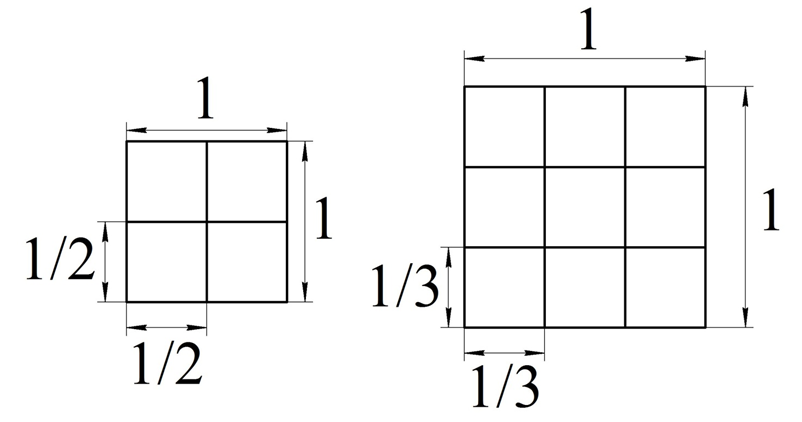
В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

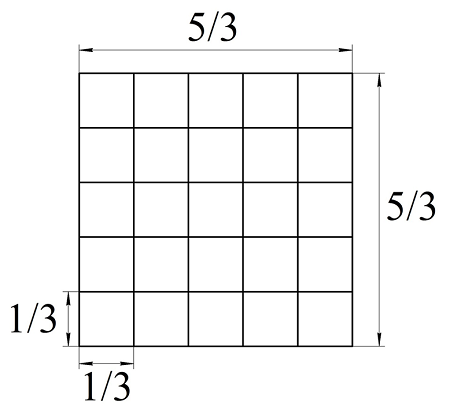
Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это . Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I2<S (случай, когда I2>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

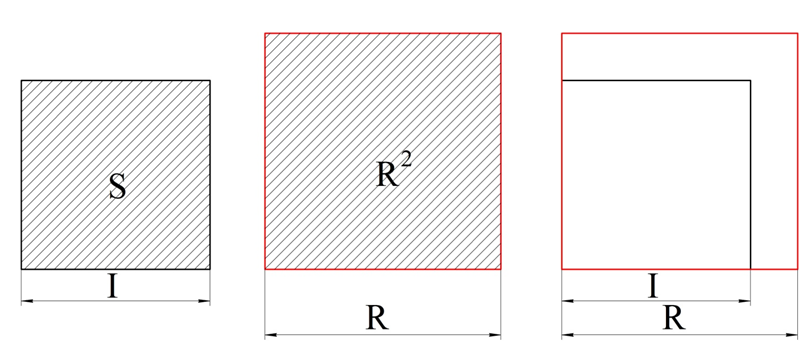
Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Ответ: 16 см2.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.

Как найти боковые стороны прямоугольника

Прямоугольник — это геометрическая фигура, которая имеет четыре стороны, из которых две параллельны и равны между собой, а две другие тоже параллельны и равны друг другу. Но что делать, если вам дана только площадь прямоугольника, а не его стороны? При этом необходимо найти длину боковых сторон.

Для того, чтобы найти боковые стороны прямоугольника по его площади, необходимо воспользоваться формулой S=a*b, где S — площадь прямоугольника, a — длина одной из сторон, b — длина другой стороны. Для нахождения конкретного значения сторон можно использовать следующие шаги:

• Узнайте площадь прямоугольника;
• Определите длину одной из сторон, деля площадь на длину другой стороны. Т.е. a=S/b;
• Найдите длину другой стороны, разделив площадь на длину первой стороны. Т.е. b=S/a;
• Проверьте полученные значения путем умножения одного значения на другое. Должна получиться исходная площадь;

Таким образом, нахождение длины боковых сторон прямоугольника по его площади не составляет большого труда, если использовать соответствующую формулу и последовательность действий.

Пример:

Дана площадь прямоугольника S=24, а одна из его сторон равна a=4. Найдем длину другой стороны:

b=S/a=24/4=6

Итак, длина боковых сторон прямоугольника равна a=4 и b=6.

Квадрат — определение и свойства

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

1. Все углы квадрата — прямые, все стороны квадрата — равны.

2. Диагонали квадрата равны и пересекаются под прямым углом.

Периметр квадрата P в 4 раза больше его стороны и равен:

Площадь квадрата равна квадрату его стороны: .

Теорема 1. Диагональ квадрата равна произведению его стороны на , то есть .

Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.

Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:

что и требовалось доказать.

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:

Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках P, M, N, K.

Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть

, что и требовалось доказать.

Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:

Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.

Тогда , что и требовалось доказать.

Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.
2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Задача 1. Найдите сторону квадрата, диагональ которого равна .

Мы знаем, что . Тогда .

Задача 2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

Тогда по формуле площади квадрата:

Второй способ решения:

Воспользуемся формулой для площади ромба:

Задача 3. Найдите радиус окружности, описанной около квадрата со стороной, равной .

Радиус описанной окружности равен половине диагонали квадрата, поэтому

Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .

Диаметр окружности равен стороне квадрата: .

Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.

Сторона квадрата в два раза больше радиуса вписанной окружности:

Диагональ найдем, зная сторону квадрата:

Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

Задача 7. Найдите периметр квадрата, если его площадь равна 9.

Найдем сторону квадрата:

Периметр квадрата со стороной 3 равен:

Задача 8. Найдите площадь квадрата, в который вписан круг площадью .

Площадь круга откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна ., то сторона малого квадрата равна . А сторона квадрата ABCD равна

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .

Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.

Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .

Формулы объема и площади поверхности. Призма, пирамида — материалы для подготовки к ЕГЭ по Математике

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

1. Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
2. Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Иногда в задаче  надо посчитать площадь поверхности куба или призмы.

Напомним, что площадь поверхности многогранника — это сумма площадей всех его граней.

В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в раз.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Структура и элементы

Окружность и круг являются двумя основными фигурами в геометрии, которые имеют схожую структуру, но отличаются своими элементами.

Окружность — это геометрическая фигура, состоящая из всех точек, равноудаленных от центра. Центр окружности — это основная точка, от которой все остальные точки окружности равноудалены. Окружность может быть представлена как замкнутая линия, образующая замкнутую кривую.

Радиус окружности — это расстояние от центра окружности до любой ее точки. Он является одним из основных элементов окружности и определяет ее размер. Любая линия, начинающаяся в центре и заканчивающаяся на окружности, будет иметь длину, равную радиусу.

Круг — это плоская геометрическая фигура, ограниченная окружностью. Круг является двумерным объектом, который имеет плоскую форму, в то время как окружность может представлять собой одномерную кривую. Круг также имеет радиус и центр, как и окружность, но в отличие от окружности, он имеет внутреннюю и внешнюю части.

Структура окружности

Окружность – это простая геометрическая фигура, состоящая из всех точек плоскости, которые находятся на одинаковом расстоянии от определенной точки, называемой центром окружности. Ключевыми элементами структуры окружности являются диаметр и радиус.

Диаметр – это отрезок, соединяющий любые две точки на окружности и проходящий через ее центр. Также диаметр можно определить, как удвоенное значение радиуса

Важно отметить, что диаметр является самой длинной линией, которую можно провести внутри окружности

Радиус – это отрезок, соединяющий центр окружности с любой точкой на ней. Радиус является половиной диаметра и определяет расстояние от центра до любой точки окружности. Радиус также является основным параметром для вычисления площади и длины окружности.

Центр окружности – это определенная точка, которая равноудалена от всех точек окружности. Центр является основным элементом, вокруг которого построена эта геометрическая фигура.

Окружность также включает в себя другие элементы, такие как хорда, дуга и связанные с ними теоретические и геометрические понятия. Эти компоненты являются частью полной структуры окружности и используются для решения различных задач в области геометрии и математики.

Структура круга

Круг — это геометрическая фигура, которая образуется на плоскости в результате движения точки с постоянным радиусом вокруг центра. Центр круга является центром симметрии этой фигуры, а радиус — расстоянием от центра до любой точки на окружности.

Окружность является частным случаем круга, при которой радиус равен половине диаметра. Диаметр — это любой отрезок, проходящий через центр и соединяющий две противоположные точки на окружности.

Круг также может быть представлен в виде таблицы, где в первом столбце указывается радиус от 1 до n, а во втором столбце — диаметр, получаемый удвоением радиуса. Такая таблица позволяет наглядно представить зависимость радиуса и диаметра в теории геометрии.

Структура круга также может быть представлена в виде списка, где основными элементами являются центр, радиус, диаметр и точка. Центр определяет положение круга на плоскости, а радиус и диаметр указывают его размеры. Точка — это элемент геометрии, которая определяет границу круга и принадлежит окружности.

Советы учителя для лучшего запоминания материала

1. Активное участие

Вовлечение учеников в процесс обучения – один из основных путей к успешному запоминанию материала. Поэтому обязательно задавайте вопросы своим ученикам, предлагайте им сами принимать решения, вырабатывать собственную точку зрения.

2. Систематическое повторение

Чтобы запомнить новый материал, нужно периодически его повторять. Постарайтесь включать в свои занятия систематические повторения. Например, ежедневный ритуал в начале каждой учебной недели – повторение основных тем прошлой недели.

3. Игры и конкурсы

Учителям стоит использовать игры и конкурсы в своей работе, особенно для учеников младшего возраста. Такой формат занятия позволяет ученикам легко и непринужденно усваивать новый материал. Это сильно упрощает работу преподавателя.

4. Помощь родителей

Своевременная помощь со стороны родителей – не менее важный фактор, влияющий на лучшее запоминание материала. Попросите родителей отводить время на повторение с детьми материала, который они изучали в школе.

5. Варьируйте формат преподавания

Разнообразьте формат проведения занятия. Это позволит ученикам лучше усваивать материал. Например, изучение темы через интерактивную доску, затем – через видеоуроки, а потом – на конференции.

Как найти сторону треугольника если известна его площадь

Для того чтобы найти сторону треугольника, если известна его площадь, необходимо использовать определенную формулу. В первую очередь, необходимо найти высоту треугольника, которая проходит через известную сторону.

Далее, можем использовать формулу S=1/2*ah, где S — площадь, а a и h — соответственно, длина известной стороны и высота. Решив эту формулу относительно стороны a, мы можем найти ее значение.

Есть также формула Герона, которая позволяет найти длину любой стороны треугольника, зная длины двух сторон и площадь. Однако, эта формула более сложная и необходима для более сложных вычислений.

Найденная сторона может быть правильной или неравнобедренной, в зависимости от данных задачи

Однако, необходимо обратить внимание, что для каждой задачи может существовать несколько способов решения и необходимо выбирать наиболее подходящий вариант

Дополнительные рекомендации

Ребёнку не всегда бывает просто уложить в голове формулы, «перевести» картинку, которую он видит, на язык символов. Лучше всего помогает многократное решение таких задач – успешные результаты хорошо закрепляются в памяти.

Заниматься удобнее дома, в спокойной обстановке, не переживая, что можно получить плохую оценку или неодобрение от учителя.

Чтобы домашние занятия были эффективными, зарегистрируйте ребёнка на платформе iSmart. Здесь собрано около тысячи примеров на эту тему. Занимаясь 15 минут в день, ваш школьник самостоятельно:

устранит пробелы в знаниях;

• доведёт до автоматизма вычислительные навыки;
• не будет бояться проверочных работ;
• повысит успеваемость на 1-2 балла.

Регистрируйте ребёнка на платформе iSmart и начинайте заниматься!

Свойства квадрата

1. Длины сторон квадрата равны.

AB=BC=CD=DA

2. Все углы квадрата прямые.

\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}

3. Противолежащие стороны квадрата параллельны друг другу.

AB \parallel CD, BC \parallel AD

4. Сумма всех углов квадрата равна 360 градусов.

\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ}

5. Величина угла между диагональю и стороной равна 45 градусов.

\angle BAC = \angle BCA = \angle CAD = \angle ACD = 45^{\circ}

Доказательство

Квадрат является ромбом \Rightarrow
AC
— биссектриса угла A
, и он равняется 45^{\circ}
. Тогда AC
делит \angle A
, и \angle C
на 2
угла по 45^{\circ}
.

6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.

AO = BO = CO = DO

\angle AOB = \angle BOC = \angle COD = \angle AOD = 90^{\circ}

AC = BD

Доказательство

Так как квадрат это прямоугольник \Rightarrow
диагонали равны; так как — ромб \Rightarrow
диагонали перпендикулярны. А так как — параллелограмм, \Rightarrow
диагонали разделены точкой пересечения пополам.

7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.

\triangle ABD = \triangle CBD = \triangle ABC = \triangle ACD

8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.

\triangle AOB = \triangle BOC = \triangle COD = \triangle AOD

9. Если сторона квадрата равна a, то, диагональ будет равна a \sqrt{2}
.

— (лат. quadratum, от quadrare сделать четырехугольным). 1) прямоугольный, равносторонний четырехугольник. 2) такое число, которое, будучи умножено само на себя, дает данное число. 3) единица для измерения плоскостей; напр.: квадратн. фут, дюйм и… … Словарь иностранных слов русского языка

В квадрате. Жарг. мол. Пренебр. О крайне тупом, безнадёжно глупом человеке. /i> Квадрат глупый, несообразительный чаловек. Никитина 1996, 82. Квадрат твою гипотенузу! Жарг. шк. Бран. Выражение досады, раздражения, негодования. ВМН 2003, 62.… … Большой словарь русских поговорок

КВАДРАТ, в биологии квадратная рама, используемая для разметки участка поверхности с целью изучения растений, находящихся на нем. Квадратом называют также и сам этот участок почвы. Как правило, такой квадрат равен 0,5 или 1 м2. Пользуясь этим… … Научно-технический энциклопедический словарь

КВАДРАТ, квадрата, муж. (лат. quadratus четырехугольный). 1. Равносторонний прямоугольник (мат.). 2. Форма такого прямоугольника у какого нибудь предмета (книжн.). Ярко освещенный квадрат окна. 3. Четырехугольный гартовый брусок мера для… … Толковый словарь Ушакова

Муж. равносторонний и прямоугольный четыреугольник; народ называет его круглым четыреугольником или клеткою. Разбить площадь на квадраты, на участки этого вида. | Квадрат числа, произведение его от умножения самого на себя. Узор квадратцами или… … Толковый словарь Даля

В полиграфии, 1) единица длины, применяемая для измерения шрифтов, формата набора. 1 квадрат = 48 пунктам (ок. 18,05 мм).2) Разновидность пробельного материала для заполнения крупных промежутков в строках … Большой Энциклопедический словарь

Параллелограмм, клетка, материал, прямоугольник, степень, квадратик Словарь русских синонимов. квадрат сущ., кол во синонимов: 9 гиперкуб (12) … Словарь синонимов

квадрат
— КВАДРАТ, а, м. Тюрьма; камера. квадрат топтать находиться в тюрьме, камере. Из уг … Словарь русского арго

квадрат
— (Quad) 1. Одна из основных единиц типометрической системы Дидо, равная 4 цицеро, или 48 пунктам. 1 квадрат равен 18,048 мм. 2. Пробельный материал, используемый при изготовлении наборных печатных форм способа высокой печати. Квадраты различают по … Шрифтовая терминология

«Квадрат»
— «Квадрат», клуб любителей джазовой музыки (джаз клуб). Создан в 1964 при ДК имени Ленсовета (с 1965 размещался в ДК имени С. М. Кирова, с 1986 во Дворце молодёжи). Объединяет музыкантов и любителей классического джаза. «Квадрат» продолжил… … Энциклопедический справочник «Санкт-Петербург»

— (от латинского quadratus четырехугольный), 1) равносторонний прямоугольник. 2) Вторая степень a2 числа a (название связано с тем, что именно так выражается площадь квадрата со стороной a) … Современная энциклопедия

Книги

• Квадрат. Из истории российского джаза , . В книге собраны избранные материалы по истории российского джаза, публиковавшиеся в 60-80-е годы прошлого века на страницах легендарного неофициального самиздатского машинописного журнала…
• Квадрат , Вилли Карлссон. Книгу видного деятеля Коммунистической партии Дании можно назвать подлинной летописью рабочего движения в стране в бурную эпоху с начала кризиса 30-X годов до оккупации Дании нацистами.…

Когда у них одинаковые длины диагоналей, сторон и равные углы.

Онлайн калькулятор площади вписанного в круг квадрата. Как узнать площадь вписанного в круг квадрата.

Вычислить площадь вписанного квадрата через:

Радиус круга R:

Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.

Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:

1. либо площадь круга, обозначаемая буквой S,
2. либо периметр круга, обозначаемый буквой P,
3. либо радиус круга, обозначаемый буквой R,
4. либо диаметр круга, обозначаемый буквой D.

Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой

Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,

мы можем узнать длину сторон квадрата используя теорему Пифагора

после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.

Выводы и рекомендации

Вывод 1: Площадь квадрата можно вычислить, зная длину одной из его сторон.

Вывод 2: Понимание понятия «площадь» и способности вычислять ее являются важными навыками для дальнейшего изучения математики.

Рекомендация 1: Родители и учителя могут использовать различные игры и задачки для развития понимания понятия «площадь» и навыков вычисления площади. Например, предлагать ребенку находить площадь различных фигур на полу или бумаге.

Рекомендация 2: Важно привлекать внимание детей к математике и ее приложениям в повседневной жизни, чтобы усовершенствовать их навыки и повысить интерес к этому предмету. Таблица 1: Некоторые способы привлечения детей к математике:СпособОписание

Таблица 1: Некоторые способы привлечения детей к математике:СпособОписание

Игры	Игры на построение фигур, игры на подсчет, игры на нахождение площади и т.д.
Практика	Помочь ребенку решать реальные задачи, связанные с математикой. Например, приготовить вместе с ребенком пиццу и поделить ее на несколько частей, чтобы ребенок мог понять, что такое дроби.
Визуальные материалы	Развивать понимание математики с помощью графиков, диаграмм, схем и картинок. Это помогает визуальным ученикам лучше понимать материал.

Следуя таким рекомендациям, дети могут более эффективно развивать свои математические навыки и увереннее себя чувствовать в учебном процессе.