Как найти объем куба через его ребро

🤔 Полезные советы

Несколько советов, которые могут помочь при вычислении объема куба:

1. Определите длину одной из сторон куба. Обычно все стороны куба одинаковые, поэтому вы можете выбрать любую.
2. Возведите длину стороны куба в квадрат. Это даст вам площадь одной грани куба.
3. Умножьте площадь одной грани куба на 6. Это даст вам общую площадь поверхности куба.
4. Определите длину любой из диагоналей куба. Вы можете использовать формулу теоремы Пифагора для нахождения длины диагонали, если известна длина стороны.
5. Возвести длину диагонали куба в куб. Это даст вам объем куба.
6. Если известна масса куба, можно использовать плотность материала для расчета его объема. Для этого нужно разделить массу на плотность.
7. Убедитесь, что вы используете одни и те же единицы измерения при расчете. Например, если длина стороны куба измеряется в сантиметрах, то и объем должен быть выражен в кубических сантиметрах.

Вопросы и ответы

Сейчас мы предлагаем вам посмотреть ответы на вопросы, которые часто задаются на данную тему.

Что такое объем куба и как его рассчитать?

Объем куба — это мера его вместимости, то есть объем пространства, которое он занимает. Он рассчитывается по формуле V = a³, где a — длина ребра куба.

Как найти длину ребра куба, если известен его объем?

Для этого нужно извлечь кубический корень из объема: a = V^(1/3). Это позволит определить длину ребра куба, зная его объем.

Что произойдет с объемом куба, если увеличить длину его ребра вдвое?

Объем куба увеличится в 8 раз. Это происходит потому, что объем куба пропорционален кубу его длины: V ~ a³. Если длина ребра увеличивается вдвое, то объем увеличивается в 222=8 раз.

Какие единицы измерения используются для объема куба?

Объем куба измеряется в кубических единицах длины, таких как кубические метры (м³), кубические сантиметры (см³), кубические дюймы (дюйм³) и т.д.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
• Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
• Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
• Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
• Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
• Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
• Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
• Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
• Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
• Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.

Как связан куб с другими фигурами и телами?

Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше. Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником. Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.

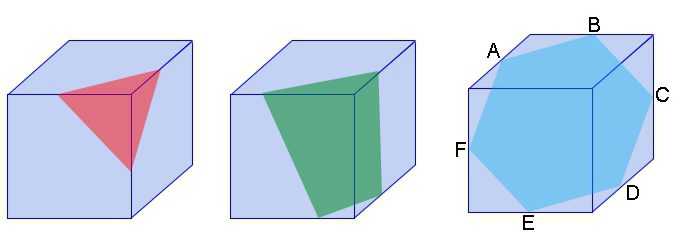
Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.

В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.

Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.

💥 Часто задаваемые вопросы

Что такое куб и как он выглядит?

Куб — это трехмерное геометрическое тело, имеющее шесть равных граней, каждая из которых является квадратом. Все грани куба пересекаются под прямым углом. Внешний вид куба можно представить себе как квадратный ящик.

Как найти объём куба?

Объём куба может быть рассчитан с использованием формулы V = a^3, где «V» обозначает объём, а «a» — длину стороны куба. Другими словами, чтобы найти объём куба, необходимо возвести длину одной из его сторон в куб.

Каковы единицы измерения объёма куба?

Объём куба обычно измеряется в кубических единицах длины, таких как кубические сантиметры (см³), кубические метры (м³) или кубические дюймы (in³), в зависимости от системы измерения, используемой в конкретном контексте.

Как объём куба связан с его длинной стороны?

Объём куба прямо пропорционален длине одной из его сторон. Если увеличить длину стороны вдвое, то объём куба увеличится в восемь раз. Например, куб со стороной в 2 см имеет объём 8 см³, а куб со стороной в 4 см — объём 64 см³.

Каковы приложения относительно объёма куба в реальной жизни?

Расчет объёма куба имеет множество практических применений. Например, при планировании хранения предметов в коробках или контейнерах, знание и расчет объема куба может помочь определить сколько объектов может вместиться или требуется конкретный объем. Также, при проектировании строений, расчет объёма помогает определить количество необходимых материалов, таких как кирпичи или бетон.

Какое значение имеет объём куба в математике?

Понимание объёма куба является важным понятием в математике и связано с понятием трехмерного пространства. Расчет объёма куба может быть расширен на другие объемные фигуры, такие как призмы и цилиндры, что применяется в многих областях, включая физику и инженерию.

Куб — это одна из самых простых и наиболее изучаемых объемных фигур в геометрии. Расчет объёма куба является одним из первых математических навыков, которые учат в школе. Этот простой пример объёма является фундаментальным для понимания более сложных понятий объема и трехмерного пространства в математике и других науках.

Немного теории о кубе

Этот многогранник относится сразу к прямым параллелепипедам и призмам. Он — частный случай того и другого. В основании куба лежит квадрат, и боковые ребра его равны стороне данного квадрата. Таким образом, все три измерения имеют одинаковые значения.

Все шесть граней куба представляют собой квадраты. Длина каждого из 12 ребер одинаковая.

В каждой из граней можно провести диагональ, длину которой легко найти по формуле Пифагора. Кроме того, сам куб имеет диагонали. Их всего четыре. Проводится диагональ куба так, чтобы начинаться из вершины нижнего основания. Конец этого отрезка оказывается в вершине верхнего основания, но так, чтобы не совпасть с диагональю квадрата.

Немного теории о кубе

Этот многогранник относится сразу к прямым параллелепипедам и призмам. Он — частный случай того и другого. В основании куба лежит квадрат, и боковые ребра его равны стороне данного квадрата. Таким образом, все три измерения имеют одинаковые значения.

Все шесть граней куба представляют собой квадраты. Длина каждого из 12 ребер одинаковая.

В каждой из граней можно провести диагональ, длину которой легко найти по формуле Пифагора. Кроме того, сам куб имеет диагонали. Их всего четыре. Проводится диагональ куба так, чтобы начинаться из вершины нижнего основания. Конец этого отрезка оказывается в вершине верхнего основания, но так, чтобы не совпасть с диагональю квадрата.

Формула площади поверхности куба

Площадь поверхности куба – это сумма площадей всех его граней:

S = S 1 + S 2 + S 3 + S 4 + S 5 + S 6 S=S_1+S_2+S_3+S_4+S_5+S_6

S = S 1 ​ + S 2 ​ + S 3 ​ + S 4 ​ + S 5 ​ + S 6 ​

Площадь каждой грани одинакова, то есть:

S 1 = S 2 = S 3 = S 4 = S 5 = S 6 = S ′ S_1=S_2=S_3=S_4=S_5=S_6=S’

S 1 ​ = S 2 ​ = S 3 ​ = S 4 ​ = S 5 ​ = S 6 ​ = S ′

S ′ — площадь любой грани куба.

Тогда полная площадь поверхности куба запишется как:

Рассмотрим на примерах разные способы вычисления полной площади поверхности куба.

Формула площади поверхности куба по длине ребра куба

Площадь каждой грани куба вычисляется как площадь квадрата, со стороной ребра куба по формуле:

a — сторона куба.

Отсюда, окончательно площадь поверхности куба:

a — длина стороны куба.

Найти площадь поверхности куба, если длина его ребра равна 12 (см.).

Решение

S = 6 ⋅ a 2 = 6 ⋅ 1 2 2 = 6 ⋅ 144 = 864 S=6cdot a^2=6cdot 12^2=6cdot 144=864

S = 6 ⋅ a 2 = 6 ⋅ 1 2 2 = 6 ⋅ 1 4 4 = 8 6 4 (см. кв.)

Ответ: 864 см. кв.

Формула площади поверхности куба по диагонали куба

По теореме Пифагора, диагональ куба связанна с длиной его ребра по формуле:

d 2 = a 2 + a 2 + a 2 d^2=a^2+a^2+a^2

d 2 = a 2 + a 2 + a 2

Подставим в формулу для площади:

S = 6 ⋅ a 2 = 6 ⋅ ( 3 ​ d ​ ) 2 = 2 ⋅ d 2

d — диагональ куба.

Одна четвертая часть диагонали куба равна 2 (см.). Найти площадь поверхности куба.

Решение

S = 2 ⋅ d 2 = 2 ⋅ 8 2 = 2 ⋅ 64 = 128 S=2cdot d^2=2cdot 8^2=2cdot 64=128

S = 2 ⋅ d 2 = 2 ⋅ 8 2 = 2 ⋅ 6 4 = 1 2 8 (см. кв.)

Ответ: 128 см. кв.

Теория

Площадь поверхности куба через ребро

Чему равна площадь поверхности куба S_пов, если длина его ребра a:

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если он имеет длину рёбер a = 5 см :

Площадь поверхности куба через диагональ

Чему равна площадь поверхности куба S_пов, если длина диагонали этого куба d:

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если длина диагонали у него d = 3 м:

S_пов = 2 ⋅ 3² = 2 ⋅ 9 = 18 м² = 180 000 см²

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если его объём V_куба = 8 см³:

S_пов = 6 ⋅ 3 √ 8² = 6 ⋅ 3 √ 64 = 6 ⋅ 4 = 24 см²

Источник

Как бы вы записали формулу площади поверхности и объема куба через длину его диагонали?

Геометрия Площадь поверхности Куб Диагональ

Рэйчел М.

Мне дана переменная d, которая представляет собой диагональ куба. Других чисел или переменных не указано. Я должен написать формулу, чтобы найти площадь поверхности куба

Подписаться

Подробнее

Отчет

3 ответа от опытных наставников

КРУЗ С.

Репетитор

4.9
(80)

Опытный заведующий кафедрой математики, стаж преподавания более 7 лет

См. таких репетиторов

Посмотреть таких репетиторов

Куб состоит из конгруэнтных сторон, и каждая грань куба является квадратом.

Площадь квадрата равна 2 , а поскольку у куба шесть сторон, площадь поверхности куба равна 6 (a 2 ) или 6a 2

Диагональ на грани куба будет создайте два треугольника 45-45-90, где катет = x и гипотенуза = x√2.

Диагональ d также является гипотенузой

d=x√2

Решение для x даст длину каждой стороны .

d/√2=x√2/√2

x = d/√2

x= (d)(√2) / (√2)(√2) = d√2/2

вычислить площадь одной стороны, определить x 2

(d√2 / 2) 2 = 2d 2 / 4 = (1/2)d 2

Площадь 6 стороны равна ( 6)(1/2)d 2 = 3d 2 , что является площадью поверхности.

SA = 3d 2

Объем равен 3 или x 3 = (d)(√2) / 2 * (d)(√2) / 2 * . (г)(√2) / 2 . = д 3 * . 2√2/8 =

V = d 3 √ 2/4

Объем равен d, умноженному на квадратный корень из 2, деленному на 4

Голосовать за 0 Понизить

Подробнее

Отчет

Исаак С.
ответил 04/29/19

Репетитор

4.9
(748)

Репетитор по физике, химии, математике и компьютерному программированию

Об этом репетиторе ›

Об этом репетиторе ›

Отношение диагонали к одной из сторон равно sqrt 3.

поэтому, чтобы найти объем, возьмите длину диагонали и разделите ее на sqrt 3, чтобы найти длину одной стороны.

Как находить сторону точного куба по объёму

Для того чтобы найти сторону точного куба по заданному объёму, необходимо выполнить следующие шаги:

1. Определить значение объёма куба.
2. Найти кубический корень из значения объёма куба. Это и будет стороной точного куба.

Например, если известен объём точного куба и он равен 125 м3, то необходимо найти кубический корень из 125. Найденное значение будет равно 5, так как 5*5*5=125. Следовательно, сторона точного куба равна 5 м.

Также можно воспользоваться формулой для вычисления объёма куба, если известна его сторона:

V = a3

где V — объём куба, a — сторона точного куба.

Таким образом, если известна сторона точного куба, можно легко вычислить его объём, а если известен объём, то можно найти сторону точного куба.

Что такое многогранник

Простейшей геометрической фигурой является прямая. Ею называется линия, которая имеет свое продолжение вправо и влево. Если эту прямую ограничить с двух сторон, получится отрезок. Для определения его величины достаточно одного измерения — длины. Прямая, ограниченная с одной стороны, имеет свое название. Это отрезок.

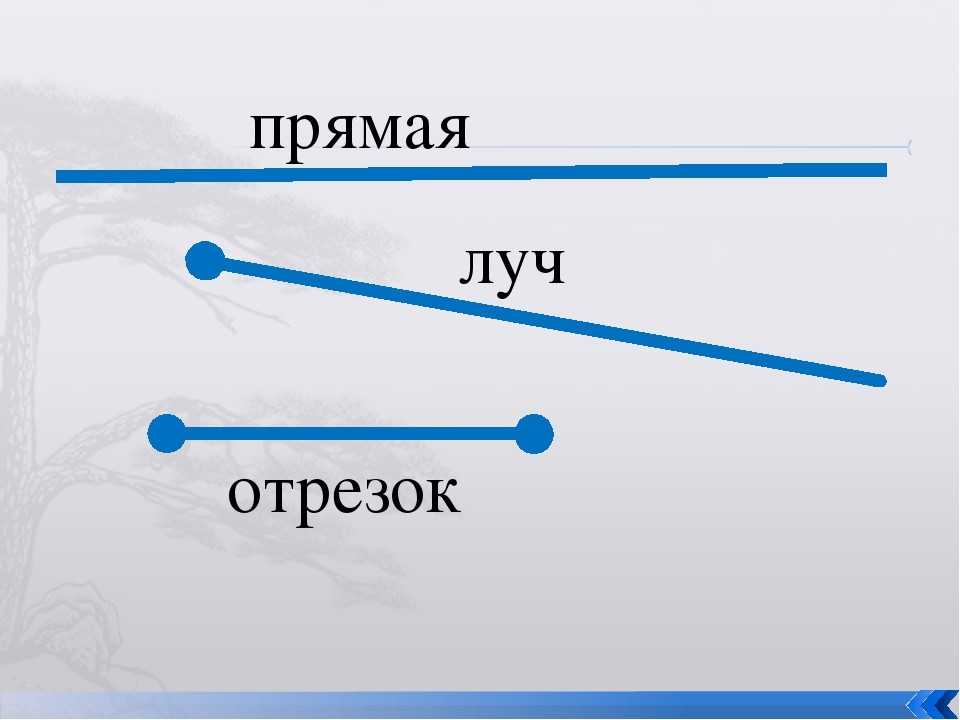
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

В пределах одной плоскости, кроме прямой, которую можно измерить одной величиной, существуют геометрические фигуры, измеряемые длиной и шириной. Это многоугольники.

Они могут иметь различное количество углов и характеризуются таким понятием как площадь.

Фигура, которая располагается в нескольких плоскостях, характеризуется пространственными величинами или трехмерным измерением. К таким фигурам относят многогранники.

Многогранник — геометрическая фигура, имеющая замкнутую поверхность, которую можно представить совокупностью многоугольников.

Для полной характеристики многогранника необходимо назвать следующие свойства:

• стороны обязательно являются смежными с одной соседней стороной;
• при необходимости можно, начав движение от одного из многоугольников, достигнуть любого другого, используя принцип смежности;
• площадь поверхности многогранника равна сумме площадей многоугольников, ограничивающих фигуру.

При этом каждый многоугольник — это грань, сторона — ребро, а вершина — вершина многогранника.

 Многогранник, как геометрическое тело, может быть представлен несколькими параллелепипедами, которые соединены по одной из граней. В таком случае их площадь будет равна сумме площадей свободных сторон и одной стороны, по которой произошло соединение. Объем такого тела будет равен сумме объемов каждого из параллелепипедов.

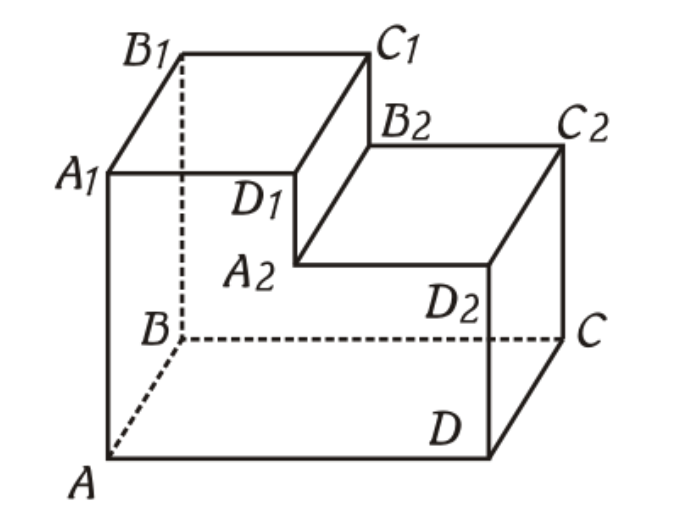
Многогранники бывают:

• выпуклыми (каждая из точек фигуры находится по одну сторону от плоскости);
• невыпуклыми (не все точки располагаются по одну сторону плоскости).

Проще говоря, выпуклый многогранник можно поставить на одну из сторон, и он будет на ней «уверенно стоять». С невыпуклым такого действия совершить нельзя.

Примечание 1

Важно помнить, что многогранник — это не только поверхность, состоящая из нескольких многоугольников. Это еще и тот внутренний объем, который ограничивает данная поверхность

Именно поэтому в стереометрии отделяют два понятия: площадь многогранника и его объем.

Куб и его свойства

В настоящее время видеоуроки нельзя просматривать или распространять среди студентов.

Чтобы получить доступ к этому и другим видеоурокам из комплекта, добавьте его в свой личный кабинет через покупку в каталоге.

Конспект урока “Куб и его свойства”

На предыдущем уроке мы узнали о таких многогранниках, как Прямоугольный параллелограмм..

Решив задачу со спичками, мы получили геометрическую фигуру под названием пирамида.

Перед этим вас познакомят и с другими многогранниками. Теперь вернемся к параллелепипеду.

Таким образом, поверхность параллелепипеда состоит из шести прямоугольников. Эти прямоугольники называются лица параллелограмм.

Обратите внимание, что два соседних прямоугольника имеют общую сторону, которую мы называем край прямоугольного параллелепипеда. Концы ребер называются вершины прямоугольного параллелепипеда

Таким образом, прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин.

Обратите внимание, что хотя многогранники различны, поверхность каждого многогранника состоит из правильных многоугольников, которые мы называем гранями многогранника. Два соседних правильных многоугольника имеют общую сторону – ребро многогранника

Концы ребер являются вершинами многогранника.

Этот многогранник называется октаэдр. Он имеет 8 ребер, которые являются треугольниками, 12 граней и 6 вершин.

Куб – это прямоугольный параллелограмм, у которого все ребра равны

Обратите внимание, что мы рисуем пунктирные линии для граней куба, которые не видны. Это дает полное представление о фигуре и ее положении относительно нас

Все грани куба – равные квадраты. Поверхность куба состоит из 6 равных квадратов. Убедитесь, что грани напротив друг друга не имеют общих ребер. Эти называются напротив.

лицакоторые имеют общее ребро, называются прилегающая территория.

Теперь давайте проведем небольшой эксперимент. Возьмите коробку, имеющую форму куба. Мы раскрываем его, затем разрезаем вдоль четырех вертикальных ребер, а затем разворачиваем.

Форма, которую мы имеем, называется Разворачивание куба.. Он состоит из 6 равных квадратов.

Фигуры ниже также являются взрывающимися кубами.

Используя каждую из разверток, вы можете сделать модель куба. Для этого выполните следующие действия. Нарисуйте чертеж куба на листе бумаги. Выключите его. Согните его вдоль секций, соответствующих граням куба, и склейте.

Теперь нарисуйте отрезок, который соединит самые удаленные вершины куба. Мы называем эти вершины противоположными вершинами.

Отрезок, соединяющий две противоположные вершины куба, называется диагональю куба.

Теперь давайте решим несколько задач.

Проблема первая. Определите, какой кубик мы получим из данной сборки.

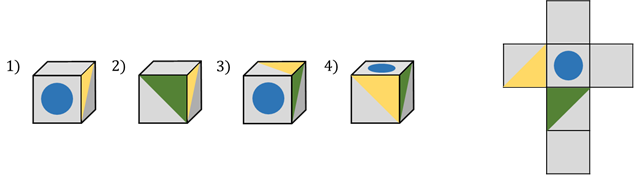
Давайте представим, какие грани куба являются смежными, то есть имеют общее ребро, и сравним с предложенными вариантами, чтобы найти правильный. Для этого нам удобнее всего сравнивать лица, которые отличаются в зависимости от рисунка на них

Обратите внимание на лицо с желтым треугольником и лицо с зеленым треугольником. Конечно, при сборке куба эти грани будут примыкать друг к другу

Следовательно, при различных поворотах куба возможны четыре варианта взаимного расположения этих граней.

Давайте теперь сравним четыре предложенных варианта. Сразу видно, что первый вариант неверен. Второй вариант неверен. Конечно, третий вариант также неверен. Однако вариант четыре является правильным, поскольку грани, на которых изображены треугольники, правильные. В этом случае на верхней поверхности должен быть синий круг. Это правильно.

Таким образом, мы выяснили, что из данного расширения получится куб с числом 4.

Вы можете решить эту проблему другим способом. Вы можете нарисовать этот контур на бумаге. Удобнее это делать на листе бумаги с квадратами, тогда вам не придется пользоваться линейкой, чтобы соблюсти размеры куба. Вы просто посчитаете количество квадратов, которое вам необходимо.

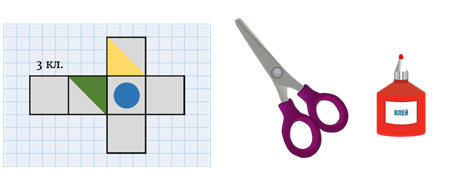
Затем вам нужно будет раскрасить и вырезать нарисованный контур. Затем скатайте его в кубик и склейте. После этого вы можете легко сравнить полученный куб с любым из предложенных вариантов и выбрать подходящий.

Вторая задача. Модель куба с длиной ребра 4 см была окрашена серой краской и разрезана вдоль ребра на кубики с длиной ребра 1 см. Сколько кубиков получилось: а) окрашенных по трем граням; б) окрашенных по двум граням?

Третья проблема. На рисунке показан скелет куба. Затем нарисуйте видимые грани так, чтобы на куб можно было смотреть: a) сверху слева; b) снизу справа.

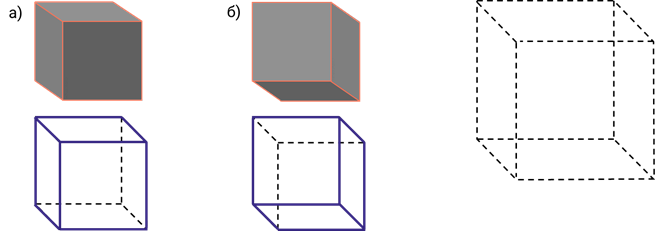
Проблема четвертая .. Фигура, показанная на рисунке, состоит из пяти кубиков. Какой формы фигура, если смотреть на нее: a) спереди; b) слева; c) сверху?

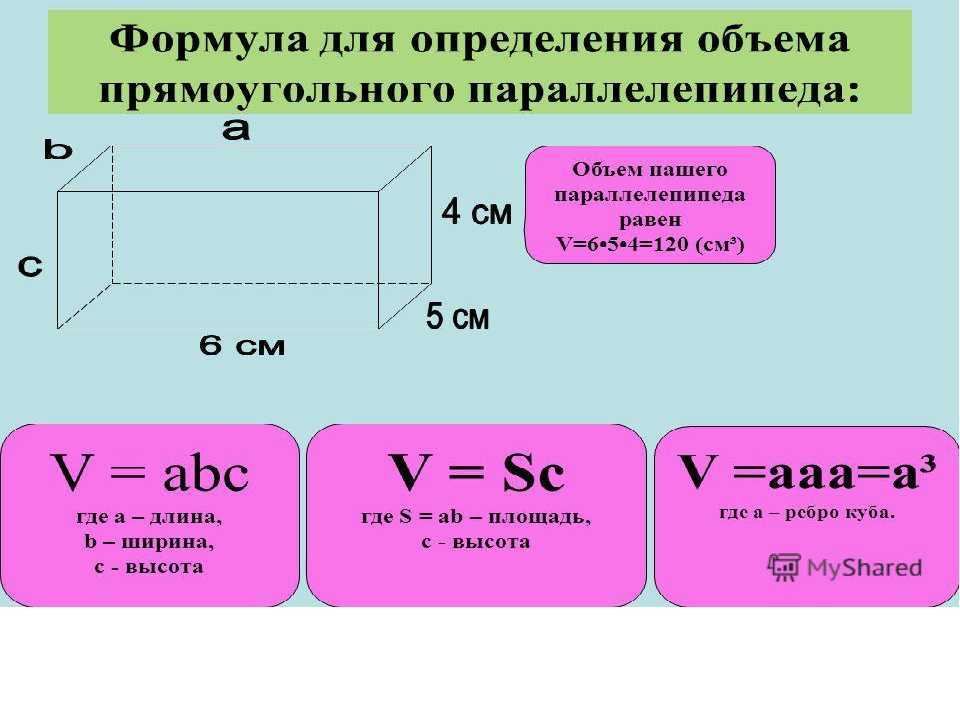
Формулы для куба

Если длина ребра куба (a) известна из условий задачи, формулу расчета длины диагонали грани (l) можно вывести из теоремы Пифагора. В кубе любые два смежных ребра образуют прямой угол, поэтому треугольник, составленный из них грани, является прямоугольным. Ребра в этом случае — катеты, а рассчитать вам нужно длину гипотенузы. Согласно упомянутой выше теореме она равна квадратному корню из суммы квадратов длин , а так как в данном случае они одинаковые размеры, просто умножьте длину ребра на квадратный корень из двойки: l = √(a²+a²) = √(2*a²) = a*√2.

Люди с каждым днем люди развиваются, но какие бы достижения ни были совершены, человечество не в бороться с различными климатическими капризами или же с природными катастрофами. Природа всегда готовит какие-то сюрпризы. Вот снег в Африке, последствием чего стало огромное количество жертв. Люди просто замерзали, ведь их оказался совершенно не приспособлен к таким условиям.

Из всего этого следует вывод: конечно же, человечество находится на грани своего развития, но и благодаря тому, что он , увеличивается и риск оказаться на грани вымирания. Поэтому не следует думать, что с проблемами нужно бороться по мере их поступления, лучше думать заранее, так, чтобы не допустить в будущем глобальной катастрофы.

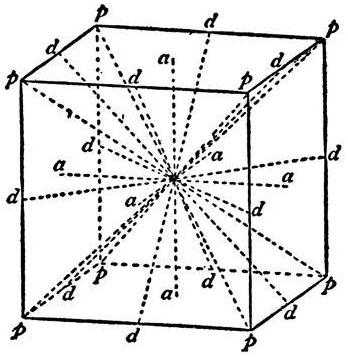
Или гексаэдр) представляет собой объемную фигуру, каждая грань — это квадрат, у которого, как нам известно, все стороны равны. Диагональю куба является отрезок, который проходит через центр фигуры и соединяет симметричные вершины. В правильном гексаэдре имеется 4 диагонали, и все они будут равны

Очень важно не путать диагональ самой фигуры с диагональю ее грани или квадрата, который лежит на его основании. Диагональ грани куба проходит через центр грани и соединяет противоположные вершины квадрата

Формула, по которой можно найти диагональ куба

Диагональ правильного многогранника можно найти по очень простой формуле, которую необходимо запомнить. D=a√3, где D обозначаем диагональ куба, а — это ребро. Приведем пример задачи, где необходимо найти диагональ, если известно, что длина его ребра равна 2 см. Здесь все просто D = 2√3, даже считать ничего не надо. Во втором примере, пусть ребро куба будет равно √3 см, то тогда получаем D = √3√3=√9=3. Ответ: D равен 3 см.

Формула, по которой можно найти диагональ грани куба

наль грани можно также найти по формуле. Диагоналей, которые лежат на гранях, всего 12 штук, и они все равны между собой. Теперь запоминаем d=a√2, где d — это диагональ квадрата, а — это также ребро куба или сторона квадрата. Понять откуда взялась эта формула, очень просто. Ведь две стороны квадрата и диагональ образуют В этом трио диагональ играет роль гипотенузы, а стороны квадрата — это катеты, которые имеют одинаковую длину. Вспомним теорему Пифагора, и все тут же встанет на свои места. Теперь задача: ребро гексаэдра равняется √8 см, необходимо найти диагональ его грани. Вставляем в формулу, и у нас получается d=√8 √2=√16=4. Ответ: диагональ грани куба равняется 4 см.

Если известна диагональ грани куба

По условию задачи, нам дана только диагональ грани правильного многогранника, которая равна, предположим, √2 см, а нам необходимо найти диагональ куба. Формула решения этой задачи немного сложнее предыдущей. Если нам известно d, то мы можем найти ребро куба, исходя из нашей второй формулы d=a√2. Получаем а= d/√2= √2/√2=1см (это наше ребро). А если известна эта величина, то найти диагональ куба не составит труда: D = 1√3= √3. Вот так мы решили нашу задачку.

Если известна площадь поверхности

Следующий алгоритм решения строится на нахождении диагонали по Предположим, что она равна 72 см 2 . Для начала найдем площадь одной грани, а всего их 6. Значит, 72 необходимо поделить на 6, получаем 12 см 2 . Это площадь одной грани. Чтобы найти ребро правильного многогранника, необходимо вспомнить формулу S=a 2 , значит a=√S. Подставляем и получаем a=√12 (ребро куба). А если мы знаем это значение, то и диагональ найти не сложно D= a√3= √12 √3 = √36 = 6. Ответ: диагональ куба равна 6 см 2 .

Если известна длина ребер куба

Бывают такие случаи, когда в задаче дана только длина всех ребер куба. Тогда необходимо это значение разделить на 12. Именно столько сторон в правильном многограннике. Например, если сумма всех ребер равна 40, то одна сторона будет равна 40/12=3,333. Вставляем в нашу первую формулу и получаем ответ!

Если шесть граней квадратной формы ограничивают некоторый объем пространства, то геометрическую форму этого пространства можно назвать кубической или гексаэдрической. Все двенадцать ребер такой пространственной фигуры имеют одинаковую длину, что значительно упрощает вычисления параметров многогранника. Длина диагонали куба — не исключение, ее можно найти многими способами.

Свойства

Диагональ куба – это отрезок, который находится во внутреннем пространстве куба, благодаря тому, что его вершины находятся на противоположных сторонах. Поэтому для того чтобы представить диагональ куба в алгебраическом виде, необходимо заключить ее в фигуру, соединив данную диагональ и боковое ребро, исходящее из любой вершины диагонали через диагональ основания. Получив, таким образом, прямоугольный треугольник, можно составить отношение сторон по теореме Пифагора и вывести формулу для диагонали куба. Ребро куба будет равно отношению диагонали к корню из трех. a^2+d^2=D^2 D^2=a^2+2a^2 D^2=3a^2 D=a√3 a=D/√3

Площадь стороны куба равна ребру куба, возведенному во вторую степень, площадь боковой поверхности представляет собой четыре таких площади стороны, а площадь полной поверхности состоит из 6 граней. Площади куба, выраженные через диагональ, принимают следующий вид: S=a^2=D^2/3 S_(б.п.)=4a^2=(4D^2)/3 S_(п.п.)=6a^2=2D^2

Объем куба равен его ребру в третьей степени, а объем куба, зная диагональ куба, будет равен диагонали, возведенной в третью степень, и деленной на три корня из трех. V=a^3=D^3/(3√3)

Чтобы вычислить периметр куба, нужно ребро куба умножить на двенадцать. Если выразить периметр грани через диагональ куба, то он примет вид отношения диагонали, умноженной на четыре корня из трех. P=12a=4√3 D

Чтобы найти диагональ стороны куба, то есть диагональ, лежащую на боковой грани, можно воспользоваться формулой диагонали квадрата, которая выглядит как произведение стороны квадрата/ребра куба на корень из двух. d=a√2=(D√2)/√3

Радиус вписанной в куб сферы равен половине ребра куба, то есть диагонали куба, деленной на два корня из трех, а радиус описанной вокруг куба сферы равен половине самой диагонали куба. (рис. 2.2, рис.2.3) r=a/2=D/(2√3) R=D/2

Примеры заданий из ЕГЭ

Они используются в части В, то есть там, где нужно выполнить развернутое решение задания. Просто выбрать ответ здесь не удастся. Поэтому придется знать формулы и уметь их применять в различных ситуациях.

Первая группа заданий.
В ней известна длина диагонали куба. Требуется вычислить его объем или узнать площадь поверхности.

К примеру, известная величина может быть равна единице. Тогда, чтобы узнать объем и площадь, нужно воспользоваться формулами № 1 и 3. Но в них идет речь о ребре, а дана диагональ. Потребуется записать еще одну формулу.

Если посмотреть на чертеж куба и проведенную в нем диагональ, то можно увидеть, что образуется прямоугольный треугольник. Один его катет совпадает с ребром, второй — с диагональю грани, а гипотенузой оказывается диагональ куба.

Тогда можно записать теорему Пифагора: квадрат гипотенузы (d 2) равен квадрату перового катета (а 2), сложенному с квадратом второго (а√2) 2 . После выполнения преобразований получается, что ребро куба а так связано с диагональю, что равно d, деленному на корень квадратный из 3.

Теперь можно начала узнать ребро, а потом подсчитать объем и площадь. В конкретной задаче а=1/√3=(√3)/3. Тогда объем получается равным (√3)/9. Площадь же — два.

Вторая группа заданий.
Обратная предыдущей, когда известны площадь или объем, а требуется вычислить значение диагонали куба.

Примером может служить задача, в которой известна площадь поверхности, и она равна 8. Необходимо будет воспользоваться формулой №3 и той зависимостью, которая выведена в предыдущей задаче.

Сначала потребуется узнать длину ребра. Она равна квадратному корню из частного S на 6. После подстановки известной величины а=√(8/6)=√(4/3). Теперь осталось вычислить диагональ куба, возведя это число в квадрат и умножив его на 3. Получится 2.

Третья группа заданий
содержит данные о диагонали грани куба. В них необходимо узнавать объем или площадь тела. Возможен также вариант, в котором потребуется вычислить диагональ самого куба. В таких задачах рассуждения идут тем же путем, который рассмотрен в предыдущих случаях.

Куб — свойства, виды и формулы » Kupuk.

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

• многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

• прямая призма, все грани которой есть квадраты;

•  прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю. 

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника. 

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Такая сфера имеет центр, совпадающий с центром куба. 

Радиус равен половине ребра:

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ.

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач.

Прочие свойства:

• у куба все грани равны, являются квадратами;

• у куба все рёбра равны;

• один центр и несколько осей симметрии.

Итог

Представлен простейший калькулятор онлайн для заданных величин рассматриваемого здесь геометрического тела. Объем его – вне зависимости от единицы, дозволяющей сделать его измерения.

Вычисления производят в:

• метрах;
• сантиметрах;
• миллиметрах.

Итог выводят в сантиметрах, метрах кубических.

Ожидая получение расчета, пользователь также может указать желаемую точность выводимого результата, то есть число знаков, идущих за запятой и до которого нужно округлить уже подсчитанный показатель.

Найти заданную величину абсолютно несложно посредством простого помощника, которым является представляемый калькулятор онлайн. Необходимое значение он выдает мгновенно, в расчетах никогда нет ошибок. Поэтому пользователь может быть стопроцентно уверен в выданных калькуляцией результатах.

Рассчитывающий объем куба калькулятор действует следующим образом: при каждом указанном значении, все прочие будут найдены автоматически. Следовательно, при вводе в ячейку (поле калькулятора онлайн), например, показателя длины грани нашей фигуры либо ее диагонали, радиуса вписываемого шара или площади, нажимают «Расчет», и все необходимые данные об иных величинах будут тотчас получены. Для удобства итоги выводятся вместе с расчетными формулами.