Стандартный метод
В зависимости от сложности вычислений, применяют одну из формул, чтобы высчитать периметр. Учащиеся начальной школы знакомятся с понятием, сталкиваясь с практическими задачами.
Задача
Найти длину забора участка прямоугольной формы, который надо построить Сидору Карловичу, если общая граница с участком Ивана Петровича составляет 3 метра, а с плантацией Марии Ивановны – 5 метров.

Решение
Чтобы решить задачу и помочь незадачливому Сидору Карловичу, ученику приходится использовать формулу периметра прямоугольника. Учитывая, что a = 3, b = 5, дети легко находят, что длина забора равна
P = 2 (a + b) = 2 * (3 + 5) = 2 * 8 = 16 (метров)
Важные требования, предъявляемые к ученикам на данном этапе изучения материала, заключаются в правильном соизмерении длины и ширины, а также в умении начертить фигуру.
Работа выполняется только при одинаковых единицах измерения, все чертежи делаются строго с использованием инструментов!
Часто длина заданного отрезка измеряется непосредственно.
Поиск периметра по заданной площади
Для найти периметр прямоугольника, зная только его площадь, необходимо использовать определенную формулу. В прямоугольнике можно выделить две стороны – длинную и короткую. Длинная сторона обозначается как а, а короткая как b. Известно, что площадь прямоугольника равна произведению длинной и короткой сторон, т.е. S = a * b.
Чтобы найти периметр, нужно знать не только площадь, но и длину одной из сторон прямоугольника. Допустим, что известна длинная сторона а, и площадь S. Тогда можно найти короткую сторону, разделив площадь на длину длинной стороны: b = S / a.
Зная обе стороны, можно найти периметр прямоугольника. Сумма всех сторон равна 2 * (a + b). Подставляя найденные значения, получаем формулу для нахождения периметра: P = 2 * (a + S / a).
Таким образом, по известной площади прямоугольника и длине одной из его сторон можно найти периметр, используя соответствующую формулу. Данная формула позволяет расчитать периметр в любом случае, когда известна площадь и хотя бы одна сторона, что является полезным инструментом при решении задач, связанных с прямоугольниками.
Варианты перестановки сторон прямоугольника
Когда мы знаем только площадь прямоугольника, мы можем сделать несколько предположений относительно его сторон и найти все возможные варианты перестановки. Один из способов — это итеративное перебор каждой возможной комбинации сторон.
- Пусть a будет длиной одной стороны, а b — длиной другой стороны. Тогда площадь S прямоугольника можно выразить формулой S = a * b.
- Если мы знаем площадь, то мы можем найти периметр прямоугольника, используя формулу P = 2 * (a + b).
- Для каждого значения a в интервале от 1 до S, мы можем вычислить соответствующее значение b, разделив S на a.
- После того, как мы найдем a и b, мы можем вычислить периметр для данной комбинации сторон.
Таким образом, мы можем найти все возможные варианты перестановки сторон прямоугольника, зная только его площадь. Этот подход особенно полезен, когда у нас есть ограничения по площади прямоугольника, и нам необходимо найти все возможные комбинации сторон.
Расчет периметра по заданной площади
Когда нам известна площадь прямоугольника, мы можем найти его периметр, используя определенные формулы и свойства этой геометрической фигуры. Для этого нам необходимо знать не только площадь прямоугольника, но и некоторые его дополнительные характеристики.
Чтобы найти периметр прямоугольника, зная его площадь, нужно обратить внимание на то, что периметр — это сумма длин всех его сторон. Очевидно, что на периметр прямоугольника влияют как его длина, так и ширина
Однако, зная только площадь прямоугольника, нам не хватит информации о его сторонах. Для полного расчета периметра нам также потребуется знать соотношение между длиной и шириной прямоугольника. Это соотношение выражается через формулу площади прямоугольника, которая равна произведению его длины на ширину.
Поэтому, чтобы найти периметр прямоугольника по заданной площади, нам потребуется провести ряд математических операций: сначала найти длину и ширину прямоугольника, используя формулу площади, а затем просуммировать все его стороны.
Таким образом, расчет периметра по заданной площади требует дополнительных данных о пропорции прямоугольника. Известная только площадь не дает нам достаточной информации для расчета периметра
Поэтому перед началом задачи стоит обратить внимание на наличие всех необходимых данных
Решение задачи: как найти длину и ширину прямоугольника зная периметр и площадь
Вычисление длины и ширины прямоугольника
Если известен периметр и площадь прямоугольника, то можно вычислить его длину и ширину. Для этого нужно знать несколько формул:
- Периметр прямоугольника равен удвоенной сумме его сторон: perimeter = 2*(a + b).
- Площадь прямоугольника равна произведению его сторон: area = a*b.
Из этих формул можно выразить длину и ширину прямоугольника:
- Длина прямоугольника равна a = (perimeter ± √(perimeter² — 16*area)) / 4
- Ширина прямоугольника равна b = area / a
Знак ± в формуле для длины означает, что нужно использовать оба значения (с плюсом и с минусом), чтобы получить два возможных решения. Из них выбирается то, которое соответствует реальной ситуации.
Примеры решения задачи
Рассмотрим несколько примеров для понимания, как применять эти формулы:
-
Пример 1: периметр прямоугольника равен 18, а площадь равна 20. Найдем длину и ширину прямоугольника.
Решение:
- Используем формулу для периметра: perimeter = 2*(a + b), подставляем известное значение: 18 = 2*(a + b).
- Используем формулу для площади: area = a*b, подставляем известное значение: 20 = a*b.
- Выразим длину из первой формулы: a = (perimeter ± √(perimeter² — 16*area)) / 4 = (18 ± √(18² — 16*20)) / 4 = 5 or 2.5.
- Используем формулу для ширины: b = area / a = 20 / 5 = 4 or 20 / 2.5 = 8.
Ответ: длина прямоугольника может быть равна 5 или 2.5, а ширина соответственно равна 4 или 8.
-
Пример 2: периметр прямоугольника равен 26, а площадь равна 84. Найдем длину и ширину прямоугольника.
Решение:
- Используем формулу для периметра: 26 = 2*(a + b).
- Используем формулу для площади: 84 = a*b.
- Выразим длину из первой формулы: a = (26 ± √(26² — 16*84)) / 4 = 10 or 4.
- Используем формулу для ширины: b = area / a = 84 / 10 = 8.4 or 84 / 4 = 21.
Ответ: длина прямоугольника может быть равна 10 или 4, а ширина соответственно равна 8.4 или 21.
Важность понимания периметра прямоугольника в повседневной жизни
Периметр прямоугольника является одним из основных понятий в геометрии, и его понимание имеет большое значение в повседневной жизни. Практически на каждом шагу мы сталкиваемся с прямоугольниками: наши дома, офисы, квартиры, мебель, электроника — все это часто имеет прямоугольную форму.
Знание периметра прямоугольника позволяет нам решать различные задачи и принимать важные решения. Например, при покупке мебели мы можем оценить, как она будет вписываться в наше помещение, исходя из ее размеров и периметра. Знание периметра также помогает в выборе материалов для строительства или ремонта, так как мы можем оценить, сколько материала нам понадобится для облицовки стен или пола.
Еще одним примером важности понимания периметра является планирование использования земельных участков. Зная периметр прямоугольника, мы можем определить его площадь и оценить, сколько места будет занимать нужное нам строение или посадки
Это позволяет оптимизировать использование зеленых насаждений, дизайна сада или планирование участка под строительство дома или гаража.
Понимание периметра прямоугольника необходимо также в повседневных задачах. Например, при обивке мебели или пошиве штор нам нужно знать периметр, чтобы правильно подобрать ткань или материал. Также, зная периметр прямоугольной огорожи или забора, мы можем определить количество материала для его строительства или расчет стоимости.
В заключение, понимание периметра прямоугольника играет важную роль в повседневной жизни, помогая решать различные задачи и принимать взвешенные решения. Знание периметра позволяет нам эффективно использовать ресурсы, оптимизировать использование пространства и достигать наилучших результатов во многих сферах нашей жизни.
Как найти периметр прямоугольника – онлайн-ресурсы
Несмотря на то, что вышеупомянутые действия легки для понимания и освоения, вам может пригодиться несколько онлайн-калькуляторов, которые помогут вам вычислить периметры (площадь, объем) разных фигур. Просто вбейте необходимые значения и мини-программа рассчитает периметр нужной вам фигуры. Ниже приведен небольшой список.
Прежде, чем решать задачи на нахождение периметра и площади геометрических фигур, напомню, что….
I уровень
1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.
2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.
5.Длина прямоугольника 8 дм, ширина 5 дм. Найди его площадь.
6.Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.
7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.
8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.
9.Длина стороны квадрата 6 см. Узнай площадь.
10.Вычисли периметр квадрата со стороной 4 см.
11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.
12.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.
14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.
15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше. Вычисли его периметр.
16.Сторона квадрата равна 3 см. Чему равен периметр?
17.Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?
18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?
19.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
20.Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.
21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?
II уровень
1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.
2.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше. Найди Р и S.
4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.
5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.
6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.
7.Периметр квадрата равен 32 см. Чему равна его сторона?
8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.
9.Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.
10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника.
11.Периметр
прямоугольника равен 54 м
.
Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.
12.
Найдите площадь квадрата, периметр которого равен 360 мм.
13.
Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?
14. Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами 2 см и 6 см.
15. Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?
16. Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?
17. У какой фигуры площадь больше и на сколько: у квадрата со стороной 4см или у прямоугольника со сторонами 2 см и 6 см?
18. Периметр прямоугольника равен 54 м. Найди площадь этого прямоугольника, если одна его сторона равна 18 м.
19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.
20. Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.
Составила
К
ислова Людмила Борисовна
Как найти периметр прямоугольника
Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.
Периметр прямоугольника — это сумма длин всех его ребер.
Основные свойства прямоугольника:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
- противоположные стороны фигуры равны и параллельны друг другу;
- сумма всех углов равна 360 градусов;
- диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
- диагонали делят фигуру на два одинаковых прямоугольных треугольника;
- по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
- стороны рассматриваемого четырехугольника также являются его высотами;
- точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
- диагональ этого четырехугольника — это диаметр описанной окружности;
- вокруг него всегда можно описать окружность.
Варианты нахождения периметра прямоугольника
По сторонам
Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:
где \(a\) и \(b\) — это две соседние стороны фигуры.
По любой стороне и площади
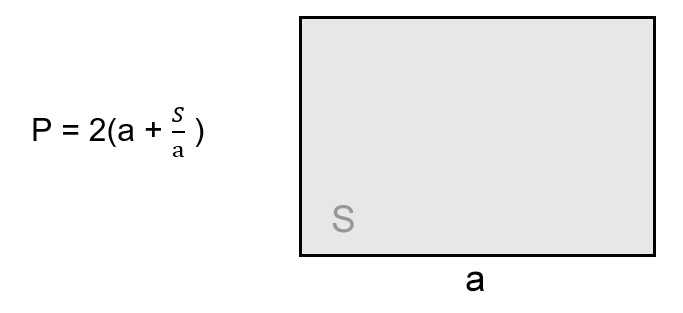
Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.
Так как площадь прямоугольника — это произведение двух его смежных сторон \((S=a\times b)\) , чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: \(b=\frac Sa\) .
Получается, что формула для расчета \(P\) рассматриваемой фигуры будет выглядеть следующим образом:
По любой стороне и диагонали
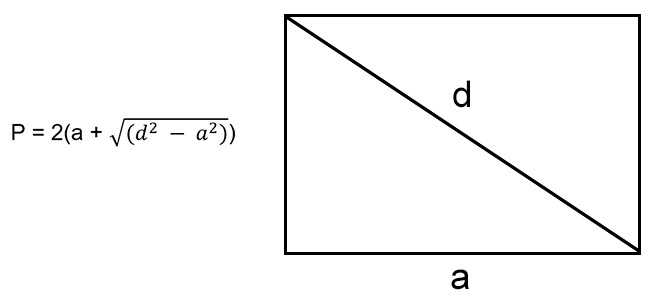
В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.
где \(d\) — диагональ прямоугольника, а \(b\) — неизвестная сторона.
Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:
По любой стороне и радиусу описанной окружности
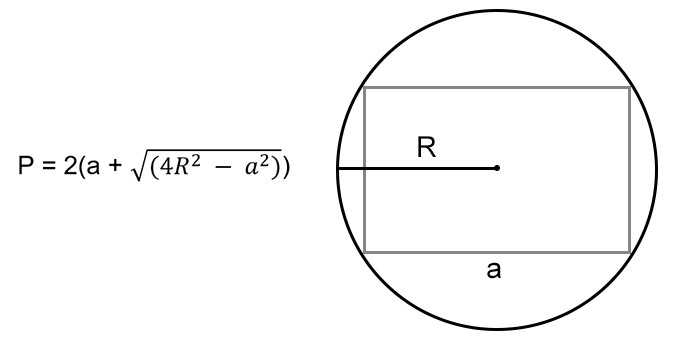
Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:
где \(R\) — радиус описанной окружности.
Тогда формула для расчета P будет выглядеть так:
Примеры решения задач
Задача 1
Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.
Решение:
Применяем самую первую формулу для расчета:
Задача 2
Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 \(см^2\) , одна из его сторон равна 6 см. Вычислить Р фигуры.
Решение:
Берем формулу \(P=2(\frac Sa+a)\) и подставляем известные значения:
Задача 3
Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.
Решение:
Вспоминаем формулу для расчета \(P=2(a+\sqrt)\) и вставляем известные величины:
Задача 4
Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.
Решение:
В этом случае для расчета суммы длин всех сторон применяем формулу \(P=2(a+\sqrt)\) . Используем известные значения и получаем:
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Методы вычисления площади прямоугольника
В прямоугольнике с известной площадью можно найти периметр, зная только его площадь. Для этого можно воспользоваться несколькими методами.
Первый метод — использовать формулу для нахождения площади прямоугольника по его сторонам. Площадь прямоугольника равна произведению длины одной стороны на длину другой стороны. Зная площадь и одну из сторон, можно найти вторую сторону путем деления площади на известную сторону. Затем, используя значения длин сторон, можно вычислить периметр прямоугольника.
Второй метод — использовать формулу для нахождения площади прямоугольника по его диагоналям. Площадь прямоугольника равна половине произведения длин его диагоналей. Зная площадь и одну из диагоналей, можно найти вторую диагональ путем деления площади на известную диагональ. Затем, используя значения диагоналей, можно вычислить периметр прямоугольника.
Третий метод — использовать формулу для нахождения площади прямоугольника по периметру и длине одной из сторон. Площадь прямоугольника равна произведению разности периметра и удвоенной длины одной из сторон на половину длины этой стороны. Зная площадь и одну из сторон, можно найти периметр путем деления площади на разность периметра и удвоенной длины этой стороны. Затем, используя значения периметра и длины стороны, можно найти вторую сторону и вычислить периметр прямоугольника.
Формула площади прямоугольника
Для того чтобы найти площадь прямоугольника, необходимо знать длину его сторон. Данная фигура имеет две параллельные стороны, измерение которых определяет ее форму и размеры.
Площадь прямоугольника вычисляется по простой формуле: S = a * b, где а и b — длины его сторон. Зная значения каждой из сторон, можно легко определить площадь этой фигуры.
Однако, если нам известна только площадь прямоугольника, найти его периметр становится сложнее. Периметр — это сумма длин всех сторон фигуры.
Площадь прямоугольника можно найти, зная его периметр, однако обратная задача, нахождение периметра по заданной площади, требует использования дополнительных данных.
Для решения данной задачи можно использовать формулу площади прямоугольника и методы математического анализа.
Таким образом, площадь прямоугольника определяется каждым его стороной, а для нахождения периметра при известной площади требуется использовать дополнительные данные и методы расчета.
Использование геометрических пропорций
Если известна площадь прямоугольника, то можно использовать геометрические пропорции для определения его периметра.
Для этого необходимо знать как связаны площадь и периметр прямоугольника. Площадь прямоугольника вычисляется как произведение его сторон. То есть, если длина сторон прямоугольника обозначить как a и b, а его площадь — как S, то можно записать уравнение: S = a * b.
Периметр прямоугольника равен сумме длин всех его сторон. Обозначим периметр как P. У прямоугольника каждая сторона противоположна другой и равна своей паре. То есть, допустим, первая сторона равна a, тогда вторая сторона будет равна b. В таком случае можно записать уравнение для периметра: P = 2a + 2b.
Используя эти формулы, можно выразить длины сторон прямоугольника через его площадь и далее вычислить периметр. Для этого необходимо найти значения a и b. Заменив в первом уравнении площадь на S и выразив одну переменную через другую, получим: a = S / b.
Подставим полученное выражение для a во второе уравнение периметра и получим: P = 2(S / b) + 2b.
Теперь, имея только значение площади S, можно найти периметр прямоугольника, зная каждую его сторону.
Периметр прямоугольника — как его найти (формула)
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.
Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.
Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.
Что такое прямоугольник и что такое периметр
Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.
Выглядит прямоугольник соответственно:
А частным случаем прямоугольника является квадрат:
У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.
Как и многие термины в математике, слово «периметр» пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,
Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.
С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.
Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».
Как найти периметр прямоугольника
Возьмем для примера такой прямоугольник:
Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.
Периметр в математике обозначается латинской буквой «Р».
С учетом равенства сторон, формулы можно существенно упростить:
или
Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:
И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника
Это могут быть миллиметры, сантиметры, метры, километры и так далее.
В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:
или
Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.
Другие формулы для расчета периметра прямоугольника
Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.
Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:
Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:
Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.
Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:
Вместо заключения
Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:
Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их периметры по отдельности и складываем друг с другом.
Вот и все, что мы хотели сегодня рассказать.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Математика




























