Основные геометрические фигуры

Три способа найти длину прямоугольника

Если вы разделите фигуру на две части диагональю, то заметите, что прямоугольник делит ее на два прямоугольных треугольника. Из этого деления следуют все формулы длины прямоугольника.

Через теорему Пифагора

Если известна длина диагонали (обозначим ее буквой d) и длина прямоугольника (примем значение за букву а). Тогда квадратный корень из разницы между квадратами диагонали и длины будет равен ширине прямоугольника.

Чтобы было понятнее, запишем решение в виде нескольких формул.

По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза — сторона, лежащая против прямого угла, две другие стороны называются катетами. В нашем случае гипотенуза — это диагональ.

Итак: d2=a2+b2 . Из этого выражения выражаем квадрат ширины (значение «b»): b2=d2-a2

Чтобы определить значение b, извлеките квадратный корень из обеих частей полученного выражения: b=(d2-a2)(-1)

При необходимости вы можете поменять местами a и b, и вы получите формулу длины.

Через площадь

Рассмотрим еще один способ нахождения длины прямоугольника — через площадь. Площадь прямоугольника равна произведению длины на ширину. То есть использовать уже известное обозначение S=a*b. Выразим значение ширины из этой формулы: b=S/b.

Как и в первом методе, вы можете поменять местами a и b, чтобы получить формулу длины: a=S/b.

Тригонометрическая функция

Один из самых быстрых, но и несколько сложных способов нахождения длины — использование тригонометрической функции.

Если это прямоугольный треугольник, существуют соотношения, известные как синус и косинус соответственно.

Выберем угол между длиной и диагональю. Обозначим его через α. Тогда sin α равен отношению между катетом, противолежащим углу α, и гипотенузой: Sin α = a/c

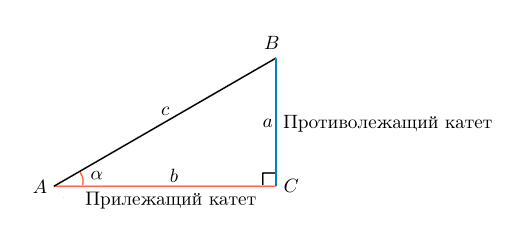
Рис. 2. Угол альфа на половине прямоугольника

Значение синуса любого угла можно найти в таблицах Брадиса или воспользовавшись калькулятором. Для удобства можно использовать онлайн-версию, которая автоматически находит значение коэффициента.

Но в формуле нет значения b, которое соответствует длине, а значит будем использовать основное тригонометрическое тождество. Косинус – это отношение катета, следующего за углом, к гипотенузе: cos a=b/c

Таким образом, вы можете найти длину, умножив косинус на гипотенузу: b=cos α*c

Угол между диагоналями прямоугольника.

Формулы для определения угла меж диагоналей прямоугольника:

1. Формула определения угла меж диагоналей прямоугольника через угол между стороной и диагональю:

2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:

8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:

Свойство 2

Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.

22.08.2020 19:32:30

2020-08-22 19:32:30

Любые данныеЛюбые данныеЛюбые данныеЛюбые данные Любые данные

Прямоугольник: что это?

Прямоугольник — это геометрическая фигура, которая имеет четыре стороны и четыре угла, где все углы равны 90 градусам. Прямоугольник имеет две пары параллельных сторон, противоположные стороны равны друг другу и его диагонали взаимно перпендикулярны.

Характеристикой прямоугольника является его площадь, которая рассчитывается как произведение длины на ширину. Определив площадь прямоугольника, можно вычислить его периметр и длину диагонали.

Прямоугольники широко используются в различных областях, таких как архитектура, инженерия, математика, дизайн и т.д. Они могут быть различных размеров, форм и цветов и используются для разных целей в зависимости от контекста применения.

Признаки прямоугольника:

1. Имеет четыре стороны и четыре угла, где все углы равны 90 градусам.
2. Имеет две пары параллельных сторон, противоположные стороны равны.
3. Диагонали взаимно перпендикулярны.
4. Площадь рассчитывается как произведение длины на ширину.

Прямоугольник — это не только геометрическая фигура на бумаге, но и часто встречающийся объект в окружающей среде, который может быть использован для решения разных задач. Например, прямоугольная форма часто используется в строительстве зданий и мебели, так как она позволяет оптимизировать потребление материалов и обеспечивает удобство использования объектов.

Определение и свойства квадрата

Квадрат — это частный случай ромба, параллелограмма или прямоугольника. Его отличие от этих фигур заключается в том, что все его углы прямые, и все четыре стороны равны. Квадрат — это правильный четырёхугольник.

Четырёхугольник называют квадратом в следующих случаях:

1. Если это прямоугольник, у которого длина a и ширина b равны.
2. Если это ромб с равными длинами диагоналей и с четырьмя прямыми углами.

К свойствам квадрата относятся все ранее рассмотренные свойства, относящиеся к прямоугольнику, а также следующие:

1. Диагонали перпендикулярны относительно друг друга (свойство ромба).
2. Точка пересечения совпадает с центром вписанной окружности.
3. Обе диагонали делят четырёхугольник на четыре одинаковых прямоугольных и равнобедренных треугольника.

Приведём часто используемые формулы для вычисления периметра, площади и элементов квадрата:

• Диагональ d = a √2.
• Периметр P = 4 a.
• Площадь S = a ².
• Радиус описанной окружности вдвое меньше диагонали: R = 0,5 a √2.
• Радиус вписанной окружности определяется как половинная длина стороны: r = a / 2.

Применение прямоугольников в повседневной жизни

Прямоугольники являются одним из наиболее распространенных геометрических фигур в нашей повседневной жизни. Мы можем встретить их в самых разных местах и ситуациях.

• В строительстве и архитектуре прямоугольники используются для построения стен, полов, оконных и дверных проемов.
• В мебельном производстве прямоугольники также являются основной формой многих предметов мебели, таких как столы, шкафы, кровати и прочее.
• В производстве электроники и бытовой техники прямоугольники встречаются как корпуса различных устройств и приборов.
• В промышленности прямоугольники используются для изготовления упаковок, ящиков и контейнеров различных видов.
• В сфере дизайна и графики прямоугольники широко используются как основные элементы оформления и композиции.

Таким образом, прямоугольники стали неотъемлемой частью нашего быта и повседневной жизни, позволяя нам производить и использовать различные предметы и конструкции.

Признаки прямоугольника

У прямоугольника всего три основных признака:

По углу. Если один из углов параллелограмма равен 90 градусам, то параллелограмм является прямоугольником.
Если три угла четырехугольника равны 90 градусам, то такой четырехугольник является прямоугольником

Обратите внимание, что в этом случае нет необходимости доказывать, что перед нами параллелограмм. Достаточно знать значения углов четырехугольника.
По диагонали: если диагонали параллелограмма равны, то такой параллелограмм является прямоугольником.

Обращайте внимание на то, к какой фигуре применяется признак, это имеет значение при доказательстве. В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других

Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки.

В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других. Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки.

Что такое прямоугольник

В предыдущих классах вы уже изучали темы о прямоугольниках. Теперь давайте освежим память и припомним, что же это за такая фигура, которая носит название прямоугольник.

Прямоугольник — это параллелограмм, четыре угла которого являются прямыми и равняются 90 градусам.

Прямоугольник — это такая геометрическая фигура, состоящая из 4-х сторон и четырех прямых углов.

Противоположные стороны прямоугольника всегда равны.

Если рассматривать определение прямоугольника по евклидовой геометрии, то чтобы четырехугольник считался прямоугольником, необходимо, чтобы в этой геометрической фигуре, хотя бы три угла были прямыми. С этого следует, что и четвертый угол тоже будет девяносто градусам.

Хотя и так понятно, что когда сумма углов четырехугольника не имеет 360 градусов, то эта фигура не является прямоугольником.

В случае, когда у правильного прямоугольника все стороны равны между собой, то такой прямоугольник носит название квадрата.

В некоторых случаях квадрат может выступать в роли ромба, если у такого ромба кроме равных между собой сторон и все углы прямые.

Чтобы доказать причастность какой-либо геометрической фигуры к прямоугольнику, достаточно чтобы эта геометрическая фигура соответствовала как минимум одному из этих требований:

1. квадрат диагонали этой фигуры должен быть равен сумме квадратов 2-х сторон, которые имеют общую точку;
2. диагонали геометрической фигуры должны иметь одинаковую длину;
3. все углы геометрической фигуры должны равняться девяносто градусам.

Если эти условия отвечают хотя бы одному требованию, то перед вами прямоугольник.

Прямоугольник в геометрии является основной базовой фигурой, у которой имеется множество подвидов, со своими особыми свойствами и характеристиками.

Задание:
Назовите геометрические фигуры, которые относятся к прямоугольникам.

Прямоугольник, свойства, признаки и формулы

Прямоугольник, свойства, признаки и формулы.

Поделиться в:

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник (понятие, определение)

Видеоурок “Прямоугольник“

Свойства прямоугольника

Признаки прямоугольника

Формулы прямоугольника

Прямоугольник (понятие, определение):

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник – это четырехугольник, у которого каждый угол является прямым.

Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.

Рис. 1. Прямоугольник

В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.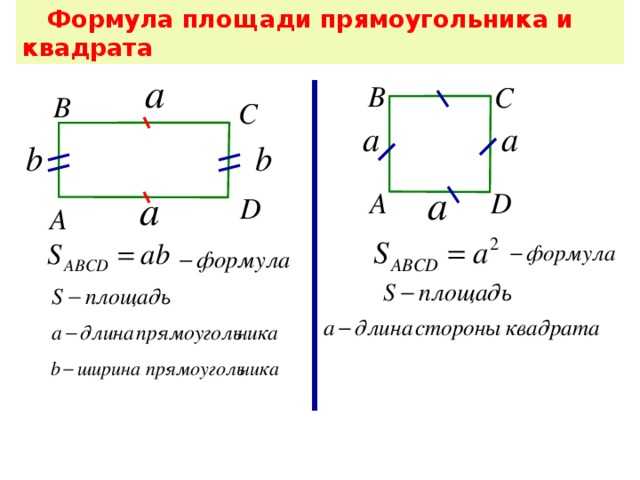

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.

Свойства прямоугольника:

1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник

AB || CD,   BC || AD

2. Противоположные стороны прямоугольника равны.

Рис. 3. Прямоугольник

AB = CD,  BC = AD

3. Стороны прямоугольника являются его высотами.

4. Прилегающие стороны прямоугольника всегда перпендикулярны.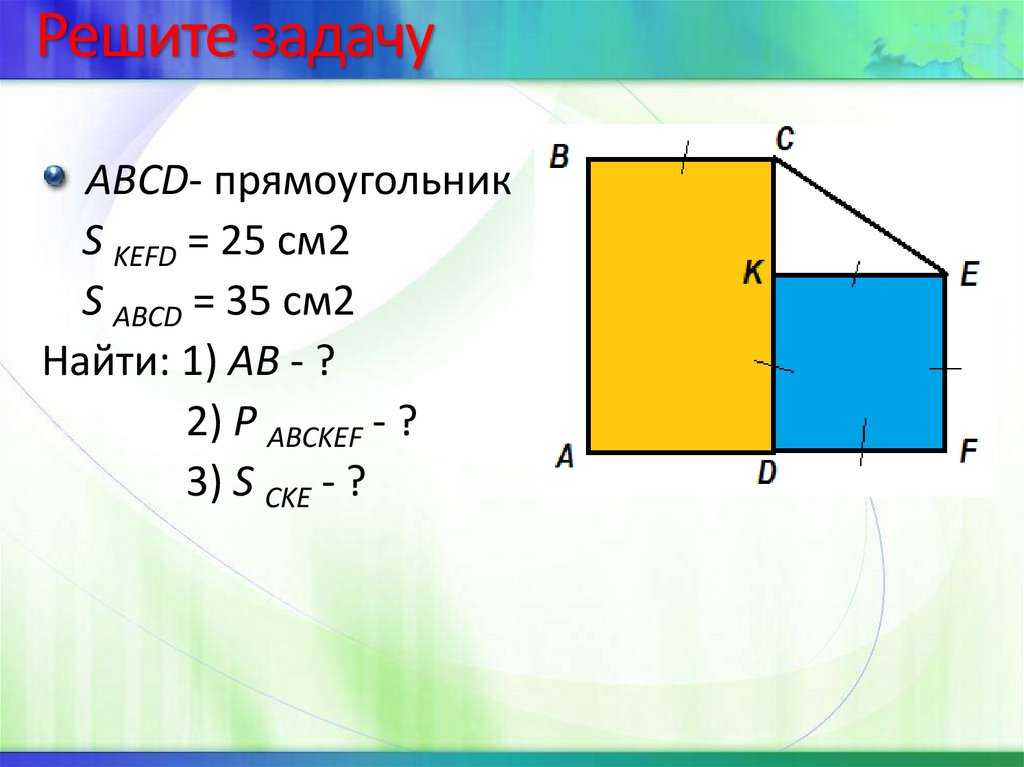

Рис. 4. Прямоугольник

AB ┴ BC,   BC ┴ CD,   CD ┴ AD,   AD ┴ AB

5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.

Рис. 5. Прямоугольник

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Диагонали прямоугольника равны.

Рис. 6. Прямоугольник

AC = BD

7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.

Рис. 7. Прямоугольник

△ABD = △BCD, △ABC = △ACD

8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).                                   

Рис. 8. Прямоугольник

AC2 ​= AD​2​​+ CD​2

9. Диагонали прямоугольника делятся точкой пересечения пополам.

Рис. 9. Прямоугольник

AO = BO = CO = DO = АС2 = BD / 2

10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.

Рис. 10. Прямоугольник

АС и BD – диаметр описанной окружности и диагональ прямоугольника

11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.

12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т. е. он является квадратом.

Рис. 11. Квадрат

AВ = ВC = AD = CD

Признаки прямоугольника:

– если диагонали параллелограмма равны, то он является прямоугольником;

– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;

– если углы параллелограмма равны, то он является прямоугольником. 

Формулы прямоугольника:

Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.

Формула стороны прямоугольника (длины и ширины прямоугольника):

,

,

,

. 

Формула диагонали прямоугольника:

,              

d = 2R.

Формулы периметра прямоугольника:

P = 2a + 2b,

P = 2(a + b). 

Формулы площади прямоугольника:

S = a · b. 

Формула радиуса окружности, описанной вокруг прямоугольника:

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Примечание:  Фото https://www.pexels.com, https://pixabay.com

Видео https://www.youtube.com/watch?v=_EVDcbOydAI

Коэффициент востребованности
4 838

Это интересно знать

Знали ли вы, что если в прямоугольнике, у которого неровные смежные стороны, провести биссектрисы углов, то при их пересечении в итоге получится прямоугольник.

А вот если проведенная биссектриса прямоугольника пересекает одну из его сторон, то она отсекает от этого прямоугольника, равнобедренный треугольник.

А известно ли вам, что еще до того, как Малевич написал свой выдающийся «Черный квадрат», в 1882 году на выставке в Париже представили картину Пола Било, на полотне которой был изображен черный прямоугольник со своеобразным названием «Битва негров в туннеле».

Такая идея с черным прямоугольником вдохновила и других деятелей культуры. Французский писатель юморист Альфонс Алле выпустил целую серию своих работ и со временем появился прямоугольный пейзаж в радикальном красном цвете под названием «Уборка урожая помидоров на берегу Красного моря апоплексическими кардиналами», который также не имел никакого изображения.

Задание

1. Назовите свойство, которое присуще только прямоугольнику?
2. В чем отличие произвольного параллелограмма от прямоугольника?
3. Верно ли утверждение, что любой прямоугольник модет быть параллелограммом? Если это так, то докажите почему?
4. Перечислите четырехугольники, которые являются прямоугольниками.
5. Сформулируйте свойства прямоугольника.

Примеры вопросов и задач

Разберём некоторые вопросы, с которыми можно столкнуться при изучении курса математики в школе, и решим несколько простых задач.

Задача 1
. Как изменится площадь прямоугольника, если увеличить длину его сторон в три раза?

Решение
Обозначим площадь исходной фигуры S0, а площадь четырёхугольника с утроенной длиной сторон — S1. По формуле, рассмотренной ранее, получаем: S0 = ab. Теперь увеличим длину и ширину в 3 раза и запишем: S1= 3 a 3 b = 9 ab. Сравнивая S0 и S1, становится очевидно, что вторая площадь больше первой в 9 раз.

Вопрос 1. Четырёхугольник с прямыми углами — это квадрат?

Решение Из определения следует, что фигура с прямыми углами является квадратом лишь тогда, когда длины всех его сторон равны. В остальных случаях фигура является прямоугольником.

Задача 2
. Диагонали прямоугольника образуют угол 60 градусов. Ширина прямоугольника — 8. Рассчитать, чему равна диагональ.

Решение:
Вспомним, что диагонали точкой пересечения разделяются пополам. Таким образом, имеем дело с равнобедренным треугольником с углом при вершине, равным 60°. Так как треугольник равнобедренный, то находящиеся при основании углы тоже будут одинаковы. Путём несложных вычислений получаем, что каждый из них равен 60°. Отсюда следует, что треугольник равносторонний. Ширина, известная нам, является основанием треугольника, следовательно, половина диагонали тоже равна 8, а длина целой диагонали в два раза больше и равна 16.

Вопрос 2. У прямоугольника все стороны равны или нет?

Решение Достаточно вспомнить, что все стороны должны быть равны у квадрата, который является частным случаем прямоугольника. Во всех остальных случаях достаточное условие — это наличие минимум 3 прямых углов. Равенство сторон не является обязательным признаком.

Задача 3
. Площадь квадрата известна и равна 289. Найти радиусы вписанной и описанной окружности.

Решение По формулам для квадрата проведём следующие расчёты:

• Определим, чему равны основные элементы квадрата: a = √ S = √289 = 17; d = a √2 =1 7√2.
• Подсчитаем, чему равен радиус описанной вокруг четырёхугольника окружности: R = 0,5 d = 8,5√2.
• Найдём радиус вписанной окружности: r = a / 2 = 17 / 2 = 8,5.

Прямоугольник уникален своей простотой. На основе этой фигуры ученики начинают познавать основы геометрии. Поэтому в старших классах теряются, не зная основных свойств и признаков прямоугольника, напрасно считая эту фигуру излишне простой.