Как найти катет по теореме пифагора онлайн

Свойство медианы прямоугольного треугольника

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Пусть СМ — медиана прямоугольного треугольника АВС с прямым углом С.
Проведем через вершину В прямую m, параллельную катету АС.
Через вершину А проведем прямую n, параллельную катету ВС.

Прямые m и n пересекаются в точке К.

Мы получили прямоугольник АКВС (параллелограмм, в котором угол С – прямой).
Диагонали прямоугольника равны и в точке пересечения делятся пополам.

Задача ЕГЭ по теме «Медиана прямоугольного треугольника»
В треугольнике ABC угол ACB равен , угол B равен , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

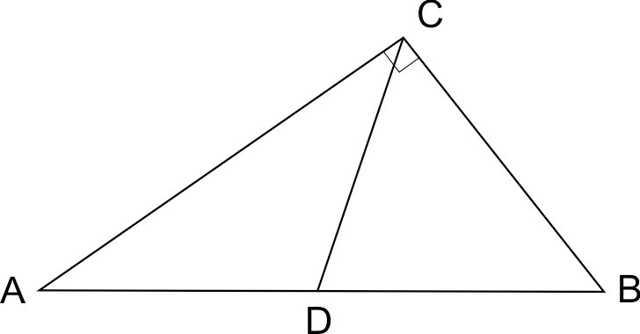
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD – равнобедренный, CD = BD. Тогда

Периметр треугольника, онлайн расчет

Как найти периметр треугольника по длине его сторон, формула периметра треугольника.

Периметр треугольника, онлайн расчет

	Прямоугольный треугольник. Свойства, признаки равенства. Задачи и решения Определение 1. Прямоугольный треугольник − это треугольник, один из углов которого прямой (т.е. 90°). Сторона, противоположная прямому углу, называется гипотенузой (сторона c (Рис.1)). Другие стороны, т.е. стороны, прилегающие к прямому углу (стороны a и b) называются катетами. Решение прямоугольного треугольника по двум сторонам Если даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме Пифагора. Острые углы определяются по формулам тригонометрических функций острого угла — Синус угла — sin(A),Косинус угла — cos(A),Тангенс угла — tg(A),Котангенс угла — ctg(A),Секанс угла — sec(A),Косеканс угла — cosec(A). Решение прямоугольного треугольника Если известны катет a и гипотенуза c Второй катет b определится по теореме Пифагора: Угол A определится по формуле синуса: Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так: Если известны катеты a и b Гипотенуза с определится по теореме Пифагора: Угол A определится по формуле тангенса: Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так: Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и катет) Катет прямоугольного треугольника a Катет прямоугольного треугольника b Угол α (градус) Угол β (градус) Некоторые свойства прямоугольных треугольников Свойство 1. Сумма двух острых углов прямоугольного треугольника равна 90°. Действительно. Поскольку сумма углов треугольника равна 180°, а прямой угол равен 90°, то сумма остальных углов равен 90°. Свойство 2. Если катет прямоугольного треугольника лежит напротив угла в 30°, то он равен половине гипотенузы. Доказательство. Рассмотрим прямоугольный треугольник ACB, у которого угол C прямой, а угол ∠ABC=30°. Приложим к этому треугольнику равному ему прямоугольный треугольник как показано на Рис.2. Рассмотрим треугольник ADB. Так как ∠A=∠D=∠ABD=60°, то треугольник ABD равносторонний. Следовательно AB=AD=BD. Тогда . Конец доказательства. Свойство 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против данного катета равен 30°. Доказательство. Пусть у прямоугольного треугольника катет AC равен половине гипотенузы AB. Аналогично вышеизложенному приложим к этому треугольнику равному ему прямоугольный треугольник BCD(Рис.2). Получим равносторонний треугольник, где AB=AD=BD. Тогда ∠A=∠D=∠ABD=60°. Но ∠ABD=2∠ABС. Следовательно . Конец доказательства.
Помощь в решении задач по геометрии, учебник онлайн (все калькуляторы по геометрии).
Калькуляторы по геометрии

Треугольник. Виды, свойства, решение треугольников.
Свойства треугольника.

Геометрические фигуры – пирамида, прямоугольник, ромб, углы, шар, параллелограмм, параллелепипед, призма, свойства, формулы геометрических фигур
Геометрические фигуры.

Мы в соцсетях Присоединяйтесь! Нашли ошибку? Есть предложения? Сообщите нам Этот калькулятор можно вставить на сайт, в блог Создадим калькулятор для вас Код для вставки без рекламы с прямой ссылкой на сайт Код для вставки с рекламой без прямой ссылки на сайт Код для вставки: Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор. Cообщение: Что-то не нашли? Ошибка? Предложения? Сообщите нам Ваш e-mail: Если нужен ответ

Примеры решения задач

Задача 1

В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.

Решение

По теореме Пифагора ВС2+АС2=АВ2, значит

\(АС\;=\;\sqrt{АВ^2\;-\;АС^2}\)

Для нахождения ответа подставим в формулу исходные значения:

\(АС\;=\;\sqrt{85^2\;-\;36^2}\;=\;\sqrt{7225\;-\;1296\;}={\;\sqrt{5929}\;=\;77\;}\)

Задача 2

Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.

Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:

• 46²+56²= 5252;
• 76²= 5776;
• 5252 ≠ 5776, значит, указанный треугольник не является прямоугольным.

Задача 3.

Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.

Решение

Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.

По теореме Пифагора:

АО2+BO2=AB2, значит

Формулы прямоугольного треугольника

Прямоугольный треугольник содержит множество полезных формул. Вы можете использовать любую из приведенных ниже формул для вычисления углов, сторон, площади или периметра прямоугольного треугольника. Мы будем ссылаться на треугольник ниже для следующих формул:

Периметр треугольника

Периметр = a + b + c
Также обратите внимание, что вам понадобится следующая таблица при использовании тригонометрических функций:

Например, если вы используете формулу tan B и рассчитываете, что ее значение равно 1, то, взглянув на таблицу выше, вы узнаете, что значение рассматриваемого угла должно быть 45 °.

Формулировка теоремы

Изначальная (геометрическая) формулировка Пифагора гласила:

Теорема

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Позднее появился алгебраический вариант:

Теорема

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.

Геометрия

Средняя линия треугольника

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Докажем теорему о средней линии треугольника.

Теорема

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Доказательство

Пусть MN — средняя линия треугольника АВС (рис. 195). Докажем, что MN || AC и MN = 1/2 AC.

Рис. 195

Треугольники BMN и ВАС подобны по второму признаку подобия треугольников (∠B — общий ). поэтому ∠1 = ∠2 и Из равенства ∠1 = ∠2 следует, что MN || АС (объясните почему), а из второго равенства — что MN = 1/2 AC. Теорема доказана.

Пользуясь этой теоремой, решим следующую задачу:

Задача 1

Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.

Решение

Рассмотрим произвольный треугольник АВС. Обозначим буквой О точку пересечения его медиан АА₁ и ВВ₁ и проведём среднюю линию А₁В₁ этого треугольника (рис. 196). Отрезок А₁В₁ параллелен стороне АВ, поэтому углы 1 и 2, а также углы 3 и 4 равны как накрест лежащие углы при пересечении параллельных прямых АВ и А₁В₁ секущими АА₁ и ВВ₁. Следовательно, треугольники АОВ и А₁ОВ₁ подобны по двум углам, и, значит, их стороны пропорциональны:

Рис. 196

Но АВ = 2А₁В₁, поэтому АО = 2А₁О и ВО = = 2В₁О. Таким образом, точка О пересечения медиан АА₁ и ВВ₁ делит каждую из них в отношении 2 : 1, считая от вершины.

Аналогично доказывается, что точка пересечения медиан ВВ₁ и СС₁ делит каждую из них в отношении 2 : 1, считая от вершины, и, следовательно, совпадает с точкой О.

Итак, все три медианы треугольника АВС пересекаются в точке О и делятся ею в отношении 2 : 1, считая от вершины.

Задача 2

Доказать, что высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Решение

Пусть ΔАВС — прямоугольный треугольник с прямым углом С, CD — высота, проведённая из вершины С к гипотенузе АВ (рис. 197). Докажем, что ΔABC ∼ ΔACD, ΔABC ∼ ΔCBD, ΔACD ∼ ΔCBD.

Рис. 197

Треугольники АВС и ACD подобны по первому признаку подобия треугольников (∠A — общий, ∠ACB = ∠ADC = 90°). Точно так же подобны треугольники АВС и CBD (∠B — общий и ∠ACB = ∠BDC- 90°), поэтому ∠A = ∠BCD. Наконец, треугольники ACD и CBD также подобны по первому признаку подобия (в этих треугольниках углы с вершиной D прямые и ∠A = ∠BCD), что и требовалось доказать.

Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если

Исходя из задачи 2, докажем следующие утверждения:

1. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

Действительно, ΔABC ∼ ΔACD (см. рис. 197), поэтому и, следовательно,

Прямоугольные треугольники

Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.

3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.

5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$

6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$/$	$/$	$/$
$cosα$	$/$	$/$	$/$
$tgα$	$/$	$1$	$√3$
$ctgα$	$√3$	$1$	$/$

Площадь прямоугольного треугольника равна половине произведения его катетов

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√$. Найдите косинус внешнего угла при вершине $В$.

Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то

Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:

Катет $ВС$ мы можем найти по теореме Пифагора:

Подставим найденное значение в формулу косинуса

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sin⁡A=/, AC=9$. Найдите $АВ$.

Распишем синус угла $А$ по определению:

Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.

Применим теорему Пифагора, чтобы отыскать $«х»$

Так как длина $АВ$ составляет пять частей, то $3∙5=15$

В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

Inverse Pythagorean Theorem

While the Pythagorean theorem relates the lengths of each side, the Inverse Pythagorean Theorem (sometimes called the Reciprocal Pythagorean Theorem) relates the side lengths to the height, or altitude, to the hypotenuse of a right triangle.

Since sides a and b are equal to the heights of the other side, the inverse Pythagorean theorem defines the relationship between the short sides and the height perpendicular to the hypotenuse.

The Inverse Pythagorean theorem states that if a right triangle with vertices A, B, and C is divided into two triangles by its height h at point D along side c, then the area of △ABC is equal to the area of △ACD plus the area of △BCD.

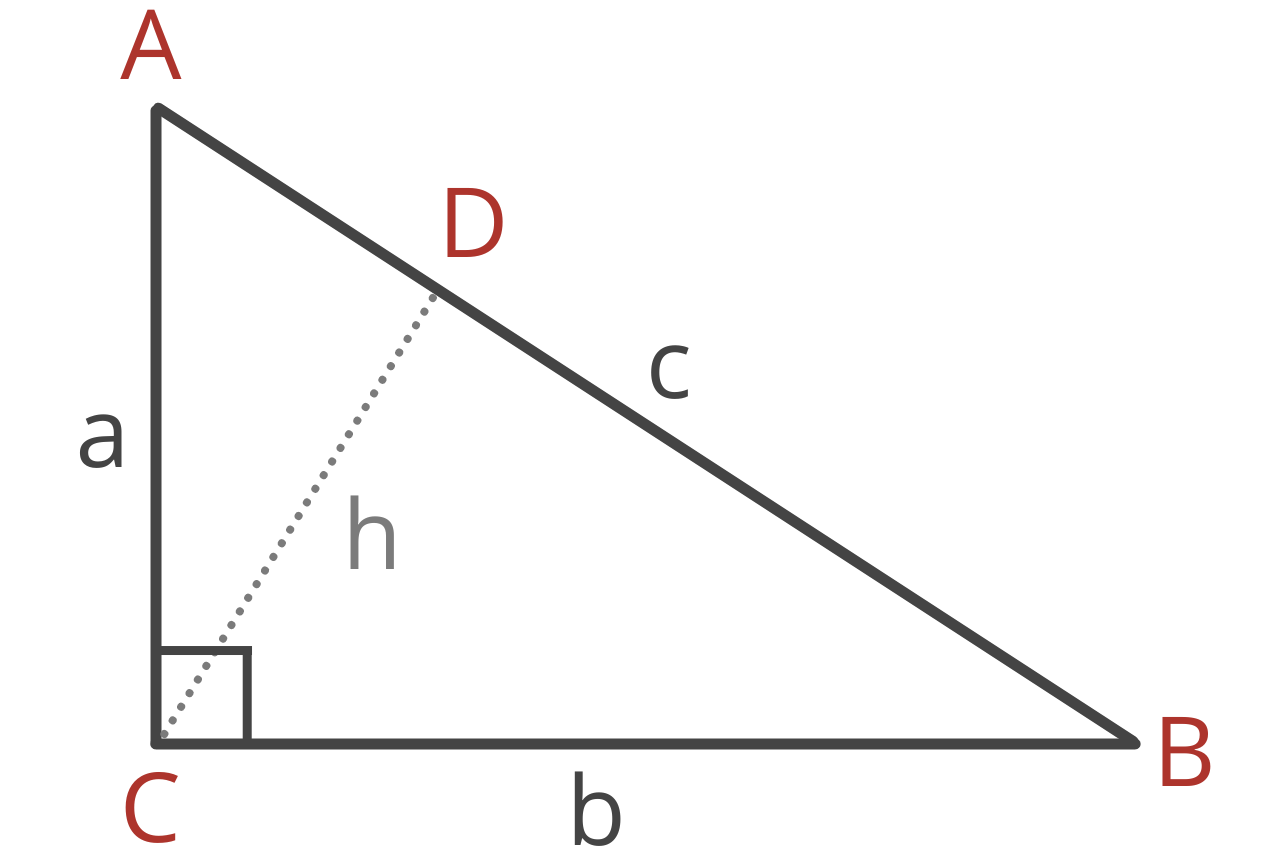
The length of the sides of these new triangles can be defined using the Pythagorean Theorem as follows:

1AC² + 1BC² = 1CD²

Note, AC, BC, and CD represent the length of the line segments connecting the respective vertices. This can be rewritten to more simply express the height of a right triangle:

1a² + 1b² = 1h²

Thus, the Inverse Pythagorean theorem says that the reciprocal of side a squared plus the reciprocal of side b squared is equal to the reciprocal of height h squared.

This can be further reduced to solve for the height given sides a, b, and c.

hc = abc = abh

You can also use our right triangle calculator to calculate the angles, area, or perimeter.

Теорема Пифагора в быту

Как ни странно, теорема Пифагора может оказаться полезной даже в бытовых делах, таких как определение высоты шкафа-купе, например. На первый взгляд, нет необходимости использовать такие сложные вычисления, ведь можно просто снять мерки с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.

Дело в том, что шкаф-купе собирается в горизонтальном положении и только потом поднимается и устанавливается к стене. Поэтому боковина шкафа в процессе подъема конструкции должна свободно проходить и по высоте, и по диагонали помещения.

Предположим, имеется шкаф-купе глубиной 800 мм. Расстояние от пола до потолка — 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше, чем высота помещения. Но почему именно на 126 мм? Рассмотрим на примере.

При идеальных габаритах шкафа проверим действие теоремы Пифагора:

АС=√АВ 2 +√ВС 2

АС=√2474 2 +800 2 =2600 мм — все сходится.

Допустим, высота шкафа равна не 2474 мм, а 2505 мм. Тогда:

АС=√2505 2 +√800 2 =2629 мм.

Следовательно, этот шкаф не подойдет для установки в данном помещении. Так как при поднятии его в вертикальное положение можно нанести ущерб его корпусу.

Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что она более чем правдива. Теперь можно использовать полученную информацию в своей повседневной жизни и быть полностью уверенным, что все расчеты будут не только полезны, но и верны.

Средний уровень

Теорема Пифагора | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Теорема Пифагора является основополагающим звеном в Евклидовой геометрии, на котором базируются большая часть всех вытекающих из теоремы Пифагора следствий и других теорем. Выведенная еще в VI веке до нашей эры, теорема связывает стороны прямоугольного треугольника простым уравнением, и имеет множество доказательств, одно из которых объединяет в себе как алгебру, так и геометрию.

Согласно теореме Пифагора, в прямоугольном треугольнике есть катеты a и b – это стороны прилегающие к прямому углу, и сумма их квадратов дает квадрат гипотенузы – третьей стороны треугольника, лежащей напротив прямого угла.

Доказать это можно, построив четыре прямоугольных треугольника так, чтобы на длинном катете каждого из них был расположен короткий катет следующего треугольника, при этом вершины углов совпадают.

Как видно из рисунка, общая фигура представляет собой квадрат со стороной c, являющей одновременно гипотенузой данных треугольников, а площадь этой фигуры равна c

2, согласно формуле площади квадрата. Помимо того, что этот квадрат включает в себя четыре прямоугольных треугольника площадью , в центре его находится еще один, маленький квадрат. Сторона маленького квадрата равна разности катетов, следовательно, его площадь будет равна квадрату этой разности.
(a-b)2=a2-2ab+b2

Представим площадь большого квадрата в виде суммы площадей маленького квадрата и четырех треугольников по принципу суперпозиции.

Таким образом, площадь квадрата одновременно равна гипотенузе во второй степени и сумме катетов во вторых степенях, что и требовалось доказать.
a2+b2=c2

Некоторые свойства прямоугольных треугольников

Свойство 1. Сумма двух острых углов прямоугольного треугольника равна 90°.

Действительно. Поскольку сумма углов треугольника равна 180°, а прямой угол равен 90°, то сумма остальных углов равен 90°.

Свойство 2. Если катет прямоугольного треугольника лежит напротив угла в 30°, то он равен половине гипотенузы.

Доказательство. Рассмотрим прямоугольный треугольник ACB, у которого угол C прямой, а угол ∠ABC=30°. Приложим к этому треугольнику равному ему прямоугольный треугольник как показано на Рис.2.

Рассмотрим треугольник ADB. Так как ∠A=∠D=∠ABD=60°, то треугольник ABD равносторонний. Следовательно AB=AD=BD. Тогда . Конец доказательства.

Свойство 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против данного катета равен 30°.

Доказательство. Пусть у прямоугольного треугольника катет AC равен половине гипотенузы AB. Аналогично вышеизложенному приложим к этому треугольнику равному ему прямоугольный треугольник BCD(Рис.2). Получим равносторонний треугольник, где AB=AD=BD. Тогда ∠A=∠D=∠ABD=60°. Но ∠ABD=2∠ABС. Следовательно . Конец доказательства.

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

следовательно: c = √ a² + b²

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Теорема Пифагора

a
b
c

c^2 = a^2 + b^2

• c — гипотенуза
• a — катет
• b — катет

Как посчитать сторону прямоугольного треугольника

Гипотенуза:

c = sqrt{a^2 + b^2}

Катеты:

a = sqrt{c^2 — b^2}

b = sqrt{c^2 — a^2}

Проверочные числа

Часто используют удобный приём магии чисел 3, 4, 5. Это ряд чисел попадает под теорему Пифагора.

Так, если взять треугольник с соотношением сторон 3 : 4 : 5

3
4
5

то этот треугольник будет прямоугольным. Доказывается это просто.

Если теорема Пифагора верна:

a^2 + b^2 = c^2

, то размеры такого треугольника подходят к теореме Пифагора:

3^2 + 4^2 = 5^2

9 + 16 = 25

Значит треугольник со сторонами 3, 4, 5 является прямоугольным.

Войдите чтобы писать комментарии

12 16 и 20 образуют прямоугольный треугольник?

Существует четвертая категория треугольников, в которых один из внутренних углов равен 90∘. Его называют прямоугольным треугольником. Это может быть либо разносторонний, либо равнобедренный. 1) 12,16,20: 202=162+122: Истина, следовательно, прямоугольный треугольник.

Что такое правило синуса и косинуса?

Правило синусов можно использовать для нахождения угла по 3 сторонам и углу или стороны по 3 углам и стороне. Чай правило косинуса можно найти сторону с 2-х сторон и прилежащий угол, или угол с 3-х сторон.

Как найти две недостающие стороны треугольника? Учитывая две стороны

1. если сторона a — недостающая сторона, преобразовать уравнение к форме, когда a находится на одной стороне, и извлечь квадратный корень: a = √ (c² — b²)
2. если нога b неизвестна, то. b = √ (c² — a²)
3. если гипотенуза c отсутствует, формула имеет вид. c = √ (a² + b²)

Как найти недостающую сторону треугольника по теореме Пифагора?